Bayesian Data Mining.pptx

1 .Bayesian Data Mining University of Belgrade School of Electrical Engineering Department of Computer Engineering and Information Theory Marko Stupar 11/3370 sm113370m@student.etf.rs 1 /40

2 .Data Mining problem Too many attributes in training set (colons of table) Existing algorithms need too much time to find solution We need to classify, estimate, predict in real time Marko Stupar 11/3370 sm113370m@student.etf.rs Target Value 1 Value 2 . . . Value 100000 2 /40

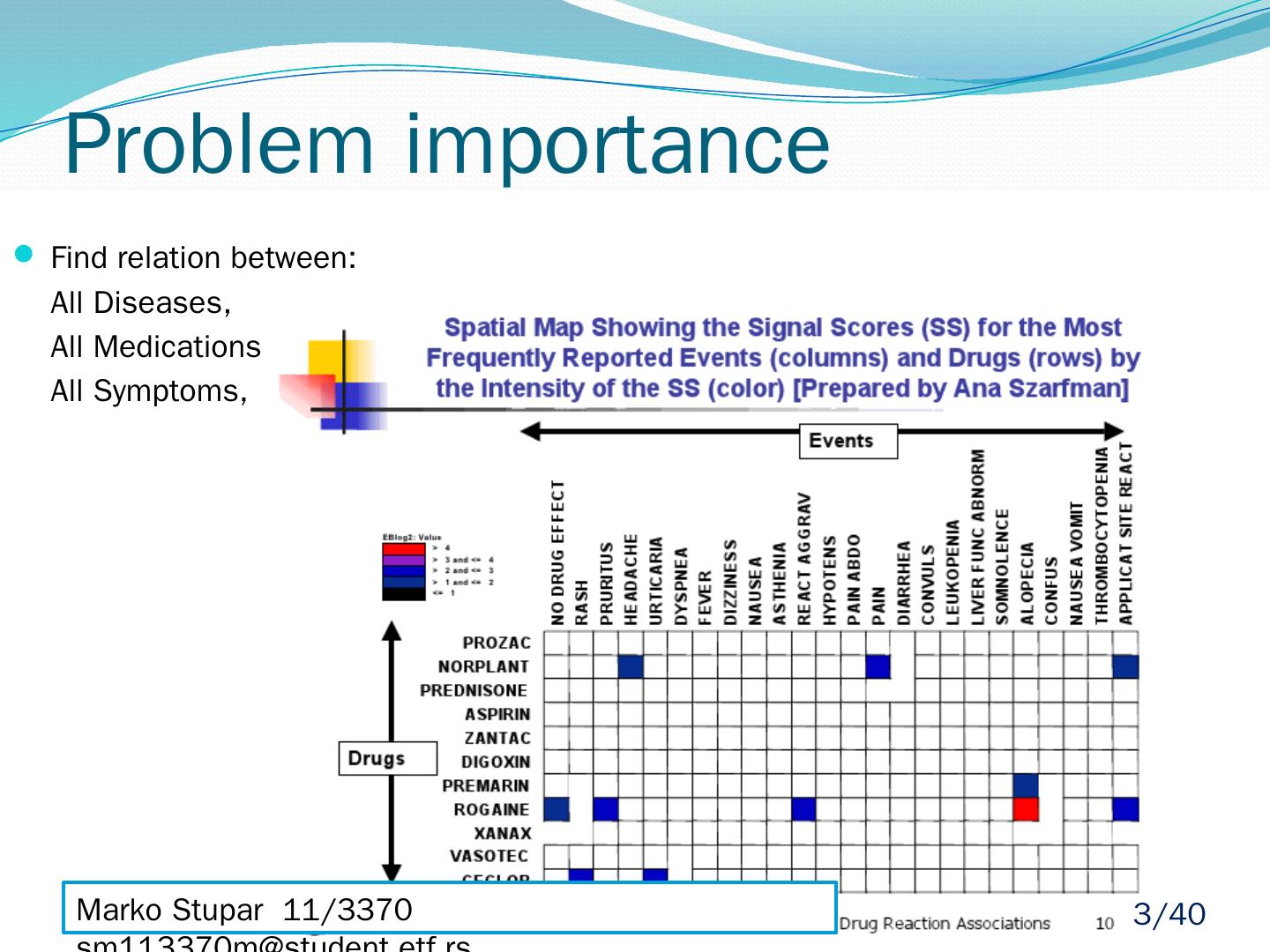
3 .Problem importance Find relation between: All Diseases, All Medications, All Symptoms, Marko Stupar 11/3370 sm113370m@student.etf.rs 3 /40

4 .Existing solutions Marko Stupar 11/3370 sm113370m@student.etf.rs CART, C4.5 Too many iterations Continuous arguments need binning Rule induction Continuous arguments need binning Neural networks High computational time K-nearest neighbor Output depends only on distance based close values 4 /40

5 .Classification, Estimation, Prediction Used for large data set Very easy to construct Not using complicated iterative parameter estimations Often does surprisingly well May not be the best possible classifier Robust, Fast, it can usually be relied on to Marko Stupar 11/3370 sm113370m@student.etf.rs Naïve Bayes Algorithm 5 /40

6 .Marko Stupar 11/3370 sm113370m@student.etf.rs Naïve Bayes algorithm Reasoning New information arrived How to classify Target? Target Attribute 1 Attribute 2 Attribute n … … … .. … … .. .. .. .. .. .. … .. … Training Set Target Attribute 1 Attribute 2 Attribute n a1 a2 an Missing 6 /40

7 .Target can be one of discrete values: t1, t2, …, tn Marko Stupar 11/3370 sm113370m@student.etf.rs Naïve Bayes algorithm Reasoning How to calculate? Did not helped very much? Naïve Bayes assumes that A1…An are independent, So: 7 /40

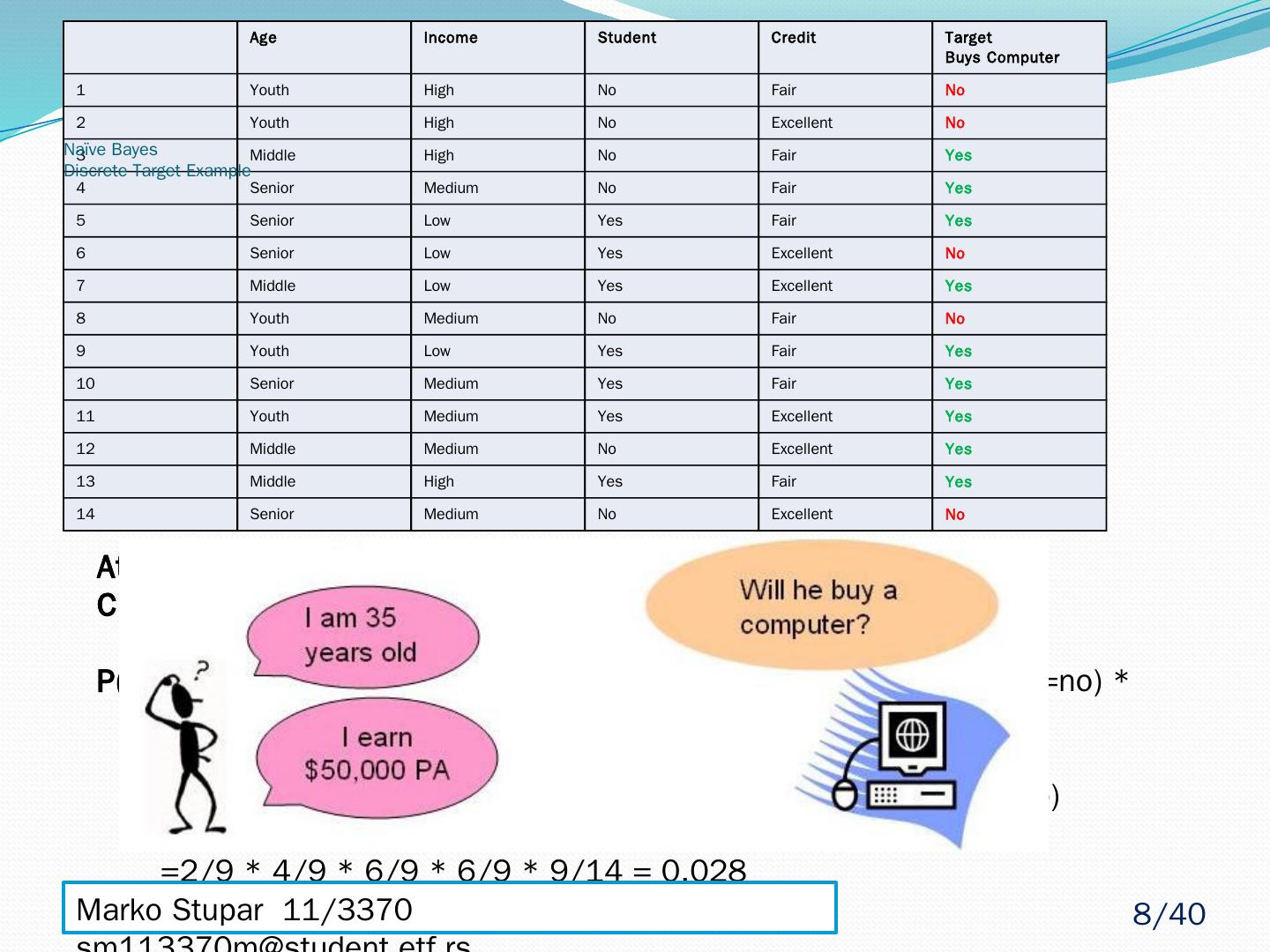
8 .Age Income Student Credit Target Buys Computer 1 Youth High No Fair No 2 Youth High No Excellent No 3 Middle High No Fair Yes 4 Senior Medium No Fair Yes 5 Senior Low Yes Fair Yes 6 Senior Low Yes Excellent No 7 Middle Low Yes Excellent Yes 8 Youth Medium No Fair No 9 Youth Low Yes Fair Yes 10 Senior Medium Yes Fair Yes 11 Youth Medium Yes Excellent Yes 12 Middle Medium No Excellent Yes 13 Middle High Yes Fair Yes 14 Senior Medium No Excellent No Attributes = (Age= youth , Income= medium , Student= yes , Credit_rating = fair ) P(Attributes, Buys_Computer =Yes) = P(Age= youth|Buys_Computer =yes) * P(Income= medium|Buys_Computer =yes) * P(Student= yes|Buys_Computer =yes) * P( Credit_rating = fair|Buys_Computer =yes) * P( Buys_Computer =yes) =2/9 * 4/9 * 6/9 * 6/9 * 9/14 = 0.028 Attributes = (Age= youth , Income= medium , Student= yes , Credit_rating = fair ) P(Attributes, Buys_Computer =No) = P(Age= youth|Buys_Computer =no) * P(Income= medium|Buys_Computer =no) * P(Student= yes|Buys_Computer =no) * P( Credit_rating = fair|Buys_Computer =no) * P( Buys_Computer =no) =3/5 * 2/5 * 1/5 * 2/5 * 5/14 = 0.007 Naïve Bayes Discrete Target Example Marko Stupar 11/3370 sm113370m@student.etf.rs 8 /40

9 .Naïve Bayes Discrete Target - Example Attributes = (Age= youth , Income= medium , Student= yes , Credit_rating = fair ) Target = Buys_Computer = [ Yes | No ] ? P(Attributes, Buys_Computer =Yes) = P(Age= youth|Buys_Computer =yes) * P(Income= medium|Buys_Computer =yes) * P(Student= yes|Buys_Computer =yes) * P( Credit_rating = fair|Buys_Computer =yes) * P( Buys_Computer =yes) =2/9 * 4/9 * 6/9 * 6/9 * 9/14 = 0.028 P(Attributes, Buys_Computer =No) = P(Age= youth|Buys_Computer =no) * P(Income= medium|Buys_Computer =no) * P(Student= yes|Buys_Computer =no) * P( Credit_rating = fair|Buys_Computer =no) * P( Buys_Computer =no) =3/5 * 2/5 * 1/5 * 2/5 * 5/14 = 0.007  P( Buys_Computer =Yes | Attributes) > P( Buys_Computer =No| Attributes) Therefore, the naïve Bayesian classifier predicts Buys_Computer = Yes for previously given Attributes Marko Stupar 11/3370 sm113370m@student.etf.rs 9 /40

10 .Naïve Bayes Discrete Target – Spam filter Attributes = Text Document = w1,w2,w3… Array of words Target = Spam = [Yes | No] ? - probability that the i-th word of a given document occurs in documents, in training set, that are classified as Spam - probability that all words of document occur in Spam documents in training set Marko Stupar 11/3370 sm113370m@student.etf.rs 10 /40

11 .Naïve Bayes Discrete Target – Spam filter - Bayes factor Sample correction – if there is a word in document that never occurred in training set the whole will be zero. Sample correction solution – put some low value for that Marko Stupar 11/3370 sm113370m@student.etf.rs 11 /40

12 .Gaussian Naïve Bayes Continuous Attributes Continuous attributes do not need binning (like CART and C4.5) Choose adequate PDF for each Attribute in training set Gaussian PDF is most likely to be used to estimate the attribute probability density function (PDF) Calculate PDF parameters by using Maximum Likelihood Method Naïve Bayes assumption - each attribute is independent of other, so joint PDF of all attributes is result of multiplication of single attributes PDFs Marko Stupar 11/3370 sm113370m@student.etf.rs 12 /40

13 .Gaussian Naïve Bayes Continuous Attributes - Example Training set Validation set sex height (feet) weight (lbs) foot size (inches) male 6 180 12 male 5.92 190 11 male 5.58 170 12 male 5.92 165 10 female 5 100 6 female 5.5 150 8 female 5.42 130 7 female 5.75 150 9 Target = male Target = female height (feet) 5.885 0.027175 5.4175 0.07291875 weight (lbs) 176.25 126.5625 132.5 418.75 foot size(inches) 11.25 0.6875 7.5 1.25 sex height (feet) weight (lbs) foot size (inches) Target 6 130 8 Marko Stupar 11/3370 sm113370m@student.etf.rs 13 /40

14 .Naïve Bayes - Extensions Easy to extend Gaussian Bayes – sample of extension Estimate Target – If Target is real number, but in training set has only few acceptable discrete values t1… tn , we can estimate Target by: A large number of modifications have been introduced, by the statistical, data mining, machine learning, and pattern recognition communities, in an attempt to make it more flexible Modifications are necessarily complications, which detract from its basic simplicity Marko Stupar 11/3370 sm113370m@student.etf.rs 14 /40

15 .Naïve Bayes - Extensions Are Attributes always really independent? A1 = Weight, A2 = Height, A3 = Shoe Size, Target = [ male|female ]? How can that influence our Naïve Bayes data mining? Assumption ? Bayesian network Marko Stupar 11/3370 sm113370m@student.etf.rs 15 /40

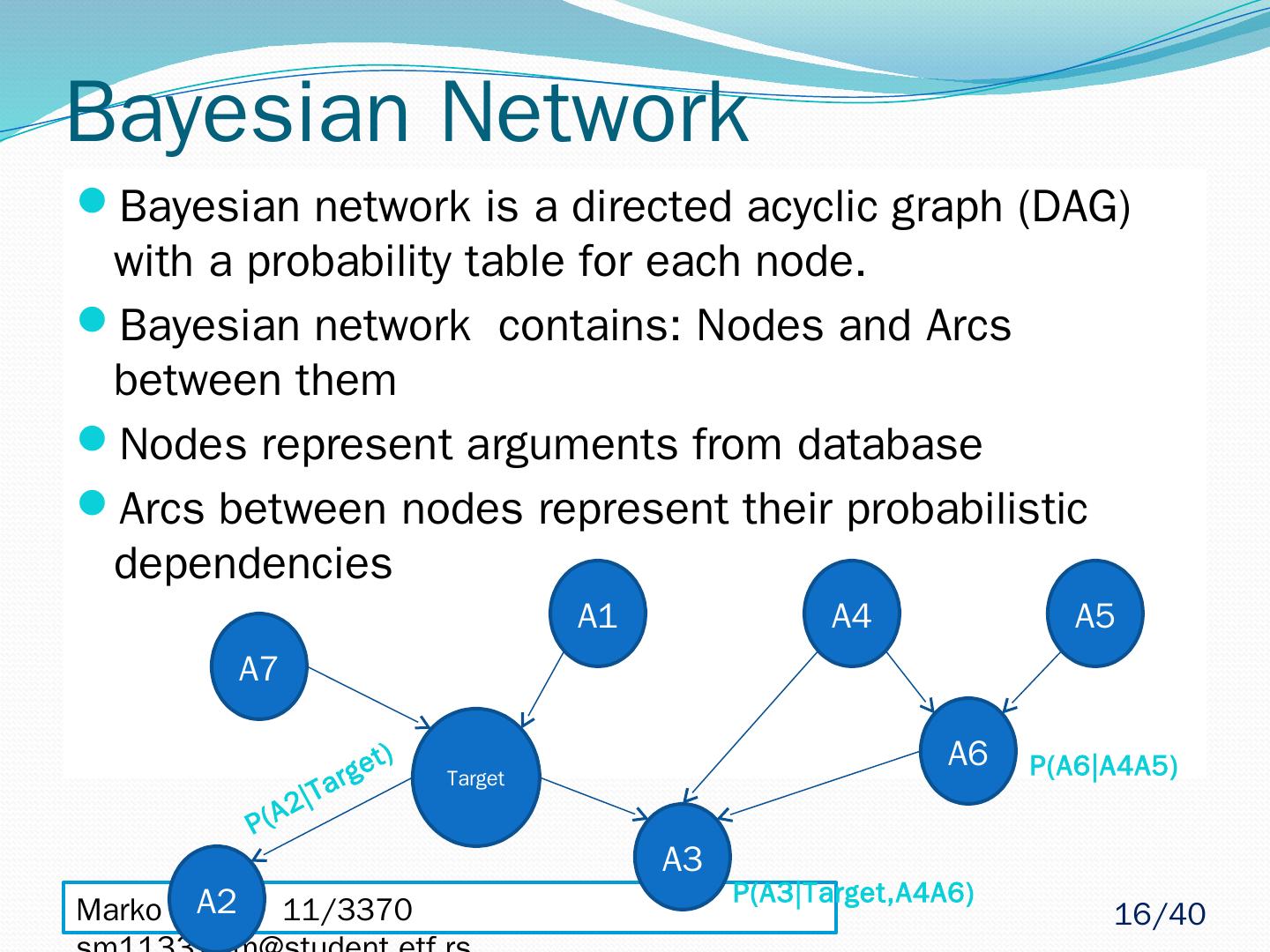
16 .Marko Stupar 11/3370 sm113370m@student.etf.rs Bayesian Network Bayesian network is a directed acyclic graph (DAG) with a probability table for each node. Bayesian network contains: Nodes and Arcs between them Nodes represent arguments from database Arcs between nodes represent their probabilistic dependencies Target A2 A1 A3 P(A2|Target) A6 A4 A5 P(A6|A4A5) A7 P(A3|Target,A4A6) 16 /40

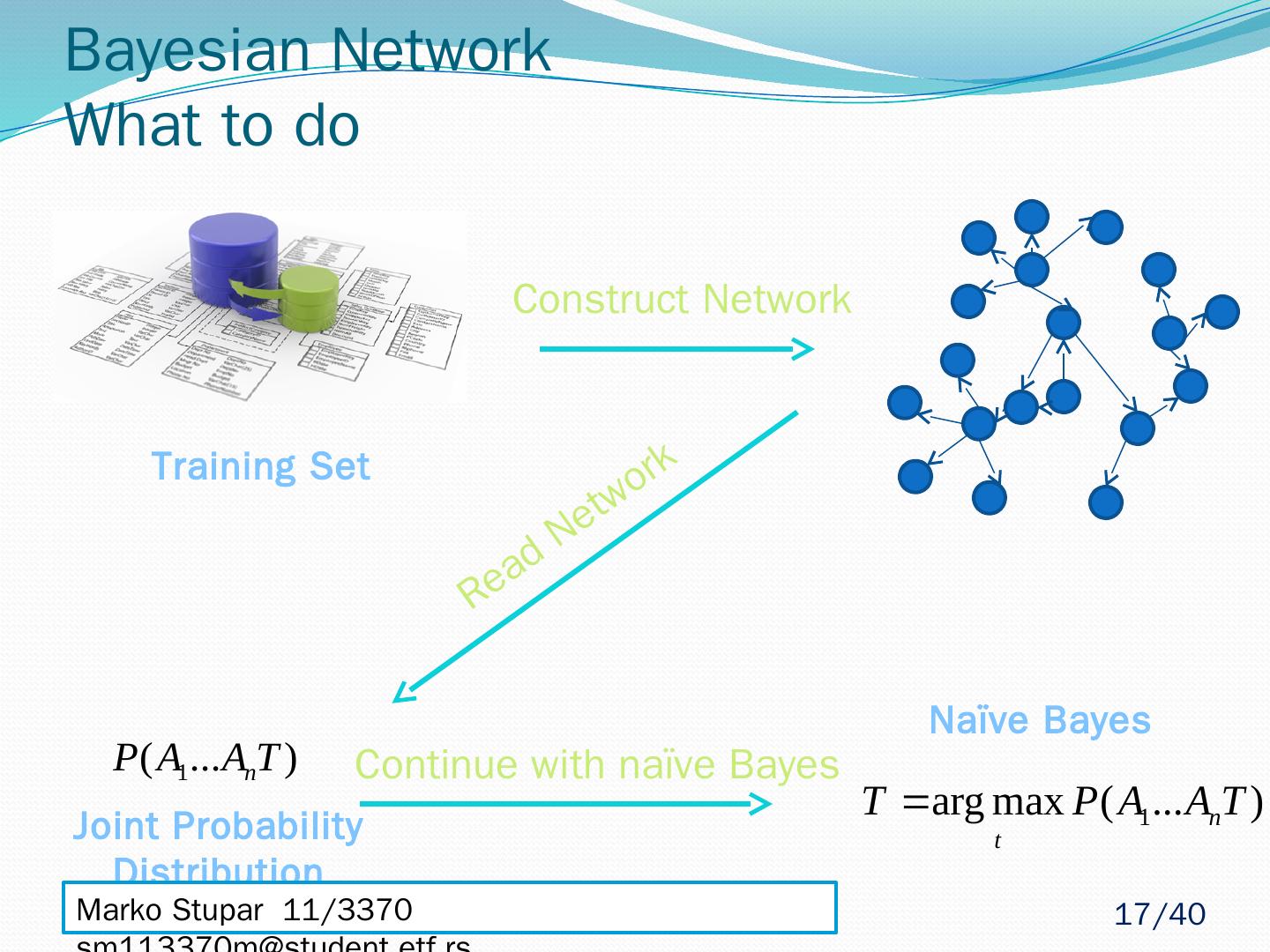
17 .Bayesian Network What to do Read Network Construct Network Training Set Continue with naïve Bayes Joint Probability Distribution Naïve Bayes Marko Stupar 11/3370 sm113370m@student.etf.rs 17 /40

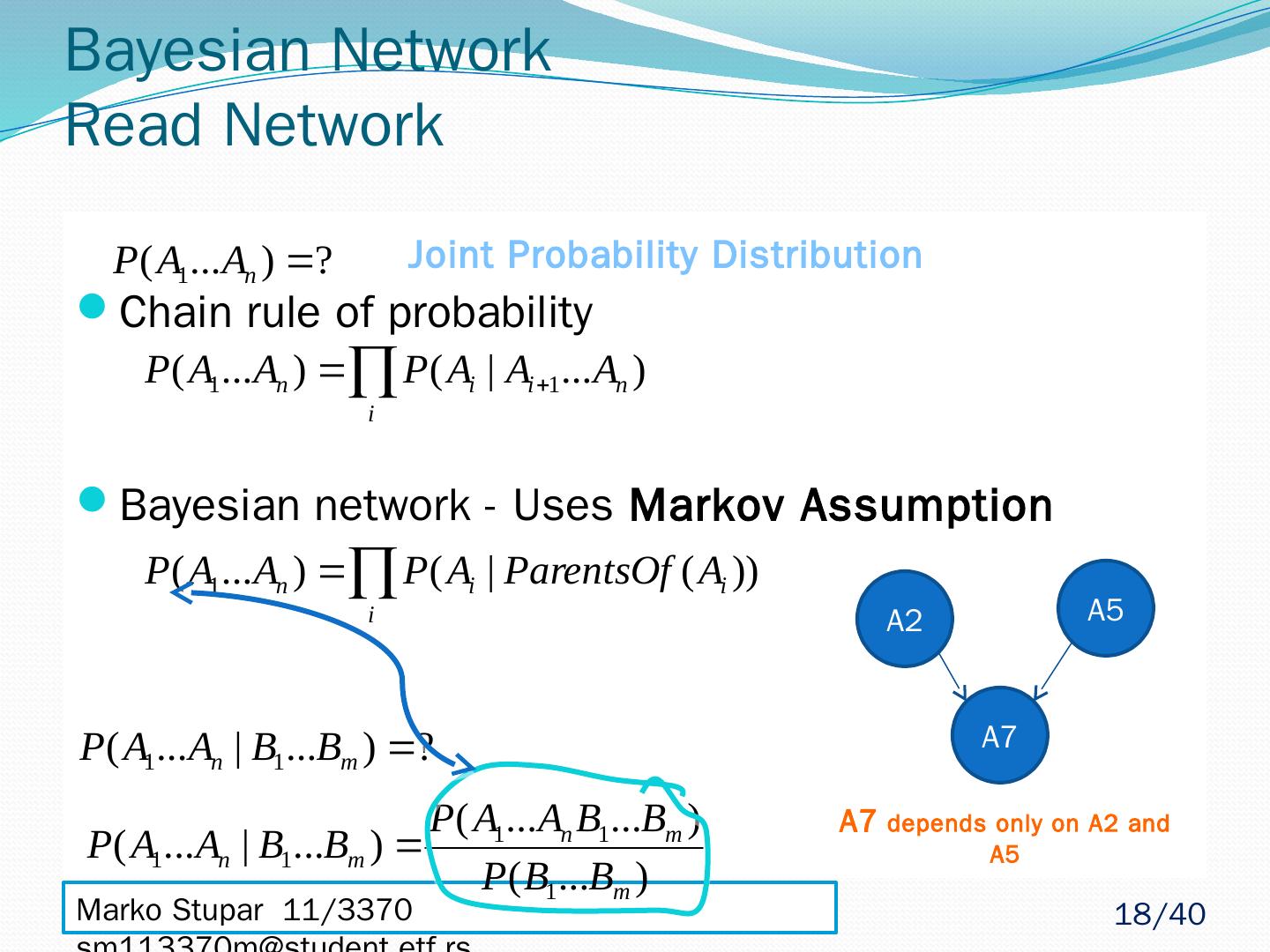
18 .Marko Stupar 11/3370 sm113370m@student.etf.rs Bayesian Network Read Network Chain rule of probability Bayesian network - Uses Markov Assumption A7 A2 A5 Joint Probability Distribution A7 depends only on A2 and A5 18 /40

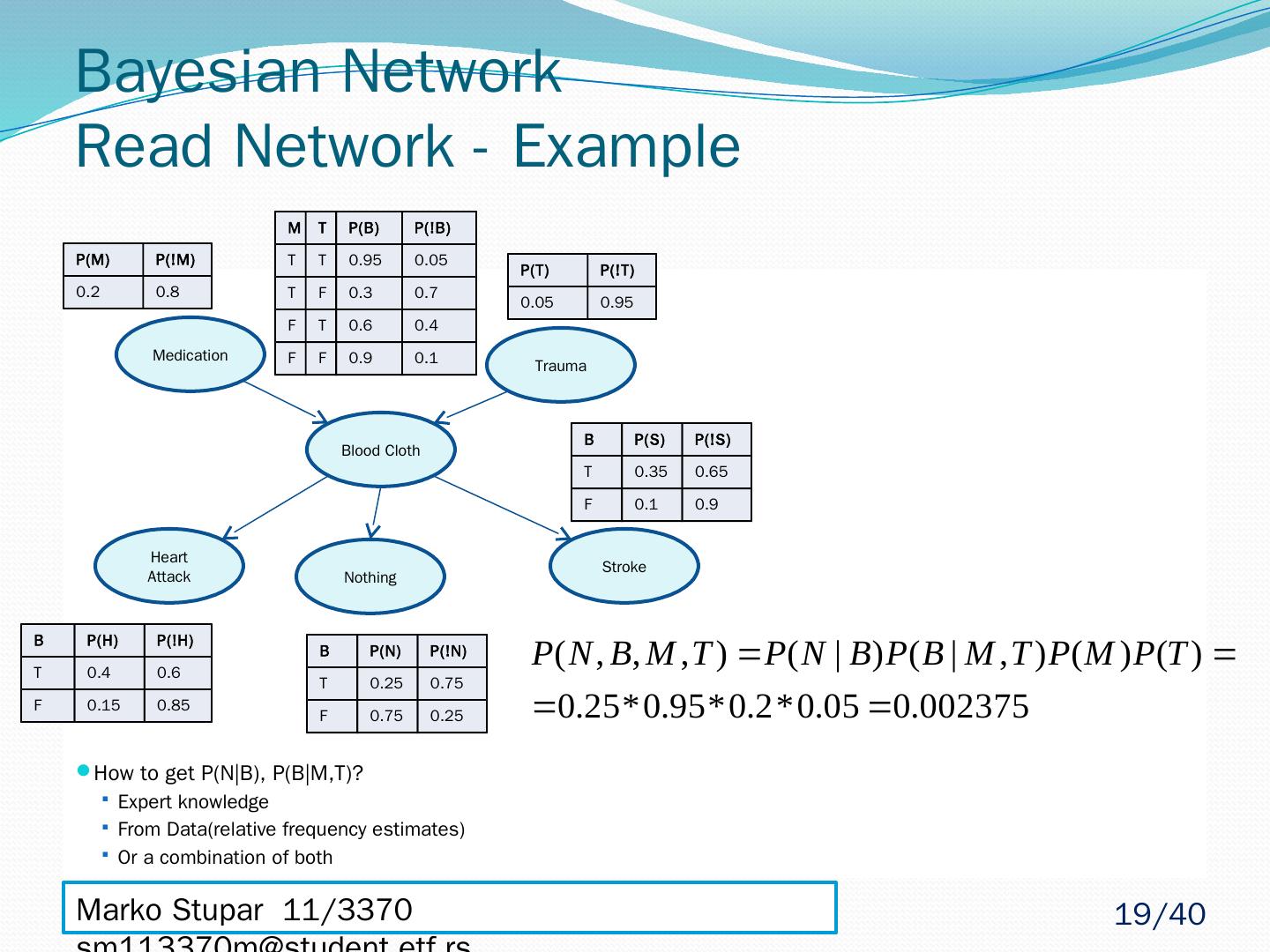
19 .Bayesian Network Read Network - Example How to get P(N|B), P(B|M,T)? Expert knowledge From Data(relative frequency estimates) Or a combination of both Medication Blood Cloth Trauma Heart Attack Nothing Stroke P(M) P(!M) 0.2 0.8 P(T) P(!T) 0.05 0.95 M T P(B) P(!B) T T 0.95 0.05 T F 0.3 0.7 F T 0.6 0.4 F F 0.9 0.1 B P(H) P(!H) T 0.4 0.6 F 0.15 0.85 B P(N) P(!N) T 0.25 0.75 F 0.75 0.25 B P(S) P(!S) T 0.35 0.65 F 0.1 0.9 Marko Stupar 11/3370 sm113370m@student.etf.rs 19 /40

20 .Manually From Database – Automatically Heuristic algorithms 1. heuristic search method to construct a model 2.evaluates model using a scoring method Bayesian scoring method entropy based method minimum description length method 3. go to 1 if score of new model is not significantly better Algorithms that analyze dependency among nodes Measure dependency by conditional independence (CI) test Bayesian Network Construct Network Marko Stupar 11/3370 sm113370m@student.etf.rs 20 /40

21 .Bayesian Network Construct Network Heuristic algorithms Advantages less time complexity in worst case Disadvantage May not find the best solution due to heuristic nature Algorithms that analyze dependency among nodes Advantages usually asymptotically correct Disadvantage CI tests with large condition-sets may be unreliable unless the volume of data is enormous. Marko Stupar 11/3370 sm113370m@student.etf.rs 21 /40

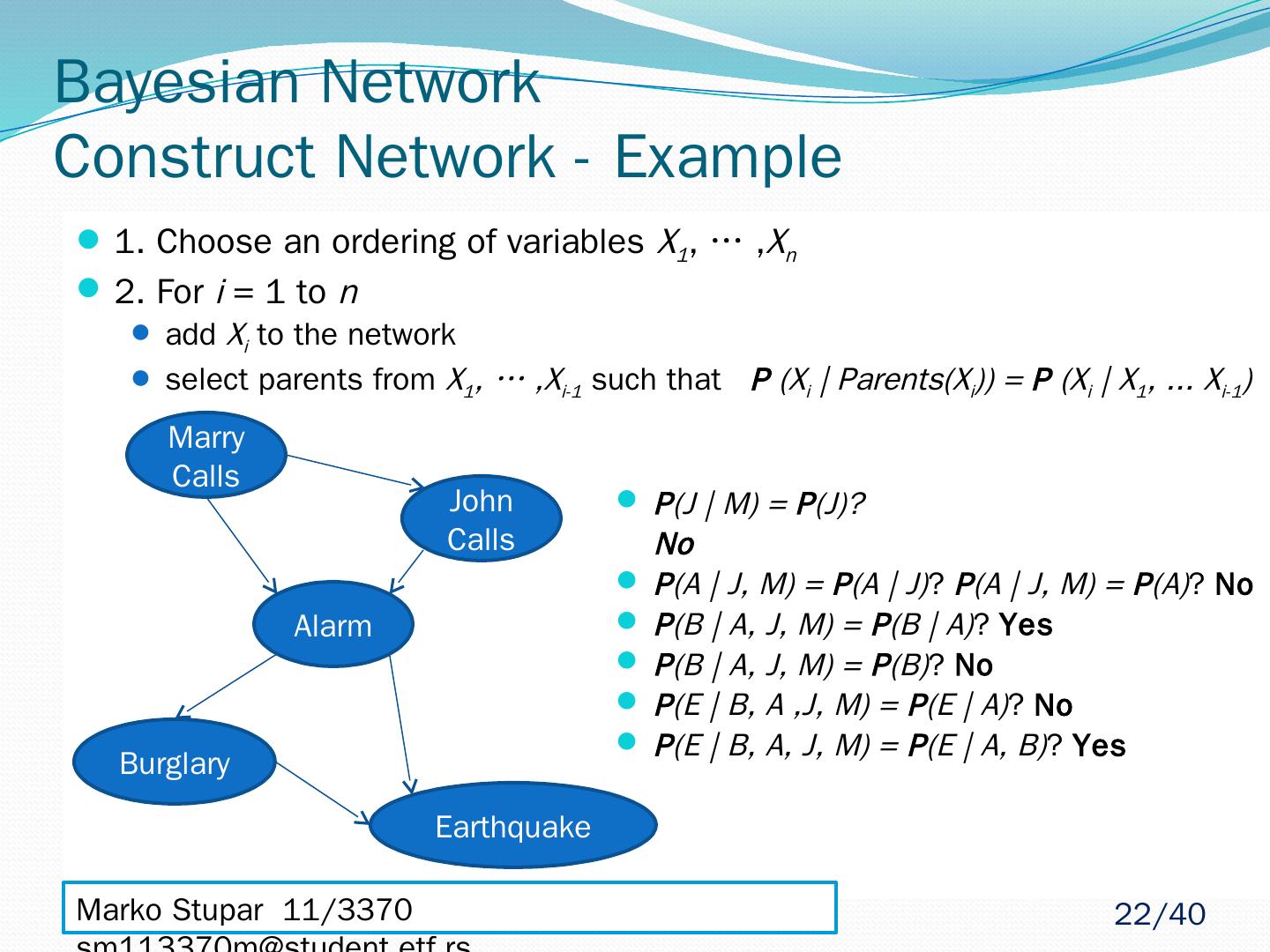
22 .Bayesian Network Construct Network - Example 1. Choose an ordering of variables X 1 , … , X n 2. For i = 1 to n add X i to the network select parents from X 1 , … ,X i-1 such that P (X i | Parents(X i )) = P (X i | X 1 , ... X i-1 ) Marko Stupar 11/3370 sm113370m@student.etf.rs Marry Calls John Calls Alarm Burglary Earthquake P (J | M) = P (J)? No P (A | J, M) = P (A | J) ? P (A | J, M) = P (A) ? No P (B | A, J, M) = P (B | A) ? Yes P (B | A, J, M) = P (B) ? No P (E | B, A ,J, M) = P (E | A) ? No P (E | B, A, J, M) = P (E | A, B) ? Yes 22 /40

23 .Create Network – from database d(Directional)-Separation d-Separation is graphical criterion for deciding, from a given causal graph(DAG), whether a disjoint sets of nodes X-set, Y-set are independent, when we know realization of third Z-set Z-set - is instantiated(values of it’s nodes are known) before we try to determine d-Separation(independence) between X-set and Y-set X-set and Y-set are d-Separated by given Z-set if all paths between them are blocked Example of Path : N1 <- N2 -> N3 -> N4 -> N5 <- N6 <- N7 N5 – “head-to-head” node Path is not blocked if every “head-to-head” node is in Z-set or has descendant in Z-set, and all other nodes are not in Z-set. Marko Stupar 11/3370 sm113370m@student.etf.rs 23 /40

24 .Create Network – from database d-Separation Example 1. Does D d -separate C and F? There are two undirected paths from C to F: ( i ) C -B -E –F This blocked given D by the node E, since E is not one of the given nodes and has both arrows on the path going into it. (ii) C - B - A - D - E - F. This path is also blocked by E (and D as well). So, D does d-separate C and F 2. Do D and E d-separate C and F? The path C - B - A - D - E - F is blocked by the node D given {D,E}. However, E no longer blocks C - B - E - F path since it “given” node. So, D and E do not d-separate C and F 3. Write down all pairs of nodes which are independent of each other. Nodes which are independent are those that are d-separated by the empty set of nodes. This means every path between them must contain at least one node with both path arrows going into it, which is E in current context. We find that F is independent of A, of B, of C and of D. All other pairs of nodes are dependent on each other. 4. Which pairs of nodes are independent of each other given B? We need to find which nodes are d-separated by B. A, C and D are all d-separated from F because of the node E. C is d-separated from all the other nodes (except B) given B. The independent pairs given B are hence: AF, AC, CD, CE, CF, DF. 5. Do we have that: P(AF|E) = P(A|E)P(F|E)? (are A and F independent given E?) A and F are NOT independent given E, since E does not d-separate A and F Marko Stupar 11/3370 sm113370m@student.etf.rs 24 /40

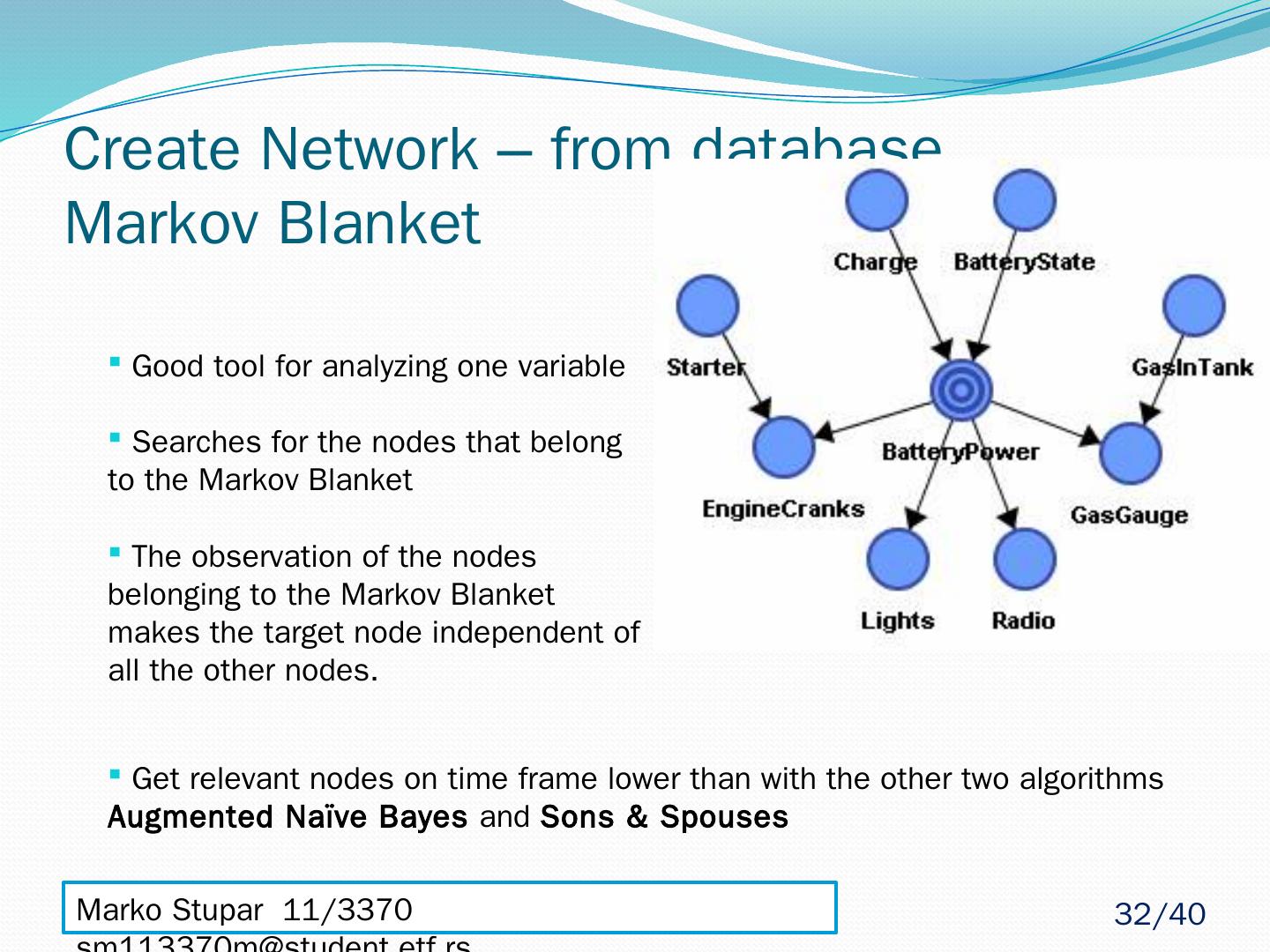
25 .Create Network – from database Markov Blanket MB(A) - set of nodes composed of A’s parents, its children and their other parents When given MB(A) every other set of nodes in network is conditionally independent or d-Separated of A MB(A) - The only knowledge needed to predict the behavior of A – Pearl 1988. Marko Stupar 11/3370 sm113370m@student.etf.rs 25 /40

26 .Mutual information Conditional mutual information Used to quantify dependence between nodes X and Y If we say that X and Y are d-Separated by condition set Z, and that they are conditionally independent Marko Stupar 11/3370 sm113370m@student.etf.rs Create Network – from database Conditional independence (CI) Test 26 /40

27 . Marko Stupar 11/3370 sm113370m@student.etf.rs Backup Slides (Not needed) 27 /40

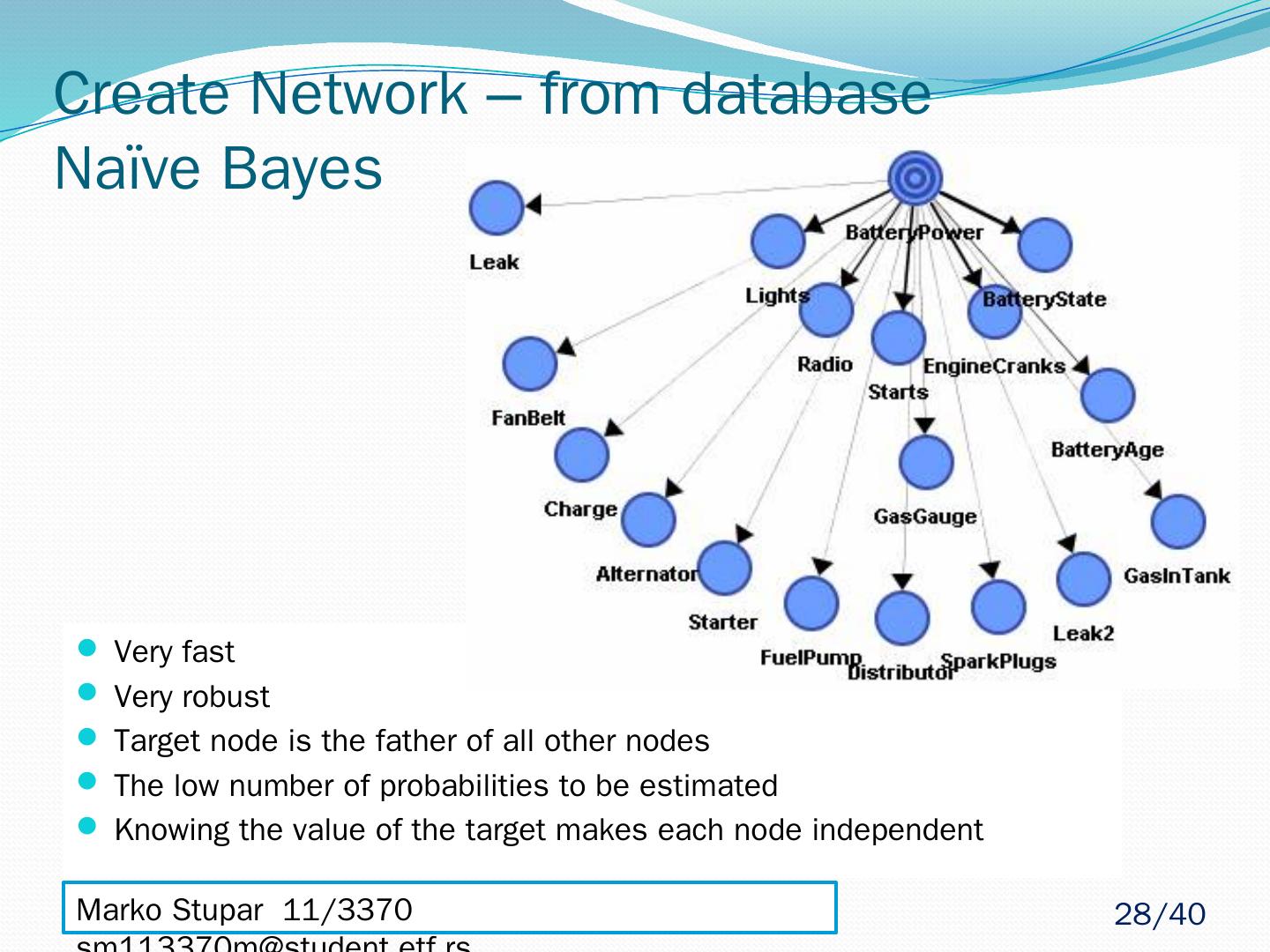
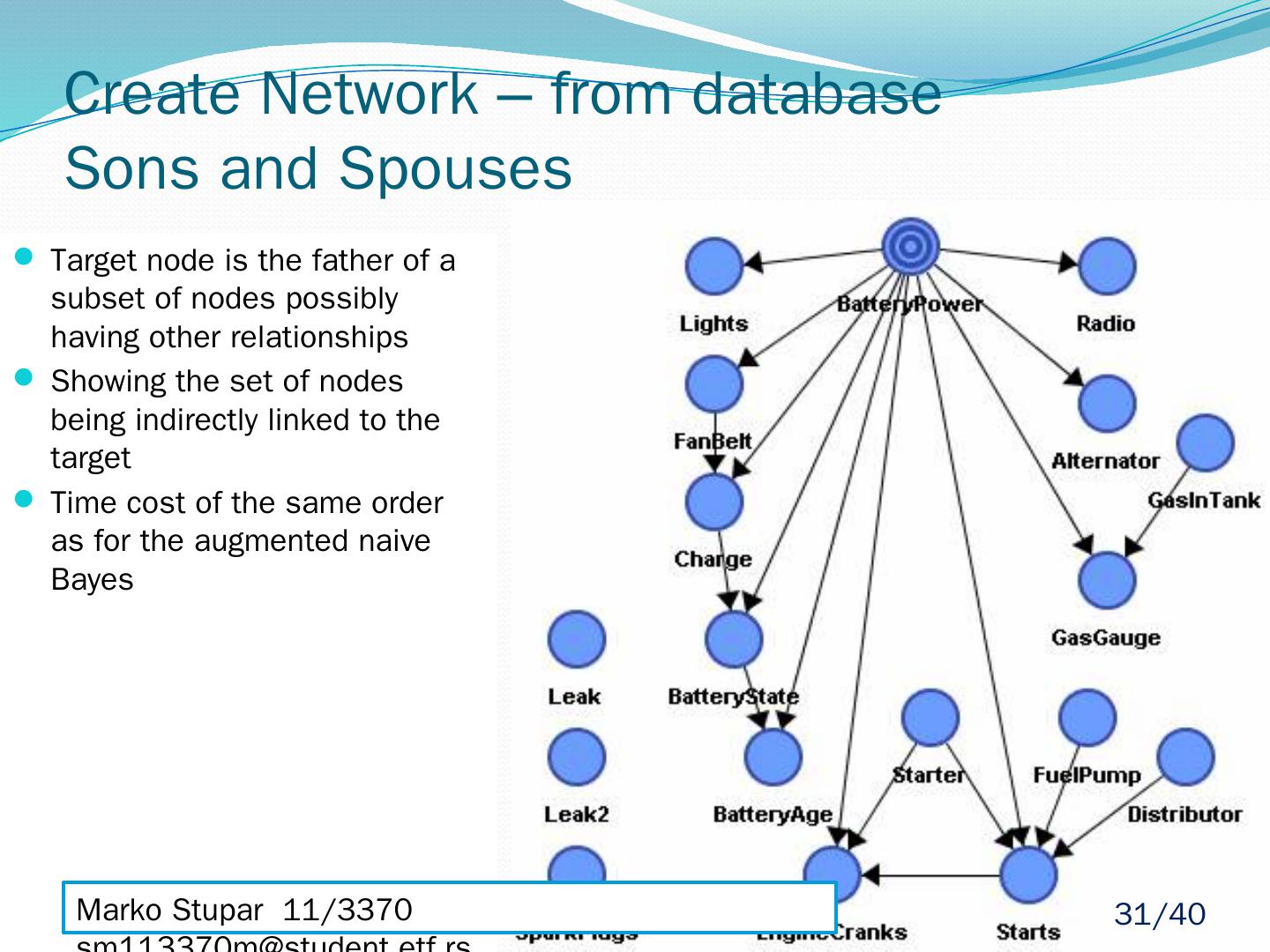
28 .Create Network – from database Naïve Bayes Very fast Very robust Target node is the father of all other nodes The low number of probabilities to be estimated Knowing the value of the target makes each node independent Marko Stupar 11/3370 sm113370m@student.etf.rs 28 /40

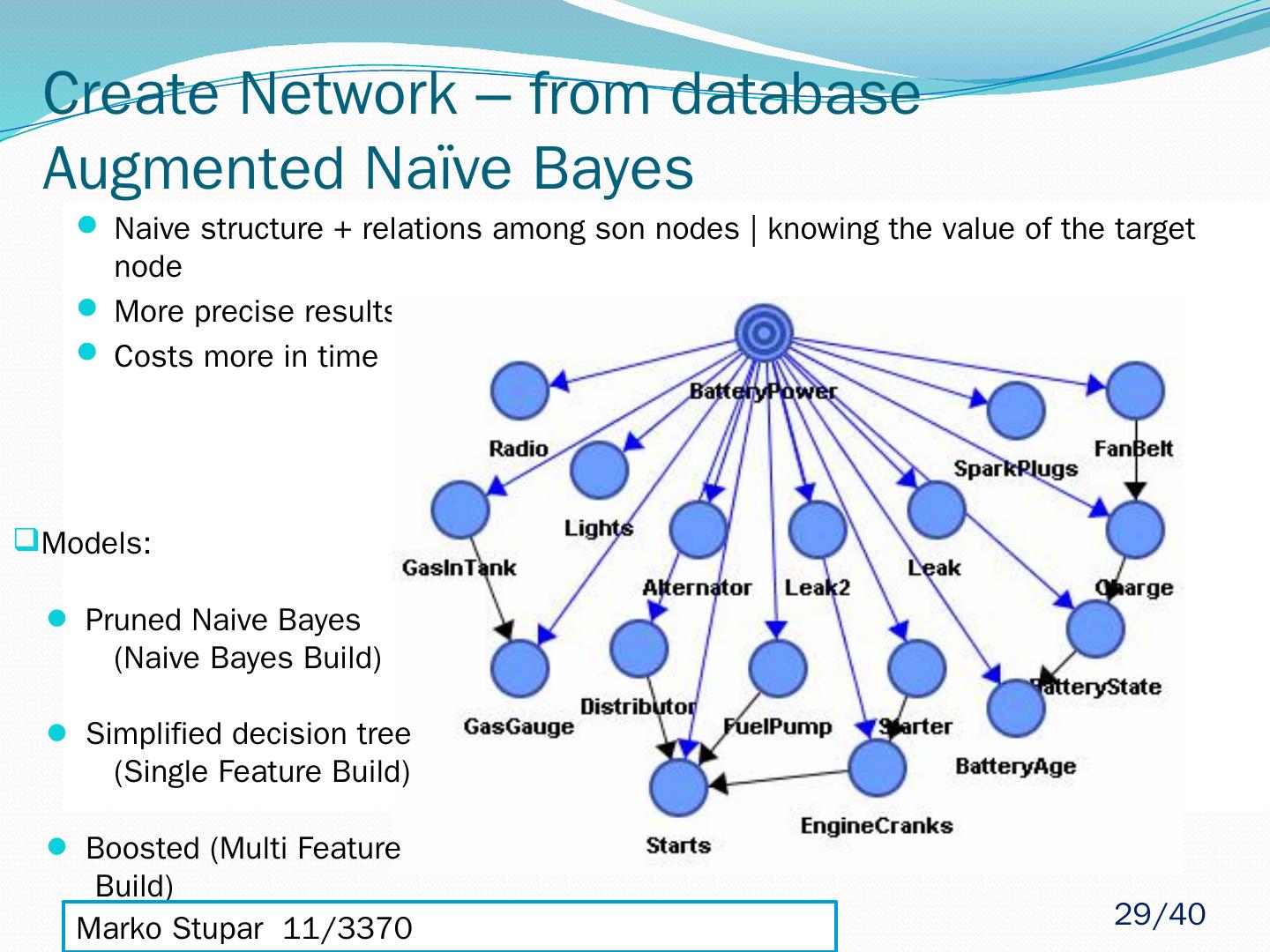
29 .Create Network – from database Augmented Naïve Bayes Naive structure + relations among son nodes | knowing the value of the target node More precise results than with the naive architecture Costs more in time Models: Pruned Naive Bayes (Naive Bayes Build) Simplified decision tree (Single Feature Build) Boosted (Multi Feature Build) Marko Stupar 11/3370 sm113370m@student.etf.rs 29 /40