Stochastic SVD on Hadoop

1 .Stochastic SVD on Hadoop Shannon Quinn (with thanks to Gunnar Martinsson and Nathan Halko of UC Boulder, and Joel Tropp of CalTech )

2 .Lecture breakdown Part I Stochastic SVD Part II Distributed stochastic SVD

3 .Part I: Stochastic SVD

4 .Basic goal Matrix A Find a low-rank approximation of A Basic dimensionality reduction Preconditioning

5 .Basic algorithm INPUT: A , k , p OUTPUT: Q Draw Gaussian n x (k + p) test matrix Ω Form product Y = AΩ Orthogonalize columns of Y  Q

6 .Basic evaluation

7 .Approximating the SVD INPUT: Q OUTPUT: Singular vectors U Form k x n matrix B = Q T A Compute SVD of B = ÛΣV T Compute singular vectors U = QÛ

8 .Demo

9 .Empirical Results 1000x1000 matrix

10 .Power iterations Affects decay of eigenvalues / singular values

11 .Empirical Results

12 .Empirical Results

13 .Part II: Distributed SSVD

14 .Algorithm Overview QR factorization Power iteration QR factorization In-core SVD

15 .SSVD Primitives Matrix-vector multiplication: y = Ax (midterm, anyone?)

16 .SSVD Primitives Matrix-matrix multiplication: y = A T Ax

17 .Matrix-matrix multiplication Very clever use of map/reduce Each Mapper outputs:

18 .SSVD Primitives Distributed o rthogonalization : Y = AΩ Givens rotation Streaming QR Sliding window Merge factorizations Merge R Merge Q T

19 .SSVD 1 2 3 4 5

20 .1: Q-job

21 .2: B T -job

22 .3: AB T -job

23 .4: U-job

24 .5: V-job

25 .Mahout SSVD Parameters

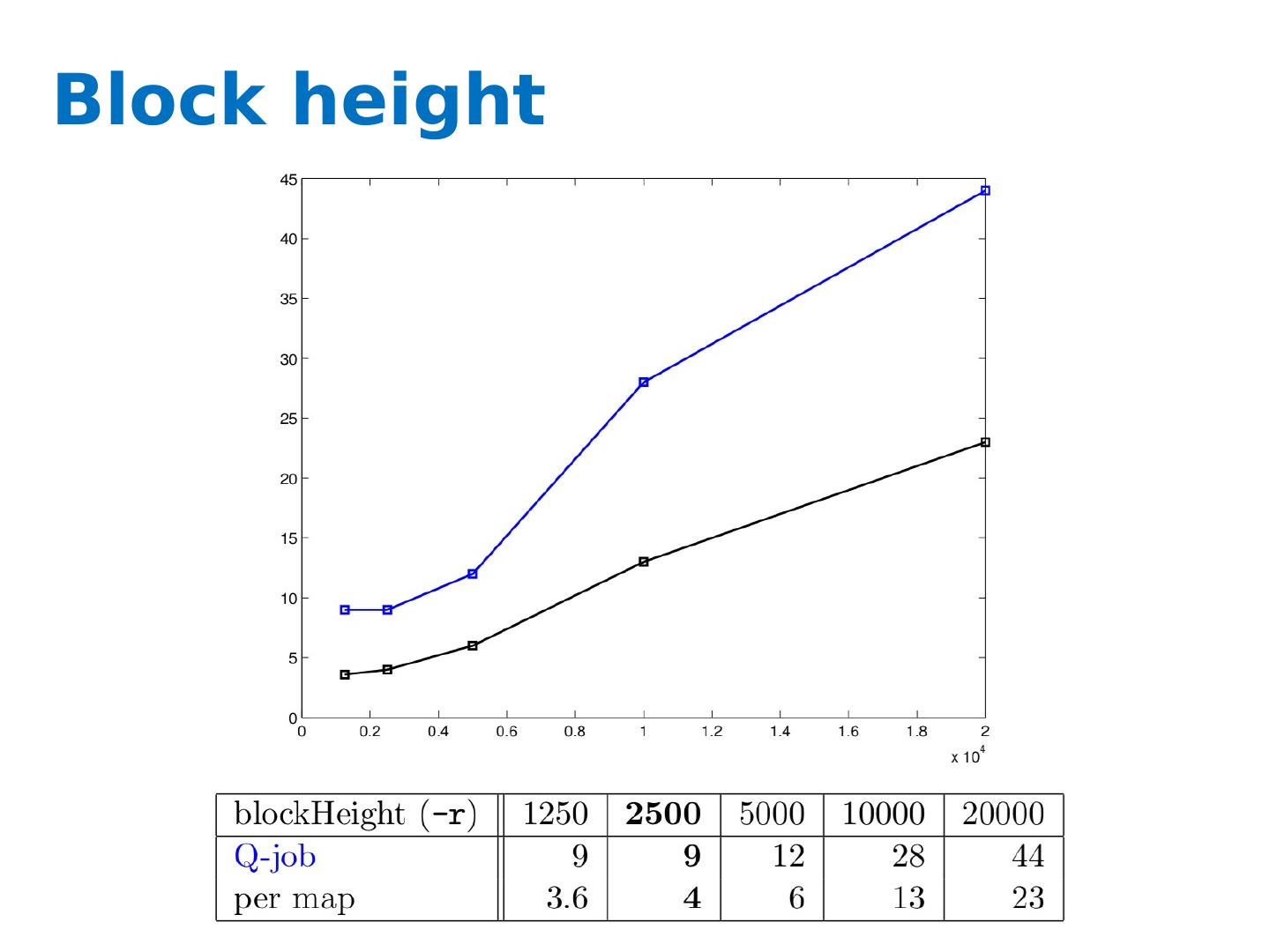
26 .Block height

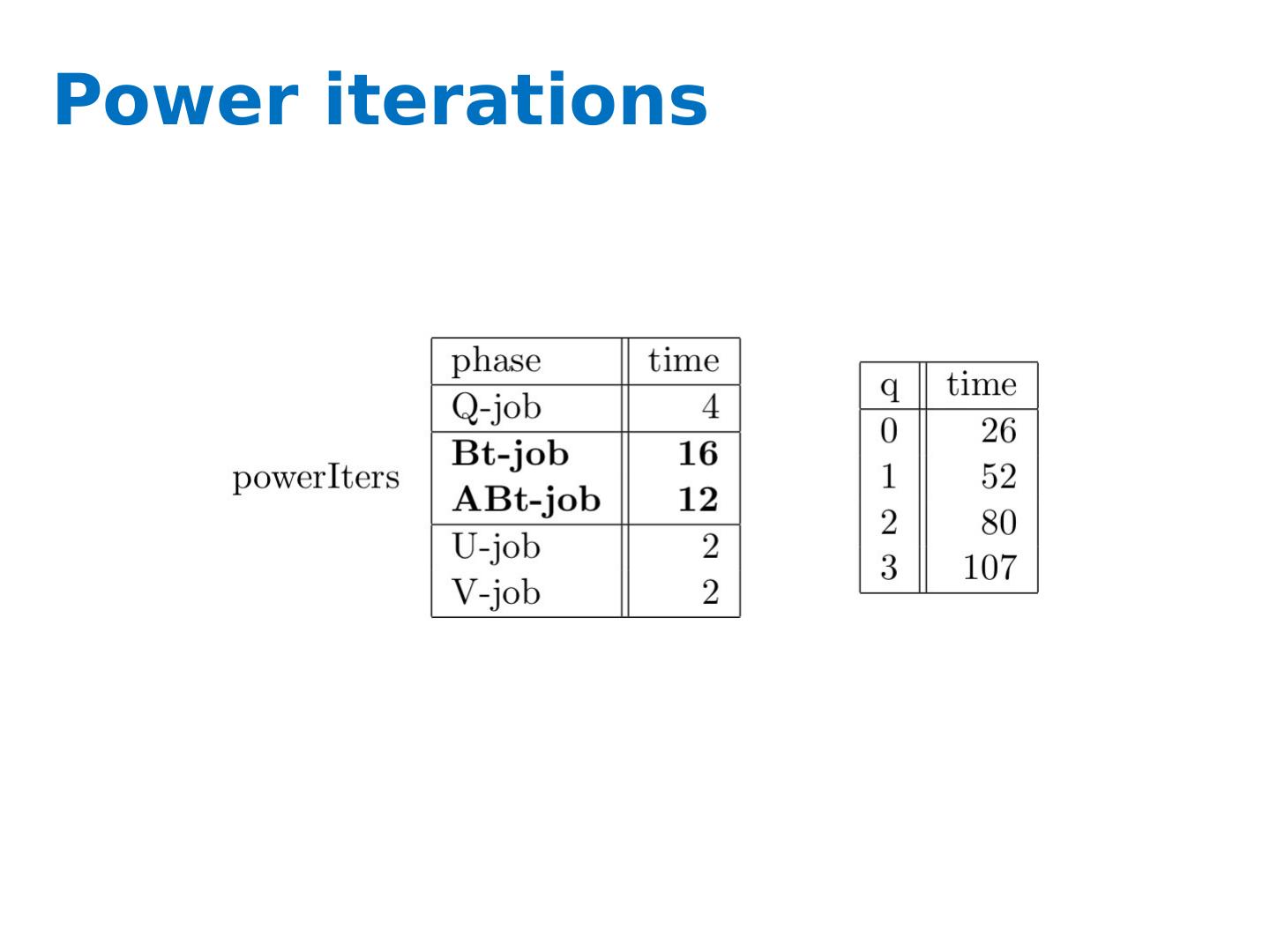
27 .Power iterations

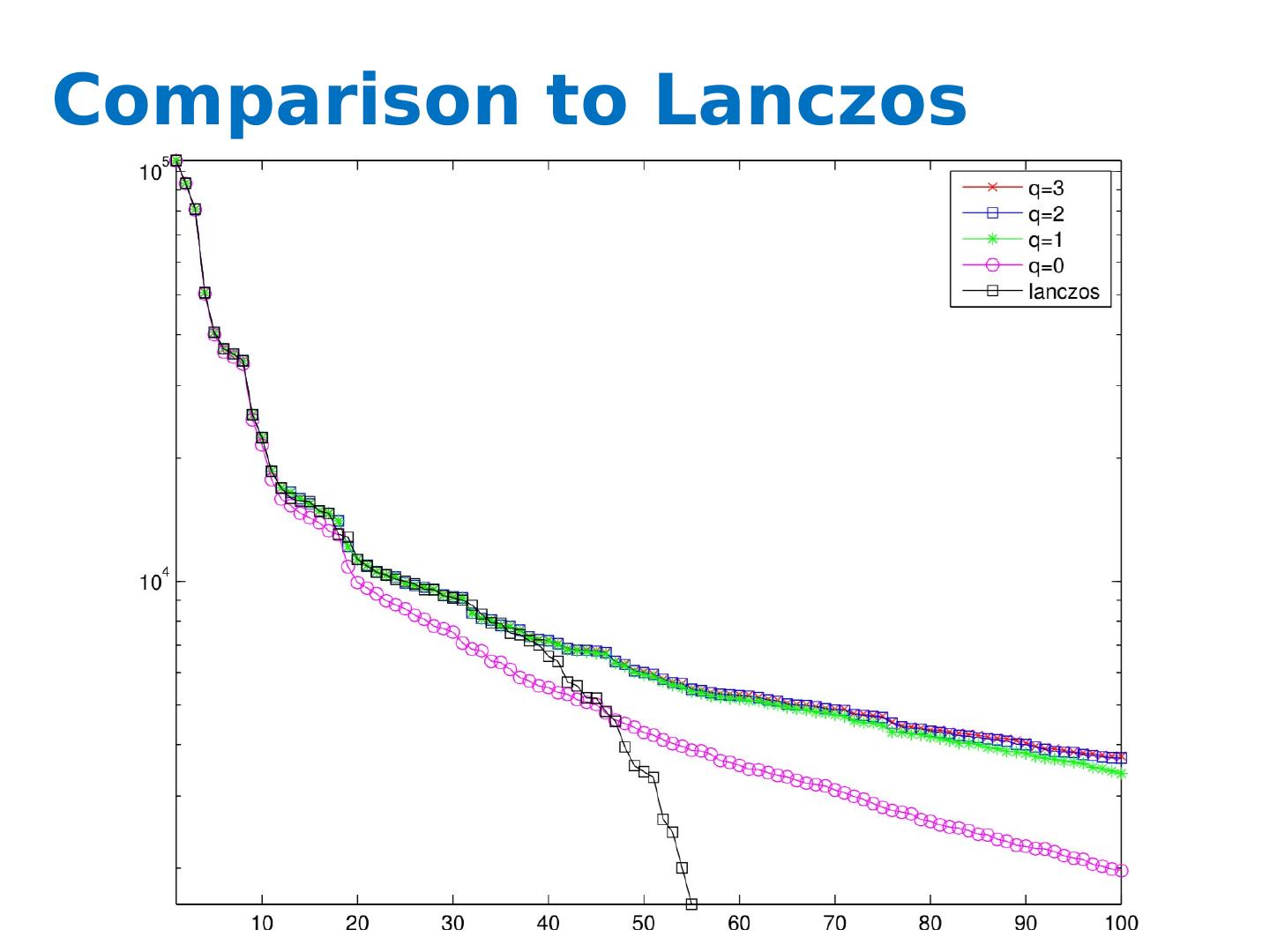
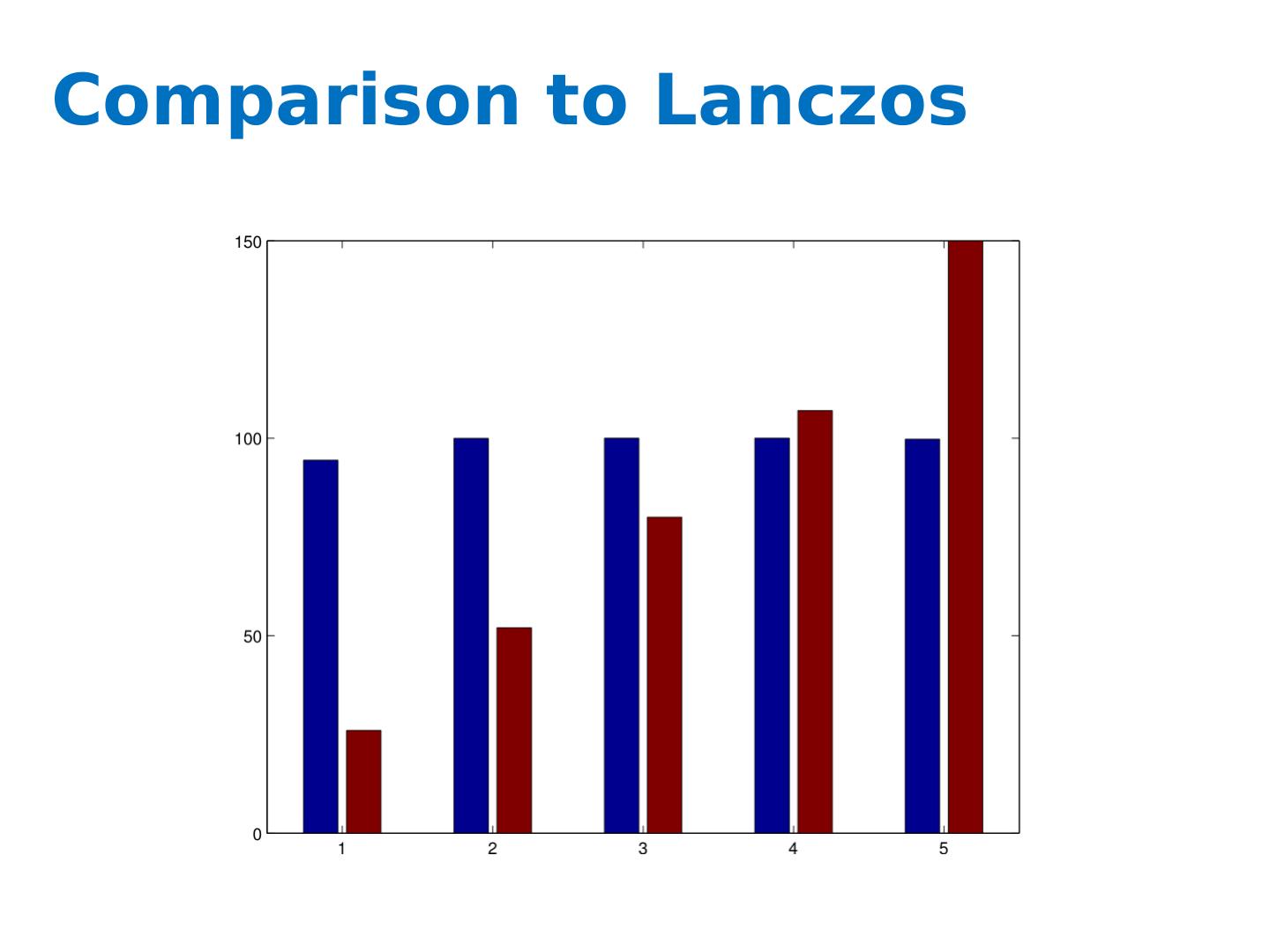
28 .Comparison to Lanczos

29 .Comparison to Lanczos