Scaling up Decision Trees

1 .Scaling up Decision Trees Shannon Quinn (with thanks to William Cohen of CMU, and B. Panda, J. S. Herbach , S. Basu , and R . J. Bayardo of IIT)

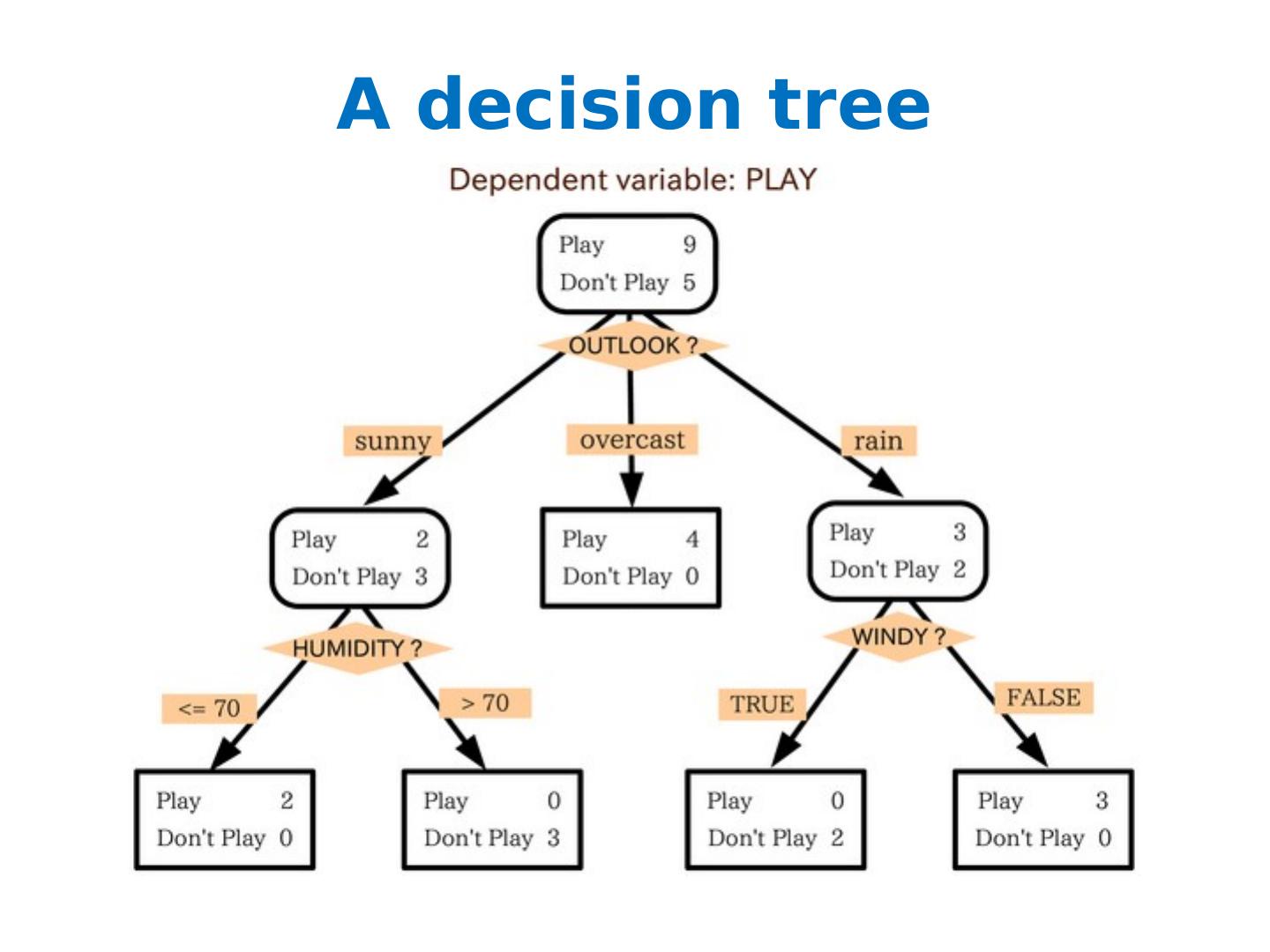
2 .A decision tree

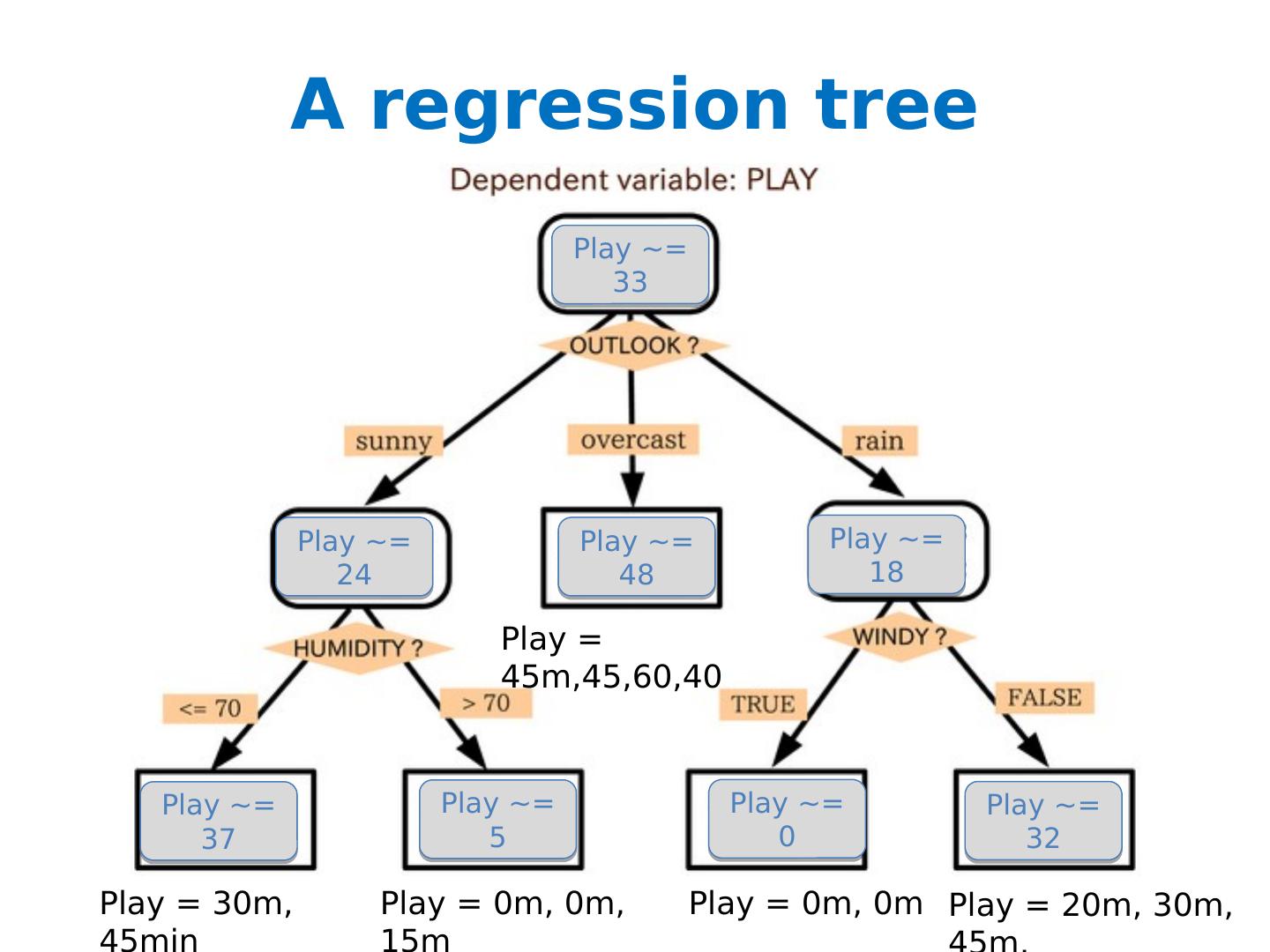
3 .A regression tree Play = 30m, 45min Play = 0m, 0m, 15m Play = 0m, 0m Play = 20m, 30m, 45m, Play ~= 33 Play ~= 24 Play ~= 37 Play ~= 5 Play ~= 0 Play ~= 32 Play ~= 18 Play = 45m,45,60,40 Play ~= 48

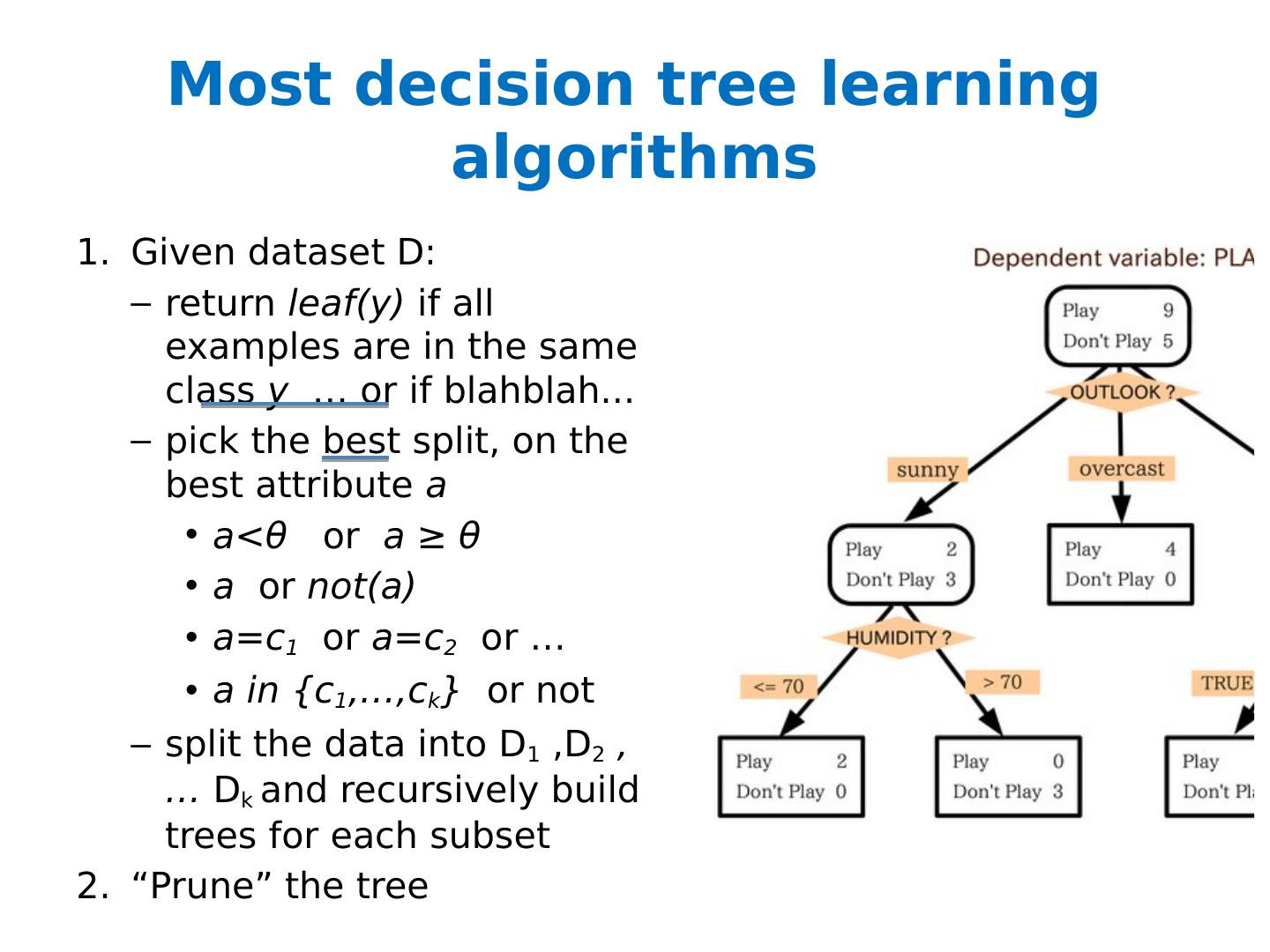
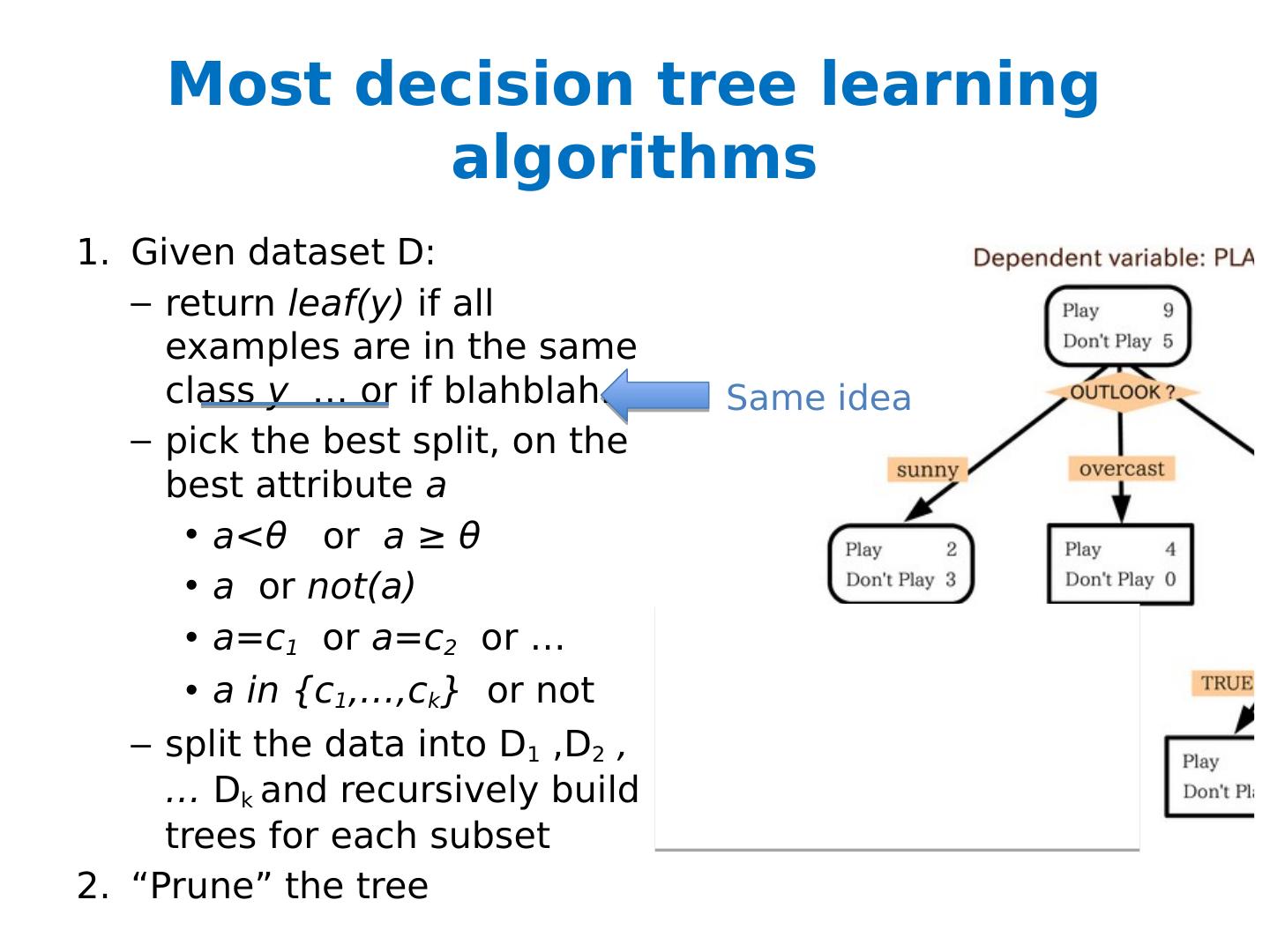
4 .Most decision tree learning algorithms Given dataset D: return leaf(y) if all examples are in the same class y … or if blahblah ... pick the best split, on the best attribute a a< θ or a ≥ θ a or not(a) a=c 1 or a=c 2 or … a in {c 1 ,…, c k } or not split the data into D 1 ,D 2 , … D k and recursively build trees for each subset “Prune” the tree

5 .Most decision tree learning algorithms Given dataset D: return leaf(y) if all examples are in the same class y … or if blahblah ... pick the best split, on the best attribute a a< θ or a ≥ θ a or not(a) a=c 1 or a=c 2 or … a in {c 1 ,…, c k } or not split the data into D 1 ,D 2 , … D k and recursively build trees for each subset “Prune” the tree Popular splitting criterion: try to lower entropy of the y labels on the resulting partition i.e., prefer splits that contain fewer labels, or that have very skewed distributions of labels

6 .Most decision tree learning algorithms Find Best Split Choose split point that minimizes weighted impurity (e.g., variance (regression) and information gain (classification) are common) Stopping Criteria (common ones ) Maximum Depth Minimum number of data points Pure data points (e.g., all have the same Y label)

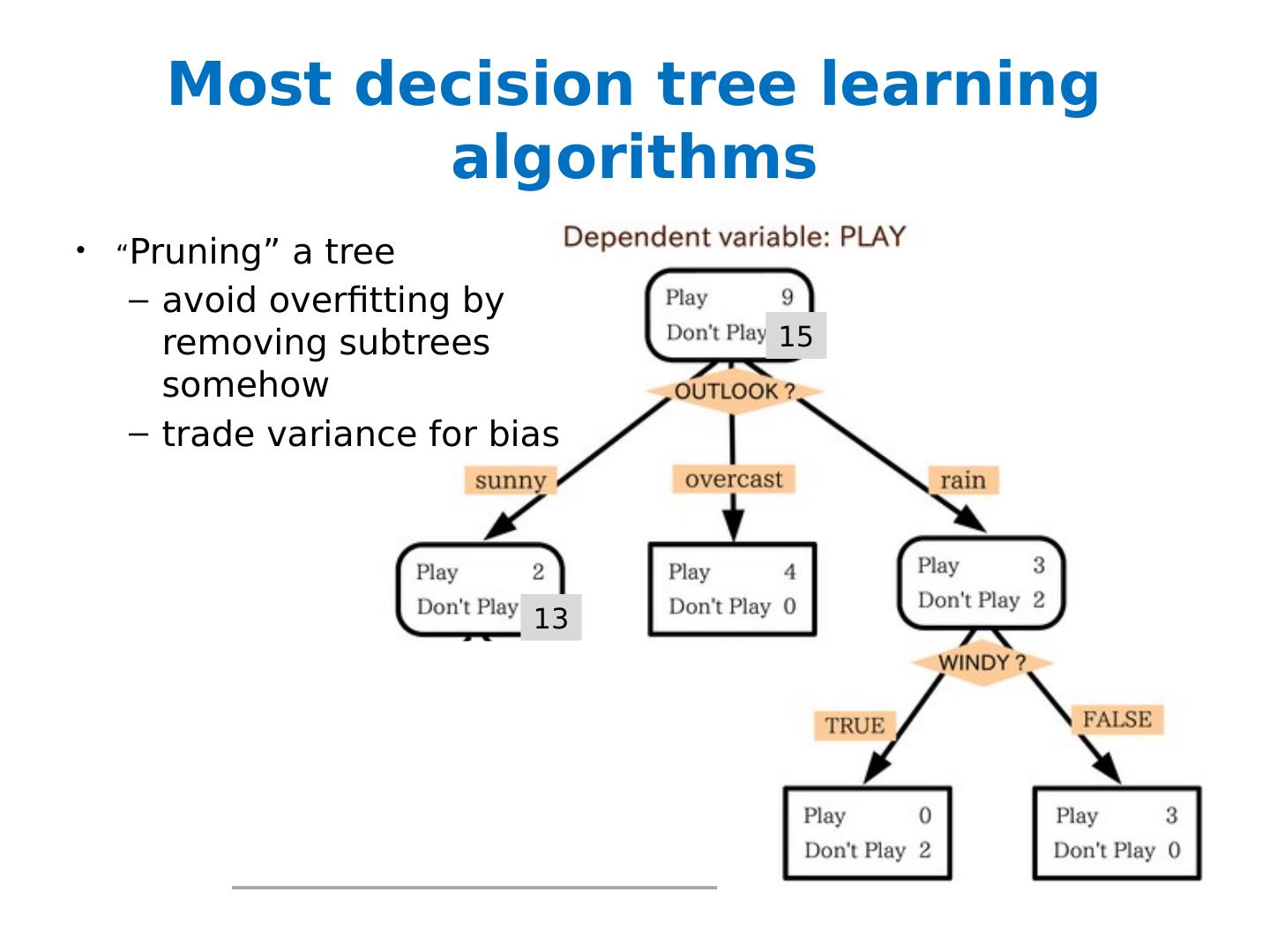
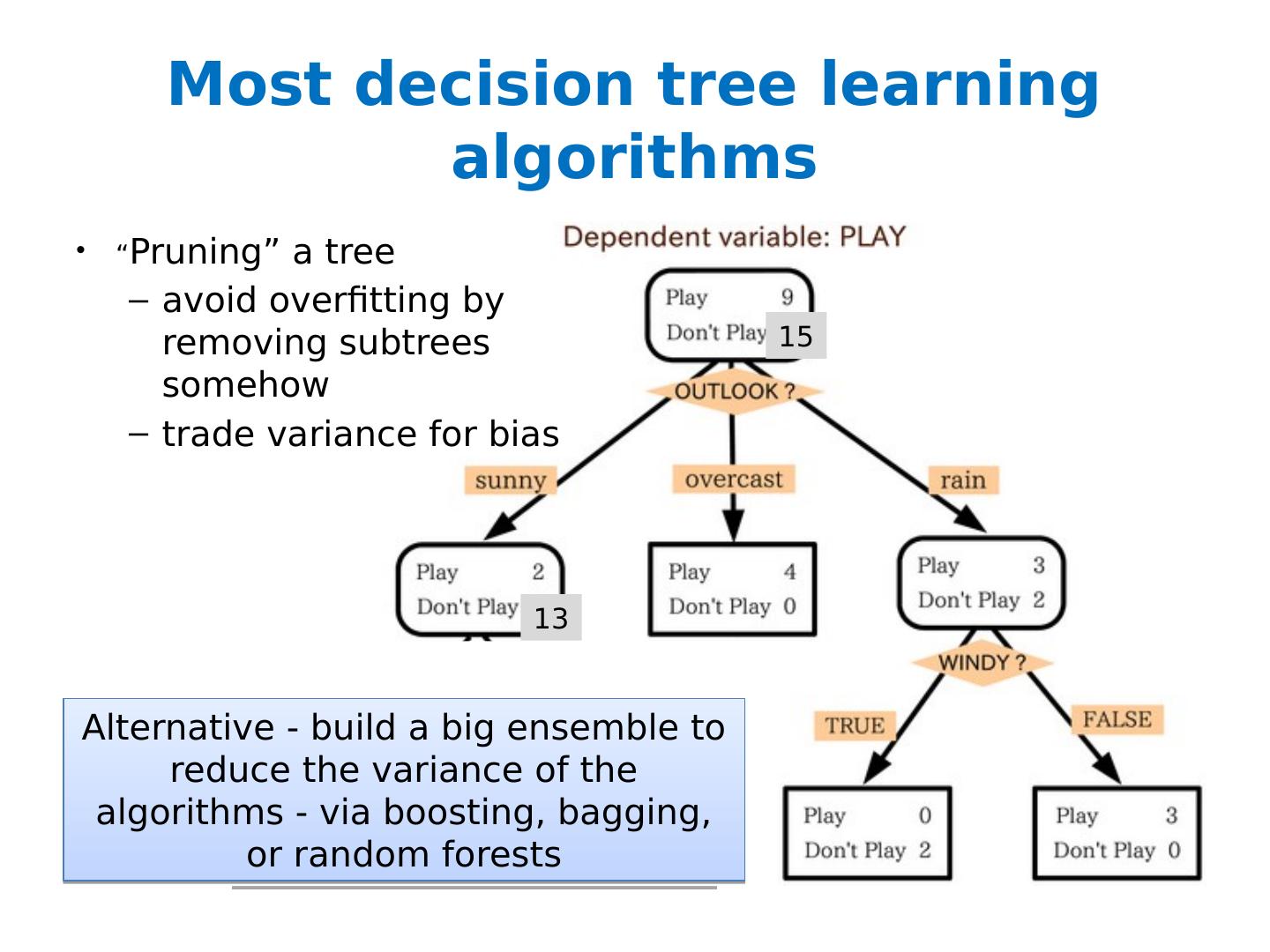
7 .Most decision tree learning algorithms “ Pruning” a tree avoid overfitting by removing subtrees somehow trade variance for bias 15 13

8 .Most decision tree learning algorithms Given dataset D: return leaf(y) if all examples are in the same class y … or if blahblah ... pick the best split, on the best attribute a a< θ or a ≥ θ a or not(a) a=c 1 or a=c 2 or … a in {c 1 ,…, c k } or not split the data into D 1 ,D 2 , … D k and recursively build trees for each subset “Prune” the tree Same idea

9 .Decision trees: plus and minus Simple and fast to learn Arguably easy to understand (if compact) Very fast to use: often you don’t even need to compute all attribute values Can find interactions between variables (play if it’s cool and sunny or ….) and hence non-linear decision boundaries Don’t need to worry about how numeric values are scaled

10 .Decision trees: plus and minus Hard to prove things about Not well-suited to probabilistic extensions Don’t (typically) improve over linear classifiers when you have lots of features Sometimes fail badly on problems that linear classifiers perform well on

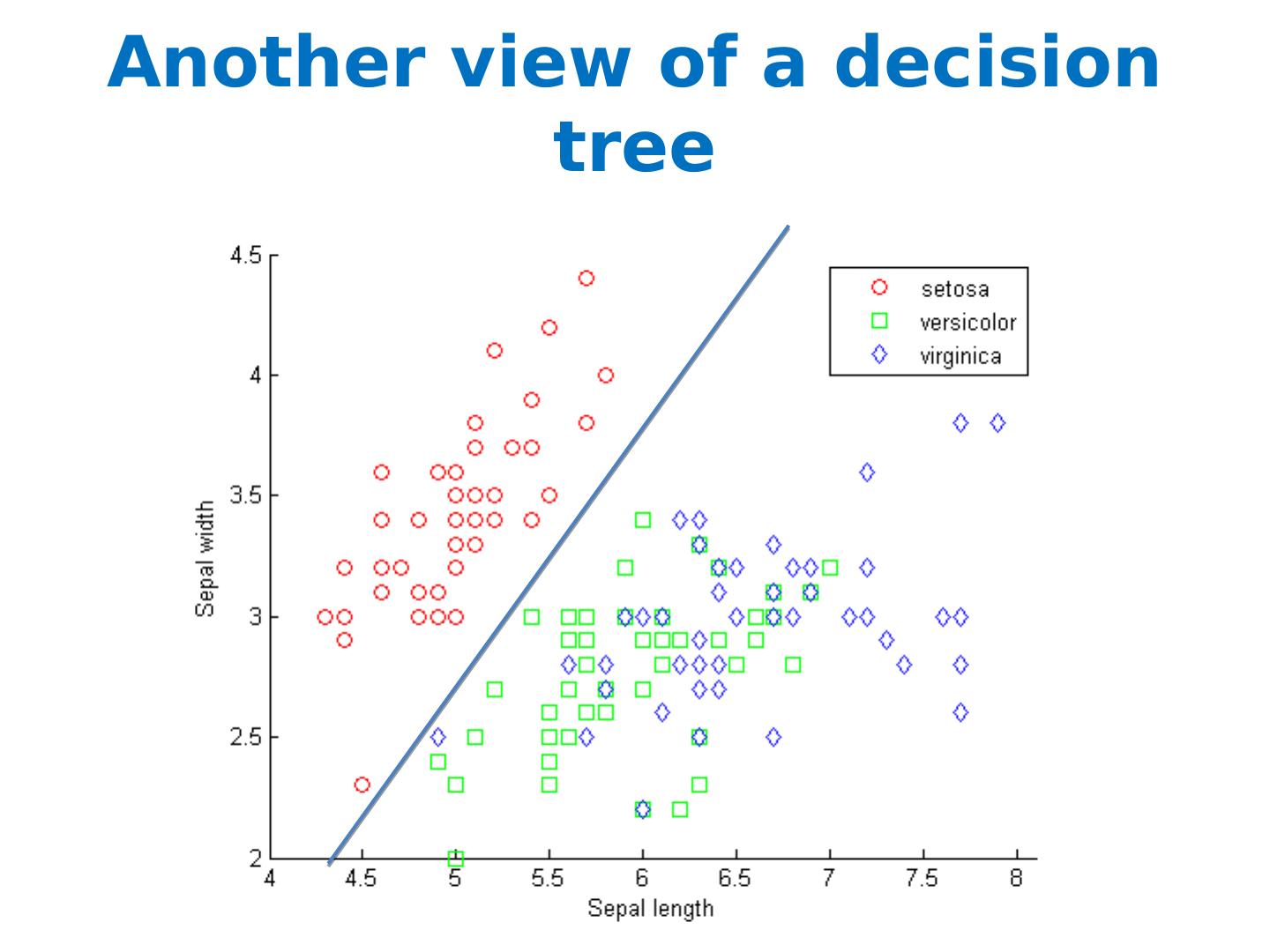
11 .Another view of a decision tree

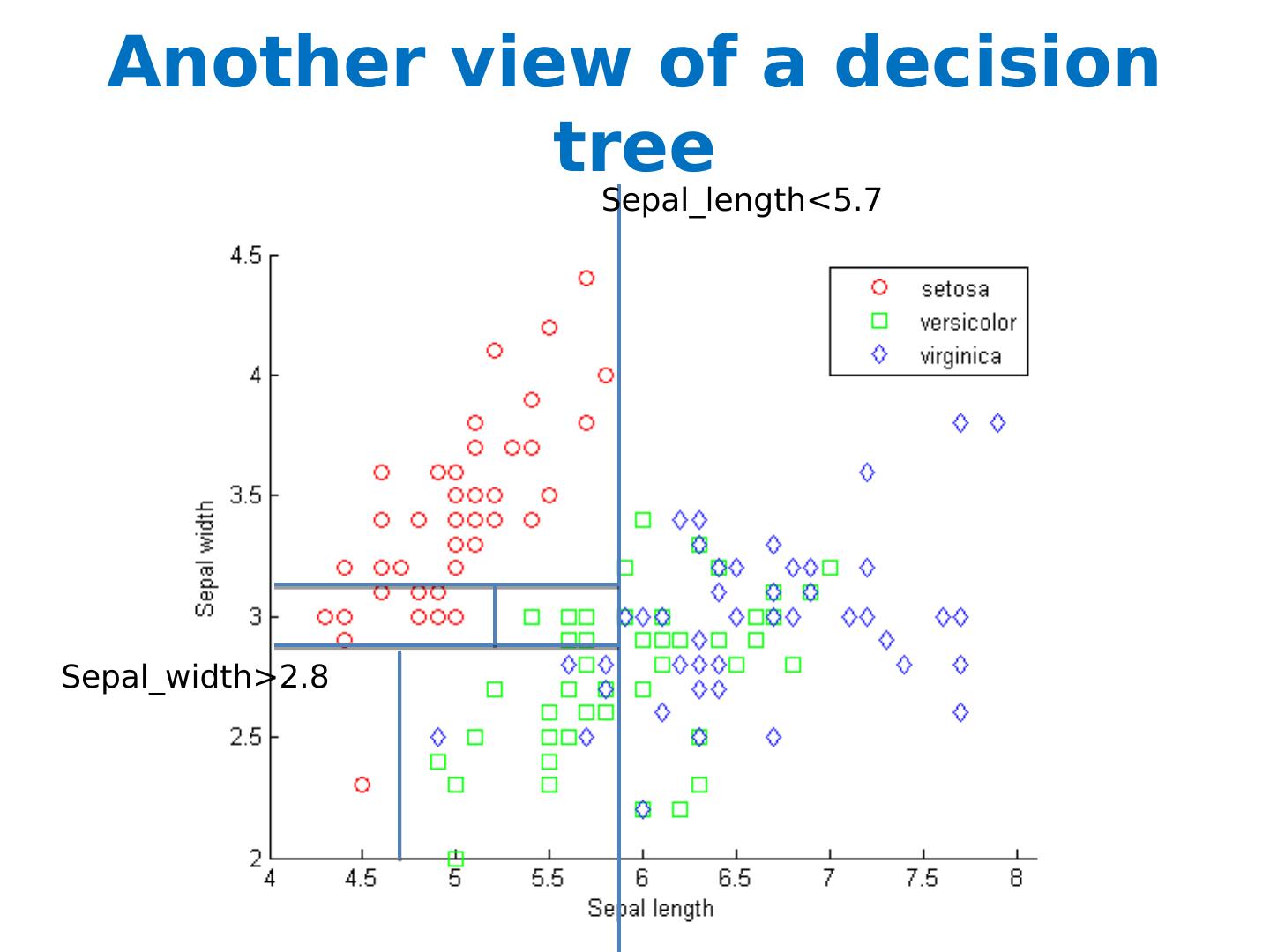
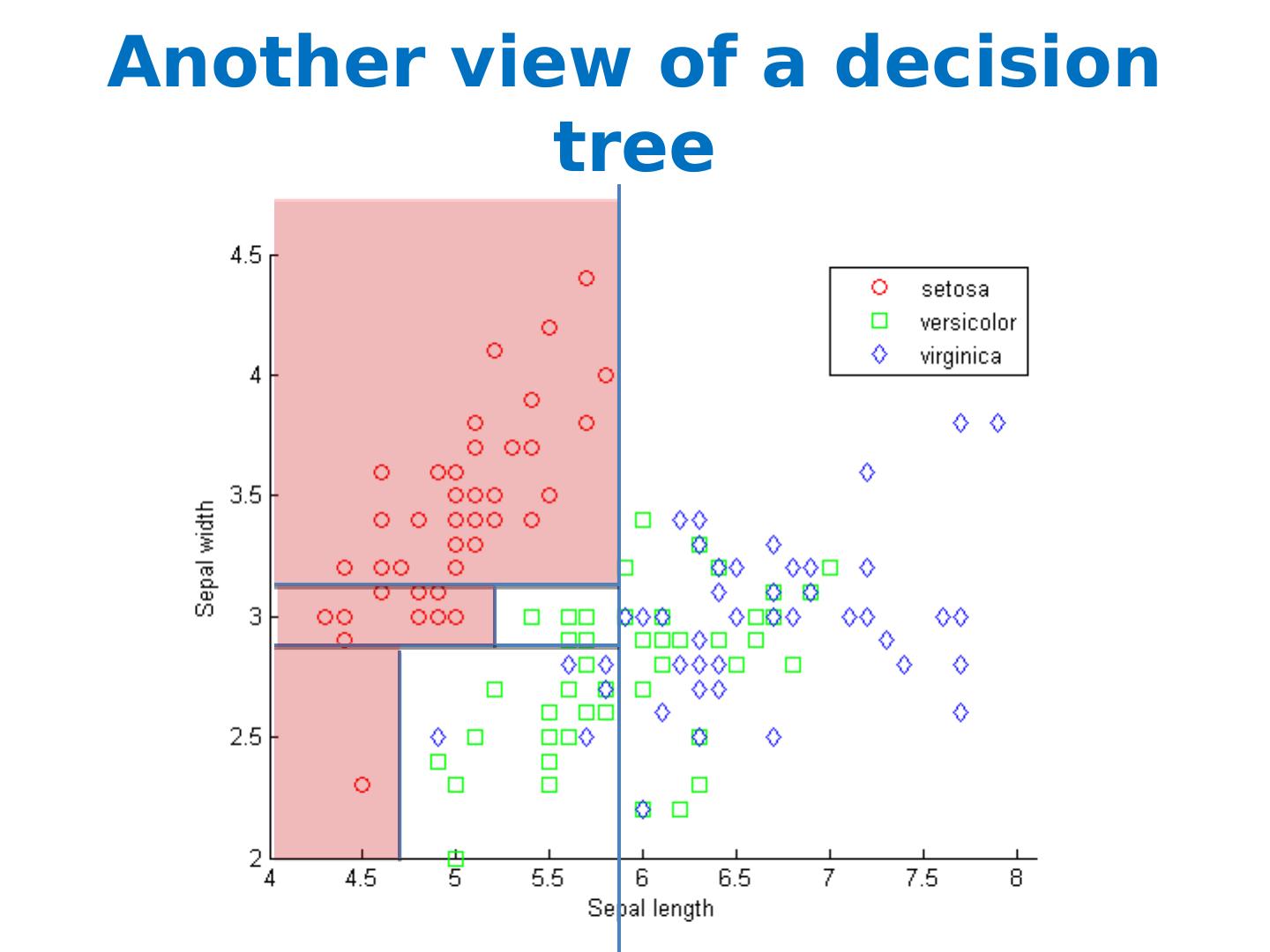
12 .Another view of a decision tree Sepal_length < 5.7 Sepal_width >2.8

13 .Another view of a decision tree Sepal_length < 5.7 Sepal_width >2.8

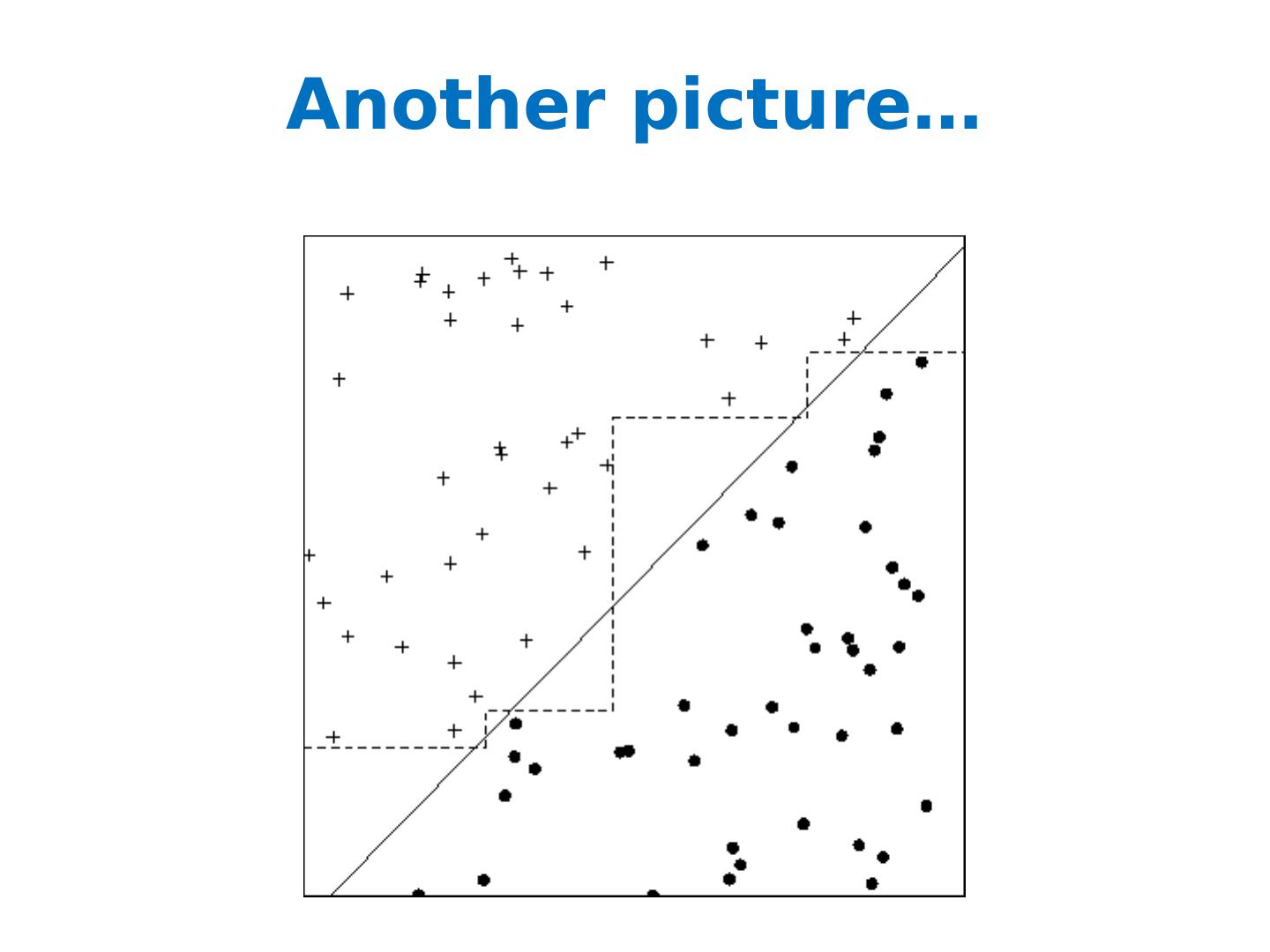
14 .Another picture…

15 .Fixing decision trees…. Hard to prove things about Don’t (typically) improve over linear classifiers when you have lots of features Sometimes fail badly on problems that linear classifiers perform well on Solution is two build ensembles of decision trees

16 .Most decision tree learning algorithms “ Pruning” a tree avoid overfitting by removing subtrees somehow trade variance for bias 15 13 Alternative - build a big ensemble to reduce the variance of the algorithms - via boosting, bagging, or random forests

17 .Example: random forests Repeat T times: Draw a bootstrap sample S ( n examples taken with replacement) from the dataset D. Select a subset of features to use for S Usually half to 1/3 of the full feature set Build a tree considering only the features in the selected subset Don’t prune Vote the classifications of all the trees at the end Ok - how well does this work?

18 .

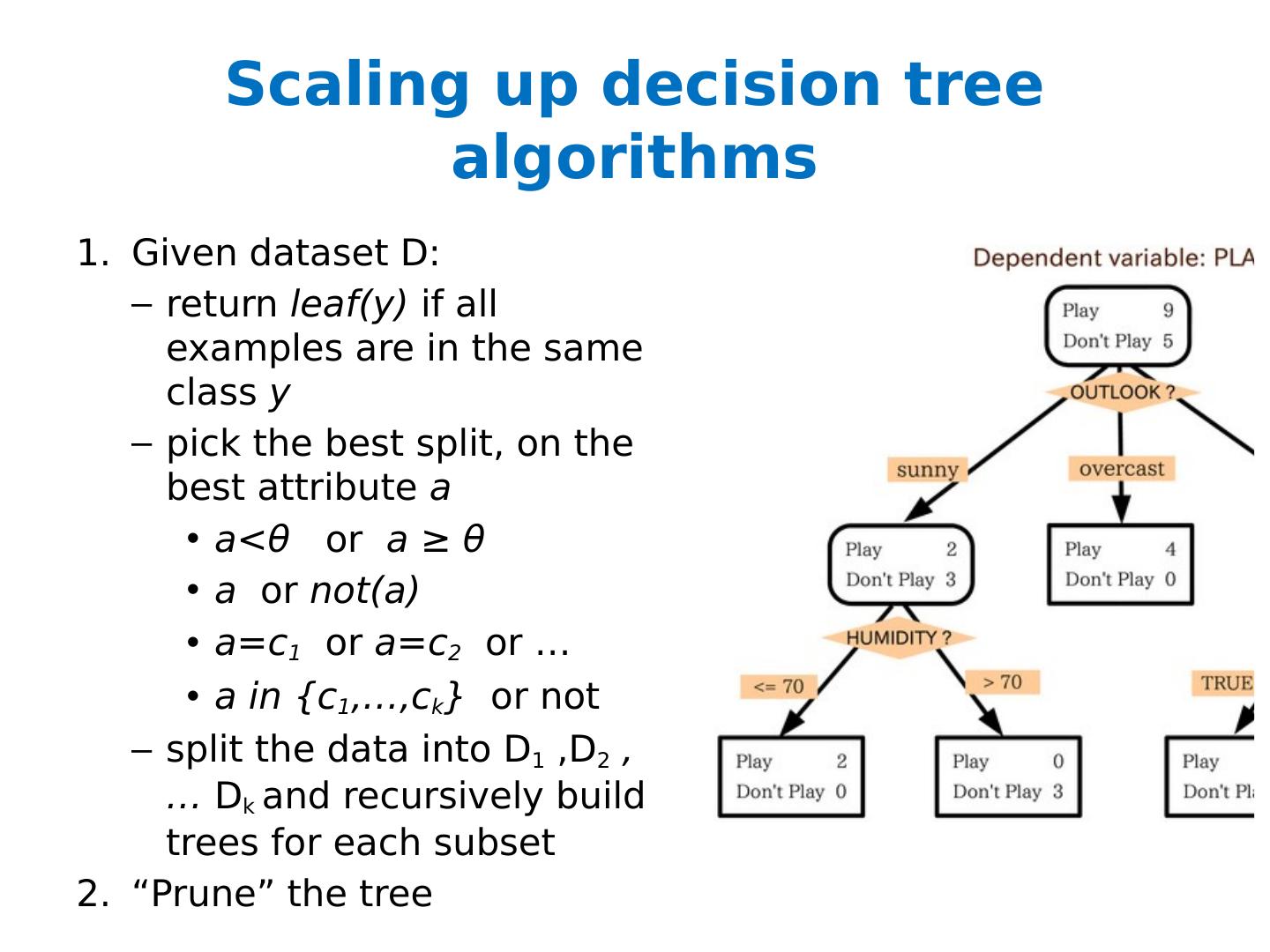
19 .Scaling up decision tree algorithms Given dataset D: return leaf(y) if all examples are in the same class y pick the best split, on the best attribute a a< θ or a ≥ θ a or not(a) a=c 1 or a=c 2 or … a in {c 1 ,…, c k } or not split the data into D 1 ,D 2 , … D k and recursively build trees for each subset “Prune” the tree

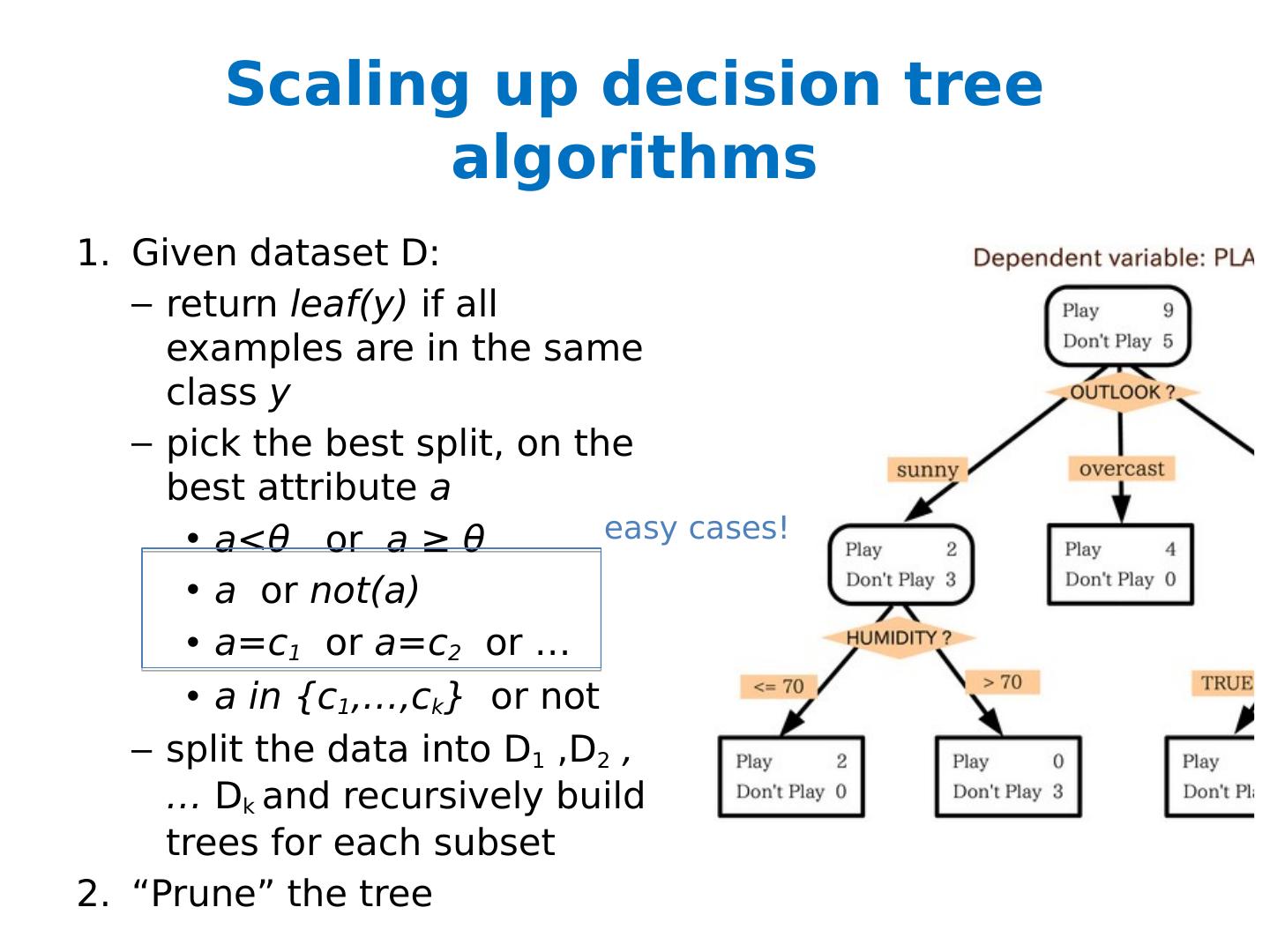
20 .Scaling up decision tree algorithms Given dataset D: return leaf(y) if all examples are in the same class y pick the best split, on the best attribute a a< θ or a ≥ θ a or not(a) a=c 1 or a=c 2 or … a in {c 1 ,…, c k } or not split the data into D 1 ,D 2 , … D k and recursively build trees for each subset “Prune” the tree easy cases!

21 .Scaling up decision tree algorithms Given dataset D: return leaf(y) if all examples are in the same class y pick the best split, on the best attribute a a< θ or a ≥ θ a or not(a) a=c 1 or a=c 2 or … a in {c 1 ,…, c k } or not split the data into D 1 ,D 2 , … D k and recursively build trees for each subset “Prune” the tree Numeric attribute: sort examples by a retain label y scan thru once and update the histogram of y| a < θ and y|a > θ at each point θ pick the threshold θ with the best entropy score O( nlogn ) due to the sort but repeated for each attribute

22 .Scaling up decision tree algorithms Given dataset D: return leaf(y) if all examples are in the same class y pick the best split, on the best attribute a a< θ or a ≥ θ a or not(a) a=c 1 or a=c 2 or … a in {c 1 ,…, c k } or not split the data into D 1 ,D 2 , … D k and recursively build trees for each subset “Prune” the tree Numeric attribute: or, fix a set of possible split-points θ in advance scan through once and compute the histogram of y’s O(n) per attribute

23 .Scaling up decision tree algorithms Given dataset D: return leaf(y) if all examples are in the same class y pick the best split, on the best attribute a a< θ or a ≥ θ a or not(a) a=c 1 or a=c 2 or … a in {c 1 ,…, c k } or not split the data into D 1 ,D 2 , … D k and recursively build trees for each subset “Prune” the tree Subset splits: expensive but useful there is a similar sorting trick that works for the regression case

24 .Scaling up decision tree algorithms Given dataset D: return leaf(y) if all examples are in the same class y pick the best split, on the best attribute a a< θ or a ≥ θ a or not(a) a=c 1 or a=c 2 or … a in {c 1 ,…, c k } or not split the data into D 1 ,D 2 , … D k and recursively build trees for each subset “Prune” the tree Points to ponder: different subtrees are distinct tasks once the data is in memory, this algorithm is fast. each example appears only once in each level of the tree depth of the tree is usually O(log n) as you move down the tree, the datasets get smaller

25 .Scaling up decision tree algorithms Given dataset D: return leaf(y) if all examples are in the same class y pick the best split, on the best attribute a a< θ or a ≥ θ a or not(a) a=c 1 or a=c 2 or … a in {c 1 ,…, c k } or not split the data into D 1 ,D 2 , … D k and recursively build trees for each subset “Prune” the tree Bottleneck points: what’s expensive is picking the attributes especially at the top levels also, moving the data around in a distributed setting

26 .Scaling up decision tree algorithms Given dataset D: return leaf(y) if all examples are in the same class y pick the best split, on the best attribute a a< θ or a ≥ θ a or not(a) a=c 1 or a=c 2 or … a in {c 1 ,…, c k } or not split the data into D 1 ,D 2 , … D k and recursively build trees for each subset “Prune” the tree Bottleneck points: what’s expensive is picking the attributes especially at the top levels also, moving the data around in a distributed setting

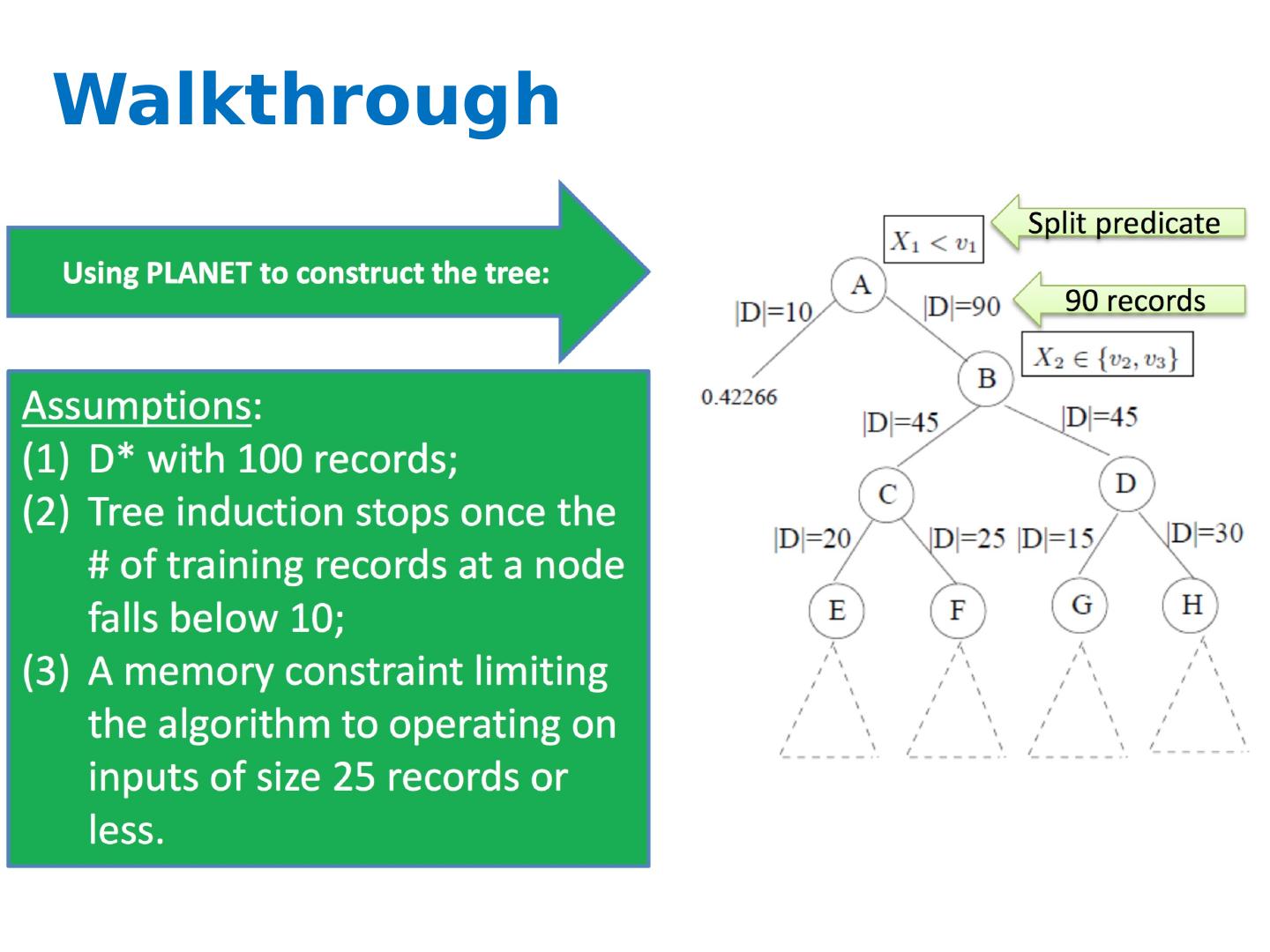
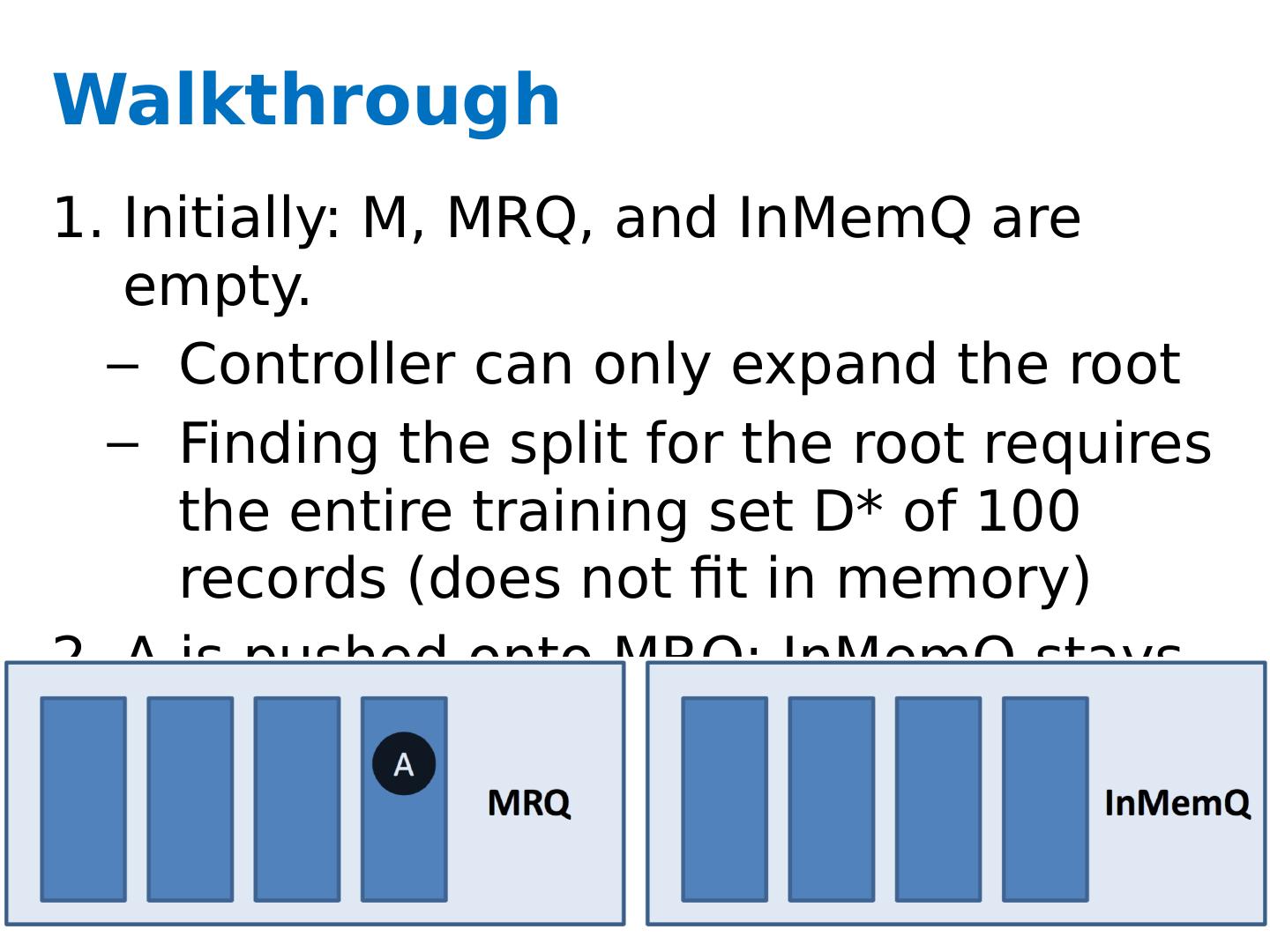
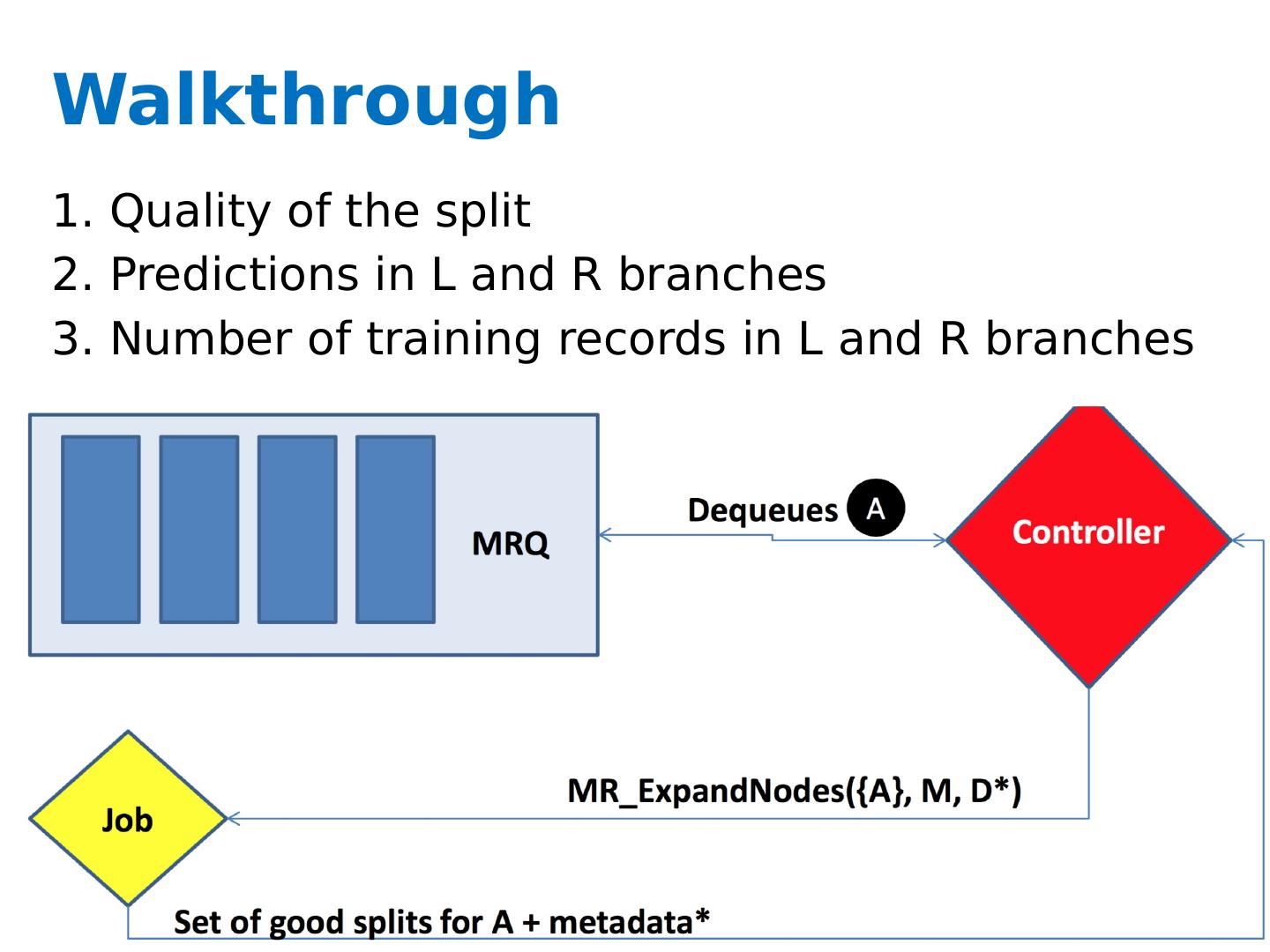
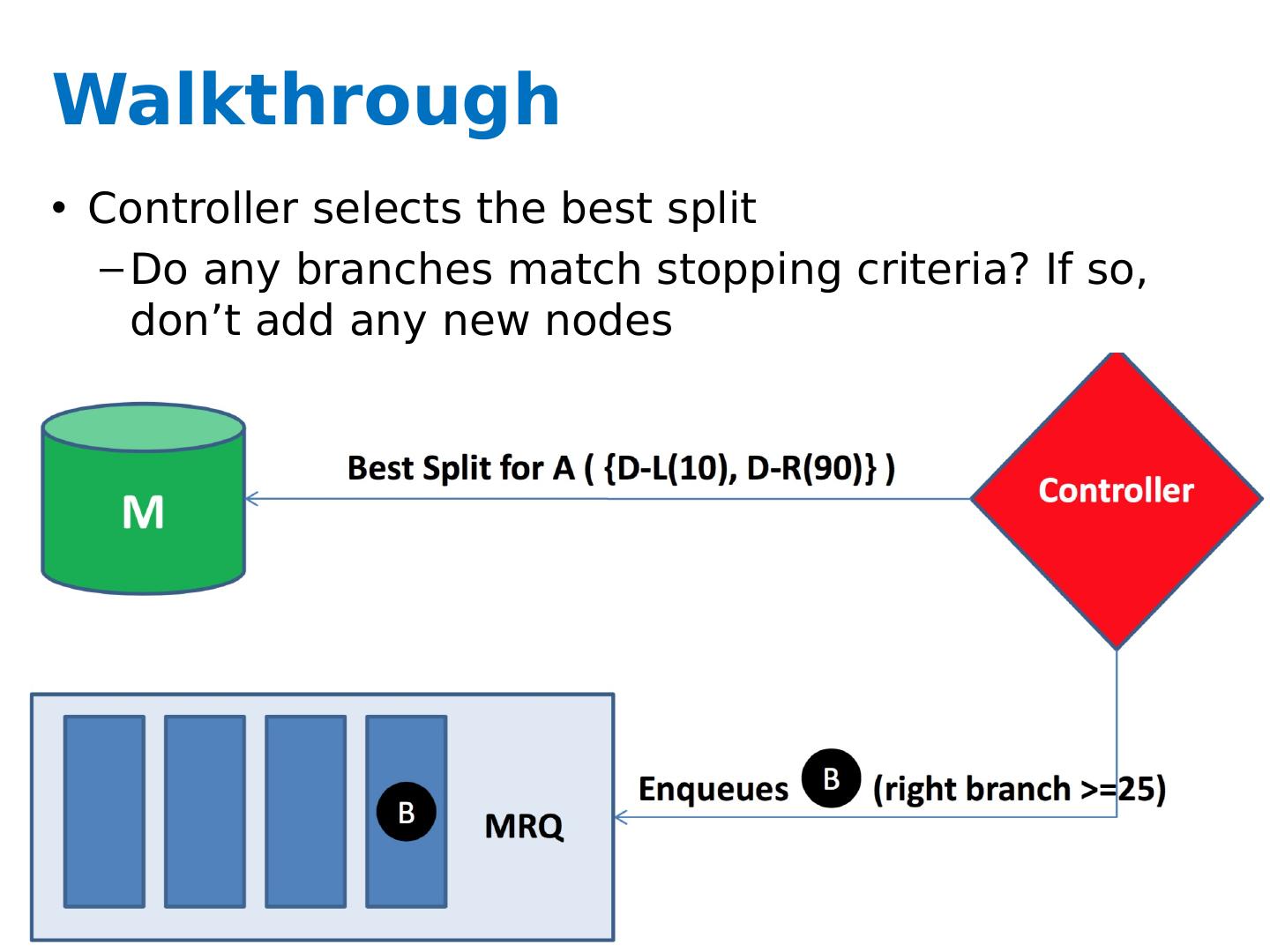
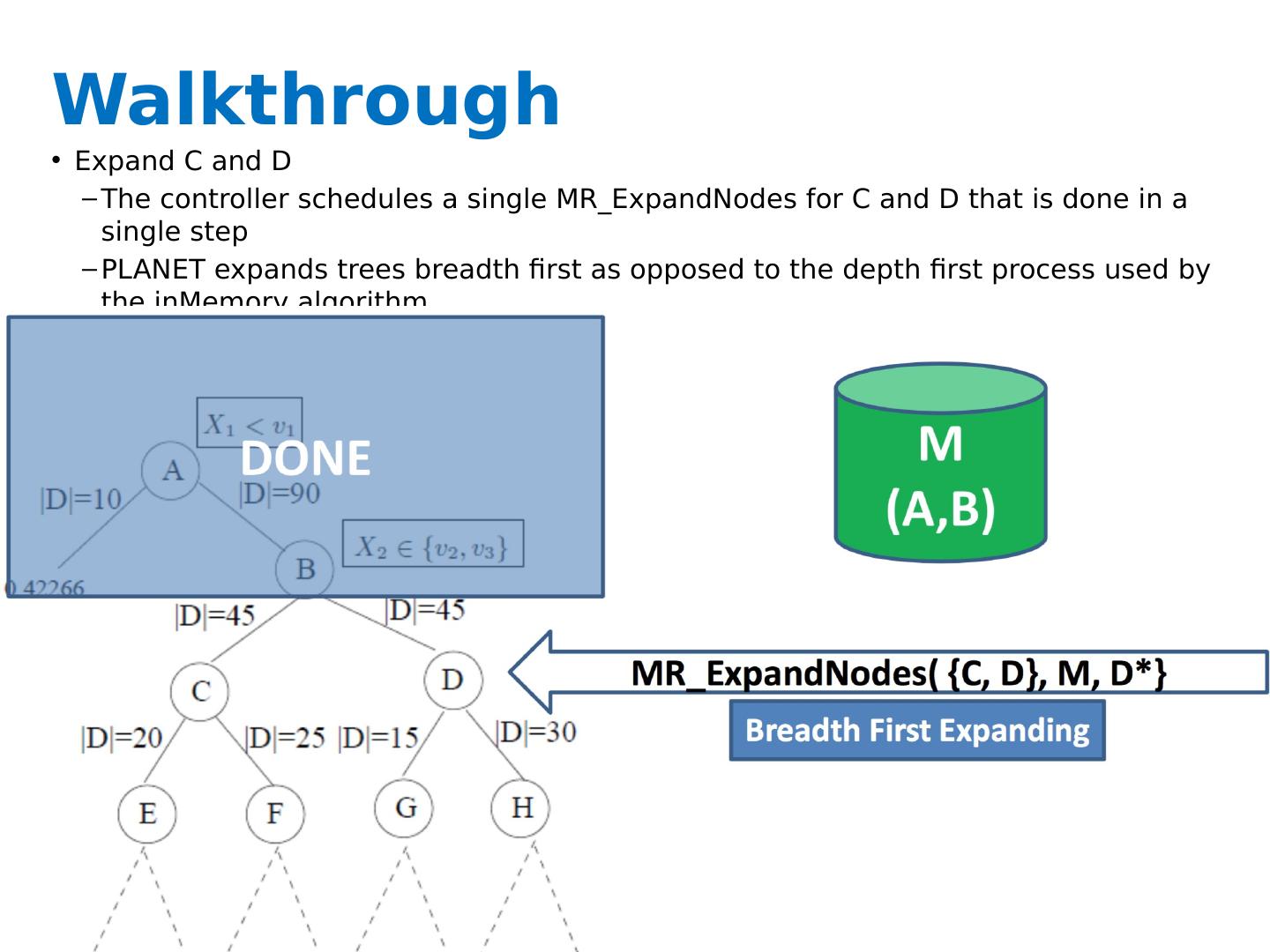
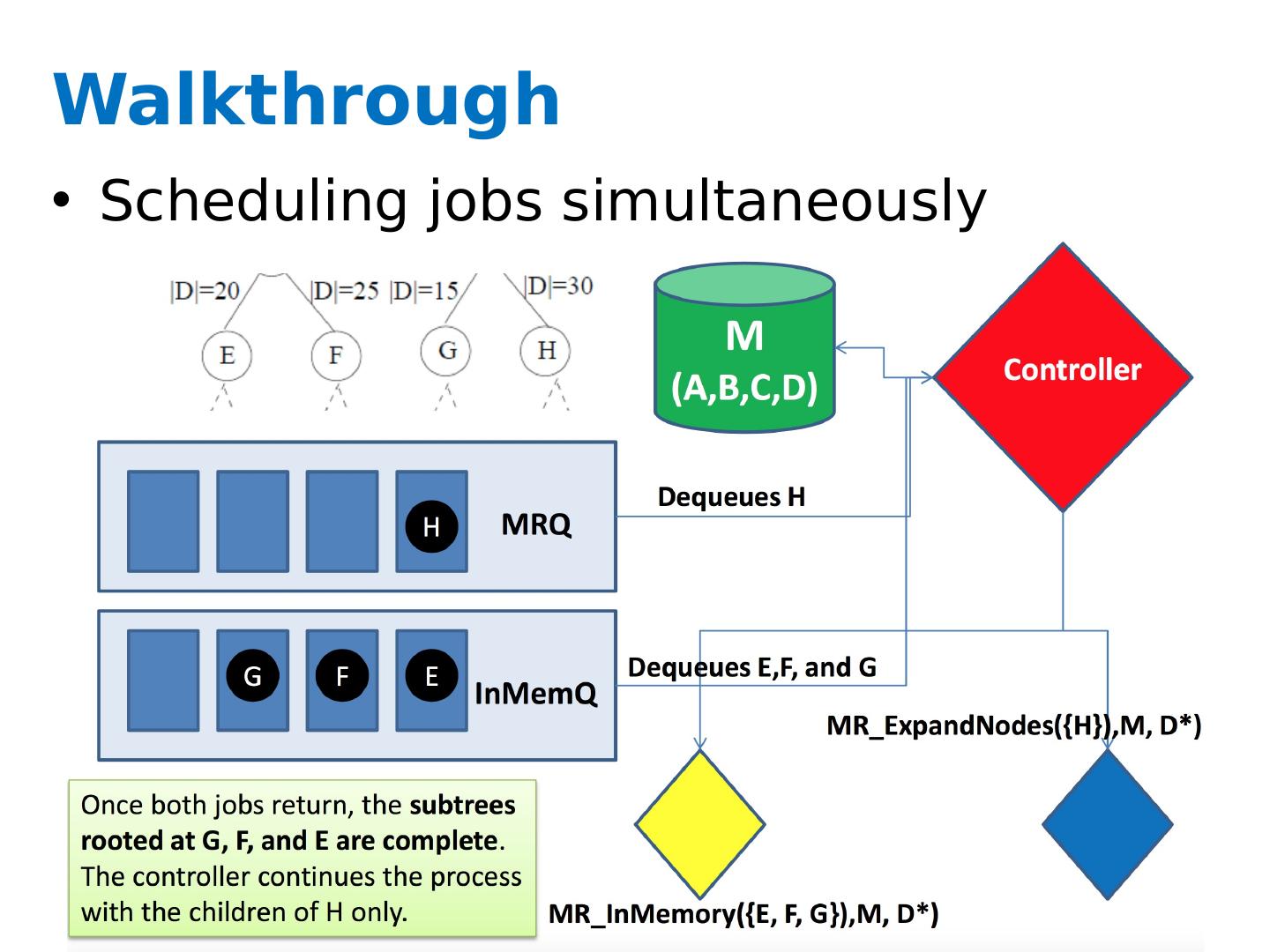
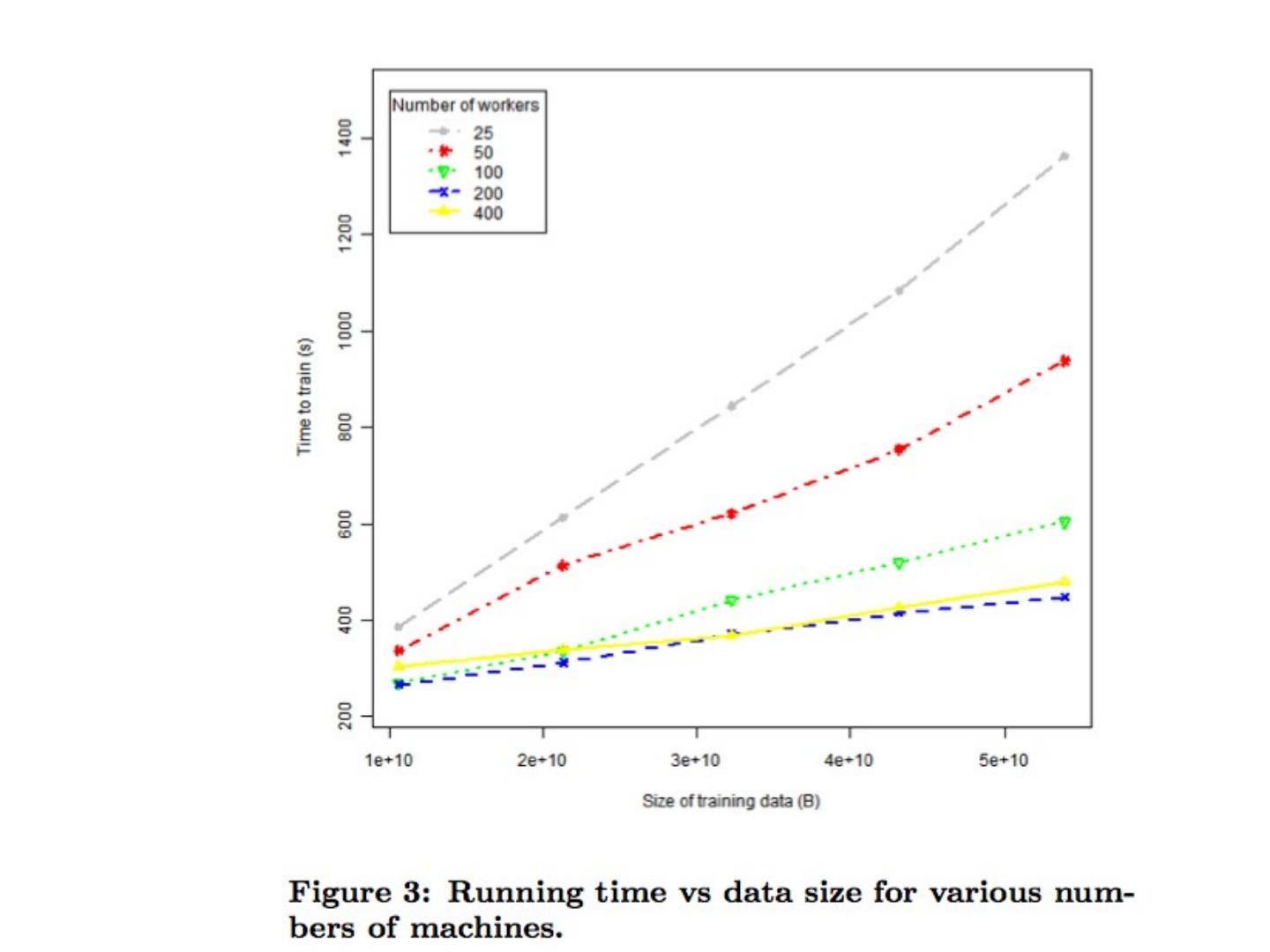
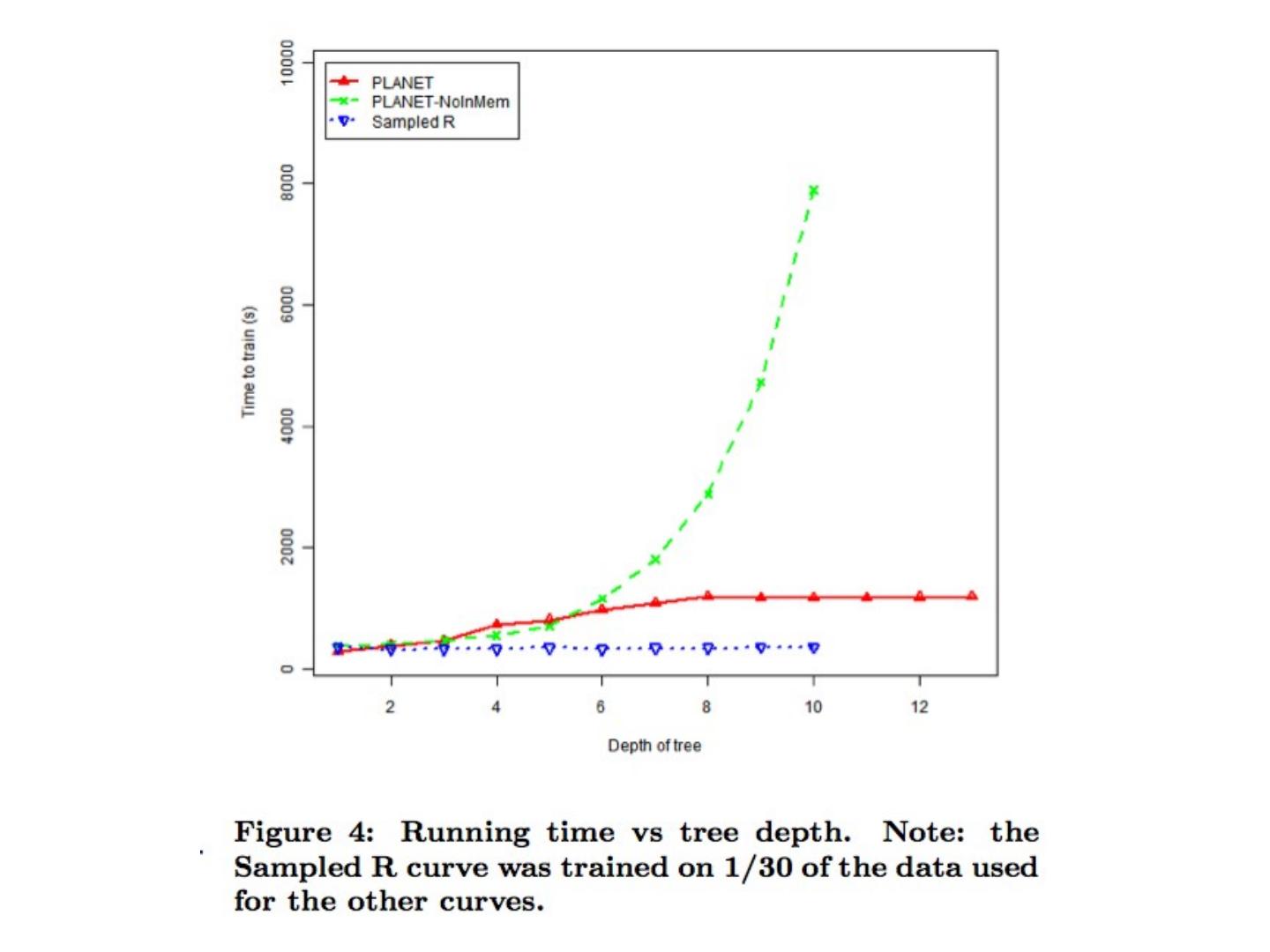
27 .Key ideas A controller to generate Map-Reduce jobs distribute the task of building subtrees of the main decision trees handle “small” and “large” tasks differently small: build tree in-memory large: build the tree (mostly) depth-first send the whole dataset to all mappers and let them classify instances to nodes on-the-fly

28 .Greedy top-down tree assembly

29 .FindBestSplit Continuous attributes Treating a point as a boundary (e.g., <5.0 or >=5.0) Categorical attributes Membership in a set of values (e.g., is the attribute value one of {Ford, Toyota, Volvo}?)