Randomized / Hashing Algorithms

1 .Randomized / Hashing Algorithms Shannon Quinn (with thanks to William Cohen of Carnegie Mellon University, and J. Leskovec , A. Rajaraman , and J. Ullman of Stanford University)

2 .Outline Bloom filters Locality-sensitive hashing Stochastic gradient descent Stochastic SVD Already covered Next Wednesday’s lecture

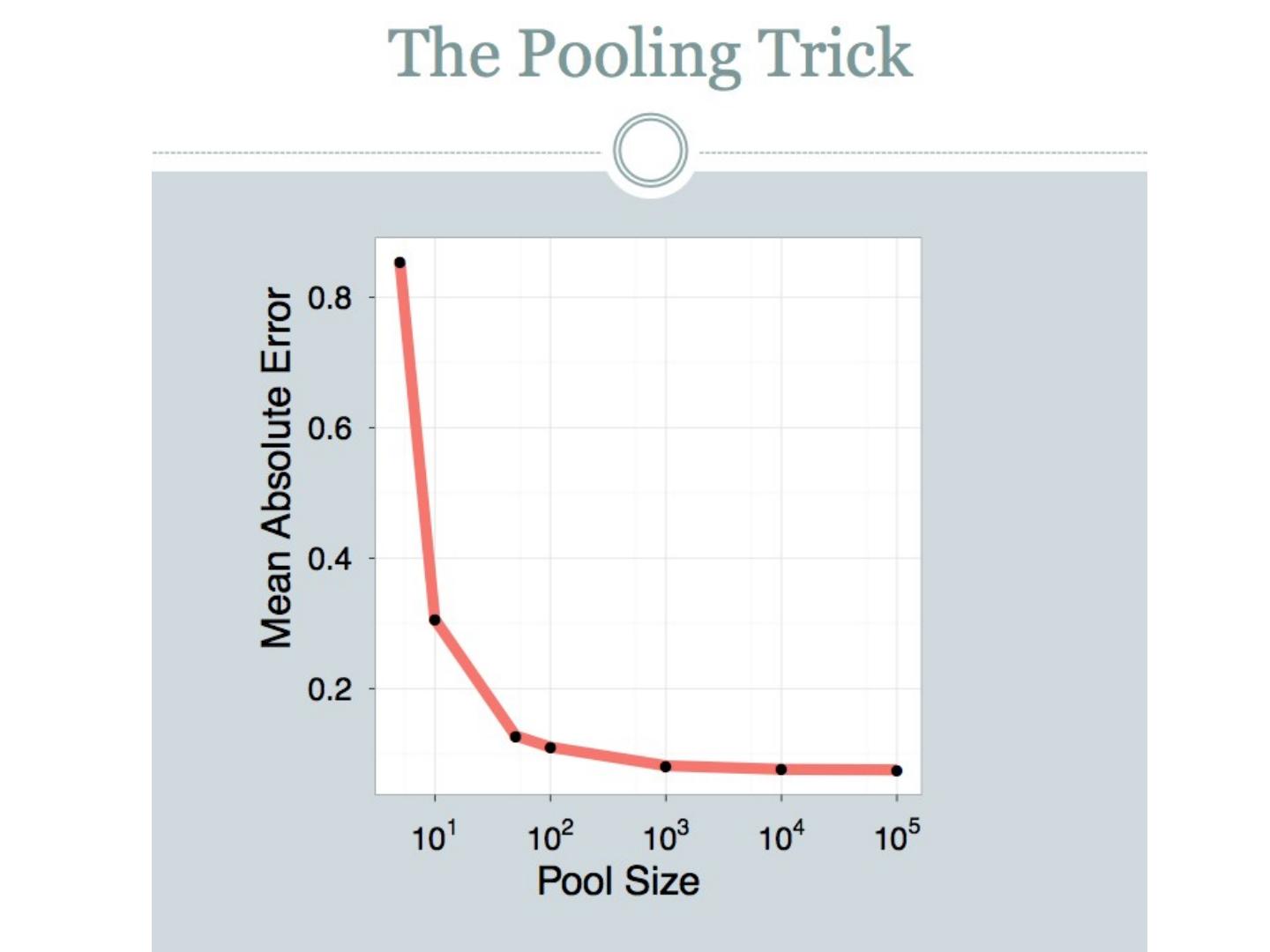
3 .Hash Trick - Insights Save memory: don’t store hash keys Allow collisions even though it distorts your data some Let the learner (downstream) take up the slack Here’s another famous trick that exploits these insights….

4 .Bloom filters Interface to a Bloom filter BloomFilter(int maxSize , double p ); void b f.add(String s ); // insert s b ool bd.contains(String s ); // If s was added return true; // else with probability at least 1-p return false; // else with probability at most p return true; I.e., a noisy “set” where you can test membership (and that’s it)

5 .One possible implementation BloomFilter(int maxSize , double p ) { set up an empty length- m array bits[]; } void bf.add(String s ) { bits[hash(s ) % m ] = 1; } bool bd.contains(String s ) { return bits[hash(s ) % m ]; }

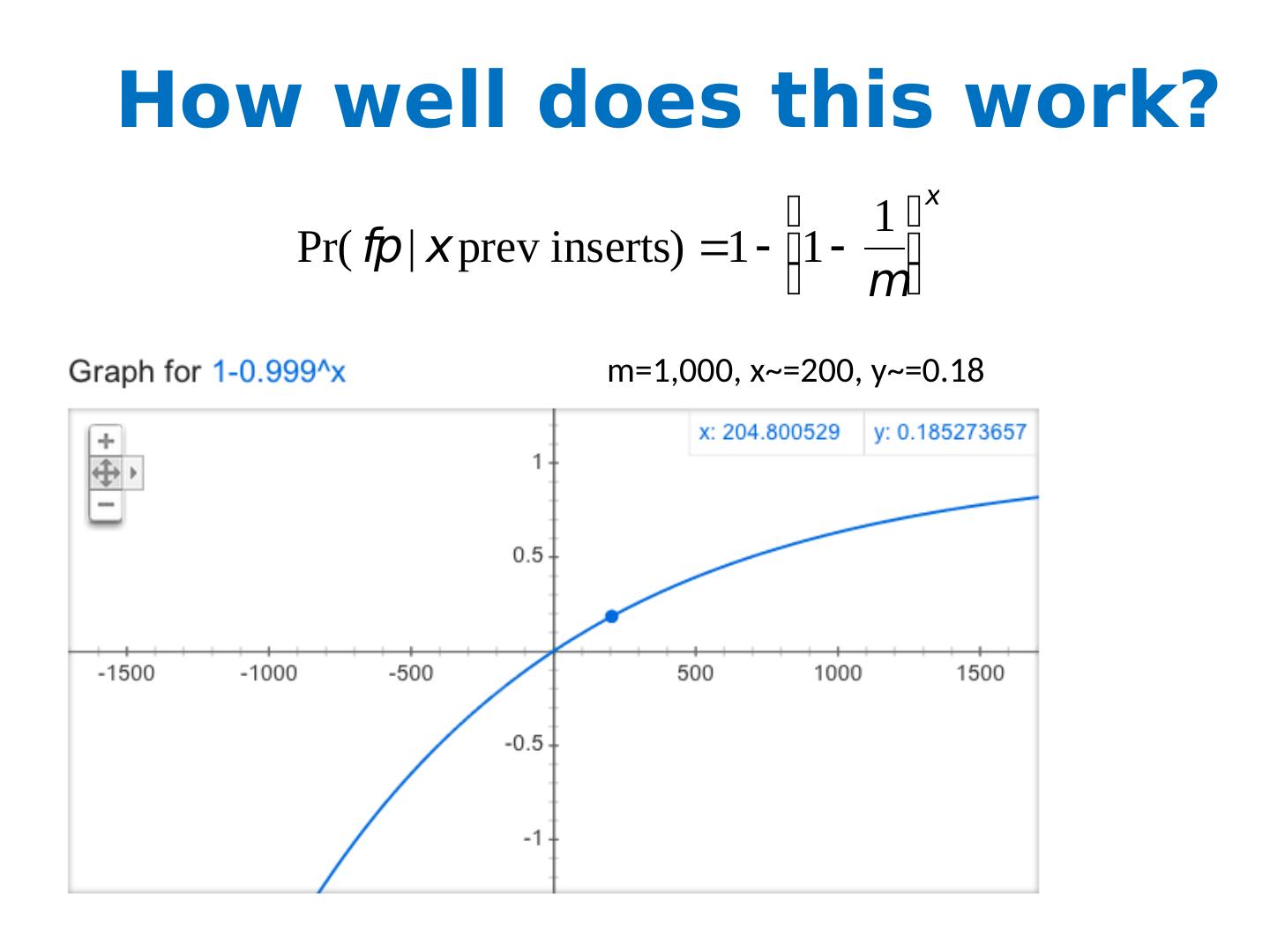
6 .How well does this work? m =1,000, x ~=200, y ~=0.18

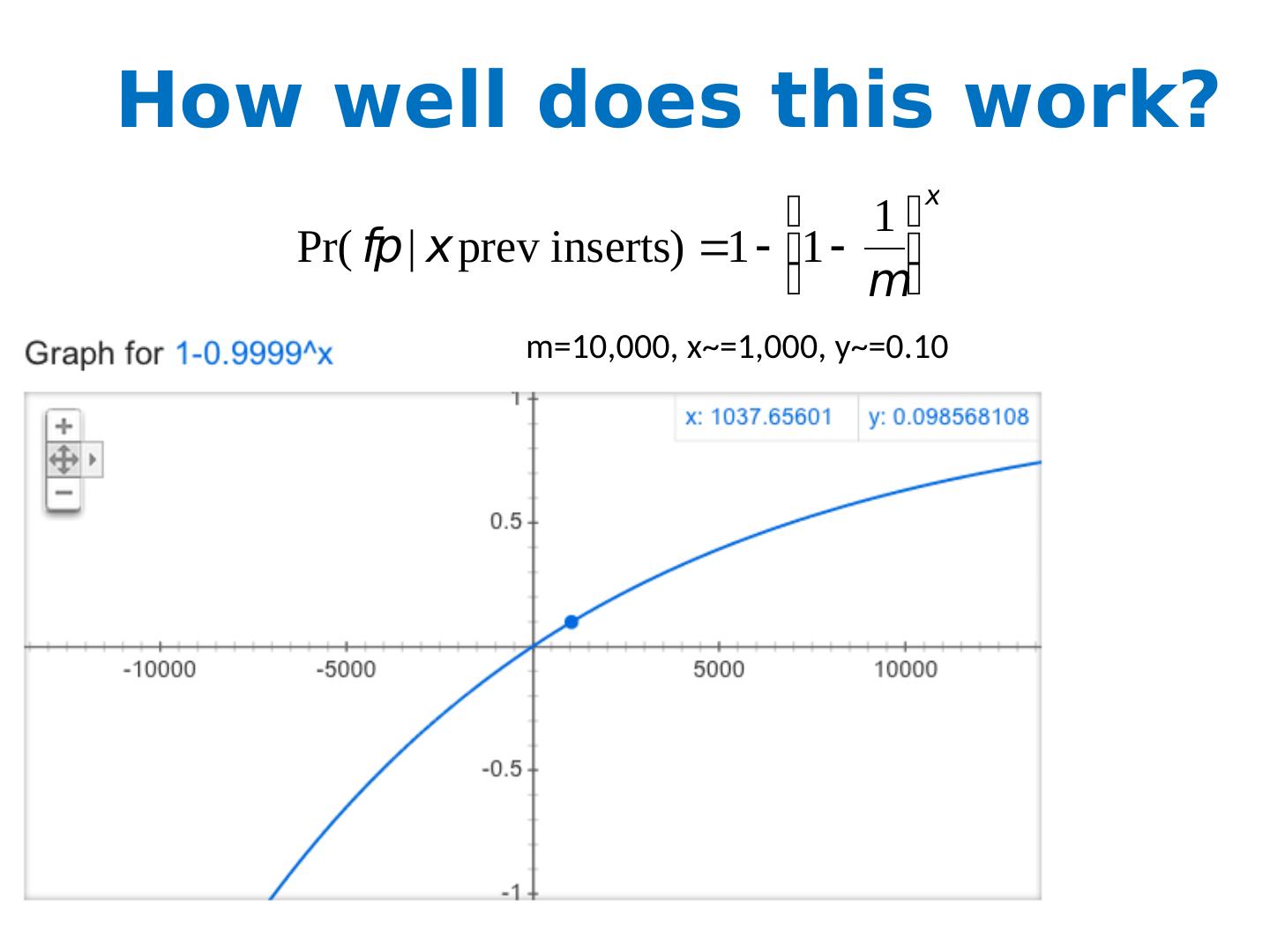
7 .How well does this work? m =10,000, x ~=1,000, y ~=0.10

8 .A better??? implementation BloomFilter(int maxSize , double p ) { set up an empty length- m array bits[]; } void bf.add(String s ) { bits[hash1(s) % m ] = 1; bits[hash2(s) % m ] = 1; } bool bd.contains(String s ) { return bits[hash1(s) % m ] && bits[hash2(s) % m ]; }

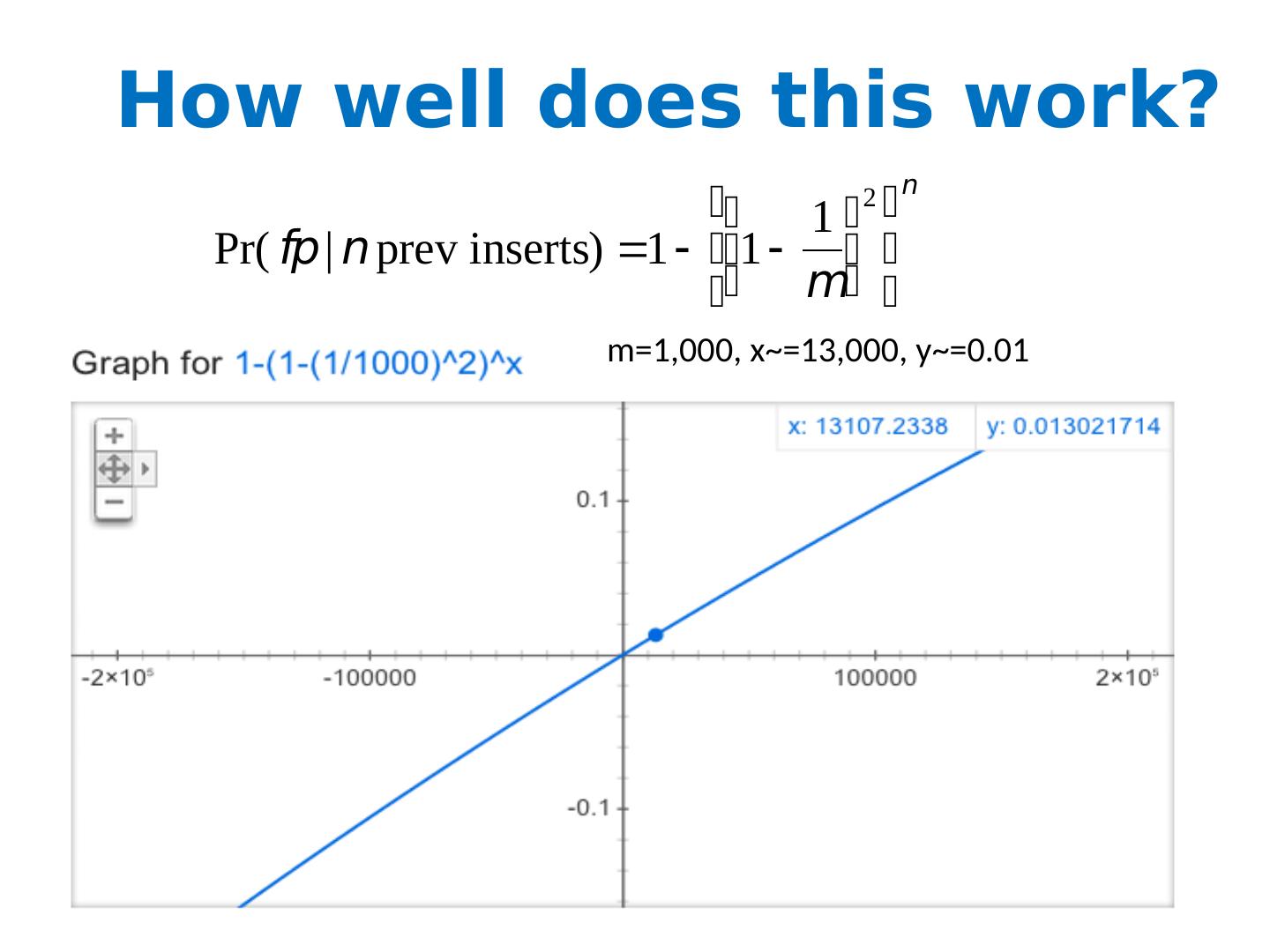
9 .How well does this work? m =1,000, x ~=200, y ~=0.18 m =1,000, x ~=13,000, y ~=0.01

10 .Bloom filters An example application Finding items in “ sharded ” data Easy if you know the sharding rule Harder if you don’t (like Google n-grams) Simple idea: Build a BF of the contents of each shard To look for key, load in the BF’s one by one, and search only the shards that probably contain key Analysis: you won’t miss anything, you might look in some extra shards You’ll hit O(1) extra shards if you set p=1/#shards

11 .Bloom filters An example application discarding rare features from a classifier seldom hurts much, can speed up experiments Scan through data once and check each w : if bf1.contains( w ): if bf2.contains(w): bf3.add( w ) else bf2.add(w) else bf1.add( w ) Now: bf2.contains(w)  w appears >= 2x bf3.contains(w)  w appears >= 3x Then train, ignoring words not in bf3

12 .Bloom filters Analysis (m bits, k hashers): Assume hash(i,s ) is a random function Look at Pr (bit j is unset after n add’s ): … and Pr (collision): …. fix m and n and minimize k: k = p =

13 .Bloom filters Analysis: Plug optimal k=m/n* ln (2) back into Pr (collision): Now we can fix any two of p, n, m and solve for the 3 rd : E.g., the value for m in terms of n and p: p =

14 .Bloom filters: demo http:// www.jasondavies.com / bloomfilter /

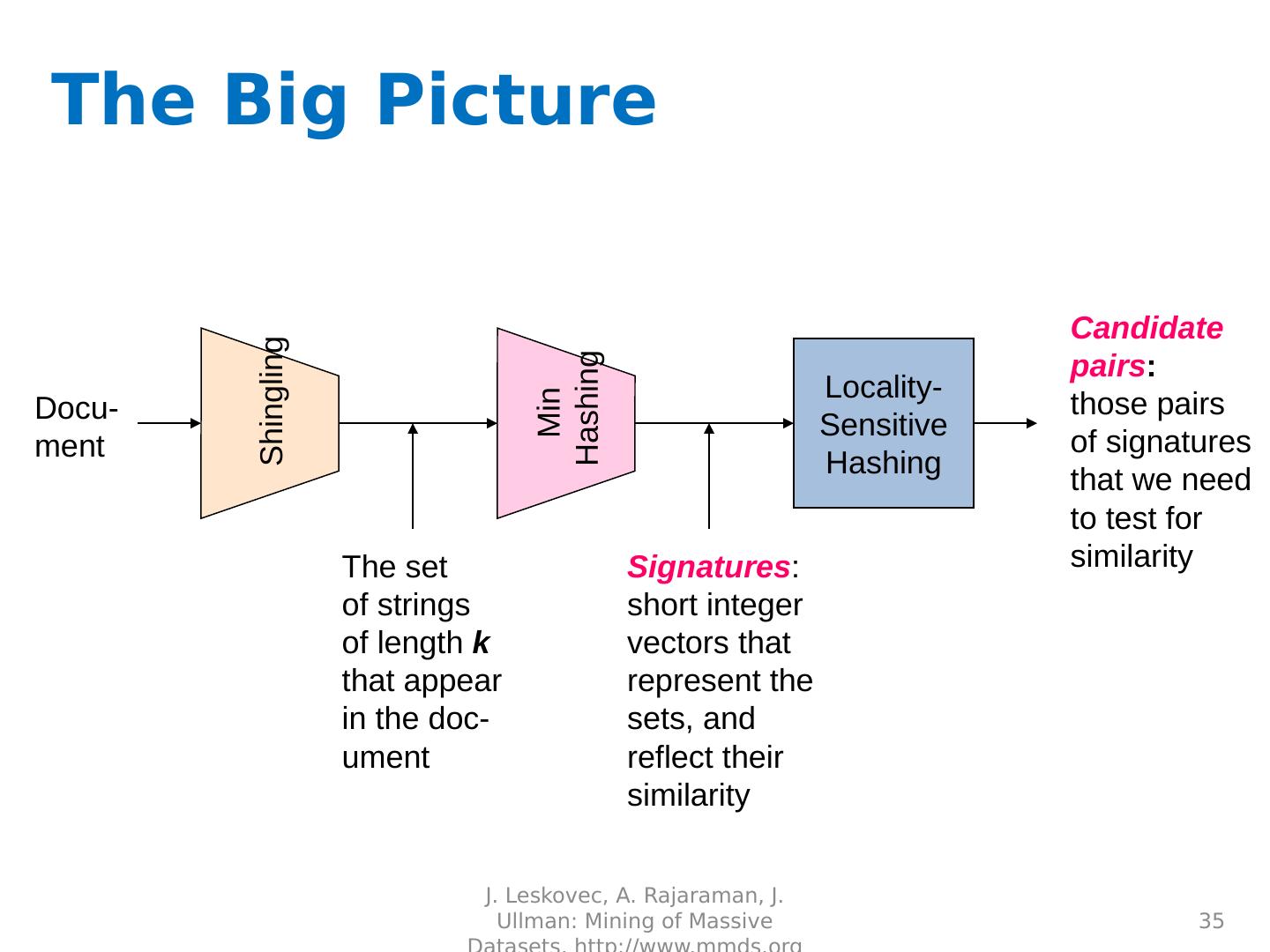
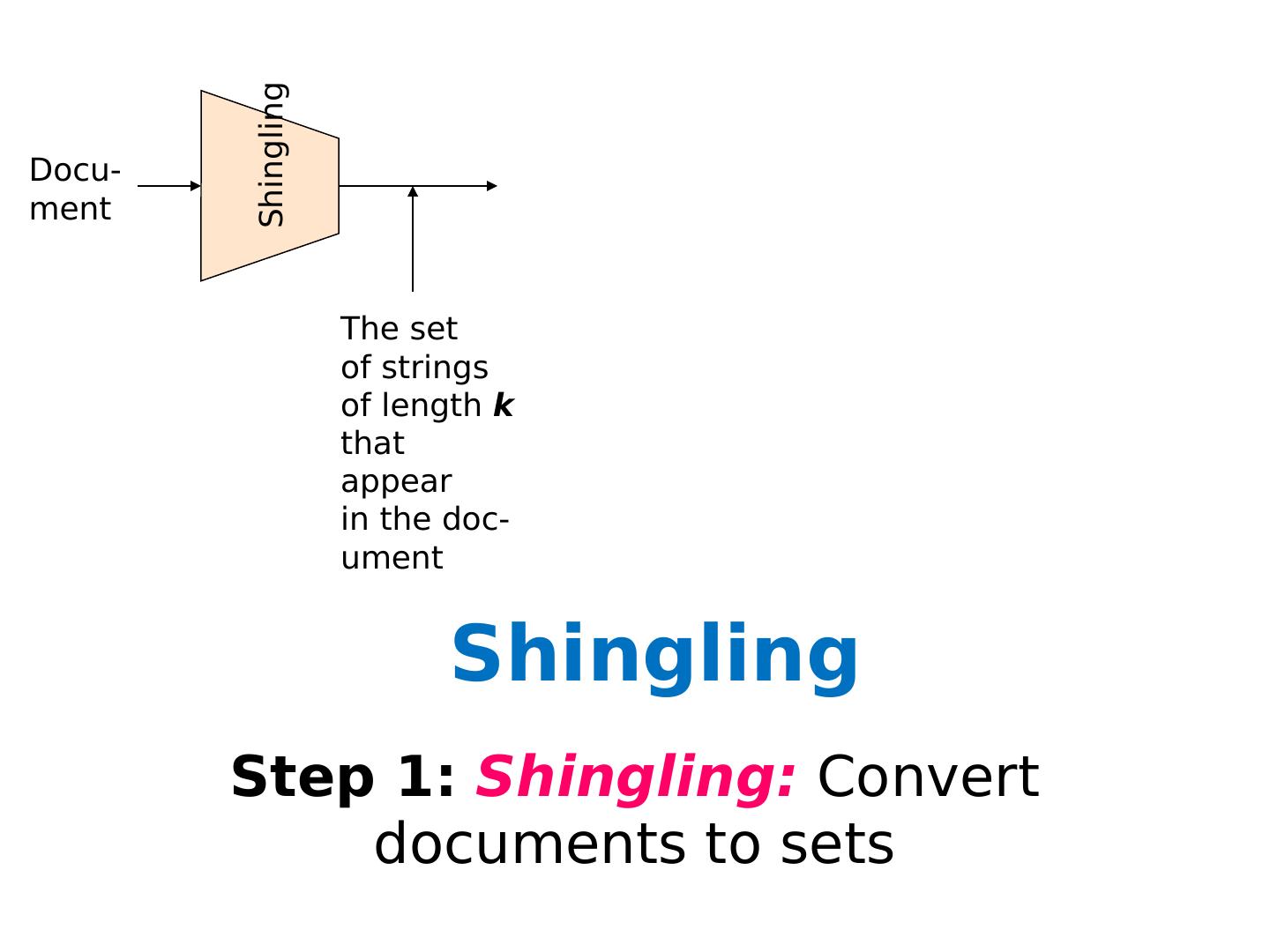
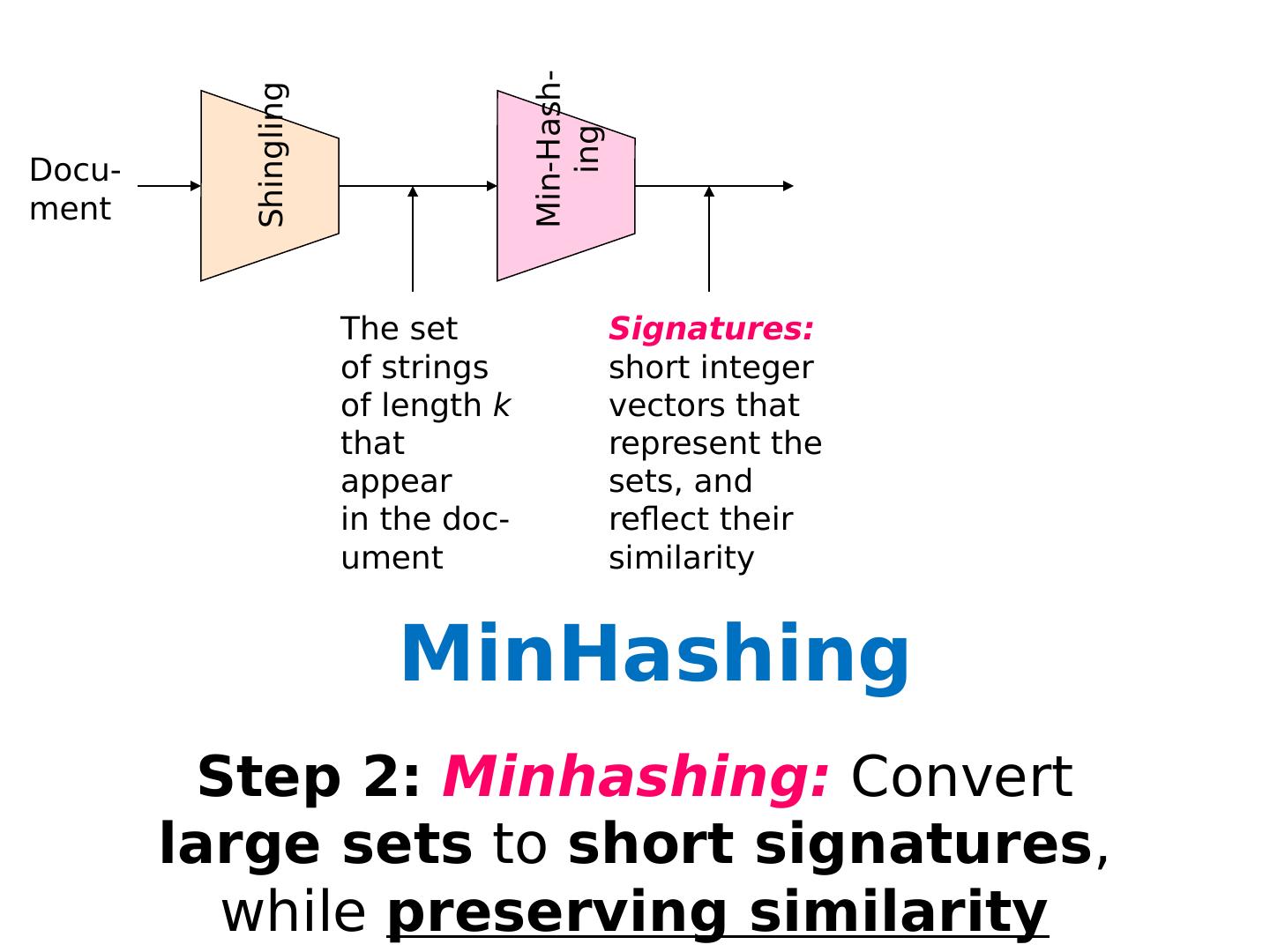
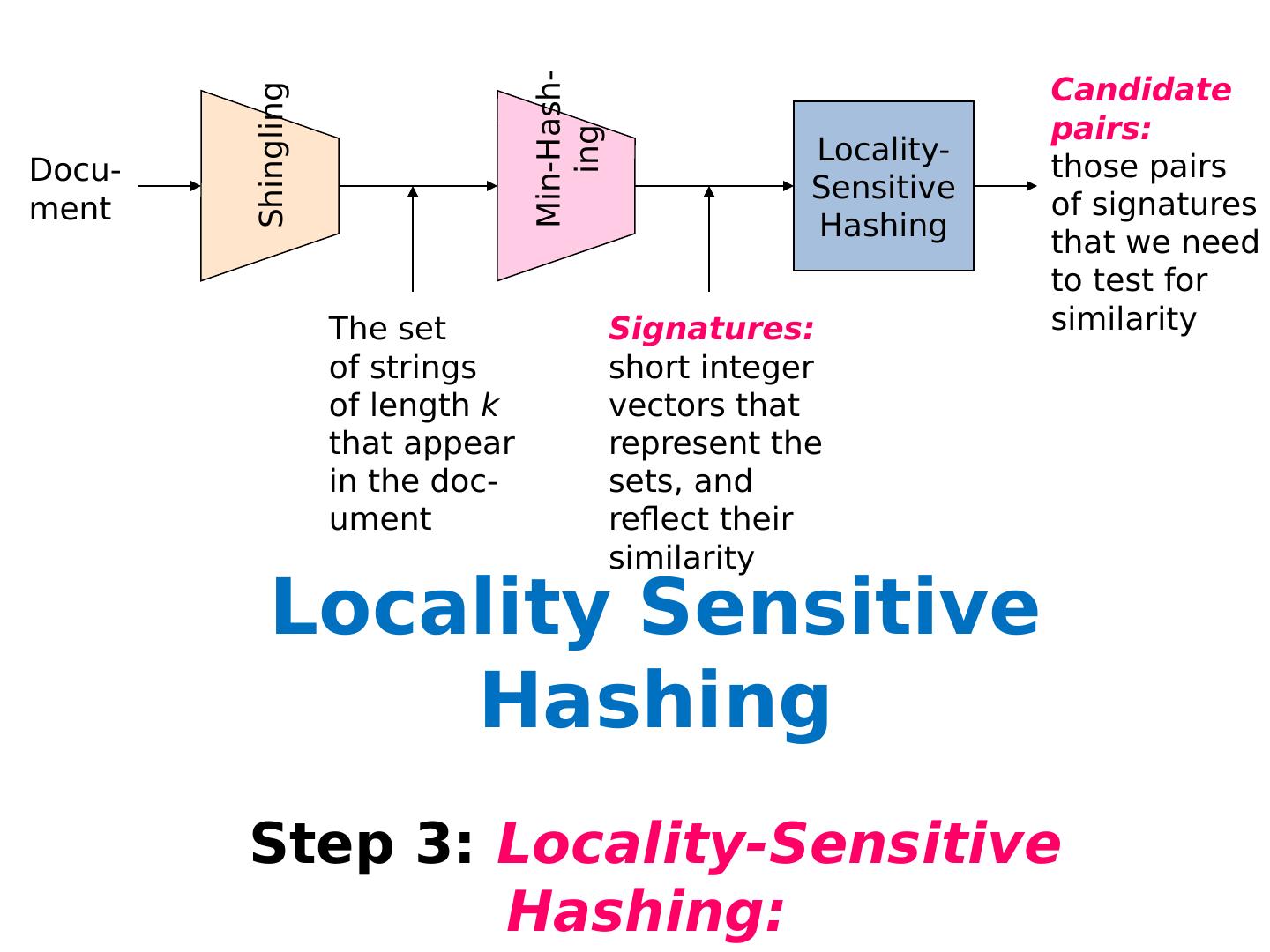
15 .Locality Sensitive Hashing (LSH) Two main approaches Random Projection Minhashing

16 .LSH: key ideas Goal: map feature vector x to bit vector bx e nsure that bx preserves “similarity”

17 .Random Projections

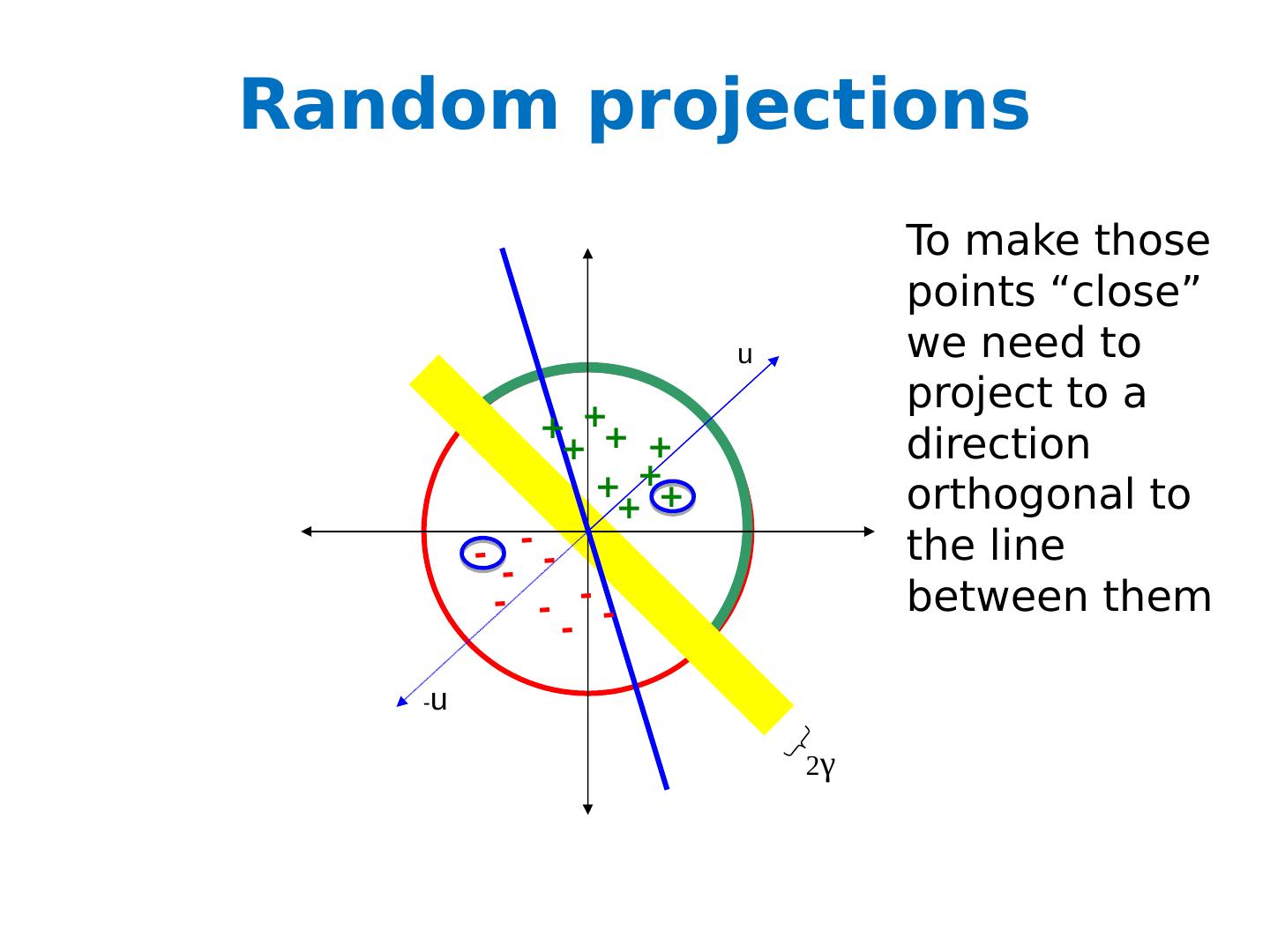
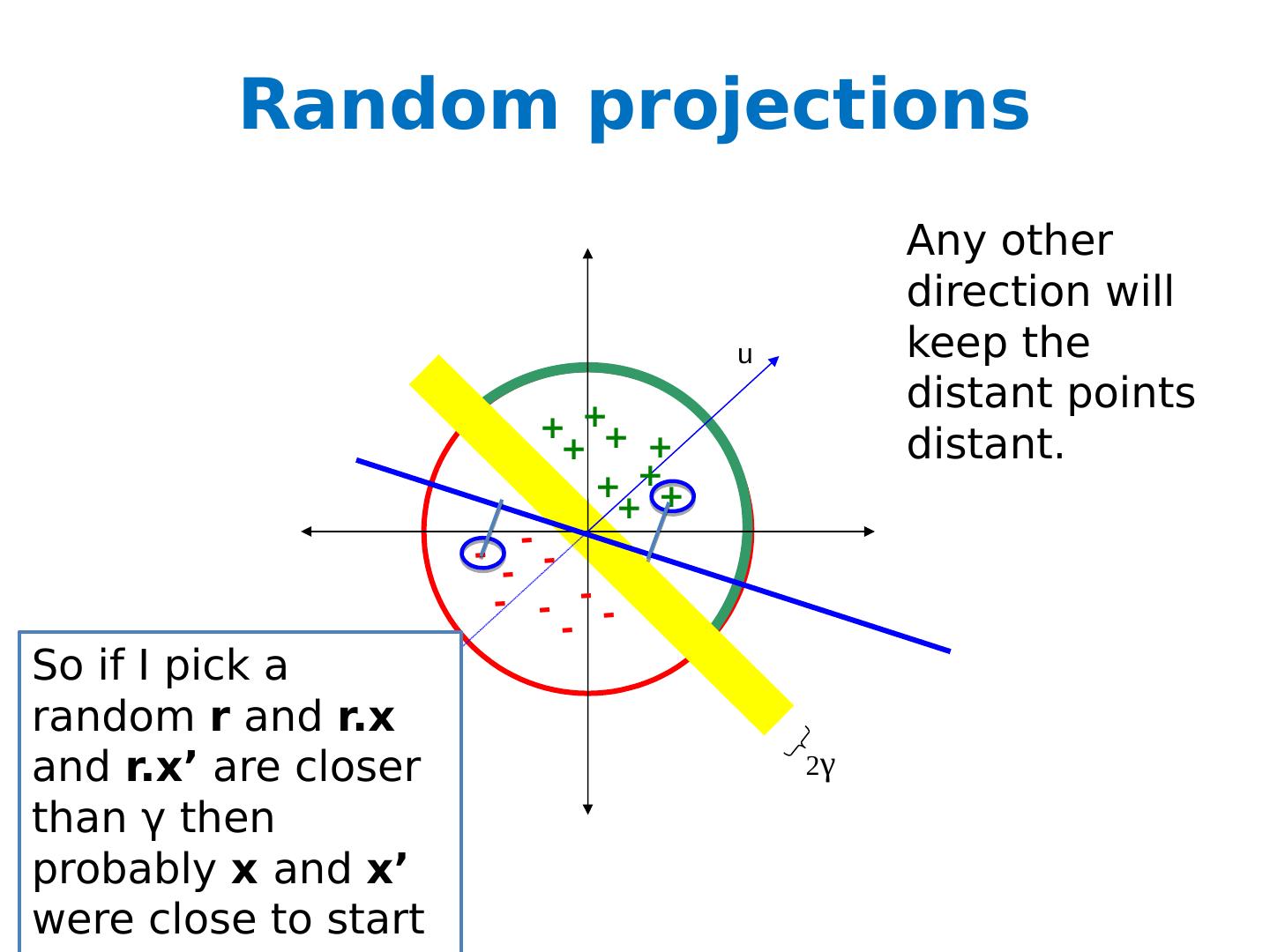
18 .Random projections u - u 2 γ + + + + + + + + + - - - - - - - - - To make those points “close” we need to project to a direction orthogonal to the line between them

19 .Random projections u - u 2 γ + + + + + + + + + - - - - - - - - - Any other direction will keep the distant points distant. So if I pick a random r and r.x and r.x ’ are closer than γ then probably x and x’ were close to start with.

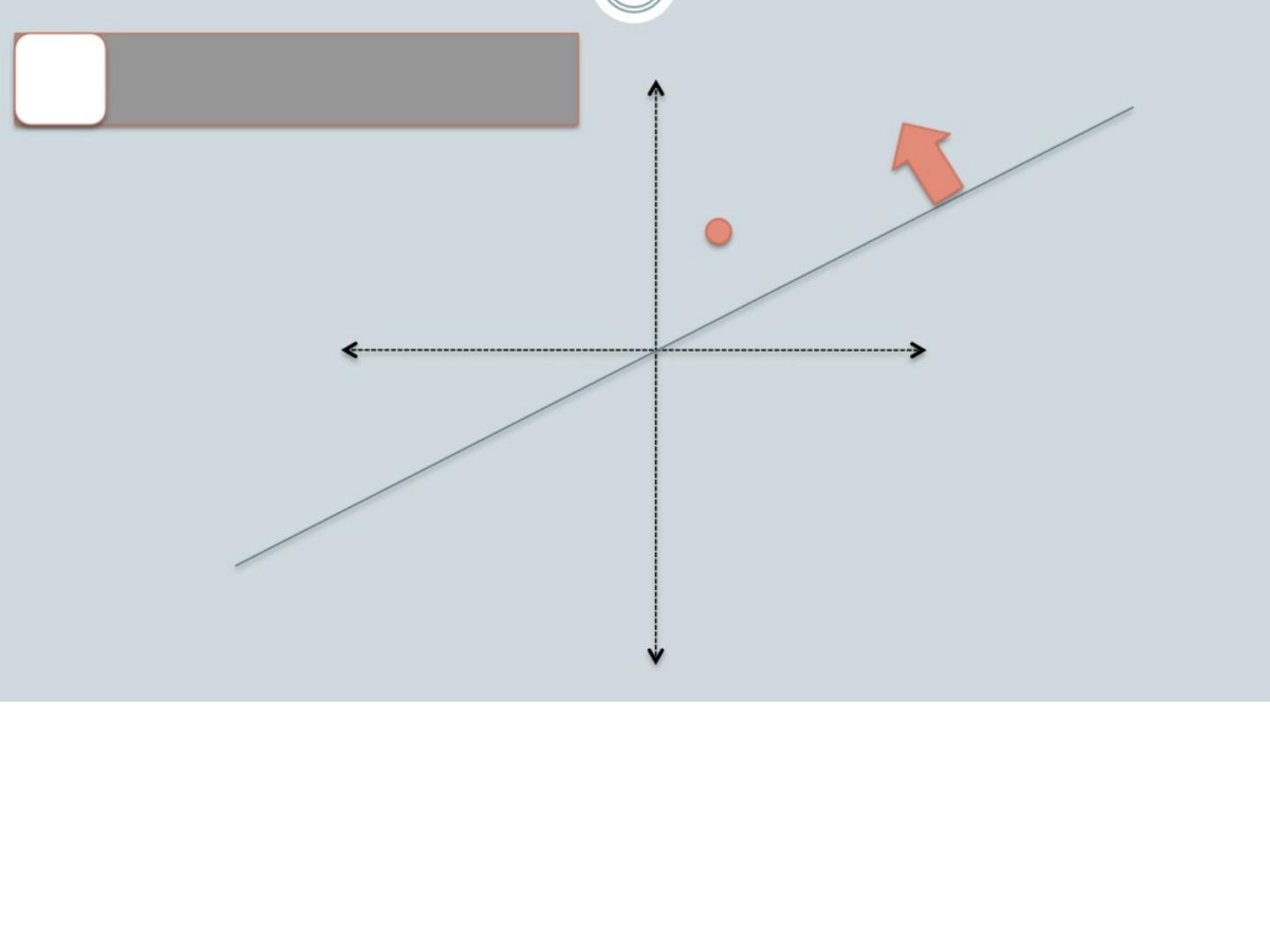
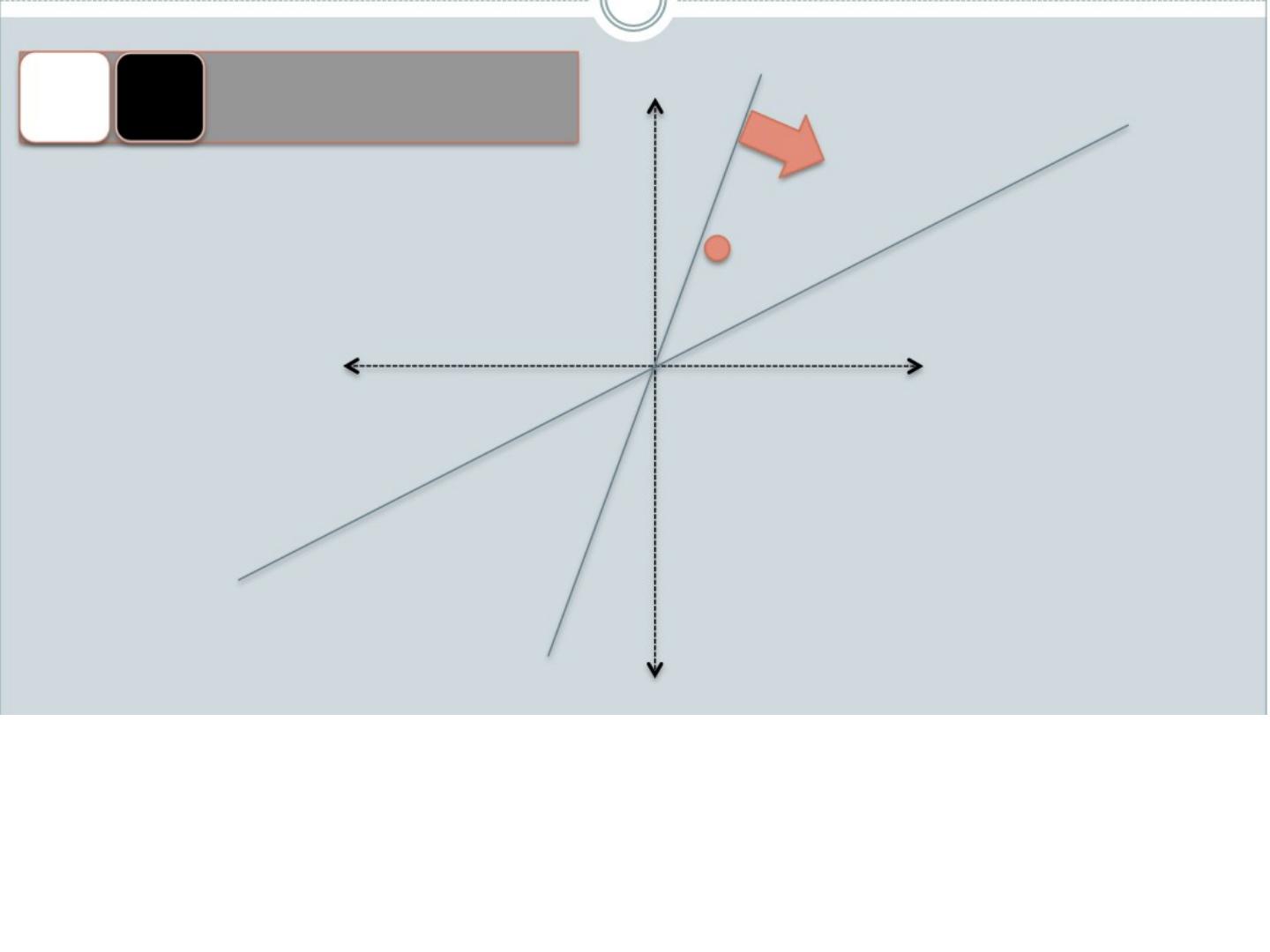
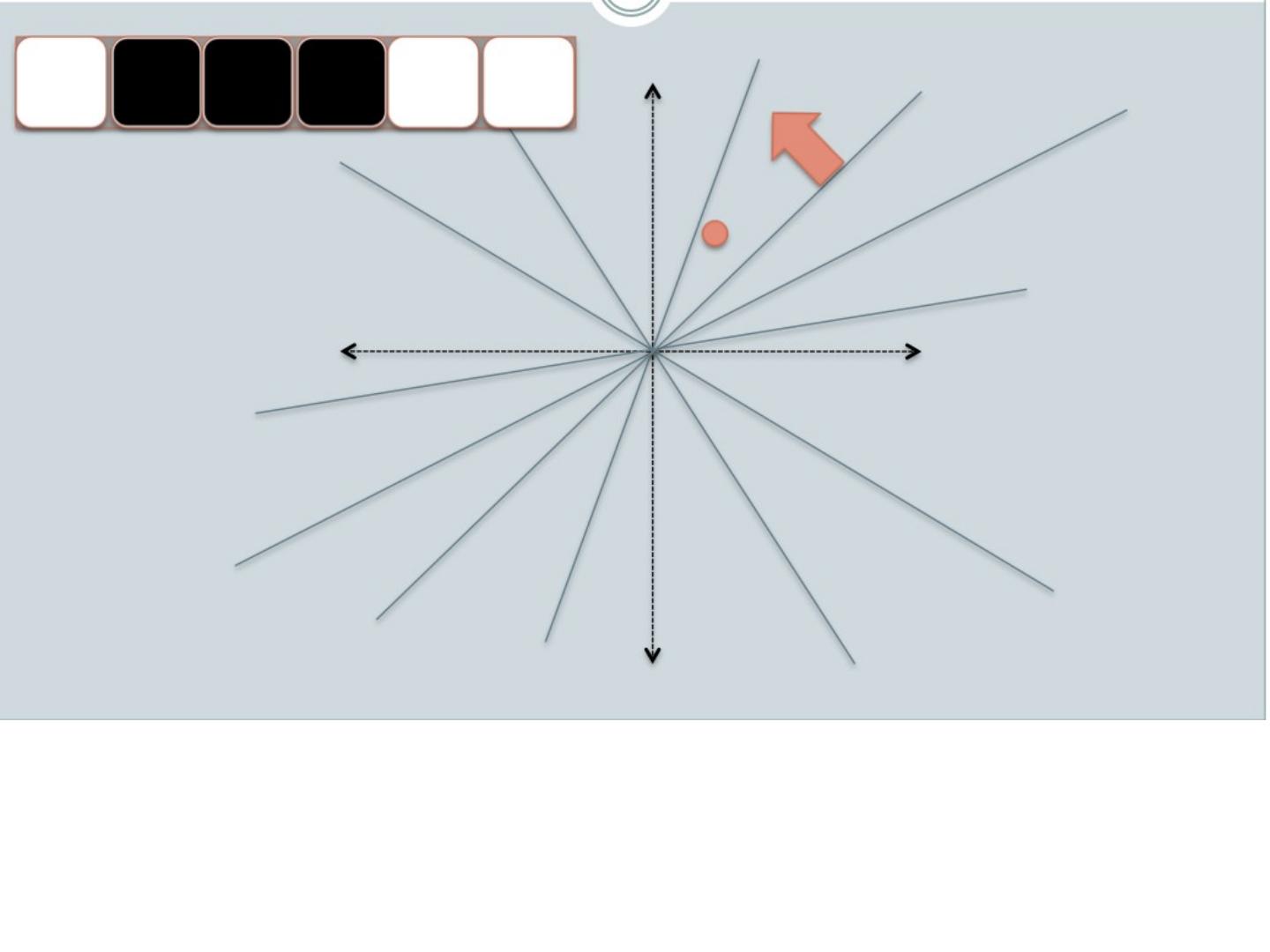
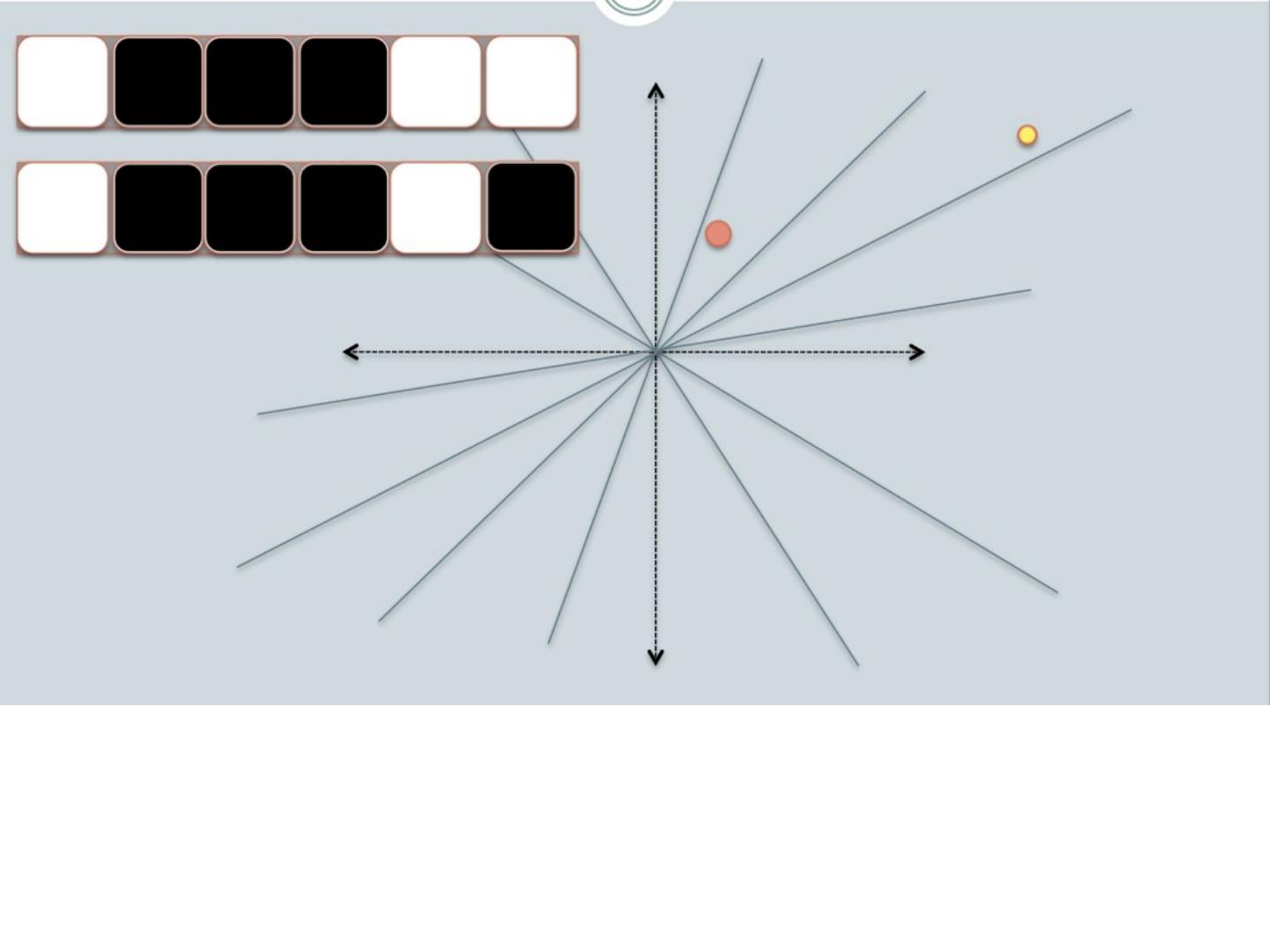
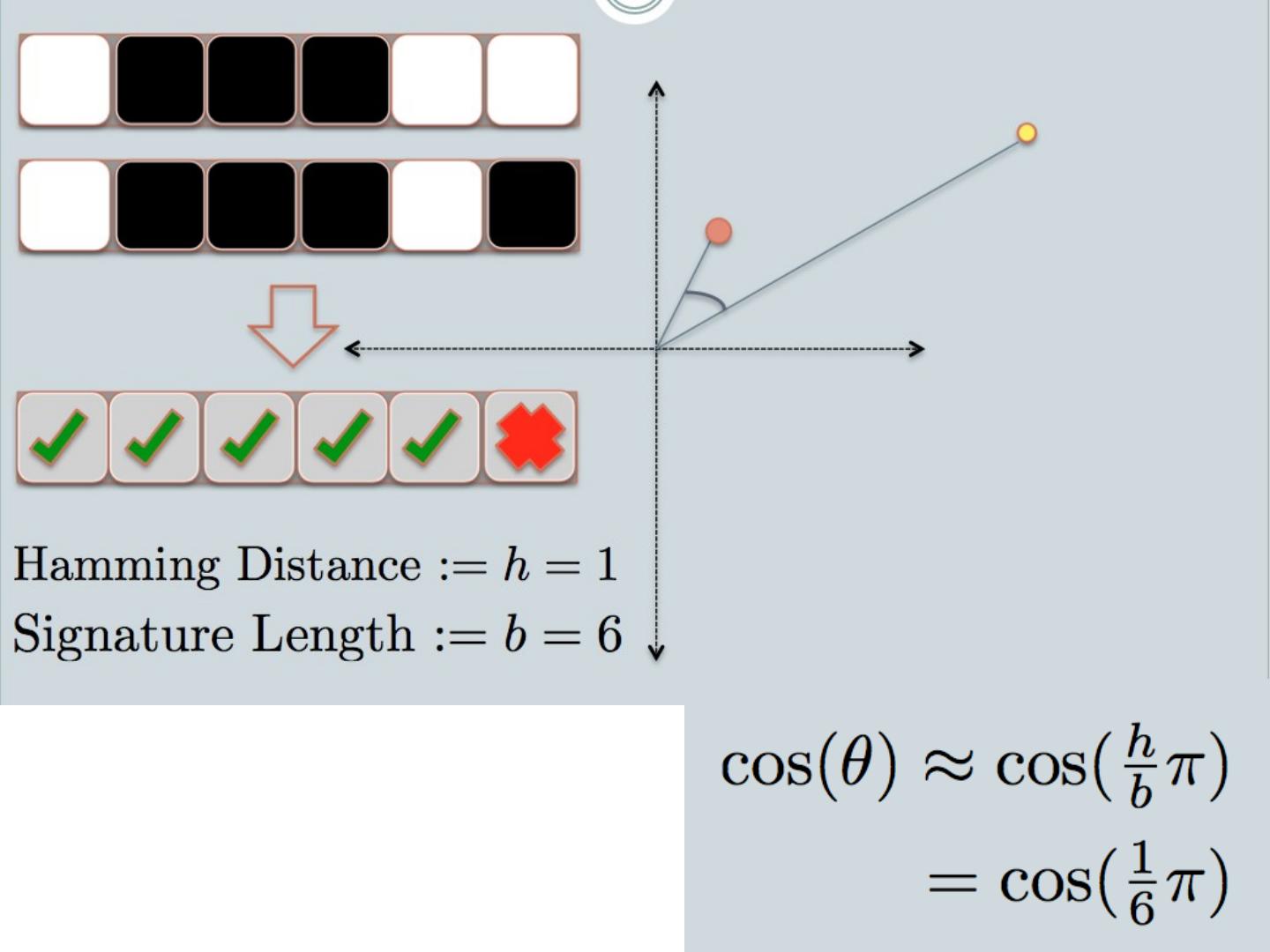
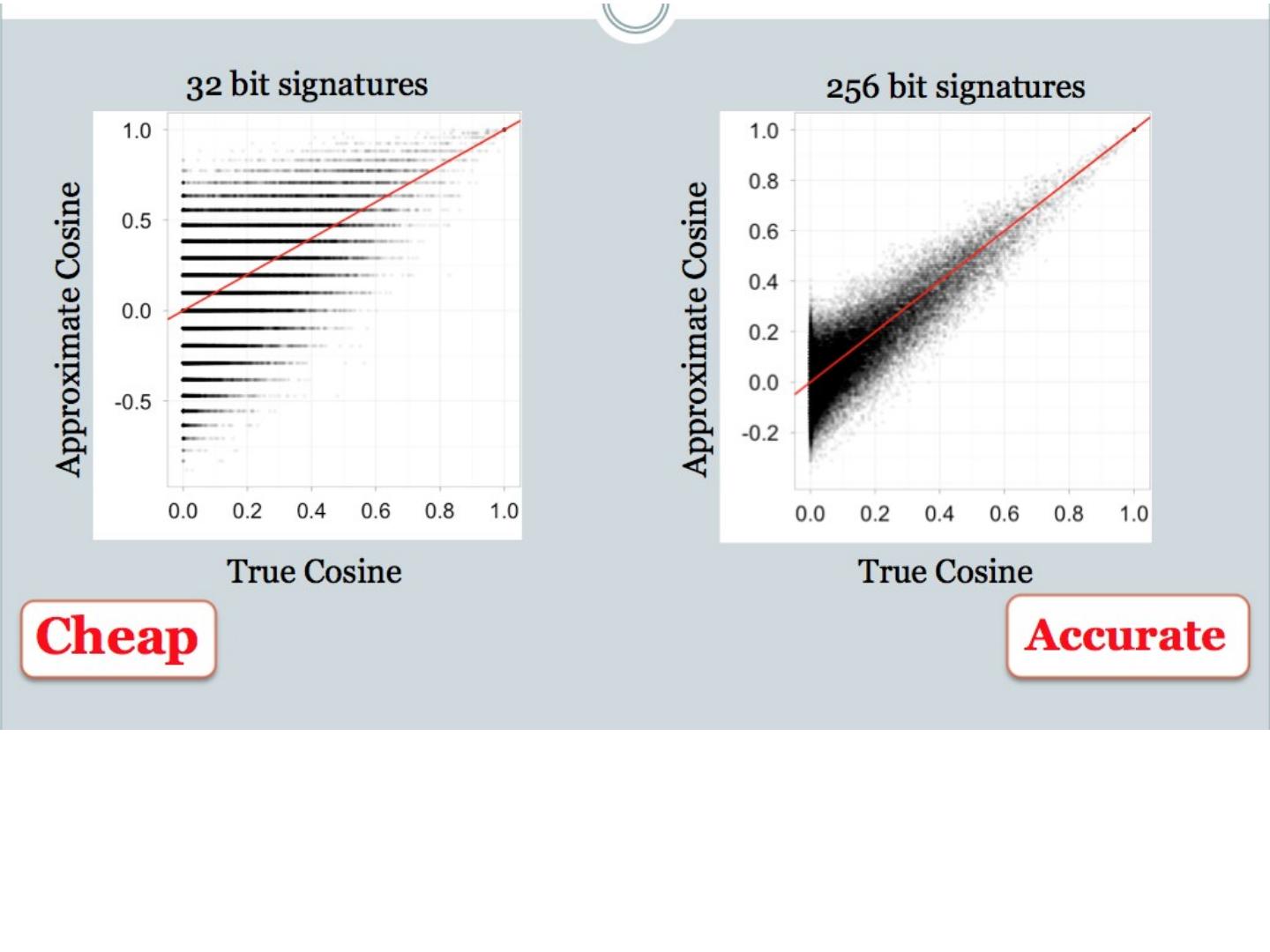
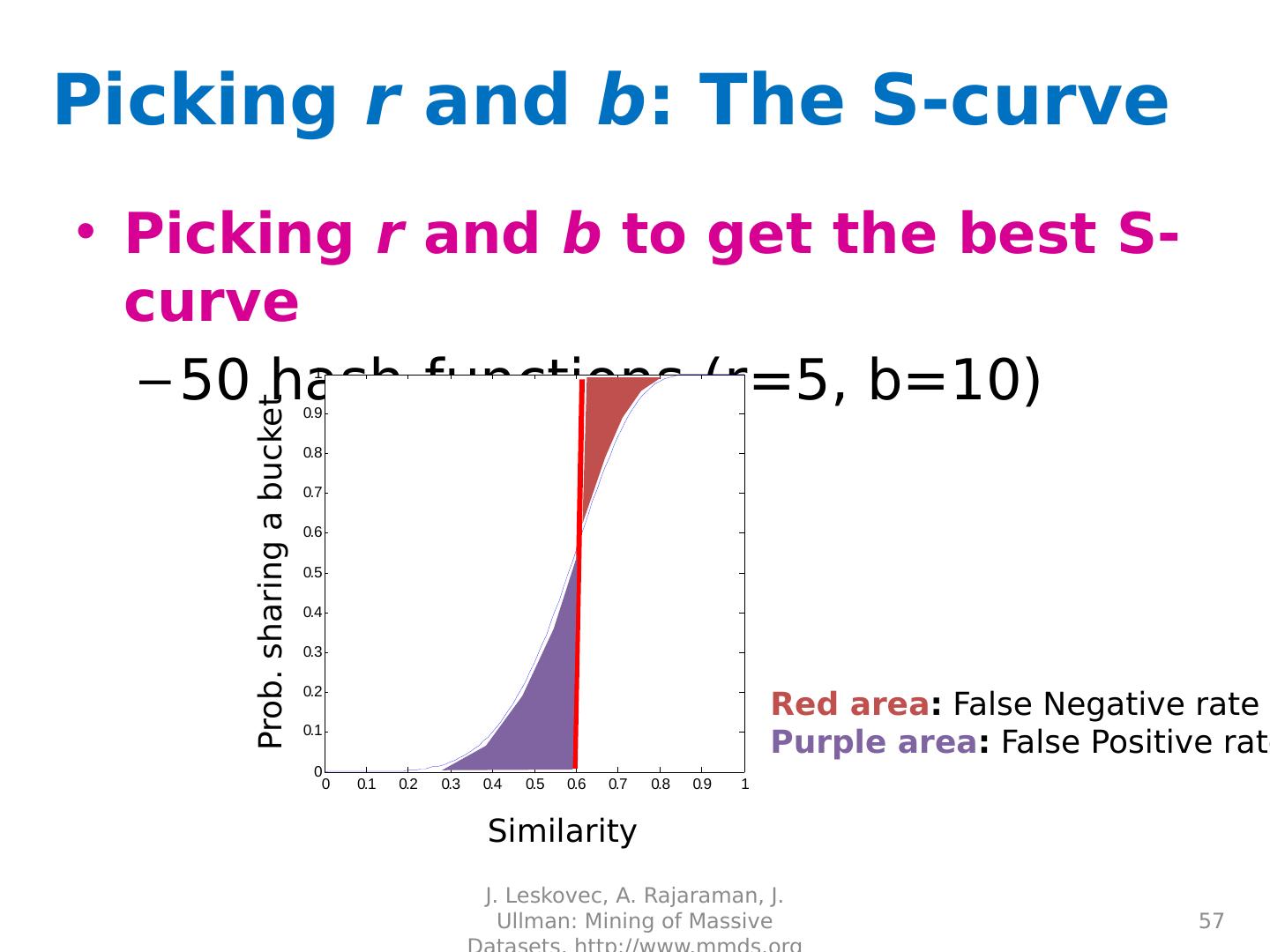
20 .LSH: key ideas Goal: map feature vector x to bit vector bx e nsure that bx preserves “similarity” Basic idea: use random projections of x Repeat many times: Pick a random hyperplane r Compute the inner product of r with x Record if x is “close to” r ( r.x >=0) the next bit in bx Theory says that is x’ and x have small cosine distance then bx and bx ’ will have small Hamming distance

21 .LSH: key ideas Naïve algorithm: Initialization: For i =1 to outputBits : For each feature f: Draw r( f,i ) ~ Normal(0,1) Given an instance x For i =1 to outputBits : LSH[ i ] = sum( x [ f ]*r[ i, f ] for f with non-zero weight in x) > 0 ? 1 : 0 Return the bit-vector LSH Problem: the array of r’s is very large

22 .

23 .

24 .

25 .

26 .

27 .

28 .

29 .Distance Measures Goal: Find near-neighbors in high-dim. space We formally define “near neighbors” as points that are a “small distance” apart For each application, we first need to define what “ distance ” means Today: Jaccard distance/similarity The Jaccard s imilarity of two sets is the size of their intersection divided by the size of their union: sim (C 1 , C 2 ) = |C 1 C 2 |/|C 1 C 2 | Jaccard distance: d (C 1 , C 2 ) = 1 - |C 1 C 2 |/|C 1 C 2 | 29 J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 3 in intersection 8 in union Jaccard similarity= 3/8 Jaccard distance = 5/8