- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Latent Dirichlet Allocation (LDA)
展开查看详情
1 .Latent Dirichlet Allocation (LDA) Shannon Quinn (with thanks to William Cohen of Carnegie Mellon University and Arvind Ramanathan of Oak Ridge National Laboratory)
2 .Processing Natural Language Text Collection of documents Each document consists of a set of word tokens, from a set of word types The big dog ate the small dog Goal of Processing Natural Language Text Construct models of the domain via unsupervised learning “Learn the structure of the domain”
3 .Structure of a Domain: What does it mean? Obtain a compact representation of each document Obtain a generative model that produces observed documents with high probability others with low probability!
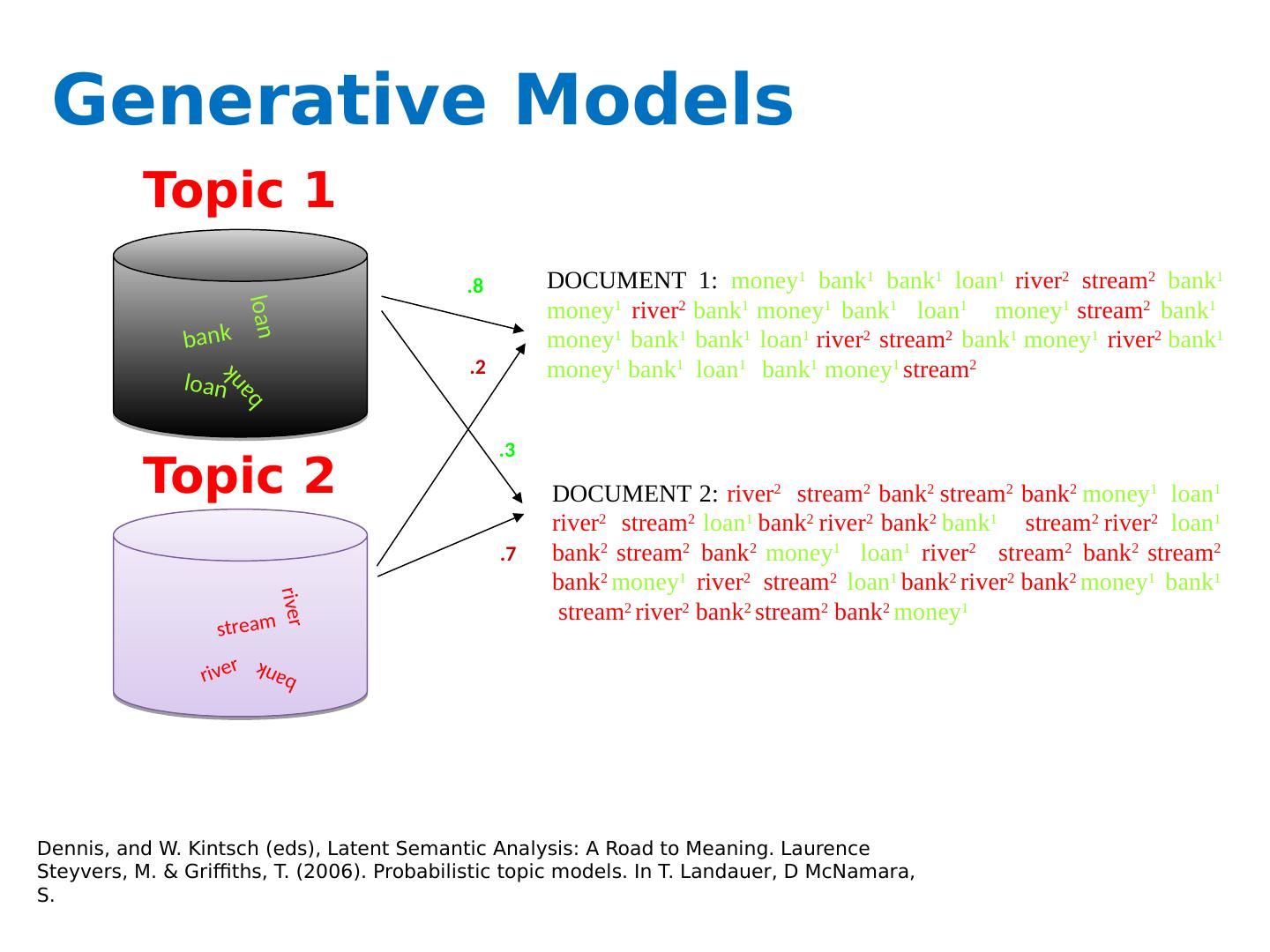
4 .Generative Models Topic 1 Topic 2 loan loan bank bank river river stream bank DOCUMENT 2: river 2 stream 2 bank 2 stream 2 bank 2 money 1 loan 1 river 2 stream 2 loan 1 bank 2 river 2 bank 2 bank 1 stream 2 river 2 loan 1 bank 2 stream 2 bank 2 money 1 loan 1 river 2 stream 2 bank 2 stream 2 bank 2 money 1 river 2 stream 2 loan 1 bank 2 river 2 bank 2 money 1 bank 1 stream 2 river 2 bank 2 stream 2 bank 2 money 1 DOCUMENT 1: money 1 bank 1 bank 1 loan 1 river 2 stream 2 bank 1 money 1 river 2 bank 1 money 1 bank 1 loan 1 money 1 stream 2 bank 1 money 1 bank 1 bank 1 loan 1 river 2 stream 2 bank 1 money 1 river 2 bank 1 money 1 bank 1 loan 1 bank 1 money 1 stream 2 .3 .8 .2 .7 Dennis, and W. Kintsch ( eds ), Latent Semantic Analysis: A Road to Meaning. Laurence Steyvers , M. & Griffiths, T. (2006). Probabilistic topic models. In T. Landauer , D McNamara, S.
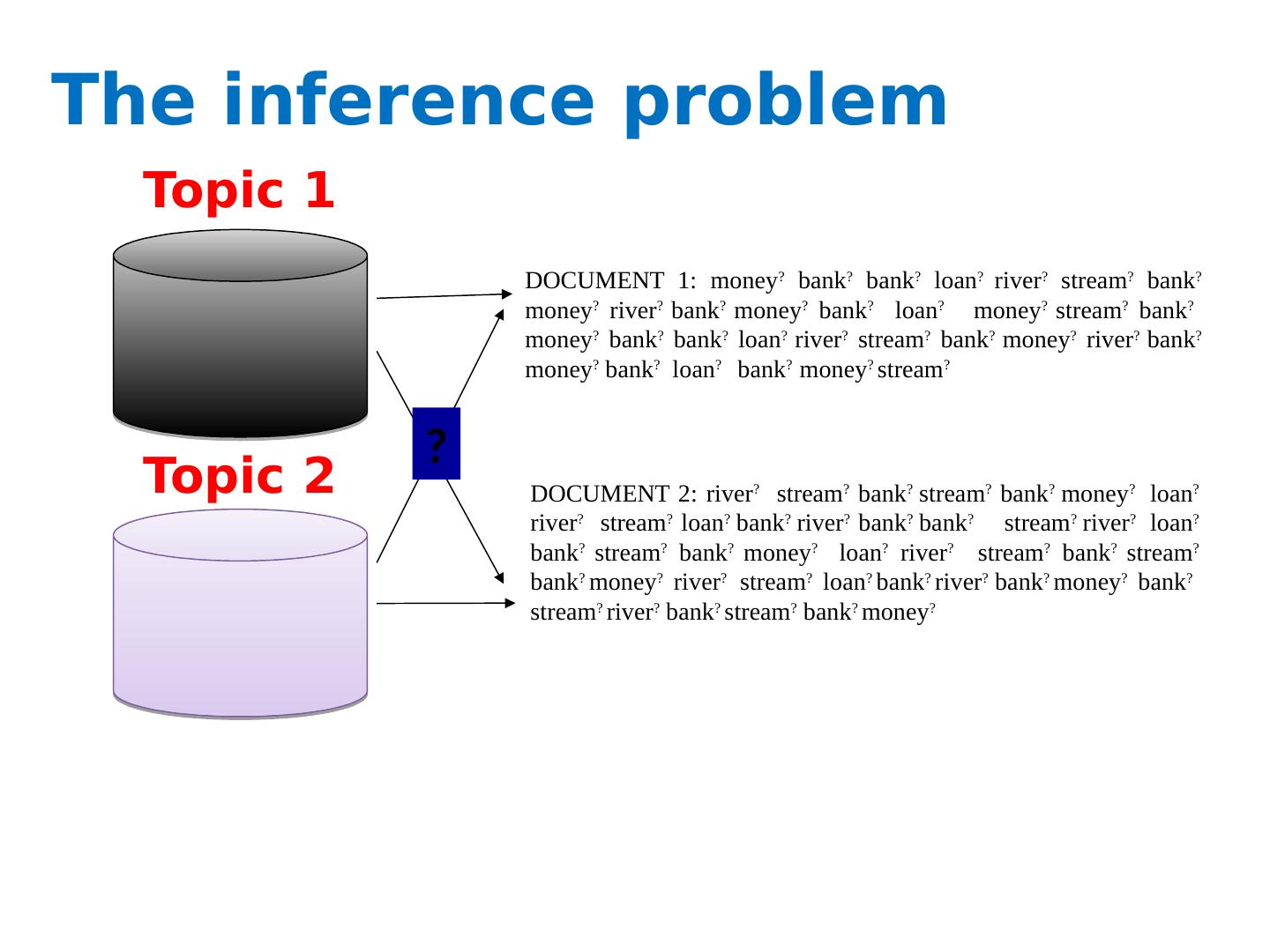
5 .The inference problem Topic 1 Topic 2 DOCUMENT 2: river ? stream ? bank ? stream ? bank ? money ? loan ? river ? stream ? loan ? bank ? river ? bank ? bank ? stream ? river ? loan ? bank ? stream ? bank ? money ? loan ? river ? stream ? bank ? stream ? bank ? money ? river ? stream ? loan ? bank ? river ? bank ? money ? bank ? stream ? river ? bank ? stream ? bank ? money ? DOCUMENT 1: money ? bank ? bank ? loan ? river ? stream ? bank ? money ? river ? bank ? money ? bank ? loan ? money ? stream ? bank ? money ? bank ? bank ? loan ? river ? stream ? bank ? money ? river ? bank ? money ? bank ? loan ? bank ? money ? stream ? ?
6 .Obtaining a compact representation: LSA Latent Semantic Analysis (LSA) Mathematical model Somewhat hacky! Topic Model with LDA Principled Probabilistic model Additional embellishments possible!
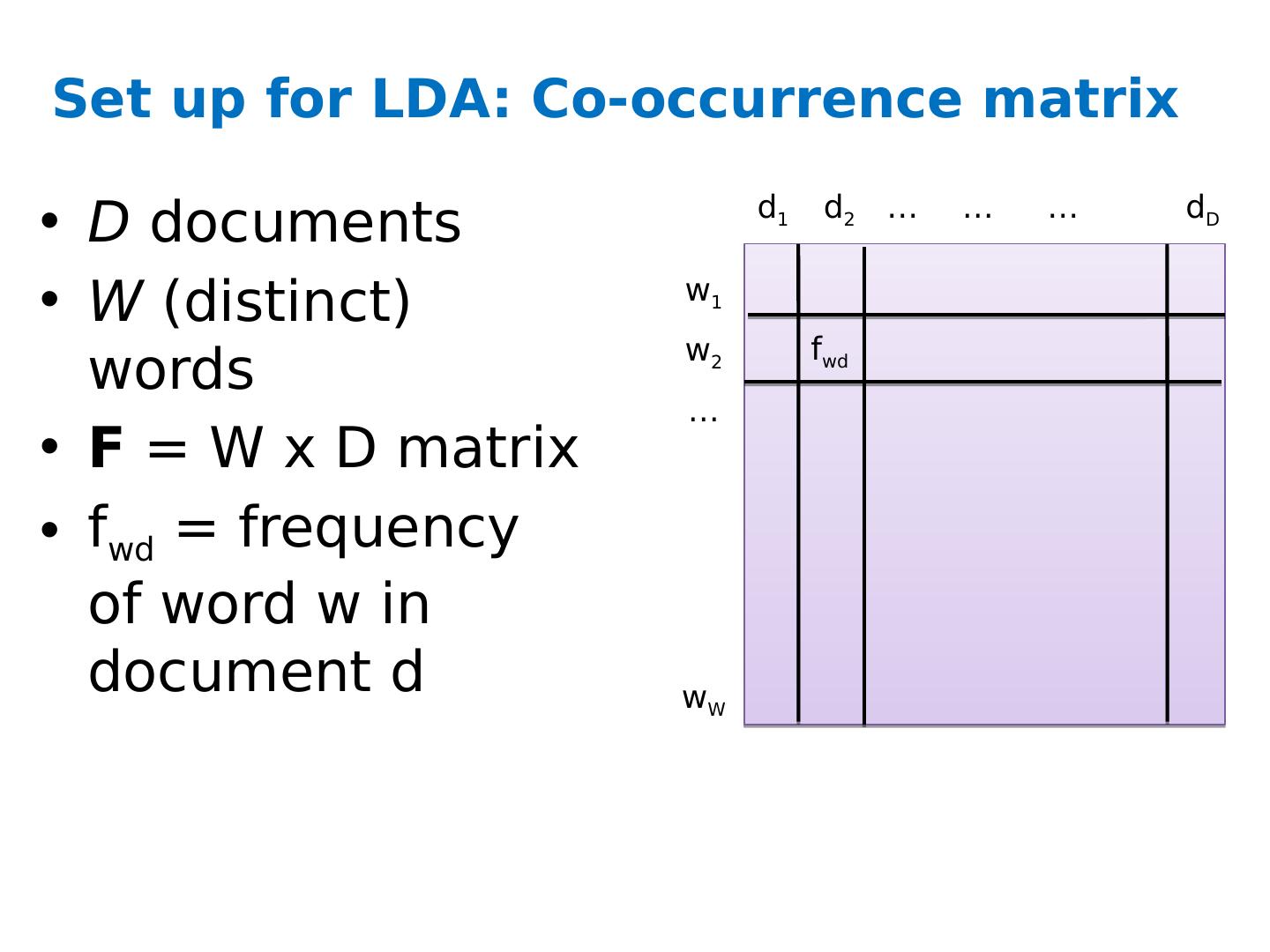
7 .Set up for LDA: Co-occurrence matrix D documents W (distinct) words F = W x D matrix f wd = frequency of word w in document d w 1 w 2 w W … d 1 d 2 d D … … … f wd
8 .LSA: Transforming the Co-occurrence matrix Compute the relative entropy of a word across documents: Are terms document specific? Occurrence reveals something specific about the document itself Hw = 0 word occurs in only one document Hw = 1 word occurs across all documents P( d|w ) [0, 1]
9 .Transforming the Co-occurrence matrix G = W x D [normalized Co-occurrence matrix] (1-Hw) is a measure of specificity: 0 word tells you nothing about the document 1 word tells you something specific about the document G = weighted matrix (with specificity) High dimensional Does not capture similarity across documents
10 .What do you do after constructing G? G (W x D) = U (W x r) Σ (r x r) V T (r x D) Singular Value decomposition if r = min(W,D) reconstruction is perfect if r < min(W, D), capture whatever structure there is in matrix with a reduced number of parameters Reduced representation of word i : row i of matrix UΣ Reduced representation of document j: column j of matrix ΣV T
11 .Some issues with LSA Finding optimal dimension for semantic space precision-recall improve as dimension is increased until hits optimal, then slowly decreases until it hits standard vector model run SVD once with big dimension, say k = 1000 then can test dimensions <= k in many tasks 150-350 works well, still room for research SVD assumes normally distributed data term occurrence is not normally distributed matrix entries are weights, not counts, which may be normally distributed even when counts are not
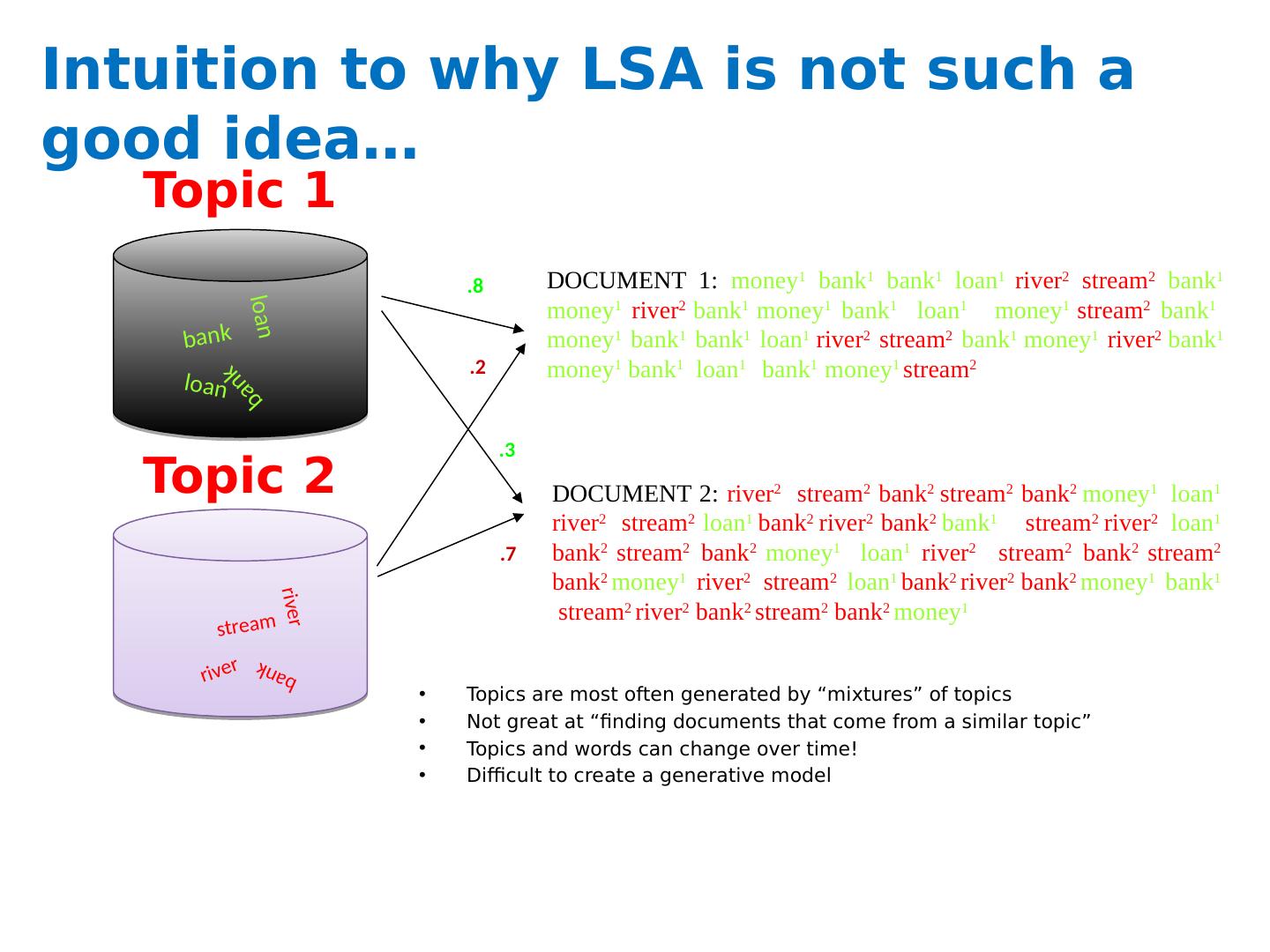
12 .Intuition to why LSA is not such a good idea… Topics are most often generated by “mixtures” of topics Not great at “finding documents that come from a similar topic” Topics and words can change over time! Difficult to create a generative model Topic 1 Topic 2 loan loan bank bank river river stream bank DOCUMENT 2: river 2 stream 2 bank 2 stream 2 bank 2 money 1 loan 1 river 2 stream 2 loan 1 bank 2 river 2 bank 2 bank 1 stream 2 river 2 loan 1 bank 2 stream 2 bank 2 money 1 loan 1 river 2 stream 2 bank 2 stream 2 bank 2 money 1 river 2 stream 2 loan 1 bank 2 river 2 bank 2 money 1 bank 1 stream 2 river 2 bank 2 stream 2 bank 2 money 1 DOCUMENT 1: money 1 bank 1 bank 1 loan 1 river 2 stream 2 bank 1 money 1 river 2 bank 1 money 1 bank 1 loan 1 money 1 stream 2 bank 1 money 1 bank 1 bank 1 loan 1 river 2 stream 2 bank 1 money 1 river 2 bank 1 money 1 bank 1 loan 1 bank 1 money 1 stream 2 .3 .8 .2 .7
13 .Topic models Motivating questions: What are the topics that a document is about? Given one document, can we find similar documents about the same topic? How do topics in a field change over time? We will use a Hierarchical Bayesian Approach Assume that each document defines a distribution over (hidden) topics Assume each topic defines a distribution over words The posterior probability of these latent variables given a document collection determines a hidden decomposition of the collection into topics.
14 .http:// dl.acm.org / citation.cfm?id =944937
15 .LDA Motivation w M N Assumptions: 1) documents are i.i.d 2) within a document, words are i.i.d. (bag of words) For each document d = 1, ,M Generate d ~ D 1 (…) For each word n = 1, , N d generate w n ~ D 2 ( ¢ | θ d n ) Now pick your favorite distributions for D 1 , D 2
16 .LDA z w M N a Randomly initialize each z m,n Repeat for t=1,…. For each doc m, word n Find Pr( z mn = k |other z’s) Sample z mn according to that distr. “Mixed membership” (k) 30? 100?
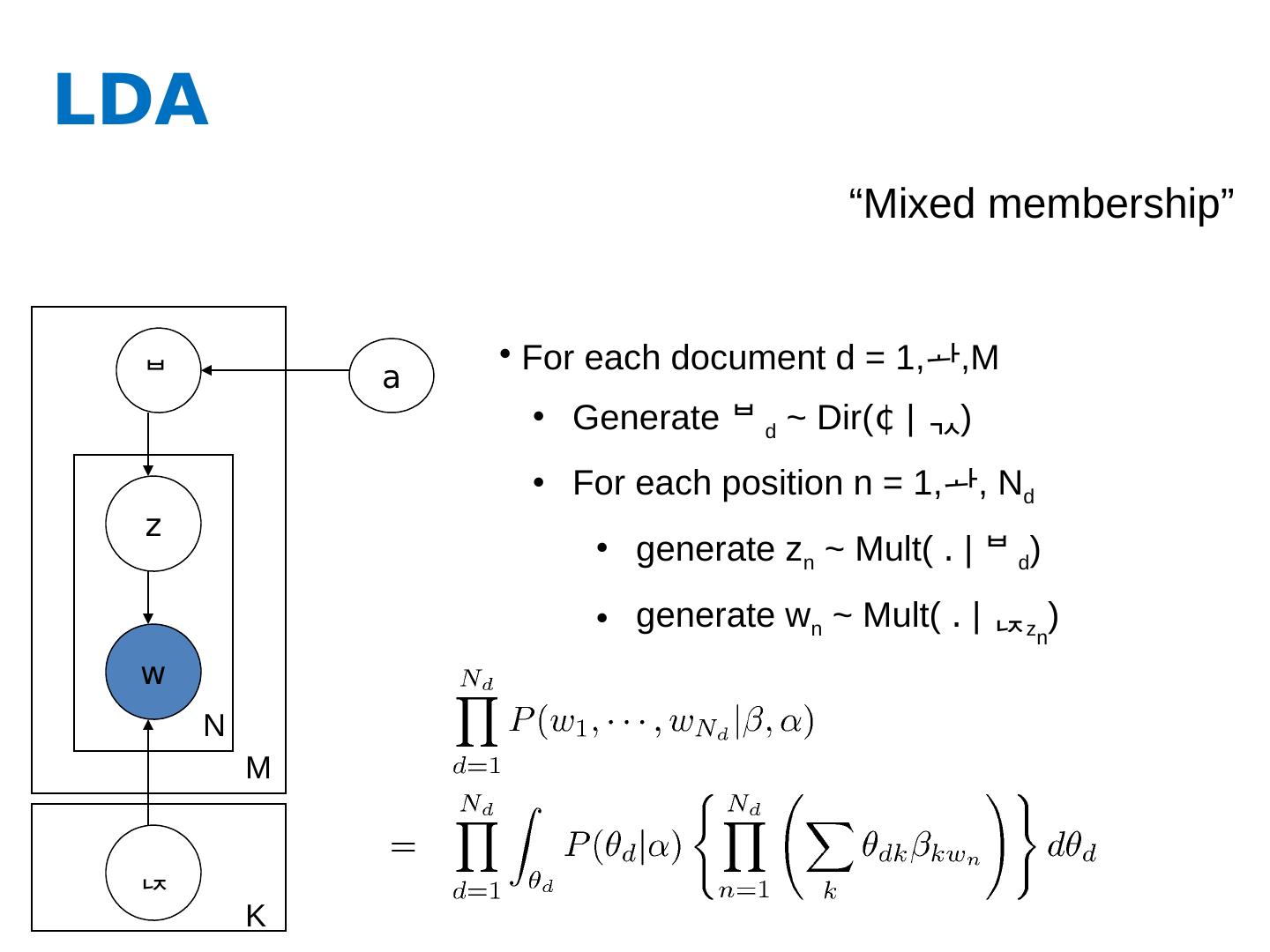
17 .LDA z w M N a For each document d = 1, ,M Generate d ~ Dir( ¢ | ) For each position n = 1, , N d generate z n ~ Mult( . | d ) generate w n ~ Mult( . | z n ) “Mixed membership” K
18 .How an LDA document looks
19 .LDA topics
20 .The intuitions behind LDA http:// www.cs.princeton.edu /~ blei /papers/Blei2011.pdf
21 .Let’s set up a generative model… We have D documents Vocabulary of V word types Each document contains up to N word tokens Assume K topics Each document has a K-dimensional multinomial θ d over topics with a common Dirichlet prior, Dir (α) Each topic has a V-dimensional multinomial β k over with a common symmetric Dirichlet prior, D( η )
22 .What is a Dirichlet distribution? Remember we called a multinomial distribution for both topic and word distributions? The space is of all of these multinomials has a nice geometric interpretation as a (k-1)-simplex, which is just a generalization of a triangle to (k-1) dimensions. Criteria for selecting our prior: It needs to be defined for a (k-1)-simplex. Algebraically speaking, we would like it to play nice with the multinomial distribution.
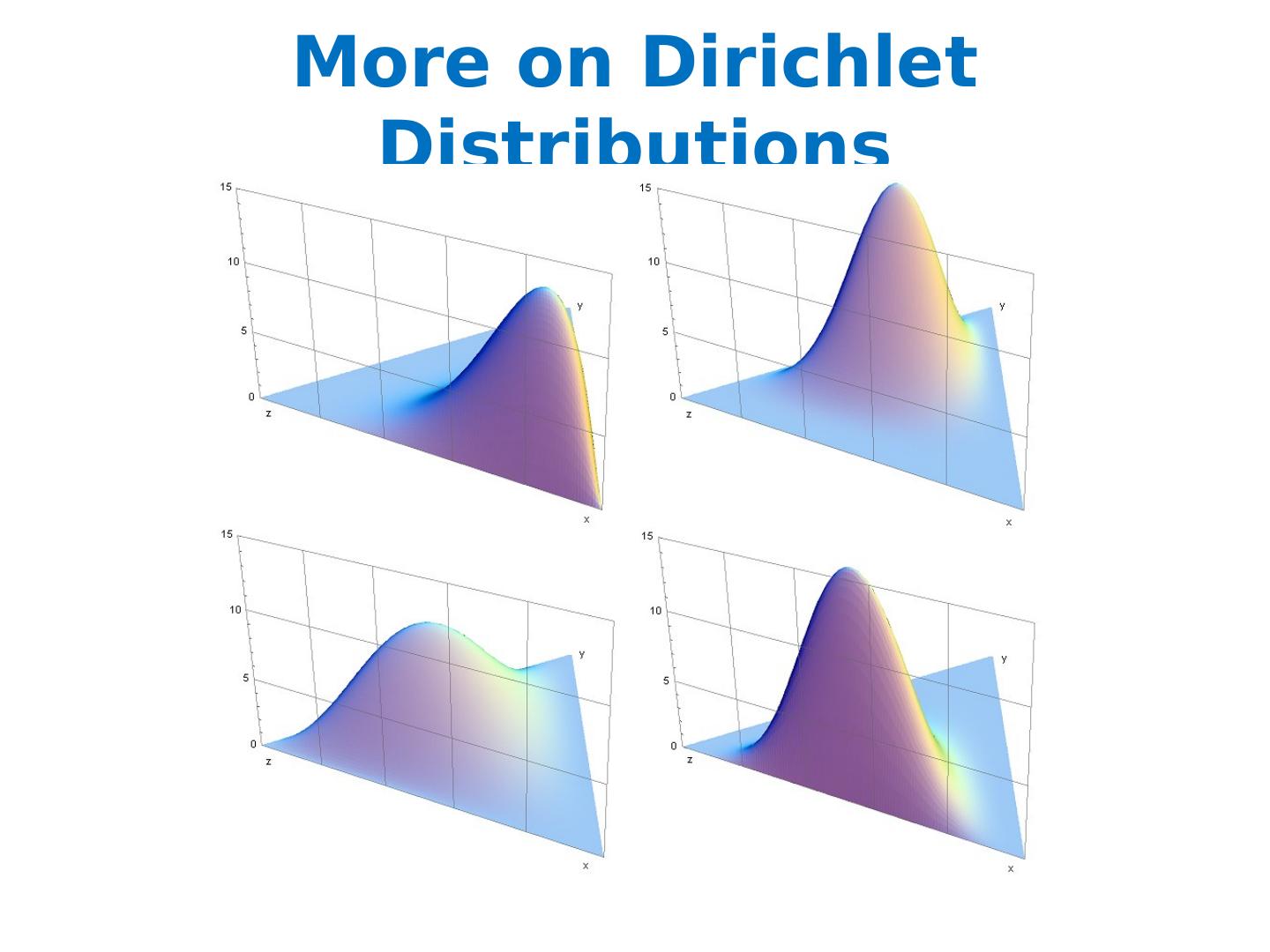
23 .More on Dirichlet Distributions Useful Facts: This distribution is defined over a (k-1)-simplex. That is, it takes k non-negative arguments which sum to one. Consequently it is a natural distribution to use over multinomial distributions. In fact, the Dirichlet distribution is the conjugate prior to the multinomial distribution. (This means that if our likelihood is multinomial with a Dirichlet prior, then the posterior is also Dirichlet !) The Dirichlet parameter i can be thought of as a prior count of the i th class.
24 .More on Dirichlet Distributions
25 .Dirichlet Distribution
26 .Dirichlet Distribution
27 .How does the generative process look like? For each topic 1…k: Draw a multinomial over words β k ~ Dir ( η ) For each document 1…d: Draw multinomial over topics θ d ~ Dir (α) For each word w dn : Draw a topic Z dn ~ Mult ( θ d ) with Z dn from [1…k] Draw a word w dn ~ Mult (β Zdn )
28 .The LDA Model z 4 z 3 z 2 z 1 w 4 w 3 w 2 w 1 b z 4 z 3 z 2 z 1 w 4 w 3 w 2 w 1 z 4 z 3 z 2 z 1 w 4 w 3 w 2 w 1
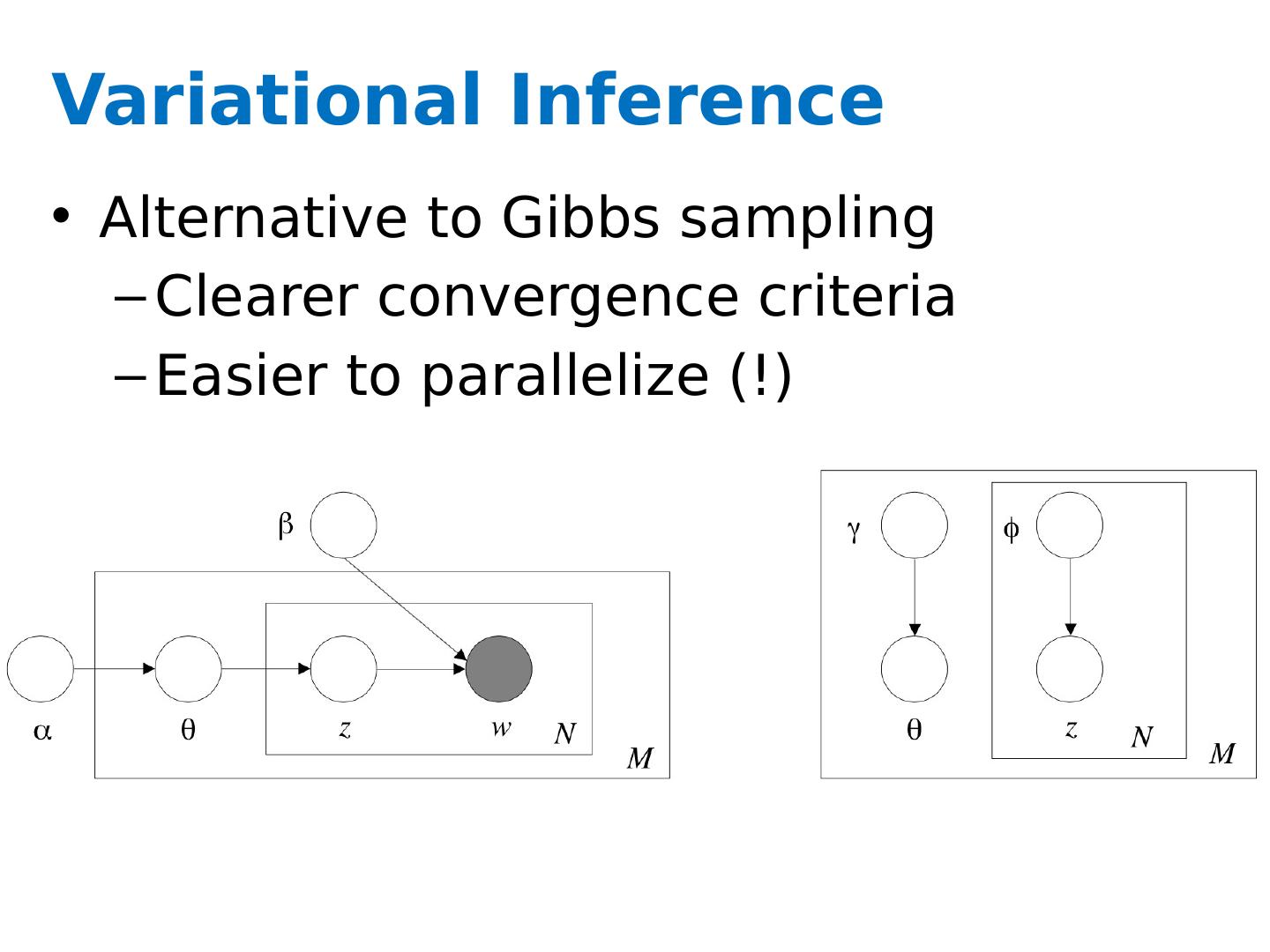
29 .What is the posterior of the hidden variables given the observed variables (and hyper-parameters)? Problem: the integral in the denominator is intractable! Solution: Approximate inference Gibbs Sampling [Griffith and Steyvers ] Variational inference [ Blei , Ng, Jordan ]