Graphs II

1 .Graphs (Part II) Shannon Quinn (with thanks to William Cohen and Aapo Kyrola of CMU, and J. Leskovec , A. Rajaraman , and J . Ullman of Stanford University)

2 .Parallel Graph Computation Distributed computation and/or multicore parallelism Sometimes confusing. We will talk mostly about distributed computation. Are classic graph algorithms parallelizable? What about distributed? Depth-first search? Breadth-first search? Priority-queue based traversals ( Djikstra’s , Prim’s algorithms)

3 .MapReduce for Graphs Graph computation almost always iterative MapReduce ends up shipping the whole graph on each iteration over the network (map->reduce->map->reduce->...) Mappers and reducers are stateless

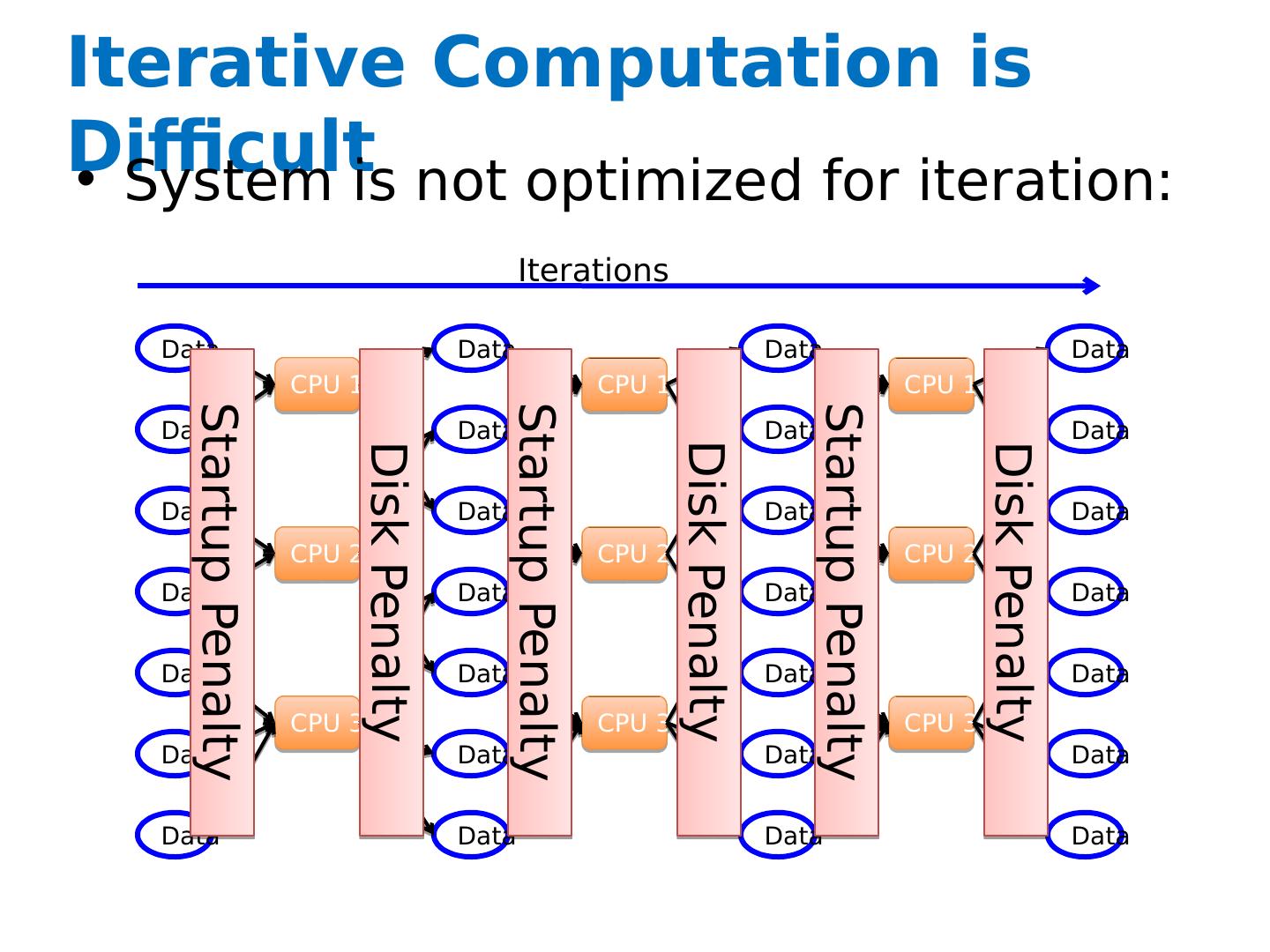
4 .Iterative Computation is Difficult System is not optimized for iteration: Data Data Data Data Data Data Data Data Data Data Data Data Data Data CPU 1 CPU 2 CPU 3 Data Data Data Data Data Data Data CPU 1 CPU 2 CPU 3 Data Data Data Data Data Data Data CPU 1 CPU 2 CPU 3 Iterations Disk Penalty Disk Penalty Disk Penalty Startup Penalty Startup Penalty Startup Penalty

5 .MapReduce and Partitioning Map-Reduce splits the keys randomly between mappers/reducers But on natural graphs, high-degree vertices (keys) may have million-times more edges than the average Extremely uneven distribution Time of iteration = time of slowest job.

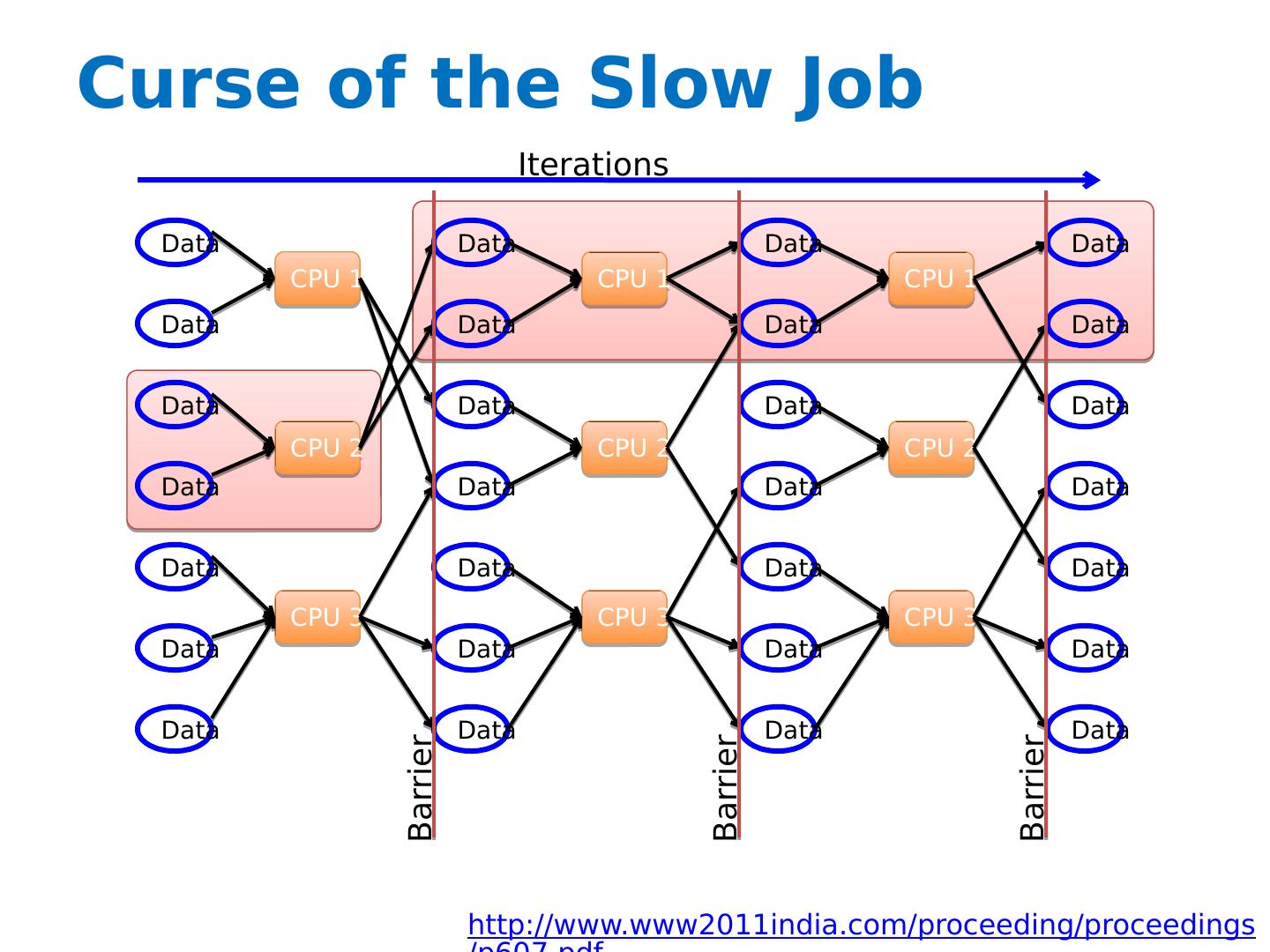
6 .Curse of the Slow Job Data Data Data Data Data Data Data Data Data Data Data Data Data Data CPU 1 CPU 2 CPU 3 CPU 1 CPU 2 CPU 3 Data Data Data Data Data Data Data CPU 1 CPU 2 CPU 3 Iterations Barrier Barrier Data Data Data Data Data Data Data Barrier http://www.www2011india.com/proceeding/proceedings/p607.pdf

7 .Map-Reduce is Bulk-Synchronous Parallel Bulk-Synchronous Parallel = BSP (Valiant, 80s) Each iteration sees only the values of previous iteration. In linear systems literature: Jacobi iterations Pros: Simple to program Maximum parallelism Simple fault-tolerance Cons: Slower convergence Iteration time = time taken by the slowest node

8 .Map-Reduce is Bulk-Synchronous Parallel Bulk-Synchronous Parallel = BSP (Valiant, 80s) Each iteration sees only the values of previous iteration. In linear systems literature: Jacobi iterations Pros: Simple to program Maximum parallelism Simple fault-tolerance Cons: Slower convergence Iteration time = time taken by the slowest node

9 .Map-Reduce is Bulk-Synchronous Parallel Bulk-Synchronous Parallel = BSP (Valiant, 80s) Each iteration sees only the values of previous iteration. In linear systems literature: Jacobi iterations Pros: Simple to program Maximum parallelism Simple fault-tolerance Cons: Slower convergence Iteration time = time taken by the slowest node

10 .Graph algorithms PageRank implementations in memory streaming, node list in memory streaming, no memory map-reduce A little like Naïve Bayes variants data in memory word counts in memory stream-and-sort map-reduce

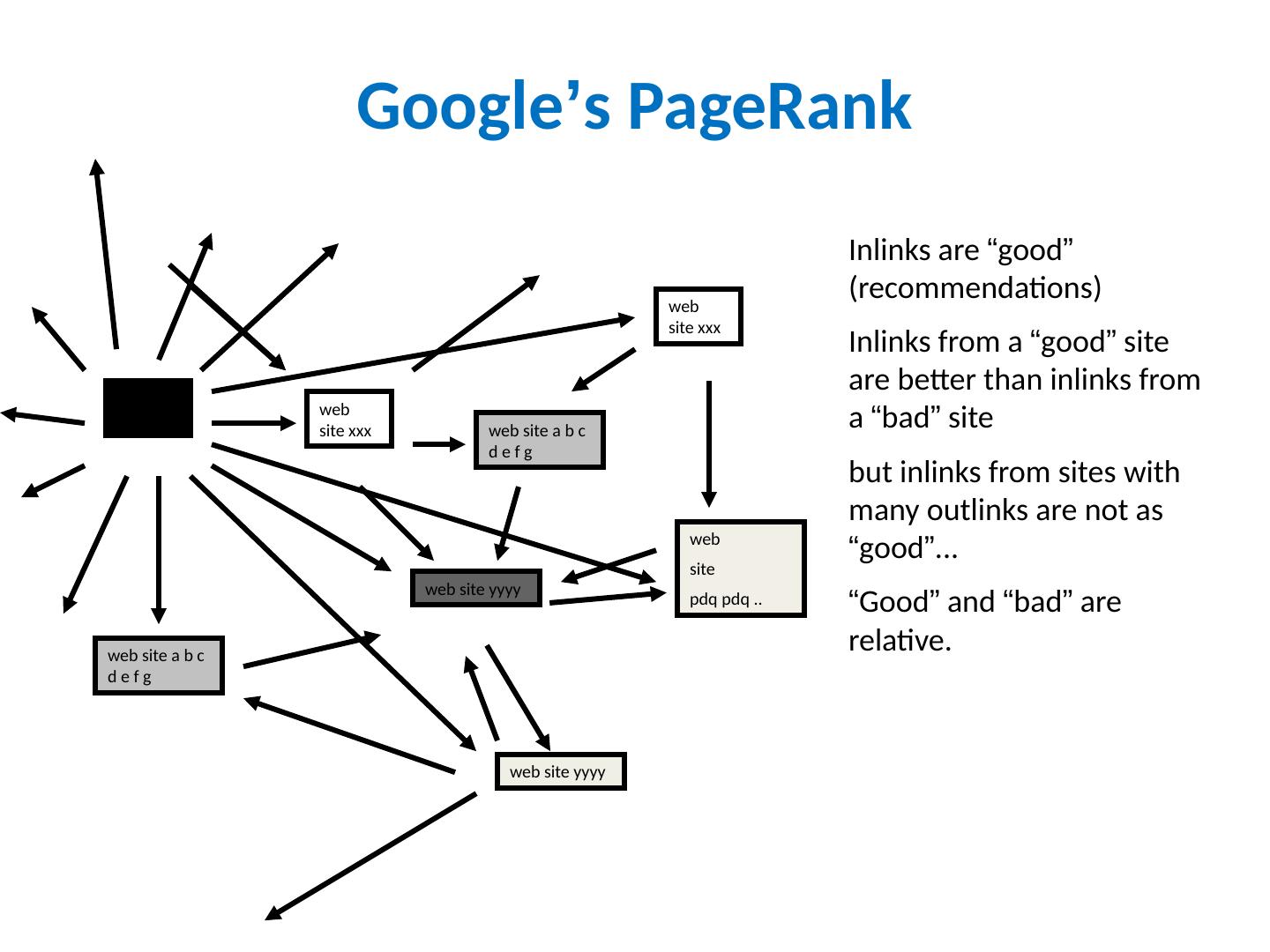
11 .Google ’ s PageRank web site xxx web site yyyy web site a b c d e f g web site pdq pdq .. web site yyyy web site a b c d e f g web site xxx Inlinks are “ good ” (recommendations) Inlinks from a “ good ” site are better than inlinks from a “ bad ” site but inlinks from sites with many outlinks are not as “ good ” ... “ Good ” and “ bad ” are relative. web site xxx

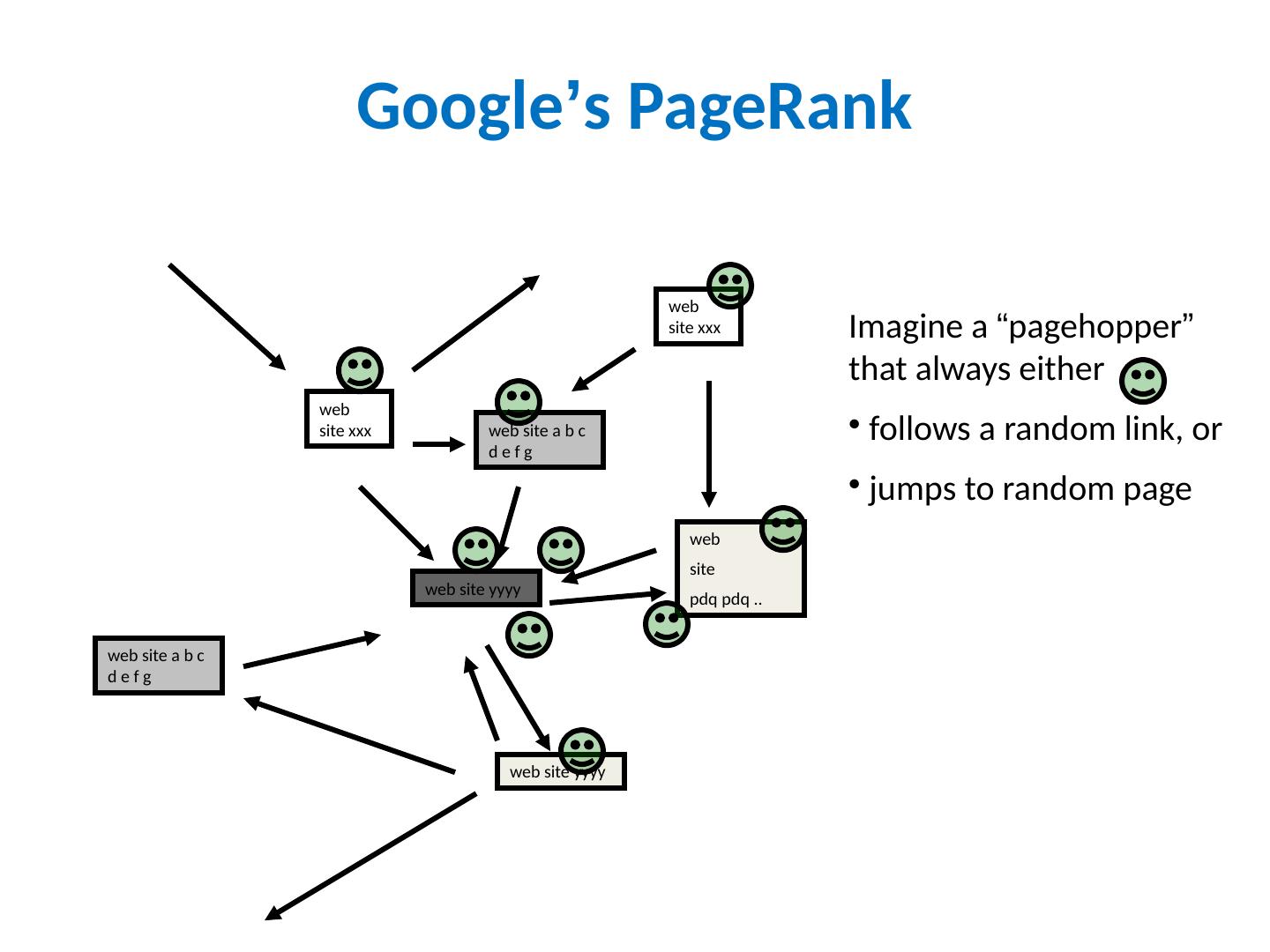
12 .Google ’ s PageRank web site xxx web site yyyy web site a b c d e f g web site pdq pdq .. web site yyyy web site a b c d e f g web site xxx Imagine a “ pagehopper ” that always either follows a random link, or jumps to random page

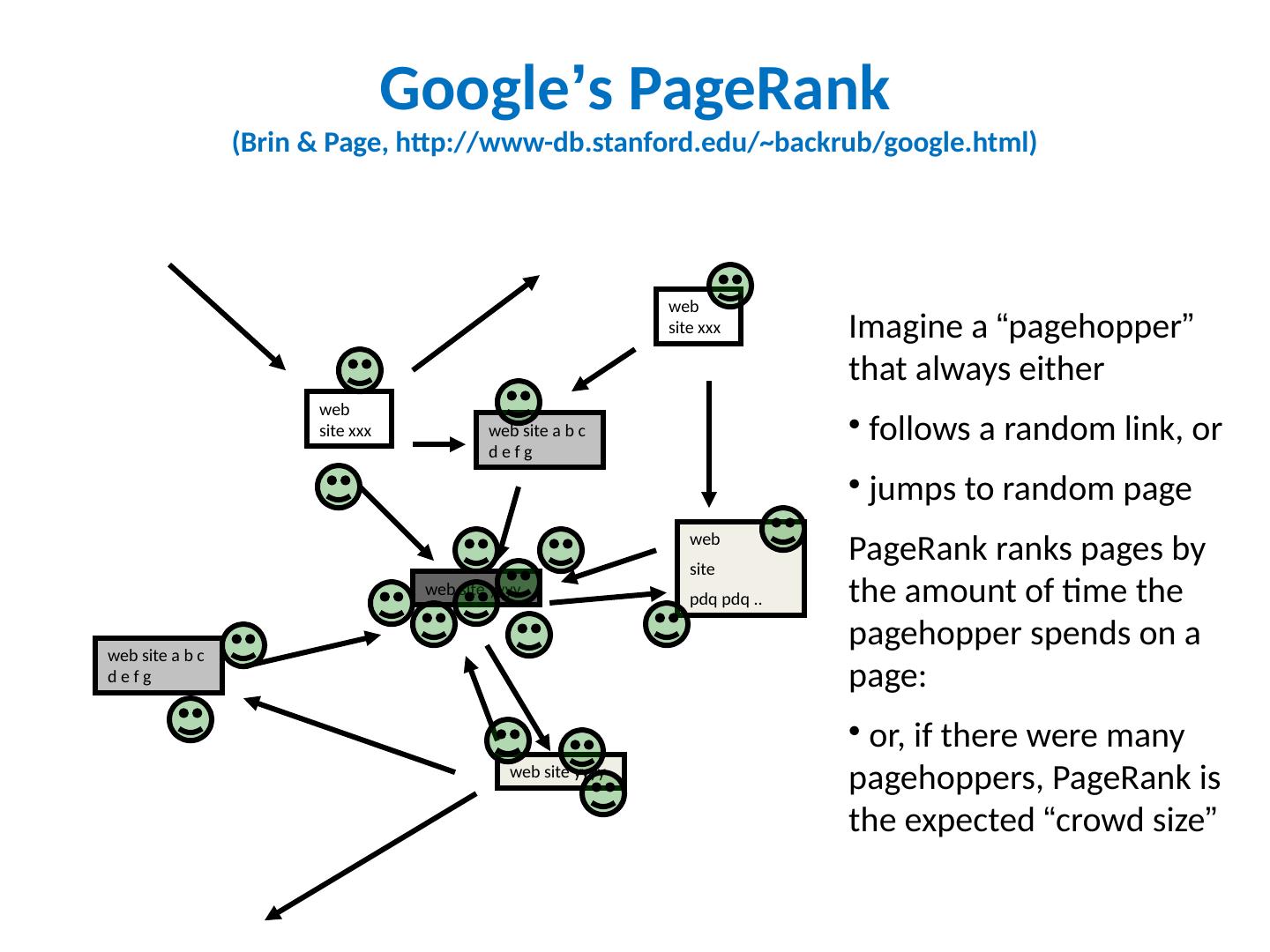
13 .Google ’ s PageRank (Brin & Page, http://www-db.stanford.edu/~backrub/google.html) web site xxx web site yyyy web site a b c d e f g web site pdq pdq .. web site yyyy web site a b c d e f g web site xxx Imagine a “ pagehopper ” that always either follows a random link, or jumps to random page PageRank ranks pages by the amount of time the pagehopper spends on a page: or, if there were many pagehoppers, PageRank is the expected “ crowd size ”

14 .Random Walks avoids messy “dead ends”….

15 .Random Walks: PageRank

16 .Random Walks: PageRank

17 .Graph = Matrix Vector = Node  Weight H A B C D E F G H I J A _ 1 1 1 B 1 _ 1 C 1 1 _ D _ 1 1 E 1 _ 1 F 1 1 1 _ G _ 1 1 H _ 1 1 I 1 1 _ 1 J 1 1 1 _ A B C F D E G I J A A 3 B 2 C 3 D E F G H I J M M v

18 .PageRank in Memory Let u = (1/N, …, 1/N) dimension = #nodes N Let A = adjacency matrix: [ a ij =1  i links to j] Let W = [ w ij = a ij / outdegree ( i )] w ij is probability of jump from i to j Let v 0 = (1,1,….,1) or anything else you want Repeat until converged: Let v t+1 = c u + (1-c) Wv t c is probability of jumping “anywhere randomly”

19 .Streaming PageRank Assume we can store v but not W in memory Repeat until converged: Let v t+1 = c u + (1-c) Wv t Store A as a row matrix: each line is i j i,1 ,…, j i,d [the neighbors of i ] Store v’ and v in memory: v’ starts out as c u For each line “ i j i,1 ,…, j i,d “ For each j in j i,1 ,…, j i,d v’ [j] += (1-c) v[ i ]/ d Everything needed for update is right there in row… .

20 .Streaming PageRank: with some long rows Repeat until converged: Let v t+1 = c u + (1-c) Wv t Store A as a list of edges: each line is: “ i d( i ) j” Store v’ and v in memory: v’ starts out as c u For each line “ i d j“ v’ [j] += (1-c) v[ i ]/ d We need to get the degree of i and store it locally

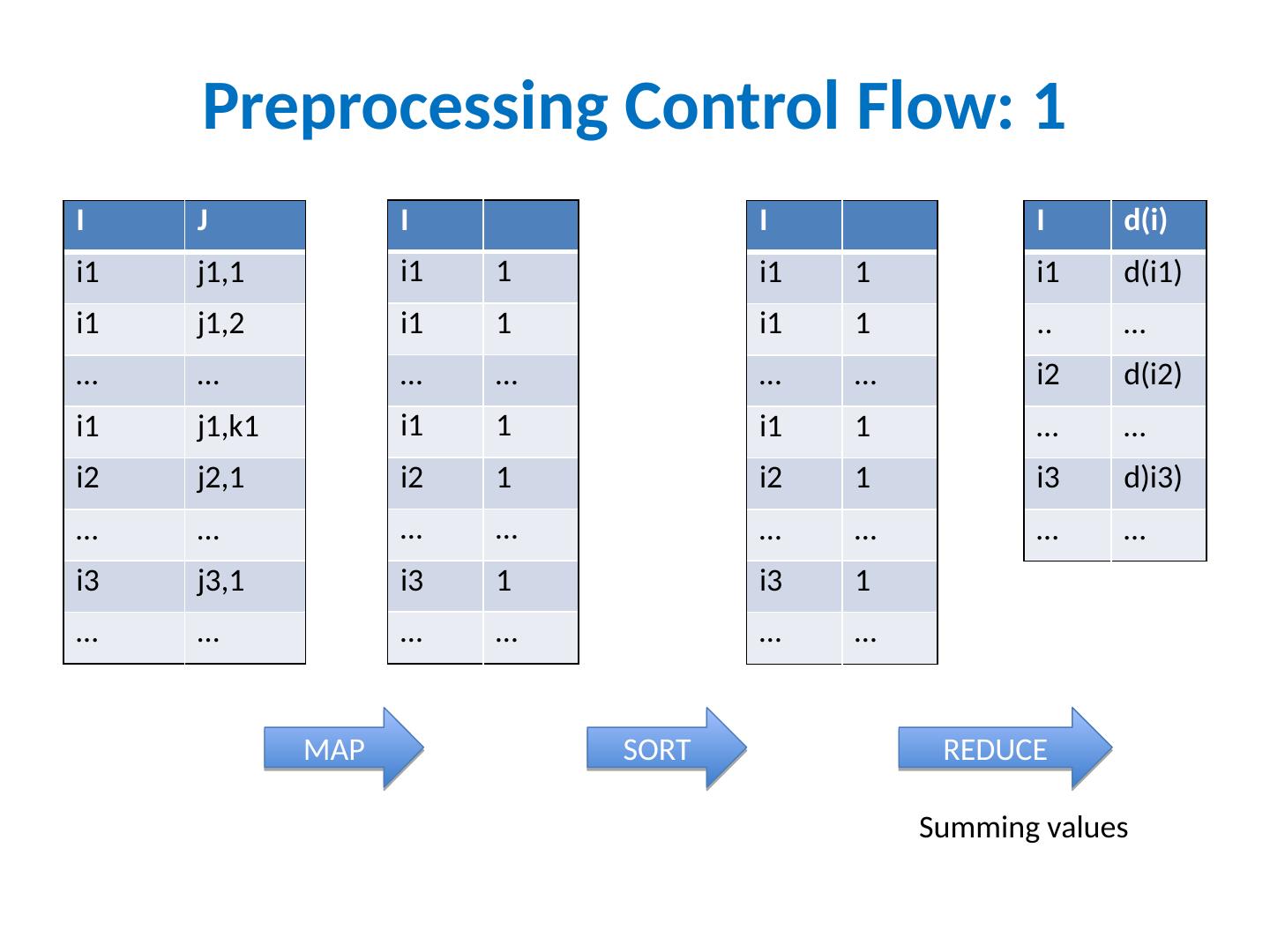
21 .Streaming PageRank: preprocessing Original encoding is edges ( i,j ) Mapper replaces i,j with i,1 Reducer is a SumReducer Result is pairs ( i,d(i )) Then: join this back with edges ( i,j ) For each i,j pair: send j as a message to node i in the degree table messages always sorted after non-messages the reducer for the degree table sees i,d(i ) first then j1, j2, …. can output the key,value pairs with key= i , value= d(i ), j

22 .Preprocessing Control Flow: 1 I J i1 j1,1 i1 j1,2 … … i1 j1,k1 i2 j2,1 … … i3 j3,1 … … I i1 1 i1 1 … … i1 1 i2 1 … … i3 1 … … I i1 1 i1 1 … … i1 1 i2 1 … … i3 1 … … I d(i ) i1 d(i1) .. … i2 d(i2) … … i3 d)i3) … … MAP SORT REDUCE Summing values

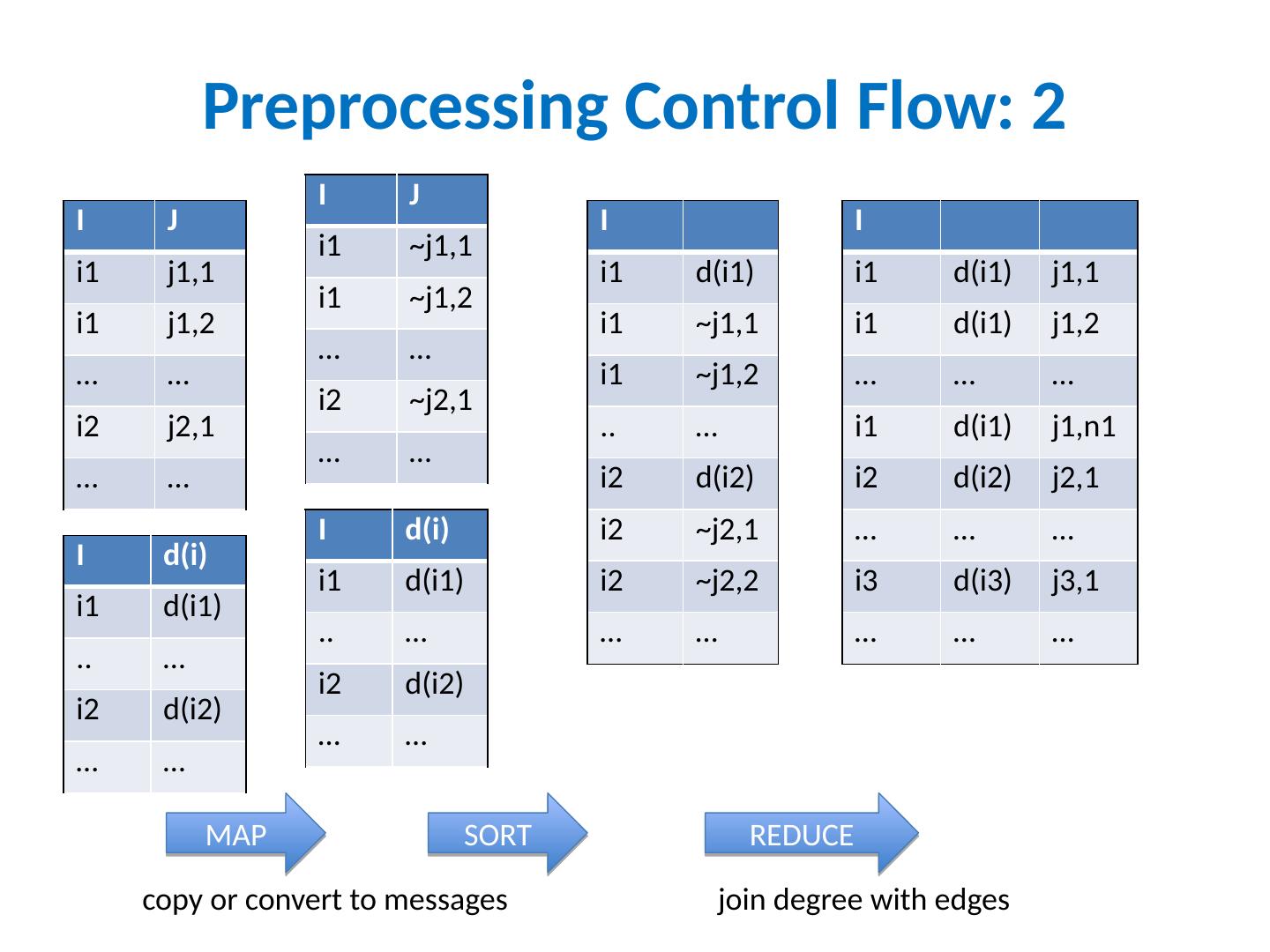
23 .Preprocessing Control Flow: 2 I J i1 j1,1 i1 j1,2 … … i2 j2,1 … … I i1 d(i1) i1 ~j1,1 i1 ~j1,2 .. … i2 d(i2) i2 ~j2,1 i2 ~j2,2 … … I i1 d(i1) j1,1 i1 d(i1) j1,2 … … … i1 d(i1) j1,n1 i2 d(i2) j2,1 … … … i3 d(i3) j3,1 … … … I d(i ) i1 d(i1) .. … i2 d(i2) … … MAP SORT REDUCE I J i1 ~j1,1 i1 ~j1,2 … … i2 ~j2,1 … … I d(i ) i1 d(i1) .. … i2 d(i2) … … copy or convert to messages join degree with edges

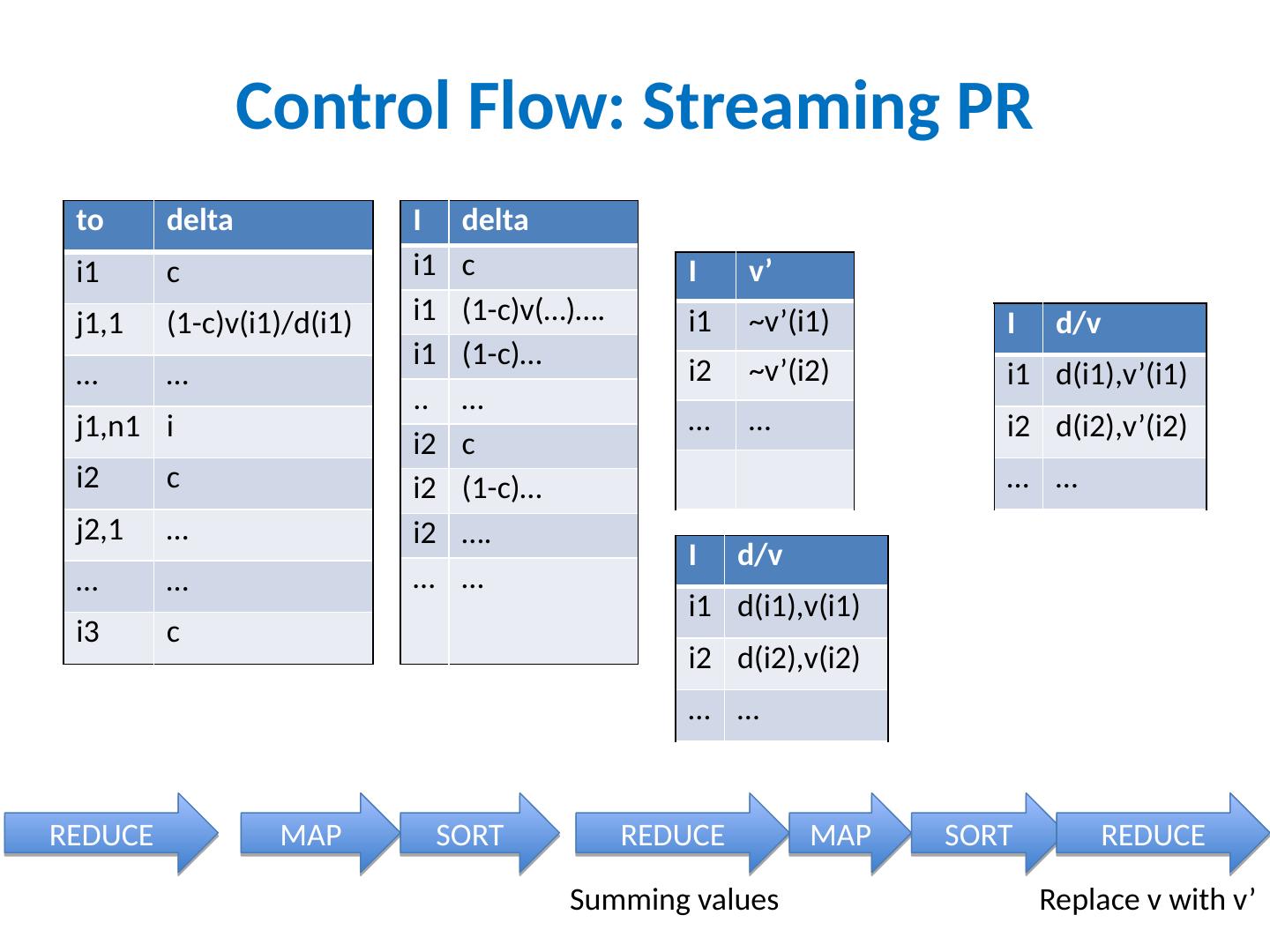
24 .Control Flow: Streaming PR I J i1 j1,1 i1 j1,2 … … i2 j2,1 … … I d/v i1 d(i1),v(i1) i1 ~j1,1 i1 ~j1,2 .. … i2 d(i2),v(i2) i2 ~j2,1 i2 ~j2,2 … … to delta i1 c j1,1 (1-c)v(i1)/d(i1) … … j1,n1 i i2 c j2,1 … … … i3 c I d/v i1 d(i1),v(i1) i2 d(i2),v(i2) … … MAP SORT REDUCE MAP SORT I delta i1 c i1 (1-c)v(…)…. i1 (1-c)… .. … i2 c i2 (1-c)… i2 …. … … copy or convert to messages send “ pageRank updates ” to outlinks

25 .Control Flow: Streaming PR to delta i1 c j1,1 (1-c)v(i1)/d(i1) … … j1,n1 i i2 c j2,1 … … … i3 c REDUCE MAP SORT I delta i1 c i1 (1-c)v(…)…. i1 (1-c)… .. … i2 c i2 (1-c)… i2 …. … … REDUCE I v ’ i1 ~v’(i1) i2 ~v’(i2) … … Summing values I d/v i1 d(i1),v(i1) i2 d(i2),v(i2) … … MAP SORT REDUCE Replace v with v ’ I d/v i1 d(i1),v’(i1) i2 d(i2),v’(i2) … …

26 .Control Flow: Streaming PR I J i1 j1,1 i1 j1,2 … … i2 j2,1 … … I d/v i1 d(i1),v(i1) i2 d(i2),v(i2) … … MAP copy or convert to messages and back around for next iteration… .

27 .PageRank in MapReduce

28 .More on graph algorithms PageRank is a one simple example of a graph algorithm but an important one personalized PageRank (aka “random walk with restart”) is an important operation in machine learning/data analysis settings PageRank is typical in some ways Trivial when graph fits in memory Easy when node weights fit in memory More complex to do with constant memory A major expense is scanning through the graph many times … same as with SGD/Logistic regression disk-based streaming is much more expensive than memory-based approaches Locality of access is very important! gains if you can pre-cluster the graph even approximately avoid sending messages across the network – keep them local

29 .Machine Learning in Graphs - 2010