Distributed Approximate Spectral Clustering for Large-Scale Data

1 .Distributed Approximate Spectral Clustering for Large-Scale Datasets Fei Gao, Wael Abd-Almageed , Mohamed Hefeeda Presented by : Bita Kazemi Zahrani 1

2 .Outline Introduction Terminologies Related Works Distributed Approximate Spectral Clustering (DASC) Analysis Evaluations Conclusion Summary References 2

3 .The idea …. Challenge : High time and Space complexity in Machine Learning algorithms Idea : propose a novel kernel-based machine learning algorithm to process large datasets Challenge : kernel-based algorithms suffer from scalability O(n 2 ) Claim : reduction in computation and memory with insignificant accuracy loss and providing a control over accuracy and reduction tradeoff Developed a spectral clustering algorithm Deployed on Amazon Elastic MapReduce service 3

4 .Terminologies Kernel based methods : one of the methods for pattern analysis, Based on kernel methods : analyzing raw representation of data by a similarity function over pairs instead of a feature vector In another word manipulating data or looking at data from another dimension Spectral clustering : using eigenvalues( characteristic values) of similarity matrix 4

5 .Introduction Proliferation of data in all fields Use of Machine Learning in science and engineering The paper introduces the class of Machine Learning Algorithms efficient for large datasets Two main techniques : Controlled Approximation ( tradeoff between accuracy and reduction) Elastic distribution of computation ( machine learning technique harnessing the distributed flexibility offered by clouds) THE PERFORMANCE OF KERNEL-BASED ALGORITHMS IMPROVES WHEN SIZE OF TRAINING DATASET INCREASES! 5

6 .Introduction Kernel-based algorithms -> O(n 2 ) similarity matrix Idea : design an approximation algorithm for constructing the kernel matrix for large datasets The steps : Design an approximation algorithm for kernel matrix computation scalable to all ML algorithms Design a Spectral Classification on top of that to show the effect on accuracy Implemented with MapReduce tested on lab cluster and EMR Experiments on both real and synthetic data 6

7 .Distributed Approximate Spectral Clustering (DASC) Overview Details Mapreduce Implementation 7

8 .Overview Kernel-based algorithms : very popular in the past decade Classification Dimensionality reduction Data clustering Compute kernel matrix i.e kernelized distance between data pair 1. create compact signatures for all data points 2. group the data with similar signature ( preprocessing) 3. compute similarity values for data in each group to construct similarity matrix 4. perform Spectral Clustering on the appx’s similarity matrix (SC can be replaces by any other kernel base approach) 8

9 .Detail The first step is preprocessing with Locality Sensitive Hashing(LSH) LSH -> probability reduction technique Dimension reduction technique : hash input, map similar items to the same bucket, reduce the size of input universe The idea : if distance of two points is less than a Threshold with probability p1, and distance of those Points is higher than the threshold by appx factor of c Then group them together or output the same hash!! Points with higher collision fall in the same bucket! 9 Courtesy: Wikipedia

10 .Details LSH : different techniques Random projection Stable distribution …. Random projection : Choose a random hyperplane Designed to appx the cosine distance when r is the hyperplane ( h is + or -) The formula is an appx of cosine( )   10 Courtesy: Wikipedia

11 .Details Given N data points Random projection hashing to produce a M-bit signature fro each data point Choose an arbitrary dimension Compare with threshold If feature value in the dimension is larger than threshold -> 1 Otherwise 0 M arbitrary dimensions, M bit 11 O(MN)

12 .Details M-bit signatures Near-duplicate signatures ( at least P bit in common )go to the same bucket Let’s say we have T buckets, each bucket N i points : = N Gaussian similarity to compute the distance between signatures Last step running Spectral Clustering on the buckets   12

13 .Detail Compute Laplacian Matrix for each similarity matrix S i The complexity is Compute the first K eigenvectors with QR decomposition QR : decomposing of a matrix A into a product   QR of an orthogonal Q and an upper triangular matrix   R ( O(K i 3 )) Reduction of Laplacian to triangular symmetric Ai QR becomes O(Ki)   13 O(Ki. )   Adding up : T DASC = O(M.N) + O(T 2 ) + O(Ki. )  

14 .Mapreduce Implementation Two MapReduce stages : 1. applies LSH on input and computes signatures Mapper : (index , inputVector ) --- > (signature, index) Reducer : ( signature,index ) ---  ( signature, listof (index)) [ based on similarity] For the approximation P is introduced to restrict the appx If P bits out of M are similar : put in the same bucket Compare two M-bit signature A and B by bit manipulation : Ans =0 -> A and B have one bit difference O(1) 2. Standard MapReduce implementation of spectral clustering in Mahout library   14

15 .15 Courtesy: reference [1]

16 .Analysis and Complexity Complexity Analysis Accuracy Analysis 16

17 .Complexity Analysis Computation analysis Memory analysis 17 Courtesy: reference [1] Courtesy: reference [1] Courtesy: reference [1]

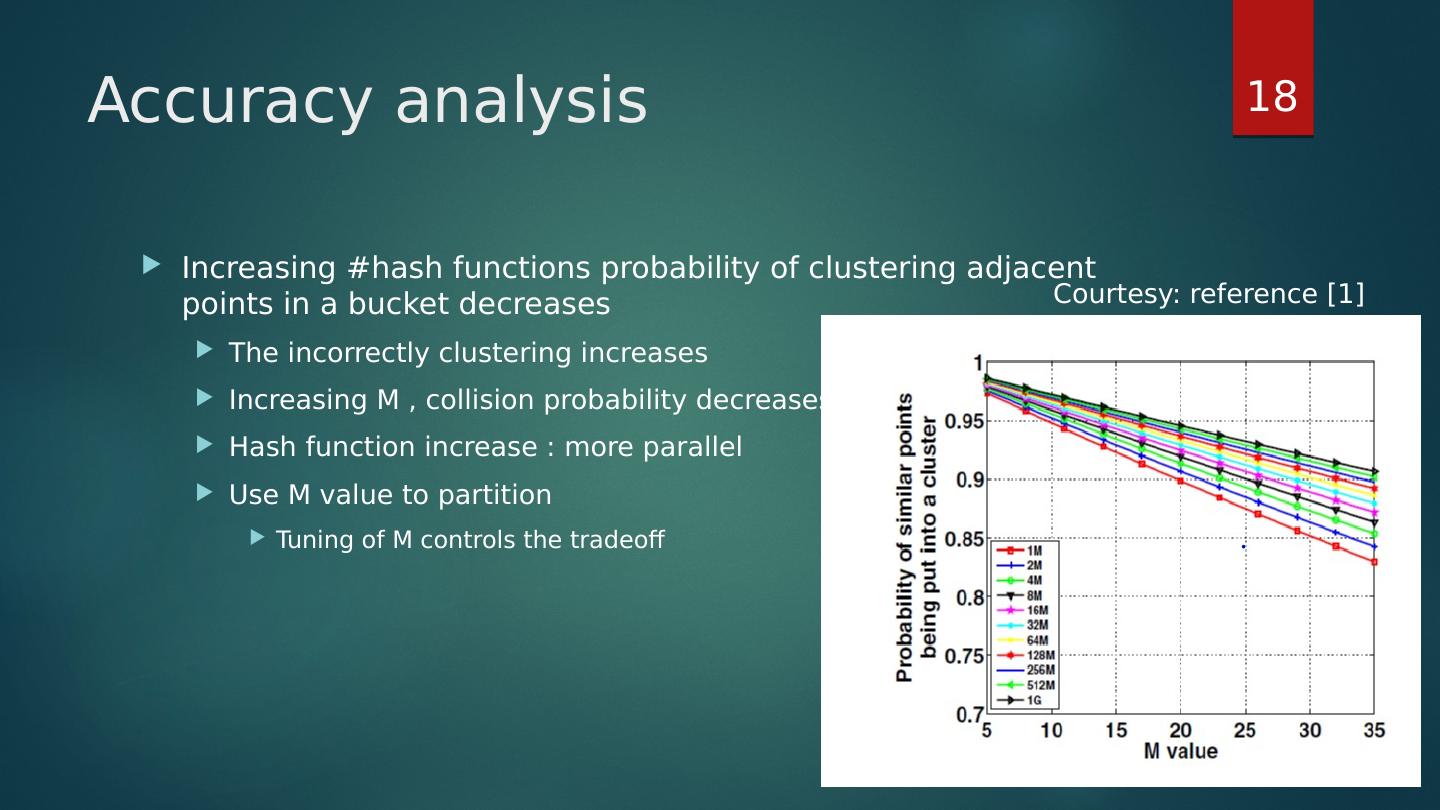
18 .Accuracy analysis Increasing #hash functions probability of clustering adjacent points in a bucket decreases The incorrectly clustering increases Increasing M , collision probability decreases Hash function increase : more parallel Use M value to partition Tuning of M controls the tradeoff 18 Courtesy: reference [1]

19 .Accuracy Analysis Randomly selected documents Ratio :Correctly classified points to the total number DASC better than PSC, close to SC NYST on MATLAB [no cluster] Clustering didn’t affect accuracy too much 19 Courtesy: reference [1]

20 .Experimental Evaluations Platform Datasets Performance Metrics Algorithm Implemented and Compared Agains Results for Clustering Results for Time and Space Complexities Elasticity and Scalability 20

21 .Platform Hadoop MapReduce Framework Local cluster and Amazon EMR Local : 5 machines (1 master/ 4 slaves) Intel Core2 Duo E6550 1GB DRAM Hadoop 0.20.2 on Ubunto , Java 1.6.0 EMR :variable configs : 16,32,64 machines 1.7GB Memory, 350 GB disk Hadoop 0.20.2 on Debian Linux 21 Courtesy: reference [1]

22 .Dataset Synthetic Real : Wikipedia 22 Courtesy: reference [1]

23 .Job flow on EMR Job Flow: collection of steps on a dataset First partition dataset into buckets with LSH Each bucket stored in a file SC applied to each bucket Partitions are processed based on mappers available Data dependent hashing can be used instead of LSH Locality is achieved through the first step LSH Highly scalable if nodes are increased or decreased dynamically allocates fewer or more number of partitions to nodes 23

24 .Algorithms and Performance metrics Computational and space complexity Clustering accuracy Ratio of correct #clustered points / #total points DBI : Davies- Bouldin Index and ASE average squared error Fnorm to similarity of original and approximate kernel matrix Implemented DASC, PSC and SC, NYST DASC modifying Mahout Library M = [( logN )/2− 1[ , and P = M-1 to have O(1) comparison SC Mahout PSC C++ implementation of SC by PARPACK lib NYST implemented by MATLAB 24

25 .Results for Clustering Accuracy Similarity between approximate and original Gram matrices Using low-level F-norm 4K to 512K data points Not able to use more than 512 K Needs square of the input size Different number of buckets ! 4 to 4K Larger the number of buckets, more partitioning Lesser accuracy Increase #buckets, decrease F-norm ratio, less similar Increase #buckets before Fnorm drops 25 Courtesy: reference [1]

26 .Results for Time and Space Complexities DASC, PSC and SC comparison: PSC implemented in C++ with MPI DASC implemented in Java with Mapreduce framework SC implemented with Mahout library Order of magnitude : DASC runs o ne order of magnitude faster than PSC Mahout SC didn’t scale to more than 15 26 Courtesy: reference [1]

27 .Conclusion Kernel-based Machine Learning Approximation for computing kernel matrix LSH to reduce the kernel computation DASC O(B) reduction in size of problem (B number of buckets) B depends on number of bits in signature Tested on real and synthetic dataset -> Real : Wikipedia 90% accuracy 27

28 .Critics The approximation factor depends on the size of the problem The algorithm is scaled just to kernel-based machine learning methods which are applicable just to a limited number of datasets Algorithms compared are each implemented in different frameworks, i.e MPI implementation might be really inefficient, thus the comparison is not really fair! 28

29 .References Hefeeda , Mohamed, Fei Gao, and Wael Abd-Almageed . "Distributed approximate spectral clustering for large-scale datasets." Proceedings of the 21st international symposium on High-Performance Parallel and Distributed Computing . ACM, 2012. Wikipedia Tom M Mitchell slides : https ://www.cs.cmu.edu/~ tom/10701_sp11/slides 29