- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
033-Path Planning
展开查看详情
1 .Lecture 14: Path Planning II Autonomous Robots, 16-200 Carnegie Mellon University Qatar
2 . Overview Logistics Movie Path Planning continued
3 . Logistics We will send you detailed feedback on your presentation and report as soon as we are done grading your reports Your project topics (title plus one paragraph) are important – come and see us if you need help with your topic HW #3 is due next Monday by 10:30a.m. Lab #3 optional second try due on Thursday during lab – sign up for slots! Timing will be very strict. We will complete the question portion of lab #3 tomorrow so come to the lab even if you don’t want to repeat it Lab #4 will be assigned tomorrow
4 .Plan Today: Path Planning II Next week: Coordination
5 . Movie A Fun Movie ☺
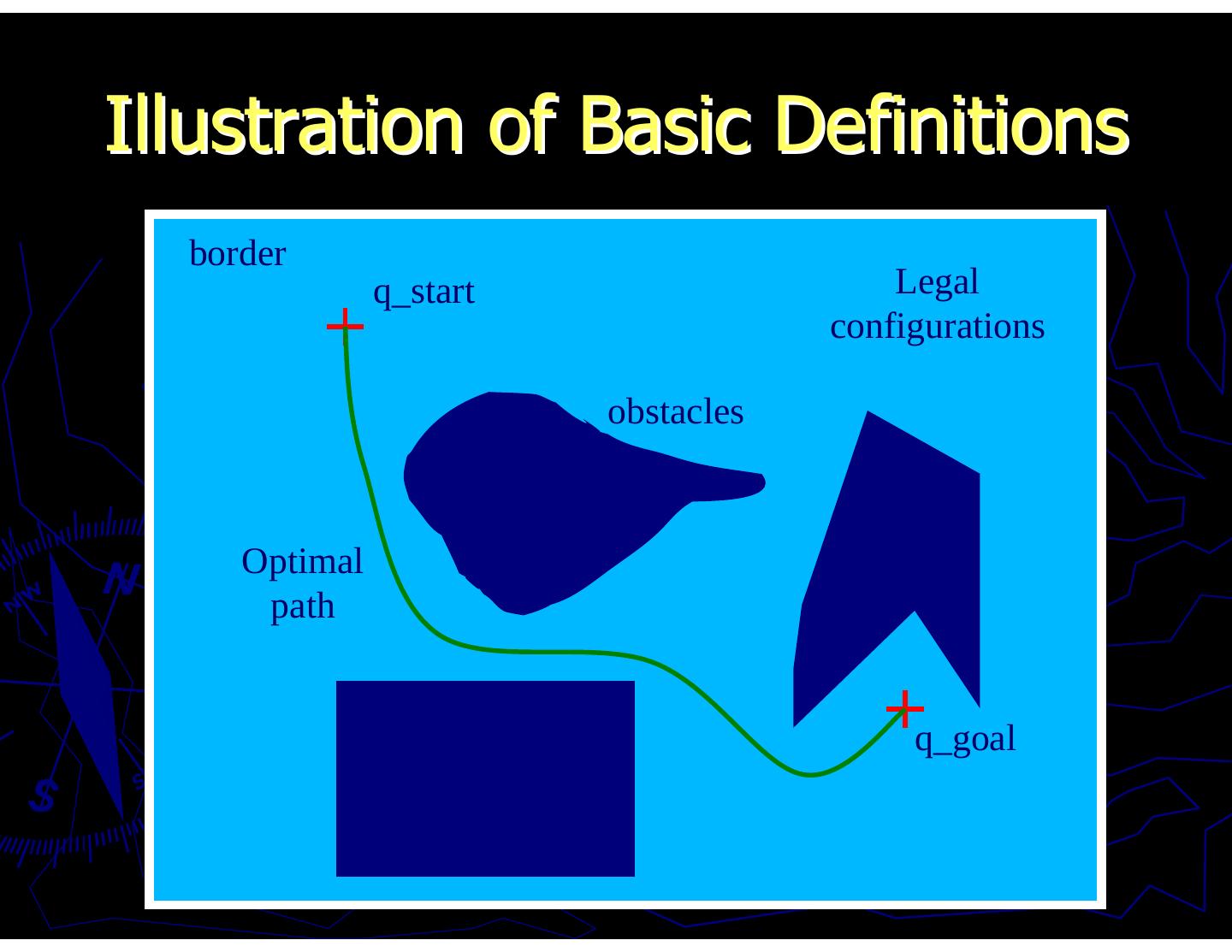
6 . Path Planning Problem Given an initial configuration q_start and a goal configuration q_goal, we must generate the best continuous path of legal configurations between these two points, if such a path exists.
7 .Illustration of Basic Definitions border q_start Legal configurations obstacles Optimal path q_goal
8 . C-Space Transform Steps For a mobile robot that only translates Choose point on the robot. Grow obstacle by translating robot around the edge of the obstacle and tracing line made by the reference point of the robot. Represent the robot only by the reference point. Legal configurations now consist of all non-obstacle points. There is a trick to make this process easier. Robots that can rotate as well are usually represented by a circle. Once the obstacles have been grown, you can plan a path!
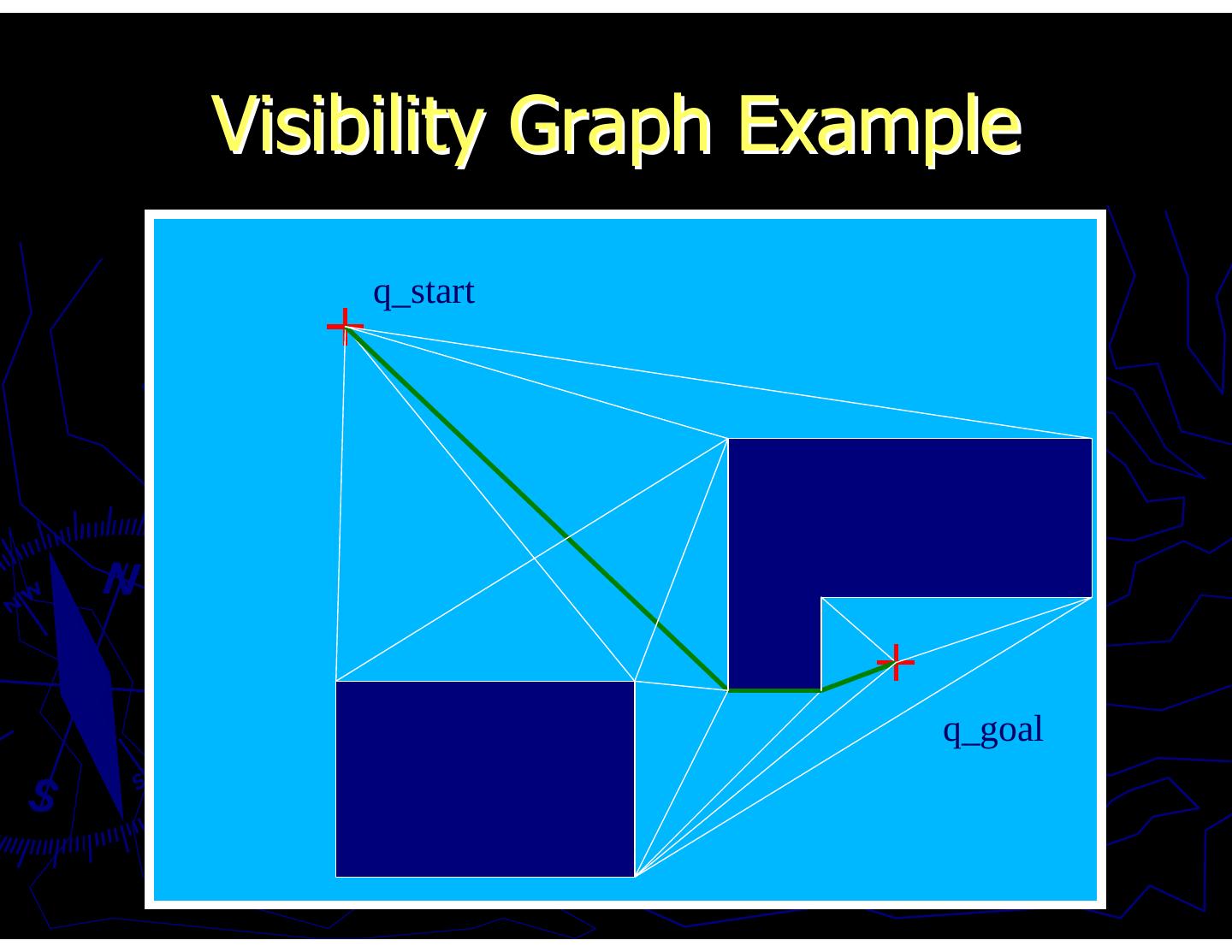
9 .Path-Planning Algorithms Potential methods Visibility graphs Voronoi diagrams Cell decomposition *Note: We don’t go over details of implementation here – just the concepts.
10 . Potential Methods We already learnt Potential Fields – these can be used for path planning! Define f(q) such that: f grows huge as the robot moves towards an obstacle f grows small as the robot moves towards the goal Possible f functions: dg(q) = distance from q to q_goal d1(q) = distance from q to nearest obstacle f(q) = d1(q) – dg(q) OR f(q) = 0.5 β(dg(q))2 + 0.5λ(d1(q))-2 Path is given by following steepest descent on f
11 .Visibility Graph Example q_start q_goal
12 .Voronoi Graph Example q_start h q_goal
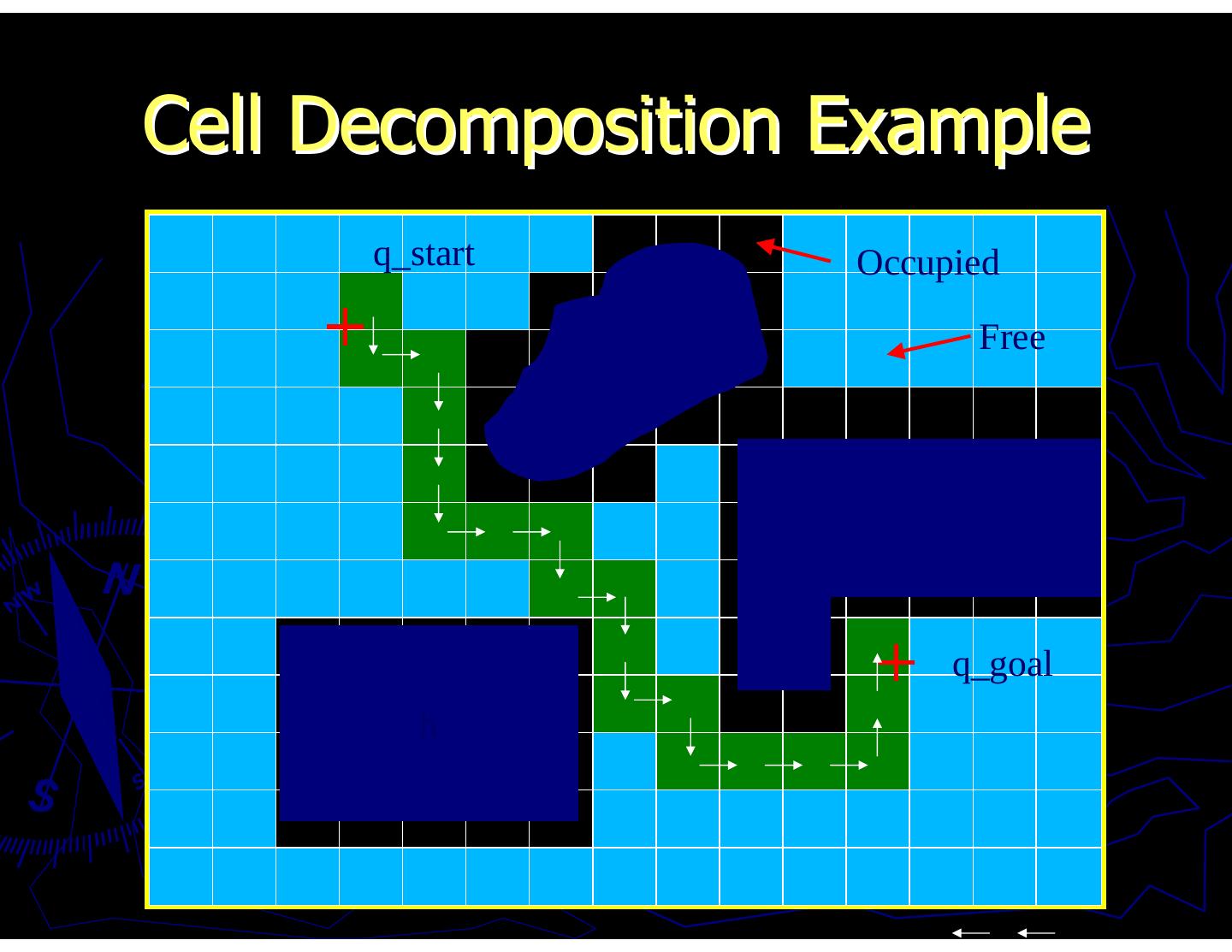
13 . Cell Decomposition Last approach: Divide C-space into convex polygons and plan between legal cells We’ll use grids…but algorithm extends to general convex polygons of different sizes Algorithm: 1. Start with C-space map 2. Divide map into polygons 3. Mark cells containing obstacles as occupied 4. Search for path to goal using unoccupied cells
14 .Cell Decomposition Example q_start Occupied Free q_goal h
15 .Cell Decomposition in Practice Multiple ways to sub-divide C-space Grids, Quad-trees Resolution is a limiting issue Too fine a grid leads to long search time Too coarse a grid misses paths May require post planning smoothing Requires a search algorithm E.g. A* and D*
16 .Quad-Tree Example
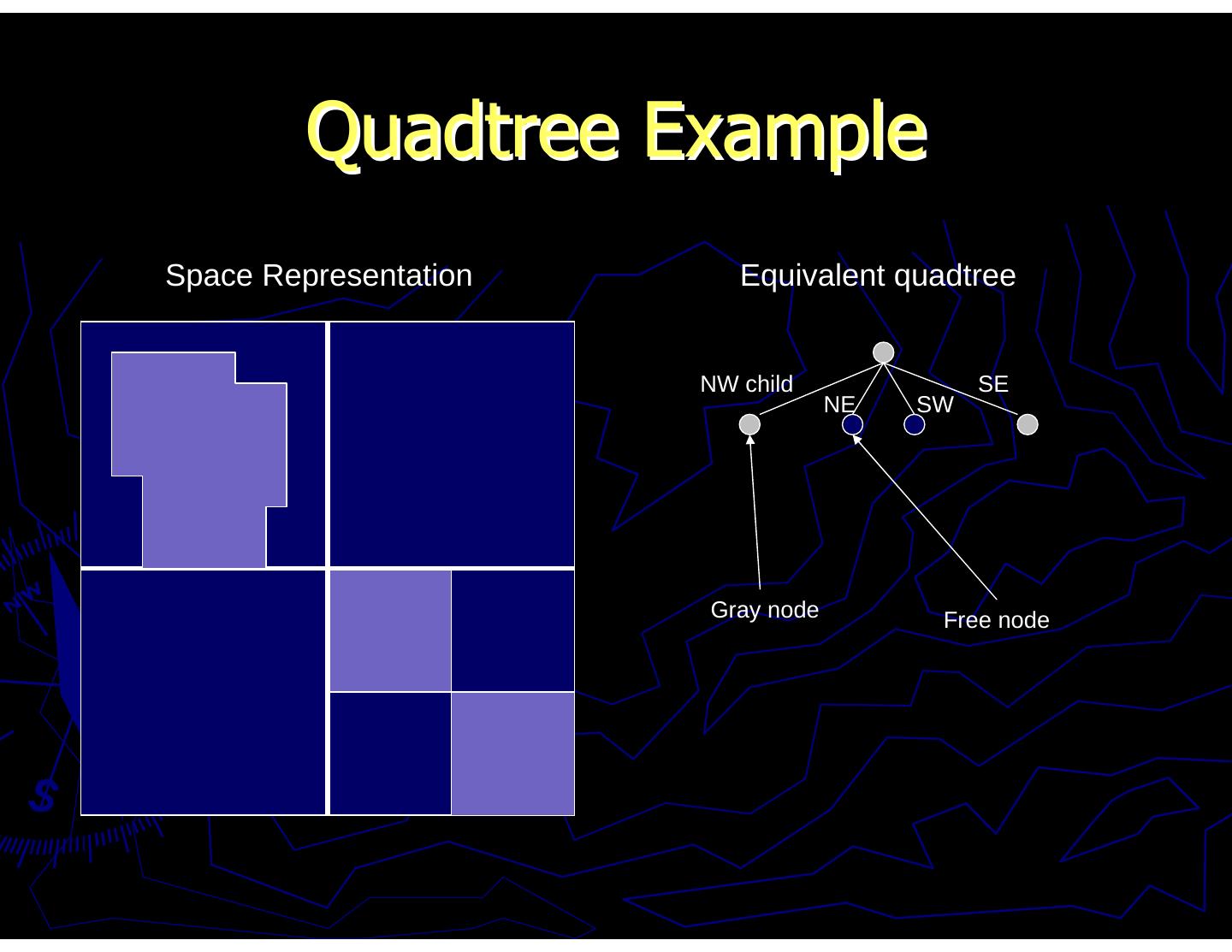
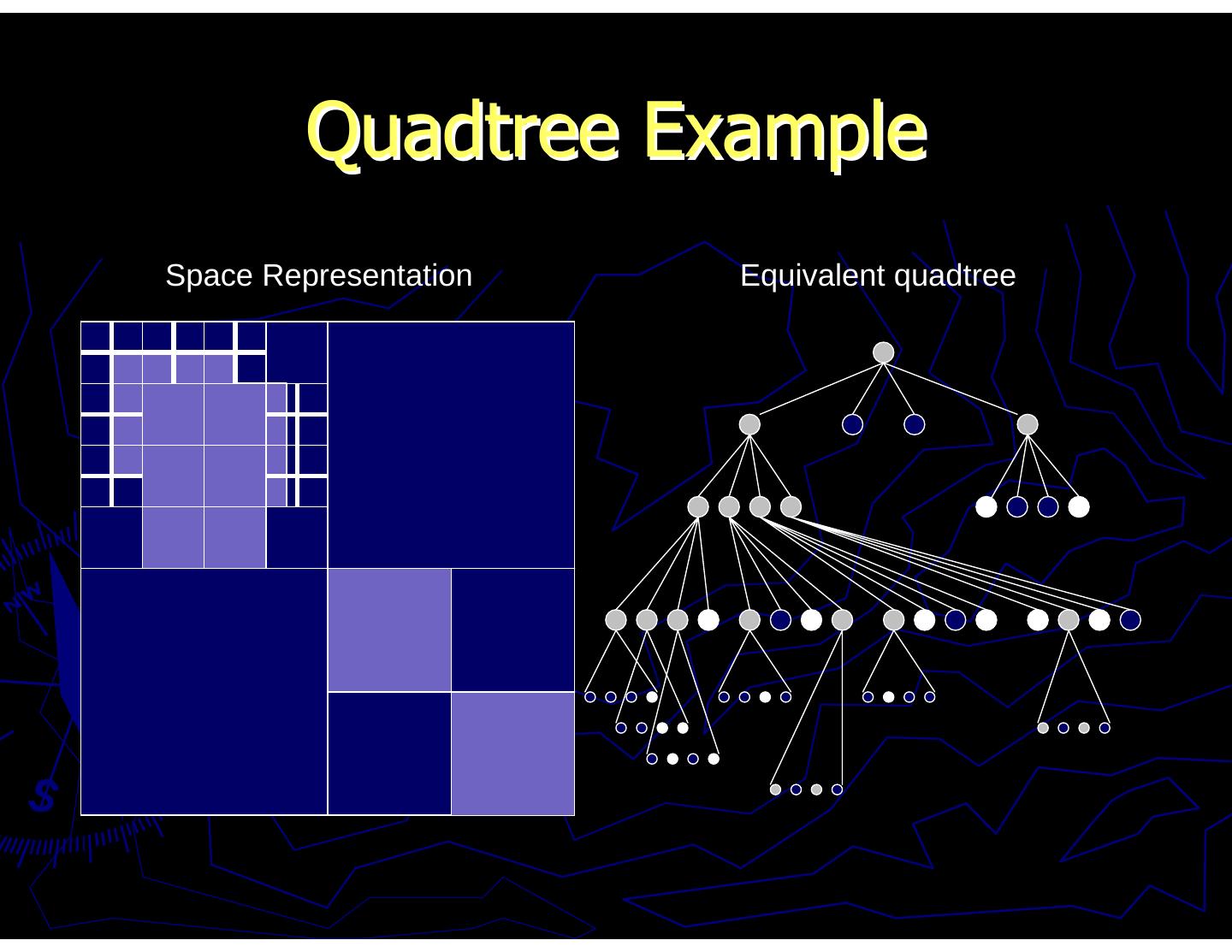
17 . Quadtree Example Space Representation Equivalent quadtree Russell Gayle, The University of North Carolina, Chapel Hill
18 . Quadtree Example Space Representation Equivalent quadtree NW child SE NE SW Gray node Free node
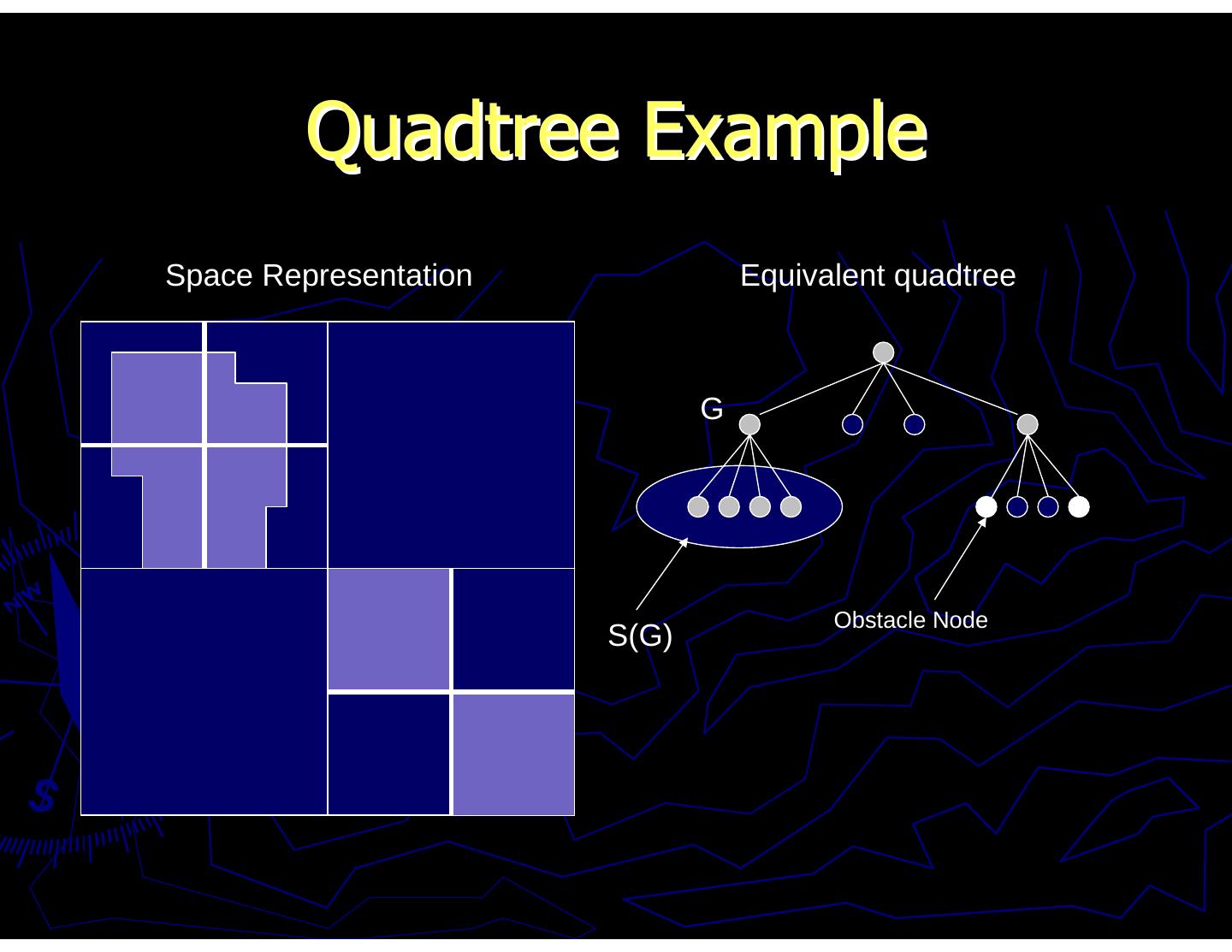
19 . Quadtree Example Space Representation Equivalent quadtree G Obstacle Node S(G)
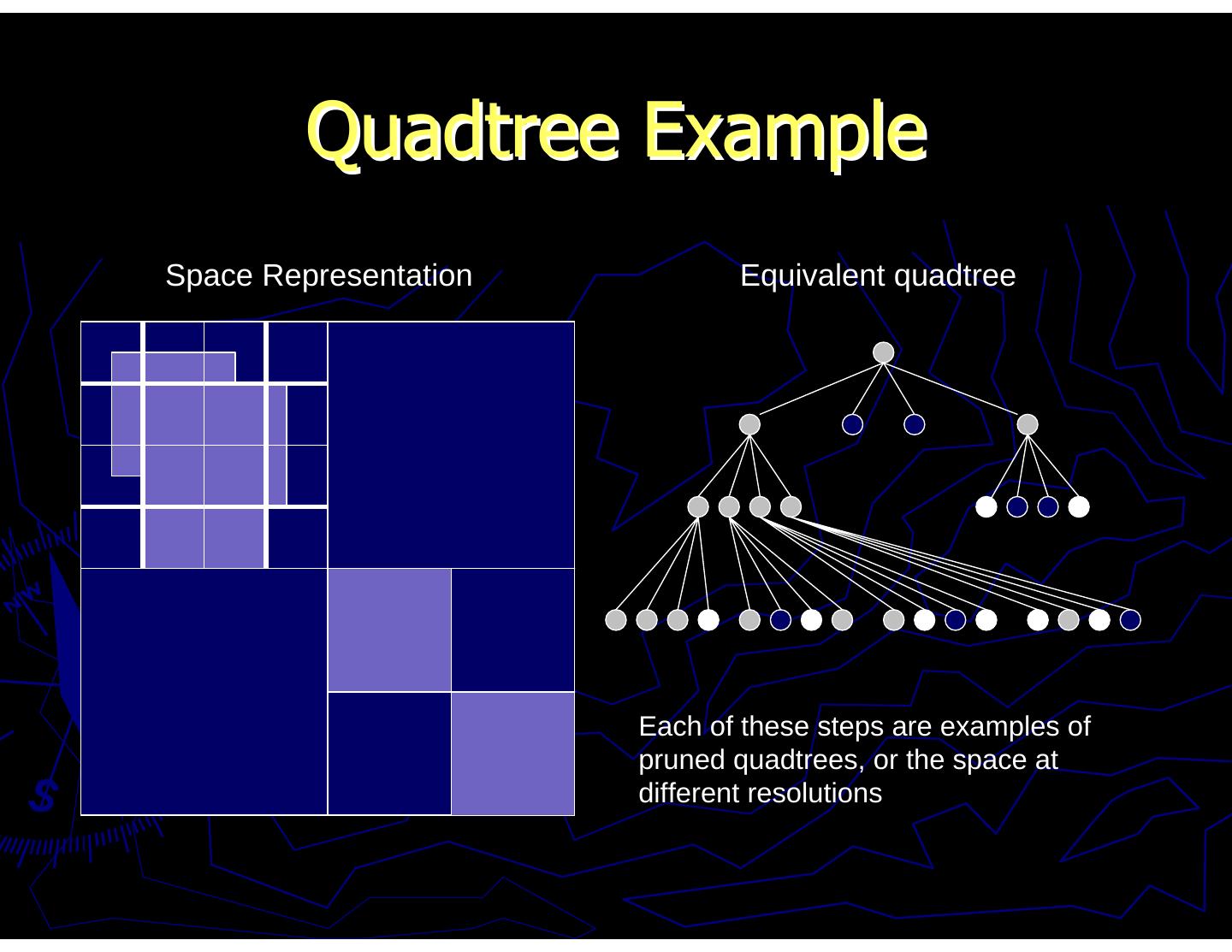
20 . Quadtree Example Space Representation Equivalent quadtree Each of these steps are examples of pruned quadtrees, or the space at different resolutions
21 . Quadtree Example Space Representation Equivalent quadtree
22 . Quadtree Example Space Representation Equivalent quadtree Complete quadtree
23 .Quadtree-Based Path Planning Preprocessing Step 1 Grow the obstacles by radius of the robot’s cross section Convert the result into a quadtree Step 2 Compute a distance transform of the free nodes (from the center of the region represented by a node to the nearest obstacle) Given start and goal points Determine the nodes S and G which contains these points Compute the minimum cost path from S to G through free nodes using the A* graph search
24 . Search Once you have your graph you need to search for the best path Several search methods can be used: A* is the most popular (we will discuss this briefly on Monday) Other options include random search, depth first search, breadth first search, etc. Good search techniques are important for a variety of reasons – you will learn more about them in 15-211 and other CS classes
25 . A Bit of Trivia The concept of a Web spider was developed by Dr. Fuzzy Mouldin Implemented in 1994 on the Web Went into the creation of Lycos Dr. Michael L. (Fuzzy) Mauldin Lycos propelled CMU into the top 5 most successful schools Commercialization proceeds Tangible evidence Newell-Simon Hall
26 . End of slides! See you tomorrow in lab!