013-epistemic logic

1 .EPISTEMIC LOGIC

2 .State Model (AKA Epistemic Model ) We introduce epistemic models Epistemic relations Epistemic relations are equivalence relations This function assigns sets of states to formulas

3 .The language of Epistemic Logic Now that we have extended concept of model we can also extend formally the concept of logic Model is first, model is the main concept in these logics. First we talked about possibility and necessity Next we talked about knowledge Now we talk about belief. Syntax of Epistemic logic sentences (formulas)

4 .Epistemic Language for Muddy Children Syntactically this can be similar to other language of logic But the most important is to know in what logic are we in, model and axioms. Now modal operators have subscript A for agent A

5 .Semantics for this language We use entailment as usually Now modal operators have subscript A for agent A

6 .Duality of modal operators is similar to classical logic quantifiers This duality is useful in proofs and formal reductions done automatically, but it is more convenient in hand transformations to keep both formulas as it helps to understand “what I am actually doing now?”

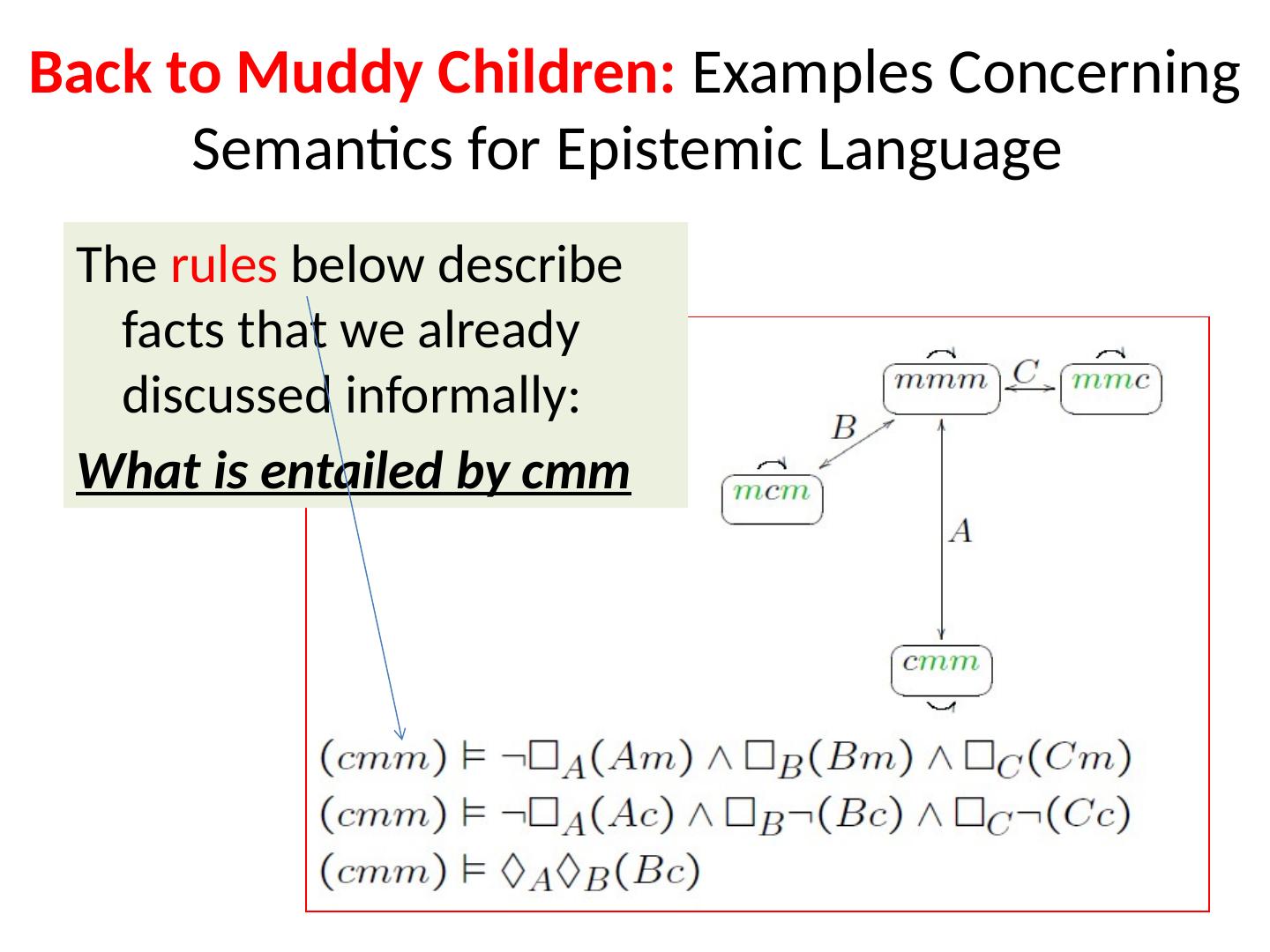
7 .Back to Muddy Children: Examples Concerning Semantics for Epistemic Language The rules below describe facts that we already discussed informally: What is entailed by cmm

8 .Adding Dynamics to epistemic logic Such a language is called Public Announcement Logic It is a kind of Dynamic Epistemic Logic. We are back to Muddy Children

9 .Semantics with Dynamics We define an entailment relation for dynamic logic

10 .Duality for Actions We define the rule for duality of actions

11 .Now we will show more examples of logics For this, we need a new example

12 .The Sum and Product Problem

13 .Sum and Product problem A P S 0 Answer 1 Answer 3 Answer 2 Answer 4 S and P are supposed to find pair x,y

14 .Let us try for small numbers… P1 thinks. 2 3 4 5 6 7 8 9 10 3 6 4 8 12 5 10 15 20 6 12 18 24 7 14 21 28 8 16 24 32 9 18 27 36 11 12 13 14 2 3 4 5 6 7 8 9 10 10 20 30 40 11 22 33 44 12 24 36 48 13 26 39 52 14 28 42 56 15 30 45 60 16 11 12 13 14 P1 would tell if the product were unieque . Like for (2,4), (2,8),,,, Pairs Non-unique after P1: 2,6 2,9 2,12 2,14 2,15 3,4 3,6 3,8 3,10 3,12 3,14 3,15….

15 .Let us try for small numbers… S1 thinks. 2 3 4 5 6 7 8 9 10 3 5 4 6 7 5 7 8 9 6 8 9 10 11 7 9 10 11 12 13 8 10 11 12 13 14 15 9 11 12 13 14 15 16 11 12 13 14 2 3 4 5 6 7 8 9 10 10 12 13 14 15 16 17 11 13 14 15 16 17 18 12 14 15 16 17 18 19 13 15 16 17 18 19 20 14 16 17 18 19 20 21 15 17 18 19 20 21 22 16 11 12 13 14 P1 excludes this pair in P1 Pairs Non-unique after P1: 2,6 2,9 2,12 2,14 2,15 3,4 3,6 3,8 3,10 3,12 3,14 3,15….

16 .Formal solution to P and S problem

17 .Adding Previous-Time Operator Such a language is called Temporal Public Announcement Logic It is “possible” type of operator of type Y

18 .Language for Sum and Product Now that we have the new operator, we can formulate language for the Sum and Product problem Necessary for S Agents are P and S Or means any of them

19 .Translation to formulas Previously it was necessary for S that P did not know

20 .Formulation of a Model for the “Sum and Product” problem Meaning of relations S and P, what S and P know Definition of set S Definitions of equalities Now we have to construct the model

21 .Formula for Sum and Product Conversation We want to find the state that this formula is always true Remember our notation

22 .Model Checker Program DEMO already exists DEMO software written in Haskell Inventing such problems and solving them is an active research area