010-muddy children problem

1 .Now, knowing classical logic we move to model checking and modal logic Muddy Children Problem

2 .The Muddy Children Puzzle n children meet their father after playing in the mud. The father notices that k of the children have mud dots on their foreheads. Each child sees everybody else’s foreheads, but not his own. The father says: “ At least one of you has mud on his forehead .” The father then says: “ Do any of you know that you have mud on your forehead? If you do, raise your hand now. ” No one raises his hand. The father repeats the question, and again no one moves. After exactly k repetitions , all children with muddy foreheads raise their hands simultaneously.

3 .Muddy Children, Dirty Kids, Wise men, Cheating Husbands, etc.

4 .Muddy Children (cont.) Suppose k = 1 The muddy child knows the others are clean When the father says at least one is muddy, he concludes that it’s him

5 .Muddy Children. BEST CASE: One child Concluding – recursion starter

6 .Muddy Children (cont.) Suppose k = 2 Suppose you are muddy After the first announcement, you see another muddy child, so you think perhaps he’s the only muddy one. But you note that this child did not raise his hand, and you realise you are also muddy. So you raise your hand in the next round, and so does the other muddy child

7 .Detailed analysis of two children Muddy Children. CASE 1: 1 child has mud dot on his head CASE 2: Both children have mud dots on their heads

8 .Now suppose there are 3 children Muddy Children.

9 .Case of three children Muddy Children.

10 .Case of three children Muddy Children.

11 .Case of three children Muddy Children.

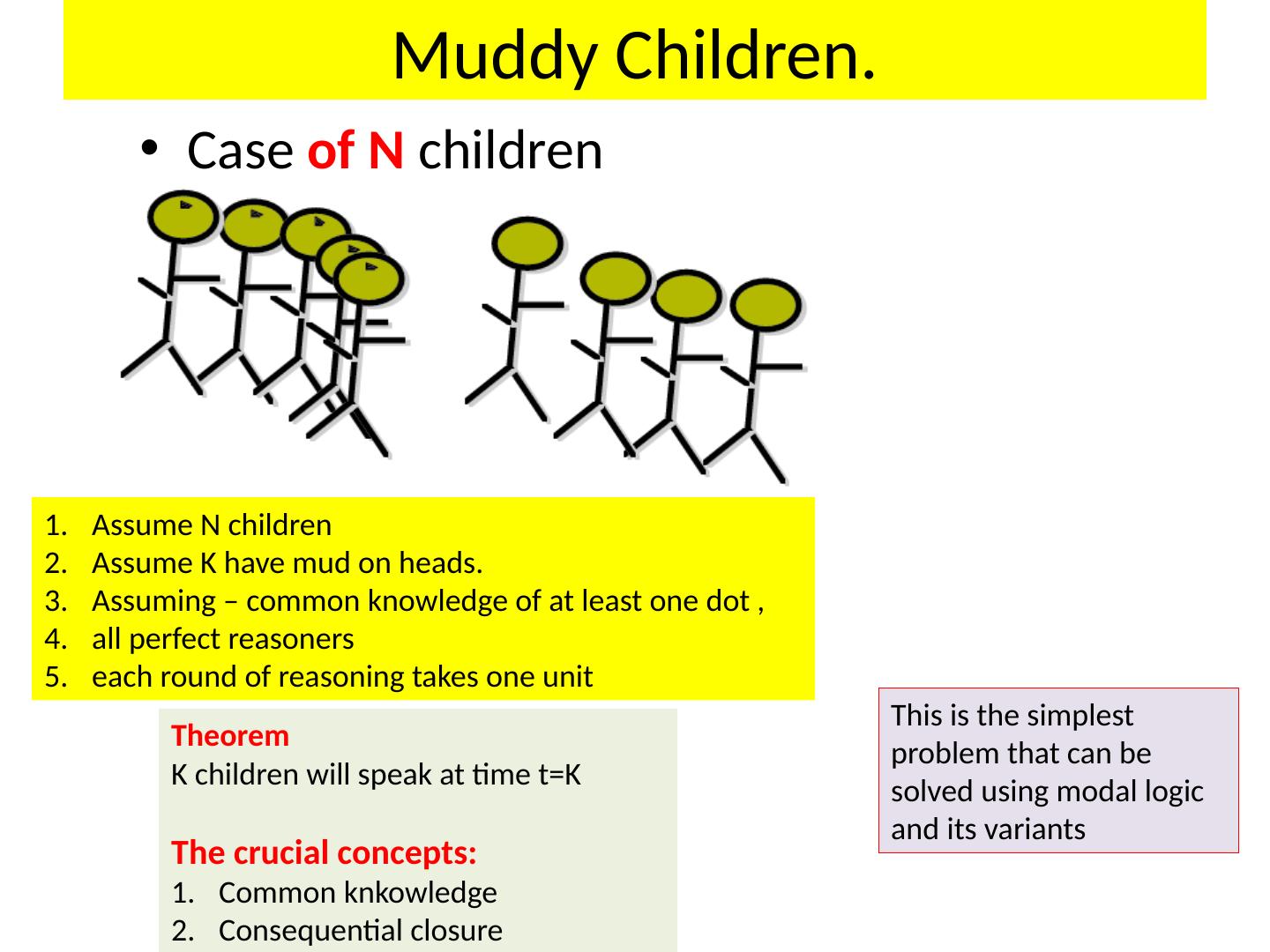
12 .Case of N children Muddy Children. Assume N children Assume K have mud on heads. Assuming – common knowledge of at least one dot , all perfect reasoners each round of reasoning takes one unit Theorem K children will speak at time t=K The crucial concepts: Common knkowledge Consequential closure This is the simplest problem that can be solved using modal logic and its variants

13 .The Partition Model of Knowledge

14 .Concepts to remind from classical logic Agent Group of agents Language Ordered tuple for definition Possible worlds Interpretation function Partitions of set

15 .Suppose there are two propositions p and q There are 4 possible worlds : w 1 : p  q w 2 : p   q w 3 :  p  q w 4 :  p   q Suppose the real world is w 1 , and that in w 1 agent i cannot distinguish between w 1 and w 2 We say that I i ( w 1 ) = { w 1 , w 2 } This means, in world w 1 agent i cannot distinguish between world w 1 and world w 2 Example of worlds Function I describes non- distinguishability of worlds Worlds and non- distinguishability of worlds W = { w 1 , w 2 , w 3 , w 4 } is the set of all worlds

16 .Partition Model of knowledge, partition of worlds in the set of all worlds W What is partition of worlds? Each I i is a partition of W for agent i Remember: a partition chops a set into disjoint sets I i ( w ) includes all the worlds in the partition of world w Intuition: if the actual world is w , then I i ( w ) is the set of worlds that agent i cannot distinguish from w i.e. all worlds in I i ( w ), all possible as far as i knows

17 .W = set of all worlds for Muddy Children with two children This is knowledge of child 2 w 1 w 3 w 4 w 2 Partition model when children see one another but before father speaks

18 .The Partition Model of Knowledge An n-agent partition model over language  is A = ( W ,  , I 1 , …, I n ) where W is a set of possible worlds  :   2 W is an interpretation function that determines which sentences are true in which worlds Each I i is a partition of W for agent i Remember: a partition chops a set into disjoint sets I i ( w ) includes all the worlds in the partition of world w Now we can define the partition model of Knowledge

19 .The Knowledge Operator It describes the knowledge of an agent By K i  we will denote that: “agent i knows that  ”

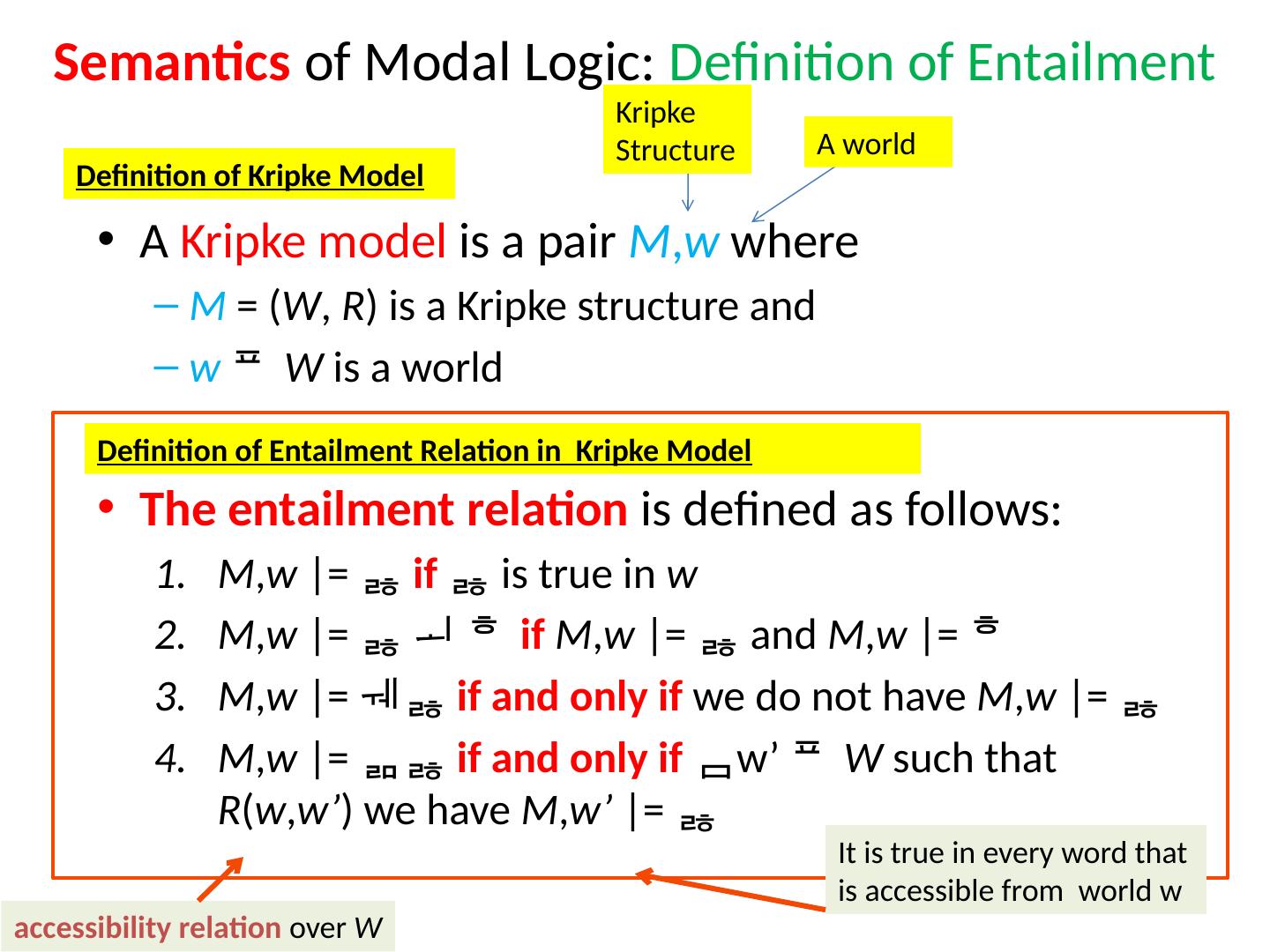
20 .Logical Entailment What is logical entailment ? Let us recall definition: We say A,w |= K i  if and only if  w’ , if w’  I i ( w ), then A,w |=  Intuition: in partition model A , if the actual world is w, agent i knows  if and only if  is true in all worlds he cannot distinguish from w

21 .The Knowledge Operator By K i  we will denote that: “agent i knows that  ” Let A = ( W ,  , I 1 , …, I n ) be a partition model over language  and let w  W We define logical entailment |= as follows: For    we say ( A,w |=  ) if and only if w   (  ) We say A,w |= K i  if and only if  w’ , if w’  I i ( w ), then A,w |=   :   2 W is an interpretation function

22 .Example of Knowledge Operator for Muddy Children Bold oval = actual world Solid boxes = equivalence classes in I 1 Dotted boxes = equivalence classes in I 2 Note: in w 1 we have: K 1 muddy2 K 2 muddy1 K 1  K 2 muddy2 … But we don’t have: K 1 muddy1 Partition for agent 2 (what child 2 knows) Partition for agent 1 Partitioning all possible worlds for agents in case of Two Muddy Children Child 1 but not child 2 knows that child 2 is muddy w 1 : muddy1  muddy2 (actual world) w 2 : muddy1   muddy2 w 3 :  muddy1  muddy2 w 4 :  muddy1   muddy2 Knowledge operators

23 .Muddy Children Revisited Now we have all background to illustrate solution to Muddy Children

24 .Muddy Children Revisited n children meet their father after playing in the mud. The father notices that k of the children have mud on their foreheads. Each child sees everybody else’s foreheads, but not his own.

25 .Muddy Children Revisited (cont .). The Case of two muddy children Suppose n = k = 2 (two children, both muddy ) As the first step we have to formalize the worlds. To formalize worlds, we need logic variables Logic variables are muddy 1 for child 1 being muddy, muddy 2 for child 2 being muddy, etc. With this all Possible Worlds w are the following : w 1 : muddy1  muddy2 (actual world) w 2 : muddy1   muddy2 w 3 :  muddy1  muddy2 w 4 :  muddy1   muddy2 These are all combinations of values of variables muddy1  muddy2 , no more are possible At the start, no one sees or hears anything, so all worlds are possible for each child After seeing each other , each child can tell apart worlds in which the other child’s state is different Formulation of logic variables and possible worlds

26 .Bold oval = actual world Solid boxes = equivalence classes in I 1 Dotted boxes = equivalence classes in I 2 Note: in w 1 we have: K 1 muddy2 K 2 muddy1 K 1  K 2 muddy2 … But we don’t have: K 1 muddy1 Partition for agent 2 (what child 2 knows) Partition for agent 1 Partitioning all possible worlds for agents in case of Two Muddy Children Child 1 but not child 2 knows that child 2 is muddy w 1 : muddy1  muddy2 (actual world) w 2 : muddy1   muddy2 w 3 :  muddy1  muddy2 w 4 :  muddy1   muddy2

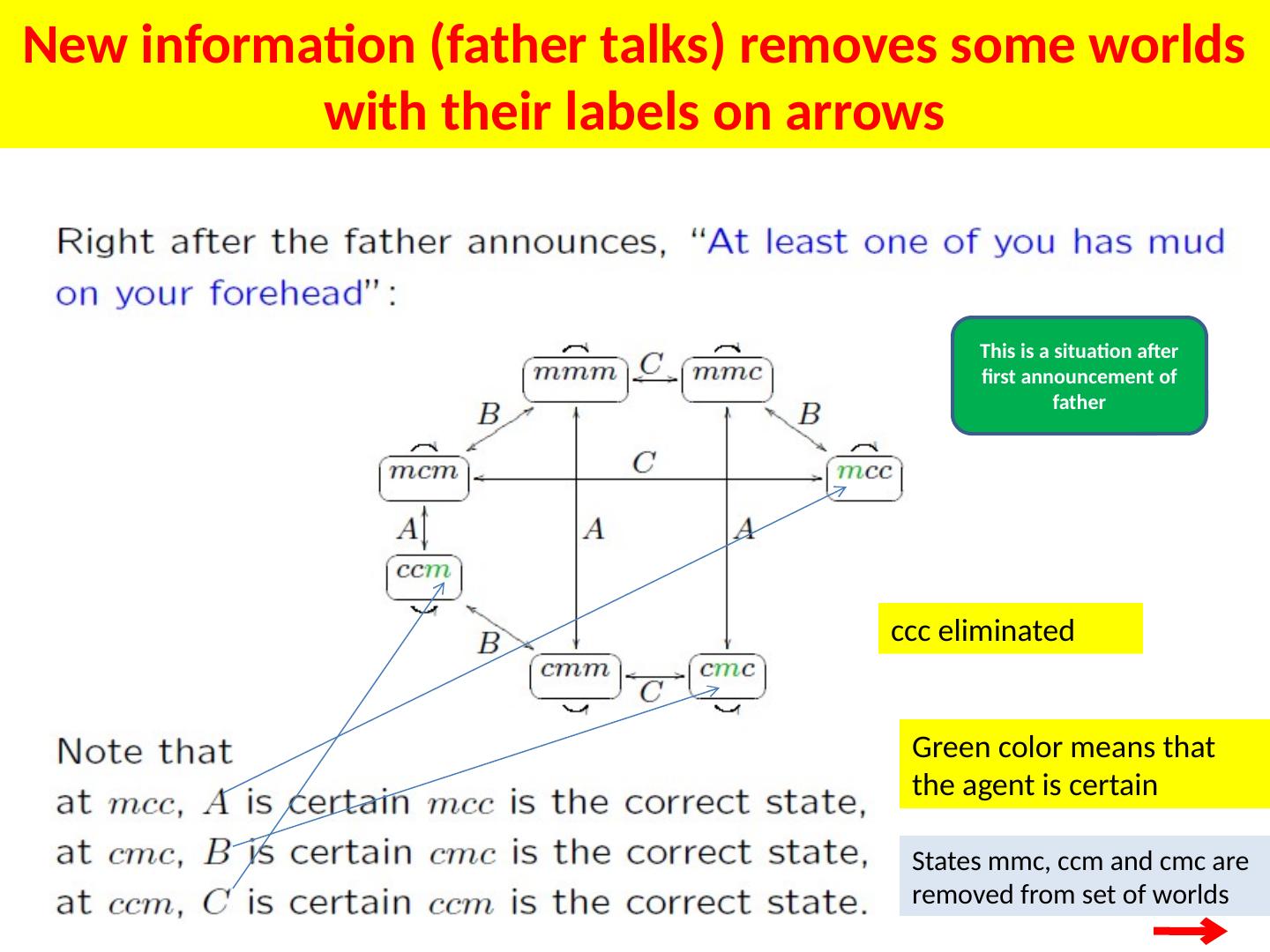
27 .Now we will consider stages of Muddy Children after each statement from father The father says: “ At least one of you has mud on his forehead .” This eliminates the world: w 4 :  muddy1   muddy2 Modification to knowledge and partitions done by the announcement of the father w 1 : muddy1  muddy2 (actual world) w 2 : muddy1   muddy2 w 3 :  muddy1  muddy2 w 4 :  muddy1   muddy2

28 .Muddy Children Revisited (cont.) Bold oval = actual world Solid boxes = equivalence classes in I 1 Dotted boxes = equivalence classes in I 2 Now, after father’s announcement, the children have only three options: Other child is muddy I am muddy We are both muddy For instance in I 2 we see that child 2 thinks as follows: Either we are both muddy Or he (child1) is muddy and I (child 2) am not muddy The same for Child 1 So each partition has more than one world and none of children can communicate any decision w 1 : muddy1  muddy2 (actual world) w 2 : muddy1   muddy2 w 3 :  muddy1  muddy2 w 4 :  muddy1   muddy2

29 .Muddy Children Revisited (cont.) The father then says: “ Do any of you know that you have mud on your forehead? If you do, raise your hand now. ” Here, no child raises his hand. But by observing that the other child did not raise his hand (i.e. does not know whether he’s muddy), each child concludes the true world state. So, at the second announcement from father, they both raise their hands. Modification to knowledge and partitions done by the SECOND announcement of the father