009-agents that reason logically

1 . Agents that Reason Logically n ts g e a c sed gi ba l o e- al dg ion le sit o w po Tim Finin Kn Pro Some material adopted from notes by Andreas Geyer-Schulz and Chuck Dyer 1 

2 . A knowledge-based agent • A knowledge-based agent includes a knowledge base and an inference system. • A knowledge base is a set of representations of facts of the world. • Each individual representation is called a sentence. • The sentences are expressed in a knowledge representation language. • The agent operates as follows: 1. It TELLs the knowledge base what it perceives. 2. It ASKs the knowledge base what action it should perform. 3. It performs the chosen action. Examples of sentences The moon is made of green cheese If A is true then B is true A is false All humans are mortal Confucius is a human 2 

3 . Architecture of a knowledge-based agent • Knowledge Level. – The most abstract level: describe agent by saying what it knows. – Example: A taxi agent might know that the Golden Gate Bridge connects San Francisco with the Marin County. • Logical Level. – The level at which the knowledge is encoded into sentences. – Example: Links(GoldenGateBridge, SanFrancisco, MarinCounty). • Implementation Level. – The physical representation of the sentences in the logical level. – Example: ‘(links goldengatebridge sanfrancisco marincounty) 3 

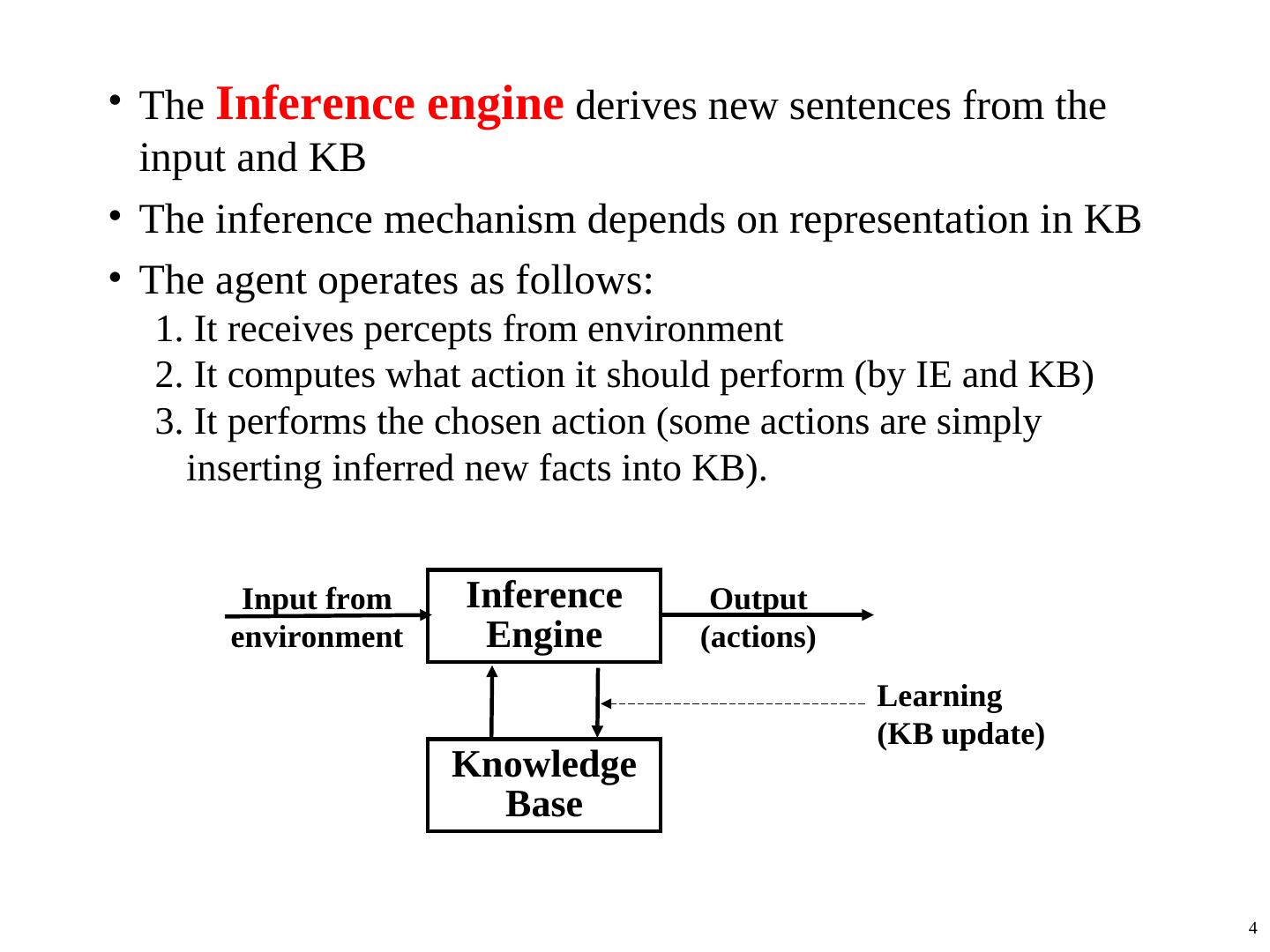
4 .• The Inference engine derives new sentences from the input and KB • The inference mechanism depends on representation in KB • The agent operates as follows: 1. It receives percepts from environment 2. It computes what action it should perform (by IE and KB) 3. It performs the chosen action (some actions are simply inserting inferred new facts into KB). Input from Inference Output environment Engine (actions) Learning (KB update) Knowledge Base 4 

5 .KB can be viewed at different levels • Knowledge Level. review – The most abstract level -- describe agent by saying what it knows. – Example: A taxi agent might know that the Golden Gate Bridge connects San Francisco with the Marin County. • Logical Level. – The level at which the knowledge is encoded into sentences. – Example: Links(GoldenGateBridge, SanFrancisco, MarinCounty). • Implementation Level. – The physical representation of the sentences in the logical level. – Example: “(Links GoldenGateBridge, SanFrancisco, MarinCounty)” 5 

6 . The Wumpus World environment • The Wumpus computer game • The agent explores a cave consisting of rooms connected by passageways. • Lurking somewhere in the cave is the Wumpus, a beast that eats any agent that enters its room. • Some rooms contain bottomless pits that trap any agent that wanders into the room. • Occasionally, there is a heap of gold in a room. • The goal is: – to collect the gold and – exit the world – without being eaten 6 

7 . Jargon file on “Hunt the Wumpus” • WUMPUS /wuhm'p*s/ n. The central monster (and, in many versions, the name) of a famous family of very early computer games called “Hunt The Wumpus,” dating back at least to 1972 • The wumpus lived somewhere in a cave with the topology of a dodecahedron's edge/vertex graph – (later versions supported other topologies, including an icosahedron and Mobius strip). • The player started somewhere at random in the cave with five “crooked arrows”; – these could be shot through up to three connected rooms, and would kill the wumpus on a hit • (later versions introduced the wounded wumpus, which got very angry). 7 

8 . Jargon file on “Hunt the Wumpus” (cont) • Unfortunately for players, the movement necessary to map the maze was made hazardous not merely by the wumpus – (which would eat you if you stepped on him) • There are also bottomless pits and colonies of super bats that would pick you up and drop you at a random location – (later versions added “anaerobic termites” that ate arrows, bat migrations, and earthquakes that randomly change pit locations). • This game appears to have been the first to use a non-random graph-structured map (as opposed to a rectangular grid like the even older Star Trek games). • In this respect, as in the dungeon-like setting and its terse, amusing messages, it prefigured ADVENT and Zork. •It was directly ancestral to both. – (Zork acknowledged this heritage by including a super-bat colony.) – Today, a port is distributed with SunOS and as freeware for the Mac. – A C emulation of the original Basic game is in circulation as freeware on the net. 8 

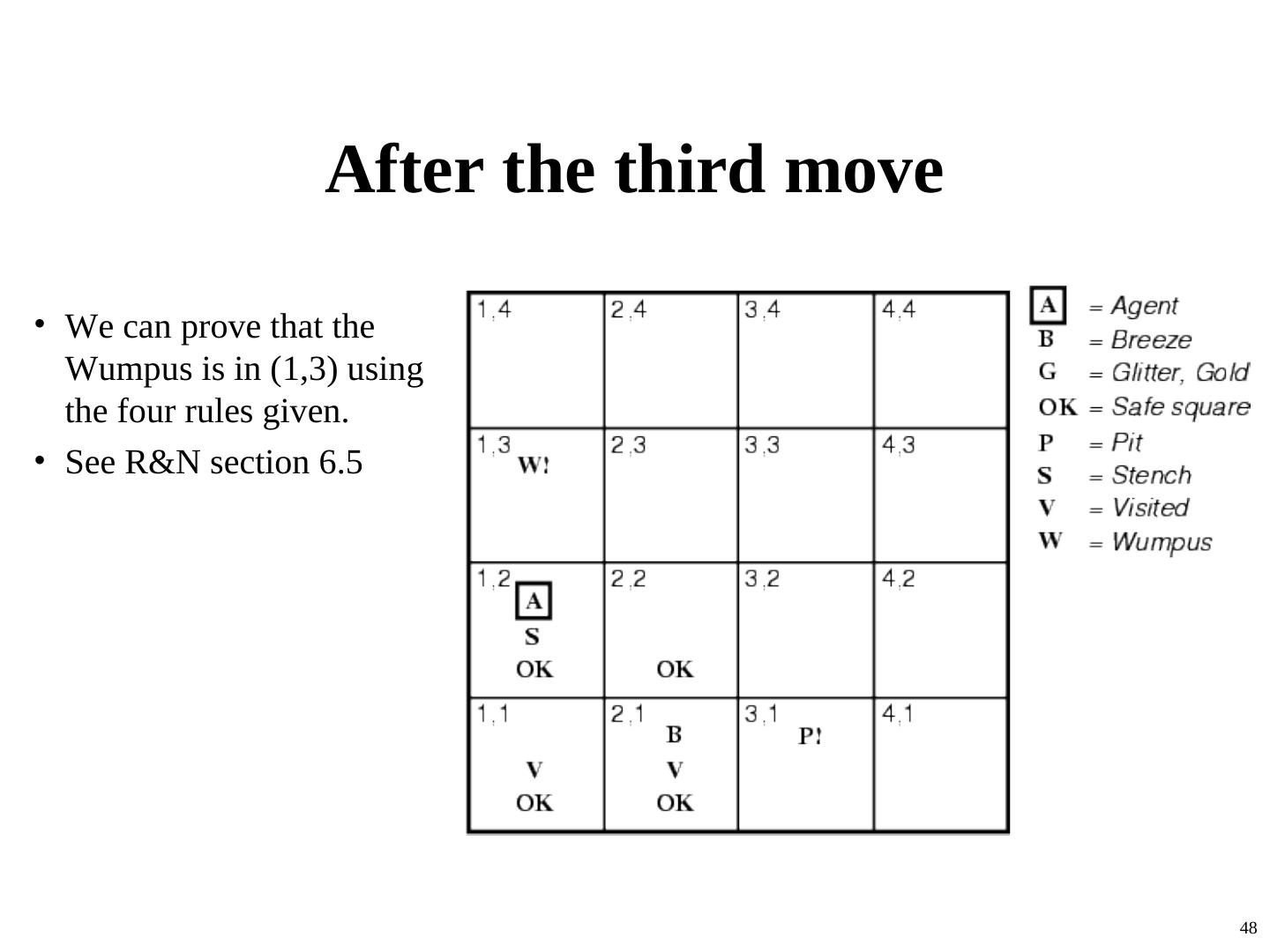
9 . A typical Wumpus world • The agent always starts in the field [1,1]. • The task of the agent is to find the gold, return to the field [1,1] and climb out of the cave. 9 

10 . Agent in a Wumpus world: Percepts • The agent perceives – a stench in the square containing the wumpus and in the adjacent squares (not diagonally) – a breeze in the squares adjacent to a pit – a glitter in the square where the gold is – a bump, if it walks into a wall – a woeful scream everywhere in the cave, if the wumpus is killed • The percepts will be given as a five-symbol list: – If there is a stench, and a breeze, but no glitter, no bump, and no scream, the percept is [Stench, Breeze, None, None, None] • The agent can not perceive its own location. 10 

11 . The actions of the agent in Wumpus game are: • go forward • turn right 90 degrees • turn left 90 degrees • grab means pick up an object that is in the same square as the agent • shoot means fire an arrow in a straight line in the direction the agent is looking. – The arrow continues until it either hits and kills the wumpus or hits the wall. – The agent has only one arrow. – Only the first shot has any effect. • climb is used to leave the cave. – Only effective in start field. • die, if the agent enters a square with a pit or a live wumpus. – (No take-backs!) 11 

12 . The agent’s goal The agent’s goal is to find the gold and bring it back to the start as quickly as possible, without getting killed. – 1000 points reward for climbing out of the cave with the gold – 1 point deducted for every action taken – 10000 points penalty for getting killed 12 

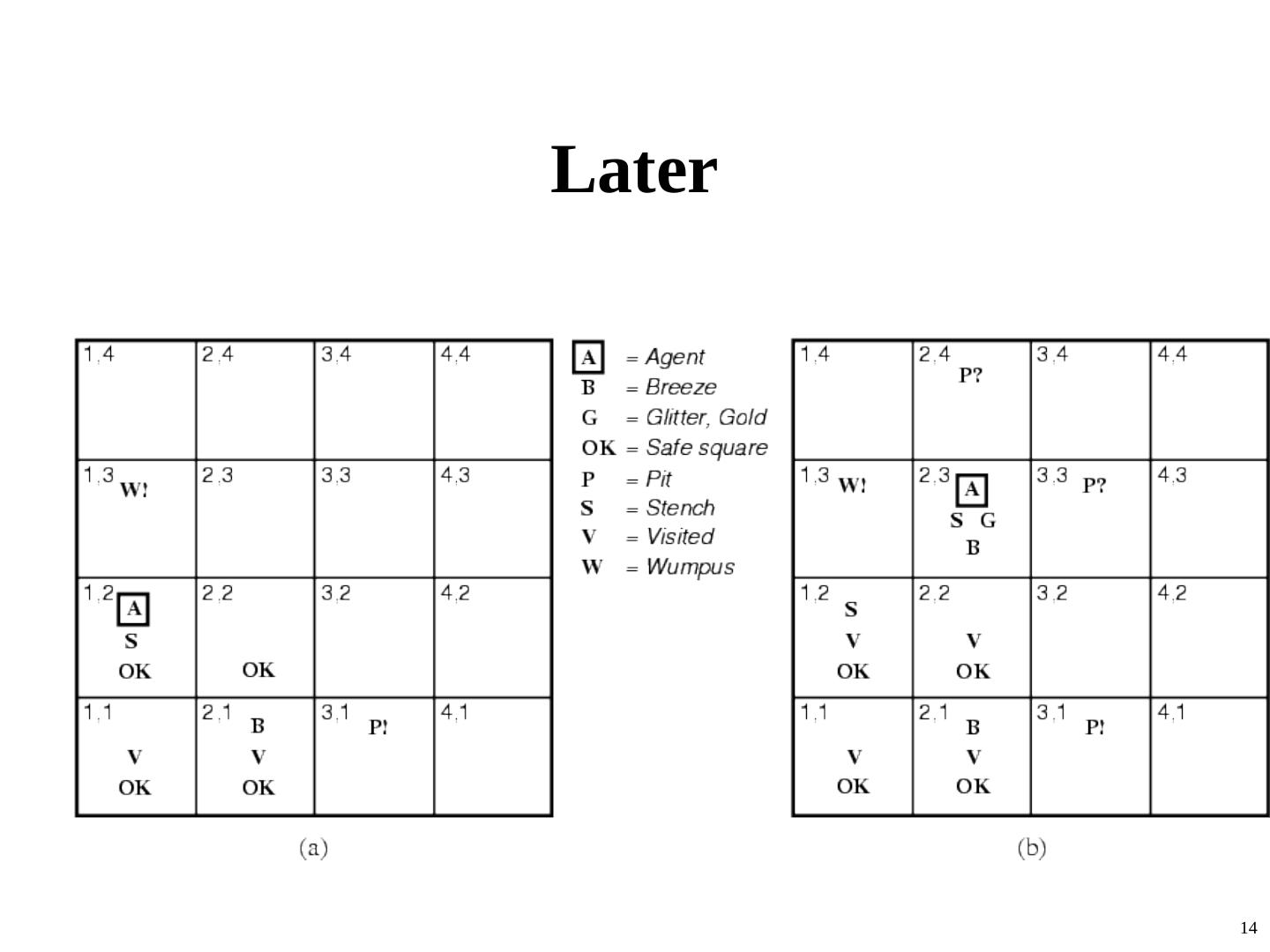
13 .The Wumpus agent’s first step 13 

14 .Later 14 

15 . World-wide web wumpuses • http://scv.bu.edu/wcl • http://216.246.19.186 • http://www.cs.berkeley.edu/~russell/code/doc/overview-AG ENTS.html 15 

16 . Representation, reasoning, and logic • The object of knowledge representation is to express knowledge in a computer-tractable form, so that agents can perform well. • A knowledge representation language is defined by: – its syntax, which defines all possible sequences of symbols that constitute sentences of the language. • Examples: Sentences in a book, bit patterns in computer memory. – its semantics, which determines the facts in the world to which the sentences refer. • Each sentence makes a claim about the world. • An agent is said to believe a sentence about the world. 16 

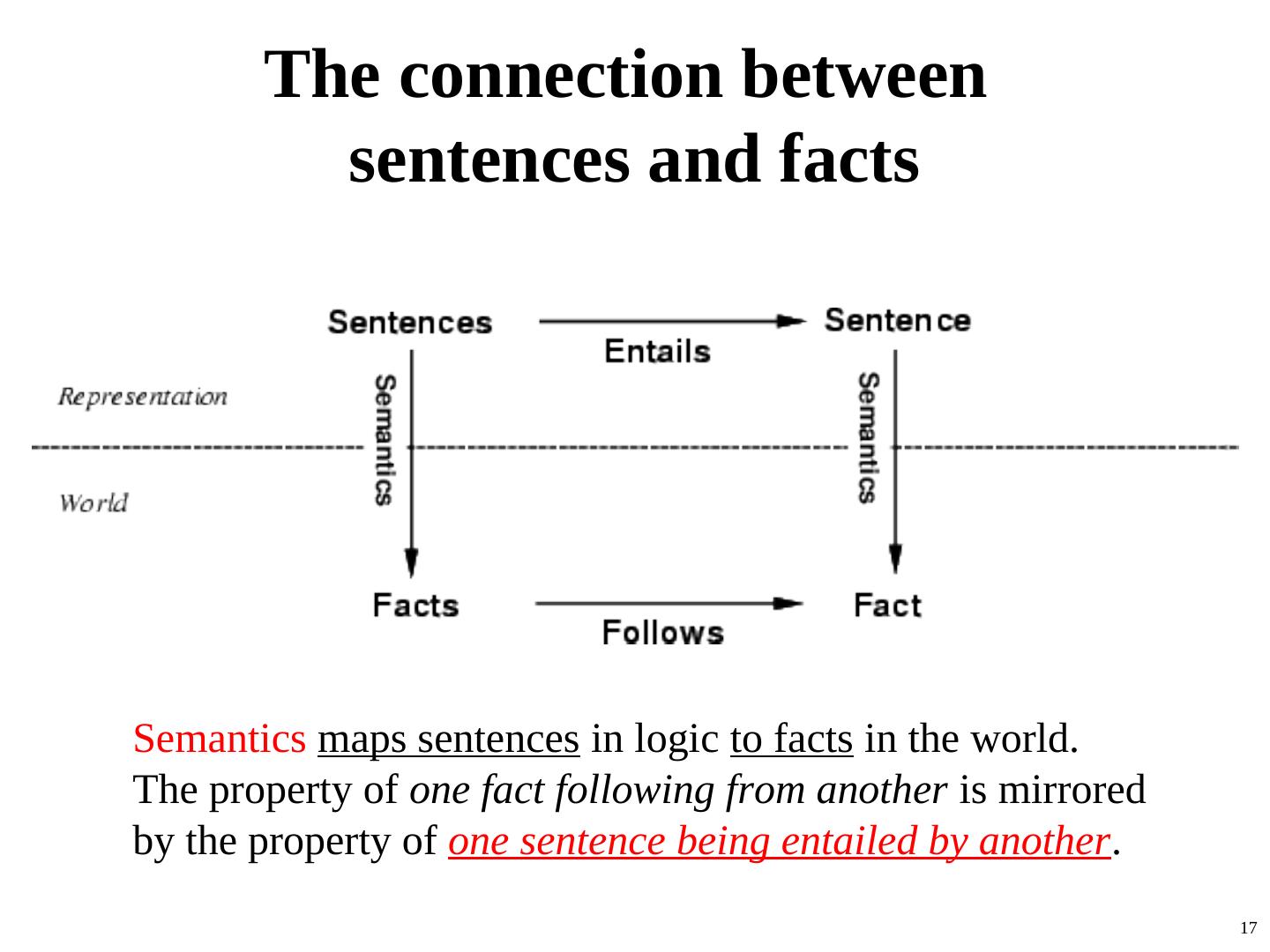
17 . The connection between sentences and facts Semantics maps sentences in logic to facts in the world. The property of one fact following from another is mirrored by the property of one sentence being entailed by another. 17 

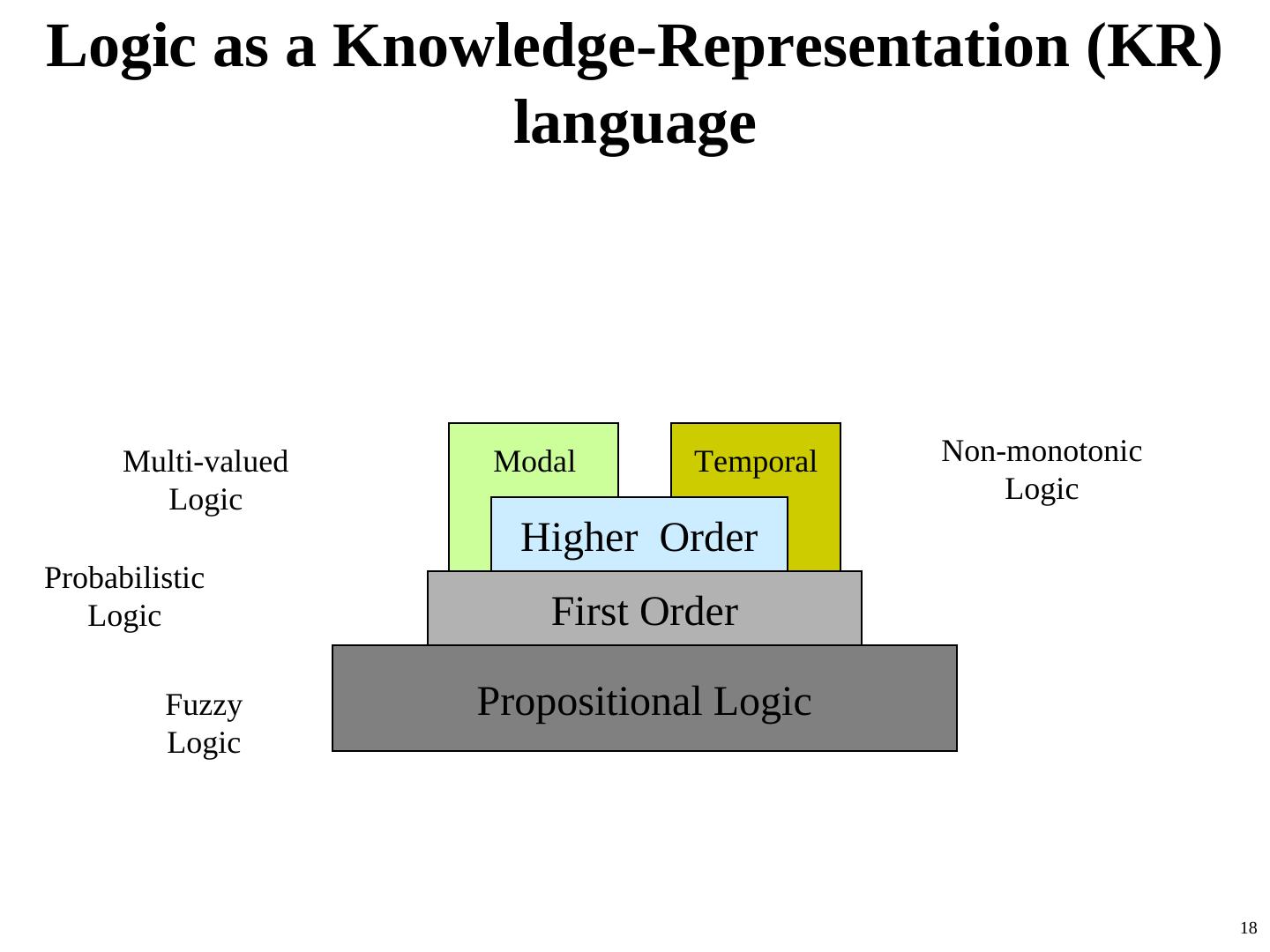
18 .Logic as a Knowledge-Representation (KR) language Multi-valued Modal Temporal Non-monotonic Logic Logic Higher Order Probabilistic Logic First Order Fuzzy Propositional Logic Logic 18 

19 . Ontology and epistemology • Ontology is the study of what there is, •an inventory of what exists. • An ontological commitment is a commitment to an existence claim. • Epistemology is major branch of philosophy that concerns the forms, nature, and preconditions of knowledge. 19 

20 . Propositional logic • Logical constants: true, false • Propositional symbols: P, Q, S, ... • Wrapping parentheses: ( … ) • Sentences are combined by connectives: ...and  ...or ...implies ..is equivalent  ...not 20 

21 . Propositional logic (PL) • A simple language useful for showing key ideas and definitions • User defines a set of propositional symbols, like P and Q. • User defines the semantics of each of these symbols, e.g.: – P means "It is hot" – Q means "It is humid" – R means "It is raining" • A sentence (aka formula, well-formed formula, wff) defined as: – A symbol – If S is a sentence, then ~S is a sentence (e.g., "not”) – If S is a sentence, then so is (S) – If S and T are sentences, then (S v T), (S ^ T), (S => T) , and (S <=> T) are sentences (e.g., "or," "and," "implies," and "if and only if”) – A finite number of applications of the above 21 

22 . Examples of PL sentences • (P ^ Q) => R “If it is hot and humid, then it is raining” • Q => P “If it is humid, then it is hot” •Q “It is humid.” • A better way: Ho = “It is hot” Hu = “It is humid” R = “It is raining” 22 

23 . A BNF grammar of sentences in propositional logic S := <Sentence> ; <Sentence> := <AtomicSentence> | <ComplexSentence> ; <AtomicSentence> := "TRUE" | "FALSE" | "P" | "Q" | "S" ; <ComplexSentence> := "(" <Sentence> ")" | <Sentence> <Connective> <Sentence> | "NOT" <Sentence> ; <Connective> := "NOT" | "AND" | "OR" | "IMPLIES" | "EQUIVALENT" ; 23 

24 .Terms: semantics, interpretation, model, tautology, contradiction, entailment • The meaning or semantics of a sentence determines its interpretation. • Given the truth values of all of symbols in a sentence, it can be “evaluated” to determine its truth value (True or False). • A model for a KB is a “possible world” in which each sentence in the KB is True. • A valid sentence or tautology is a sentence that is True under all interpretations, no matter what the world is actually like or what the semantics is. – Example: “It’s raining or it’s not raining.” • An inconsistent sentence or contradiction is a sentence that is False under all interpretations. – The world is never like what it describes, as in “It’s raining and it's not raining.” • P entails Q, written P |= Q, means that whenever P is True, so is Q. – In other words, all models of P are also models of Q. 24 

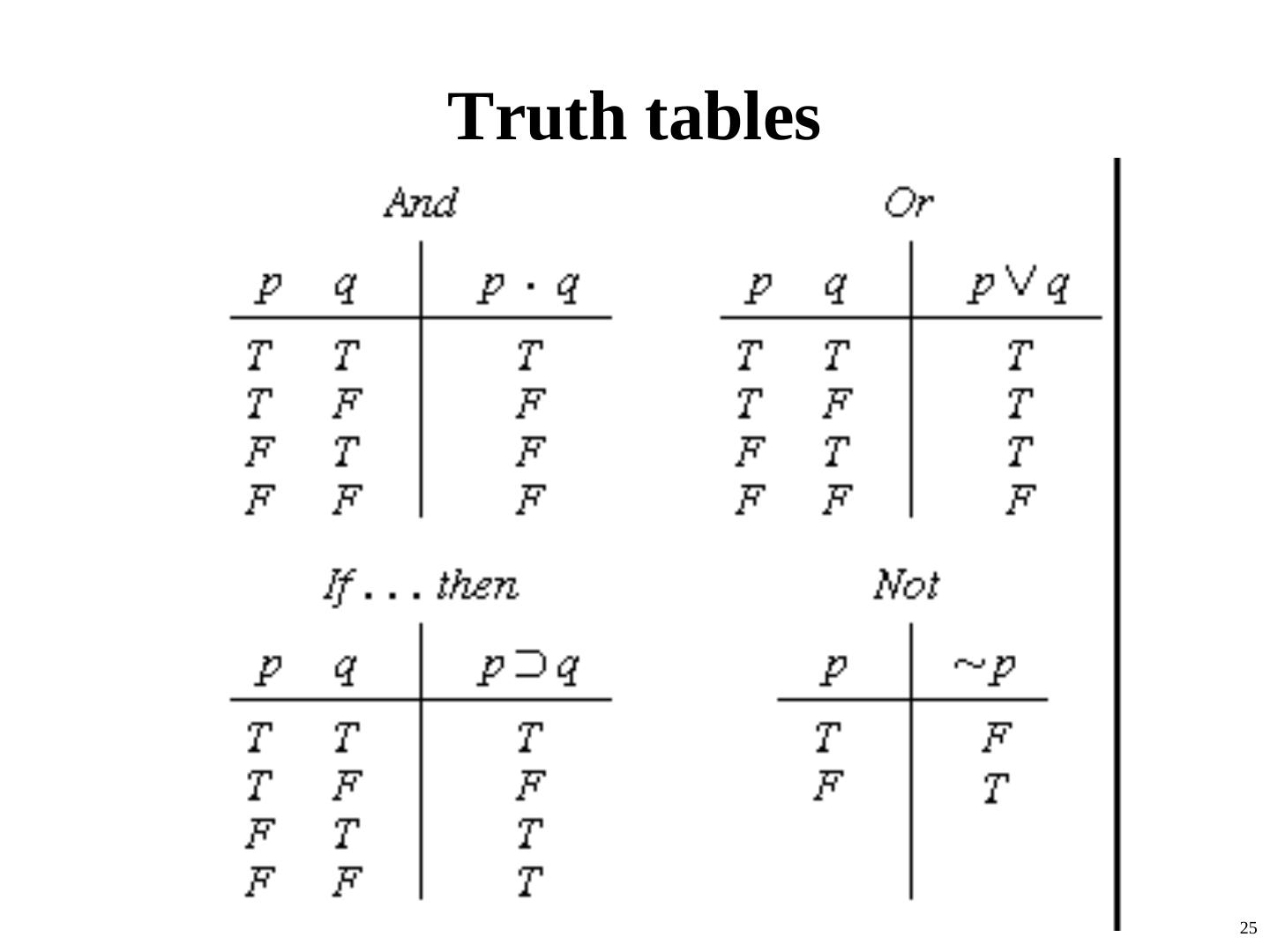
25 .Truth tables 25 

26 . Truth tables II The five logical connectives: A complex sentence: 26 

27 .Models of complex sentences 27 

28 . Agents have no independent access to the world • The reasoning agent often gets its knowledge about the facts of the world as a sequence of logical sentences. • It must draw conclusions only from them , without independent access to the world. • Thus it is very important that the agent’s reasoning is sound! reasoning agent 28 

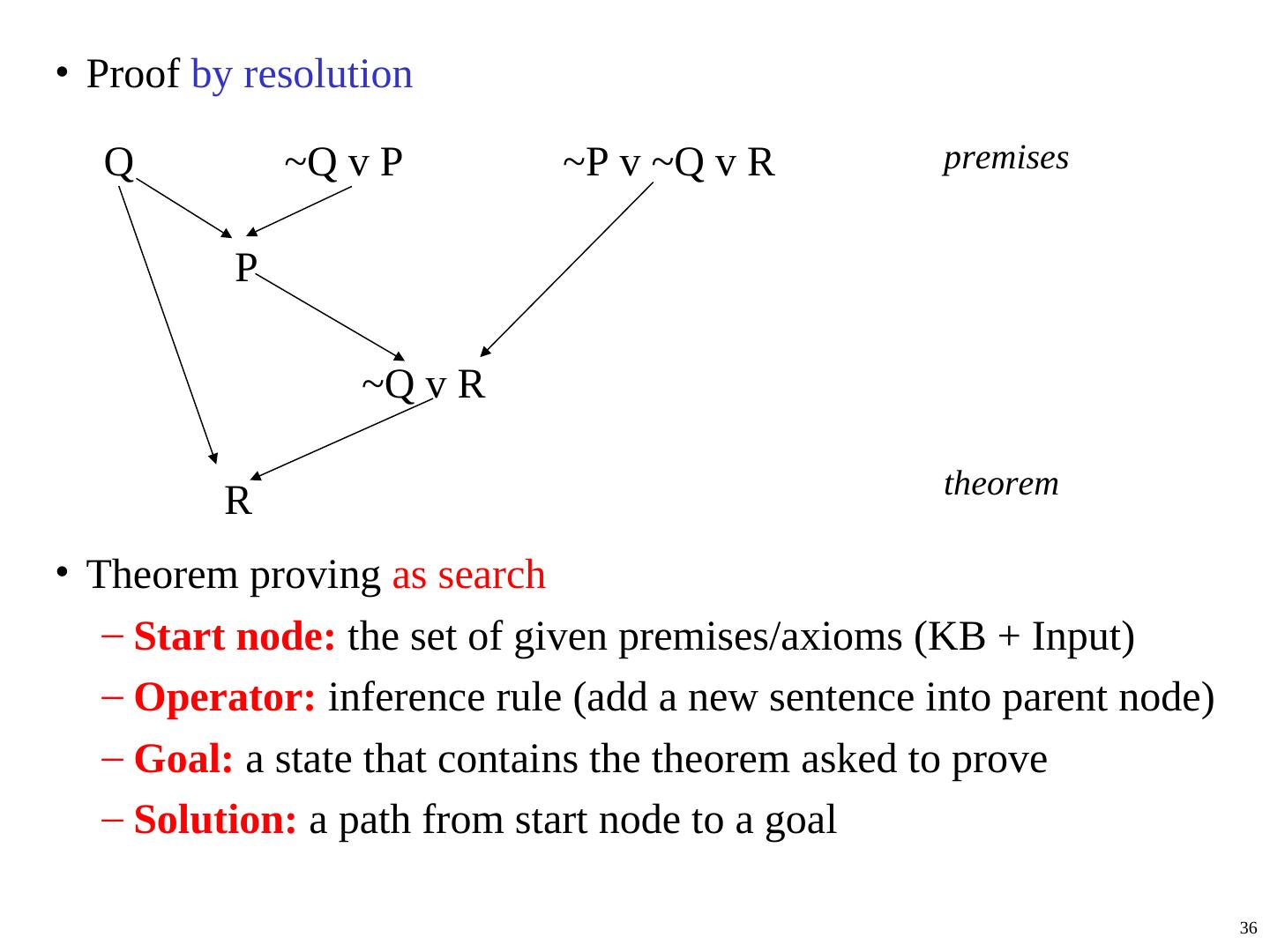
29 . Inference rules • Logical inference is used to create new sentences that logically follow from a given set of predicate calculus sentences (KB). • An inference rule is sound if every sentence X produced by an inference rule operating on a KB logically follows from the KB. – (That is, the inference rule does not create any contradictions) • An inference rule is complete if it is able to produce every expression that logically follows from the KB. – We also say - “expression is entailed by KB”. – Pleas note the analogy to complete search algorithms. 29