- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
007-introduction to modal and epistemic logic for beginners
展开查看详情
1 .Marek Perkowski INTRODUCTION TO MODAL AND EPISTEMIC LOGIC for beginners
2 .Overview Why we need moral robots Review of classical Logic The Muddy Children Logic Puzzle The partition model of knowledge Introduction to modal logic The S5 axioms Common knowledge Applications to robotics Knowledge and belief
3 .The goals of this series of lectures My goal is to teach you everything about modal logic, deontic logic, temporal logic, proof methods etc that can be used in the following areas of innovative research : Robot morality (assistive robots, medical robots, military robots) Natural language processing (robot assistant, robot-receptionist) Mobile robot path planning (in difficult “game like” dynamically changeable environments) General planning, scheduling and allocation (many practical problems in logistics, industrial, military and other areas) Hardware and software verification (of Verilog or VHDL codes) Verifying laws and sets of rules (like consistency of divorce laws in Poland) Analytic philosophy (like proving God’ Existence, free will, the problem of evil, etc) Many other… At this point I should ask all students to give another examples of similar problems that they want to solve
4 .Big hopes Modal logic is a very hot topic in recent ~12 years. In my memory I see new and new areas that are taken over by modal logic Let us hope to find more applications Every problem that was formulated or not previously in classical logic, Bayesian logic, Hiden Markov models, automata, etc can be now rewritten to modal logic.
5 .The Tokyo University of Science: Saya Morality for non-military robots that deal directly with humans. At this point I should ask all students to give another examples of dialogs, that would include reasoning, to have with Saya
6 .6 MechaDroyd Typ C3 Business Design, Japan At this point I should ask all students to give another examples of dialogs, that would include reasoning, to have with MechaDroyd
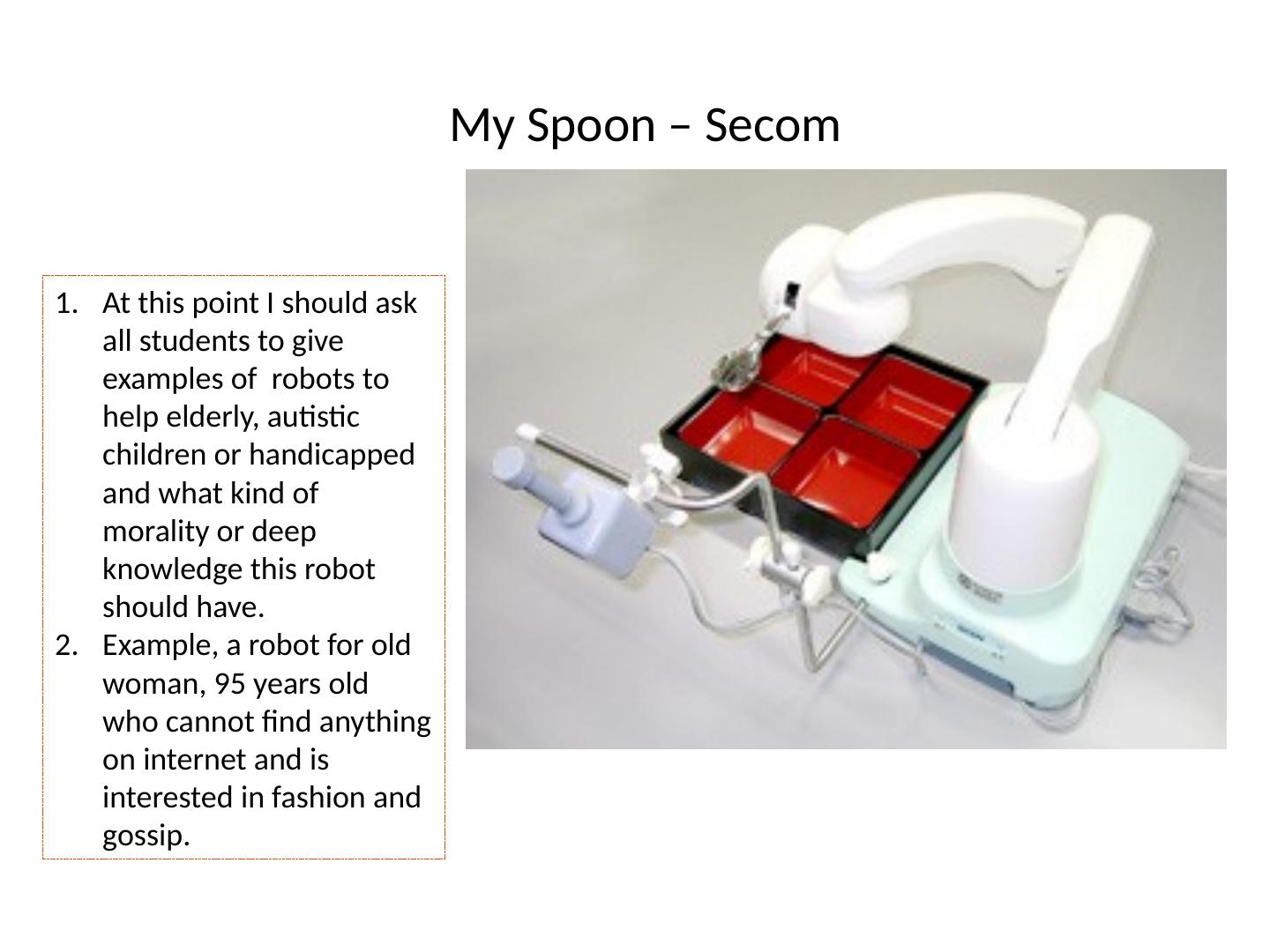
7 .My Spoon – Secom in Japan http://www.secom.co.jp/english/myspoon/index.html
8 .My Spoon – Secom At this point I should ask all students to give examples of robots to help elderly, autistic children or handicapped and what kind of morality or deep knowledge this robot should have. Example, a robot for old woman, 95 years old who cannot find anything on internet and is interested in fashion and gossip.
9 .Robot IPS
10 .Fuji Heavy Industries/Sumitomo Cleaning lawn-moving, and similar robots will have contact with humans and should be completely safe What kind of deep knowledge and morality a robot should have for standard large US hospital?
11 .Care robot How much trust you need to be in arms of a strong big robot like this? How to build this trust? What kind morality you would expect from this robot? R. Capurro: Cybernics Salon
12 .Robots and War Congress : one-third of all combat vehicles to be robots by 2015 Future Combat System (FCS) Development cost by 2014 : $130-$250 billion
13 .Robotex (Palo Alto, California) by Terry Izumi We urgently need robot morality for military robots It is expected that these robots will be more moral than contemporary US soldiers in case of accidental shootings of civilians, avoiding panic behaviors, etc
14 .
15 .Review of classical logic
16 .Classical logic What is logic? A set of techniques for representing, transforming, and using information. What is classical logic? A particular kind of logic that has been well understood since ancient times . (Details to follow…)
17 .Classical vs non-classcial logic I should warn you that non-classical logic is not as weird as you may think. I’m not going to introduce “new ways of thinking” that lead to bizarre beliefs. What I want to do is make explicit some non-classical ways of reasoning that people have always found useful. I will be presenting well-accepted research results, not anything novel or controversial.
18 .Classical logic in Ancient times 300s B.C.: ARISTOTLE and other Greek philosophers discover that some methods of reasoning are truth-preserving. That is, if the premises are true, the conclusion is guaranteed true, regardless of what the premises are.
19 .Example of Classical logic Syllogism All hedgehogs are spiny. Matilda is a hedgehog. ∴ Matilda is spiny. You do not have to know the meanings of “hedgehog” or “spiny” or know anything about Matilda in order to know that this is a valid argument.
20 .What Classical logic can really do? VALID means TRUTH-PRESERVING. Logic cannot tell us whether the premises are true. The most that logic can do is tell us that IF the premises are true, THEN the conclusions must also be true.
21 .Classical logic since 1854 1854: George Boole points out that inferences can be represented as formulas and there is an infinite number of valid inference schemas. (∀ x) hedgehog(x) ⊃ spiny(x) hedgehog(Matilda) ∴ spiny(Matilda) Proving theorems (i.e., proving inferences valid) is done by manipulating formulas .
22 .What is an argument? An argument is any set of statements one of which, the conclusion , is supposed to be epistemically supported by the remaining statements, the premises .
23 .Is this an argument? Ms. Malaprop left her house this morning. Whenever she does this, it rains. _____________ Therefore, the moon is made of blue cheese.
24 .What is a good argument? An argument is valid if and only if the conclusion must be true, given the truth of the premises.
25 .Is this argument valid? If the moon is made of blue cheese, then pigs fly. The moon is made of blue cheese. ______________ Therefore, pigs fly.
26 .What we aim for An argument is sound if and only if the argument is valid and, in addition, all of its premises are true.
27 .Logical Negation Consider the following sentences “2 plus 2 is 4” is true “2 plus 2 isn’t 4” is false “2 plus 2 is 5” is false “2 plus 2 isn’t 5” is true
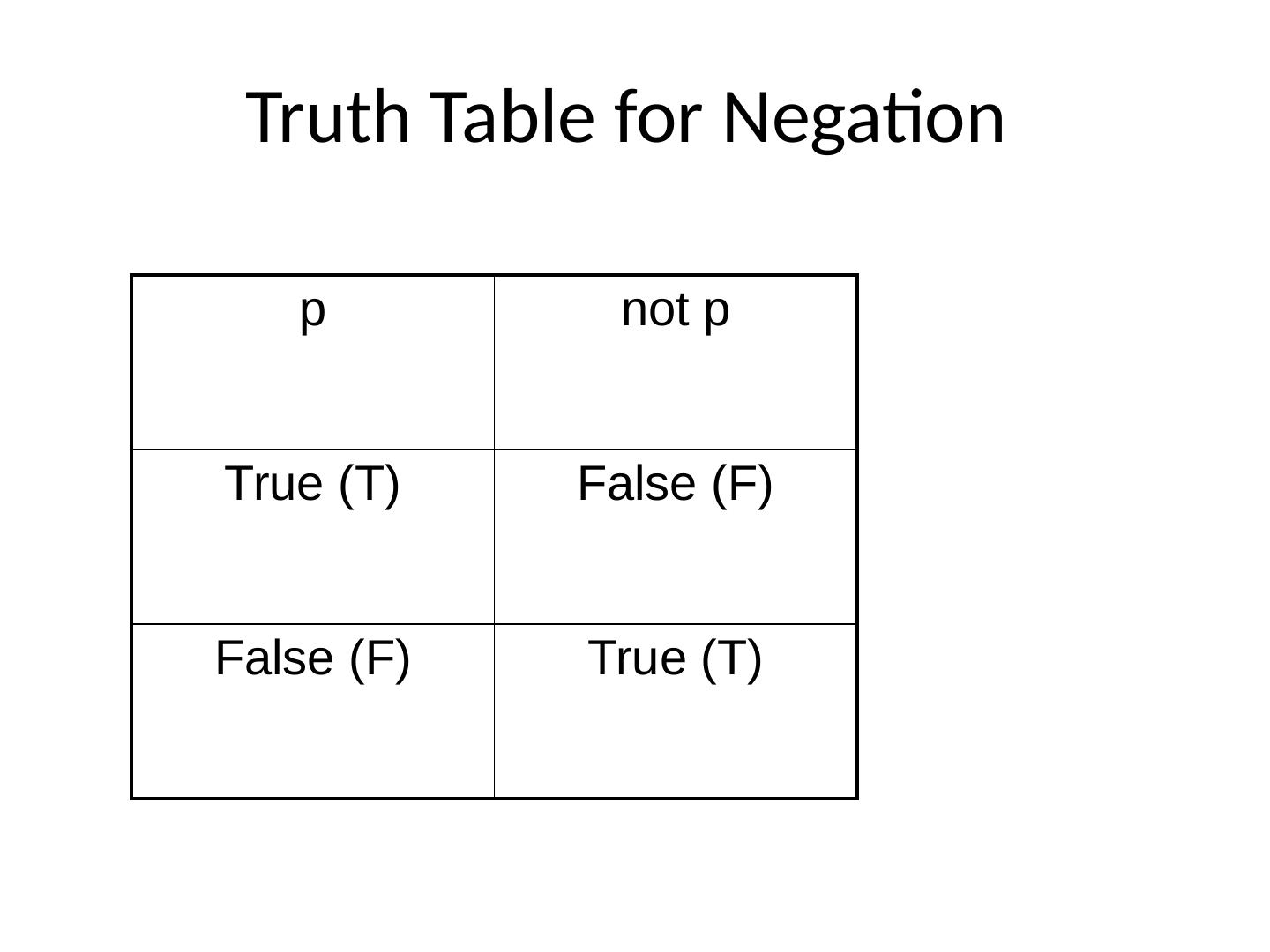
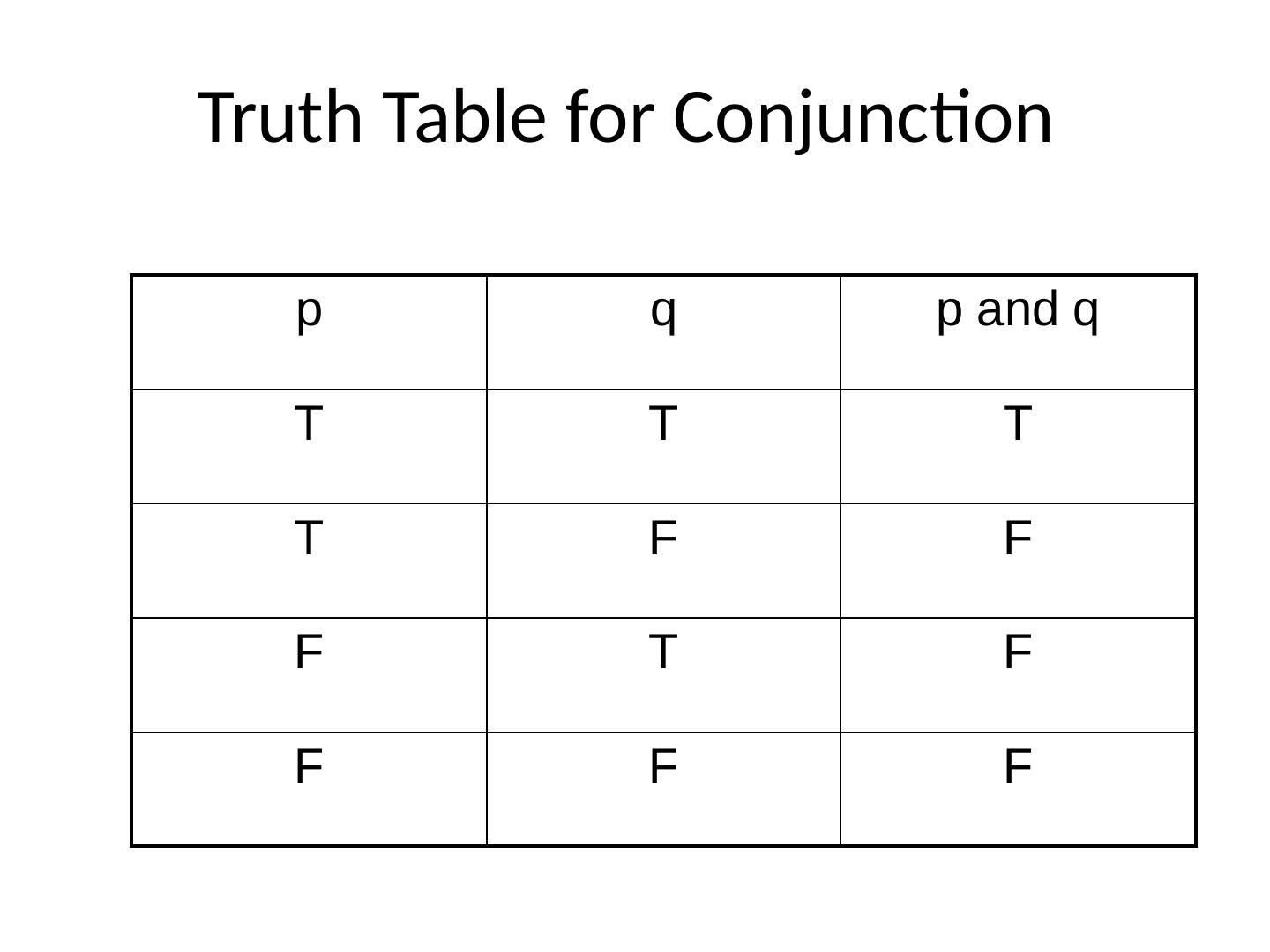
28 .Truth Table for Negation p not p True (T) False (F) False (F) True (T)
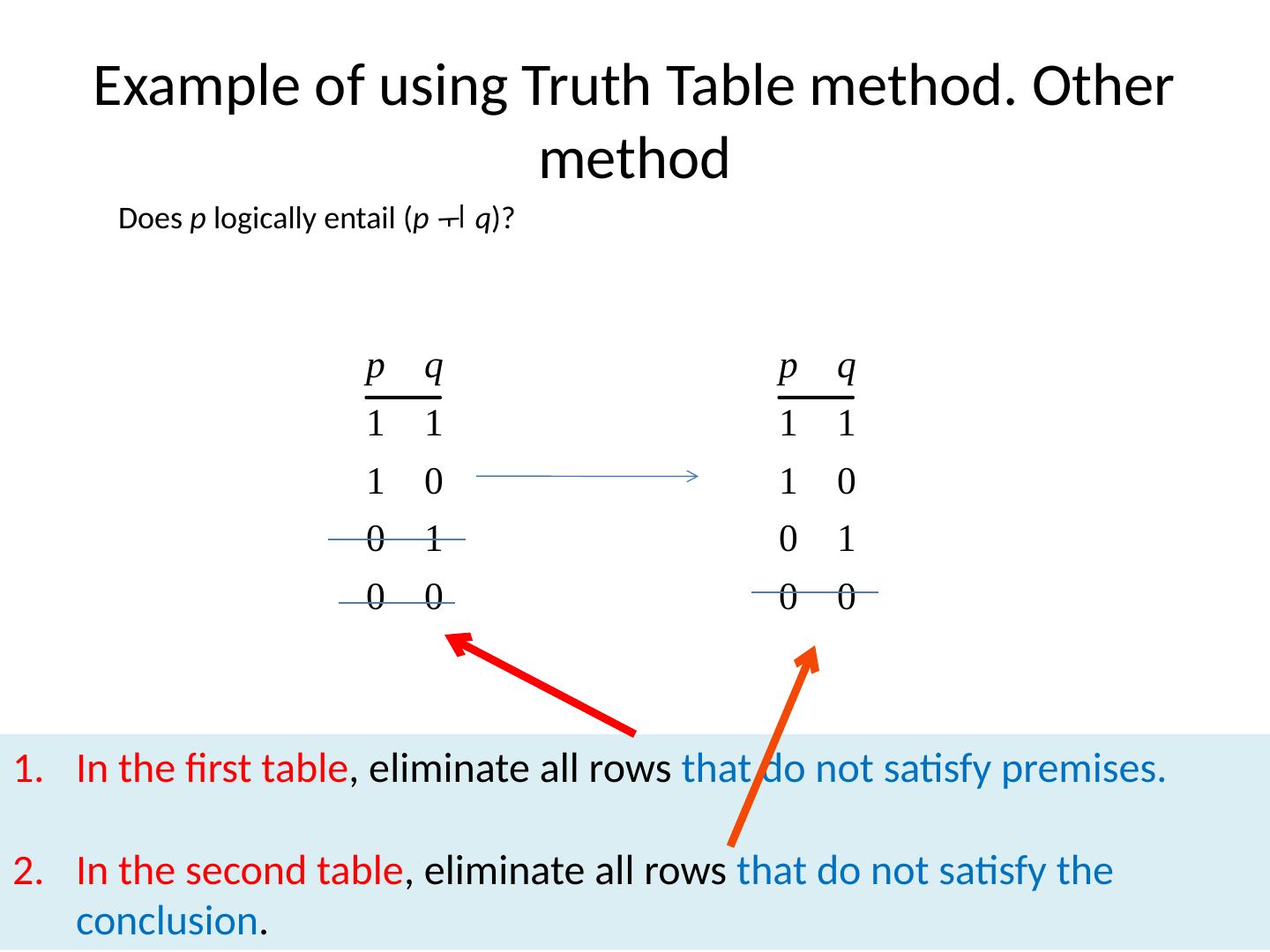
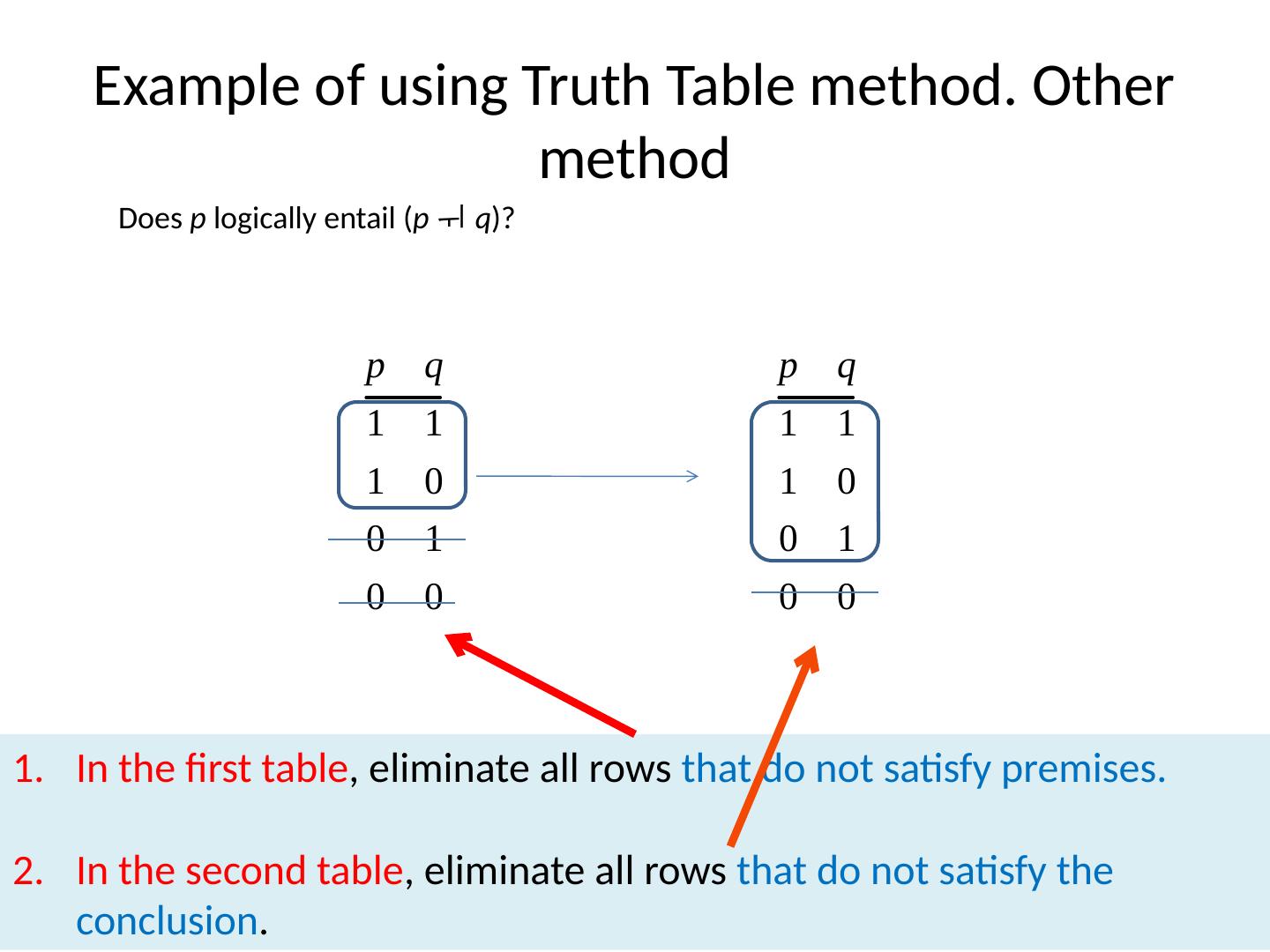
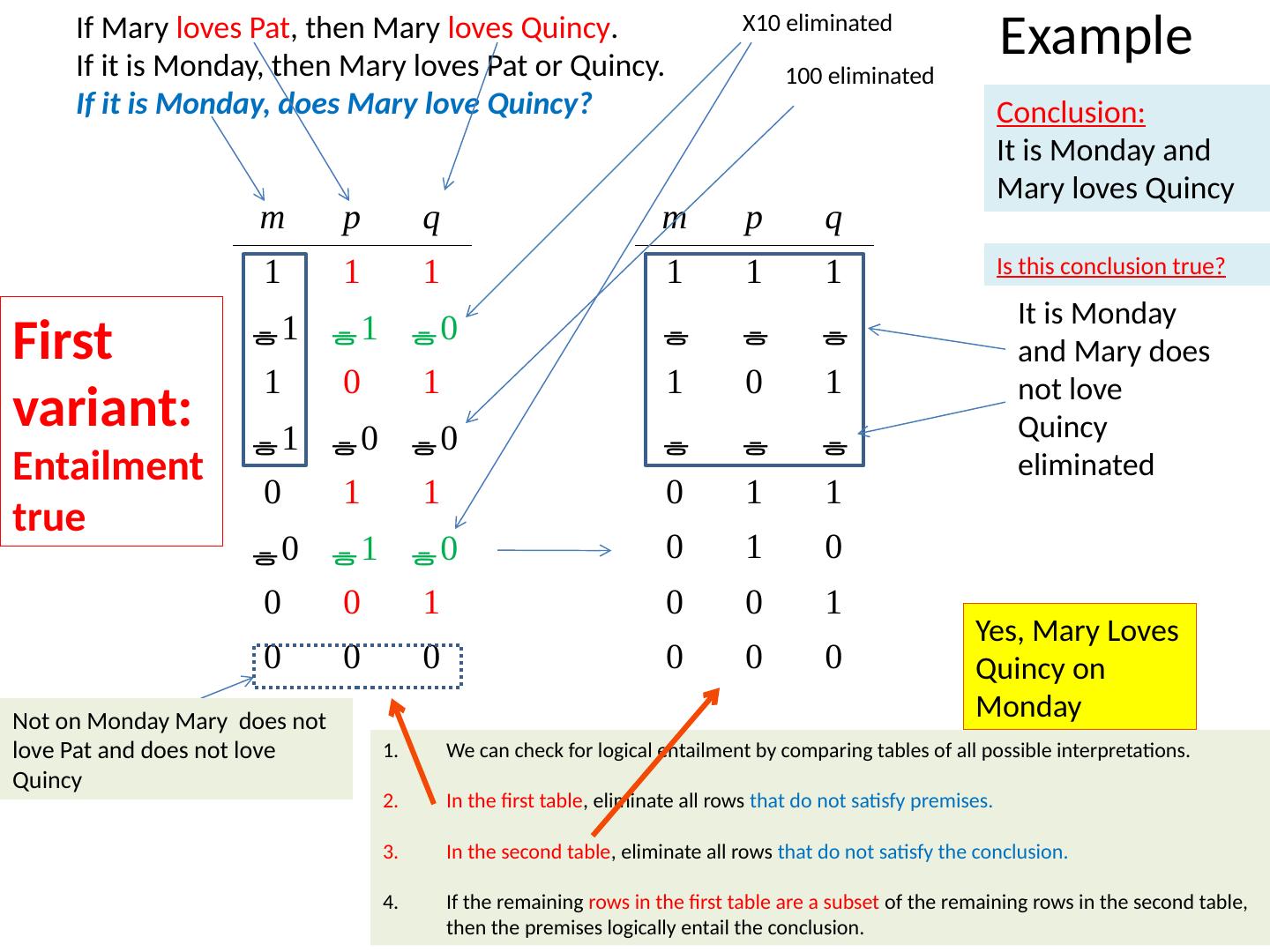
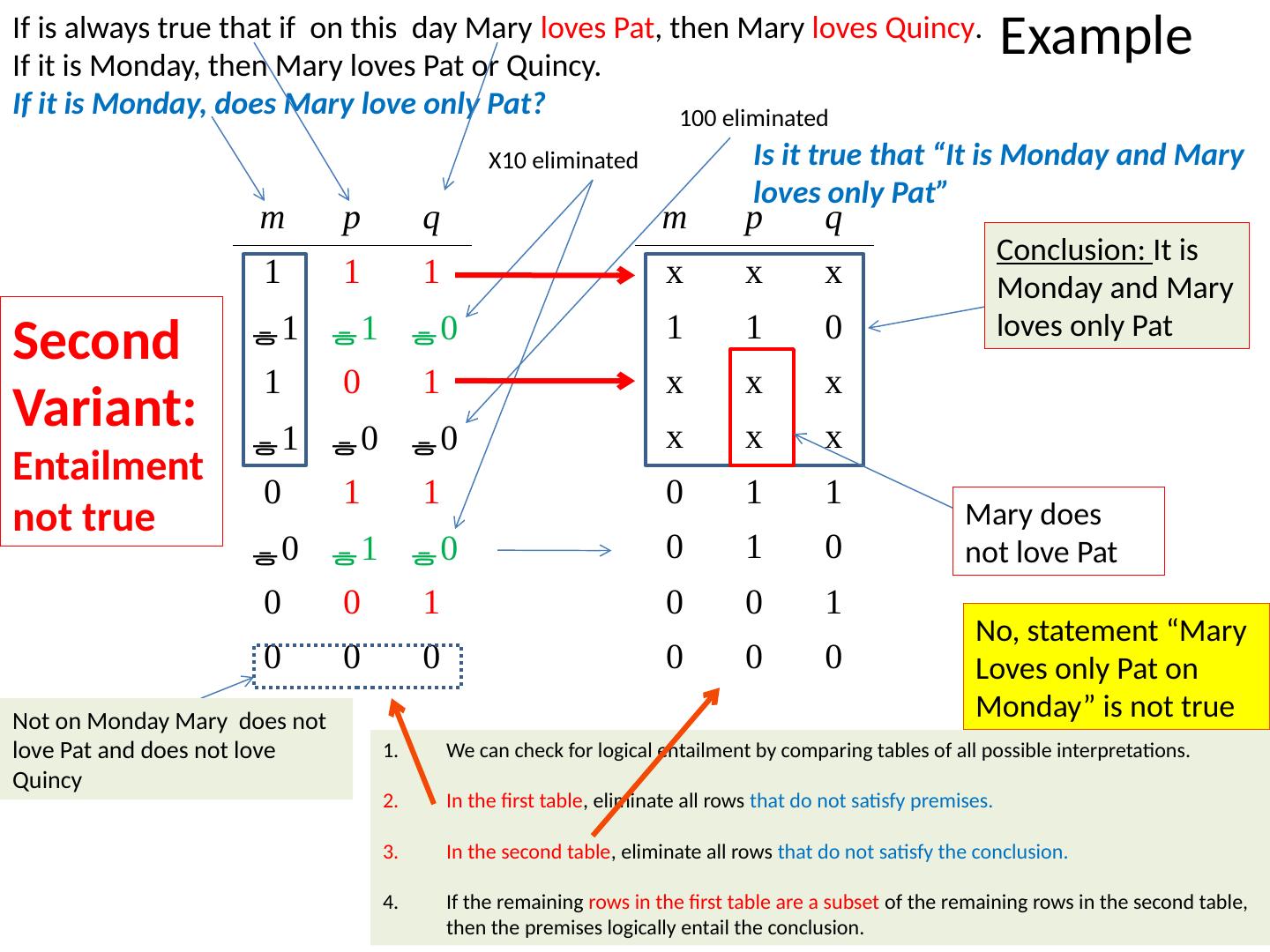
29 .Definition of Logical Negation A sentence of the form “not-p” is true if and only if p is false; otherwise, it is false. So logically speaking negation has the effect of switching the truth-value of any sentence in which it occurs.