- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
006-boolean algebra
展开查看详情
1 .1 Chapter 11 Boolean Algebra Rosen 6 th ed., ch. 11
2 .2 What is Boolean Algebra? A minor generalization of propositional logic. In general, an algebra is any mathematical structure satisfying certain standard algebraic axioms. Such as associative/commutative/transitive laws, etc. General theorems that are proved about an algebra then apply to any structure satisfying these axioms. Boolean algebra just generalizes the rules of propositional logic to sets other than { T , F } . E.g. , to the set {0,1} of base-2 digits, or the set { V L , V H } of low and high voltage levels in a circuit. We will see that this algebraic perspective lends itself to the design of digital logic circuits . Claude Shannon’s Master’s thesis!
3 .3 Boolean Algebra Sections of chapter 11: §1 – Boolean Functions §2 – Representing Boolean Functions §3 – Logic Gates §4 – Minimization of Circuits
4 .4 §11.1 – Boolean Functions Boolean complement, sum, product. Boolean expressions and functions. Boolean algebra identities. Duality. Abstract definition of a Boolean algebra.
5 .5 Complement, Sum, Product Correspond to logical NOT, OR, and AND. We will denote the two logic values as 0 : ≡ F and 1 : ≡ T , instead of False and True . Using numbers encourages algebraic thinking. New, more algebraic-looking notation for the most common Boolean operators: Precedence order→
6 .6 Boolean Functions Let B = { 0 , 1 } , the set of Boolean values. For all n Z + , any function f : B n → B is called a Boolean function of degree n . There are 2 2 ⁿ (wow!) distinct Boolean functions of degree n . B/c 2 n rows in truth table, w. 0 or 1 in each. Degree How many Degree How many 0 2 4 65,536 1 4 5 4,294,967,296 2 16 6 18,446,744,073,709,551,616. 3 256
7 .7 Boolean Expressions Let x 1 , …, x n be n different Boolean variables. n may be as large as desired. A Boolean expression (recursive definition) is a string of one of the following forms: Base cases: 0 , 1 , x 1 , …, or x n . Recursive cases: E 1 , ( E 1 E 2 ) , or ( E 1 + E 2 ) , where E 1 and E 2 are Boolean expressions. A Boolean expression represents a Boolean function. Furthermore, every Boolean function (of a given degree) can be represented by a Boolean expression.
8 .8 Hypercube Representation A Boolean function of degree n can be represented by an n -cube (hypercube) with the corresponding function value at each vertex. (0,0,0) (0,0,1) (0,1,0) (0,1,1) (1,0,0) (1,0,1) (1,1,0) (1,1,1) 0 1 0 1 0 1 0 1 ( a , b , c )
9 .9 Boolean equivalents, operations on Boolean expressions Two Boolean expressions e 1 and e 2 that represent the exact same function f are called equivalent. We write e 1 e 2 , or just e 1 = e 2 . Implicitly, the two expressions have the same value for all values of the free variables appearing in e 1 and e 2 . The operators ¯ , + , and · can be extended from operating on expressions to operating on the functions that they represent, in the obvious way.
10 .10 Some popular Boolean identities Double complement: x = x Idempotent laws: x + x = x , x · x = x Identity laws: x + 0 = x , x · 1 = x Domination laws: x + 1 = 1 , x · 0 = 0 Commutative laws: x + y = y + x , x · y = y · x Associative laws: x + ( y + z ) = ( x + y ) + z x · ( y · z ) = ( x · y ) · z Distributive laws: x + y · z = ( x + y )·( x + z ) x · ( y + z ) = x · y + x · z De Morgan’s laws: ( x · y ) = x + y , ( x + y ) = x · y Absorption laws: x + x · y = x , x · ( x + y ) = x ← Not true in ordinary algebras. also, the Unit Property: x + x = 1 and Zero Property: x · x = 0
11 .11 Duality The dual e d of a Boolean expression e representing function f is obtained by exchanging + with · , and 0 with 1 in e . The function represented by e d is denoted f d . Duality principle: If e 1 e 2 then e 1 d e 2 d . Example: The equivalence x ( x + y ) = x implies (and is implied by) x + xy = x .
12 .12 Boolean Algebra, in the abstract A general Boolean algebra is any set B having elements 0 , 1 , two binary operators , , and a unary operator that satisfies the following laws: Identity laws: x 0 = x , x 1 = x Complement laws: x x = 1 , x x = 0 Associative laws: ( x y ) z = x ( y z ) , ( x y ) z = x ( y z ) Commutative laws: x y = y x , x y = y x Distributive laws: x ( y z ) = ( x y ) ( x z ) , x ( y z )=( x y ) ( x z ) . Note that B may generally have other elements besides 0 , 1 , and we have not fully defined any of the operators!
13 .13 §11.2 – Representing Boolean Functions Sum-of-products Expansions A.k.a. Disjunctive Normal Form (DNF) Product-of-sums Expansions A.k.a. Conjunctive Normal Form (CNF) Functional Completeness Minimal functionally complete sets of operators.
14 .14 Sum-of-Products Expansions Theorem: Any Boolean function can be represented as a sum of products of variables and their complements. Proof: By construction from the function’s truth table. For each row that is 1, include a term in the sum that is a product representing the condition that the variables have the values given for that row. Show an example on the board.
15 .15 Literals, Minterms, DNF A literal is a Boolean variable or its complement. A minterm of Boolean variables x 1 ,…, x n is a Boolean product of n literals y 1 … y n , where y i is either the literal x i or its complement x i . Note that at most one minterm can have the value 1. The disjunctive normal form (DNF) of a degree- n Boolean function f is the unique sum of minterms of the variables x 1 ,…, x n that represents f . A.k.a. the sum-of-products expansion of f .
16 .16 Conjunctive Normal Form A maxterm is a sum of literals. CNF is a product-of-maxterms representation. To find the CNF representation for f , take the DNF representation for complement f , f = ∑ i ∏ j y i , j and then complement both sides & apply DeMorgan’s laws to get: f = ∏ i ∑ j y i , j Can also get CNF more directly, using the 0 rows of the truth table.
17 .17 Functional Completeness Since every Boolean function can be expressed in terms of · , + , ¯ , we say that the set of operators {·,+,¯} is functionally complete . There are smaller sets of operators that are also functionally complete. We can eliminate either · or + using DeMorgan’s law. NAND | and NOR ↓ are also functionally complete, each by itself (as a singleton set). E.g. , x = x | x , and xy = ( x | y )|( x | y ) .
18 .18 § 11.3 – Logic Gates Inverter, Or, And gate symbols. Multi-input gates. Logic circuits and examples. Adders, “half,” “full,” and n -bit.
19 .19 Logic Gate Symbols Inverter (logical NOT, Boolean complement). AND gate (Boolean product). OR gate (Boolean sum). XOR gate (exclusive-OR, sum mod 2). x x y x ·y x y x+y y x x ⊕ y
20 .20 Multi-input AND, OR, XOR Can extend these gates to arbitrarily many inputs. Two commonly seen drawing styles: Note that the second style keeps the gate icon relatively small. x 1 x 1 x 2 x 3 x 2 x 3 x 1 ⋮ x 5 x 1 …x 5
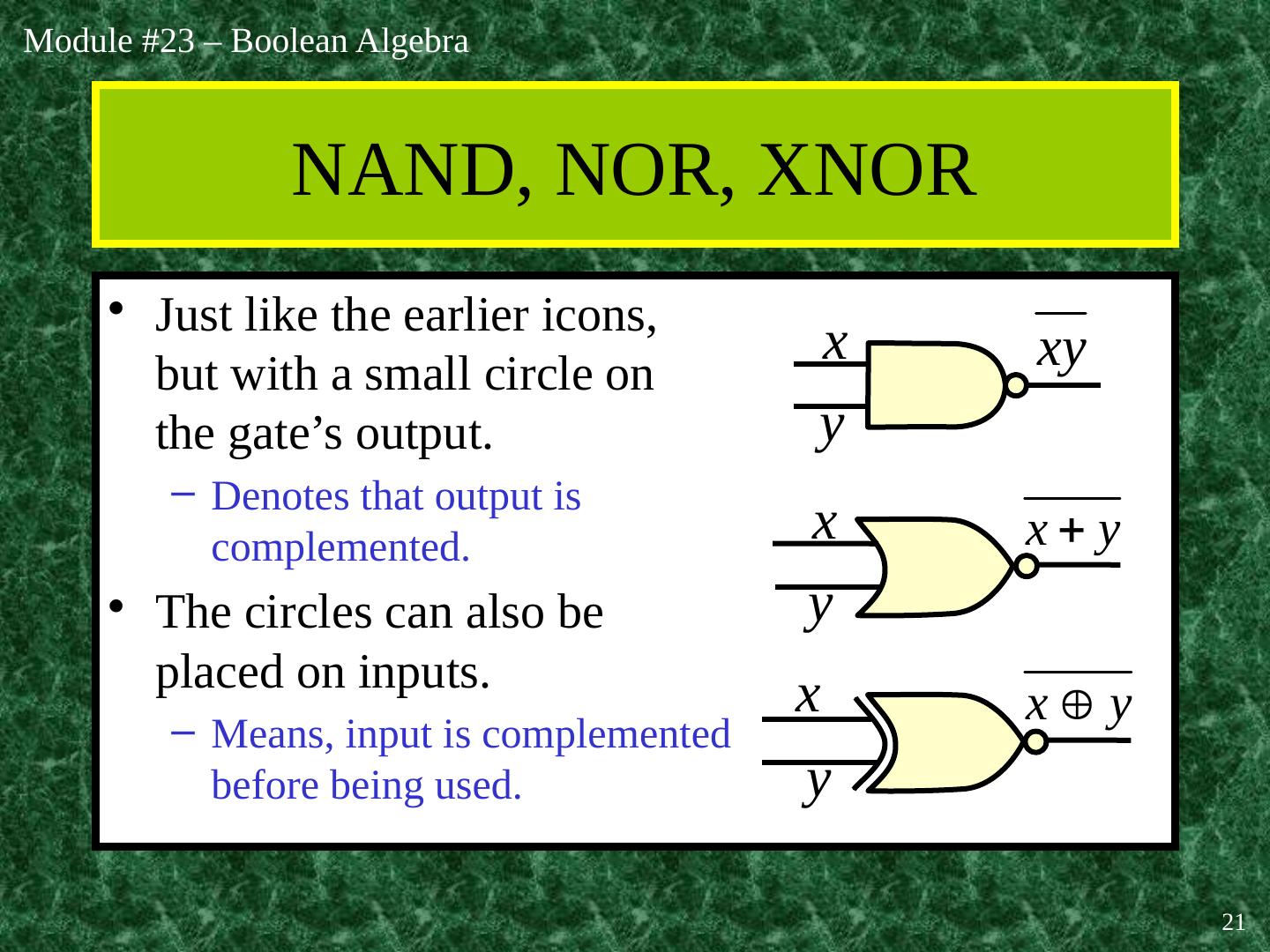
21 .21 NAND, NOR, XNOR Just like the earlier icons, but with a small circle on the gate’s output. Denotes that output is complemented. The circles can also be placed on inputs. Means, input is complemented before being used. x y x y y x
22 .22 Buffer What about an inverter symbol without a circle? This is called a buffer . It is the identity function. It serves no logical purpose, but… It represents an explicit delay in the circuit. This is sometimes useful for timing purposes. All gates, when physically implemented, incur a non-zero delay between when their inputs are seen and when their outputs are ready. x x
23 .23 Combinational Logic Circuits Note: The correct word to use here is “combinat ion al,” NOT “combinat ori al!” Many sloppy authors get this wrong. These are circuits composed of Boolean gates whose outputs depend only on their most recent inputs, not on earlier inputs. Thus these circuits have no useful memory. Their state persists while the inputs are constant, but is irreversibly lost when the input signals change.
24 .24 Combinational Circuit Examples Draw a few examples on the board: Majority voting circuit. XOR using OR / AND / NOT. 3-input XOR using OR / AND / NOT. Also, show some binary adders: Half adder using OR/AND/NOT. Full adder from half-adders. Ripple-carry adders.
25 .25 §11.4 – Minimizing Circuits Karnaugh Maps Don’t care conditions The Quine-McCluskey Method
26 .26 Goals of Circuit Minimization (1) Minimize the number of primitive Boolean logic gates needed to implement the circuit. Ultimately, this also roughly minimizes the number of transistors, the chip area, and the cost. Also roughly minimizes the energy expenditure among traditional irreversible circuits. This will be our focus. (2) It is also often useful to minimize the number of combinational stages or logical depth of the circuit. This roughly minimizes the delay or latency through the circuit, the time between input and output.
27 .27 Minimizing DNF Expressions Using DNF (or CNF) guarantees there is always some circuit that implements any desired Boolean function. However, it may be far larger than needed! We would like to find the smallest sum-of-products expression that yields a given function. This will yield a fairly small circuit. However, circuits of other forms (not CNF or DNF) might be even smaller for complex functions.