004-representation and logic

1 .

2 .Representation ❧We need a way to enter “world facts” into the computer in such a manner that the computer can reason (“make inferences”) with and about them ❧normal English is insufficient ● too hard currently • ambiguity • how do we draw inferences in natural languages? 

3 . Physical Symbol Hypothesis (again) ❧Intelligence can be achieved by ● symbols that represent the significant aspects of the given problem domain ● operations on these basic & compound symbols that generate potential solutions ● search to find the a solution among solutions ❧We’ve looked at #3; now we examine #1 & #2 

4 . Requirements for an AI language ❧ Handle qualitative knowledge ❧ Allow inference ● inference rules save us from explicitly writing down every fact (“deductive database”) ❧ Allow representation of general principles (rules) and specific situations (facts) ❧ capture complex situations (time, change, etc.) ❧ support meta-level reasoning ● analyzing one’s knowledge, reasoning, learning, etc. ● stepping outside the system 

5 .First-order predicate calculus (FOPC) ❧The core representation language ❧In terms of representation, it is well-defined (mathematical logic) ❧In terms of reasoning, it is ● sound: inferences are correct ● complete: all possible inferences can be mechanically (syntactically) produced ❧ Note: one can & often does use FOPC as a representation language while using a more efficient (but less sound & complete) reasoning system 

6 .Russell & logical atomism ❧The belief that “the world can be analyzed into a number of separate things with relations and so forth” (1918) ● in opposition to a sort of holism which holds that not everything can be analyzed into parts & put back together to form the original whole ❧Methodology: take complex entities & dissolve them into simple atoms ● we take a seemingly complex thing & enumerate all of its properties & relationships 

7 .Language ❧Problem: what are the atoms? ❧Solution: a logically perfect (ideal) language ● one-to-one mapping between facts in the world & “words” (symbols) • thus there is no ambiguity & no inter-dependence regarding facts ● relations between facts ❧Two categories ● atoms, relationships ● logical connectives: and, or, if-then, not, etc. 

8 .Propositional calculus ❧Rather than jumping right into FOPC, we begin with propositional calculus ❧FOPC’s little brother ● No quantification ● No equality 

9 .“Data types” ❧Propositions ● Boolean-valued ● P, Q, R,… • statements about the world • R : it’s-raining-now • needn’t be a single letter ❧Truth symbols ● true, false ● same meaning as in English 

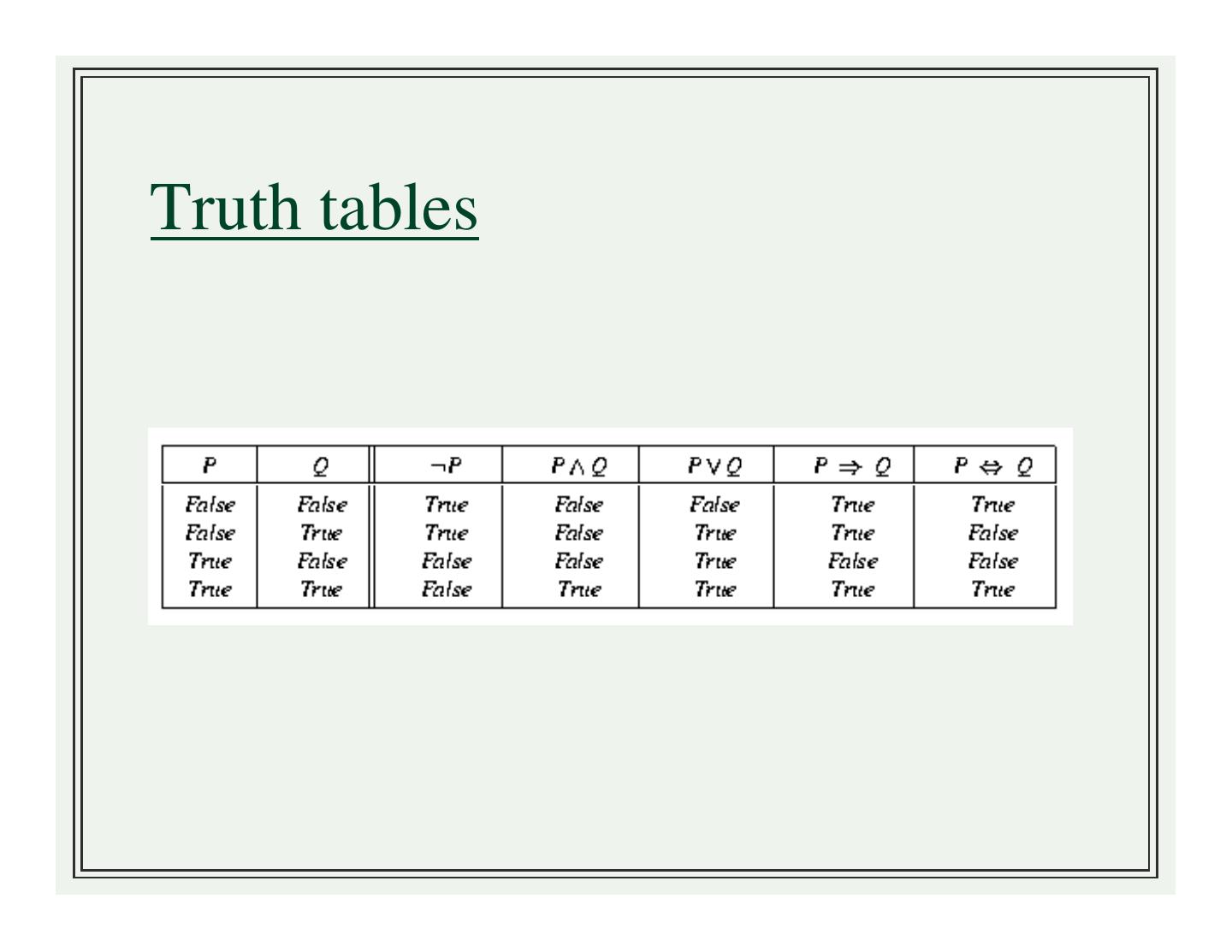
10 .Connectives ❧and (∧) ❧or (∨) ❧implies (⇒) ❧equivalent (⇔) ❧not (¬) ❧used to combine simple statements into more complex ones 

11 .Truth tables 

12 .Well-formed formulae (wffs) ❧Sentences ● just like in a programming language, there are rules (syntax) for legally creating compound statements ● remember: we’re always stating a truth about the world, • hence every wff is something that has a Boolean value (it is either a true or a false statement about the world) 

13 .Syntax rules ❧Propositions (P, Q, R, …) are wffs ❧Truth symbols (true, false) are wffs ❧If A is a wff, so are ¬A and (A) ❧If A and B are wffs, so are ● A∧B ● A∨B ● A⇒ B ● A⇔B 

14 .Interpretation example ❧[(P ∨ Q) ∧ R] ⇒ (S ⇔ V) ❧First, we need an interpretation ● truth values for our “atomic” sentences ● P : T; Q : F; R : T; S : F; V : T ❧Then evaluate ● P∨Q:T ● (P ∨ Q) ∧ R : T ● S⇔V:F ● whole thing : F 

15 .Connectives ❧Think of connectives as functions that take truth values as their arguments and return a truth value ❧The output of these functions is determined by the previous truth tables ❧Just like a normal function that maps inputs to outputs; ● in this case, since the possible values are relatively few, we can enumerate all of them 

16 .Are these WFFs? ❧P Q R ❧(P ∧ Q) ∨ (R ∨ S) ❧P ⇒ ∨ (Q ∧ R) 

17 .Example of k-rep in prop calc ❧R : “It is raining” ❧B : “Take the bus to class” ❧W : “Walk to class” ❧Some things to tell our agent ● R ⇒ B (“If it is raining, (then) take the bus to class”) ● ¬R ⇒ W (“If it is not raining, (then) walk to class”) ❧Ideally, we would like our agent to sense that it is raining & then decide to take the bus 

18 .Validity ❧A wff is valid if it is true under all possible interpretations (i.e., all possible “variable settings”) [use truth table to show this] ● P ∨ ¬ P is valid • if P is true, then the whole sentence is true • if P is false, then ~P is true and the whole sentence is true ● (P ∧ ¬Q) ∨ (¬ ¬P ∧ Q) isn’t valid • when P is true & Q is true, the sentence isn’t true • in order to not be valid, there only need exist one counter-example ● valid is also called a tautology 

19 . Satisfiable ❧A wff is satisfiable if some interpretation makes it true ❧Examples: ● P is satisfiable • simply let P be true ● P ∧ ¬P is not satisifiable • if P is true, ¬P is false, the whole sentence is false • if P is false, the whole sentence is false ● P ⇒ Q is satisfiable • several ways: P is true, Q is true; etc. ● A wff that cannot be satisfied is called a contradiction 

20 .

21 . What is soundness? ❧An inference procedure is sound if it only generates entailed wffs ● a wff is entailed if it is necessarily true given the previously true wffs ● “necessarily true” means it is true given the previously true wffs on any interpretation (on any truth assignment to the symbols) ● this is written as KB |= A • for example, {A ⇒ B, A} |= B ● examples of sound inference procedures are: modus ponens, resolution, and-introduction, etc. • the wffs they generate a true under any interpretation 

22 . Why do we care about soundness? ❧Sound inference procedures are truth-preserving ● none of the wffs produced by the inference procedure contradict any of the given wffs or any of the other derived wffs ● all the wffs produced are consistent with all the wffs given or generated ● thus, any model for the original set of wffs is also a model for the derived set of wffs ● we can write this as: “For every KB |- A, KB |= A” 

23 .

24 .What is a model? ❧A model is an interpretation that makes all the wffs in a set true ● for example, a model for {A ∧ B, ¬B ∨ C} is • A : true, B : true, C : true • note: there may be more than one model ● thus, KB |= A means every model of KB is also a model of A • every assignment of truth values to the wffs in KB that make all of the wffs in KB true, also make A true 

25 .What is an interpretation? ❧An interpretation is the assignment of facts to symbols (or: proposition letters) ● a fact is taken to be either true or false about the world ● thus, by providing an interpretation, we also provide the truth value of each of symbol ● example • P : it-is-raining-here-now • since this is either a true statement about the world or a false statement, the value of P is either true or false 

26 .

27 .Completeness ❧We have shown what it means to be a sound inference procedure: we only generate entailed wffs ❧One other question we can ask is whether using our inference procedure we can generate all of the entailed wffs ❧If we are able to do so, we say that our inference procedure is complete 

28 .What is completeness? ❧An inference procedure is complete if it can find a proof for any sentence that is entailed ● that is, that it can generate all the wffs consistent with the “givens” using it’s “operations” ❧What is complete? ● Are truth tables complete? ● When are the inference rules in some set of rules complete? 

29 .Truth tables ❧Truth tables are sound and complete ● they enumerate every combination of truth values • as the number of literals increases, the size of the truth table grows exponentially (2(# of literals)) ● thus, they will be able to “prove” every entailed wff (using the definitions of the connectives) • for a truth table, a proof is simply the truth table itself ● they are sound because they simply enumerate all of the truth possibilities