- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
001-introduction to logic
展开查看详情
1 .
2 . Aristotle Aristotle (3000 years ago) was a Greek philosopher, scientist, and mathematician. He wanted to create a system for explaining reality - and he called this system “Logos” or “Logic”
3 . Aristotle’s system • Was very popular for the ancient Greeks. • The system of logic became the basis for Western thought and Western writing.
4 . It’s like Mathematics If A, then B If B, then C Therefore...... If A, then C
5 . Anatomy of an argument • The bottom statement after the “therefore” is called the “conclusion” of the argument • Conclusions are often called “thesis statements” • The top two statements are called “premises” • Premises are often called “supporting statements”
6 . Why do we argue??? To make people believe the same thing we do
7 . Meet Fred the Dog • If Fred is a healthy dog, then he has four legs • If he has four legs, then he can run quickly • Therefore, if Fred is a healthy dog, he can run quickly.
8 . See the flow? • If Fred is a healthy • If A then B dog, then he has four legs. • If Fred Has four legs, then he can run • If B then C quickly • If Fred is a healthy dog, then he can run • If A then C quickly
9 . We See a “Z” • If Fred is a healthy • If A then B dog , then he has four legs • If Fred has four legs, then he can run fast • If A then C • If Fred is a healthy dog, then he can run fast • If B then C
10 . Let’s try it with another form • If Fred is a healthy • If A then B dog , then he has four legs • If Fred is a healthy dog, then he can run • If A then C fast • If fred has four legs, then he can run fast • If B then C
11 . It Doesn’t Work • If Fred is a healthy • If A then B dog , then he has four legs • If Fred is a healthy dog, then he can run • If A then C fast • If Fred has four legs, then he can run fast • If B then C
12 . Connecting the Ideas • When the Ideas flow together in a “Z” chain, then we say the argument has a good “form” • There are many kinds of forms that work • We will learn two more forms
13 . An argument is VALID when • The argument has a proper form that chains together without interruption • The premises are true. IF THESE RULES ARE MET, THEN THE ARGUMENT IS VALID, AND THE CONCLUSION MUST BE TRUE!!!!
14 .Argument form #1 - Hypothetical Syllogism (the Fred argument) If A, then B If B, then C If C, then D If A, then D
15 . Something a little more real.. • If the United Nations help Poochnia develop it’s economy, then Poochnia can make enough food for it’s people. • If Poochnia can make enough food, then it won’t attack it’s neighbors for food. • If the United Nations help Poochnia develop it’s economy, it won’t attack it’s neighbors for food.
16 .Argument form #2 - Modus Ponens If A, then B If B, then C A C
17 . Example • If you throw a ball at Fred, he will try to catch it. • You throw a ball to Fred. Therefore • He will try to catch it.
18 . A little more real • If we help Poochnia develop it’s economy, it will be able to make enough food. • If Poochnia can make enough food, then it won’t attack it’s neighbors for food. • If Poochnia doesn’t attack it’s neighbors, then there will be peace in that region. • We will help Poochnia develop it’s economy. Therefore • There will be peace in the region.
19 .Argument form #3 - Transitive Syllogism A=B B=C C=D A=D
20 . Meet Fred’s friend -- Fluffy • Fluffy is a cat • cats are meat eaters • meat eaters are killers therefore • Fluffy is a killer
21 . Another trip to Poochnia • Poochnia is a poor country • Poor countries have bad economies • Bad economies are the result of bad political systems therefore • Poochnia has a bad political system
22 . Argument Grammar • Infinitives - ‘to protect our society’ • Prediction Modals - ‘may/will/would/shall’ • Suasive verbs - ‘agree, demand, prove recommend, suggest, indicate, show’ • Conditional subordination - ‘if - then’, ‘either - or’, ‘unless’ • Necessity modals - ‘will/would/shall ’ • Possibility modals - ‘can/may/might/could’
23 .
24 . The Statement The fundamental unit in symbolic logic is the statement which is a declarative statement that may be assigned a value of being either False (0) or True (1) The following are examples of statements: p: The sky is blue. q: The sky is black r: The cat is fat. s: The cat ate the rat. t: The cat is black. u: Today is Thursday.
25 . Not a Statement What time is it? (Interrogative not declarative.)
26 . Not a Statement Stop making that noise. (Imperative not declarative.)
27 . Not a Statement Pow! Holy Cow, Batman! (Exclamatory not declarative)
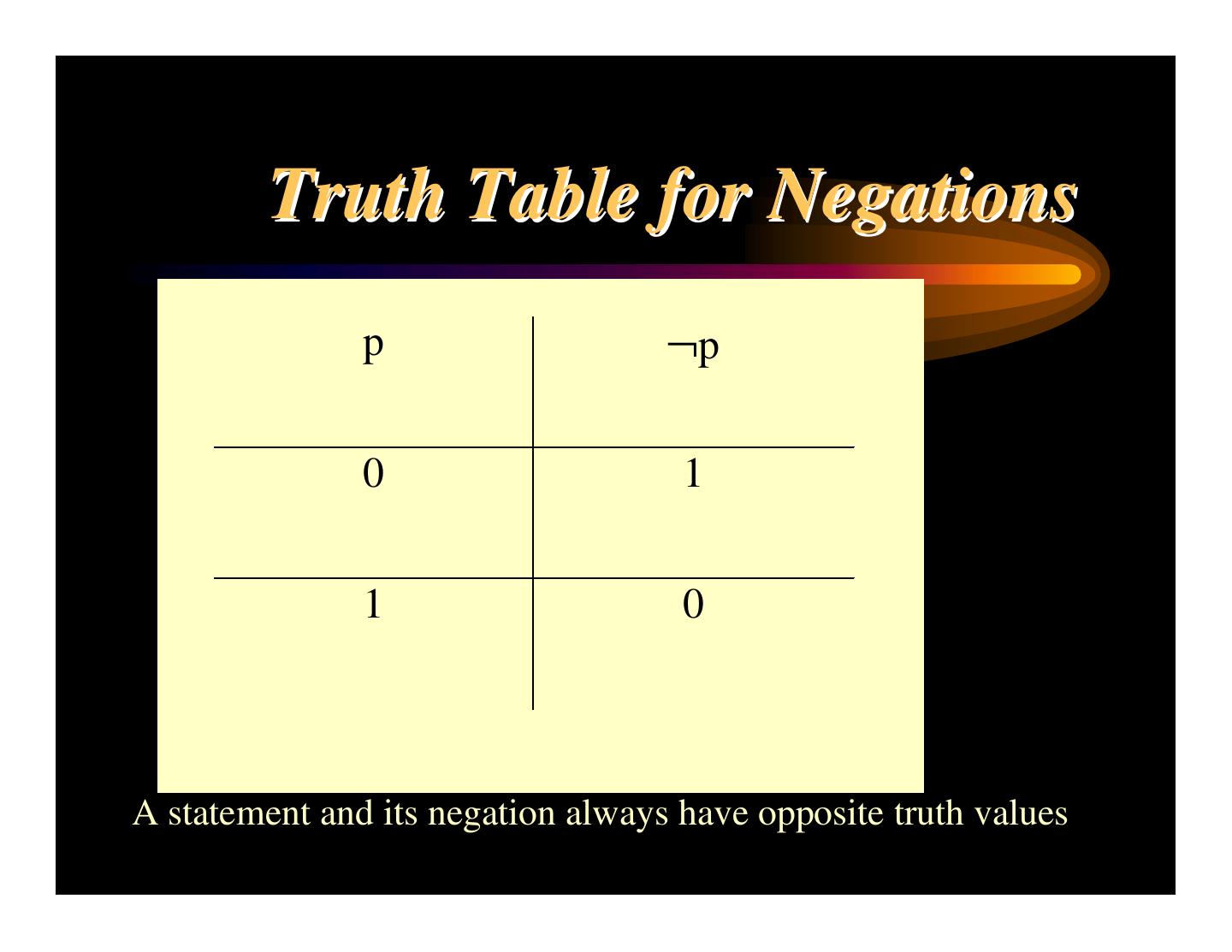
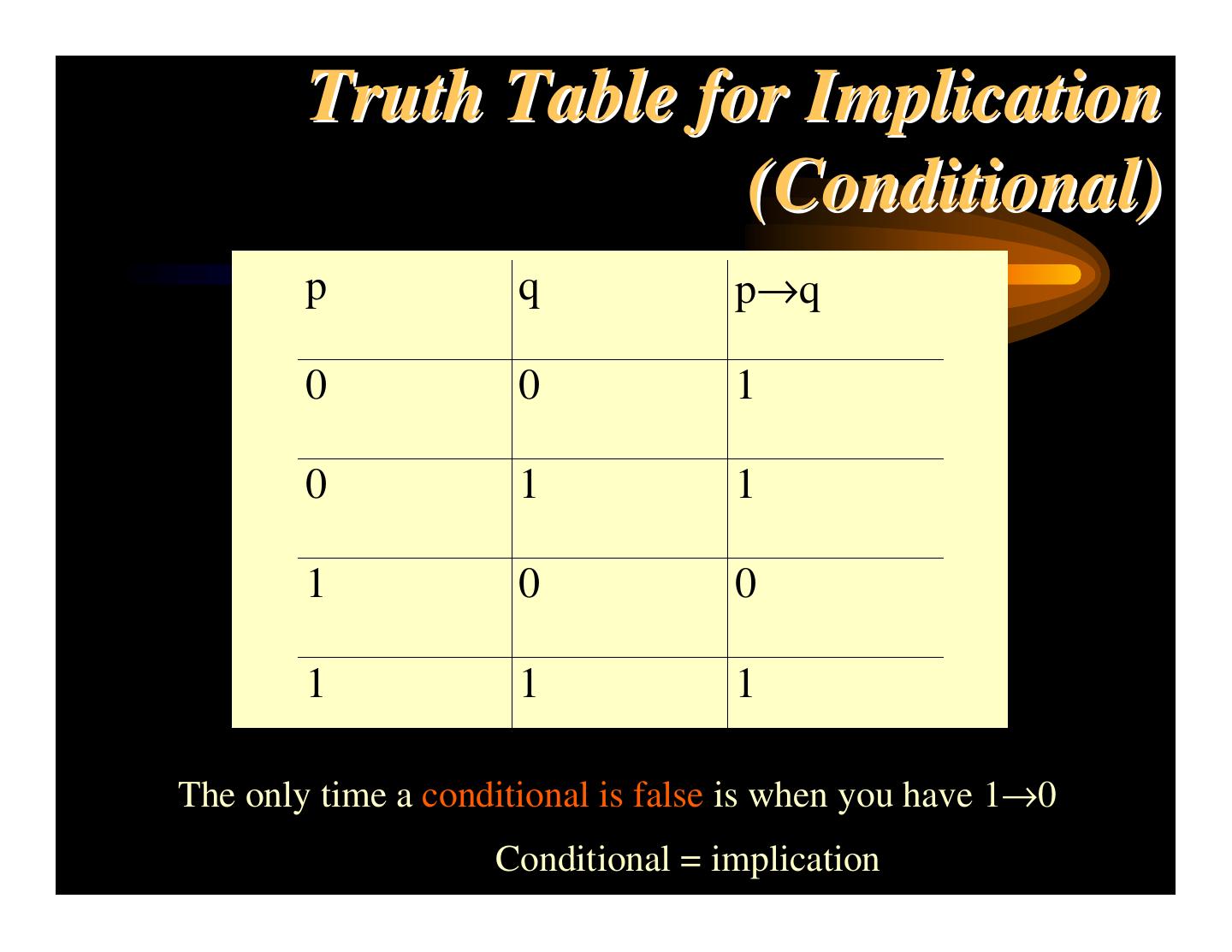
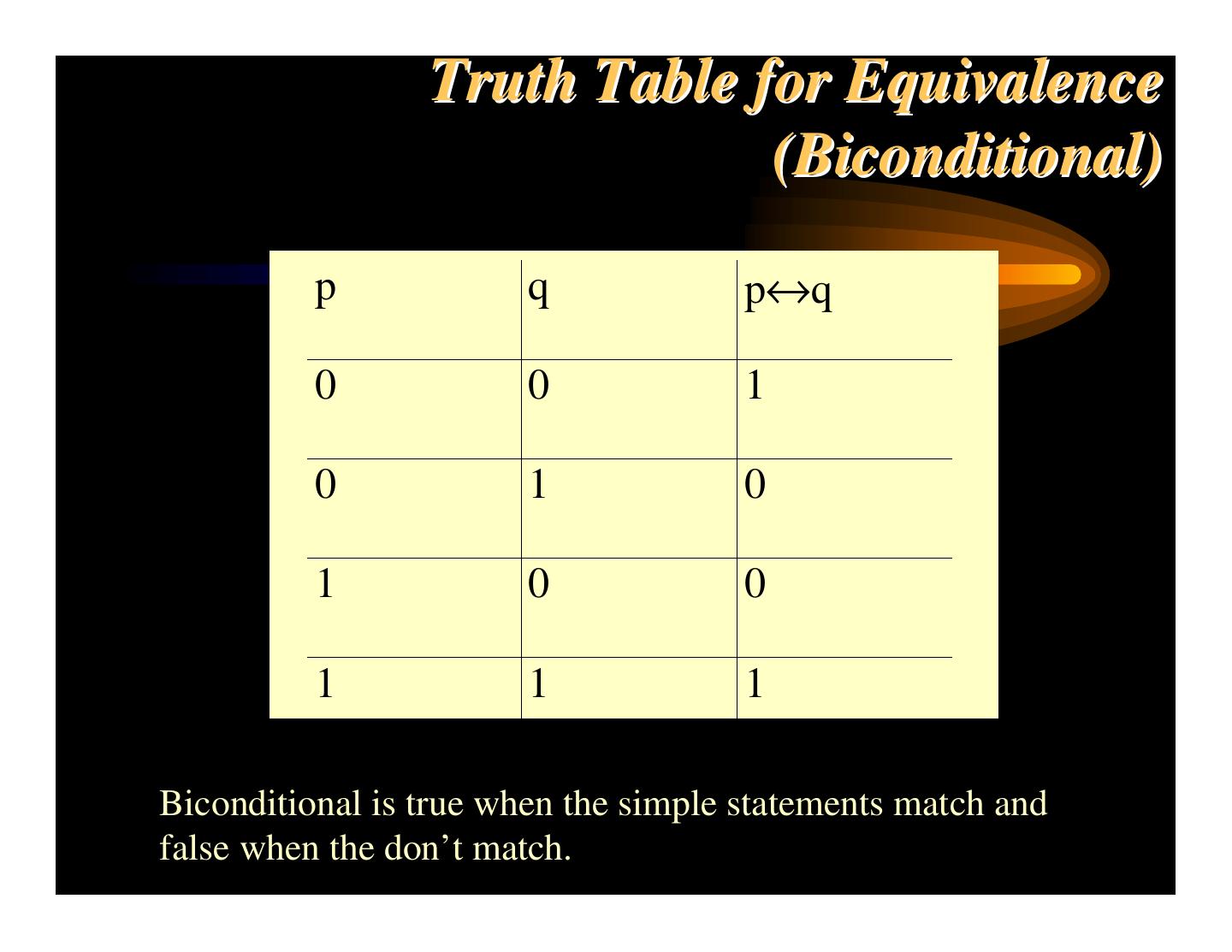
28 . The Statement At different times the same statement may take on different truth values. For example tonight statement t is True (1) but tomorrow it will be False (0). A statement is simple if it has a single subject and predicate and if it doesn’t use the words we define as connectives. The connectives are: not, and, or, if…then, if and only if A statement that uses connectives is compound.
29 . Simple & Compound Statements Simple Statements: Today is Thursday. Tomorrow is Friday. The cat is black. Compound Statements: Today is not Thursday. The cat is fat and black. If the cat ate the rat then the cat is fat. We have a class today, if and only if today is Thursday.