022-Prolog

1 .PROLOG 

2 . Contents 1. PROLOG: The Robot Blocks World. 2. PROLOG: The Monkey and Bananas problem. 3. What is Planning? 4. Planning vs. Problem Solving 5. STRIPS and Shakey 6. Planning in Prolog 7. Operators 8. The Frame Problem 9. Representing a plan 10. Means Ends Analysis 

3 .PROLOG PROGRAM FOR BLOCKS WORLD • Consider a robot that manipulates blocks on table • Robot can see blocks by a camera mounted on ceiling • Robot wants to know: 1. blocks’ coordinates, 2. whether a block is graspable (nothing on top), 3. etc. 

4 . PROLOG PROGRAM FOR ROBOT’S WORLD a Y % see( Block, X, Y) b see( a, 2, 5). 5 c d 4 see( d, 5, 5). 3 e see( e, 5, 2). 2 1 1 2 3 4 5 6 X % on( Block, BlockOrTable) on( a, b). on( b, c). on( c, table). on( d, table). on( e, table). 

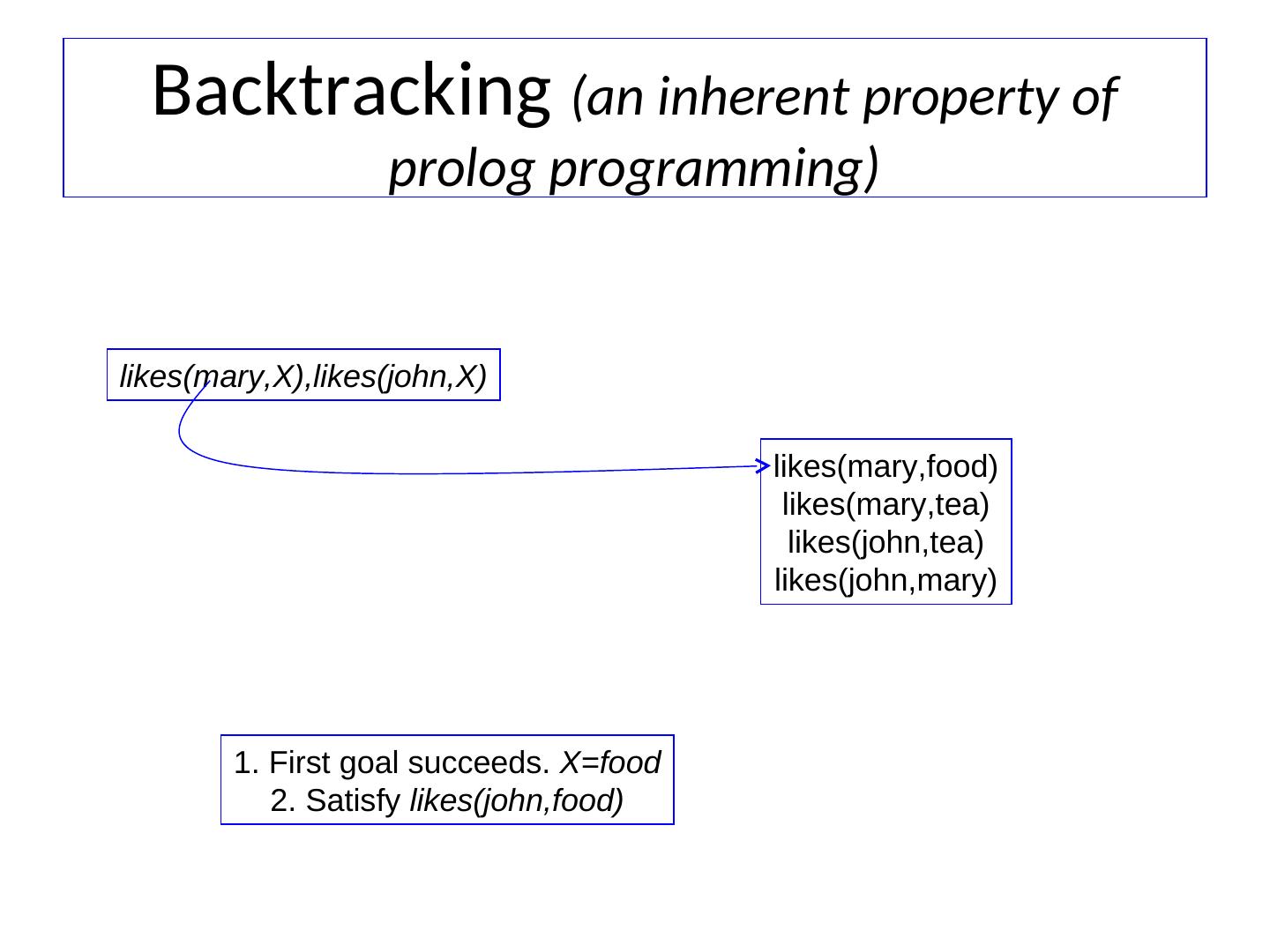
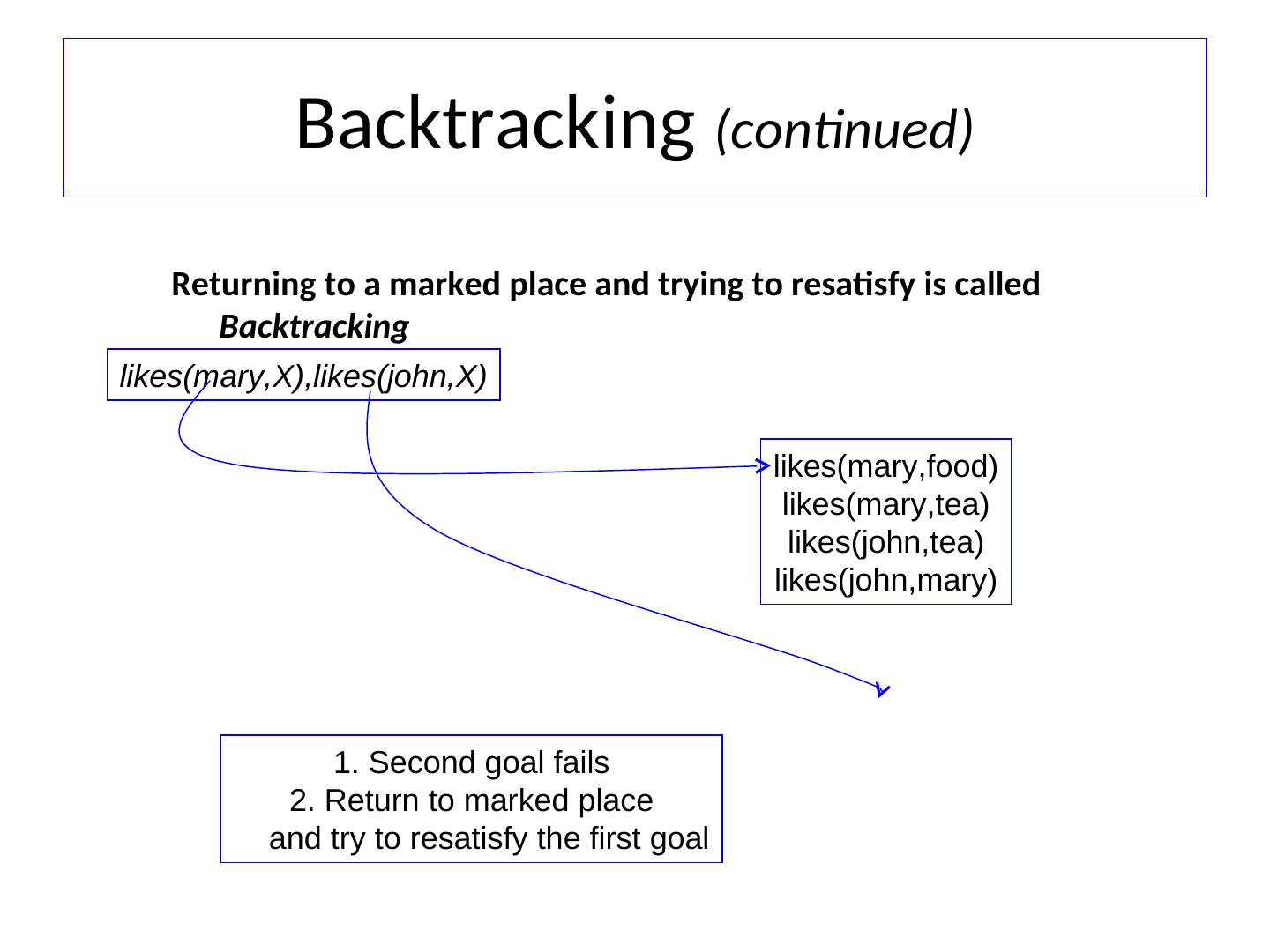
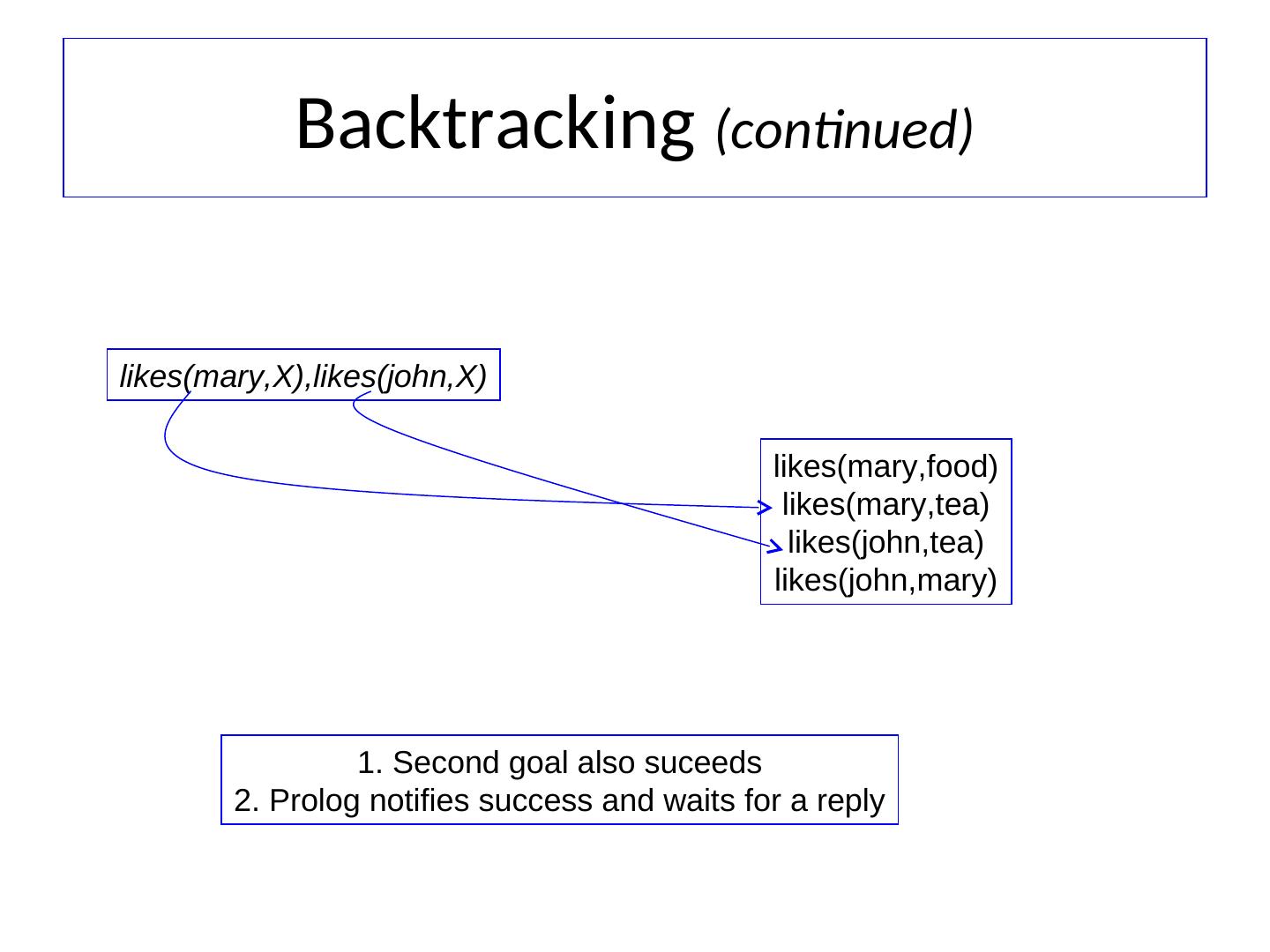
5 . INTERACTION WITH ROBOT PROGRAM Start Prolog interpreter ?- [robot]. % Load file robot.pl File robot consulted ?- see( a, X, Y). % Where do you see block a X=2 Y=5 ?- see( Block, _, _). % Which block(s) do you see? Block = a; % More answers? Block = d; Block = e; no 

6 . INTERACTION, CTD. ?- see( B1, _, Y), see( B2, _, Y). % Blocks at same Y? % Prolog’s answers may surprise! % Perhaps this was intended: ?- see( B1, _, Y), see( B2, _, Y), B1 \== B2. 

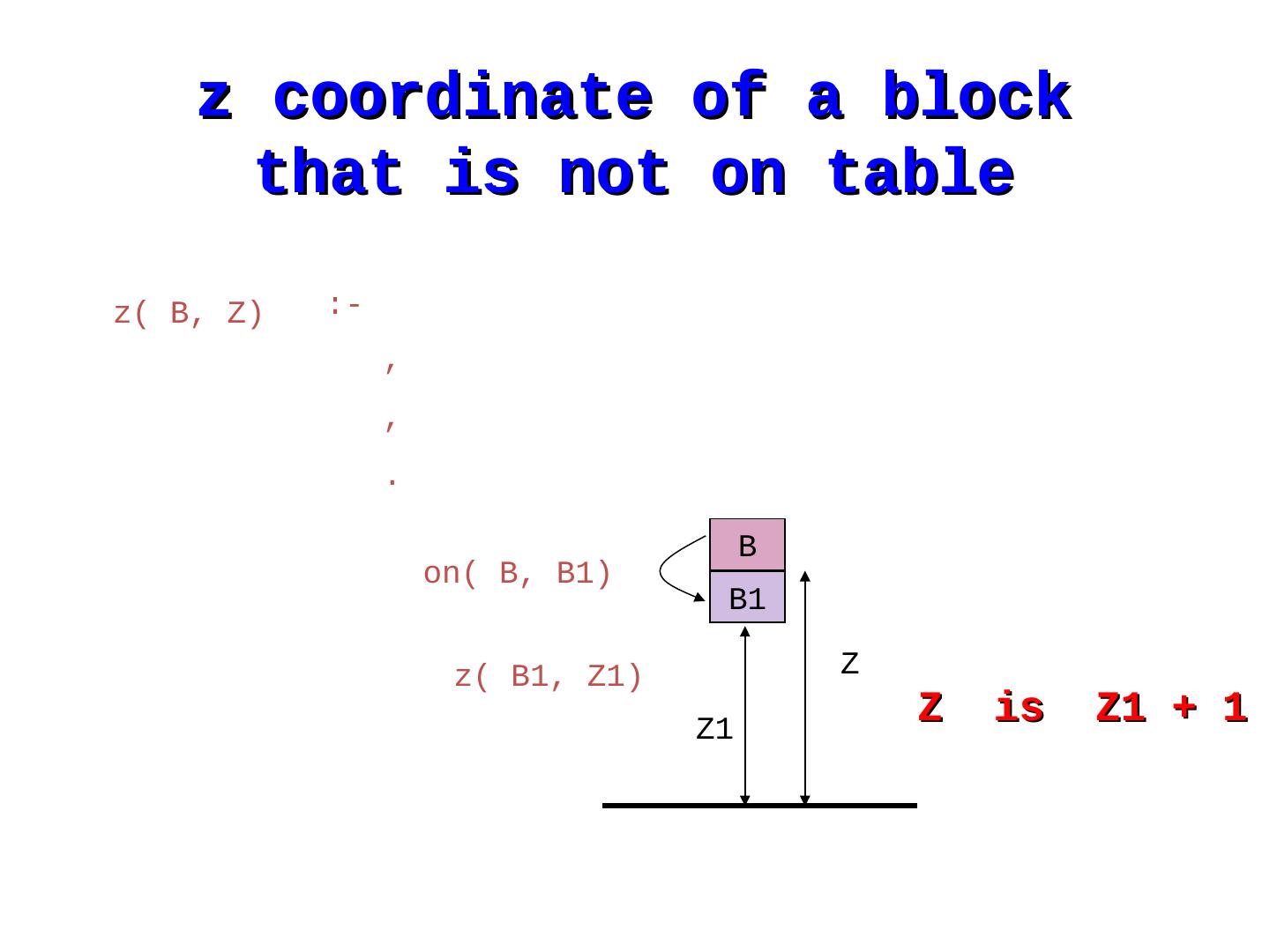
7 . z coordinate of a block that is not on table z( B, Z) :- , , . B on( B, B1) B1 z( B1, Z1) Z Z1 Z is Z1 + 1 

8 . EXTRACT X, Y, Z COORD. % z( Block, Z): z-coord. of Block z( B, 0) :- on( B, table). z( B, Z) :- on( B, B0), B on B0 z( B0, Z0), Z is Z0 + 1 Z is Z0 + 1. Z0 

9 . Prolog tends to keep results in symbolic form % An attempt at shortening this z( B, Z0 + 1) :- on( B, B0), z( B0, Z0). ?- z( a, Za). Za = 0+1+1 % Prolog constructs a formula! 

10 .Prolog can easily construct general formula z( B, Z0 + height( B)) :- % Add hight of block B on( B, B0), z( B0, Z0). ?- z( a, Za). Za = 0 + height(c) + height( b) 

11 .% xy( Block, X, Y): X, Y coord. of Block xy( B, X, Y) :- see( B, X, Y). xy( B, X, Y) :- on( B0, B), xy( B0, X, Y). % Blocks in stack same xy-coord. 

12 .?- z( c, Z). Z=0 ?- z( a, Z). Z=2 % Trace proof tree of this execution 

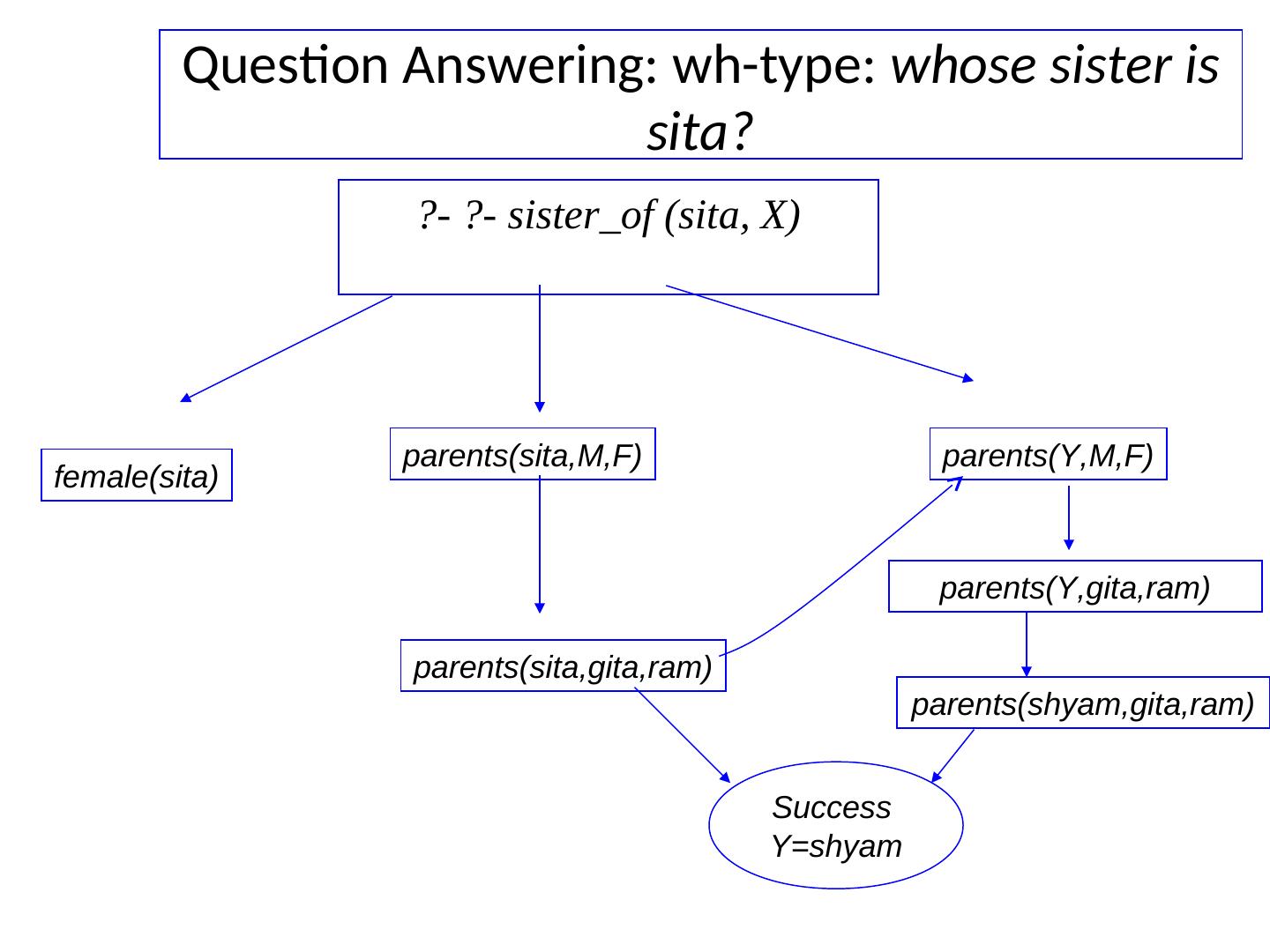
13 . RELATION ABOVE % above( Block1, Block2): Block1 above Block2 in the same stack above( B1, B2) :- on( B1, B2). above( B1, B2) :- on( B1, B), above( B, B2). ?- above( a, c). % Trace proof tree for this 

14 . DECLARATIVE vs PROCEDURAL MEANING • A & B is logically equal to B & A • Declarative meaning of Prolog program = logical meaning • Order of goals in clauses does not affect declarative meaning • Procedural meaning of Prolog = algorithm for searching for proof • Order of goals and clauses does affect procedural meaning 

15 . A VARIANT OF ABOVE above2( B1, B2) :- above2( B, B2), on( B1, B). above2( B1, B2) :- on( B1, B2). ?- above( a, c). % Trace to see what happens 

16 . TRY SIMPLE THINGS FIRST • Why above2 fails procedurally? • above2 always tries complicated things first • This is a bad idea • A principle that often works: Try simple things first • Do we always have to study procedural details in Prolog? No, usually not! • In fact, quite the opposite: we shouldn’t! • Programmer encouraged to think declaratively - this is the point of a declarative language! 

17 . Prolog Programming 

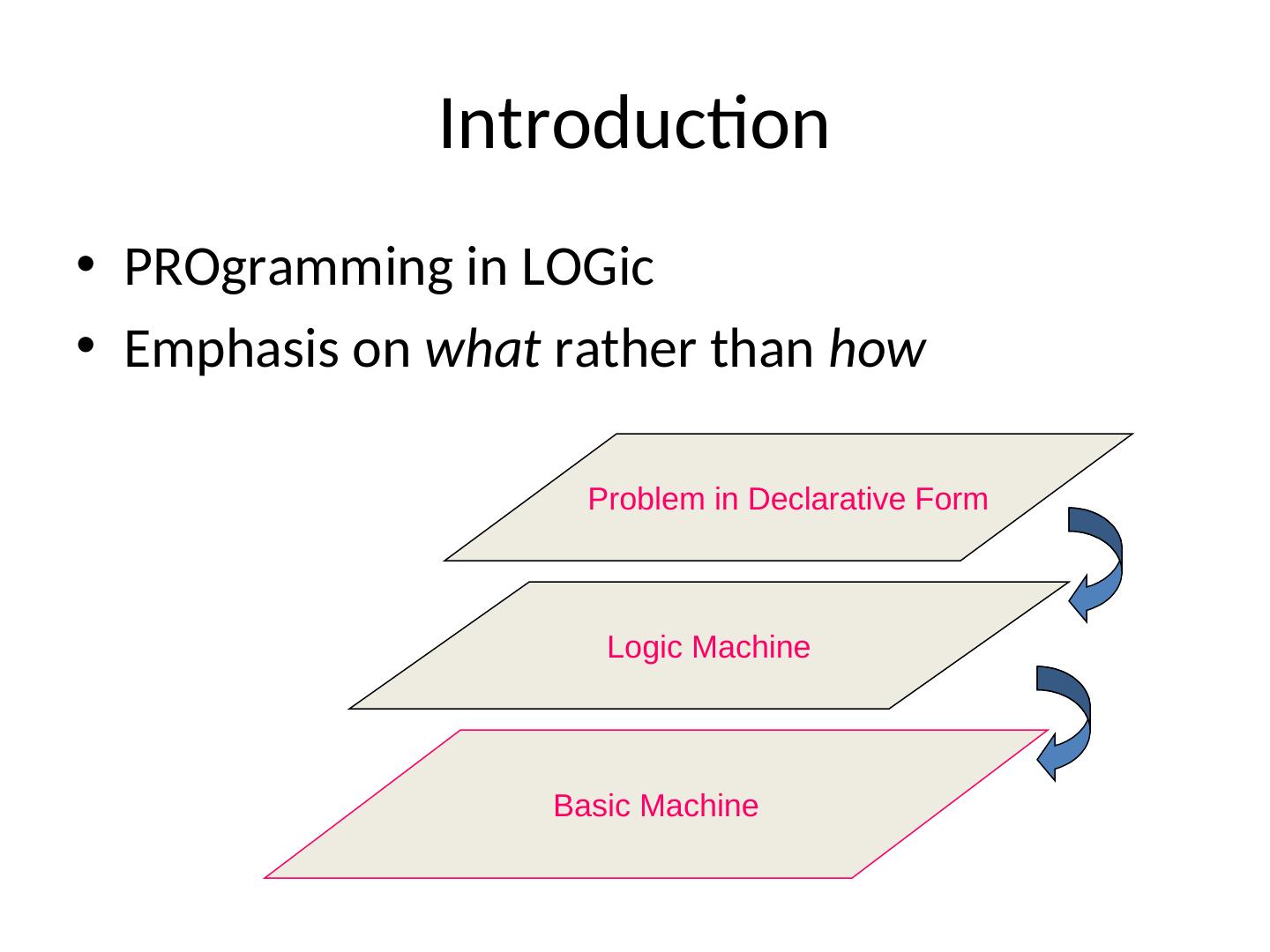
18 . Introduction • PROgramming in LOGic • Emphasis on what rather than how Problem in Declarative Form Logic Machine Basic Machine 

19 . Prolog’s strong and weak points • Assists thinking in terms of objects and entities • Not good for number crunching • Useful applications of Prolog in – Expert Systems (Knowledge Representation and Inferencing) – Natural Language Processing – Relational Databases 

20 . A Typical Prolog program Compute_length ([],0). Compute_length ([Head|Tail], Length):- Compute_length (Tail,Tail_length), Length is Tail_length+1. High level explanation: The length of a list is 1 plus the length of the tail of the list, obtained by removing the first element of the list. This is a declarative description of the computation. 

21 .Planning and Prolog 

22 . Planning • To solve this problem the monkey needed to devise a plan, a sequence of actions that would allow him to reach the desired goal. • Planning is a topic of traditional interest in Artificial Intelligence as it is an important part of many different AI applications, such as robotics and intelligent agents. • To be able to plan, a system needs to be able to reason about the individual and cumulative effects of a series of actions. – This is a skill that is only observed in a few animal species and only mastered by humans. • The planning problems we will be discussing today are mostly Toy- World problems but they can be scaled up to real-world problems such as a robot negotiating a space. 

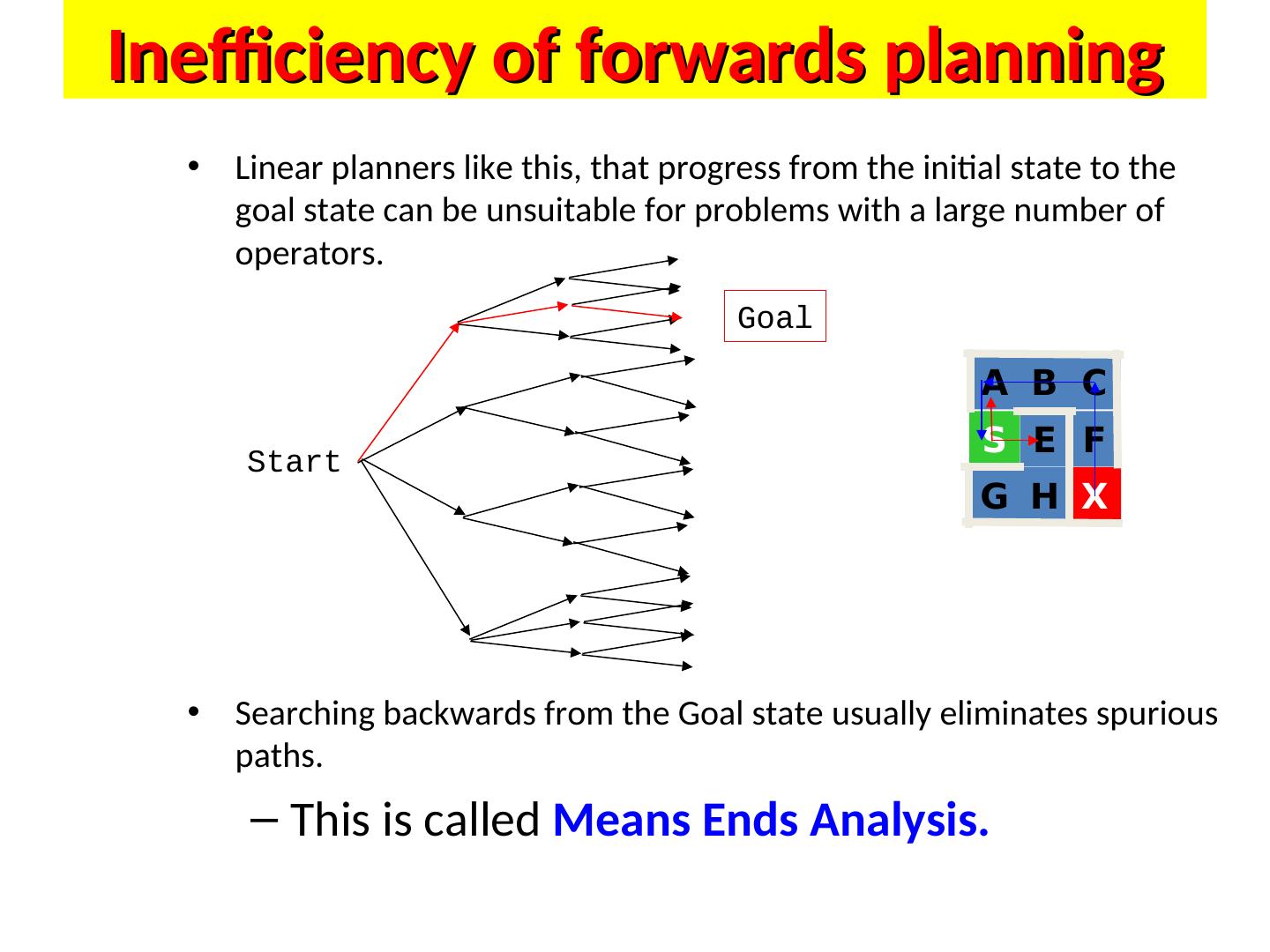
23 . Planning vs. Problem Solving • Planning and problem solving (Search) are considered as different approaches even though they can often be applied to the same problem. • Basic problem solving (as discussed in the Search lectures) searches a state-space of possible actions, starting from an initial state and following any path that it believes will lead it the goal state. • Planning is distinct from this in three key ways: 1. Planning “opens up” the representation of states, goals and actions so that the planner can deduce direct connections between states and actions. 2. The planner does not have to solve the problem in order (from initial to goal state) it can suggest actions to solve any sub-goals at anytime. 3. Planners assume that most parts of the world are independent so they can be stripped apart and solved individually (turning the problem into practically sized chunks). 

24 .Shakey • Shakey.ram 

25 .Planning using STRIPS • The “classical” approach most planners use today is derived from the STRIPS language. • STRIPS was devised by SRI in the early 1970s to control a robot called Shakey. • Shakey’s task was to negotiate a series of rooms, move boxes, and grab objects. • The STRIPS language was used to derive plans that would control Shakey’s movements so that he could achieve his goals. • The STRIPS language is very simple but expressive language that lends itself to efficient planning algorithms. • The representation we will use in Prolog is derived from the original STRIPS representation. 

26 . STRIPS 1. Stanford Research Institute Problem Solver (1970s) 1. Planning system for a robotics project : SHAKEY (by Nilsson et.al.) 2. Knowledge Representation : First Order Logic. 3. Algorithm : Forward chaining on rules. 4. Any search procedure : Finds a path from start to goal. 1. Forward Chaining : Data-driven inferencing 2. Backward Chaining : Goal-driven 

27 . Forward & Backward Chaining 1. Rule : man(x)  mortal(x) 2. Data : man(Shakespeare) 3. To prove : mortal(Shakespeare) 4. Forward Chaining: 5. man(Shakespeare) matches LHS of Rule. 6. X = Shakespeare 1. mortal( Shakespeare) added 7. Forward Chaining used by design expert systems 8. Backward Chaining: uses RHS matching 9. - Used by diagnostic expert systems 

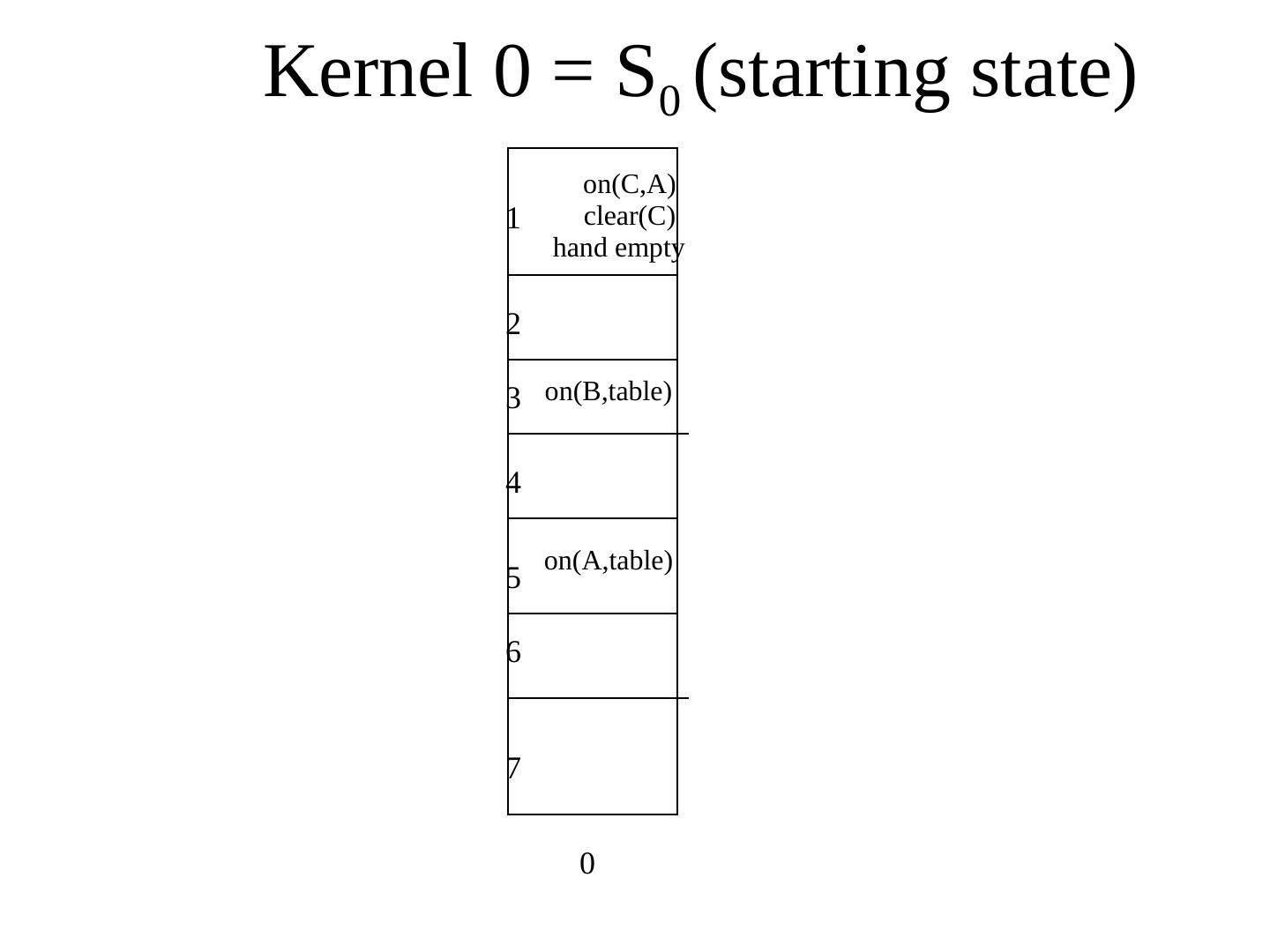
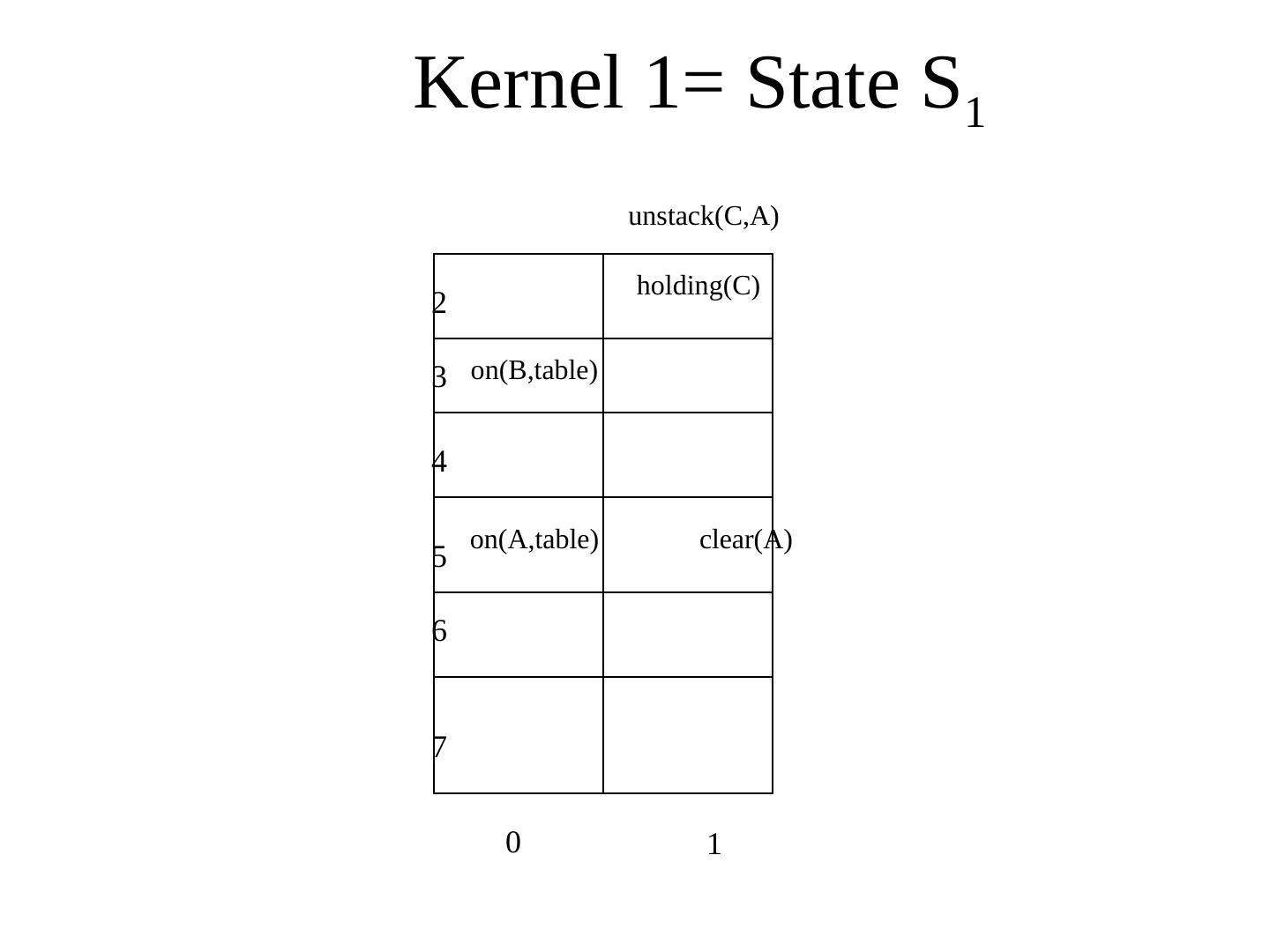
28 . Triangular Table • For n operations in the plan, there are : • (n+1) rows : 1  n+1 • (n+1) columns : 0  n • At the end of the ith row, place the ith component of the plan. • The row entries for the ith step contain the pre-conditions for the ith operation. • The column entries for the jth column contain the add list for the rule on the top. • The <i,j> th cell (where 1 ≤ i ≤ n+1 and 0≤ j ≤ n) contain the pre- conditions for the ith operation that are added by the jth operation. • The first column indicates the starting state and the last row indicates the goal state. 

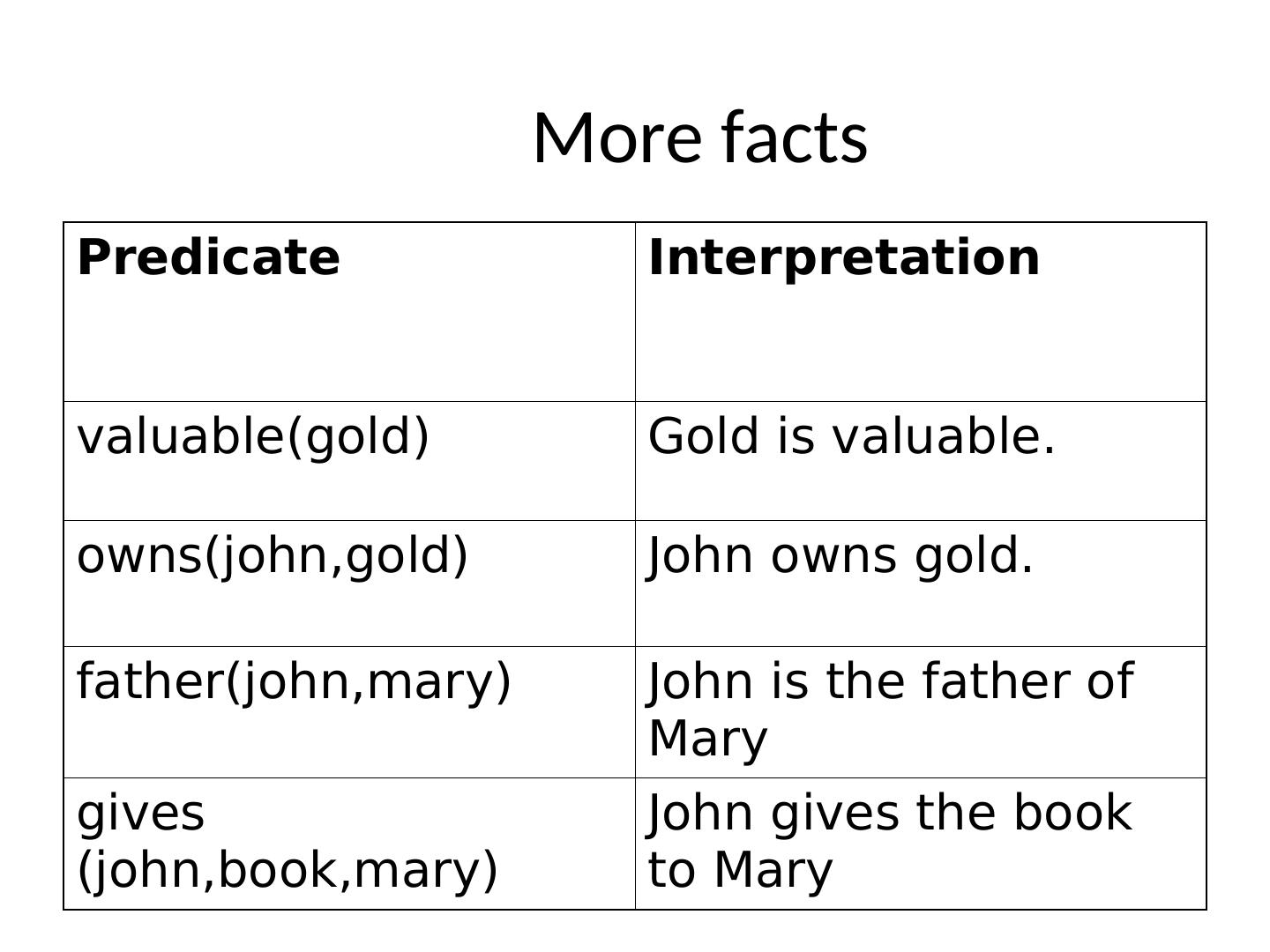
29 . STRIPS Representation • Planning can be considered as a logical inference problem: – a plan is inferred from facts and logical relationships. • STRIPS represented planning problems as a series of state descriptions and operators expressed in first-order predicate logic. State descriptions represent the state of the world at three points during the plan: – Initial state, the state of the world at the start of the problem; – Current state, and – Goal state, the state of the world we want to get to. Operators are actions that can be applied to change the state of the world. – Each operator has outcomes i.e. how it affects the world. – Each operator can only be applied in certain circumstances. – These are the preconditions of the operator.