032-Planning-to-move

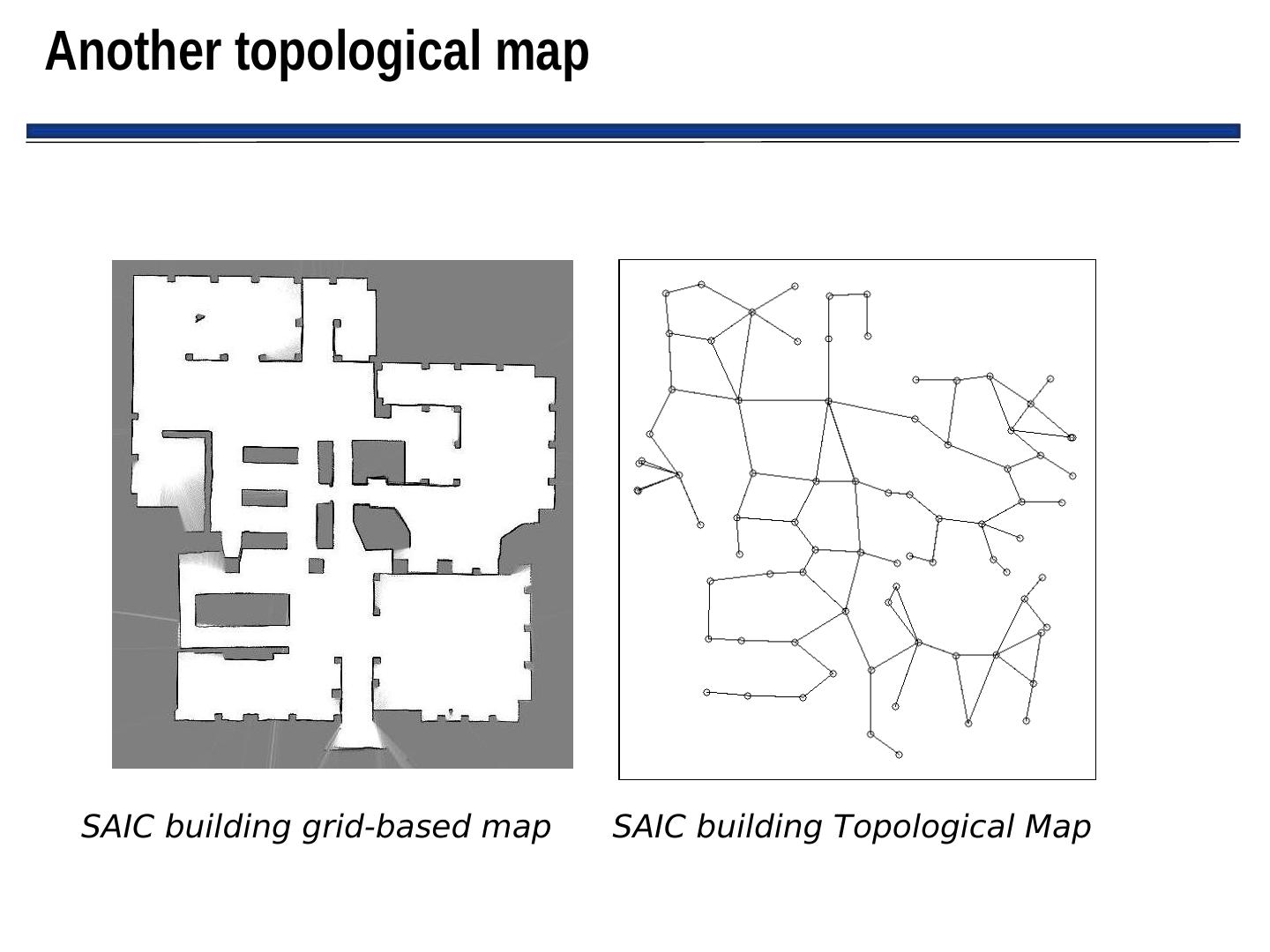
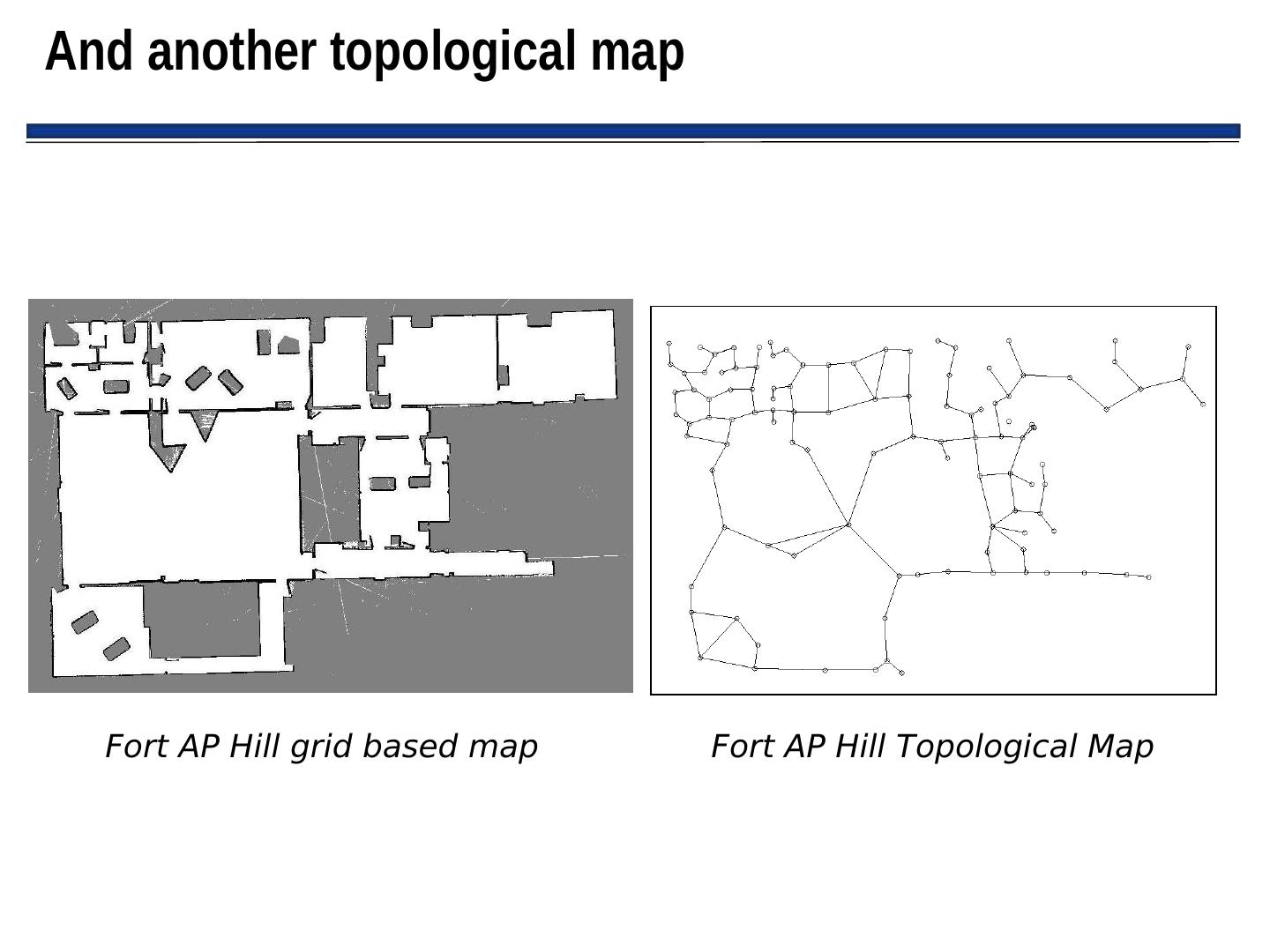
1 . Navigation and Metric Path Planning Minerva tour guide robot (CMU): Example of Minerva’s occupancy Gave tours in Smithsonian’s National Museum of History map used for navigation 

2 . Objectives • Understand techniques for metric path planning: – Configuration space – Meadow maps – Generalized Voronoi graphs – Grids – Quadtrees – Graph-based planners: A* – Wavefront-based planners 

3 . Introduction to Navigation • Navigation is fundamental ability in autonomous mobile robotics • Primary functions of navigation: – Where am I going? • Usually defined by human operator or mission planner – What’s the best way to get there? • Path planning: qualitative and quantitative – Where have I been? • Map making – Where am I? • Localization: relative or absolute 

4 . Introduction to Navigation (con’t.) • Navigation is a fundamental robotics problem because it involves almost everything about AI robotics: – Sensing – Acting – Planning – Architectures – Hardware – Computational efficiencies – Problem solving 

5 . Introduction to Navigation (con’t.) • Path Planning Research – goes back to 1970s • Lots of approaches: proper choice depends upon ecological niche • Criteria for Evaluating Path Planners: – Complexity – Sufficiently represents the terrain – Sufficiently represents the physical limitations of the robot platform – Compatible with the reactive layer – Supports corrections to the map and re-planning 

6 . Intro. (con’t.): Impact of Sensor Uncertainty • Early path planning research (in simulation) assumed: – Sensors give an accurate representation of world – Robot ability to localize • But, as we’ve learned, these assumptions aren’t true • Therefore, robot has to operate in presence of uncertainty • Result: new techniques for dealing with sensor noise in localization, map building, and path planning 

7 . Intro. (con’t.): Spatial Memory • Spatial memory: – World representation used by robot – Provides methods and data structures for processing and storing information derived from sensors – Organized to support methods that extract relevant expectations about a navigational task 

8 . Intro. (con’t.): Spatial Memory (con’t.) • Four basic functions of Spatial memory: – Attention: What features, landmarks to look for next? – Reasoning: E.g., can I fit through that door? – Path Planning: What is the best way through this building? – Information collection: What does this place look like? Have I ever seen it before? What has changed since I was here before? 

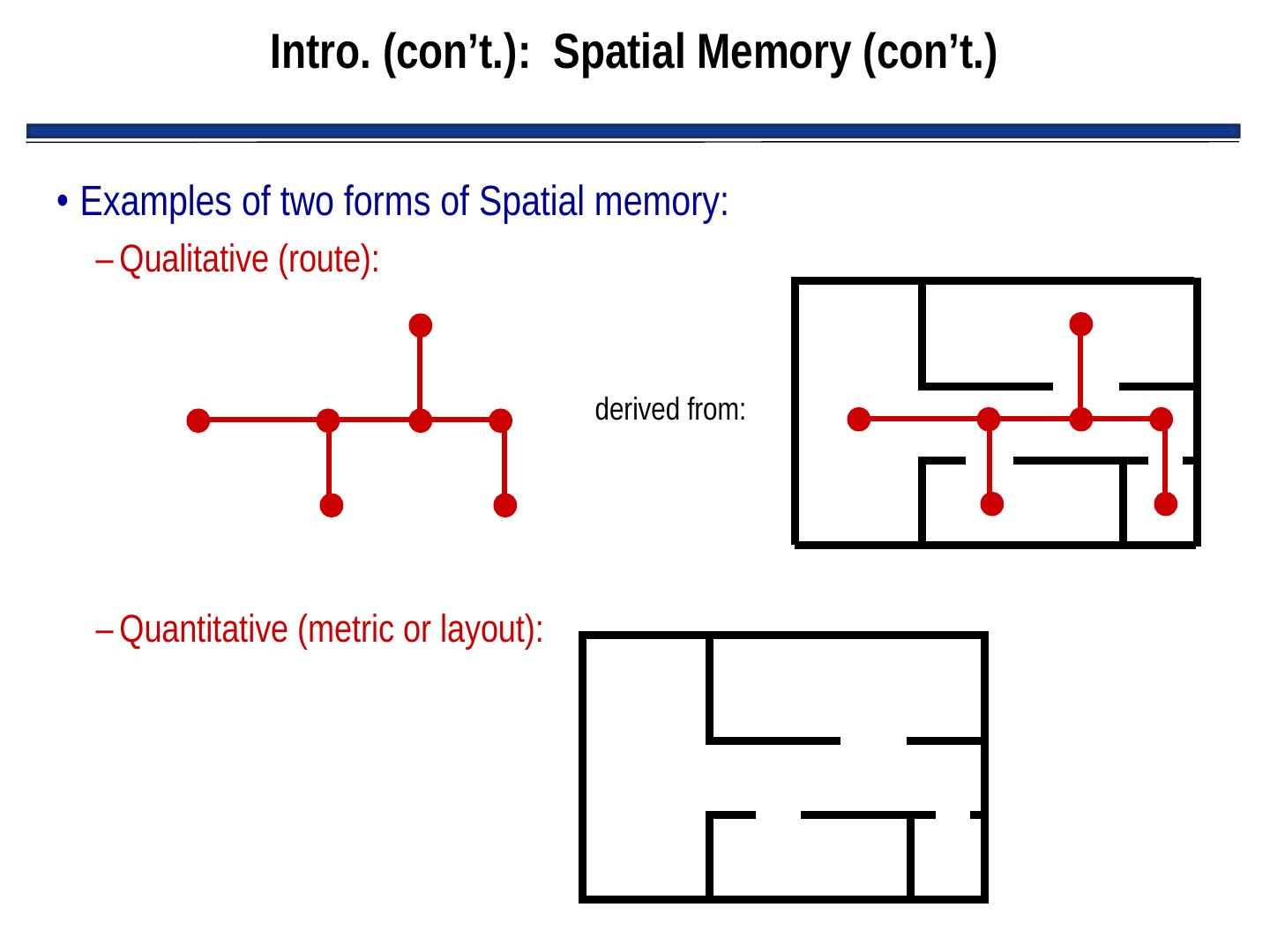
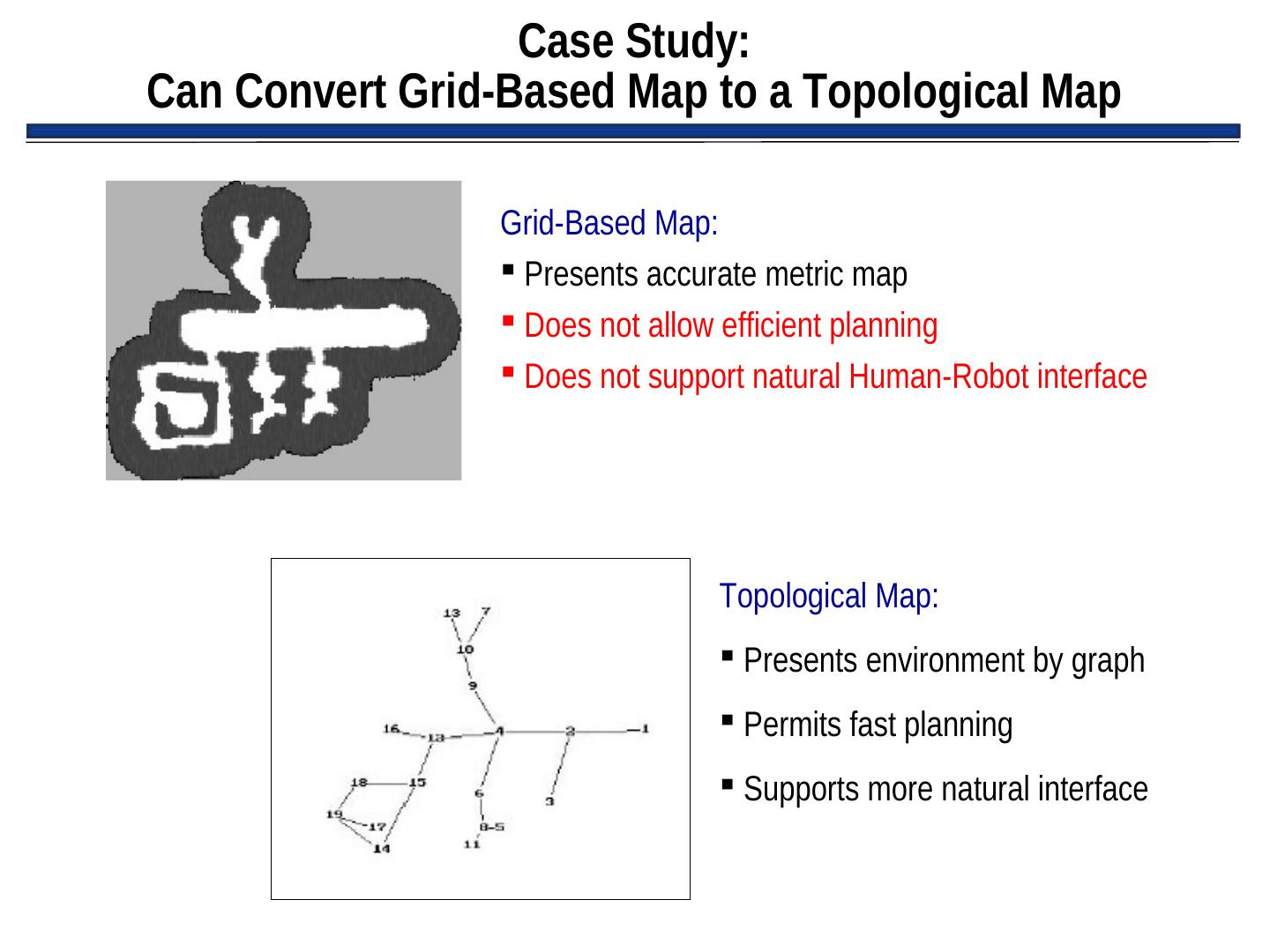
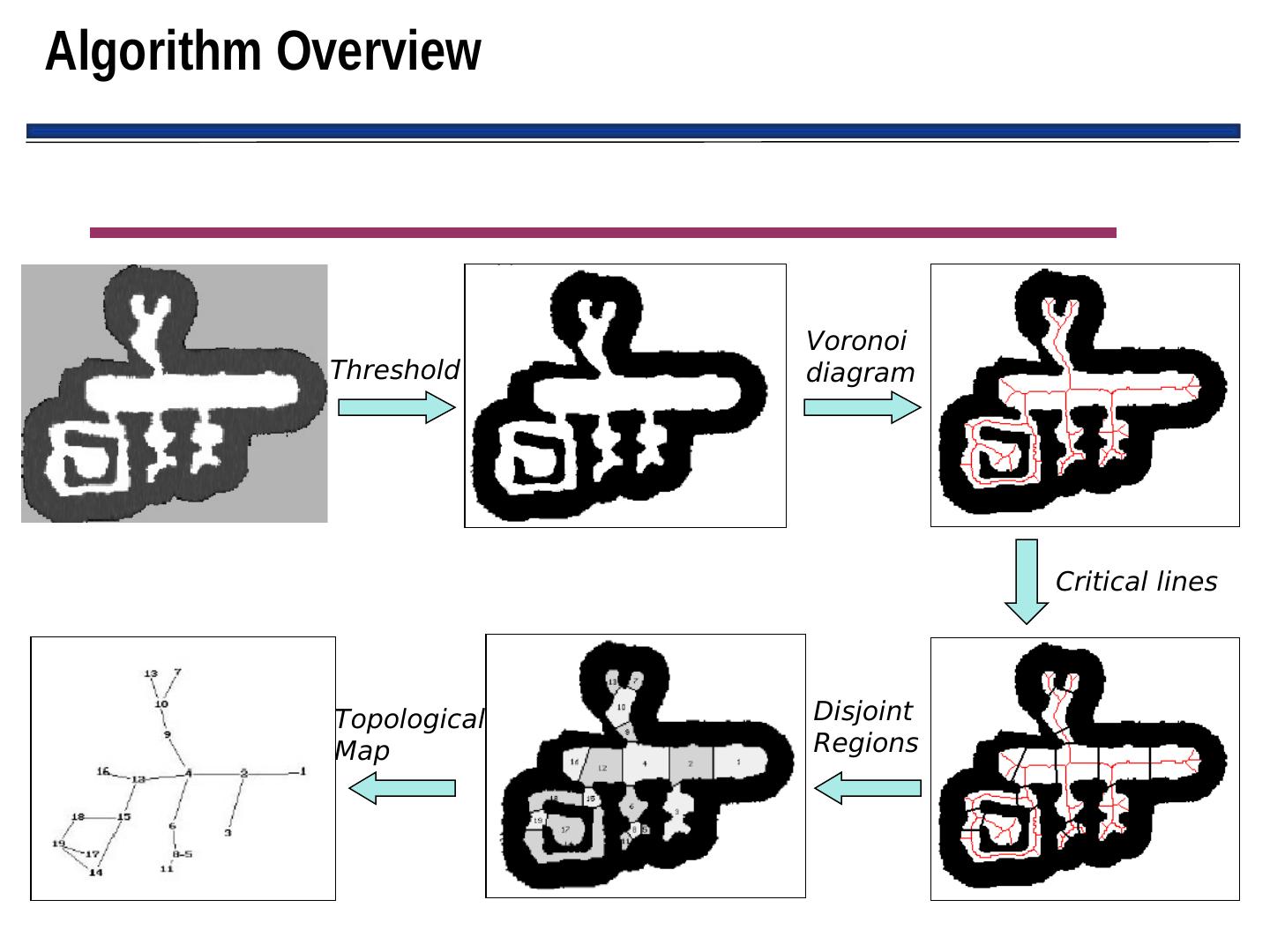
9 . Intro. (con’t.): Spatial Memory (con’t.) • Examples of two forms of Spatial memory: – Qualitative (route): derived from: – Quantitative (metric or layout): 

10 . Intro. (con’t.): Spatial Memory (con’t.) • Two forms of Spatial memory: – Qualitative (route): • Express space in terms of connections between landmarks • Dependent upon perspective of the robot • Orientation clues are egocentric • Usually cannot be used to generate quantitative (metric/layout) representations – Quantitative (metric or layout): • Express space in terms of physical distances of travel • Bird’s eye view of the world • Not dependent upon the perspective of the robot • Independent of orientation and position of robot • Can be used to generate qualitative (route) representations 

11 . Intro. (con’t.): Spatial Memory (con’t.) • Questions regarding spatial memory: – How accurately and efficiently does robot need to navigate? – Is navigation time-critical, or is a slightly sub-optimal route acceptable? – What are the characteristics of the environment? – Are there landmarks to provide orientation cues? – Are distances known accurately? – What are the sources of information about the environment that specify terrains, surface properties, obstacles, etc.? – What are the properties of the available sensors in the environment? 

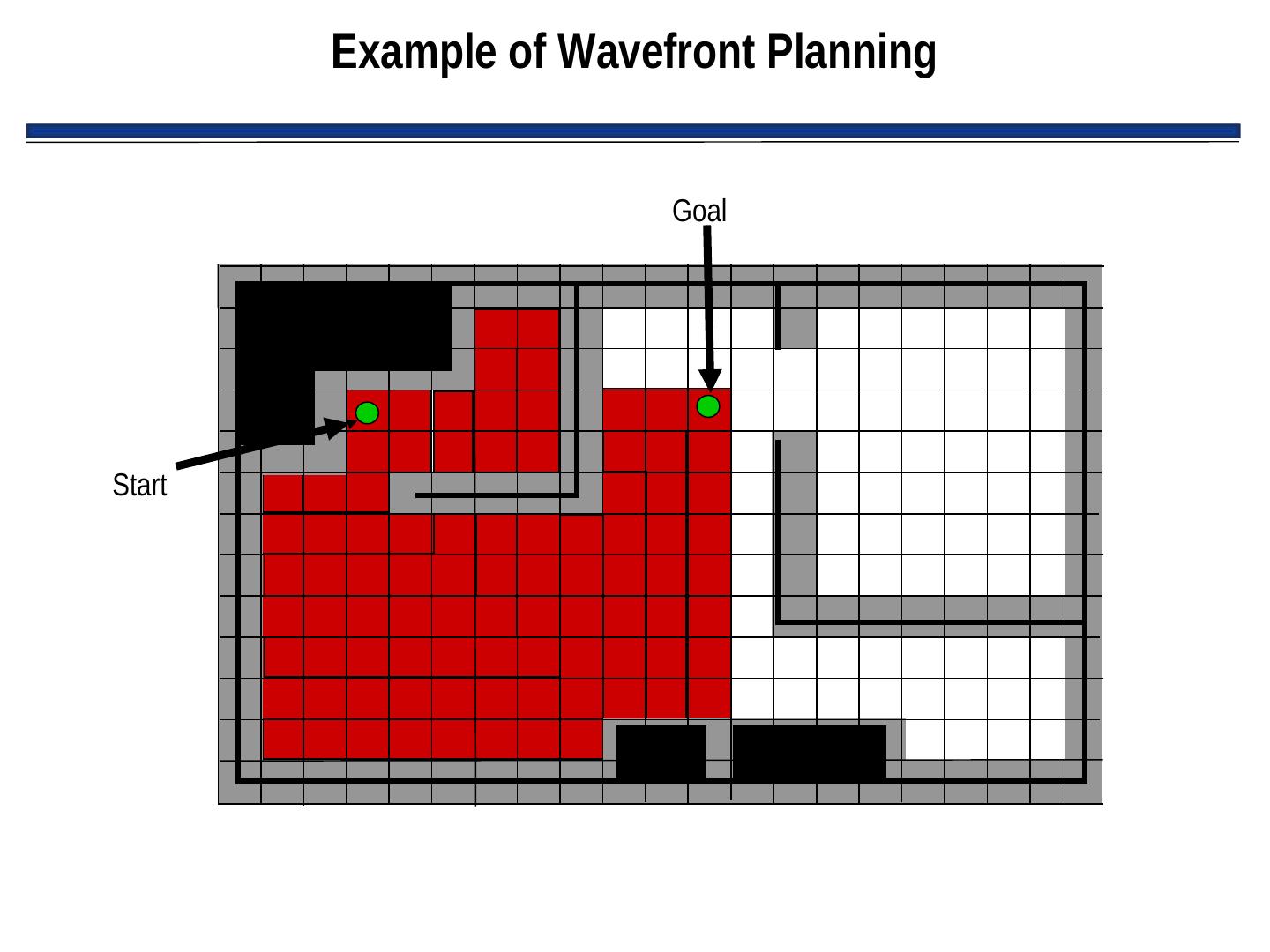
12 . Metric Path Planning • Objective: determine a path to a specified goal • Metric methods: – Tend to favor techniques that produce an optimal path – Usually decompose path into subgoals called waypoints • Two components to metric methods for path planning: – Representation (i.e., data structure) – Algorithm 

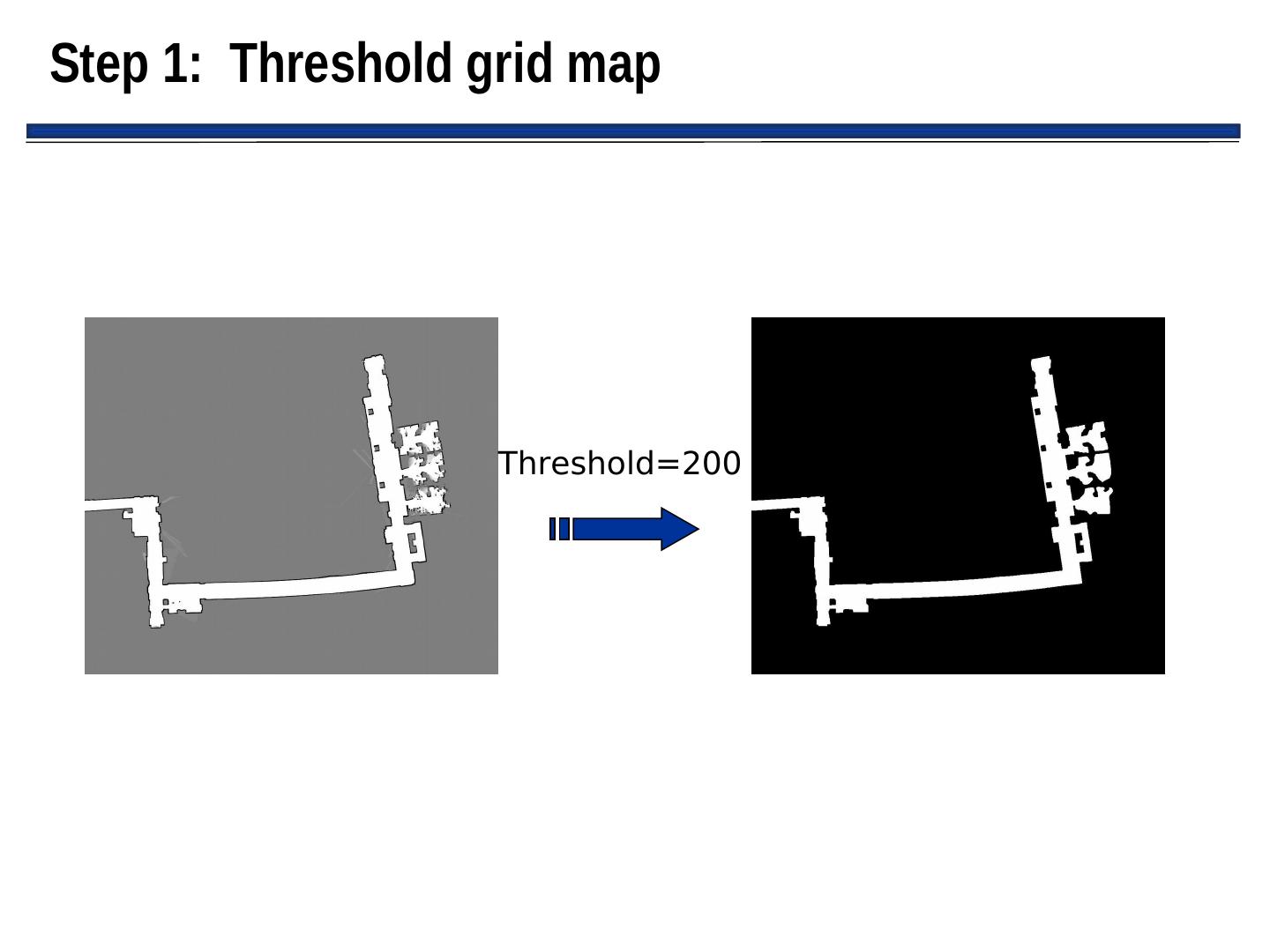
13 . Configuration Space • Configuration Space (abbreviated: “Cspace”): – Data structure that allows robot to specify position and orientation of objects and robot in the environment – “Good Cspace”: Reduces # of dimensions that a planner has to deal with – Typically, for indoor mobile robots: • Assume 2 DOF for representation • Assume robot is round, so that orientation doesn’t matter • Assumes robot is holonomic (i.e., it can turn in place) – (Although there is much research dealing with path planning in non- holonomic robots) – Typically represents “occupied” and “free” space • “Occupied”  object is in that space • “Free”  space where robot is free to move without hitting any modeled object 

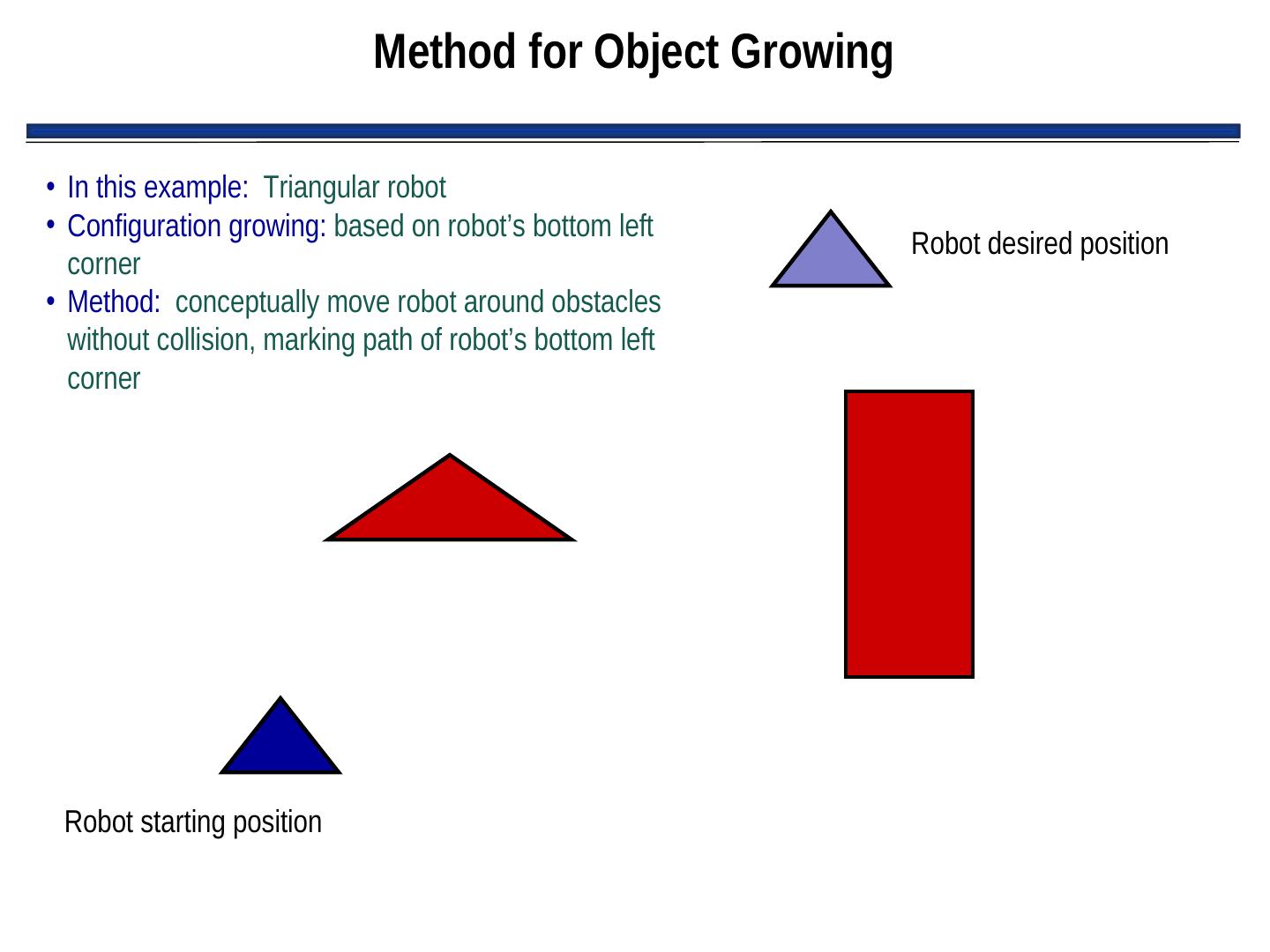
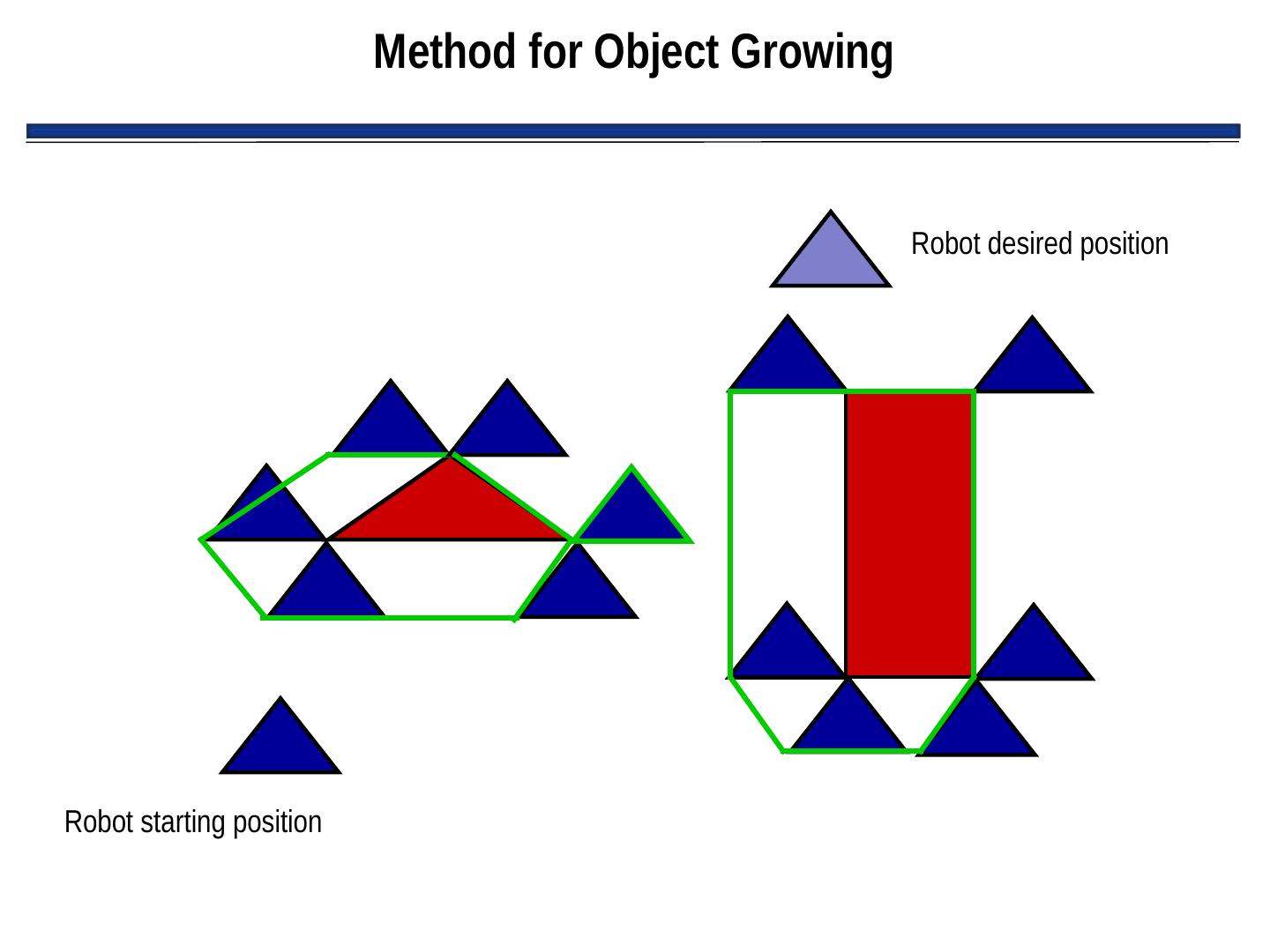
14 . Object Growing • Since we assume robot is round, we can “grow” objects by the width of the robot and then consider the robot to be a point • Greatly simplifies path planning • New representation of objects typically called “configuration space object” 

15 . Method for Object Growing • In this example: Triangular robot • Configuration growing: based on robot’s bottom left Robot desired position corner • Method: conceptually move robot around obstacles without collision, marking path of robot’s bottom left corner Robot starting position 

16 . Method for Object Growing Robot desired position Robot starting position 

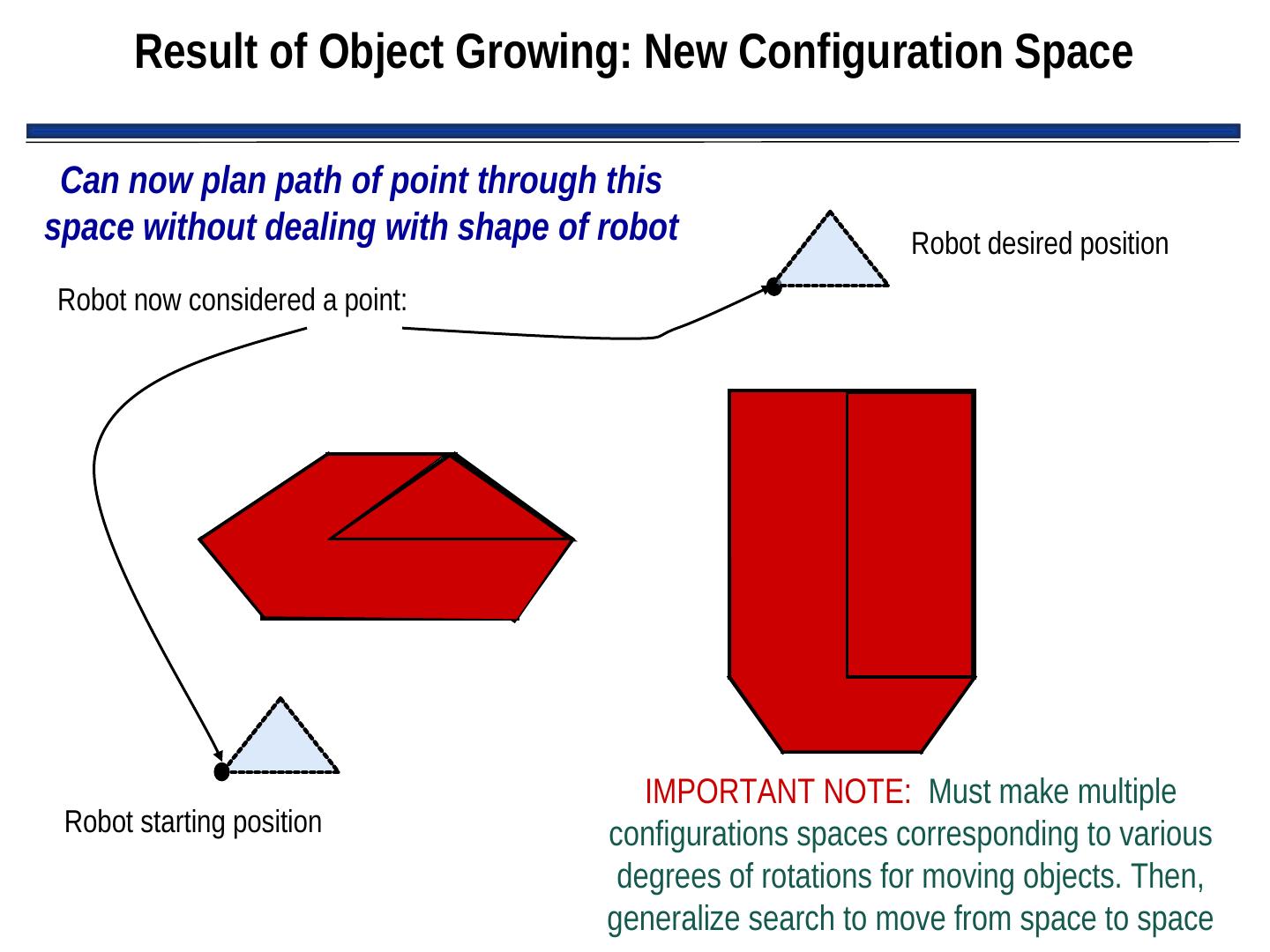
17 . Result of Object Growing: New Configuration Space Can now plan path of point through this space without dealing with shape of robot Robot desired position Robot now considered a point: IMPORTANT NOTE: Must make multiple Robot starting position configurations spaces corresponding to various degrees of rotations for moving objects. Then, generalize search to move from space to space 

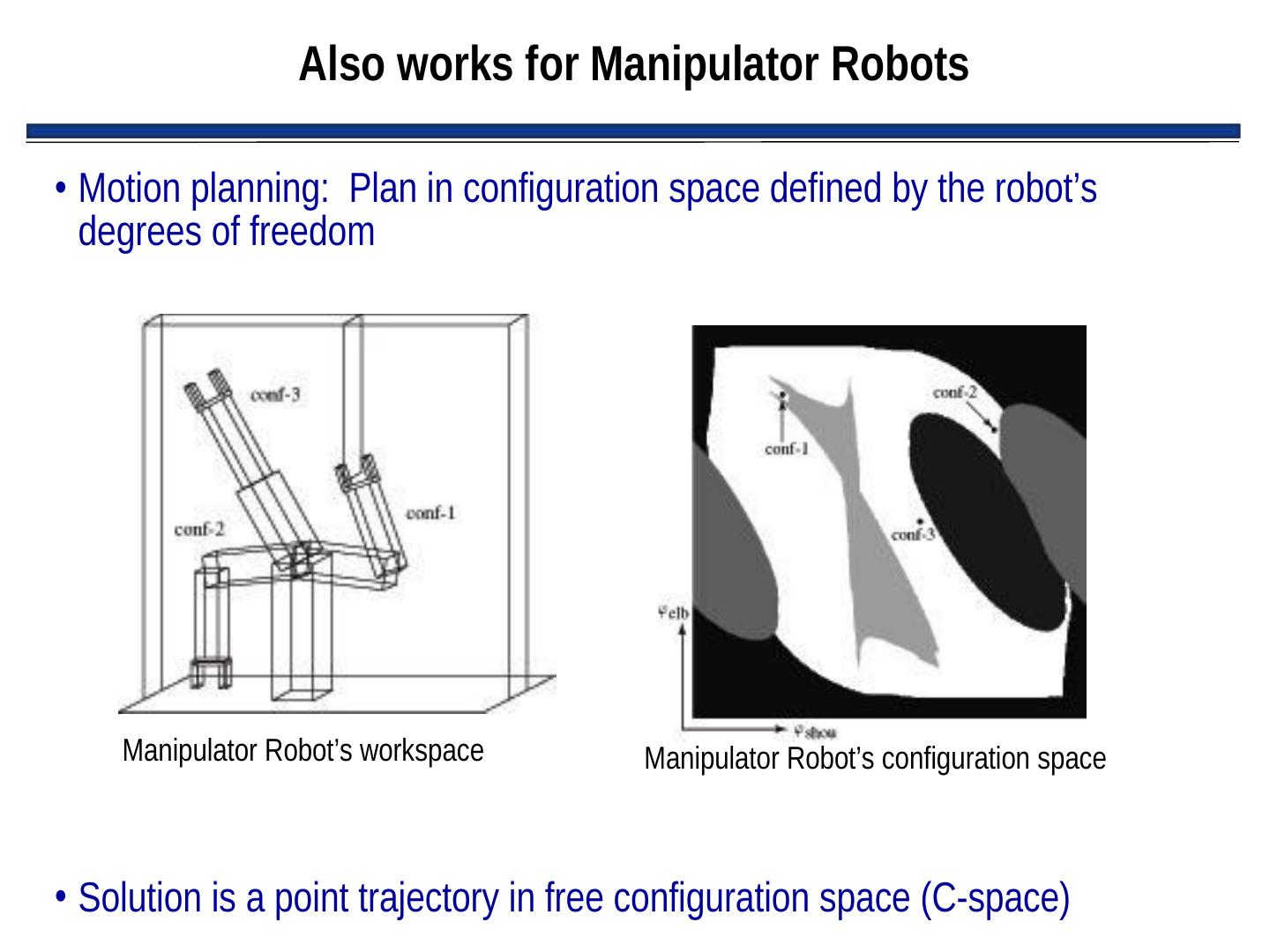
18 . Also works for Manipulator Robots • Motion planning: Plan in configuration space defined by the robot’s degrees of freedom Manipulator Robot’s workspace Manipulator Robot’s configuration space • Solution is a point trajectory in free configuration space (C-space) 

19 . Examples of Cspace Representations • Voronoi diagrams • Regular grids • Quadtrees/octtrees • Vertex graphs • Hybrid free space/vertex graphs (meadow map) 

20 . Meadow Maps (Hybrid Vertex-graph Free-space) • Transform space into convex polygons – Polygons represent safe regions for robot to traverse • Important property of convex polygons: – If robot starts on perimeter and goes in a straight line to any other point on the perimeter, it will not go outside the polygon • Path planning: – Involves selecting the best series of polygons to transit through 

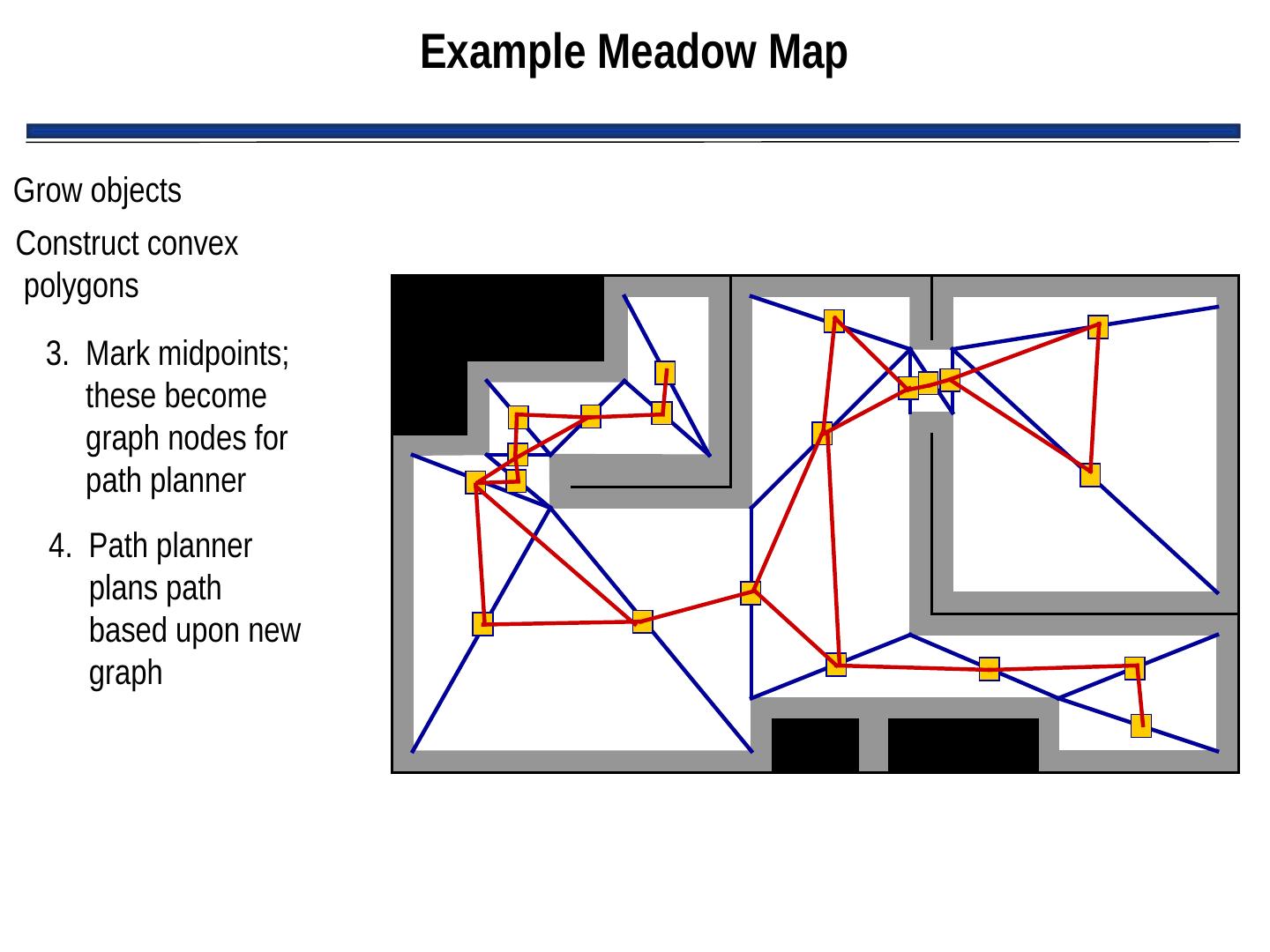
21 . Example Meadow Map Grow objects Construct convex polygons 3. Mark midpoints; these become graph nodes for path planner 4. Path planner plans path based upon new graph 

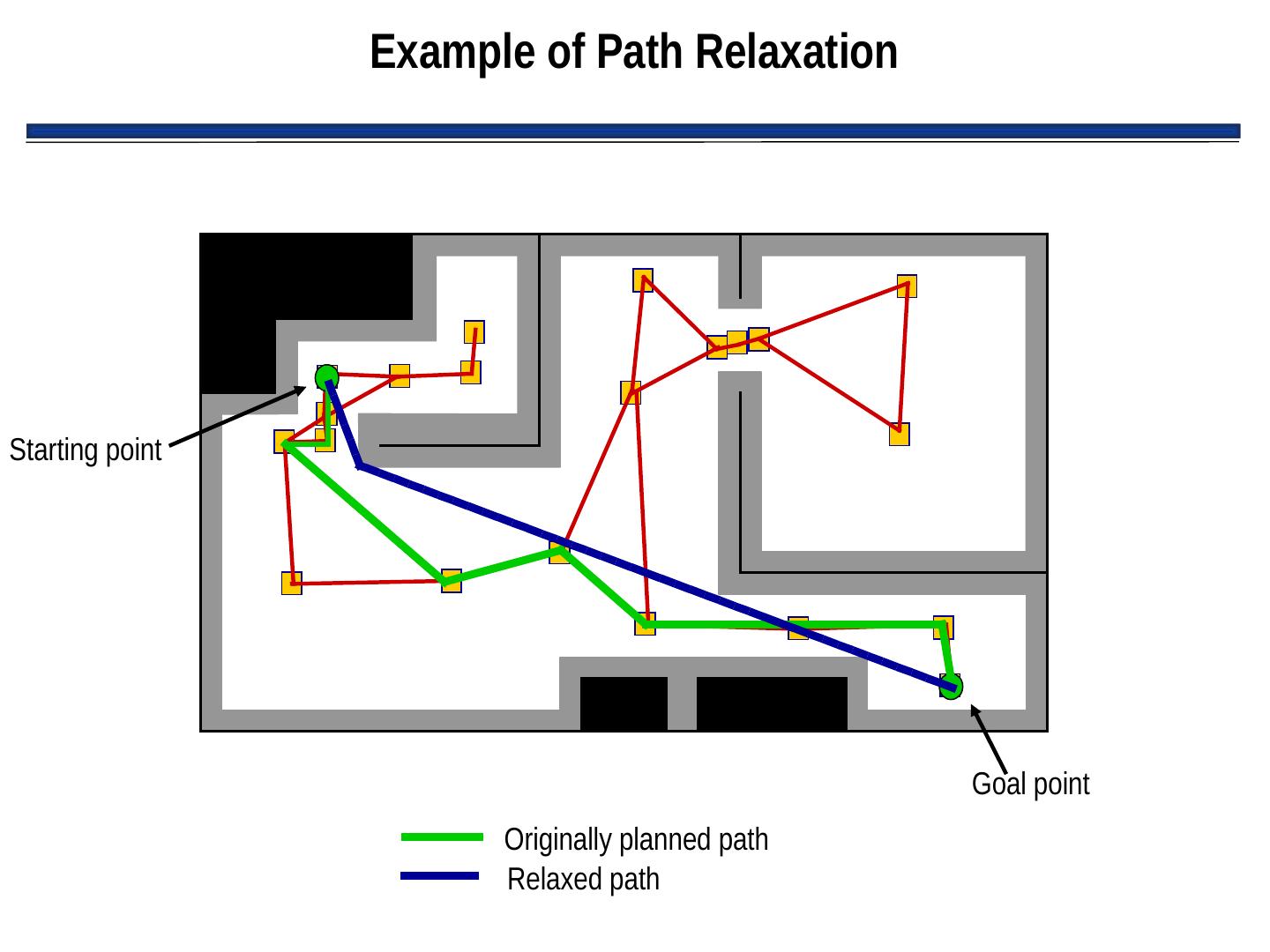
22 . Path Relaxation • Disadvantage of Meadow Map: – Resulting path is jagged • Solution: path relaxation – Technique for smoothing jagged paths resulting from any discretization of space • Approach: – Imagine path is a string – Imagine pulling on both ends of the string to tighten it – This removes most of “kinks” in path 

23 . Example of Path Relaxation Starting point Goal point Originally planned path Relaxed path 

24 . Limited Usefulness of Meadow Maps • Three problems with meadow maps: – Technique to generate polygons is computationally complex – Uses artifacts of the map to determine polygon boundaries, rather than things that can be sensed – Unclear how to update or repair diagrams as robot discovers differences between a priori map and the real world 

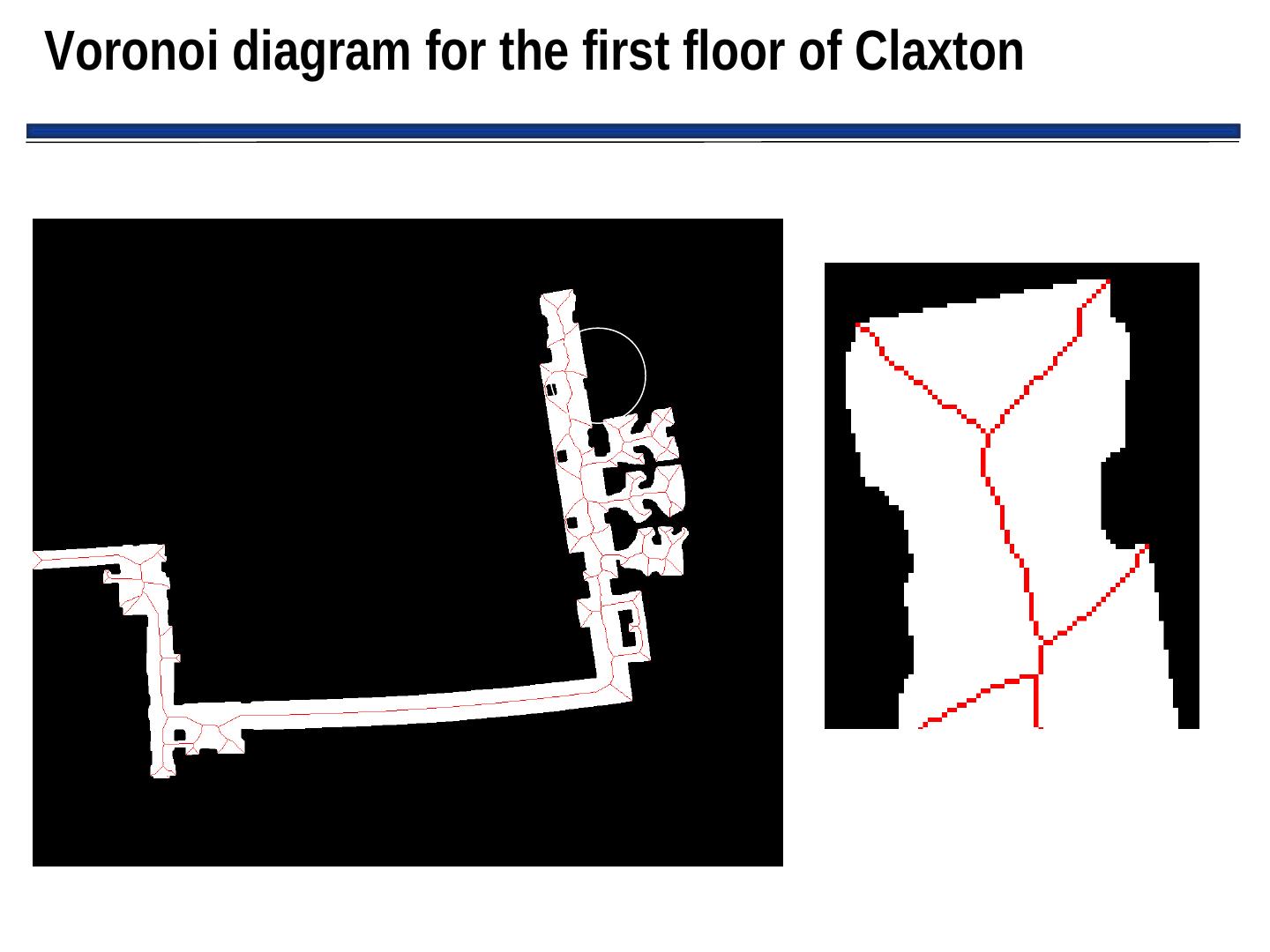
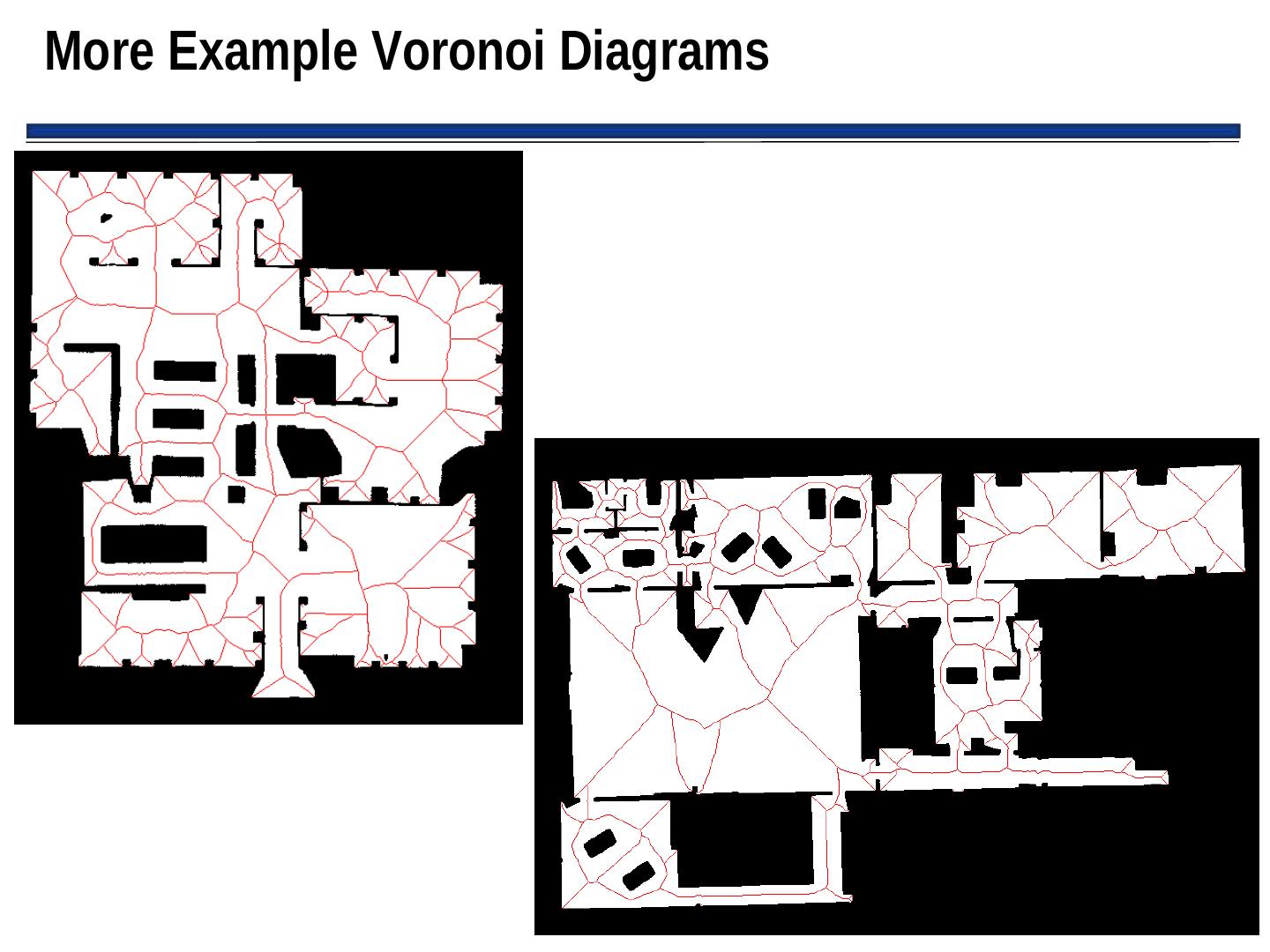
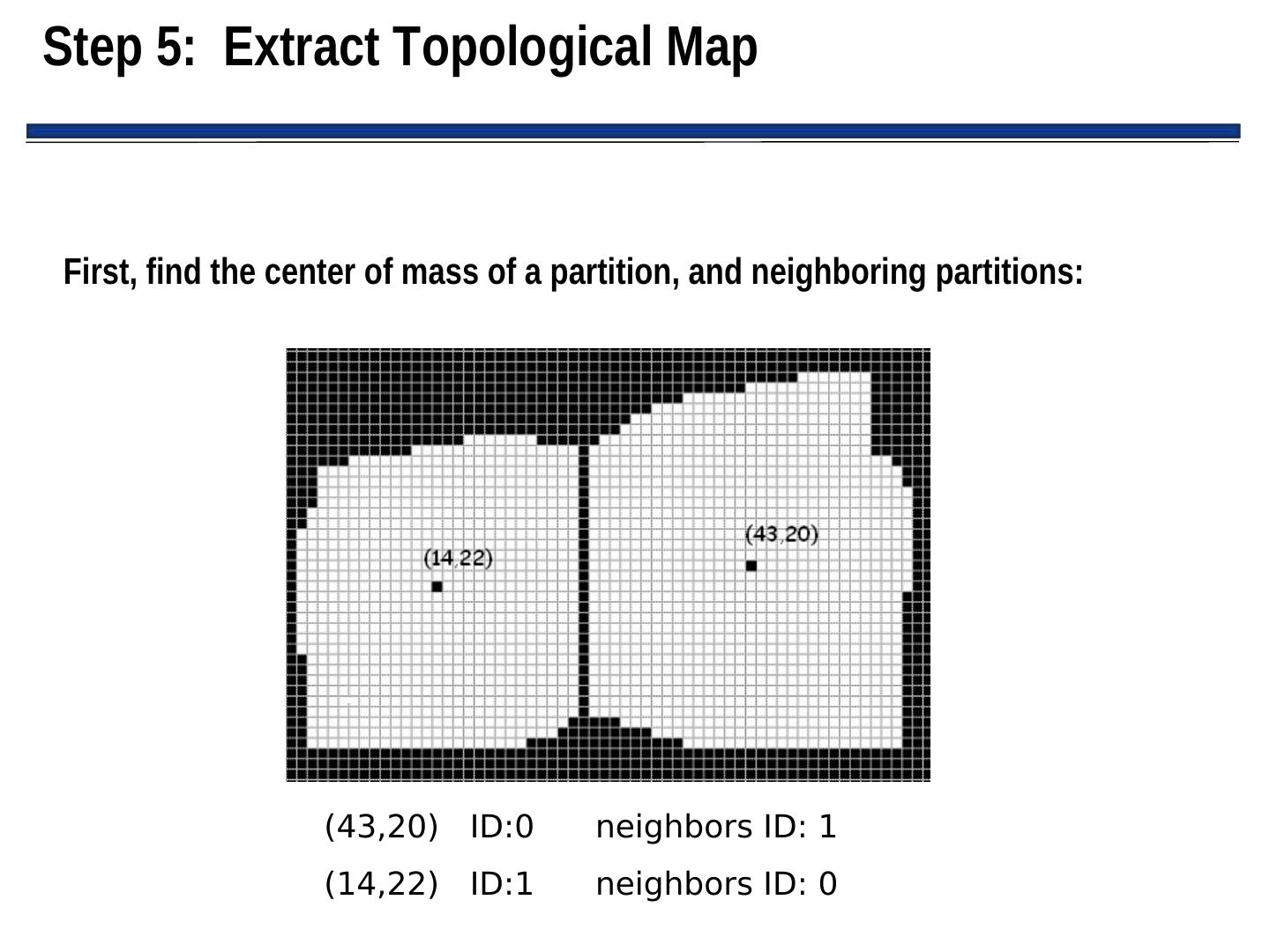
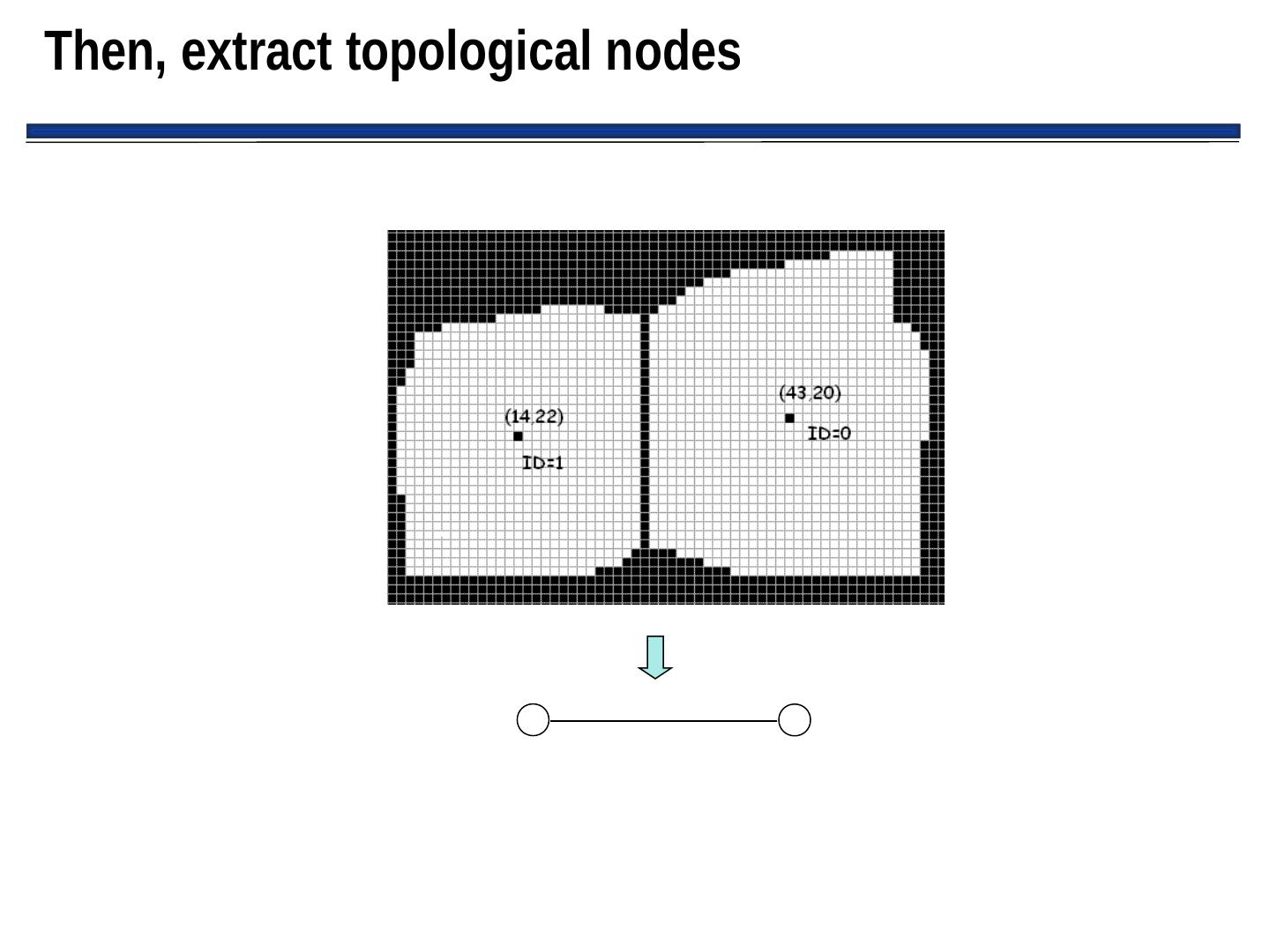
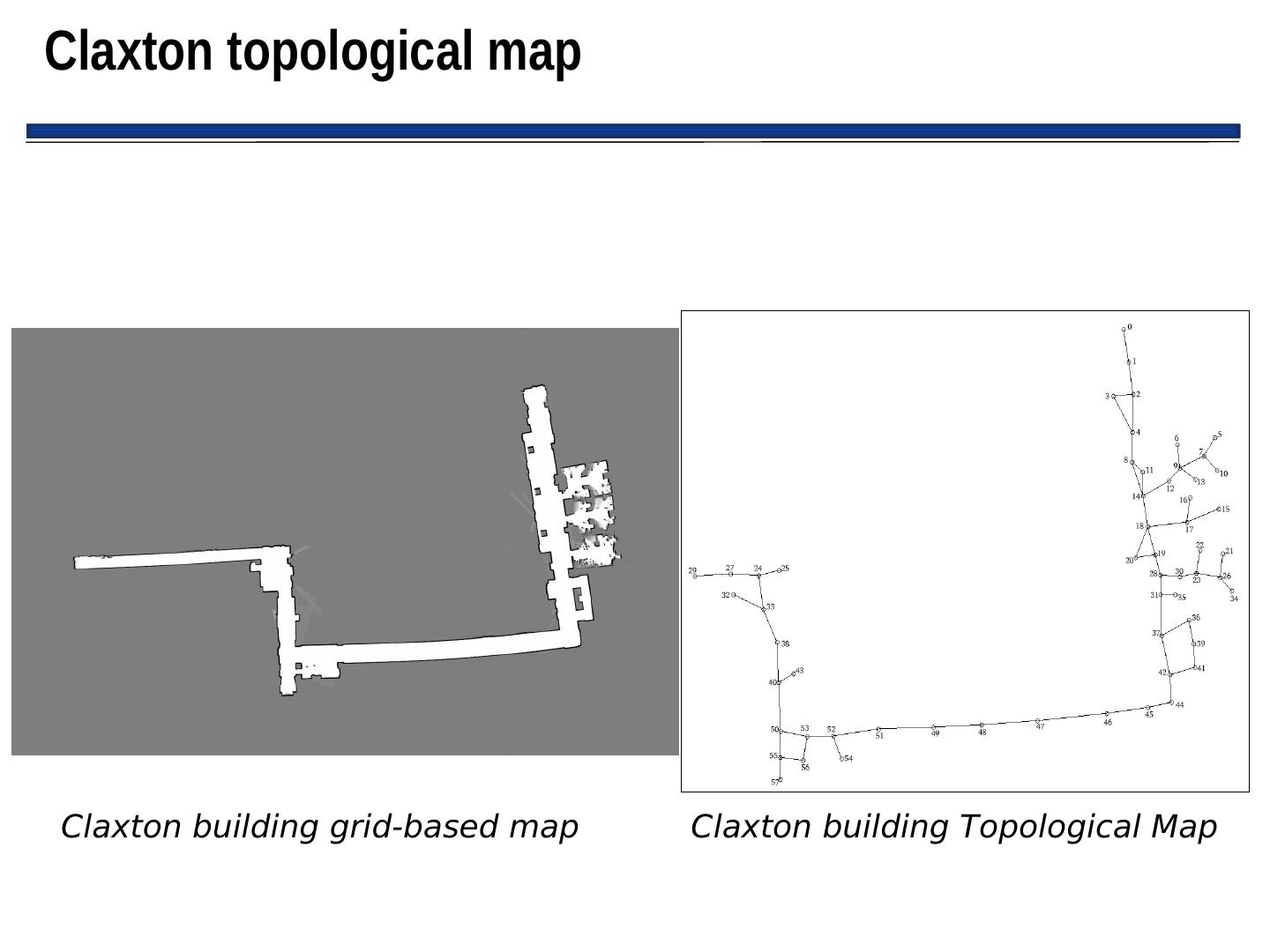
25 . Generalized Voronoi Diagrams (GVGs) • GVGs: – Popular mechanism for representing Cspace and generating a graph – Can be constructed as robot enters new environment • Basic GVG approach: – Generate a Voronoi edge, which is equidistant from all points – Point where Voronoi edge meets is called a Voronoi vertex – Note: vertices often have physical correspondence to aspects of environment that can be sensed – If robot follows Voronoi edge, it won’t collide with any modeled obstacles  don’t need to grow obstacle boundaries 

26 .Example Generalized Voronoi Graph (More on this next time) 

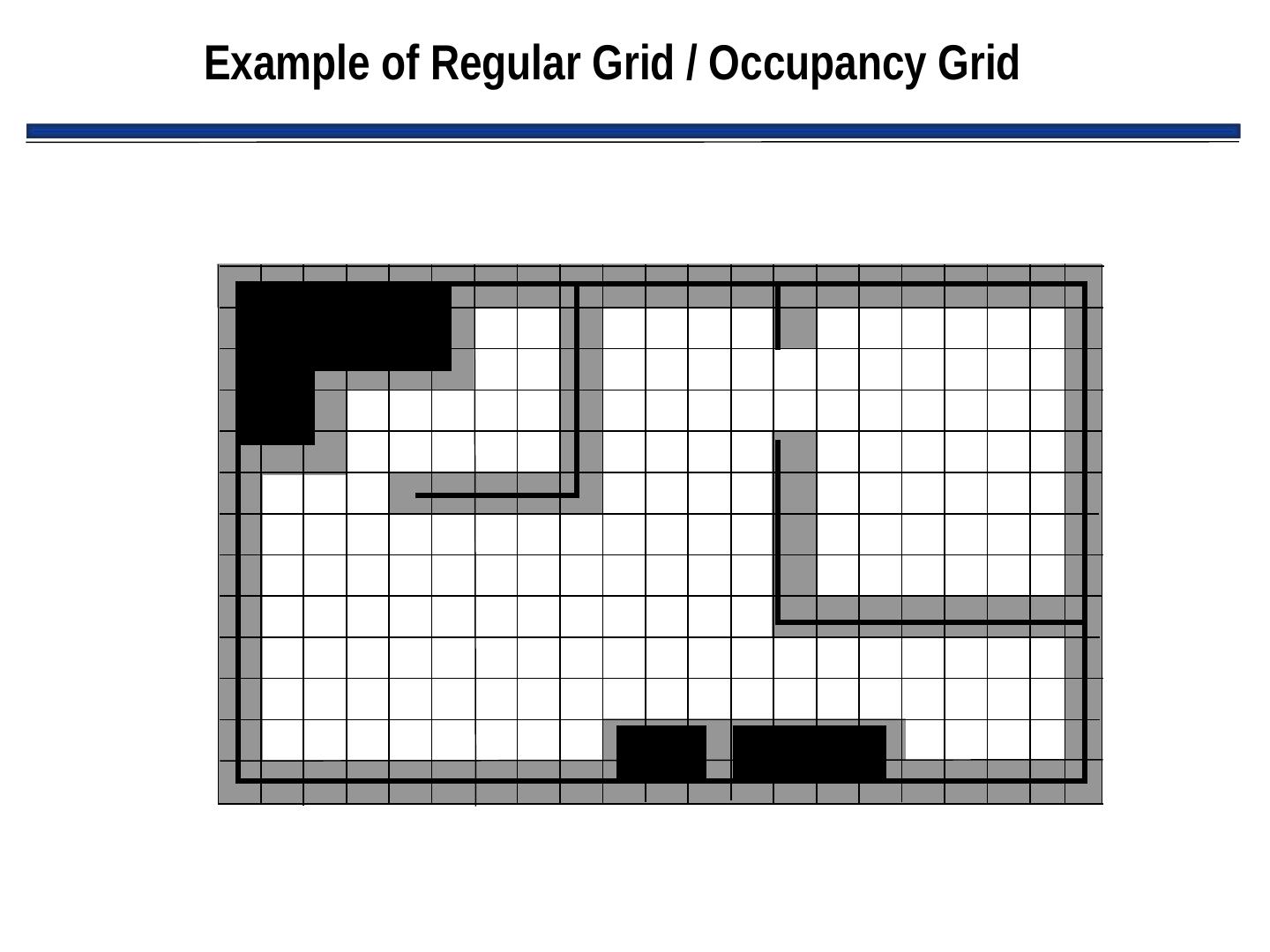
27 . Regular Grids / Occupancy Grids • Superimposes a 2D Cartesian grid on the world space • If there is any object in the area contained by a grid element, that element is marked as occupied • Center of each element in grid becomes a node, leading to highly connected graph • Grids are either considered 4-connected or 8-connected 

28 .Example of Regular Grid / Occupancy Grid 

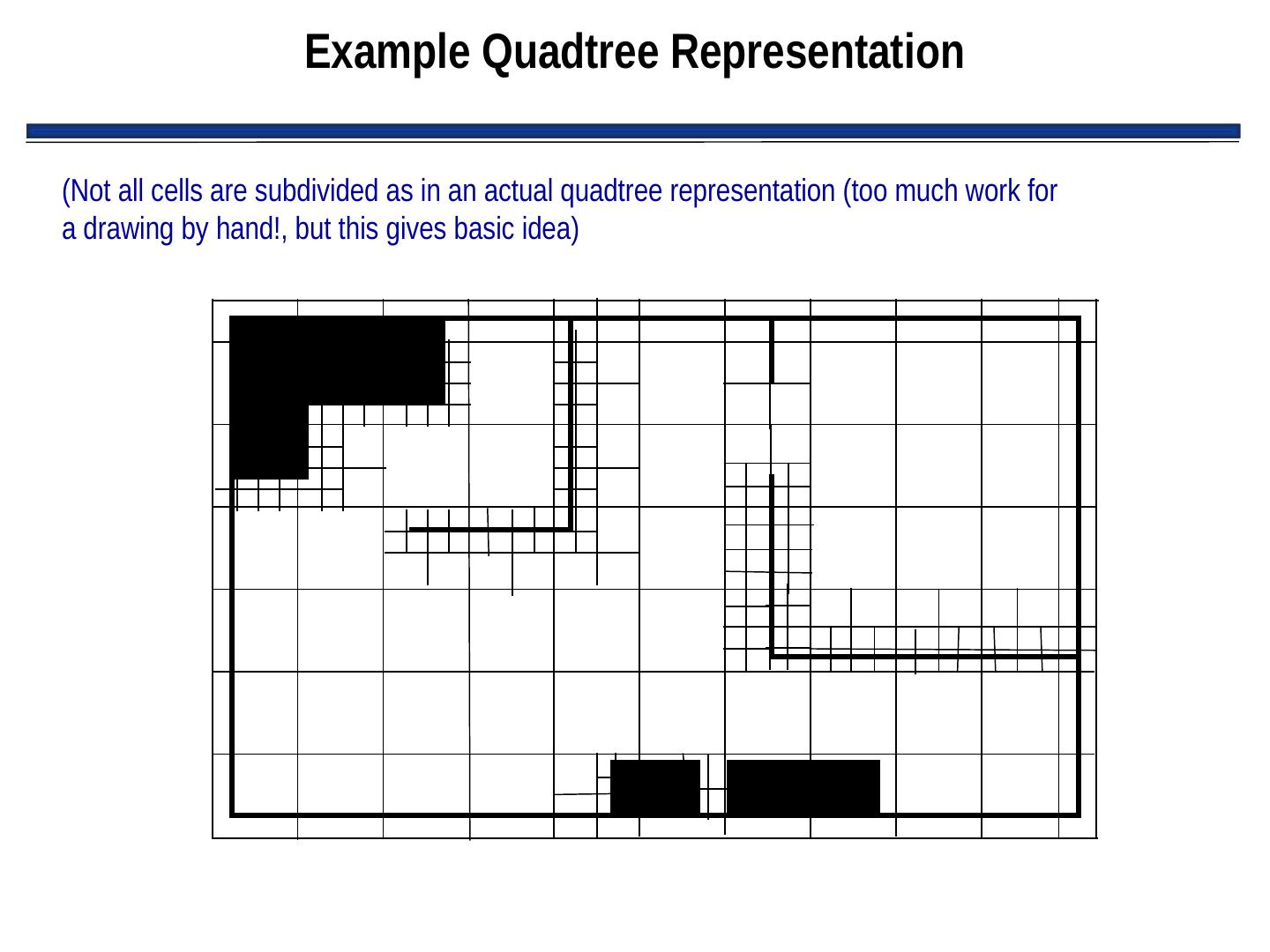
29 . Disadvantages of Regular Grids • Digitization bias: – If object falls into even small portion of grid element, the whole element is marked as occupied – Leads to wasted space • Solution: use fine-grained grids (4-6 inches) • But, this leads to high storage cost and high # nodes for path planner to consider • Partial solution to wasted space: Quadtrees