023-Modal Logic and Its Applications

1 .Modal Logic and Its Applications, explained using Puzzles and Examples

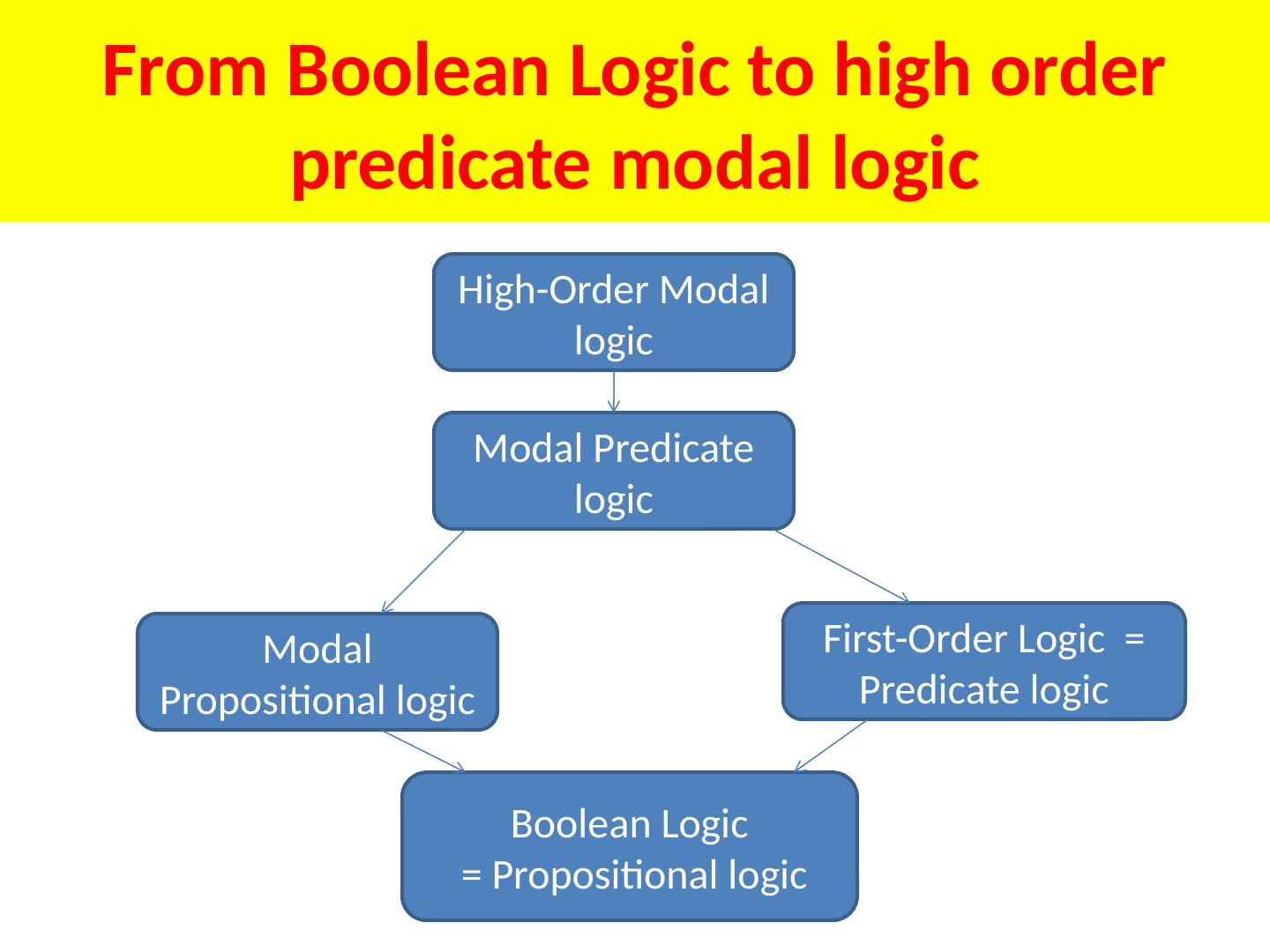
2 .From Boolean Logic to high order predicate modal logic Boolean Logic = Propositional logic Modal Propositional logic First-Order Logic = Predicate logic Modal Predicate logic High-Order Modal logic

3 .From Boolean Logic to high order predicate modal logic

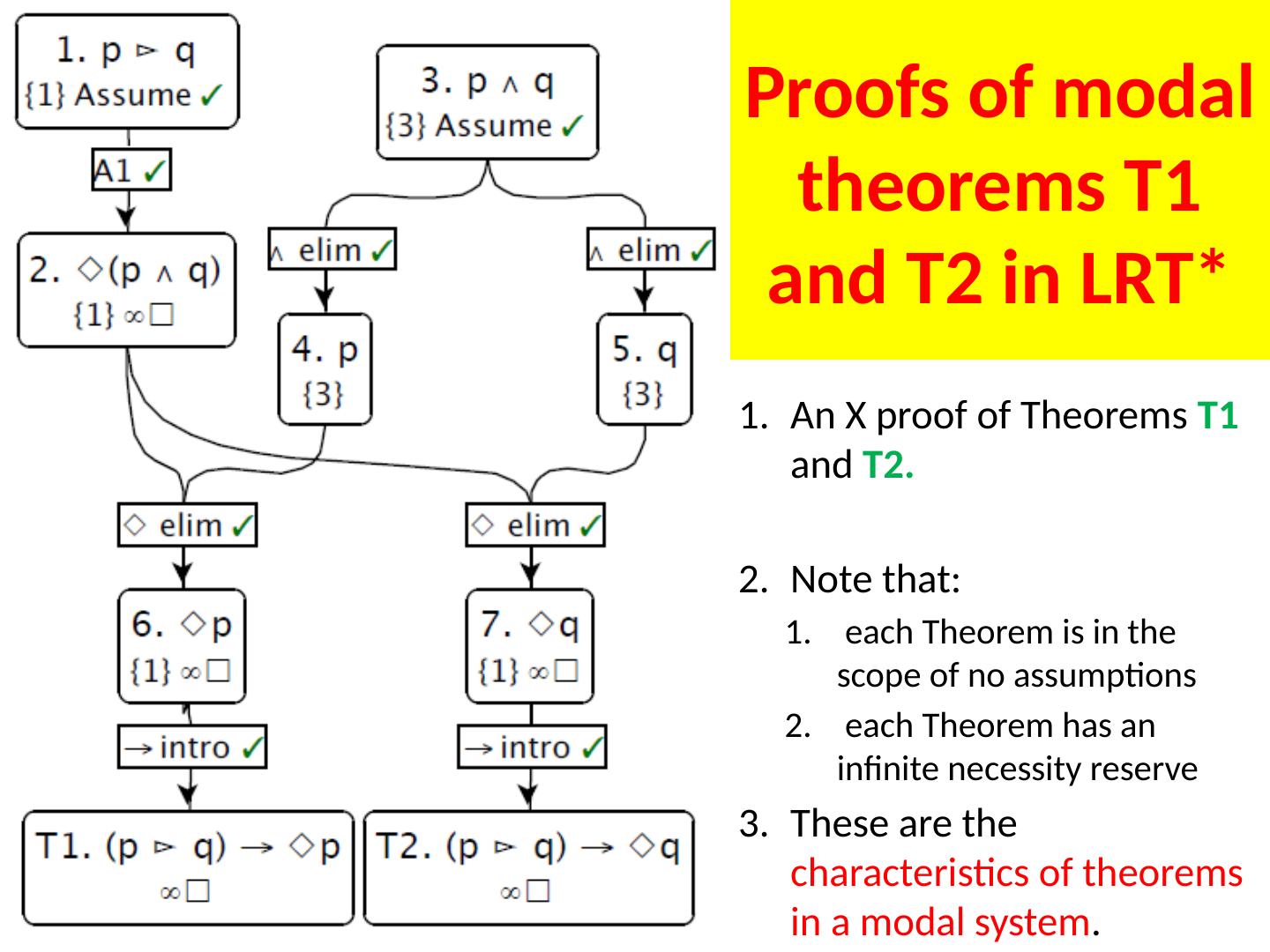
4 .1. p 2. q 3. p/\q 4. p 5. q  p 6. p  ( q  p) As an illustration, consider the following proof which establishes the theorem p  (q  p): 7. q 8. p  q 9. q ( p  q)

5 .

6 .We shall be concerned with alethic modal logic, or modal logic tout court . The starting point, once again, is Aristotle , who was the first to study the relationship between modal statements and their validity . However, the great discussion it enjoyed in the Middle Ages . The official birth date of modal logic is 1921, when Clarence Irving Lewis wrote a famous essay on implication .

7 .Modal logics has Roots in C. I. Lewis As is widely known and much celebrated, C. I. Lewis invented modal logic. Modal logic sprang in no small part from his disenchantment with material implication Material implication was accepted and indeed taken as central in Principia by Russell and Whitehead. In the modern propositional calculus (PC), implication is of this sort; hence a statement like “ If the moon is composed of Jarlsberg cheese, then Selmer is Norwegian" is symbolized by m  s ; where of course the propositional variables can vary with personal choice. Aristotle St. Anselm C.I. Lewis Saul Kripke Modern Engineering Temporal Logic and Model Checking

8 .Proof Rules for Modal Logic

9 .Proof Rules for Modal Logic Modal Generalization A  A Monotonicity of  A  B  A   B Monotonicity of  A  B    A    B

10 .An Axiom System for Prepositional Logic (A  (B  C))  (A  B)  (A  C) A  (B  A) (( A  false )  false )  A Modus Ponens A, A -> B B

11 .An Axiom System for Predicate Logic  x (A(x)  B(x))  (  xA (x)   xB (x))  x A(x)  A[t/x] provided t is free for x in A A   x A(x) provided x is not free in A Modus Ponens A, A  B B Generalization A x A(x)

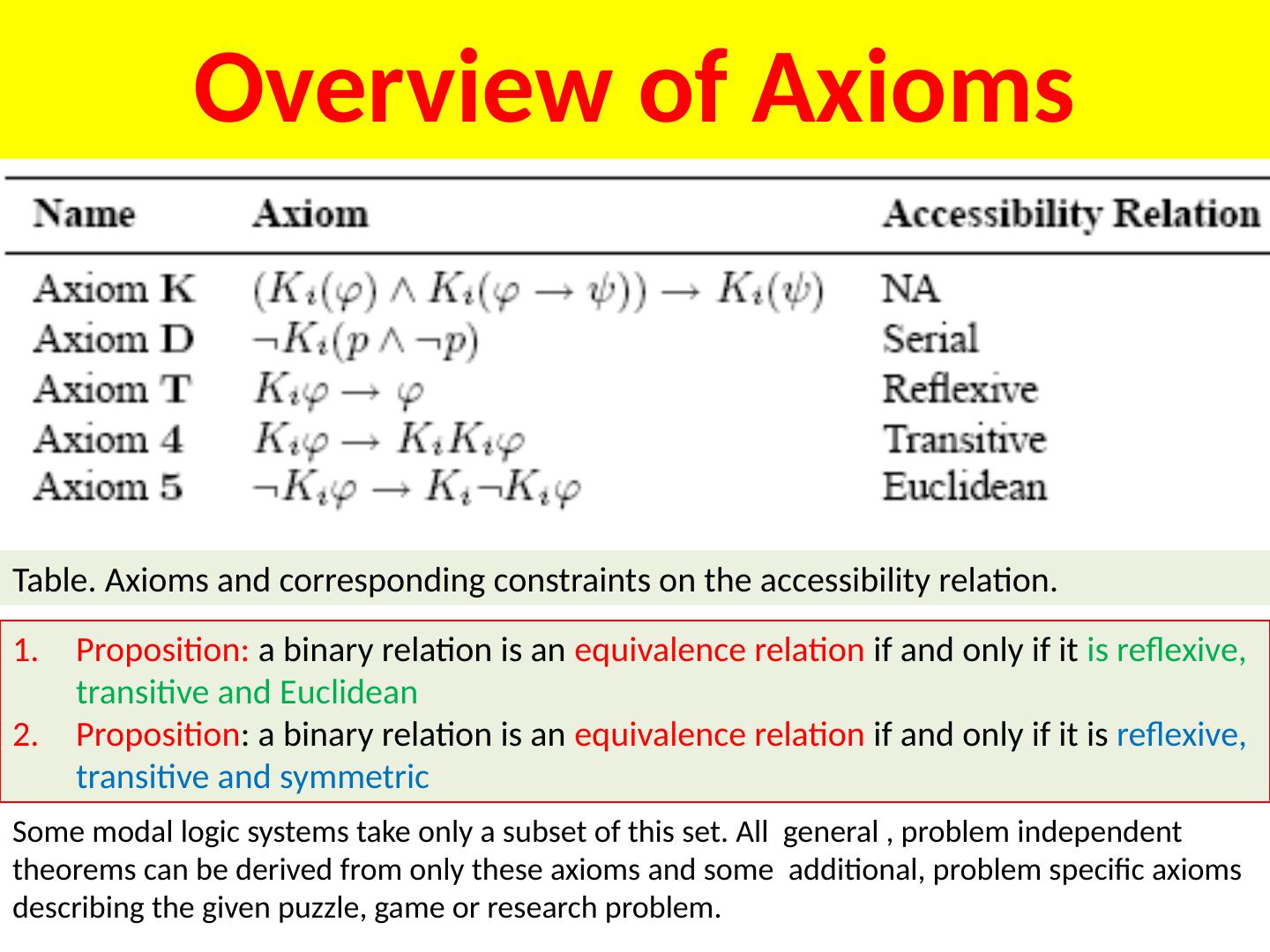
12 .Some Facts About Modal Logic A couple of Valid Modal Formulas:  (A  B )  (  A)  (  B) (A  B )  (  A)  (  B) [](A  B )  ( [] A)  ( [] B) [K](A  B )  ( [K] A)  ( [K] B)  (false) (false) ( A)  ([]B)   (A  B ) Counter-examples to invalid modal formulas ( A)  ( [] A )

13 .Some Facts About Modal Logic A couple of Valid Modal Formulas:  (A  B )  (  A)  (  B) (A  B )  (  A)  (  B) [](A  B )  ( [] A)  ( [] B) [K](A  B )  ( [K] A)  ( [K] B)  (false) (false) ( A)  ([]B)   (A  B ) Counter-examples to invalid modal formulas ( A)  ( [] A )

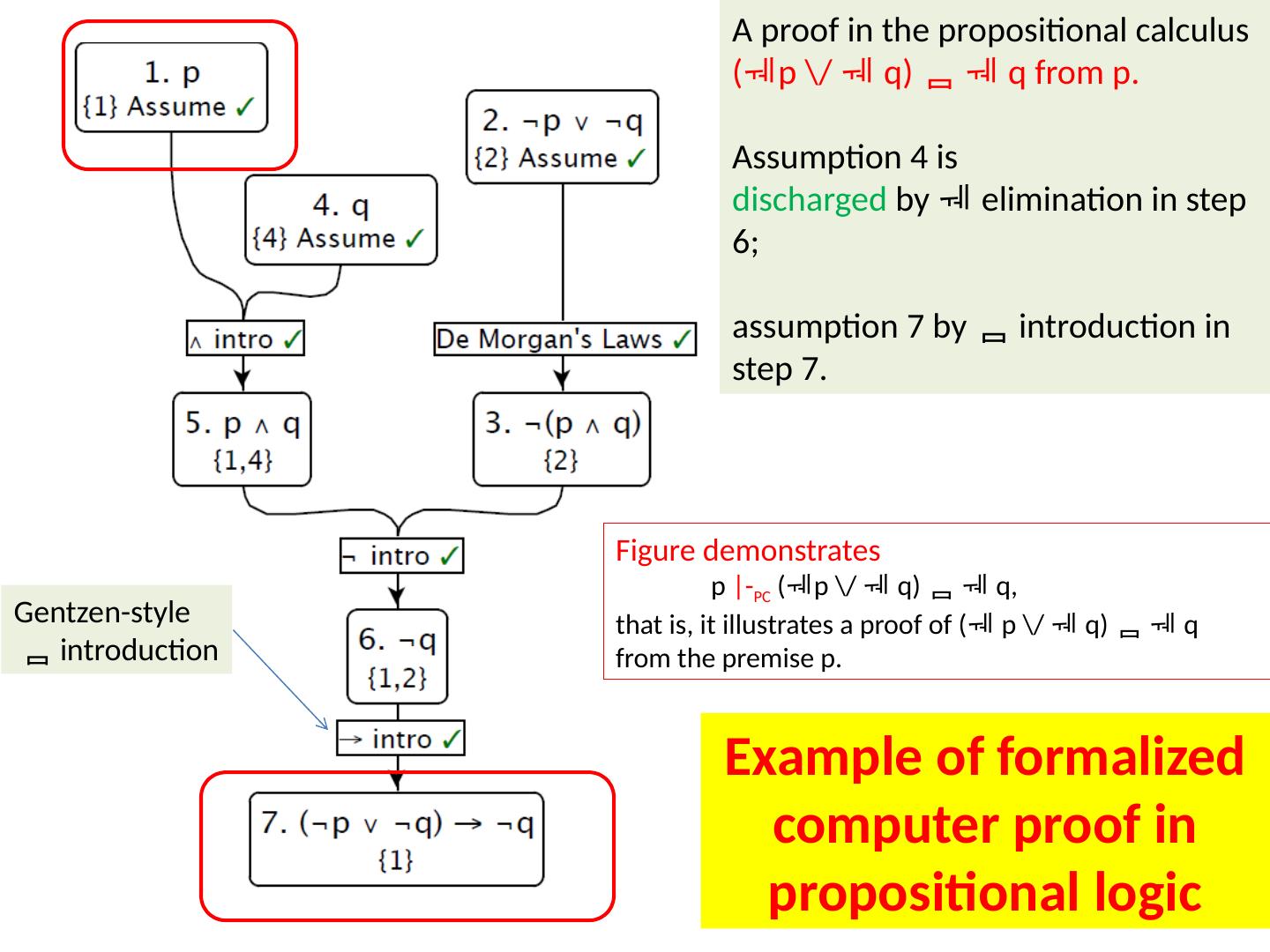
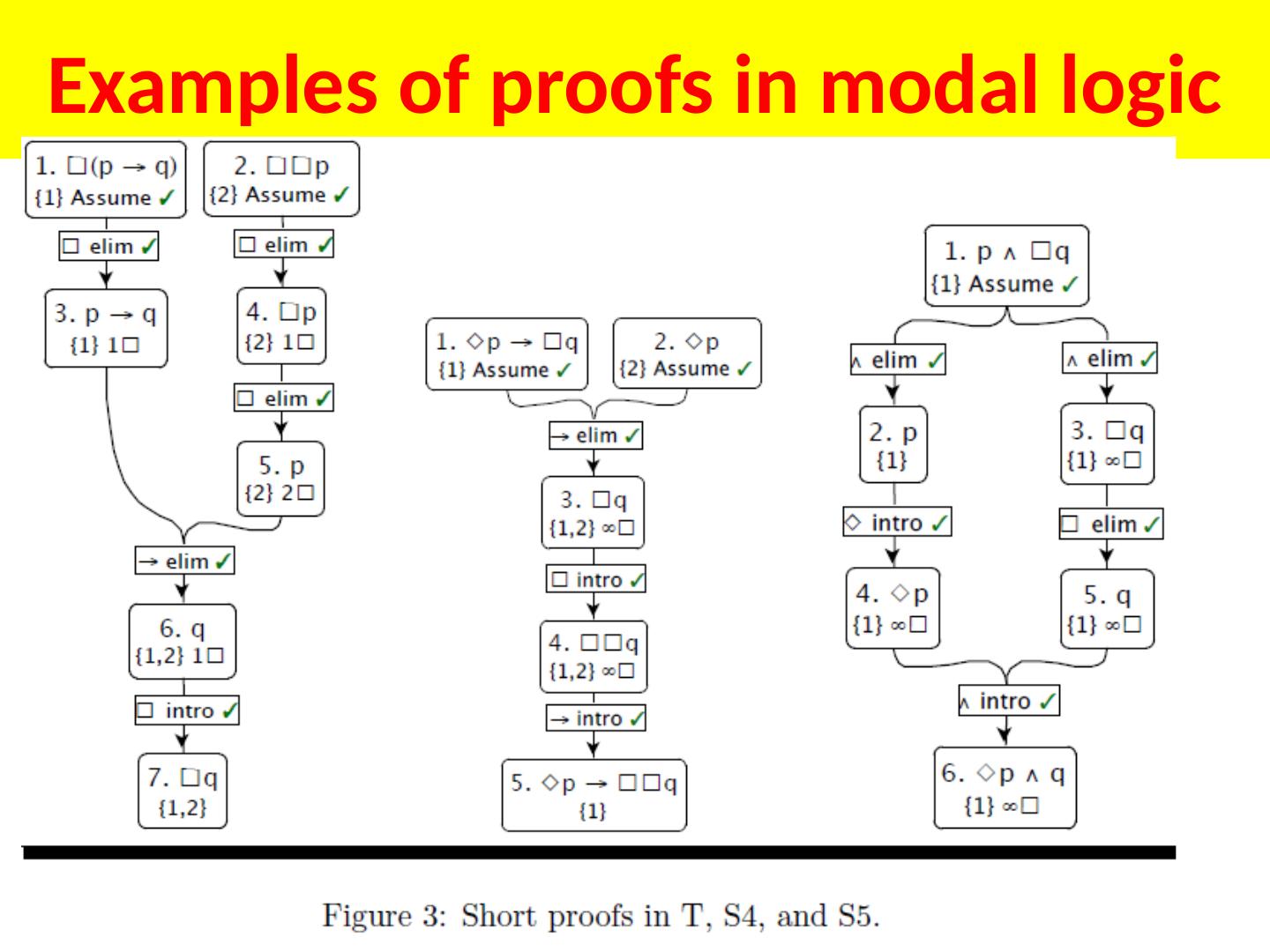
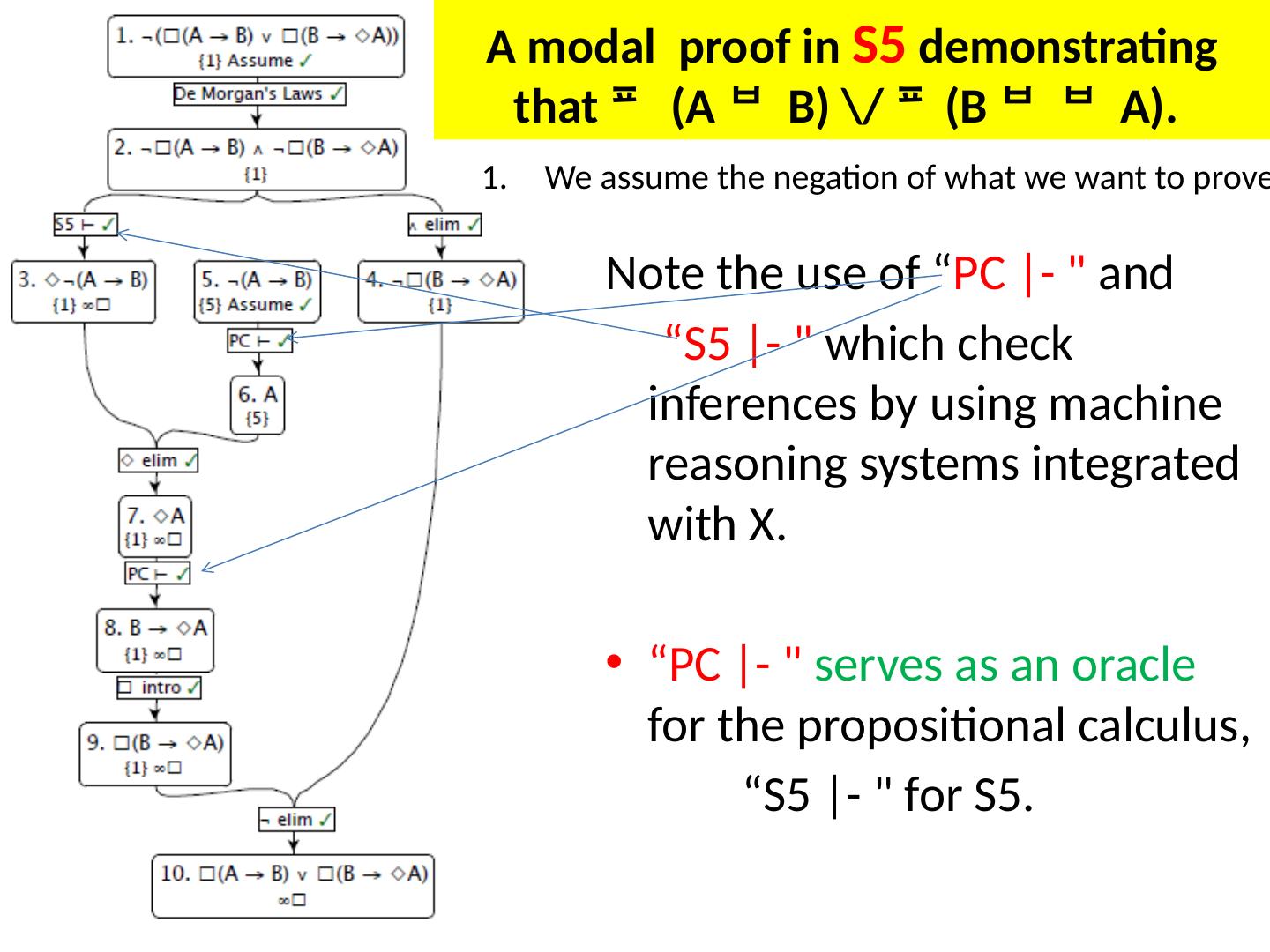
14 .A proof in the propositional calculus (  p \/  q )   q from p. Assumption 4 is discharged by  elimination in step 6; assumption 7 by  introduction in step 7. Figure demonstrates p |- PC (  p \/  q)   q, that is, it illustrates a proof of (  p \/  q)   q from the premise p. Gentzen -style  introduction Example of formalized computer proof in propositional logic

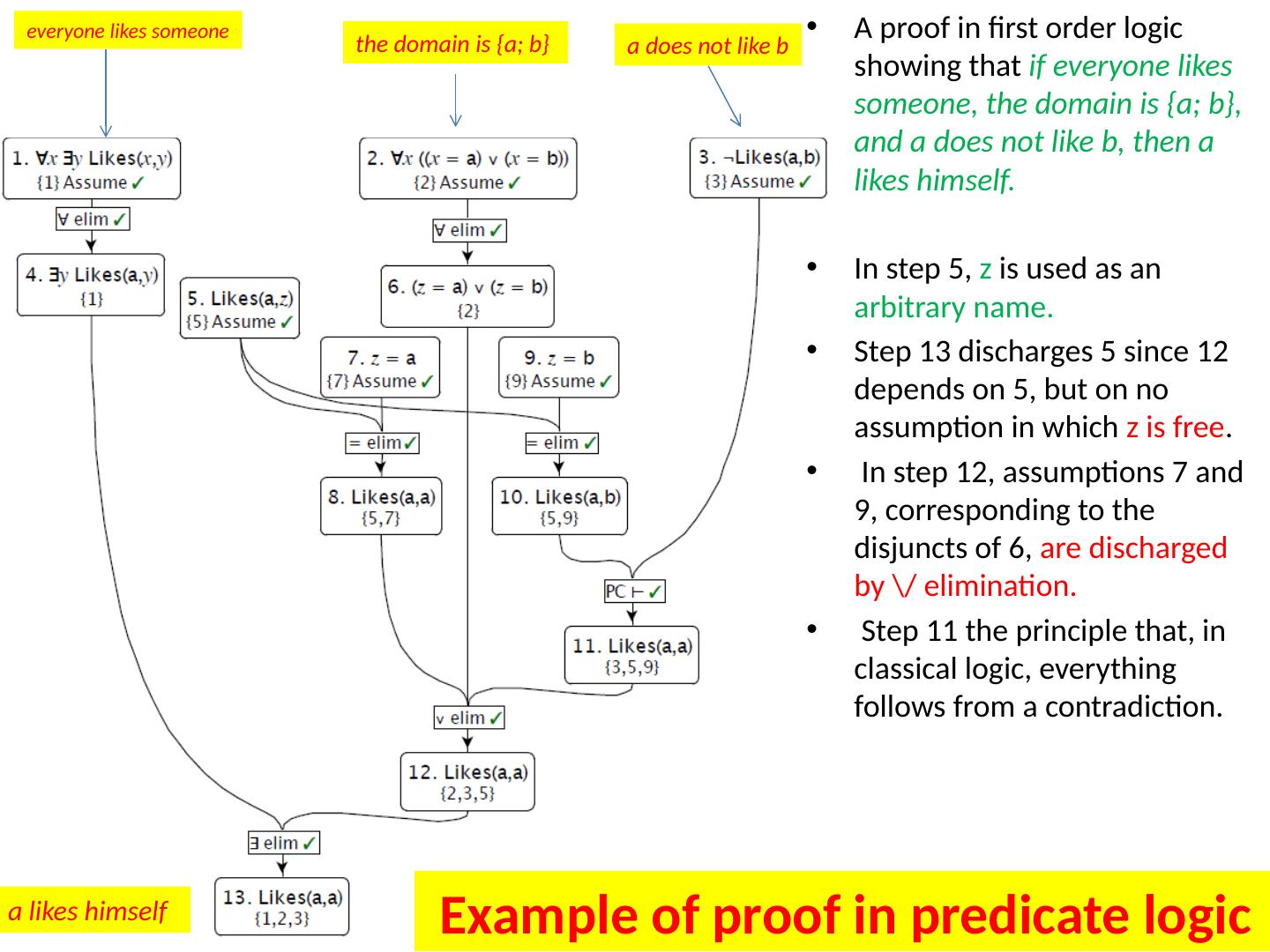
15 .A proof in first order logic showing that if everyone likes someone, the domain is {a ; b}, and a does not like b, then a likes himself. In step 5, z is used as an arbitrary name. Step 13 discharges 5 since 12 depends on 5, but on no assumption in which z is free . In step 12, assumptions 7 and 9, corresponding to the disjuncts of 6, are discharged by \/ elimination . Step 11 the principle that, in classical logic, everything follows from a contradiction. the domain is {a; b } everyone likes someone a does not like b a likes himself Example of proof in predicate logic

16 . TYPES OF MODAL LOGIC

17 . TYPES OF MODAL LOGIC Modal logic is extremely important both for its philosophical applications and in order to clarify the terms and conditions of arguments. The label “ modal logic ” refers to a variety of logics: alethic modal logic , dealing with statements such as “It is necessary that p ”, “It is possible that p ”, etc. epistemic modal logic , that deals with statements such as “I know that p ”, “I believe that p ”, etc.

18 . TYPES OF MODAL LOGIC (cont) deontic modal logic , dealing with statements such as “It is compulsory that p ”, “It is forbidden that p ”, etc temporal modal logic , dealing with statements such as “It is always true that p ”, “It is sometimes true that p ”, etc. ethical modal logic , dealing with statements such as “It is good that p ”, “It is bad that p ”

19 . Main Concepts of MODAL LOGIC

20 .We introduced two modal terms such as impossible and necessary . In order to define strict implication, that is, we need two new symbols,  and  . Given a statement p , by “  p ” we mean “It is necessary that p ” and by “  p ” we mean “It is possible that p ” Now we can define strict implication : p  q := ¬ ( p Λ ¬ q ) that is it is not possible that both p and ¬q are true Reminder on Modal Strict Implication

21 .Both operators, that of necessity  and that of possibility  , can be reciprocally defined. If we take  as primitive, we have:  p := ¬ ¬ p that is “ it is necessary that p ” means “it is not possible that non- p ” Therefore, we can define strict implication as : p  q := (¬ p Λ q ) but since p  q is logically equivalent to ¬ ( p Λ ¬ q ), or (¬ p Λ q ), we have p  q := ( p  q ) Reciprocal definitions

22 .Analogously, if we take  as primitive, we have:  p := ¬¬ p that is “ it is possible that p ” means “ it is not necessary that non- p ” And again, from the definition of strict implication and the above definition, we can conclude that p  q := ( p  q ) Taking  as primitive

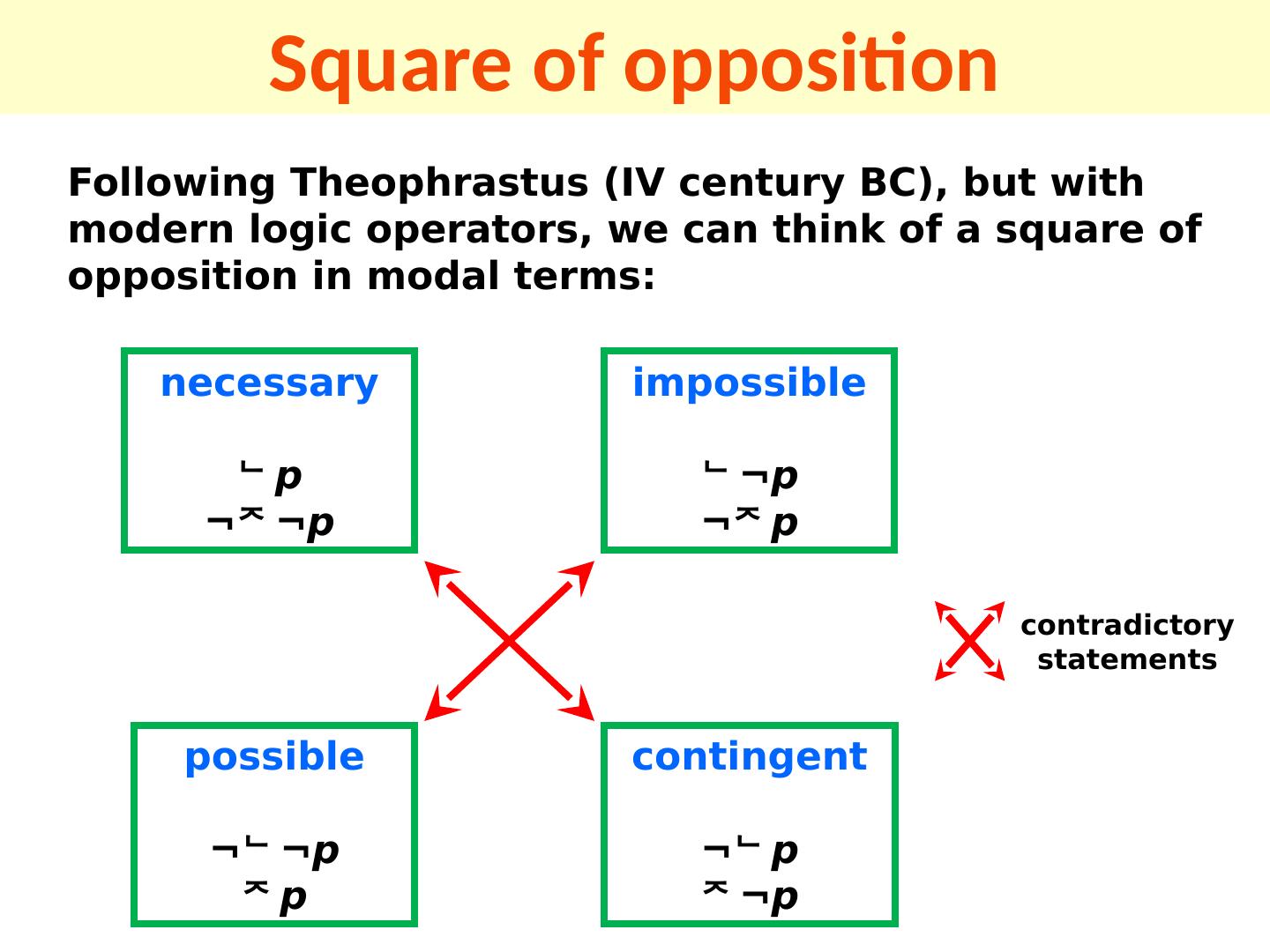
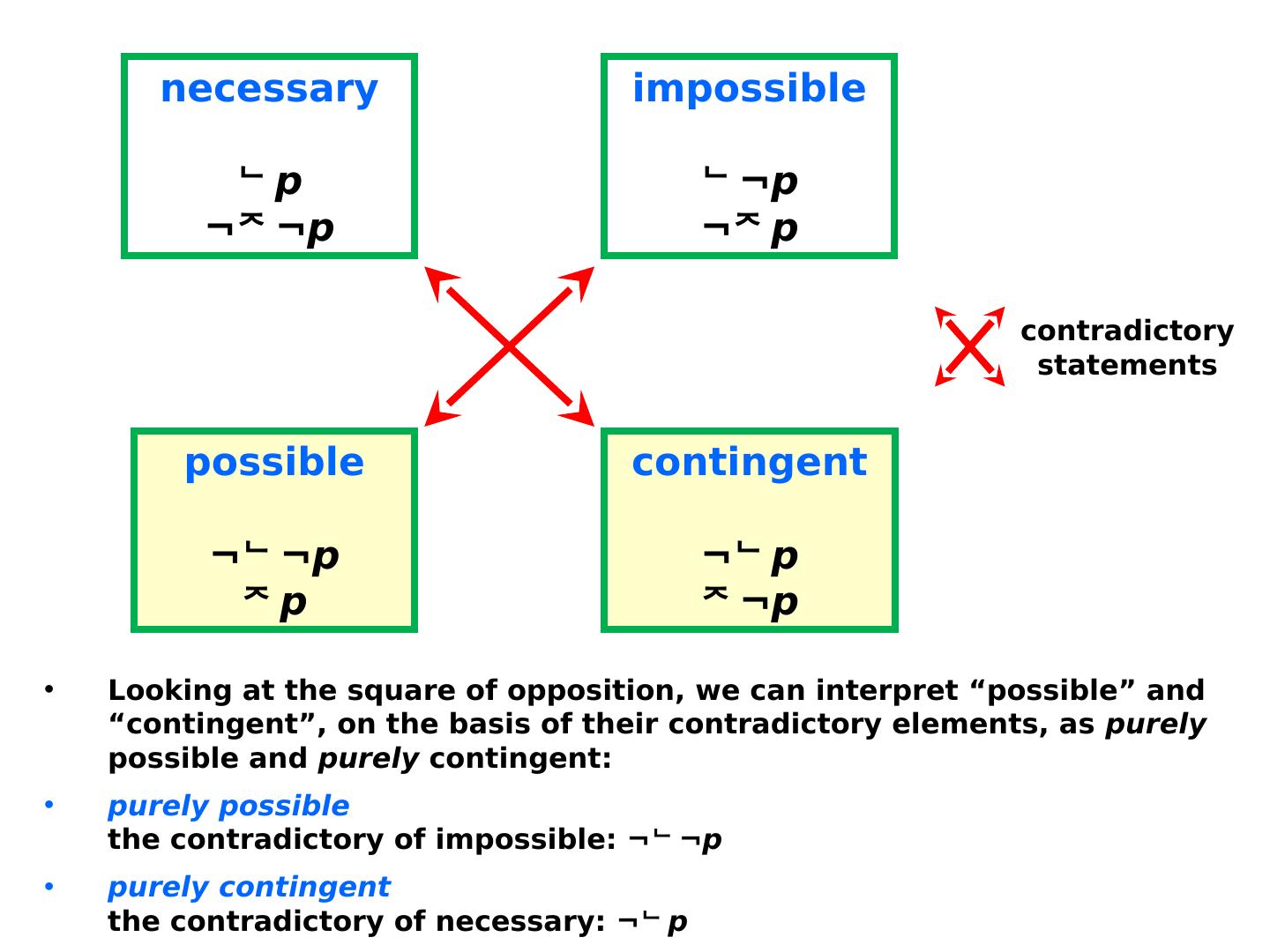
23 .necessary  p ¬ ¬ p impossible  ¬ p ¬  p possible ¬ ¬ p  p contingent ¬  p ¬ p contradictory statements Following Theophrastus (IV century BC), but with modern logic operators, we can think of a square of opposition in modal terms: Square of opposition

24 . What is logical Necessity? By logical necessity we do not refer either to physical necessity (such as “bodies attract according to Newton’s formula”, or “heated metals dilate”) nor philosophical necessity (such as an a priori reason, independent from experience, or “ cogito ergo sum ”). What we have in mind, by contrast, the kind of relationship linking premises and conclusion in a mathematical proof, or formal deduction: if the deduction is correct and the premises are true, the conclusion is true.

25 .In this sense we say that “true mathematical and logical statements are necessary”. In Leibniz’s terms, a necessary statement is true in every possible world ; a possible statement is true in at least one of the possible worlds . Necessary is true in every possible world

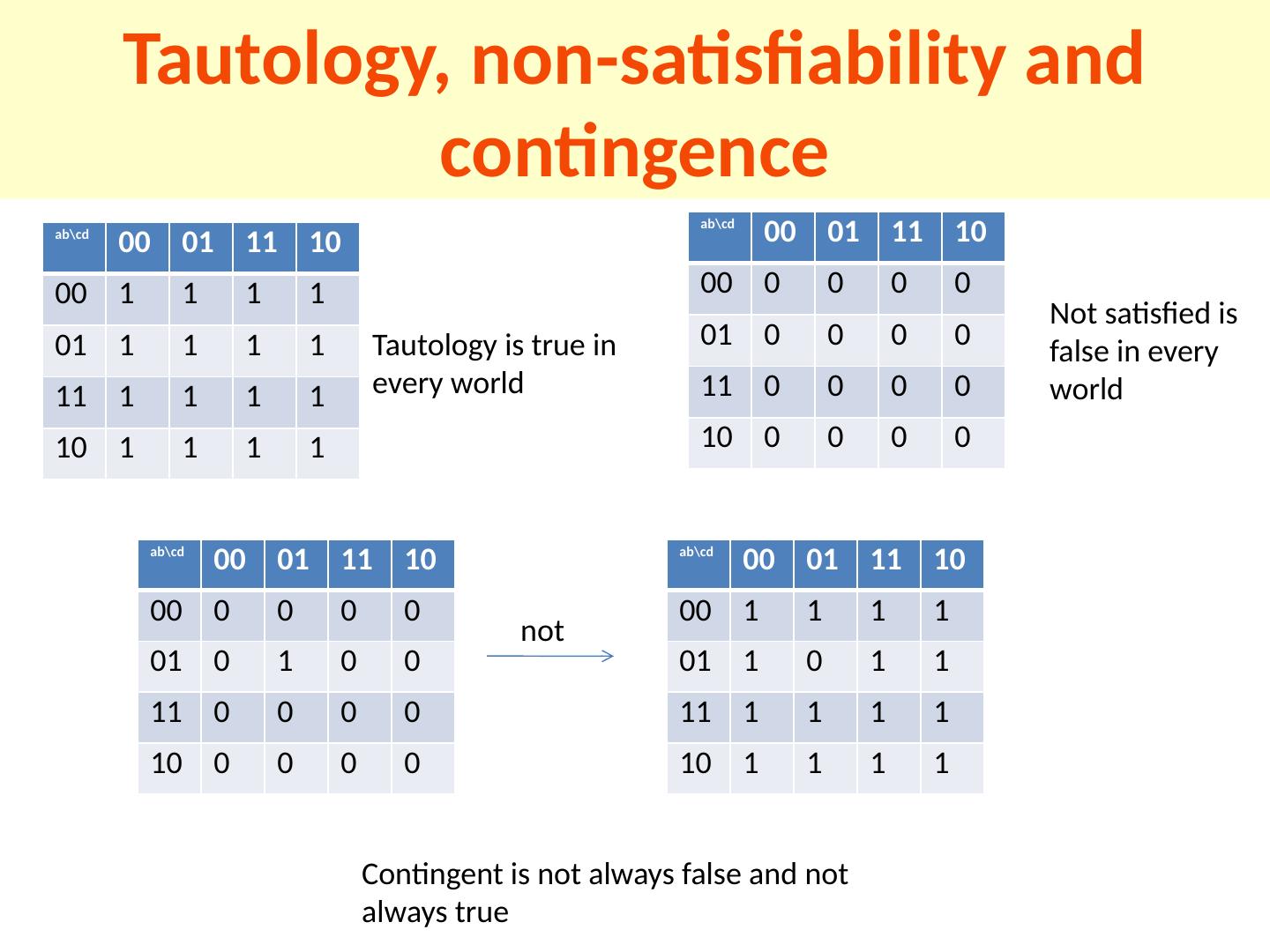
26 .Tautology, non- satisfiability and contingence ab \ cd 00 01 11 10 00 1 1 1 1 01 1 1 1 1 11 1 1 1 1 10 1 1 1 1 ab \ cd 00 01 11 10 00 0 0 0 0 01 0 0 0 0 11 0 0 0 0 10 0 0 0 0 ab \ cd 00 01 11 10 00 0 0 0 0 01 0 1 0 0 11 0 0 0 0 10 0 0 0 0 ab \ cd 00 01 11 10 00 1 1 1 1 01 1 0 1 1 11 1 1 1 1 10 1 1 1 1 Tautology is true in every world Not satisfied is false in every world not Contingent is not always false and not always true

27 .CONTINGENT and POSSIBLE According to Aristotle, “ p is contingent ” is to be understood as  p Λ  ¬ p . Looking at the square of opposition, we can interpret “possible” and “contingent”, on the basis of their contradictory elements, as purely possible and purely contingent: purely possible the contradictory of impossible: ¬ ¬ p purely contingent the contradictory of necessary: ¬ p

28 .necessary  p ¬ ¬ p impossible  ¬ p ¬  p possible ¬ ¬ p  p contingent ¬  p ¬ p contradictory statements Looking at the square of opposition, we can interpret “possible” and “contingent”, on the basis of their contradictory elements, as purely possible and purely contingent: purely possible the contradictory of impossible: ¬ ¬ p purely contingent the contradictory of necessary: ¬ p

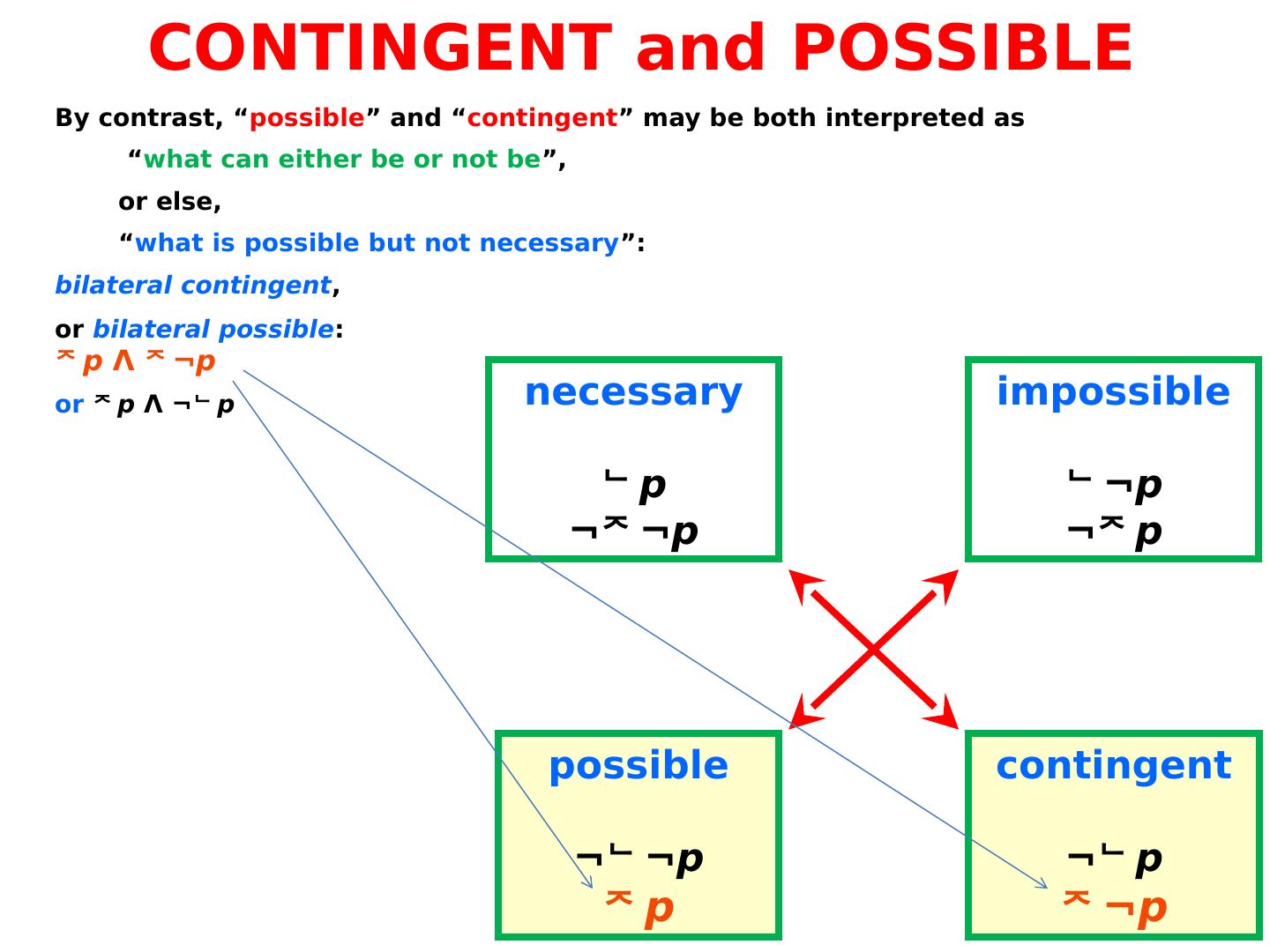
29 .CONTINGENT and POSSIBLE By contrast, “ possible ” and “ contingent ” may be both interpreted as “ what can either be or not be ”, or else, “ what is possible but not necessary ”: bilateral contingent , or bilateral possible :  p Λ  ¬ p or  p Λ ¬ p necessary  p ¬ ¬ p impossible  ¬ p ¬  p possible ¬ ¬ p  p contingent ¬  p ¬ p