018-Inference in First Order Logic

1 .• April 23 • Alan Cheng, Justin Cheng, Matthew Mglej, Anika Raghuvanshi 1 

2 . Inference in First Order Logic Some material adopted from notes by Tim Finin, Andreas Geyer-Schulz, and Chuck Dyer 2 

3 . Inference Rules for FOL • Inference rules for PL apply to FOL as well (Modus Ponens, And-Introduction, And-Elimination, etc.) • New (sound) inference rules for use with quantifiers: 1. Universal Elimination 2. Existential Introduction 3. Existential Elimination 4. Generalized Modus Ponens (GMP) • Resolution 1. Clause form (CNF in FOL) 2. Unification (consistent variable substitution) 3. Refutation resolution (proof by contradiction) 3 

4 .1.Universal Elimination 2.Existential Introduction 3.Existential Elimination 4 

5 .Universal Elimination (x) P(x) |– P(c). • If (x) P(x) is true, then P(c) is true for any constant c in the domain of x, i.e., (x) P(x) |= P(c). • Replace all occurrences of x in the scope of x by the same ground term (a constant or a ground function). • Example: (x) eats(Ziggy, x) |– eats(Ziggy, IceCream) Existential Introduction P(c) |– (x) P(x) • If P(c) is true, so is (x) P(x), i.e., P(c) |= (x) P(x) • Replace all instances of the given constant symbol by the same new variable symbol. • Example eats(Ziggy, IceCream) |– (x) eats(Ziggy, x) Existential Elimination • From (x) P(x) infer P(c), i.e., (x) P(x) |= P(c), where c is a new constant symbol, – All we know is there must be some constant that makes this true, so we can introduce a brand new one to stand in for that constant, even though we don’t know exactly what that constant refer to. – Example: (x) eats(Ziggy, x) |= eats(Ziggy, Stuff) 5 

6 .SKOLEMIZATION; Skolem constants and Skolem Variables • Things become more complicated when there are universal quantifiers (x)(y) eats(x, y) |= (x)eats(x, Stuff) ??? (x)(y) eats(x, y) |= eats(Ziggy, Stuff) ??? – Introduce a new function food_sk(x) to stand for y because that y depends on x (x)(y) eats(x, y) |– (x)eats(x, food_sk(x)) (x)(y) eats(x, y) |– eats(Ziggy, food_sk(Ziggy)) – What exactly the function food_sk(.) does is unknown, except that it takes x as its argument • The process of existential elimination is called “Skolemization”, and the new, unique constants (e.g., Stuff) and functions (e.g., food_sk(.)) are called skolem constants and skolem functions 6 

7 .Generalized Modus Ponens (GMP)  7 

8 . Generalized Modus Ponens (GMP) • Combines And-Introduction, Universal-Elimination, and Modus Ponens • Ex: P(c), Q(c), (x)(P(x) ^ Q(x)) => R(x) |– R(c) P(c), Q(c) |– P(c) ^ Q(c) (by and-introduction) (x)(P(x) ^ Q(x)) => R(x) |– (P(c) ^ Q(c)) => R(c) (by universal-elimination) P(c) ^ Q(c), (P(c) ^ Q(c)) => R(c) |– R(c) (by modus ponens) • All occurrences of a quantified variable must be instantiated to (or substituted by) the same constant. P(a), Q(c), (x)(P(x) ^ Q(x)) => R(x) |– R(c) because all occurrences of x must be either instantiated to a or c which makes the modus ponens rule not applicable. applicable Cannot be different constants 8 

9 . Resolution for FOL • Resolution rule operates on two clauses – A clause is a disjunction of literals (without explicit quantifiers) – Relationship between clauses in KB is conjunction – Variables in a clause are considered universally quantified • Resolution Rule for FOL: there can be just one pair of opposing literals, not more, as the sums of literals – clause C1: (l_1, l_2, ... l_i, ... l_n) and must have Hamming distance one – recall consensus, show examples on Kmaps clause C2: (l’_1, l’_2, ... l’_j, ... l’_m) – if l_i and l’_j are two opposite literals (e.g., P and ~P) and their argument lists can be be made the same (unified) by a set of variable bindings {x1/y1, ... xk/yk} where x1, ... xk are variables and x1/y1, ... xk/yk} where x1, ... xk are variables and y1, ... yk are terms, – then derive a new clause (called resolvent) subst((l_1, l_2, ... l_n, l’_1, l’_2, ... l’_m),  where function subst(expression, returns a new expression by applying all variable bindings in  to the original expression 9 

10 .We need answers to the following questions 1.How to convert FOL sentences to clause form (especially how to remove quantifiers): normalization and skolemization 2.How to unify two argument lists, – i.e., how to find their most general unifier (mgu) unification 3.How to determine which two clauses in KB should be resolved next (among all resolvable pairs of clauses) – and how to determine a proof is completed: resolution strategy 10 

11 .Converting FOL sentences to clause form • Clauses are quantifier free CNF of FOL sentences • Basic ideas – How to handle quantifiers • Careful on quantifiers with preceding negations (explicit or implicit) ~x P(x) is really x ~P(x) (x P(x)) => (y Q(y))  ~(x P(x)) v (y Q(y))  x ~P(x) v y Q(y) • Eliminate true existential quantifier by Skolemization • For true universally quantified variables, treat them as such without quantifiers – How to convert to CNF (similar to PL after all quantifiers are removed) 11 

12 .Conversion procedure to CNF step 1: remove all “=>” and “<=>” operators (using P => Q make ~P v Q and P <=> Q make to P => Q ^ Q => P) step 2: move all negation signs to individual predicates (using de Morgan’s law) step 3: remove all existential quantifiers y case 1: y is not in the scope of any universally quantified variable, then replace all occurrences of y by a skolem constant case 2: if y is in scope of universally quantified variables x1, ... xi, then replace all occurrences of y by a skolem function with x1, ... xi are its argument step 4: remove all universal quantifiers x (with the understanding that all remaining variables are universally quantified) step 5: convert the sentence into CNF (using distribution law, etc) step 6: use parenthesis to separate all disjunctions, then drop all v’s and ^’s 

13 . Conversion examples x (P(x) ^ Q(x) => R(x)) y rose(y) ^ yellow(y) x ~(P(x) ^ Q(x)) v R(x) (by step 1) rose(c) ^ yellow(c) x ~P(x) v ~Q(x) v R(x) (by step 2) (where c is a skolem constant) constant ~P(x) v ~Q(x) v R(x) (by step 4) (rose(c)), (yellow(c)) (~P(x), ~Q(x), R(x)) (by step 6) x [person(x) => y (person(y) ^ father(y, x))] x [~person(x) v y (person(y) ^ father(y, x))] (by step 1) x [~person(x) v (person(f_sk(x)) ^ father(f_sk(x), x))] (by step 3) ~person(x) v (person(f_sk(x)) ^ father(f_sk(x), x)) (by step 4) (~person(x) v person(f_sk(x)) ^ (~person(x) v father(f_sk(x), x)) (by step 5) (~person(x), person(f_sk(x)), (~person(x), father(f_sk(x), x)) (by step 6) (where f_sk(.) is a skolem function) 13 

14 .Rules for Unification of two clauses • Basic idea: x P(x) => Q(x), P(a) |– Q(a) (~P(x), Q(x)), (P(a)) {x1/y1, ... xk/yk} where x1, ... xk are variables and x/a} a substitution in which variable x is bound to a (Q(a)) – The goal is to find a set of variable bindings so that the argument lists of two opposite literals (in two clauses) can be made the same. – Only variables can be bound to other things. things 1. a and b cannot be unified (different constants in general refer to different objects) 2. a and f(x) cannot be unified (unless the inverse function of f is known, which is not the case for general functions in FOL) 3. f(x) and g(y) cannot be unified (function symbols f and g in general refer to different functions and their exact definitions are different in different interpretations) 

15 .Rules for Unification of two clauses (cont) – Cannot bind variable x to y if x appears anywhere in y • Try to unify x and f(x). If we bind x to f(x) and apply the binding to both x and f(x), we get f(x) and f(f(x)) which are still not the same (and will never be made the same no matter how many times the binding is applied) – Otherwise, bind variable x to y, written as x/y (this guarantees to find the most general unifier, or mgu) • Suppose both x and y are variables, then they can be made the same by binding both of them to any constant c or any function f(.). Such bindings are less general and impose unnecessary restriction on x and y. – To unify two terms of the same function symbol, unify their argument lists (unification is recursive) Ex: to unify f(x) and f(g(b)), we need to unify x and g(b) 15 

16 .Rules for Unification of two clauses (cont) – When the argument lists contain multiple terms, unify each pair of terms Ex. To unify (x, f(x), ...) (a, y, ...) 1. unify x and a (x/a}) 2. apply  to the remaining terms in both lists, resulting (f(a), ...) and (y, ...) 3. unify f(a) and y with binding y/f(a) 4. apply the new binding y/f(a) to and to the rest of the two lists 5. add y/f(a) to new  most general unifier 16 

17 . Unification Examples • parents(x, father(x), mother(Bill)) and parents(Bill, father(Bill), y) – unify x and Bill:  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/Bill} – unify father(Bill) and father(Bill):  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/Bill} – unify mother(Bill) and y:  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/Bill}, y/mother(Bill)} • parents(x, father(x), mother(Bill)) and parents(Bill, father(y), z) – unify x and Bill:  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/Bill} – unify father(Bill) and father(y):  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/Bill, y/Bill} – unify mother(Bill) and z:  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/Bill, y/Bill, z/mother(Bill)} • parents(x, father(x), mother(Jane)) and parents(Bill, father(y), mother(y)) – unify x and Bill:  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/Bill} – unify father(Bill) and father(y):  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/Bill, y/Bill} – unify mother(Jane) and mother(Bill): Failure because Jane and Bill are different constants 

18 . More Unification Examples • P(x, g(x), h(b)) and P(f(u, a), v, u)) – unify x and f(u, a):  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/ f(u, a)}; remaining lists: (g(f(u, a)), h(b)) and (v, u) – unify g(f(u, a)) and v:  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/f(u, a), v/g(f(u, a))}; remaining lists: (h(b)) and (u) – unify h(b) and u:  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/f(h(b), a), v/g(f(h(b), a)), u/h(b)}; • P(f(x, a), g(x, b)) and P(y, g(y, b)) – unify f(x, a) and y:  = {x1/y1, ... xk/yk} where x1, ... xk are variables and y/f(x, a)} remaining lists: (g(x, b)) and (g(f(x, a), b)) – unify x and f(x, a): failure because x is in f(x, a) 18 

19 .Pseudo-Code of the Unification Algorithm procedure unify(p, q, ) /* p and q are two lists of terms and |p| = |q| */ if p = empty then return ; /* success */ let r = first(p) and s = first(q); if r = s then return unify(rest(p), rest(q), ); if r is a variable then temp = unify-var(r, s); else if s is a variable then temp = unify-var(s, r); else if both r and s are functions of the same function name then temp = unify(arglist(r), arglist(s), empty); else return “failure”; if temp = “failure” then return “failure”; /* p and q are not unifiable */ else  = subst(temp) temp; /* apply tmp to old then insert it into  */  return unify(subst(rest(p), tmp), subst(rest(q), tmp), ); end{x1/y1, ... xk/yk} where x1, ... xk are variables and unify} procedure unify-var(x, y) if x appears anywhere in y then return “failure”; else return (x/y) end{x1/y1, ... xk/yk} where x1, ... xk are variables and unify-var} Recursive algorithm Interesting hardware realization 19 

20 .Informal example of Resolution in FOL • Convert all sentences in KB (axioms, definitions, and known facts) and the goal sentence (the theorem to be proved) to clause form • Two clauses C1 and C2 can be resolved if and only if r in C1 and s in C2 are two opposite literals, and their argument lists arglist_r and arglist_s are unifiable with mgu = . • Then derive the resolvent sentence: subst((C1 – {x1/y1, ... xk/yk} where x1, ... xk are variables and r}, C2 – {x1/y1, ... xk/yk} where x1, ... xk are variables and s}), ) (substitution is applied to all literals in C1 and C2, but not to any other clauses) • Example (P(x, f(a)), Q(x, f(y)), R(y)) (~P(z, f(a)), ~S(z))  = {x1/y1, ... xk/yk} where x1, ... xk are variables and x/z} (Q(z, f(y)), R(y), ~S(z)) 

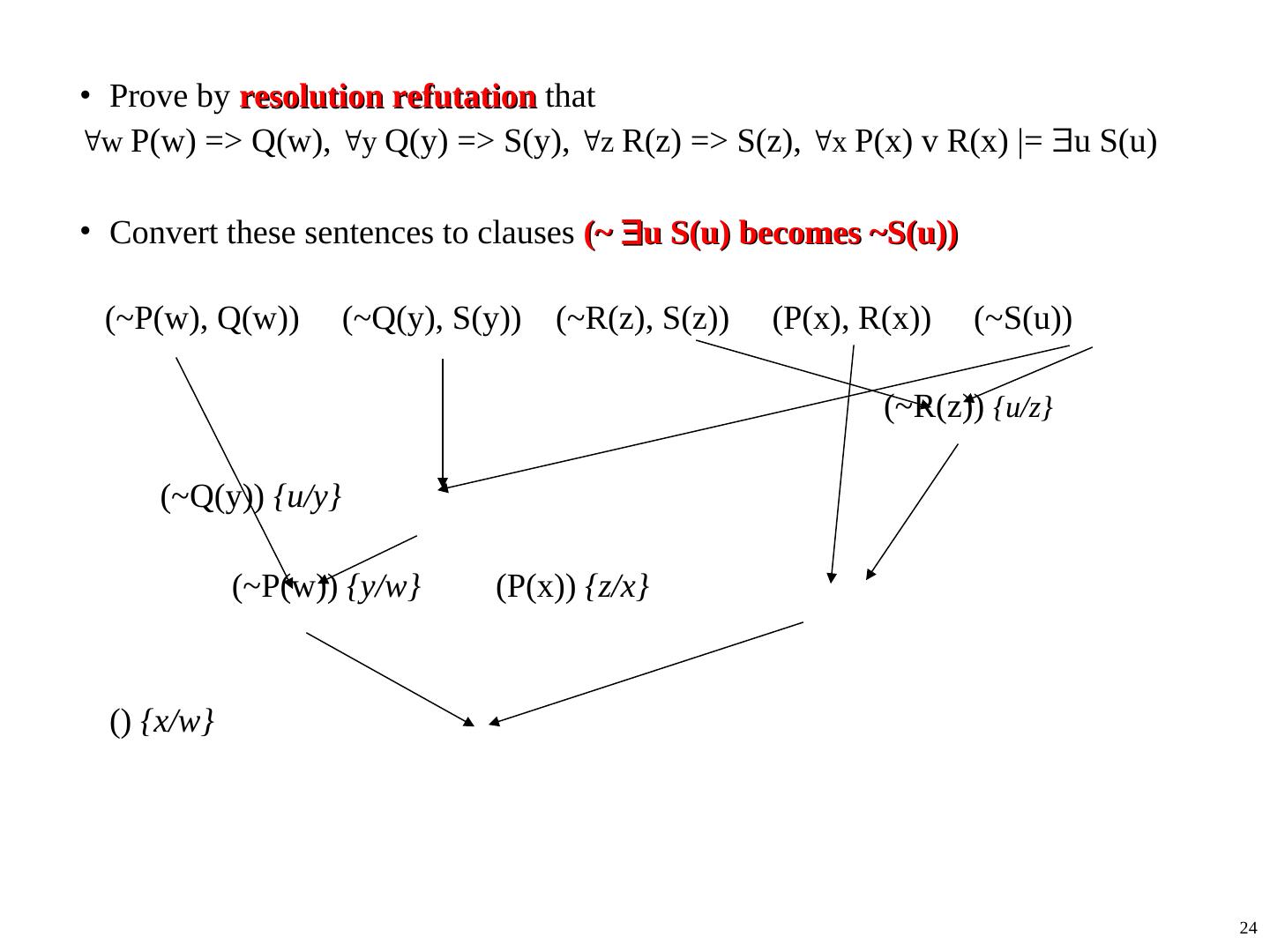
21 . Resolution example with Skolem constant • Prove that w P(w) => Q(w), y Q(y) => S(y), z R(z) => S(z), x P(x) v R(x) |= u S(u) • Convert these sentences to clauses (u S(u) skolemized to S(a)) • Apply resolution z/a (~P(w), Q(w)) (~Q(y), S(y)) (~R(a), S(a)) (P(x), R(x)) (~P(y), S(y)) {w/y} a resolution (S(x), R(x)) {y/x} proof tree (S(a)) {x/a, z/a} • Problems 1. The theorem S(a) does not actively participate in the proof 2. Hard to determine if a proof (with consistent variable bindings) is completed if the theorem consists of more than one clause Resolution Refutation: a better proof strategy 21 

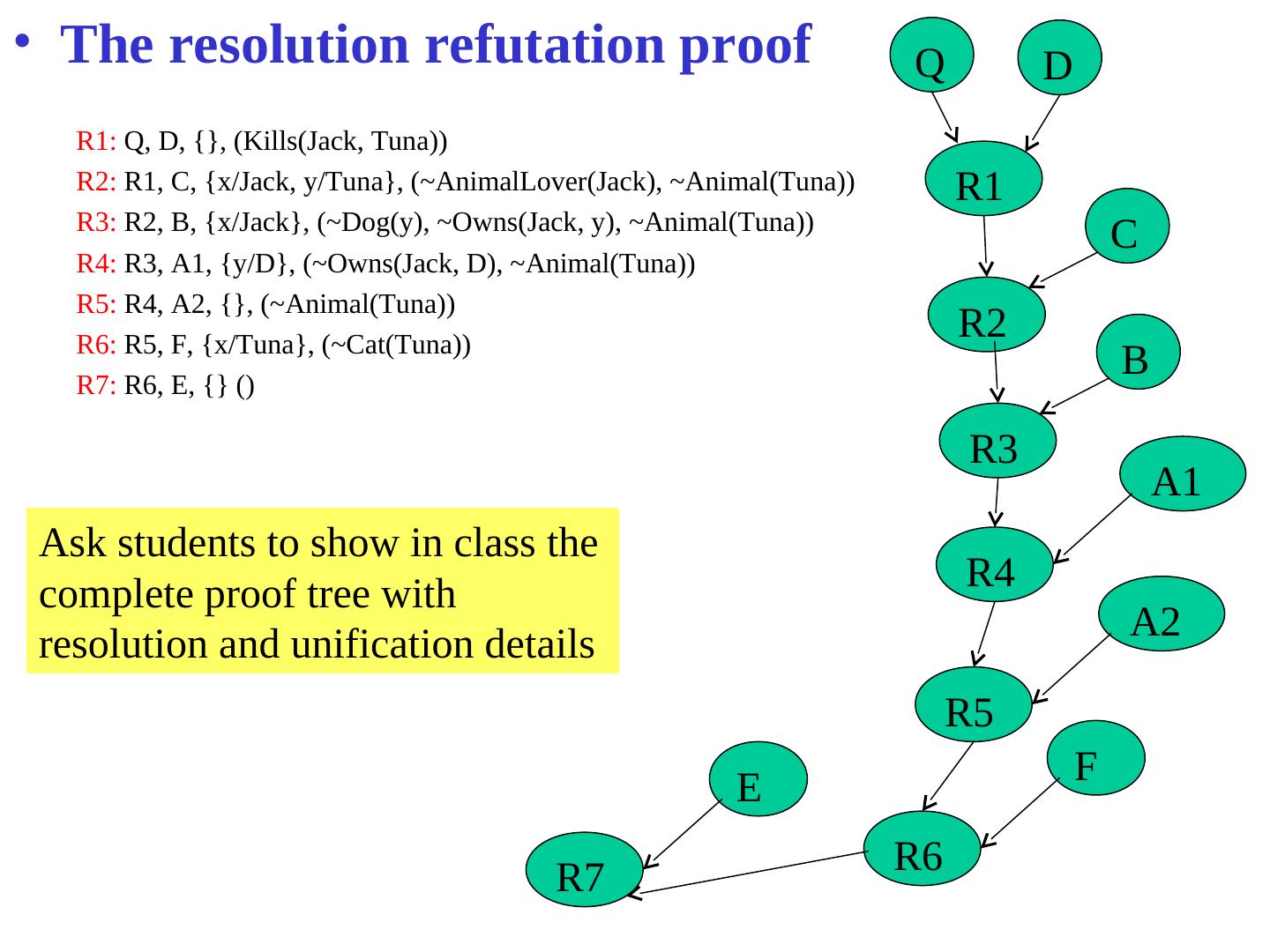
22 . Resolution Refutation: a better proof strategy • We want: – Given a consistent set of axioms KB and goal sentence Q, show that KB |= Q. • We do: – Proof by contradiction: 1. Add ~Q to KB and try to prove false. 2. because (KB |= Q) <=> (KB ^ ~Q |= False) 3. KB ^ ~Q |= False means the same as KB ^ ~Q is inconsistent • We will illustrate proof by contradiction • “false” in clause form is represented by null (empty) clause 22 

23 . Resolution Refutation: a better proof strategy – Proof by contradiction: 1. Add ~Q to KB and try to prove false. 2. because (KB |= Q) <=> (KB ^ ~Q |= False) 3. KB ^ ~Q |= False means the same as KB ^ ~Q is inconsistent • We will illustrate below a proof by contradiction • How to represent “false” in clause form Explain this in  x P(x) ^ y ~P(y) is inconsistent English using terms of data – Convert them to clause form then apply resolution base KB and (P(x)) (~P(y)) prolog program with goal Q {x1/y1, ... xk/yk} where x1, ... xk are variables and x/y} ( ) a null clause – A null clause represents false (inconsistence/contradiction) – KB |= Q if we can derive a null clause from KB ^ ~Q by resolution 23 

24 .• Prove by resolution refutation that w P(w) => Q(w), y Q(y) => S(y), z R(z) => S(z), x P(x) v R(x) |= u S(u) • Convert these sentences to clauses (~ u S(u) becomes ~S(u)) (~P(w), Q(w)) (~Q(y), S(y)) (~R(z), S(z)) (P(x), R(x)) (~S(u)) (~R(z)) {u/z} (~Q(y)) {u/y} (~P(w)) {y/w} (P(x)) {z/x} () {x/w} 24 

25 . Refutation Resolution Procedure procedure resolution(KB, Q) /* KB is a set of consistent, true FOL sentences, Q is a goal sentence. It returns success if KB |-- Q, and failure otherwise */ KB = clause(union(KB, {x1/y1, ... xk/yk} where x1, ... xk are variables and ~Q})) /* convert KB and ~Q to clause form */ while null clause is not in KB do pick 2 sentences, S1 and S2, in KB that contain a pair of opposite literals whose argument lists are unifiable if none can be found then return "failure" resolvent = resolution-rule(S1, S2) KB = union(KB, {x1/y1, ... xk/yk} where x1, ... xk are variables and resolvent}) return "success " end{x1/y1, ... xk/yk} where x1, ... xk are variables and resolution} 25 

26 . Control Strategies for Resolution • At any given time, there are multiple pairs of clauses that are resolvable. • Therefore, we need a systematic way to select one such pair at each step of proof 1. May lead to a null clause 2. Without losing potentially good threads (of inference) • There are a number of general (domain independent) strategies that are useful in controlling a resolution theorem prover. • We’ll briefly look at the following resolution strategies: 1. Breadth first 2. Set of support 3. Unit resolution 4. Input Resolution 5. Ordered resolution 6. Subsumption 26 

27 . Breadth first resolution strategy 1.Level 0 clauses are those from the original KB and the negation of the goal. 2.Level k clauses are the resolvents computed from two clauses, one of which must be from level k-1 and the other from any earlier level. 3.Compute all level 1 clauses possible, then all possible level 2 clauses, etc. 4.Complete, but very inefficient. inefficient 27 

28 . Set of Support Resolution Strategy 1.At least one parent clause must be from the negation of the goal or one of the "descendents" of such a goal clause (i.e., derived from a goal clause). 2.Complete (assuming all possible set-of-support clauses are derived) 3.Gives a goal directed character to the search 28 

29 . Unit Resolution Strategy 1.At least one parent clause must be a "unit clause," i.e., a clause containing a single literal. 2.Not complete in general 3.But complete for Horn clause KBs 29