- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
016-Fundamentals of Logic
展开查看详情
1 . Chapter 2 Fundamentals of Logic 1. What is a valid argument or proof? 2. Study system of logic 3. In proving theorems or solving problems, creativity and insight are needed, which cannot be taught
2 .2.1 Basic connectives and truth tables 2.1 Basic connectives and truth tables statements (propositions): declarative sentences that are either true or false--but not both. Eg. Margaret Mitchell wrote Gone with the Wind. 2+3=5. not statements: What a beautiful morning! Get up and do your exercises.
3 .2.1 Basic connectives and truth tables primitive and compound statements combined from primitive statements by logical connectives or by negation ( p , p) logical connectives: (a) conjunction (AND): p q (b) disjunction(inclusive OR): p q (c) exclusive or: p q (d) implication: p q (if p then q) (e) biconditional: p q (p if and only if q, or p iff q)
4 .2.1 Basic connectives and truth tables "The number x is an integer." is not a statement because its truth value cannot be determined until a numerical value is assigned for x. First order logic vs. predicate logic
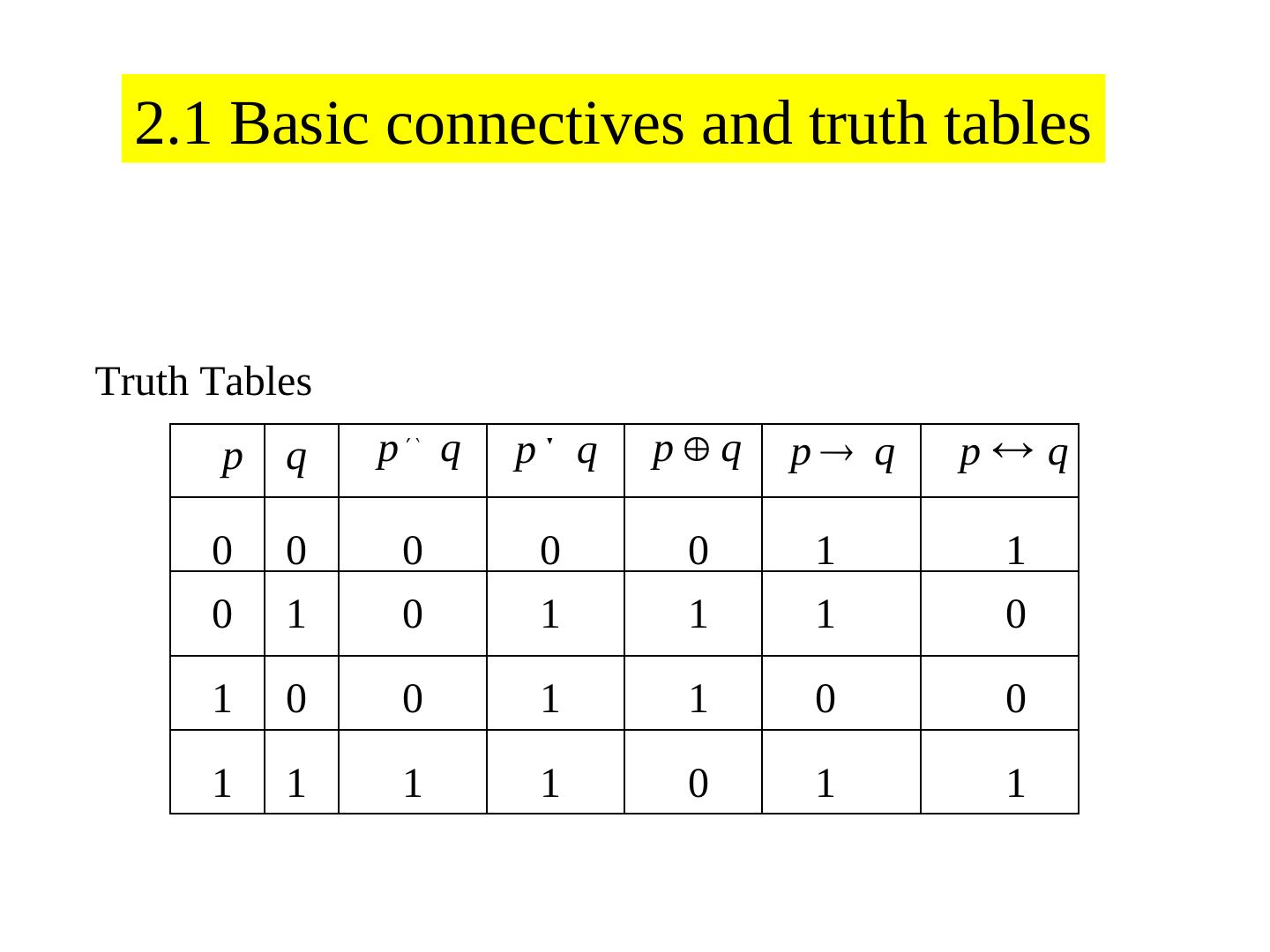
5 . 2.1 Basic connectives and truth tables Truth Tables p q p q p q pq p q p q 0 0 0 0 0 1 1 0 1 0 1 1 1 0 1 0 0 1 1 0 0 1 1 1 1 0 1 1
6 .2.1 Basic connectives and truth tables Ex. 2.1 s: Phyllis goes out for a walk. t: The moon is out. u: It is snowing. ( t u ) s : If the moon is out and it is not snowing, then Phyllis goes out for a walk. If it is snowing and the moon is not out, then Phyllis will not go out for a walk. ( u t ) s
7 .2.1 Basic connectives and truth tables Def. 2.1. A compound statement is called a tautology(T0) if it is true for all truth value assignments for its component statements. If a compound statement is false for all such assignments, then it is called a contradiction(F0). p ( p q ) : tautology p ( p q ) : contradiction
8 .2.1 Basic connectives and truth tables an argument: ( p1 p 2 p n ) q premises conclusion If any one of p1 , p 2 , , p n is false, then no matter what truth value q has, the implication is true. Consequently, if we start with the premises p1 , p 2 , , p n --each with truth value 1--and find that under these circumstances q also has value 1, then the implication is a tautology and we have a valid argument.
9 . 2.2 Logical Equivalence: The Laws of Logic Ex. 2.7 p q p q p q p 0 0 1 1 1 0 1 1 1 1 1 0 0 0 0 1 1 0 1 1 Def 2.2 . logically equivalent s1 s2
10 .2.2 Logical Equivalence: The Laws of Logic logically equivalent ( p q) p q ( p q) ( p q) (q p ) ( p q ) ( p q ) ( q p ) ( p q) ( p q) ( p q) ( p q ) ( p q ) We can eliminate the connectives and from compound statements. (and,or,not) is a complete set.
11 .2.2 Logical Equivalence: The Laws of Logic Ex 2.8. DeMorgan's Laws ( p q) p q ( p q) p q p and q can be any compound statements.
12 .2.2 Logical Equivalence: The Laws of Logic (1) p p Law of Double Negation ( 2) ( p q) p q Demorgan's Laws ( p q) p q ( 3) p q q p Commutative Laws p q q p ( 4) p ( q r ) ( p q) r Associative Laws p ( q r ) ( p q) r
13 .2.2 Logical Equivalence: The Laws of Logic ( 5) p ( q r ) ( p q ) ( p r ) Distributive Law p ( q r ) ( p q) ( p r ) ( 6) p p p , p p p Idempotent Law ( 7 ) p F0 p , p T0 p Identity Law ( 8) p p T0 , p p F0 Inverse Law ( 9 ) p T0 T0 , P F0 F0 Domination Law (10) p ( p q ) p , p ( p q ) p Absorption Law
14 .2.2 Logical Equivalence: The Laws of Logic All the laws, aside from the Law of Double Negation, all fall naturally into pairs. Def. 2.3 Let s be a statement. If s contains no logical connectives other than and , then the dual of s, denoted sd, is the statement obtained from s by replacing each occurrence of and by and , respectively, and each occurrence of T0 and F0 by F0 and T0, respectively. Eg. s: ( p q ) ( r T0 ), s d : ( p q ) ( r F0 ) The dual of p q is ( p q ) d p q
15 .2.2 Logical Equivalence: The Laws of Logic Theorem 2.1 (The Principle of Duality) Let s and t be statements. If s t , then s d t d . First Substitution Rule (replace each p by another statement q) Ex. 2.10 P: ( p q ) ( p q ) is a tautology. Replace each occurrence of p by r s P1: [( r s) q ] [ ( r s) q ] is also a tautology.
16 .2.2 Logical Equivalence: The Laws of Logic Second Substitution Rule Ex. 2.11 P: ( p q ) r Then, P P1 P1: ( p q ) r because ( p q ) ( p q ) Ex. 2.12 Negate and simplify the compound statement ( p q ) r [( p q ) r ] [ ( p q ) r ] [( p q ) r ] ( p q ) r ( p q) r
17 .2.2 Logical Equivalence: The Laws of Logic Ex. 2.13 What is the negation of "If Joan goes to Lake George, then Mary will pay for Joan's shopping spree."? Because ( p q ) ( p q ) p q The negation is "Joan goes to Lake George, but (or and) Mary does not pay for Joan's shopping spree."
18 .2.2 Logical Equivalence: The Laws of Logic Ex. 2.15 contrapositive of p q p q p q q p q p p q 0 0 1 1 1 1 0 1 1 1 0 0 1 0 0 0 1 1 1 1 1 1 1 1 converse inverse
19 . 2.2 Logical Equivalence: The Laws of Logic Compare the efficiency of two program segments. z:=4; . for i:=1 to 10 do Number of comparisons? . begin 20 vs. 10+3=13 . x:=z-1; if x>0 then y:=z+3*i; if y>0 then if ((x>0) and (y>0)) then … writeln(‘The value of the sum x+y is’, x+y) end ( p q ) r logically equivalent p (q r )
20 .2.2 Logical Equivalence: The Laws of Logic simplification of compound statement Ex. 2.16 ( p q ) ( p q ) Demorgan's Law ( p q ) ( p q ) ( p q) ( p q) Law of Double Negation p (q q) Distributive Law p F0 p Inverse Law and Identity Law
21 . 2.3 Logical Implication: Rules of Inference an argument: ( p1 p 2 p n ) q premises conclusion is a valid argument ( p1 p 2 p n ) q is a tautology
22 .2.3 Logical Implication: Rules of Inference Ex. 2.19 statements: p: Roger studies. q: Roger plays tennis. r: Roger passes discrete mathematics. premises: p1: If Roger studies, then he will pass discrete math. p2: If Roger doesn't play tennis, then he'll study. p3: Roger failed discrete mathematics. Determine whether the argument ( p1 p 2 p 3 ) q is p1: p r , p 2 : q p , p 3 : r valid. which is a tautology, ( p1 p 2 p 3 ) q the original argument is true [( p r ) ( q p ) r ] q
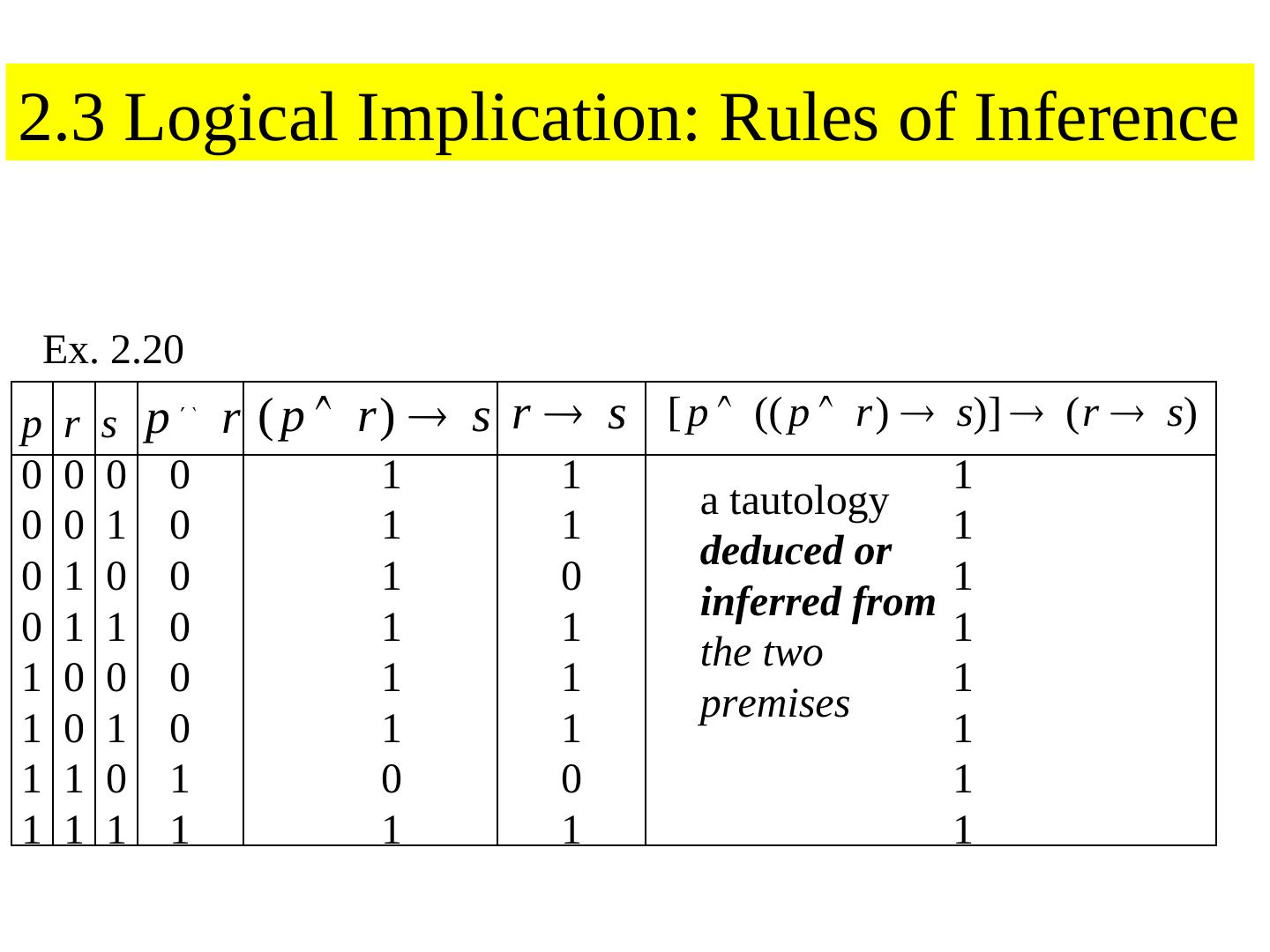
23 .2.3 Logical Implication: Rules of Inference Ex. 2.20 p r s p r ( p r ) s r s [ p (( p r ) s)] ( r s) 0 0 0 0 1 1 1 a tautology 0 0 1 0 1 1 1 deduced or 0 1 0 0 1 0 1 inferred from 0 1 1 0 1 1 1 the two 1 0 0 0 1 1 1 premises 1 0 1 0 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1
24 .2.3 Logical Implication: Rules of Inference Def. 2.4. If p, q are any arbitrary statements such that p q is a tautology, then we say that p logically implies q and we write p q to denote this situation. p q means p q is a tautology. p q means p q is a tautology.
25 .2.3 Logical Implication: Rules of Inference rule of inference: use to validate or invalidate a logical implication without resorting to truth table (which will be prohibitively large if the number of variables are large) Ex 2.22 Modus Ponens (the method of affirming) or the Rule of Detachment p [ p ( p q )] q p q q
26 .2.3 Logical Implication: Rules of Inference Example 2.23 Law of the Syllogism p q q r [( p q ) ( q r )] ( p r ) p r Ex 2.25 p p q q r r
27 . 2.3 Logical Implication: Rules of Inference Ex. 2.25 Modus Tollens (method of denying) p q [( p q ) q ] p q example: p r p p s r s p u t s s t s u t u t u p u p
28 .2.3 Logical Implication: Rules of Inference Ex. 2.25 Modus Tollens (method of denying) p q [( p q ) q ] p q example: p r p p s r s t s p s t u t u another reasoning p
29 .2.3 Logical Implication: Rules of Inference fallacy p q q p (1) If Margaret Thatcher is the president of the U.S., then she is at least 35 years old. (2) Margaret Thatcher is at least 35 years old. (3) Therefore, Margaret Thatcher is the president of the US.