017-Basic Knowledge Representation in First Order Logic

1 .Basic Knowledge Representation in First Order Logic Some material adopted from notes by Tim Finin And Andreas Geyer-Schulz 

2 . First Order (Predicate) Logic (FOL) • First-order logic is used to model the world in terms of – objects which are things with individual identities e.g., individual students, lecturers, companies, cars ... – properties of objects that distinguish them from other objects e.g., mortal, blue, oval, even, large, ... – classes of objects (often defined by properties) e.g., human, mammal, machine, red-things... – relations that hold among objects e.g., brother of, bigger than, outside, part of, has color, occurs after, owns, a member of, ... – functions which are a subset of the relations in which there is only one ``value'' for any given ``input''. e.g., father of, best friend, second half, one more than ... 

3 . Syntax of FOL • Predicates: P(x[1], ..., x[n]) – P: predicate name; (x[1], ..., x[n]): argument list – A special function with range = {T, F}; – Examples: human(x), /* x is a human */ father(x, y) /* x is the father of y */ – When all arguments of a predicate is assigned values (said to be instantiated), the predicate becomes either true or false, i.e., it becomes a proposition. • Ex. Father(Fred, Joe) – A predicate, like a membership function, defines a set (or a class) of objects • Terms (arguments of predicates must be terms) – Constants are terms (e.g., Fred, a, Z, “red”, etc.) – Variables are terms (e.g., x, y, z, etc.), a variable is instantiated when it is assigned a constant as its value – Functions of terms are terms (e.g., f(x, y, z), f(x, g(a)), etc.) – A term is called a ground term if it does not involve variables – Predicates, though special functions, are not terms in FOL 

4 .• Quantifiers Universal quantification  (or forall) – (x)P(x) means that P holds for all values of x in the domain associated with that variable. – E.g., (x) dolphin(x) => mammal(x) (x) human(x) => mortal(x) – Universal quantifiers often used with "implication (=>)" to form "rules" about properties of a class (x) student(x) => smart(x) (All students are smart) – Often associated with English words “all”, “everyone”, “always”, etc. – You rarely use universal quantification to make blanket statements about every individual in the world (because such statement is hardly true) (x)student(x)^smart(x) means everyone in the world is a student and is smart. 

5 .Existential quantification  – (x)P(x) means that P holds for some value(s) of x in the domain associated with that variable. – E.g., (x) mammal(x) ^ lays-eggs(x) (x) taller(x, Fred) (x) UMBC-Student (x) ^ taller(x, Fred) – Existential quantifiers usually used with “^ (and)" to specify a list of properties about an individual. (x) student(x) ^ smart(x) (there is a student who is smart.) – A common mistake is to represent this English sentence as the FOL sentence: (x) student(x) => smart(x) It also holds if there no student exists in the domain because student(x) => smart(x) holds for any individual who is not a student. – Often associated with English words “someone”, “sometimes”, etc. 

6 . Scopes of quantifiers • Each quantified variable has its scope – (x)[human(x) => (y) [human(y) ^ father(y, x)] ] – All occurrences of x within the scope of the quantified x refer to the same thing. – Better to use different variables for different things, even if they are in scopes of different quantifiers • Switching the order of universal quantifiers does not change the meaning: – (x)(y)P(x,y) <=> (y)(x)P(x,y), can write as (x,y)P(x,y) • Similarly, you can switch the order of existential quantifiers. – (x)(y)P(x,y) <=> (y)(x)P(x,y) • Switching the order of universals and existential does change meaning: – Everyone likes someone: (x)(y)likes(x,y) – Someone is liked by everyone: (y)(x) likes(x,y) 

7 . Sentences are built from terms and atoms • A term (denoting a individual in the world) is a constant symbol, a variable symbol, or a function of terms. • An atom (atomic sentence) is a predicate P(x[1], ..., x[n]) – Ground atom: all terms in its arguments are ground terms (does not involve variables) – A ground atom has value true or false (like a proposition in PL) • A literal is either an atom or a negation of an atom • A sentence is an atom, or, – ~P, P v Q, P ^ Q, P => Q, P <=> Q, (P) where P and Q are sentences – If P is a sentence and x is a variable, then (x)P and (x)P are sentences • A well-formed formula (wff) is a sentence containing no "free" variables. i.e., all variables are "bound" by universal or existential quantifiers. (x)P(x,y) has x bound as a universally quantified variable, but y is free. 

8 . A BNF for FOL Sentences S := <Sentence> ; <Sentence> := <AtomicSentence> | <Sentence> <Connective> <Sentence> | <Quantifier> <Variable>,... <Sentence> | ~ <Sentence> | "(" <Sentence> ")"; <AtomicSentence> := <Predicate> "(" <Term>, ... ")" | <Term> "=" <Term>; <Term> := <Function> "(" <Term>, ... ")" | <Constant> | <Variable>; <Connective> := ^ | v | => | <=>; <Quantifier> :=  | ; <Constant> := "A" | "X1" | "John" | ... ; <Variable> := "a" | "x" | "s" | ... ; <Predicate> := "Before" | "HasColor" | "Raining" | ... ; <Function> := "Mother" | "LeftLegOf" | ... ; <Literal> := <AutomicSetence> | ~ <AutomicSetence> 

9 . Translating English to FOL • Every gardener likes the sun. (x) gardener(x) => likes(x,Sun) • Not Every gardener likes the sun. ~((x) gardener(x) => likes(x,Sun)) • You can fool some of the people all of the time. (x)(t) person(x) ^ time(t) => can-be-fooled(x,t) • You can fool all of the people some of the time. (x)(t) person(x) ^ time(t) => can-be-fooled(x,t) (the time people are fooled may be different) • You can fool all of the people at some time. (t)(x) person(x) ^ time(t) => can-be-fooled(x,t) (all people are fooled at the same time) • You can not fool all of the people all of the time. ~((x)(t) person(x) ^ time(t) => can-be-fooled(x,t)) • Everyone is younger than his father (x) person(x) => younger(x, father(x)) 

10 .• All purple mushrooms are poisonous. (x) (mushroom(x) ^ purple(x)) => poisonous(x) • No purple mushroom is poisonous. ~(x) purple(x) ^ mushroom(x) ^ poisonous(x) (x) (mushroom(x) ^ purple(x)) => ~poisonous(x) • There are exactly two purple mushrooms. (x)(Ey) mushroom(x) ^ purple(x) ^ mushroom(y) ^ purple(y) ^ ~(x=y) ^ (z) (mushroom(z) ^ purple(z)) => ((x=z) v (y=z)) • Clinton is not tall. ~tall(Clinton) • X is above Y if X is directly on top of Y or there is a pile of one or more other objects directly on top of one another starting with X and ending with Y. (x)(y) above(x,y) <=> (on(x,y) v (z) (on(x,z) ^ above(z,y))) 

11 . Example: A simple genealogy KB by FOL • Build a small genealogy knowledge base by FOL that – contains facts of immediate family relations (spouses, parents, etc.) – contains definitions of more complex relations (ancestors, relatives) – is able to answer queries about relationships between people • Predicates: – parent(x, y), child(x, y), father(x, y), daughter(x, y), etc. – spouse(x, y), husband(x, y), wife(x,y) – ancestor(x, y), descendent(x, y) – Male(x), female(y) – relative(x, y) • Facts: – husband(Joe, Mary), son(Fred, Joe) – spouse(John, Nancy), male(John), son(Mark, Nancy) – father(Jack, Nancy), daughter(Linda, Jack) – daughter(Liz, Linda) – etc. 

12 .• Rules for genealogical relations – (x,y) parent(x, y) <=> child (y, x) (x,y) father(x, y) <=> parent(x, y) ^ male(x) (similarly for mother(x, y)) (x,y) daughter(x, y) <=> child(x, y) ^ female(x) (similarly for son(x, y)) – (x,y) husband(x, y) <=> spouse(x, y) ^ male(x) (similarly for wife(x, y)) (x,y) spouse(x, y) <=> spouse(y, x) (spouse relation is symmetric) – (x,y) parent(x, y) => ancestor(x, y) (x,y)(z) parent(x, z) ^ ancestor(z, y) => ancestor(x, y) – (x,y) descendent(x, y) <=> ancestor(y, x) – (x,y)(z) ancestor(z, x) ^ ancestor(z, y) => relative(x, y) (related by common ancestry) (x,y) spouse(x, y) => relative(x, y) (related by marriage) (x,y)(z) relative(z, x) ^ relative(z, y) => relative(x, y) (transitive) (x,y) relative(x, y) <=> relative(y, x) (symmetric) • Queries – ancestor(Jack, Fred) /* the answer is yes */ – relative(Liz, Joe) /* the answer is yes */ – relative(Nancy, Mathews) /* no answer in general, no if under closed world assumption */ – (z) ancestor(z, Fred)^ancestor(z, Liz) 

13 . Connections between Forall and Exists • “It is not the case that everyone is ...” is logically equivalent to “There is someone who is NOT ...” • “No one is ...” is logically equivalent to “All people are NOT ...” • We can relate sentences involving forall and exists using De Morgan’s laws: ~(x)P(x) <=> (x) ~P(x) ~(x) P(x) <=> (x) ~P(x) (x) P(x) <=> ~(x) ~P(x) (x) P(x) <=> ~ (x) ~P(x) • Example: no one likes everyone – ~ (x)(y)likes(x,y) – (x)(y)~likes(x,y) 

14 . Semantics of FOL • Domain M: the set of all objects in the world (of interest) • Interpretation I: includes – Assign each constant to an object in M – Define each function of n arguments as a mapping M^n => M – Define each predicate of n arguments as a mapping M^n => {T, F} – Therefore, every ground predicate with any instantiation will have a truth value – In general there are infinite number of interpretations because |M| is infinite • Define of logical connectives: ~, ^, v, =>, <=> as in PL • Define semantics of (x) and (x) – (x) P(x) is true iff P(x) is true under all interpretations – (x) P(x) is true iff P(x) is true under some interpretation 

15 .• Model: – an interpretation of a set of sentences such that every sentence is True • A sentence is: – satisfiable if it is true under some interpretation – valid if it is true under all possible interpretations – inconsistent if there does not exist any interpretation under which the sentence is true • logical consequence: – S |= X if all models of S are also models of X 

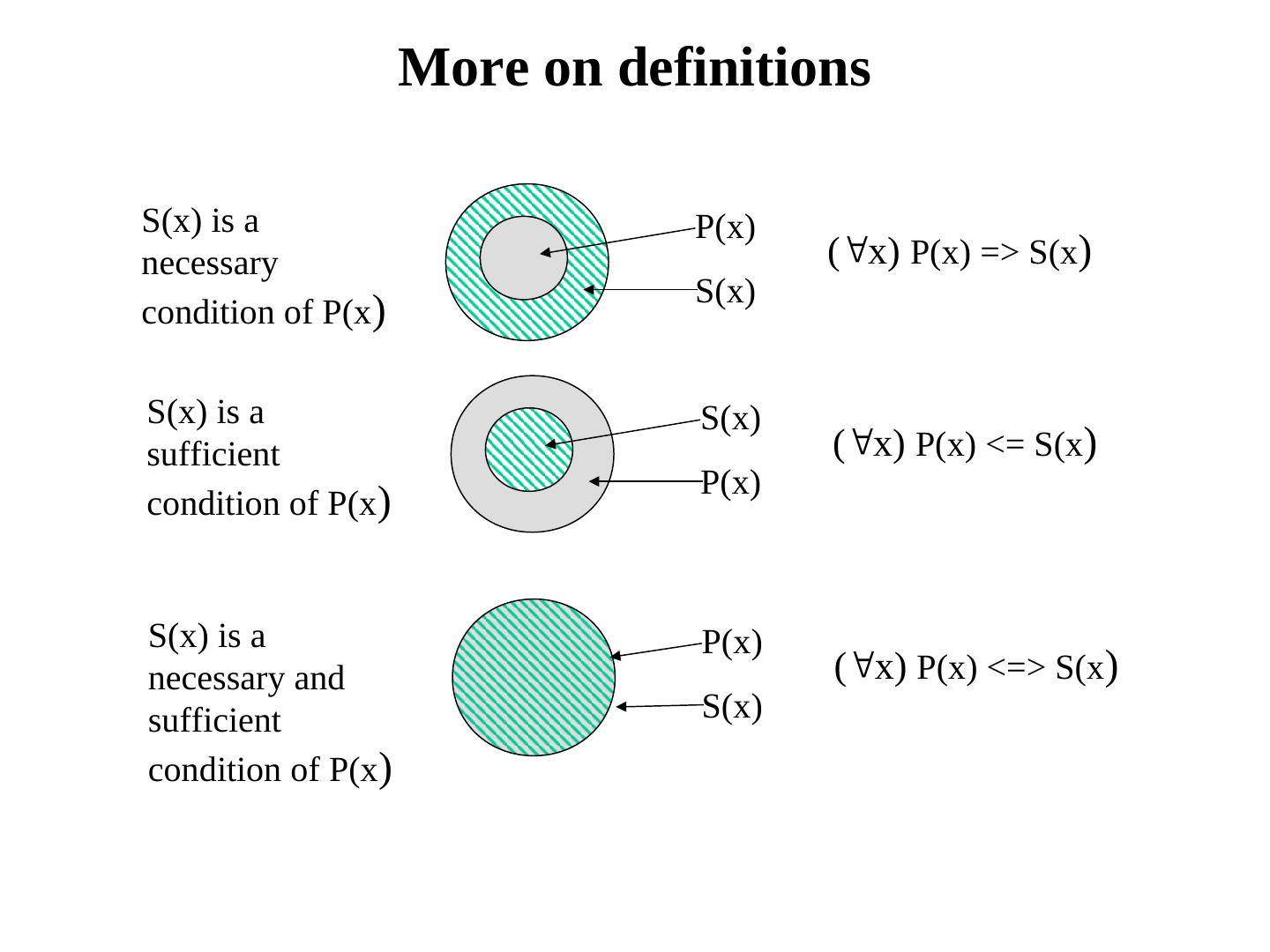
16 . Axioms, definitions and theorems •Axioms are facts and rules which are known (or assumed) to be true facts and concepts about a domain. –Mathematicians don't want any unnecessary (dependent) axioms -- ones that can be derived from other axioms. –Dependent axioms can make reasoning faster, however. –Choosing a good set of axioms for a domain is a kind of design problem. •A definition of a predicate is of the form “P(x) <=> S(x)” (define P(x) by S(x)) and can be decomposed into two parts –Necessary description: “P(x) => S(x)” (only if) –Sufficient description “P(x) <= S(x)” (if) –Some concepts don’t have complete definitions (e.g. person(x)) •A theorem S is a sentence that logically follows the axiom set A, i.e. A |= S. 

17 . More on definitions • A definition of P(x) by S(x)), denoted (x) P(x) <=> S(x), can be decomposed into two parts – Necessary description: “P(x) => S(x)” (only if, for P(x) being true, S(x) is necessarily true) – Sufficient description “P(x) <= S(x)” (if, S(x) being true is sufficient to make P(x) true) • Examples: define father(x, y) by parent(x, y) and male(x) – parent(x, y) is a necessary (but not sufficient ) description of father(x, y) father(x, y) => parent(x, y), parent(x, y) => father(x, y) – parent(x, y) ^ male(x) is a necessary and sufficient description of father(x, y) parent(x, y) ^ male(x) <=> father(x, y) – parent(x, y) ^ male(x) ^ age(x, 35) is a sufficient (but not necessary) description of father(x, y) because father(x, y) => parent(x, y) ^ male(x) ^ age(x, 35) 

18 . More on definitions S(x) is a P(x) necessary (x) P(x) => S(x) S(x) condition of P(x) S(x) is a S(x) sufficient (x) P(x) <= S(x) P(x) condition of P(x) S(x) is a P(x) necessary and (x) P(x) <=> S(x) sufficient S(x) condition of P(x) 

19 . Higher order logic (HOL) • FOL only allows to quantify over variables. • In FOL variables can only range over objects. • HOL allows us to quantify over relations • Example: (quantify over functions) “two functions are equal iff they produce the same value for all arguments” f g (f = g) <=> (x f(x) = g(x)) • Example: (quantify over predicates) r transitive( r ) => (xyz) r(x,y) ^ r(y,z) => r(x,z)) • More expressive, but undecidable. 

20 . Representing Change • Representing change in the world in logic can be tricky. • One way is to change the KB – add and delete sentences from the KB to reflect changes. – How do we remember the past, or reason about changes? • Situation calculus is another way • A situation is a snapshot of the world at some instant in time • When the agent performs an action A in situation S1, the result is a new situation S2. 

21 . Situation Calculus • A situation is a snapshot of the world at an interval of time when nothing changes • Every true or false statement is made with respect to a particular situation. – Add situation variables to every predicate. • E.g., feel(x, hungry) becomes feel(x, hungry, s0) to mean that feel(x, hungry) is true in situation (i.e., state) s0. – Or, add a special predicate holds(f,s) that means "f is true in situation s.” • e.g., holds(feel(x, hungry), s0) • Add a new special function called result(a,s) that maps current situation s into a new situation as a result of performing action a. – For example, result(eating, s) is a function that returns the successor state in which x is no longer hungry • Example: The action of eating could be represented by • (x)(s)(feel(x, hungry, s) => feel(x, not-hungry,result(eating(x),s)) 

22 . Frame problem • An action in situation calculus only changes a small portion of the current situation – after eating, x is not-hungry, but many other properties related to x (e.g., his height, his relations to others such as his parents) are not changed – Many other things unrelated to x’s feeling are not changed • Explicit copy those unchanged facts/relations from the current state to the new state after each action is inefficient (and counterintuitive) • How to represent facts/relations that remain unchanged by certain actions is known as “frame problem”, a very tough problem in AI • One way to address this problem is to add frame axioms. – (x,s1,s2)P(x, s1)^s2=result(a(s1)) =>P(x, s2))P(x, s1)^s2)P(x, s1)^s2=result(a(s1)) =>P(x, s2)=result(a(s1)) =>P(x, s2)P(x, s1)^s2=result(a(s1)) =>P(x, s2)) • We may need a huge number of frame axioms