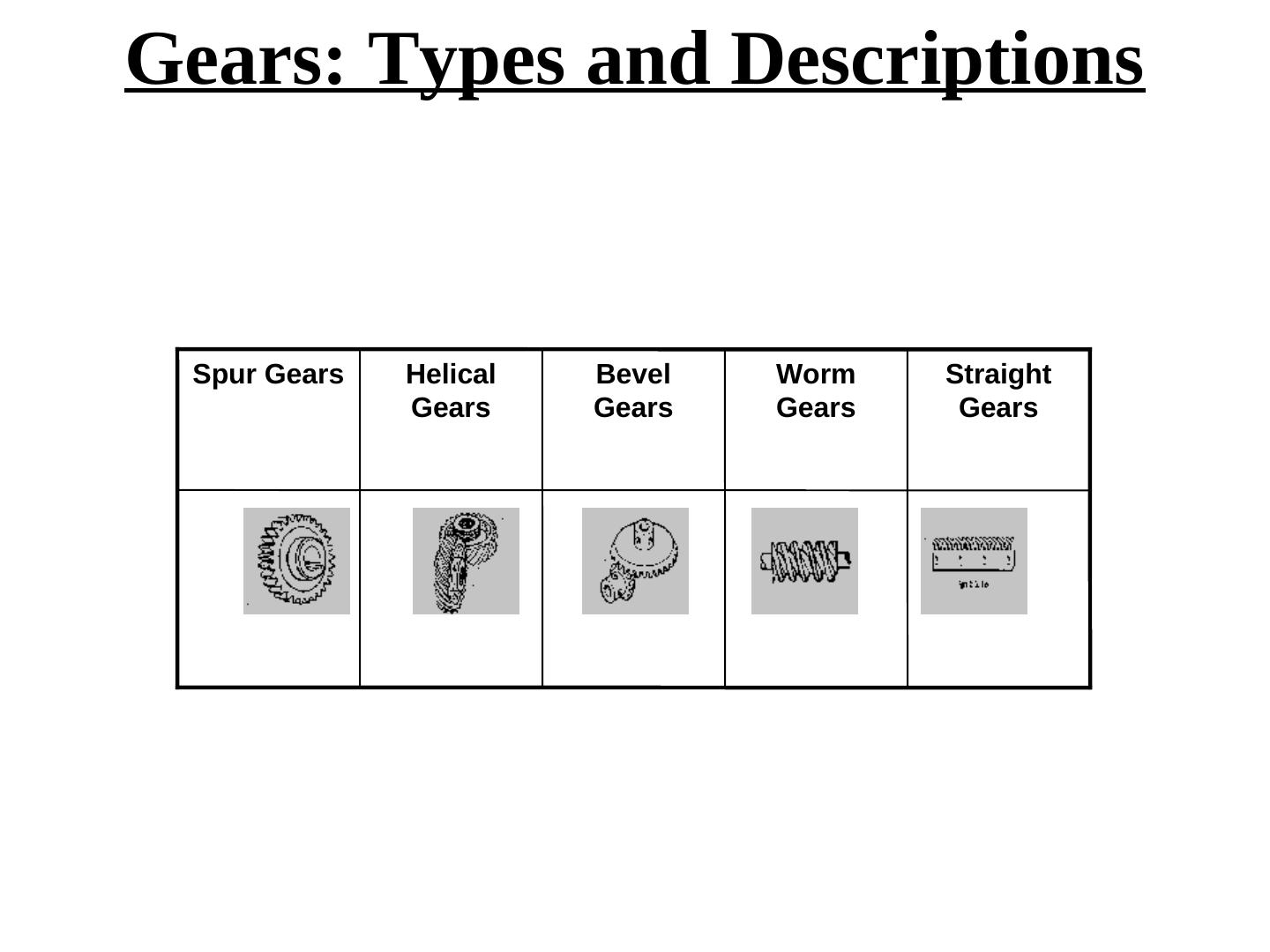
simple gears in robot design

1 .Gearing 

2 .Very Simple Chain Theory 16 32 Let us start with a very simple example 

3 .Building a Robot Chain Theory 16 32 

4 .Building a Robot Chain Theory 16 32 

5 .Building a Robot Chain Theory 16 32 

6 .Building a Robot Chain Theory 16 32 

7 .Building a Robot Chain Theory 16 32 

8 .Building a Robot Chain Theory 16 32 

9 .Building a Robot Chain Theory 16 32 

10 .Building a Robot Chain Theory 16 32 

11 .Building a Robot Chain Theory 16 32 

12 .Building a Robot Chain Theory 16 32 

13 .Building a Robot Chain Theory 16 32 

14 .Building a Robot Chain Theory 16 32 

15 .Building a Robot Chain Theory 16 32 

16 .Building a Robot Chain Theory 16 32 

17 .Building a Robot Chain Theory 16 32 

18 .Building a Robot Chain Theory 16 32 

19 .Building a Robot Chain Theory 16 32 

20 . The Effect on Speed 1. When gears are combined, there is also an effect on the output speed. 2. To measure speed we are interested in the circumference of the gear, C= 2  r. 3. If the circumference of Gear1 is twice that of Gear2, then Gear2 must turn twice for each full rotation of Gear1. 4. => Gear2 must turn twice as fast to keep up with Gear1. 

21 . Gearing Law for Speed • If the output gear is larger than the input gear, the speed decreases. • If the output gear is smaller than the input gear, the speed increases. • => Gearing up decreases speed • => Gearing down increases speed 

22 .Gearing Laws rpmoutput rpminput * ? torqueoutput torqueinput * ? 

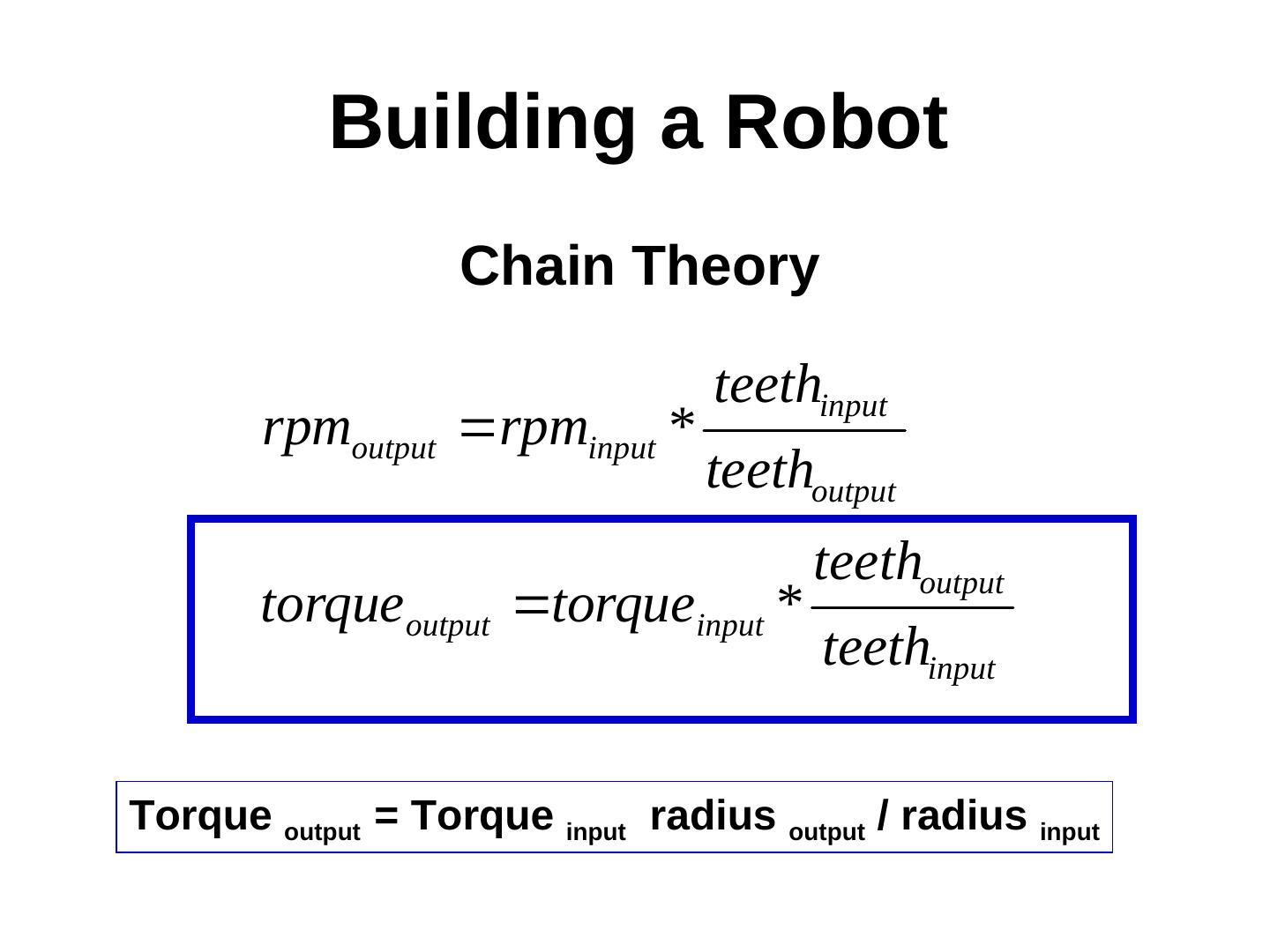
23 .Gearing Law for Speed teethinput rpmoutput rpminput * teethoutput torqueoutput torqueinput * ? • These are all important when you are building a robot 

24 . Gearing in robots 1. Gears are used to alter the output torque of a motor. force F=T/ r 2. The force generated at the edge of a gear is equal to the ratio the torque and the radius r of the gear (T = F r), in the line tangential to its circumference. T=Fr 3. This is the underlying law behind gearing mechanisms. 

25 . Building a Robot Chain Theory teethinput rpmoutput rpminput * teethoutput teethoutput torqueoutput torqueinput * teethinput Torque output = Torque input radius output / radius input 

26 . Gear Radii and Force/Torque 1. By combining gears with different radii, we can manipulate the amount of force/torque the mechanism generates. 2. The relationship between the radii and the resulting torque is well defined 3. The torque generated at the output gear is proportional to the torque on the input gear and the ratio of the two gear's radii. 

27 . Example of Gearing 1. Suppose Gear1 with radius r1 turns with torque t1, generating a force of torque t1 t1/r1 perpendicular to its r1 circumference. force of t1/r1 2. If we mesh it with Gear2, with r2, which generates t2/r2, then t1/r1 = t2/r2 r2 1. To get the torque generated by Gear2, we get: t2 = t1 r2/r1 2. If r2 > r1, we get a bigger torque, 3. if r1 > r2, we get a smaller torque. Forces are equal 

28 . Gearing Law for Torque 1. If the output gear is larger than the input gear, the torque increases. 2. If the output gear is smaller than the input gear, the torque decreases. 3. => Gearing up increases torque 4. => Gearing down decreases torque 

29 . Exchanging Speed for Torque • When a small gear drives a large one, torque is increased and speed is decreased. Analogously, when a large gear drives a small one, torque is decreased and speed is increased. • Gears are used in DC motors (which are fast and have low torque) to trade off extra speed for additional torque. • How?