Mobile robots - minimal Kinematics

1 .Kinematics of Mobile Robots 

2 . Forward Kinematics of Differential drive 

3 .Where can we find differential drives? 1. Braitenberg Vehicles 2. Micromouse 3. Most of our robots 4. Unicycle 5. Segway 6. Many many others 

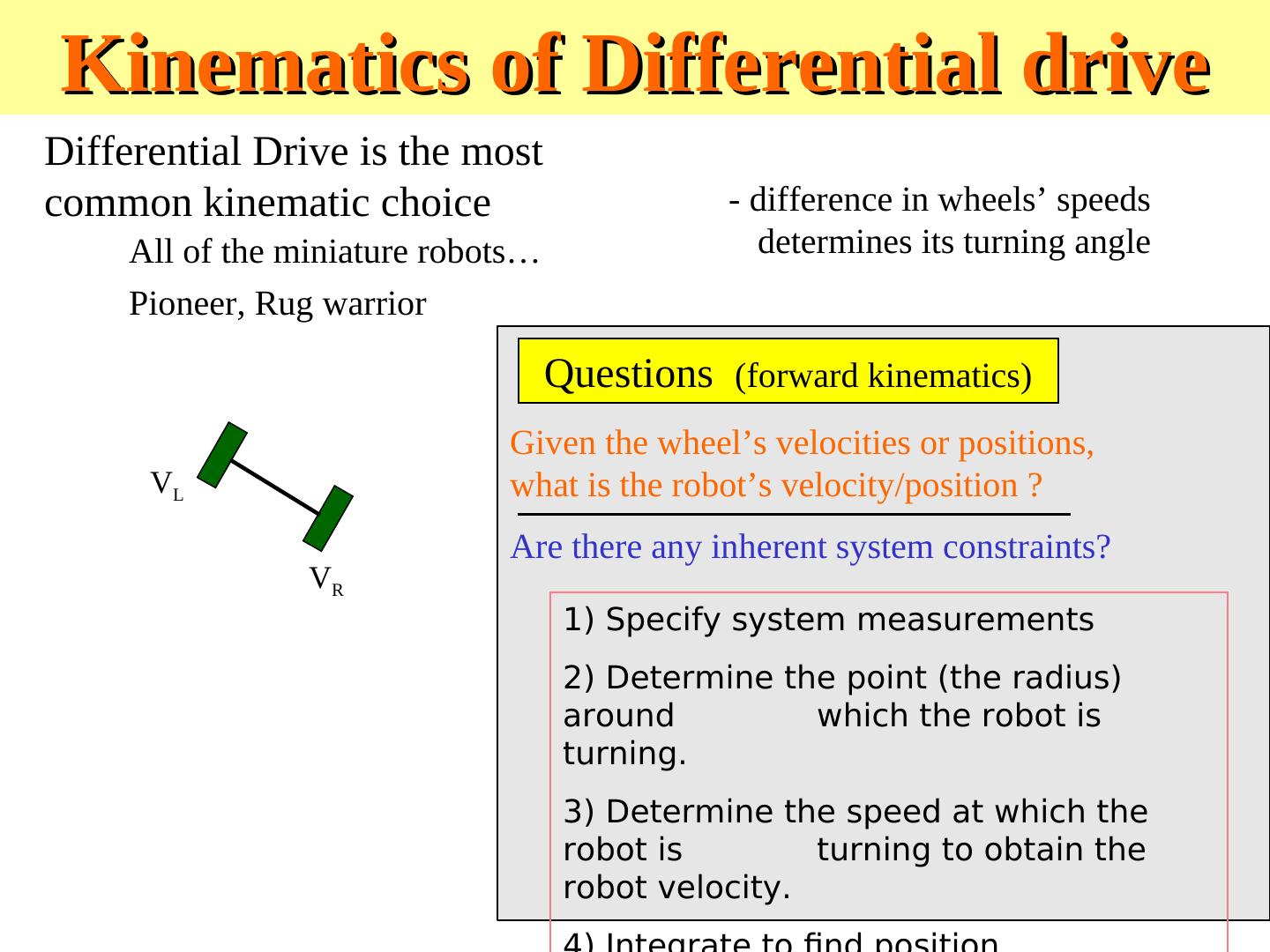
4 .Kinematics of Differential drive Differential Drive is the most common kinematic choice - difference in wheels’ speeds All of the miniature robots… determines its turning angle Pioneer, Rug warrior Questions (forward kinematics) Given the wheel’s velocities or positions, VL what is the robot’s velocity/position ? Are there any inherent system constraints? VR 1) Specify system measurements 2) Determine the point (the radius) around which the robot is turning. 3) Determine the speed at which the robot is turning to obtain the robot velocity. 

5 .Kinematics of Differential drive 1) Specify system measurements y - consider possible coordinate systems VL x  2d VR (assume a wheel radius of 1) 

6 .Kinematics of Differential drive – radius of turning 1) Specify system measurements y - consider possible coordinate systems 2) Determine the point (the radius) around which the robot is turning. VL x  2d VR ICC “instantaneous center of curvature” (assume a wheel radius of 1) 

7 .Kinematics of Differential drive – angular velocity 1) Specify system measurements y - consider possible coordinate systems 2) Determine the point (the radius) around which the robot is turning. - to minimize wheel slippage, this point (the ICC) must lie at the intersection of the wheels’ axles VL x - each wheel must be traveling at  the same angular velocity 2d VR ICC “instantaneous center of curvature” (assume a wheel radius of 1)  = angular velocity 

8 .Kinematics of Differential drive 1) Specify system measurements y - consider possible coordinate systems 2) Determine the point (the radius)  around which the robot is turning. - to minimize wheel slippage, this point (the ICC) must lie at the intersection of the wheels’ axles VL x - each wheel must be traveling at  the same angular velocity around 2d VR the ICC ICC “instantaneous center of curvature” (assume a wheel radius of 1) 

9 .Kinematics of Differential drive 1) Specify system measurements y - consider possible coordinate systems 2) Determine the point (the radius)  around which the robot is turning. - each wheel must be traveling at the same angular velocity around the ICC VL 3) Determine the robot’s speed x around the ICC and its linear velocity 2d VR ICC R+d) = VL R robot’s turning radius R-d) = VR (assume a wheel radius of 1) 

10 .Kinematics of Differential drive 1) Specify system measurements y - consider possible coordinate systems 2) Determine the point (the radius)  around which the robot is turning. - each wheel must be traveling at the same angular velocity around the ICC VL 3) Determine the robot’s speed x around the ICC and then linear 2d velocity VR ICC “instantaneous center of curvature” ICC R+d) = VL R robot’s turning radius R-d) = VR Thus,  = ( VR - VL ) / 2d R = 2d ( VR + VL ) / ( VR - VL ) (assume a wheel radius of 1) 

11 .Kinematics of Differential drive – robot’s velocity 1) Specify system measurements y - consider possible coordinate systems 2) Determine the point (the radius)  around which the robot is turning. - each wheel must be traveling at the same angular velocity around the ICC VL 3) Determine the robot’s speed x around the ICC and then linear 2d velocity VR ICC R+d) = VL R robot’s turning radius R-d) = VR Thus,  = ( VR - VL ) / 2d R = 2d ( VR + VL ) / ( VR - VL ) So, the robot’s velocity is V = R = ( VR + VL ) / 2 

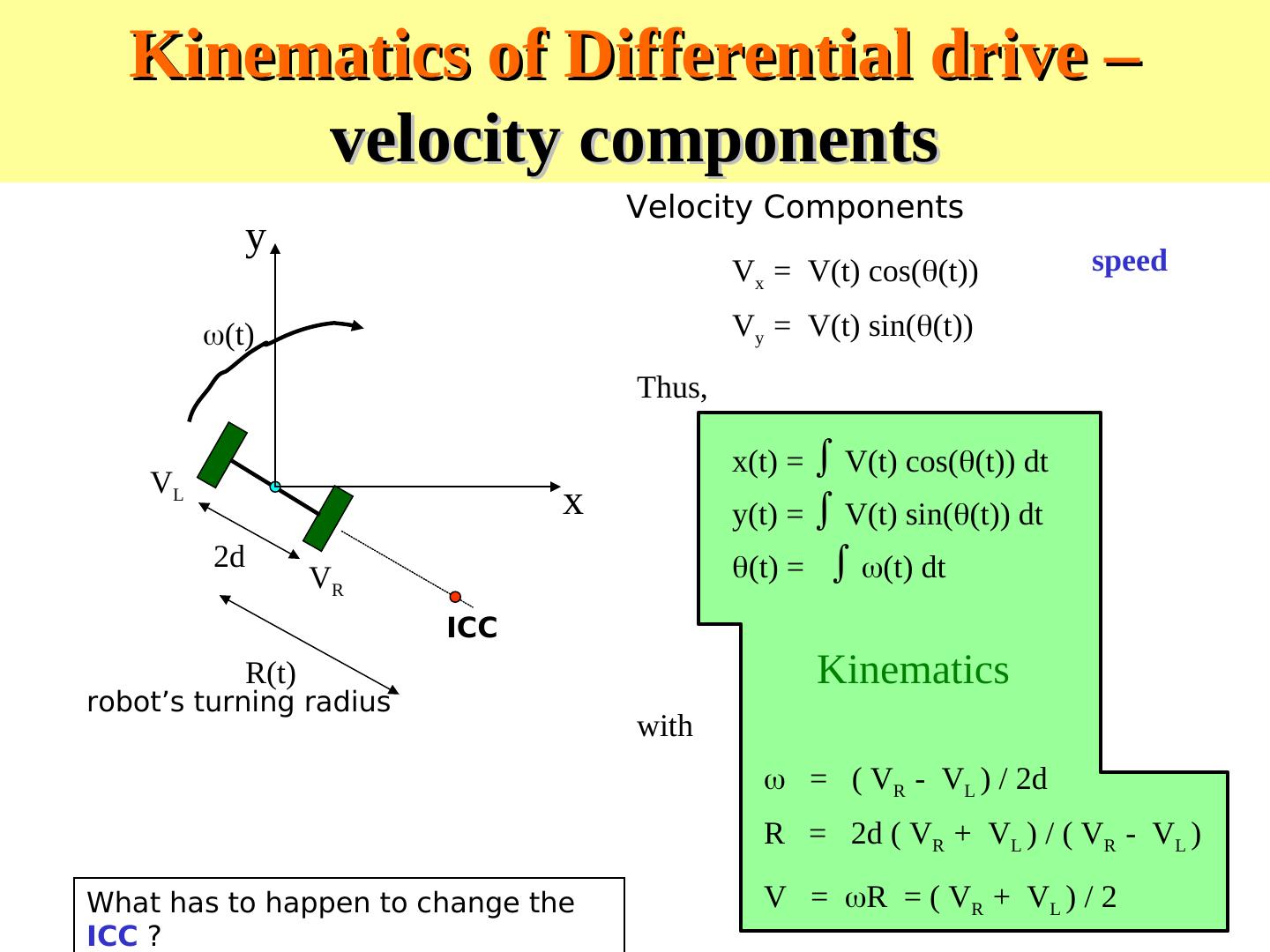
12 . Kinematics of Differential drive – integrate to obtain position 4) Integrate to obtain position y Vx = V(t) cos((t)) (t) Vy = V(t) sin((t)) V(t) (t) VL Vx x 2d VR ICC “instantaneous center of curvature” ICC R(t) robot’s turning radius with  = ( VR - VL ) / 2d R = 2d ( VR + VL ) / ( VR - VL ) What has to happen to change the V = R = ( VR + VL ) / 2 ICC ? 

13 .Kinematics of Differential drive 4) Integrate to obtain position y Vx = V(t) cos((t)) (t) Vy = V(t) sin((t)) Thus, x(t) = ∫ V(t) cos((t)) dt VL x y(t) = ∫ V(t) sin((t)) dt 2d (t) = ∫ (t) dt VR ICC R(t) robot’s turning radius with  = ( VR - VL ) / 2d R = 2d ( VR + VL ) / ( VR - VL ) V = R = ( VR + VL ) / 2 

14 . Kinematics of Differential drive – velocity components Velocity Components y Vx = V(t) cos((t)) speed (t) Vy = V(t) sin((t)) Thus, x(t) =  V(t) cos((t)) dt VL x y(t) =  V(t) sin((t)) dt 2d (t) =  (t) dt VR ICC R(t) Kinematics robot’s turning radius with  = ( VR - VL ) / 2d R = 2d ( VR + VL ) / ( VR - VL ) What has to happen to change the V = R = ( VR + VL ) / 2 ICC ? 

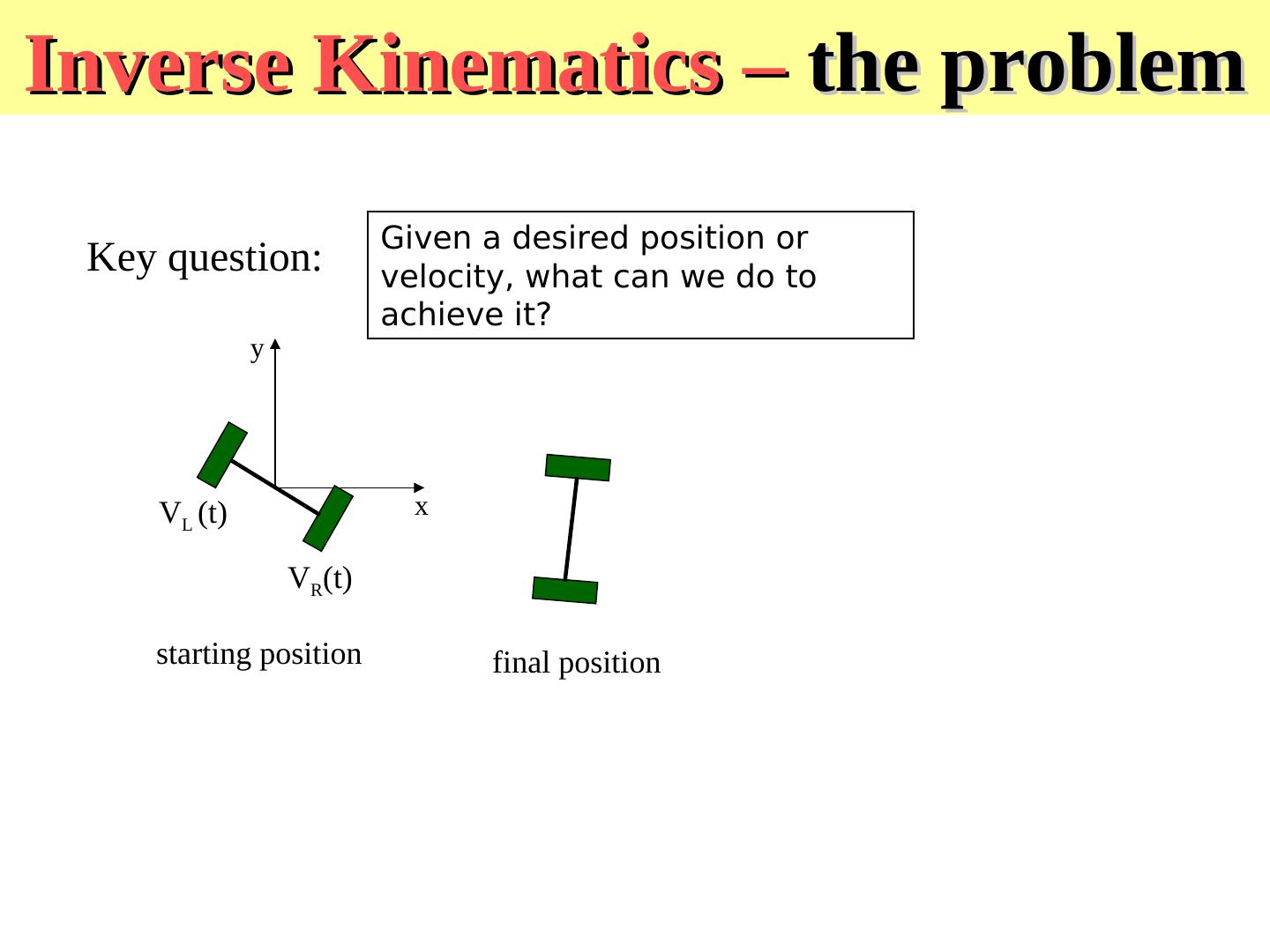
15 . Inverse Kinematics of Differential Drive 

16 .Inverse Kinematics – the problem Given a desired position or Key question: velocity, what can we do to achieve it? y VL (t) x VR(t) starting position final position 

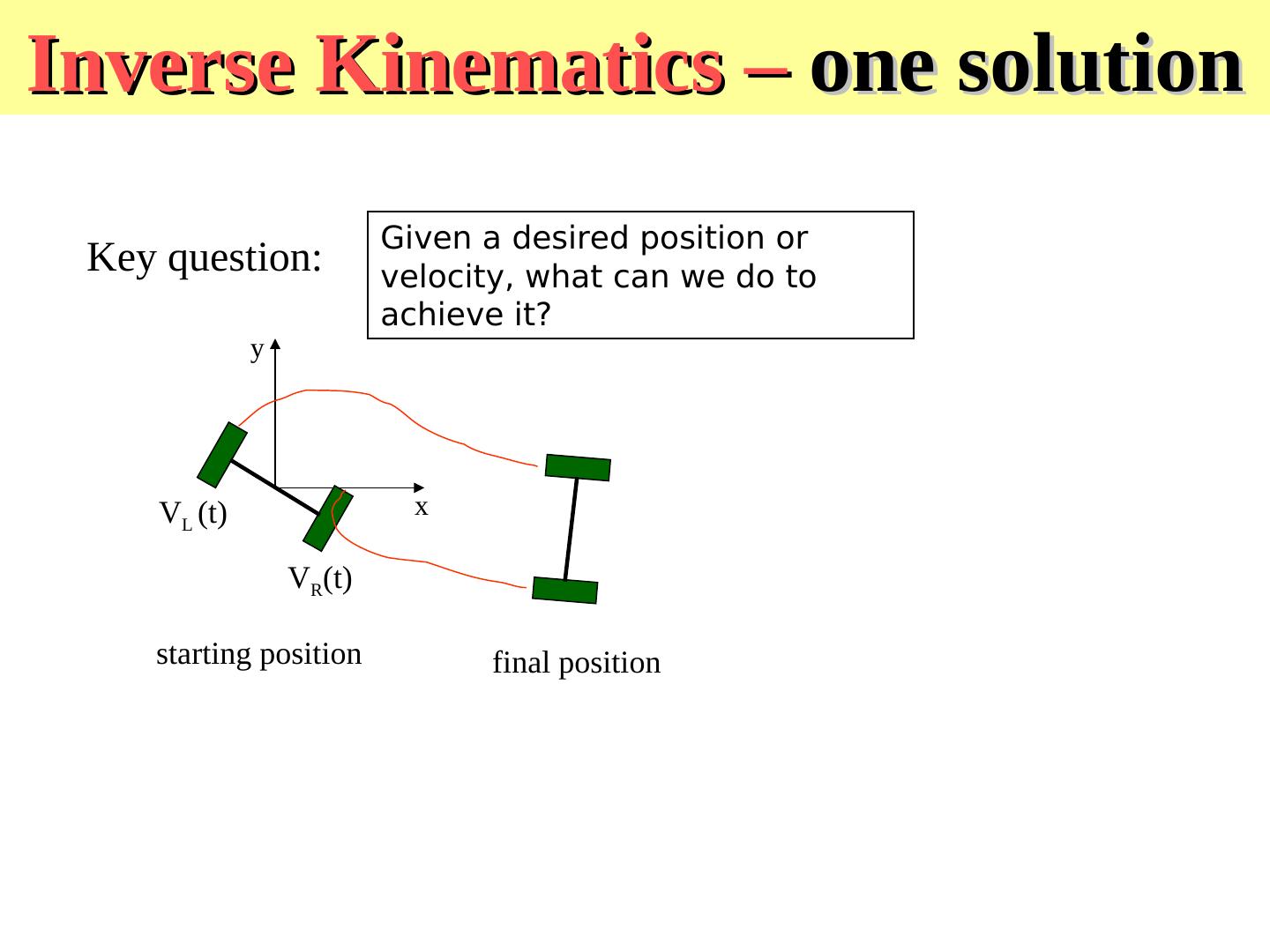
17 .Inverse Kinematics – one solution Given a desired position or Key question: velocity, what can we do to achieve it? y VL (t) x VR(t) starting position final position 

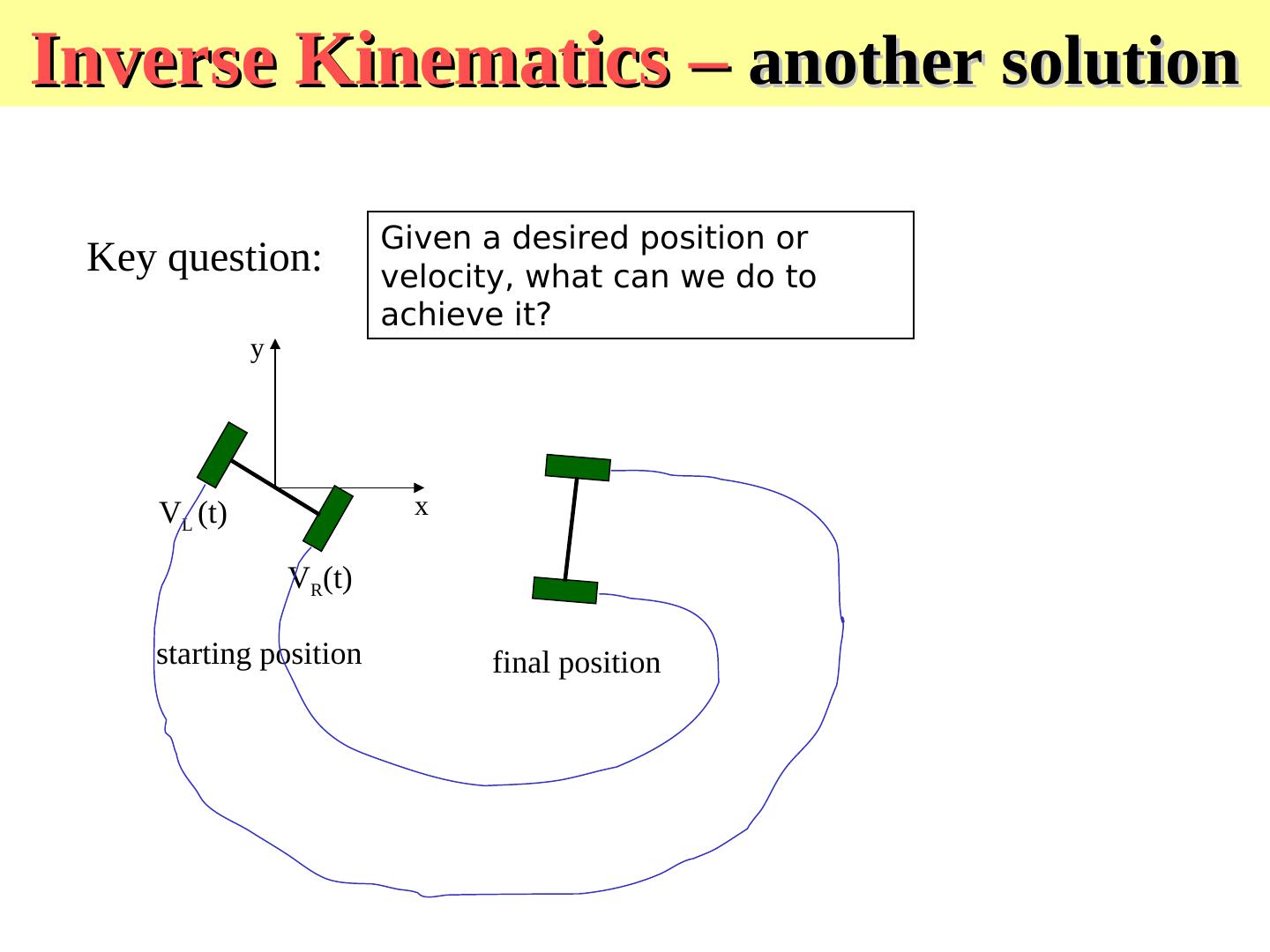
18 .Inverse Kinematics – another solution Given a desired position or Key question: velocity, what can we do to achieve it? y VL (t) x VR(t) starting position final position 

19 .Inverse Kinematics – many numerical solutions to equations Given a desired position or Key question: velocity, what can we do to achieve it? y Need to solve these equations: x =  V(t) cos((t)) dt y =  V(t) sin((t)) dt VL (t) x  =  (t) dt VR(t)  = ( VR - VL ) / 2d V = R = ( VR + VL ) / 2 starting position final position for VL (t) and VR(t) . There are lots of solutions... 

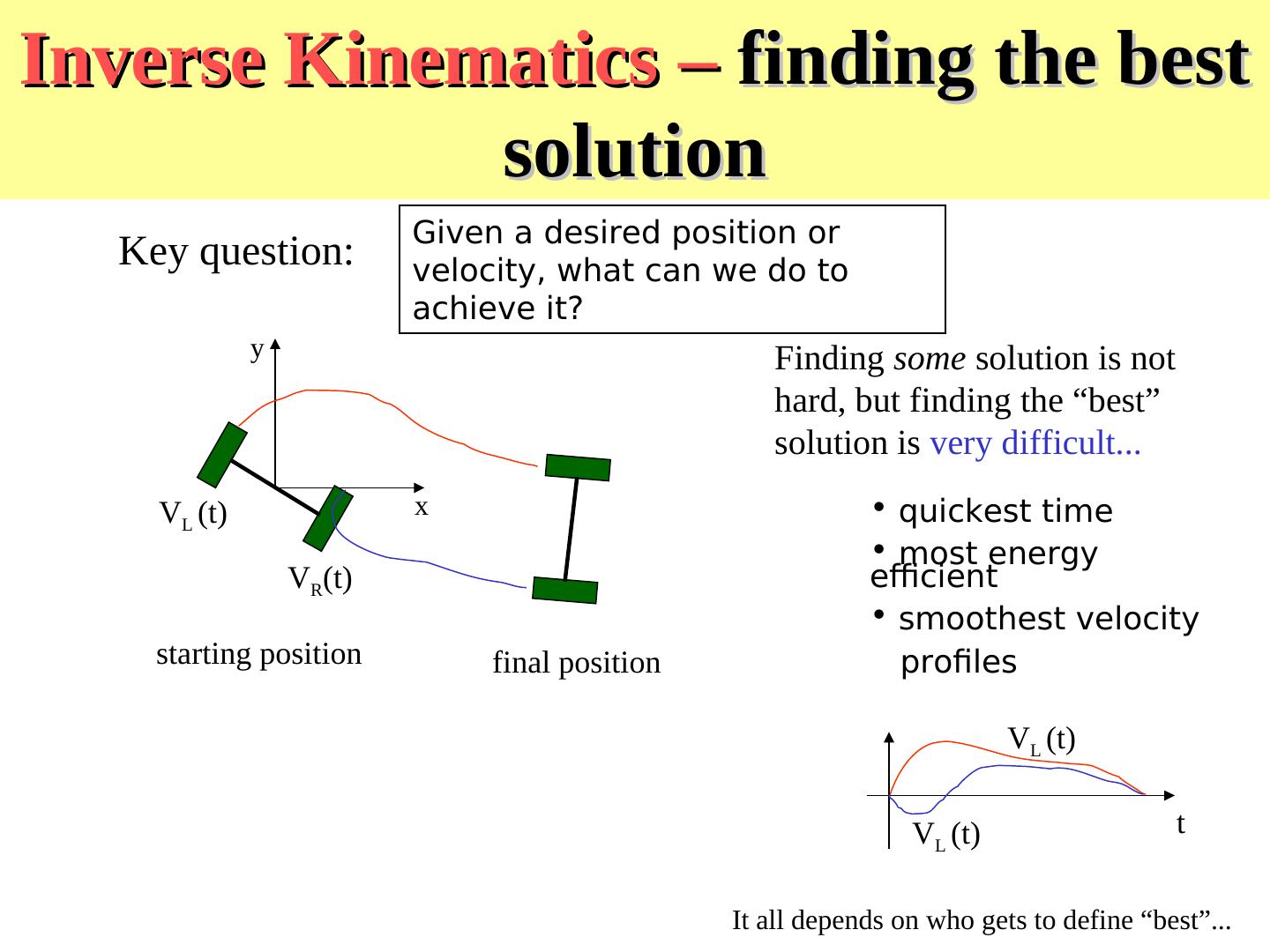
20 .Inverse Kinematics – finding the best solution Given a desired position or Key question: velocity, what can we do to achieve it? y Finding some solution is not hard, but finding the “best” solution is very difficult... VL (t) x • quickest time • most energy VR(t) efficient • smoothest velocity starting position final position profiles VL (t) VL (t) t It all depends on who gets to define “best”... 

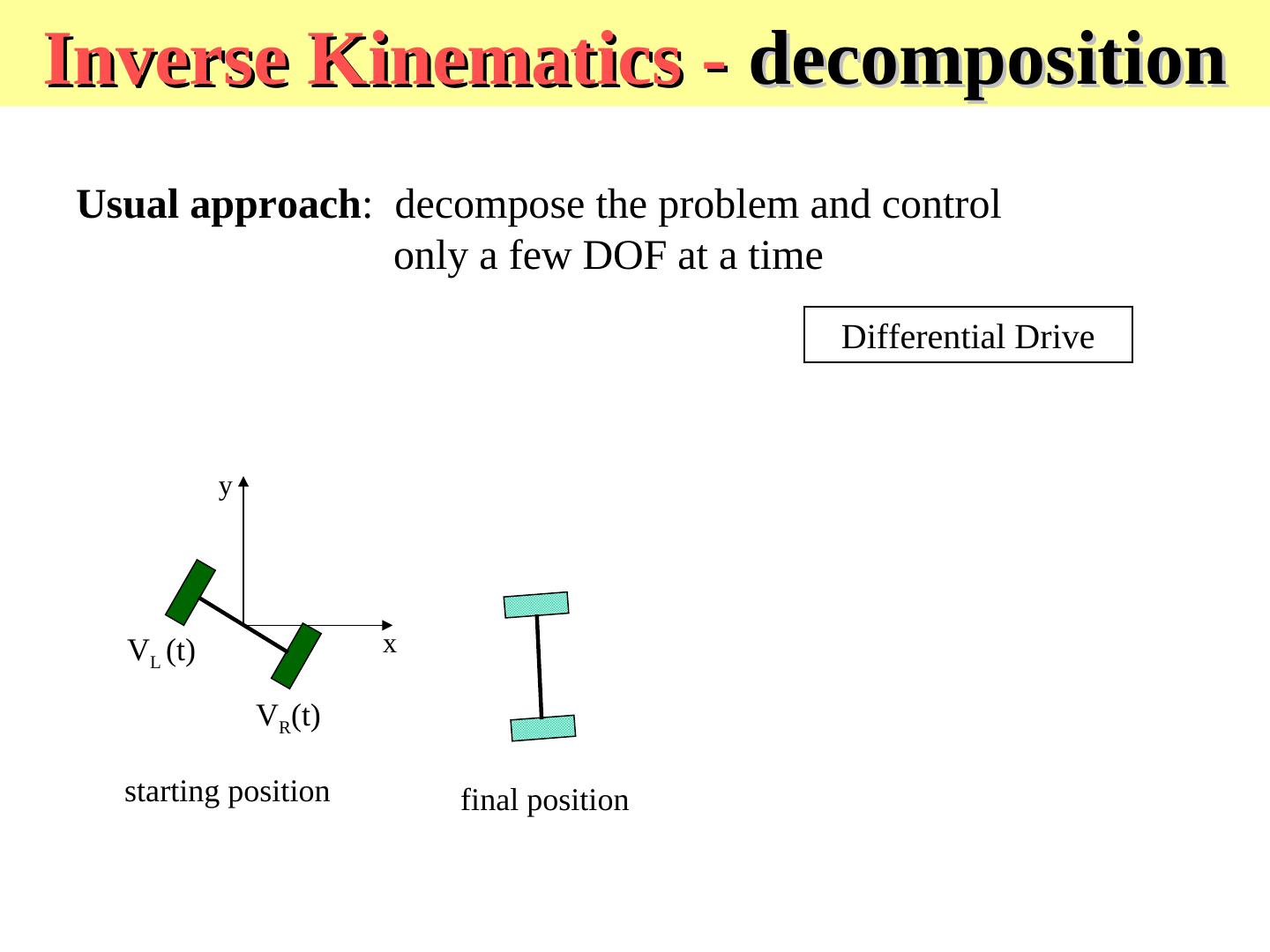
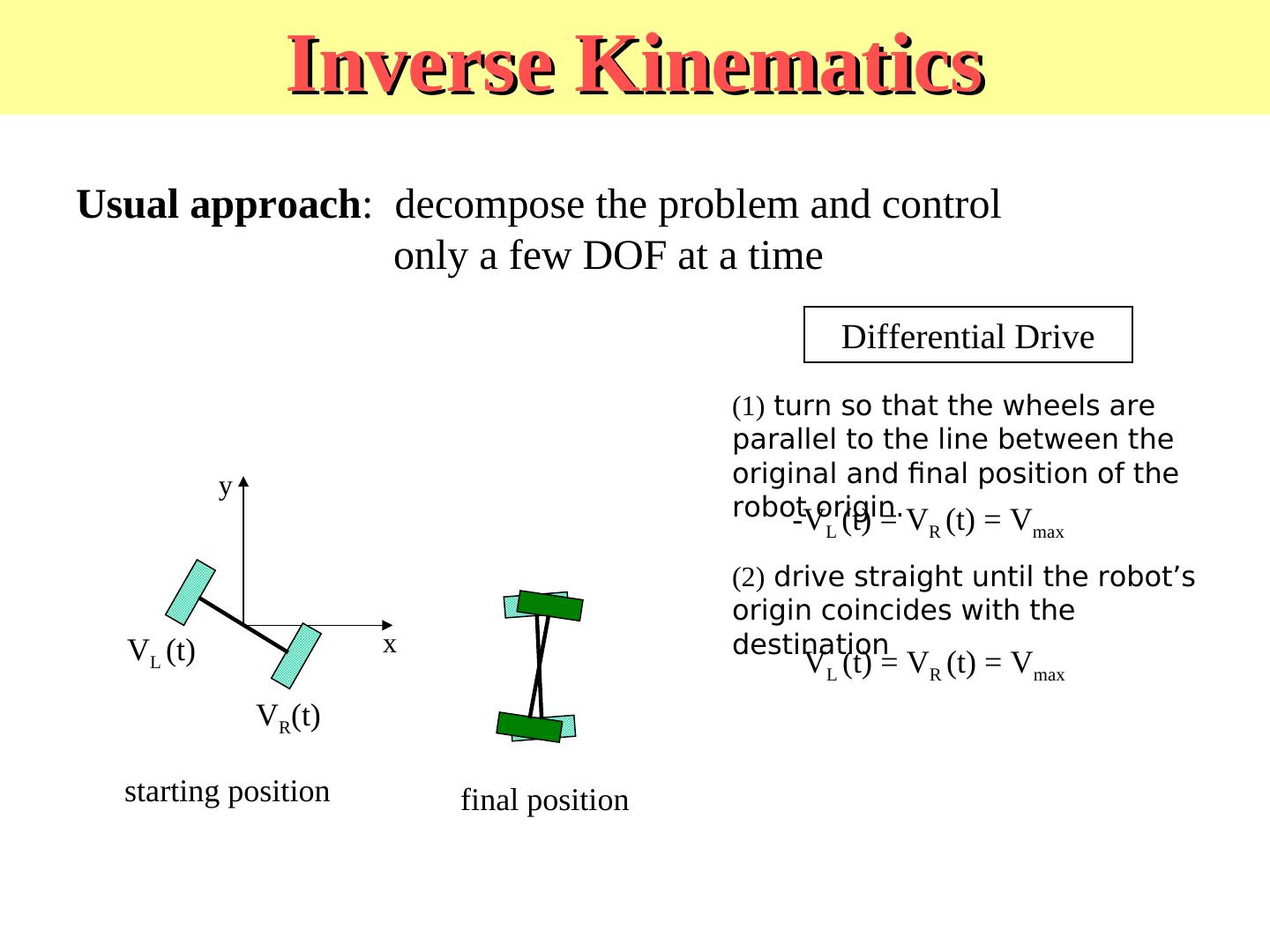
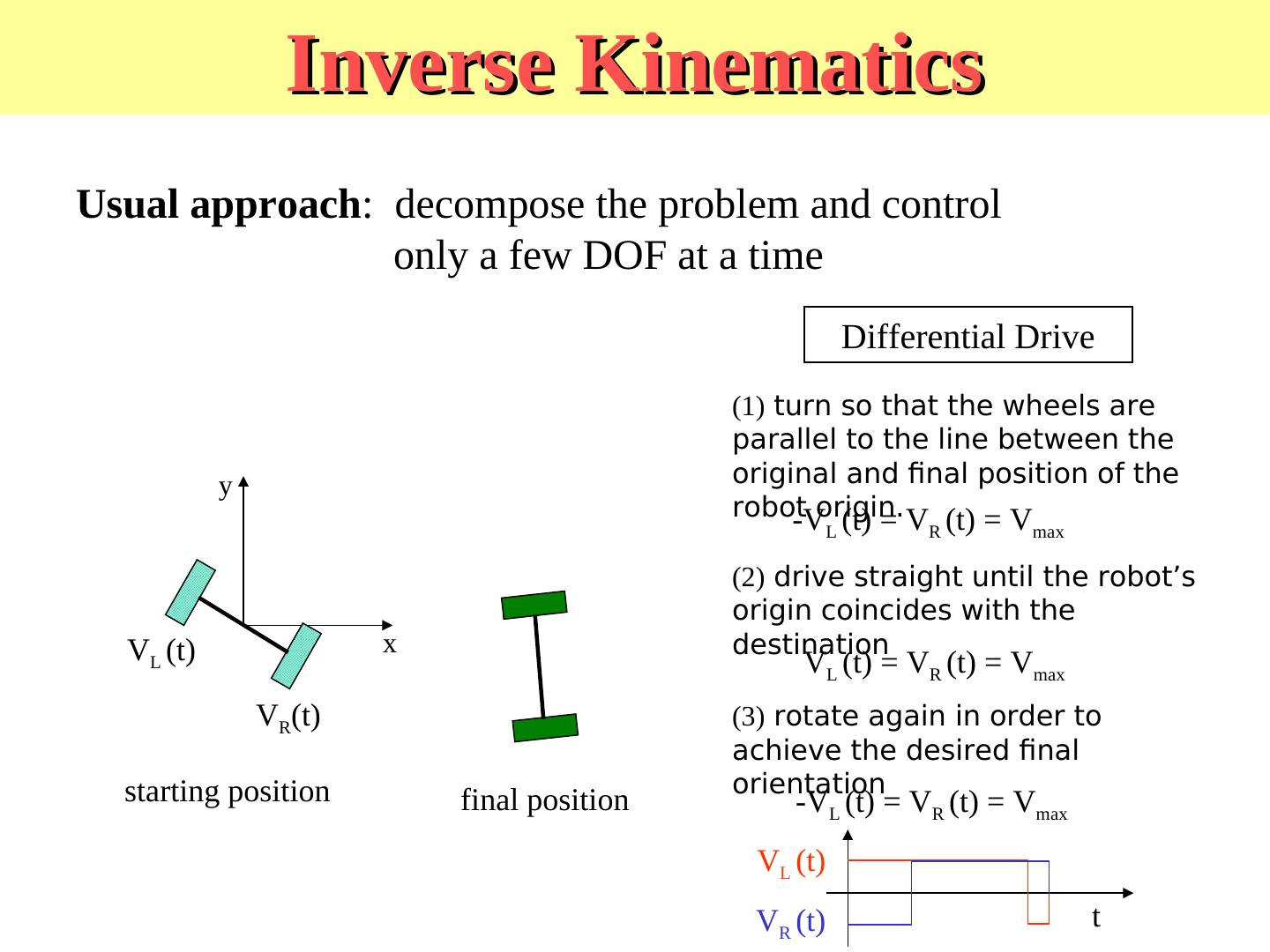
21 .Inverse Kinematics - decomposition Usual approach: decompose the problem and control only a few DOF at a time Differential Drive y VL (t) x VR(t) starting position final position 

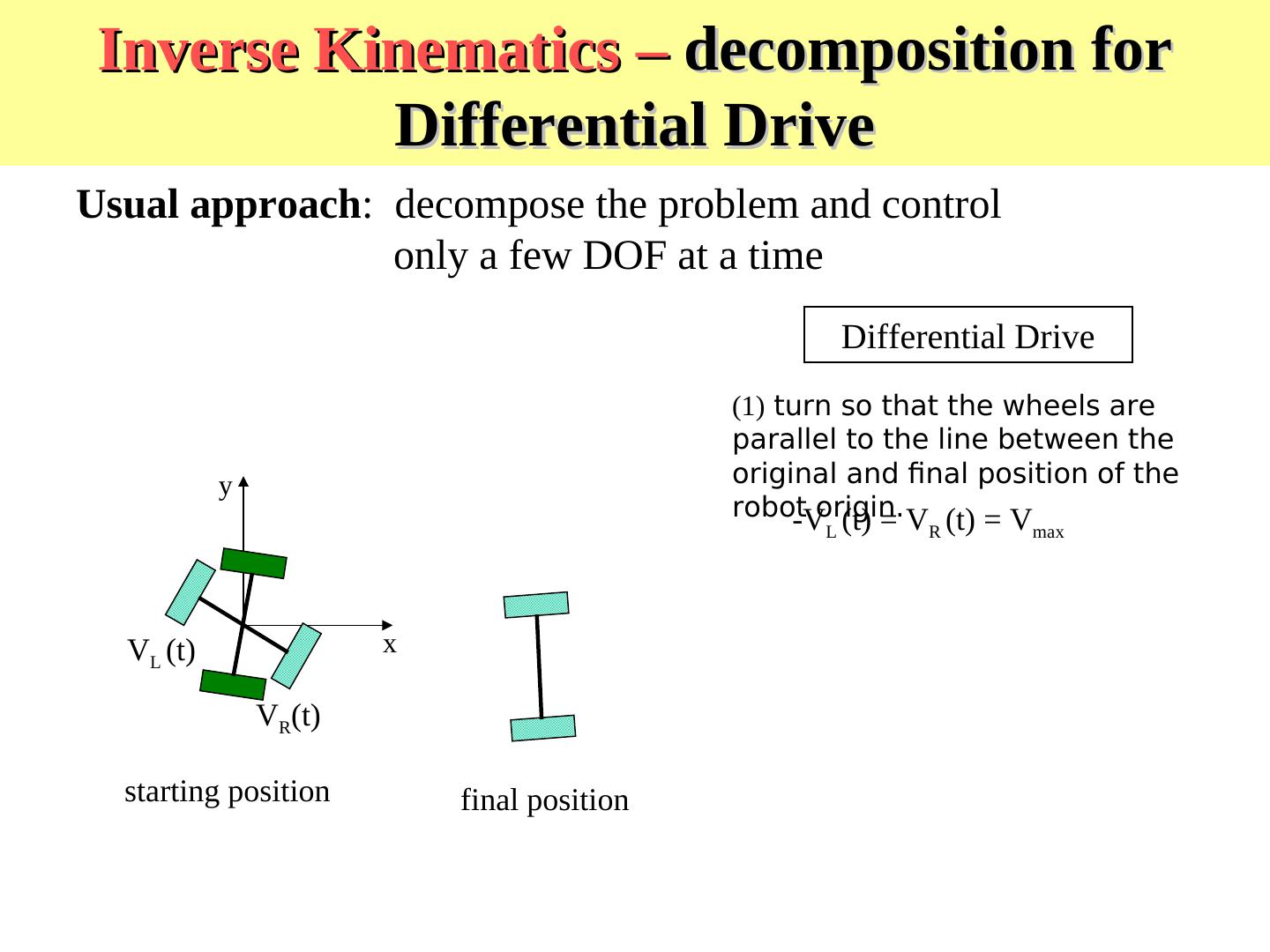
22 . Inverse Kinematics – decomposition for Differential Drive Usual approach: decompose the problem and control only a few DOF at a time Differential Drive (1) turn so that the wheels are parallel to the line between the y original and final position of the robot-Vorigin. (t) = V (t) = V L R max VL (t) x VR(t) starting position final position 

23 . Inverse Kinematics Usual approach: decompose the problem and control only a few DOF at a time Differential Drive (1) turn so that the wheels are parallel to the line between the y original and final position of the robot-Vorigin. (t) = V (t) = V L R max (2) drive straight until the robot’s origin coincides with the VL (t) x destination VL (t) = VR (t) = Vmax VR(t) starting position final position 

24 . Inverse Kinematics Usual approach: decompose the problem and control only a few DOF at a time Differential Drive (1) turn so that the wheels are parallel to the line between the y original and final position of the robot-Vorigin. (t) = V (t) = V L R max (2) drive straight until the robot’s origin coincides with the VL (t) x destination VL (t) = VR (t) = Vmax VR(t) (3) rotate again in order to achieve the desired final starting position orientation final position -VL (t) = VR (t) = Vmax VL (t) VR (t) t 

25 . Problem Represent the forward and inverse kinematics for this robot using notation from the previous lecture. 

26 . Sources • Prof. Maja Mataric • Dr. Fred Martin • Bryce Tucker and former PSU students • A. Ferworn, • Prof. Gaurav Sukhatme, USC Robotics Research Laboratory • Paul Hannah • Reuven Granot, Technion • Dodds, Harvey Mudd College