35_Servos and Control- applications

1 . Robot Motion • Forward and Inverse Kinematics – Next quarter • PID Control • Frame-Based Motions on the AIBO • Modeling Effects of Motions 

2 . Automatic Control Systems, Servos, Automatic Tracking, Feedback Control 

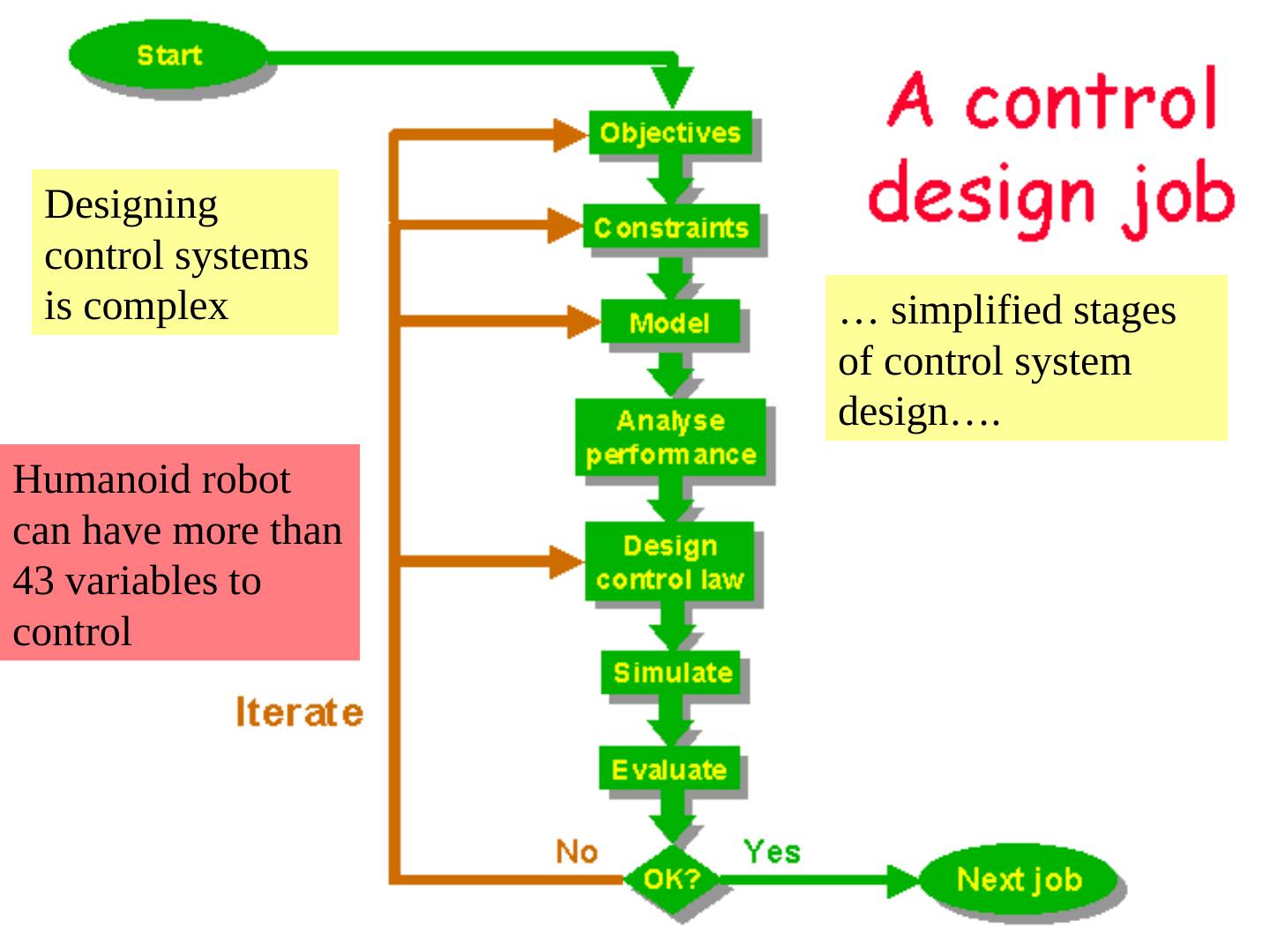
3 .VOCABULARY: Automatic Control Systems  Automatic: able to activate, move or regulate itself.  Control: command, direct, rule, check, limit, restrain, regulate or operate.  System: a group or combination of interrelated, independent, or interacting elements forming a collective entity. • Control engineering is concerned with modifying the behavior of dynamical systems to achieve desired goals. 

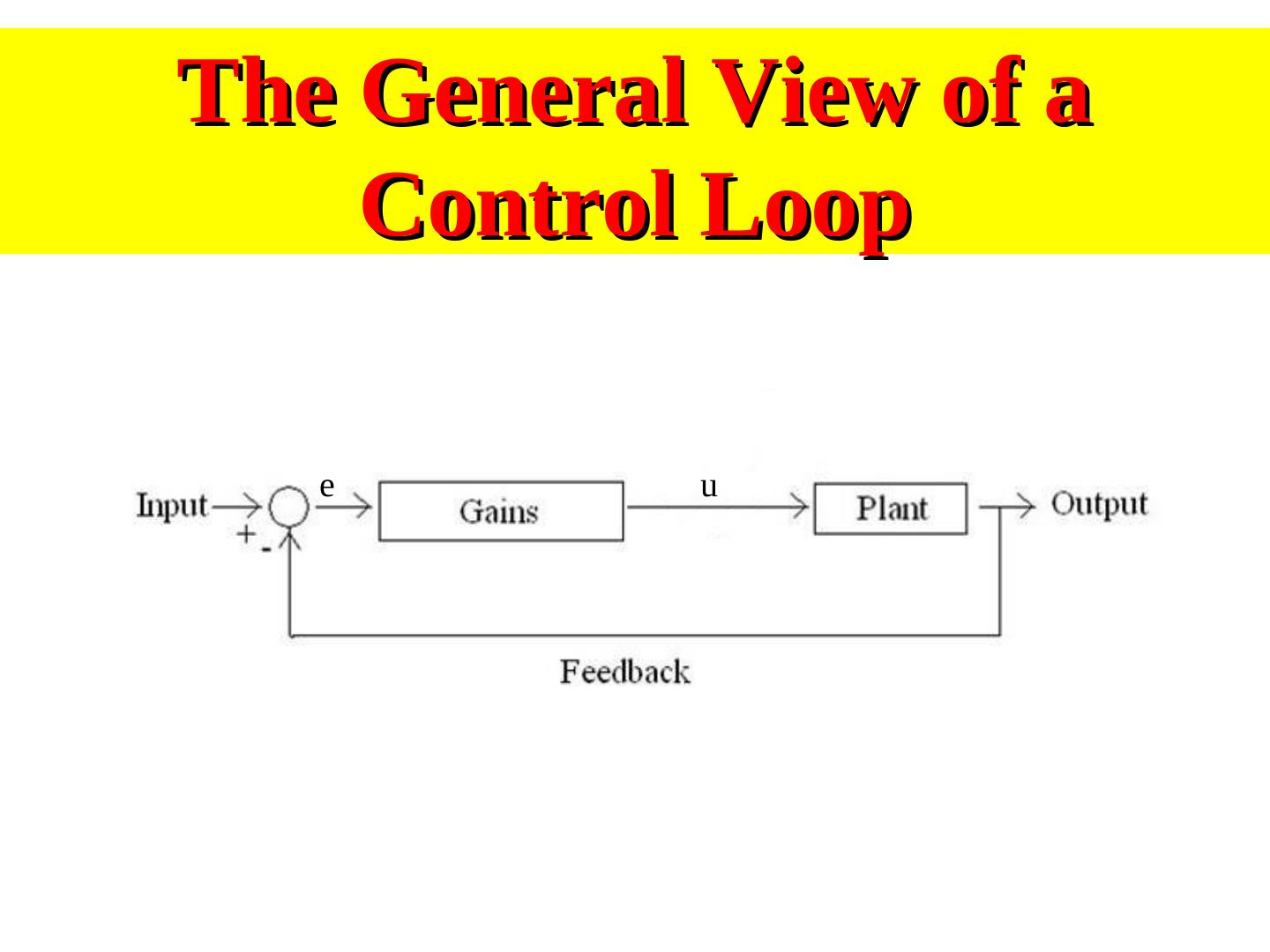
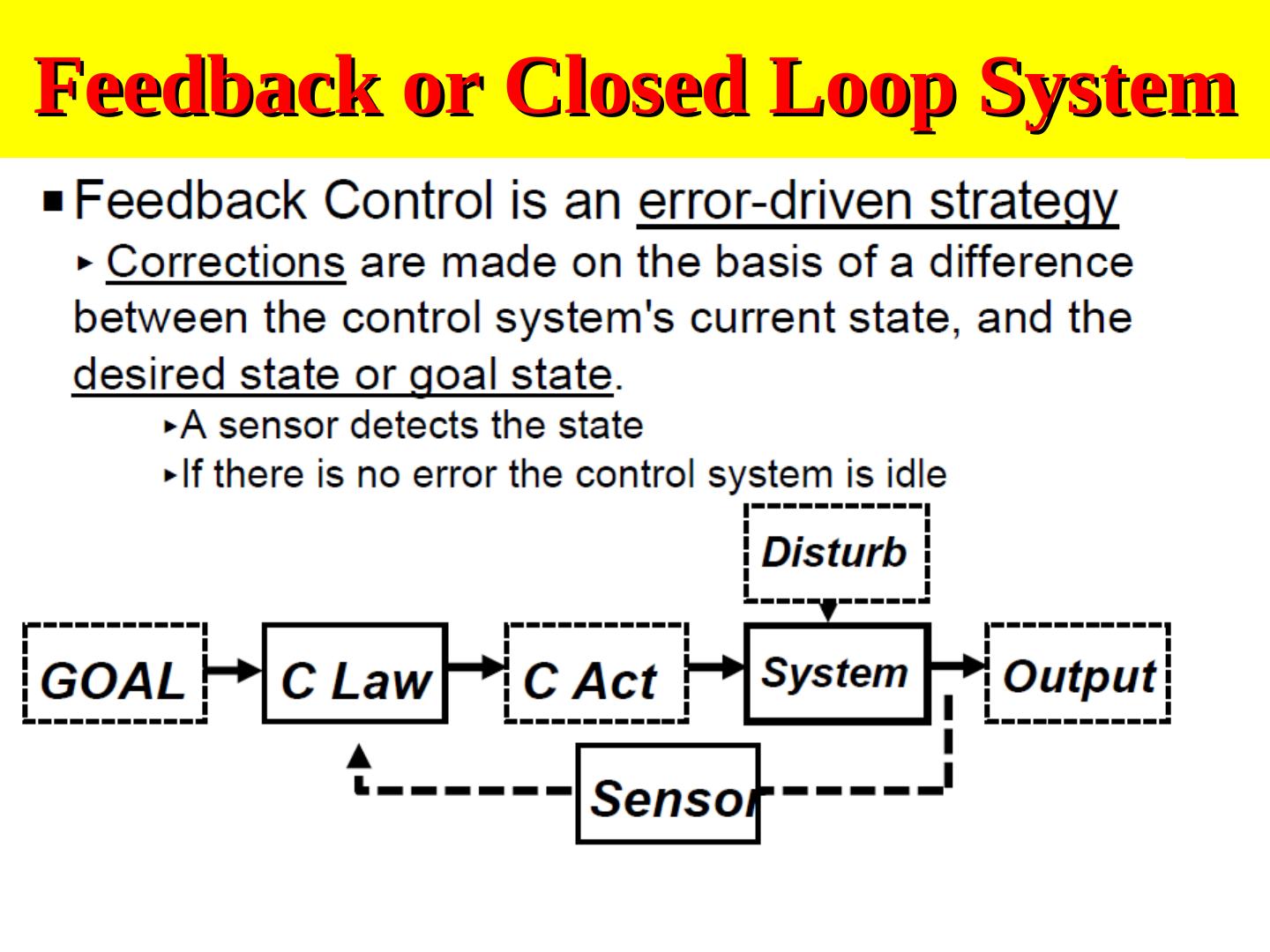
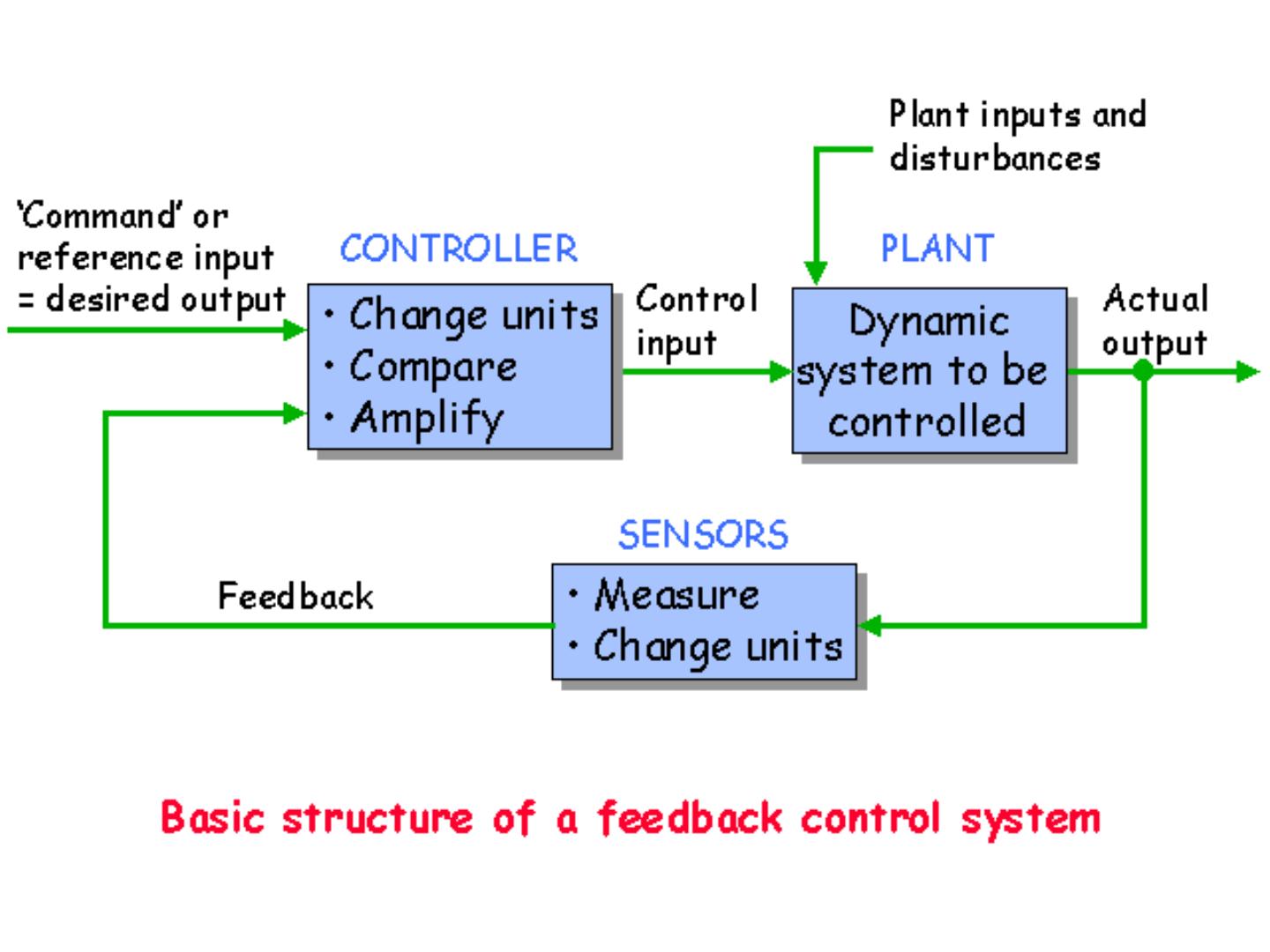
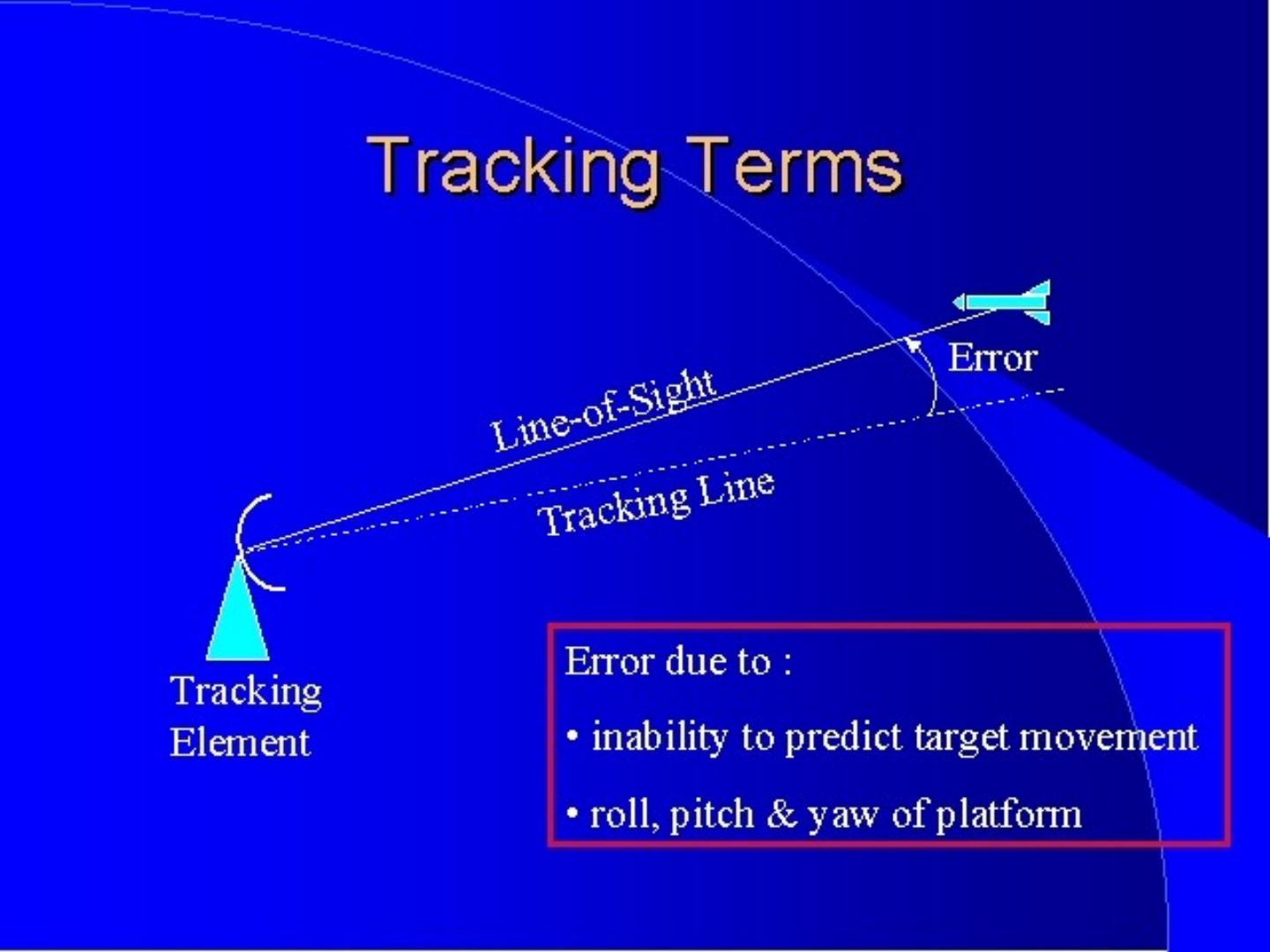
4 . Control System Terminology • Input - Excitation applied to a control system from an external source. • Output - The response obtained from a system • Feedback - The output of a system that is returned to modify the input. • Error - The difference between the input and the output. 

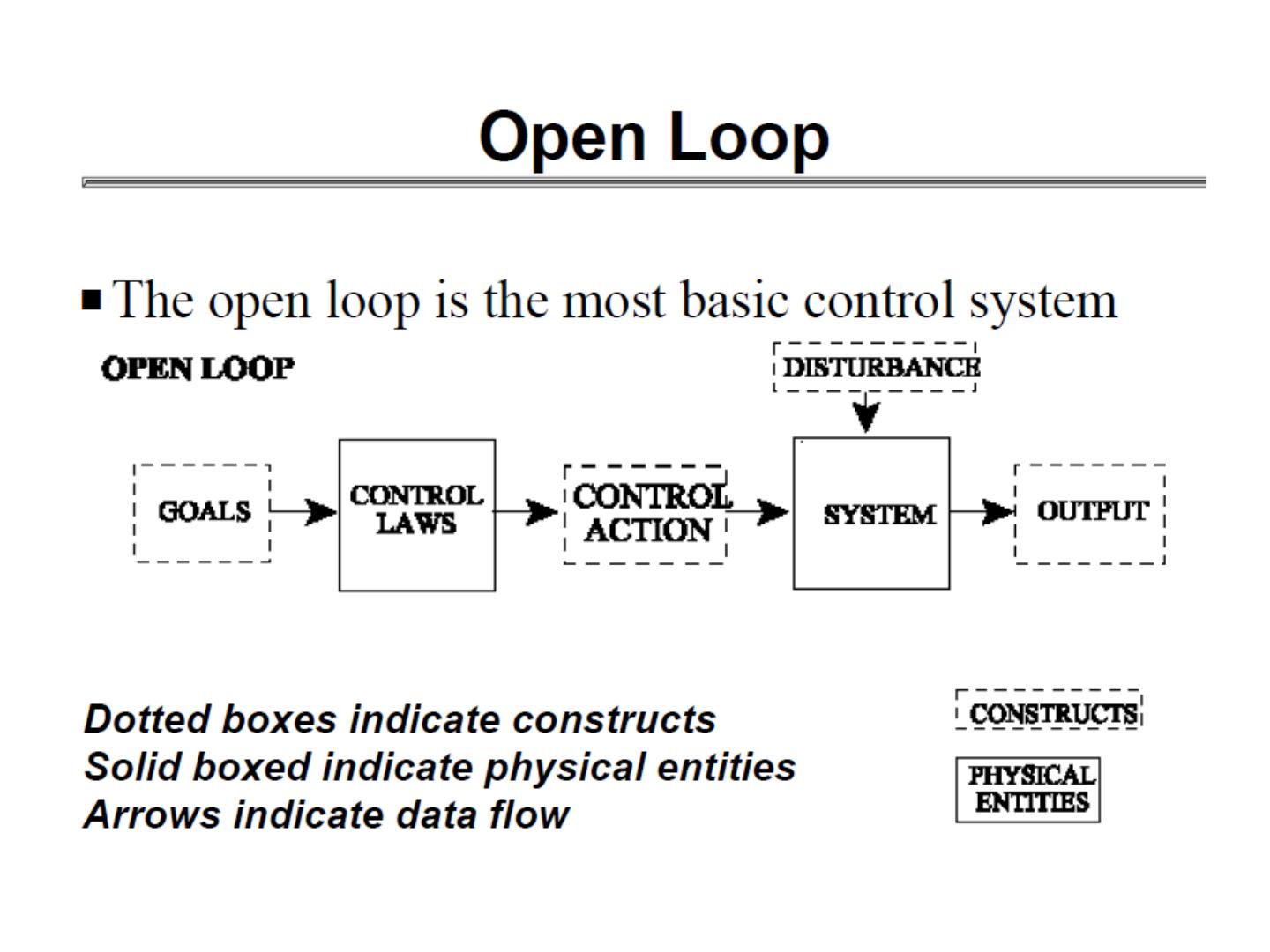
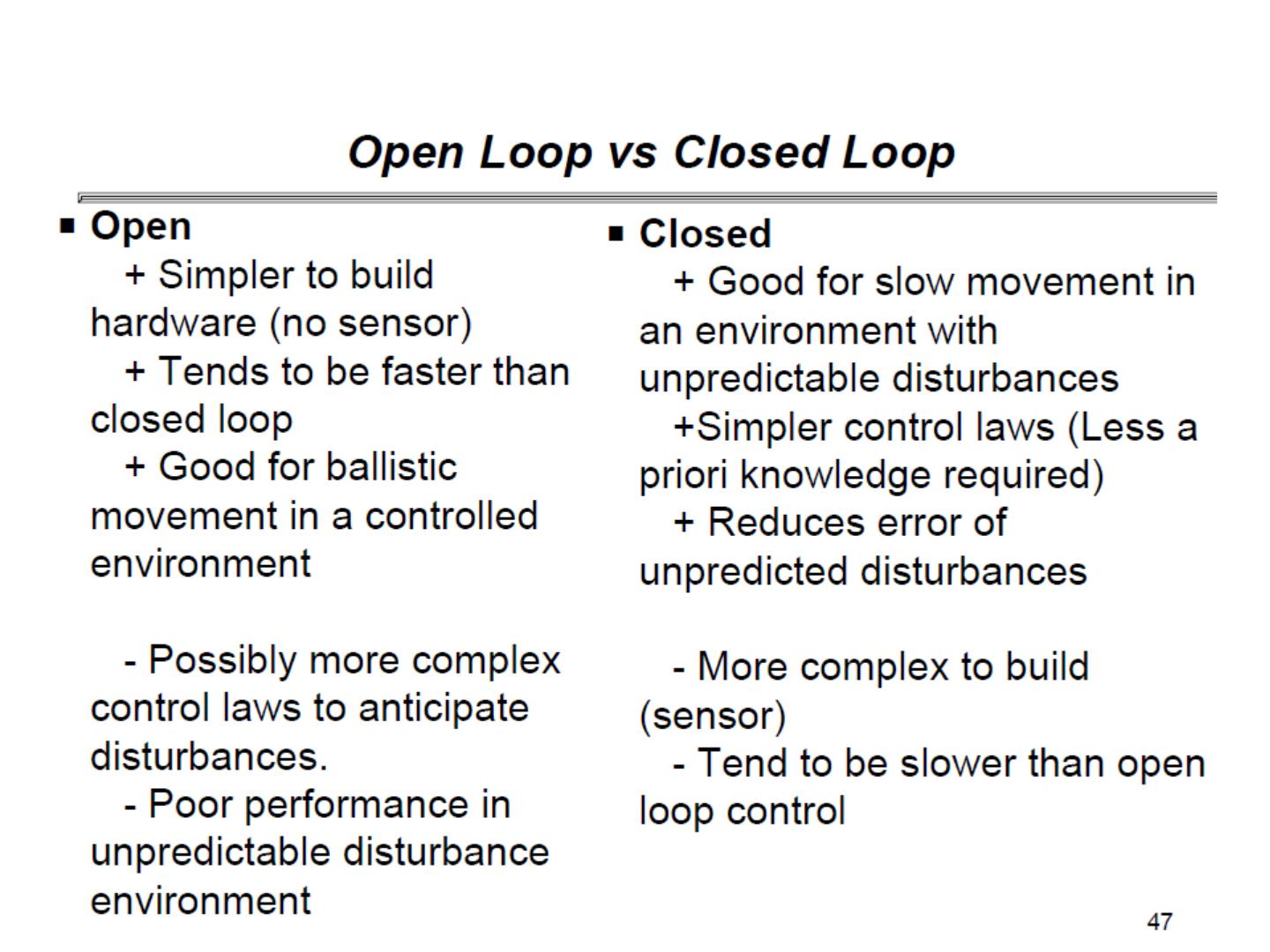
5 . Types of Control Systems • Open-Loop  Simple control system which performs its function without concerns for initial conditions or external inputs.  Must be closely monitored. • Closed-Loop (feedback)  Uses the output of the process to modify the process to produce the desired result.  Continually adjusts the process. 

6 .Control Systems 

7 .Transducer or Sensor Factors 

8 .Open Loop Controller 

9 .

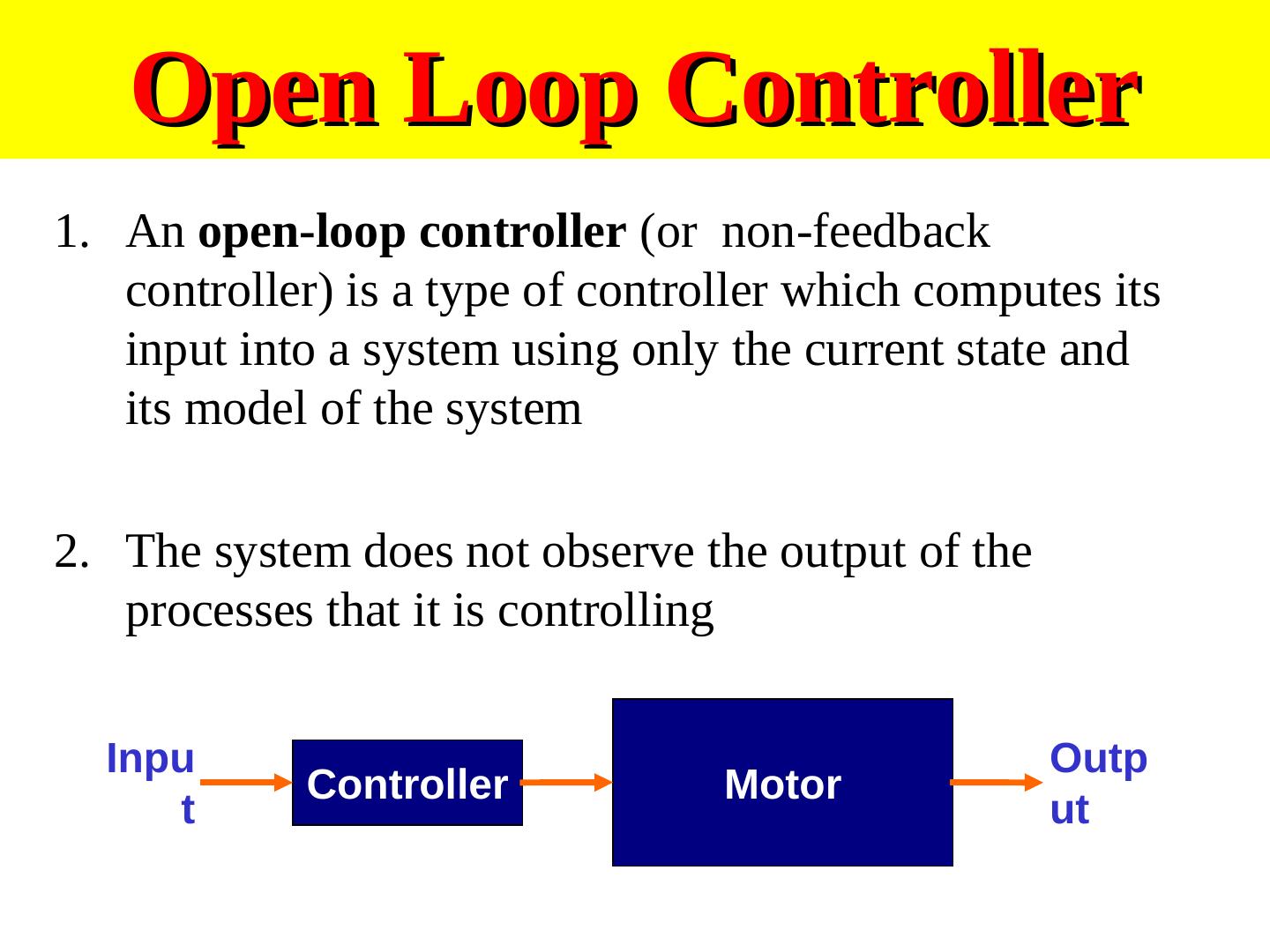
10 . Open Loop Controller 1. An open-loop controller (or non-feedback controller) is a type of controller which computes its input into a system using only the current state and its model of the system 2. The system does not observe the output of the processes that it is controlling Inpu Outp Controller Motor t ut 

11 .

12 . Open Loop Controller (cont…) 1. Open-loop control is useful for well-defined systems where the relationship between input and the resultant state can be modeled by a mathematical formula 2. For example determining the voltage to be fed to an electric motor that drives a constant load, in order to achieve a desired speed would be a good application of open-loop control 

13 . Open Loop Controller (cont…) 1. An open-loop controller is often used in simple processes because of its simplicity and low-cost, especially in systems where feedback is not critical 2. Generally, to obtain a more accurate or more adaptive control, it is necessary to feed the output of the system back to the inputs of the controller 

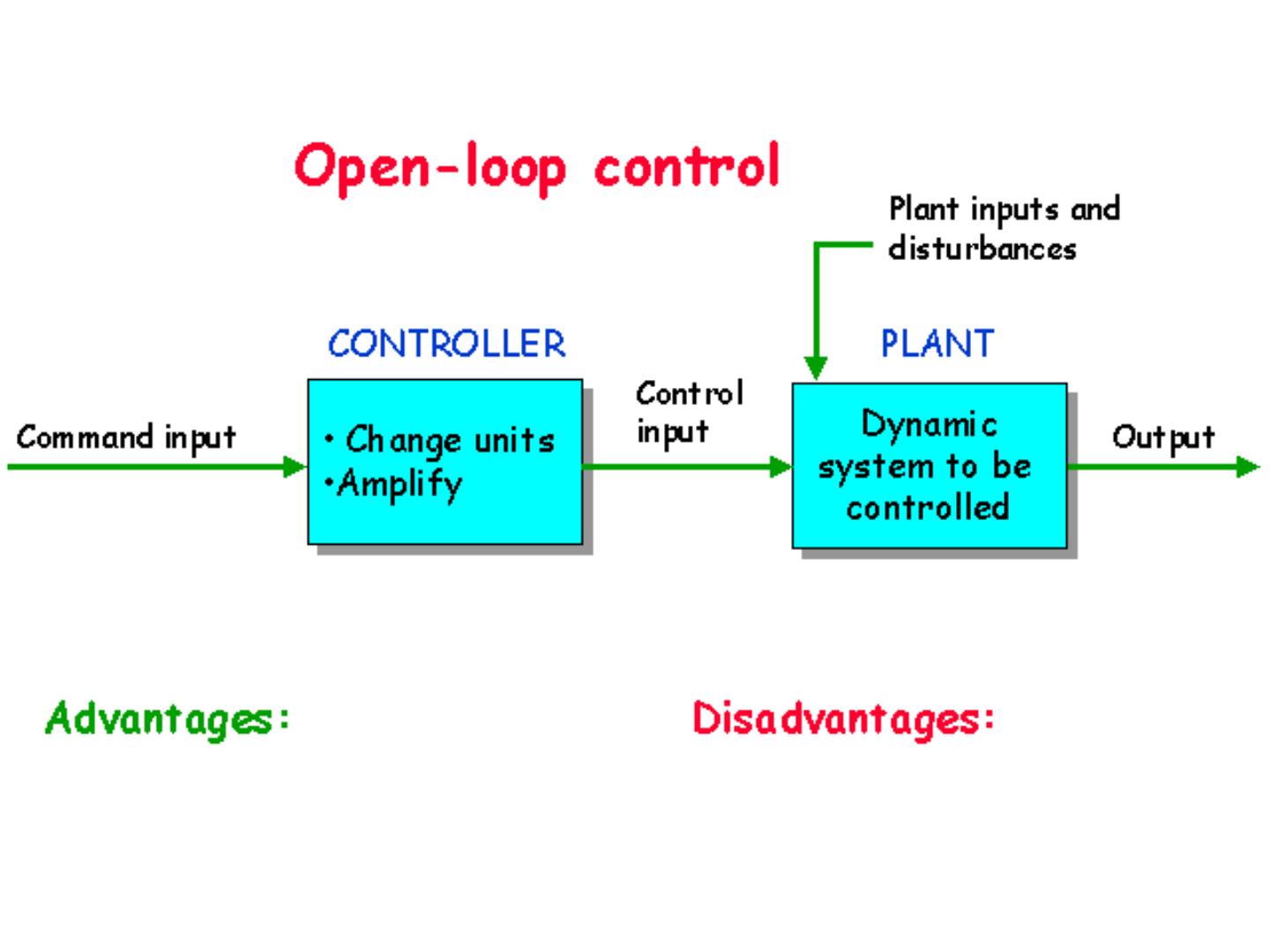
14 . Open-loop control • Advantages:  Stability not a problem  Cheaper than closed-loop  Can be used even if output cannot be measured • Disadvantages:  Changes in system or disturbances ? errors  Periodic calibration required 

15 .Closed Loop Controller 

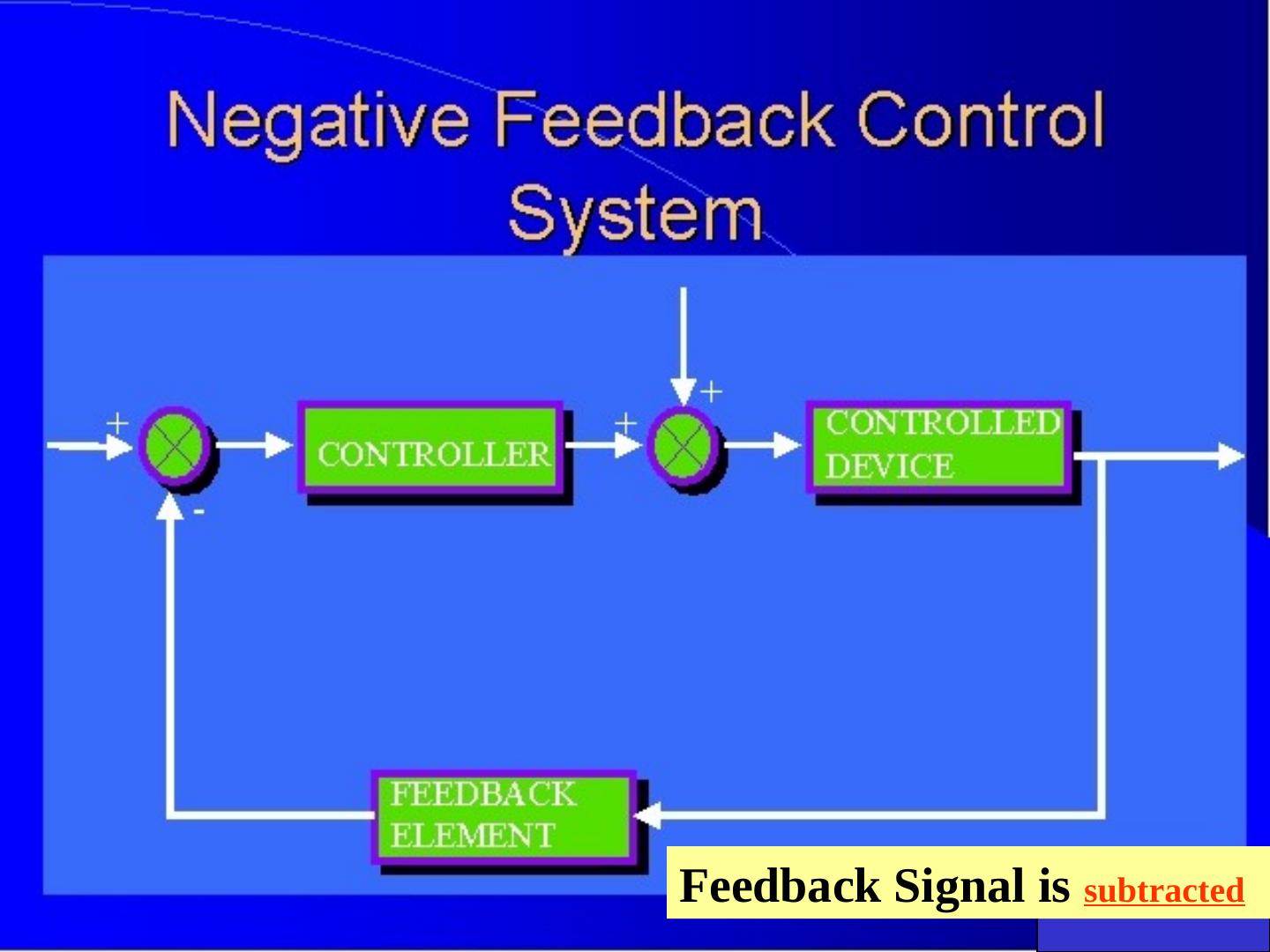
16 .Example of a simple Control in Closed Loop 

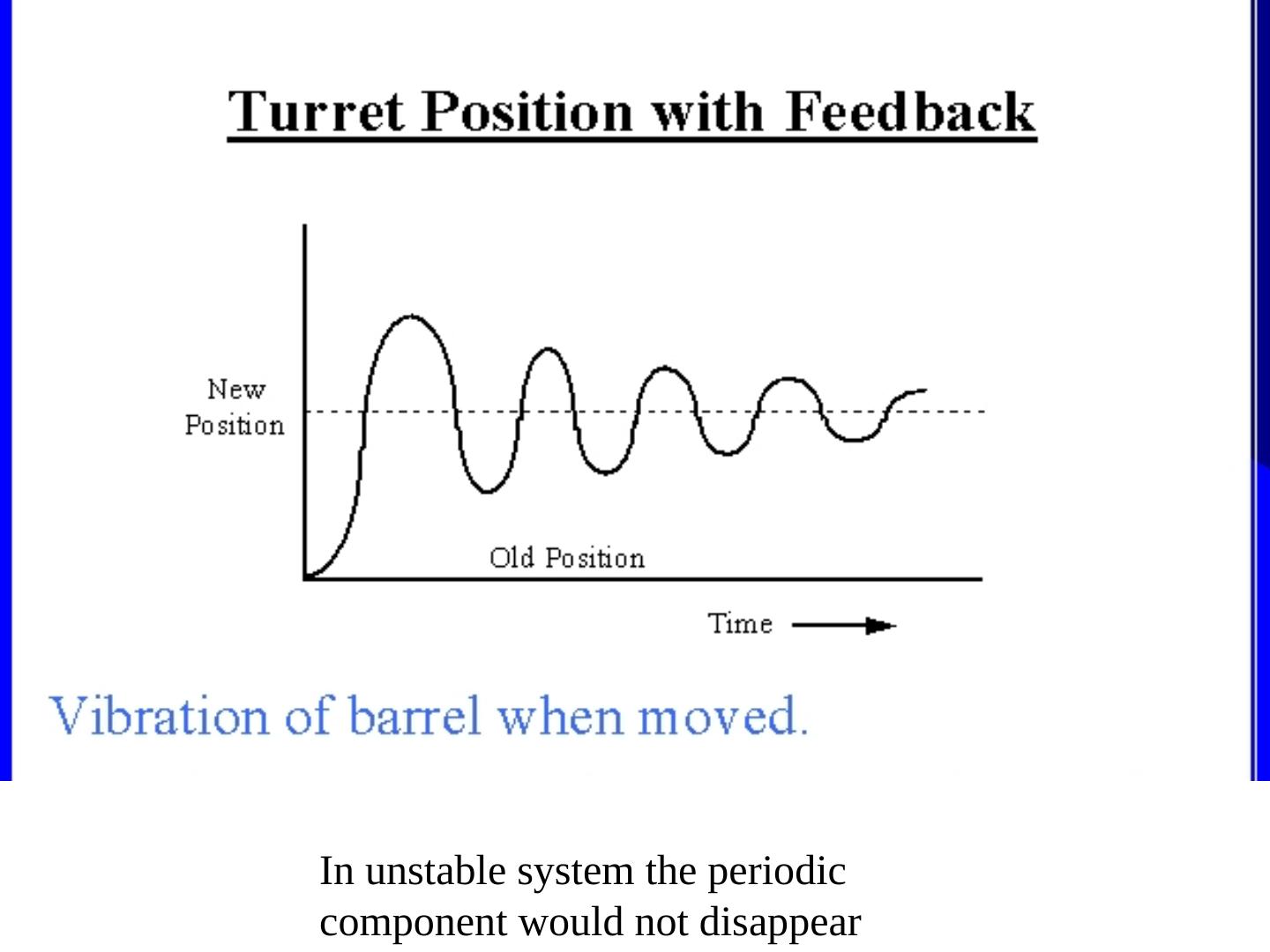
17 . Closed Loop Controller 1. Closed-loop controllers have the following advantages over open- loop controllers: 1. Disturbance rejection (such as unmeasured friction in a motor) 2. Guaranteed performance even with model uncertainties, when the model structure does not match perfectly the real process and the model parameters are not exact 3. Unstable processes can be stabilized 4. Reduced sensitivity to parameter variations 5. Improved reference tracking performance 

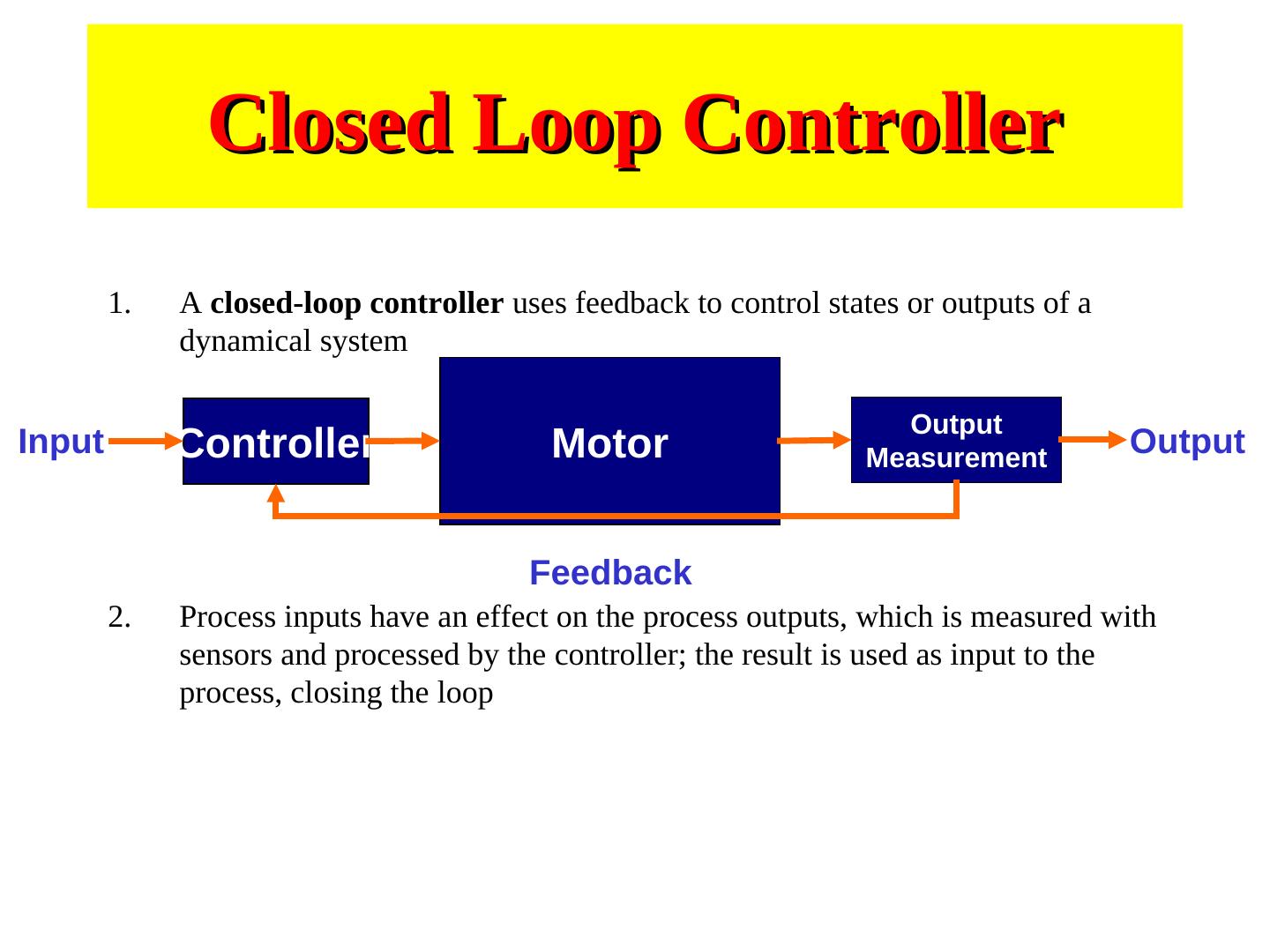
18 . Closed Loop Controller 1. A closed-loop controller uses feedback to control states or outputs of a dynamical system Output Input Controller Motor Measurement Output Feedback 2. Process inputs have an effect on the process outputs, which is measured with sensors and processed by the controller; the result is used as input to the process, closing the loop 

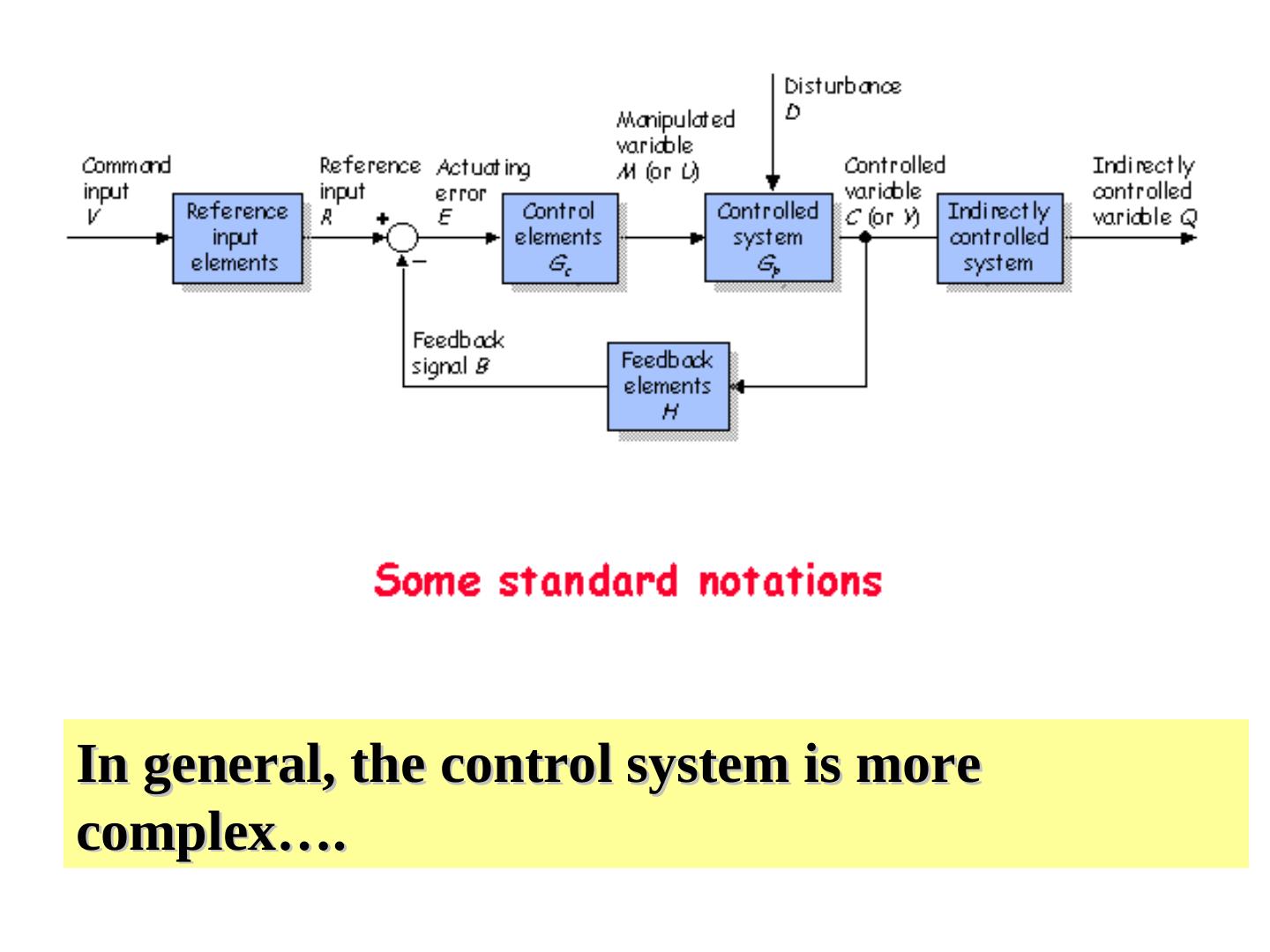
19 .The General View of a Control Loop e u 

20 .Feedback or Closed Loop System 

21 . PID Control • Proportional Integral Derivative Control • The Basic Problem: – We have n joints, each with a desired position which we have specified – Each joint has an actuator which is given a command in units of torque – Most common method for determining required torques is by feedback from joint sensors 

22 . What is PID Control? • Proportional, Integral, & Derivative Control – Proportional: Multiply current error by constant to try to resolve error – Integral: Multiply sum of previous errors by constant to resolve steady state error (error after system has come to rest) – Derivative: Multiply time derivative of error change by constant to resolve error as quickly as possible 

23 .Feedback Signal is subtracted 

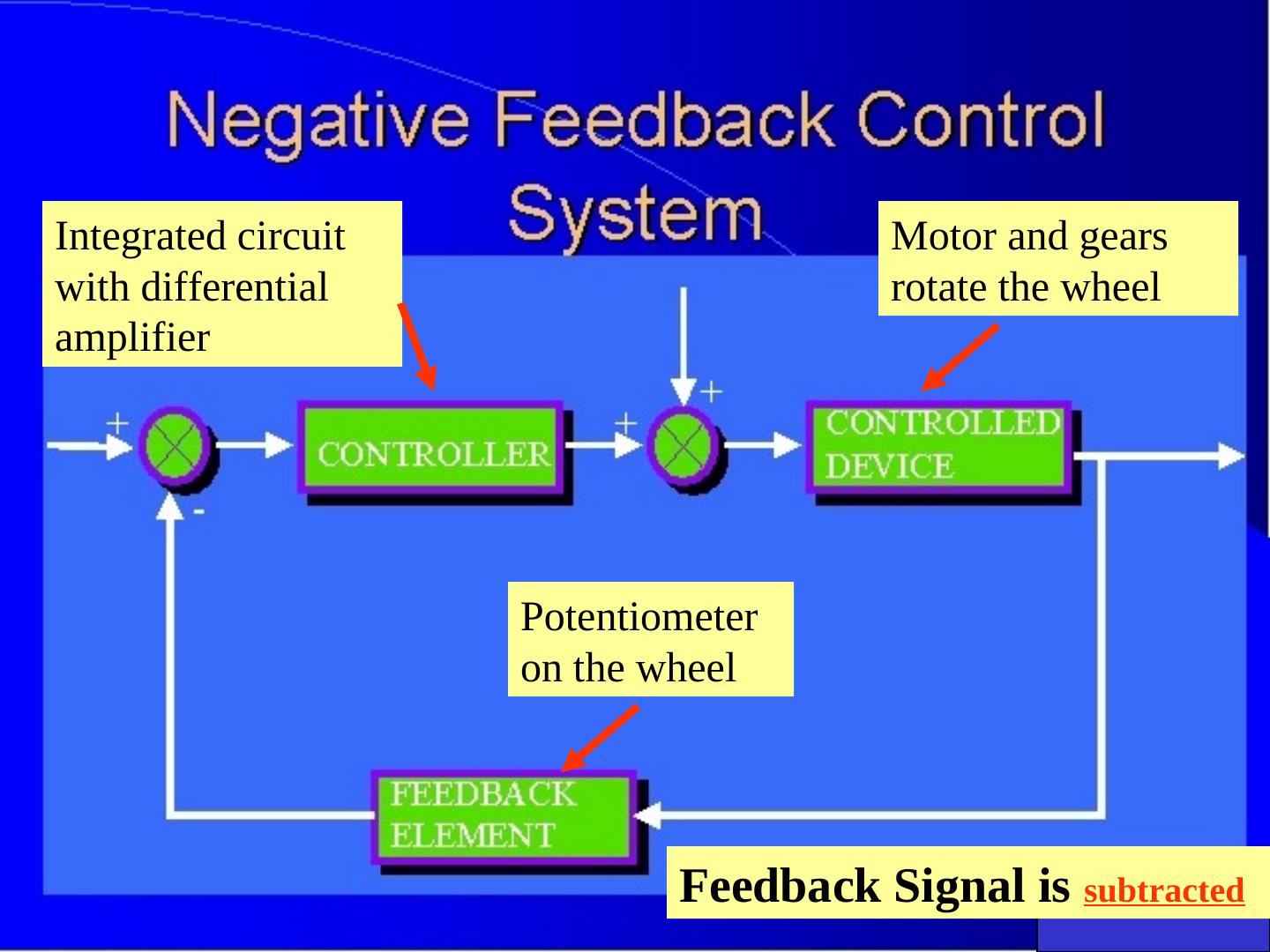
24 .Integrated circuit Motor and gears with differential rotate the wheel amplifier Potentiometer on the wheel Feedback Signal is subtracted 

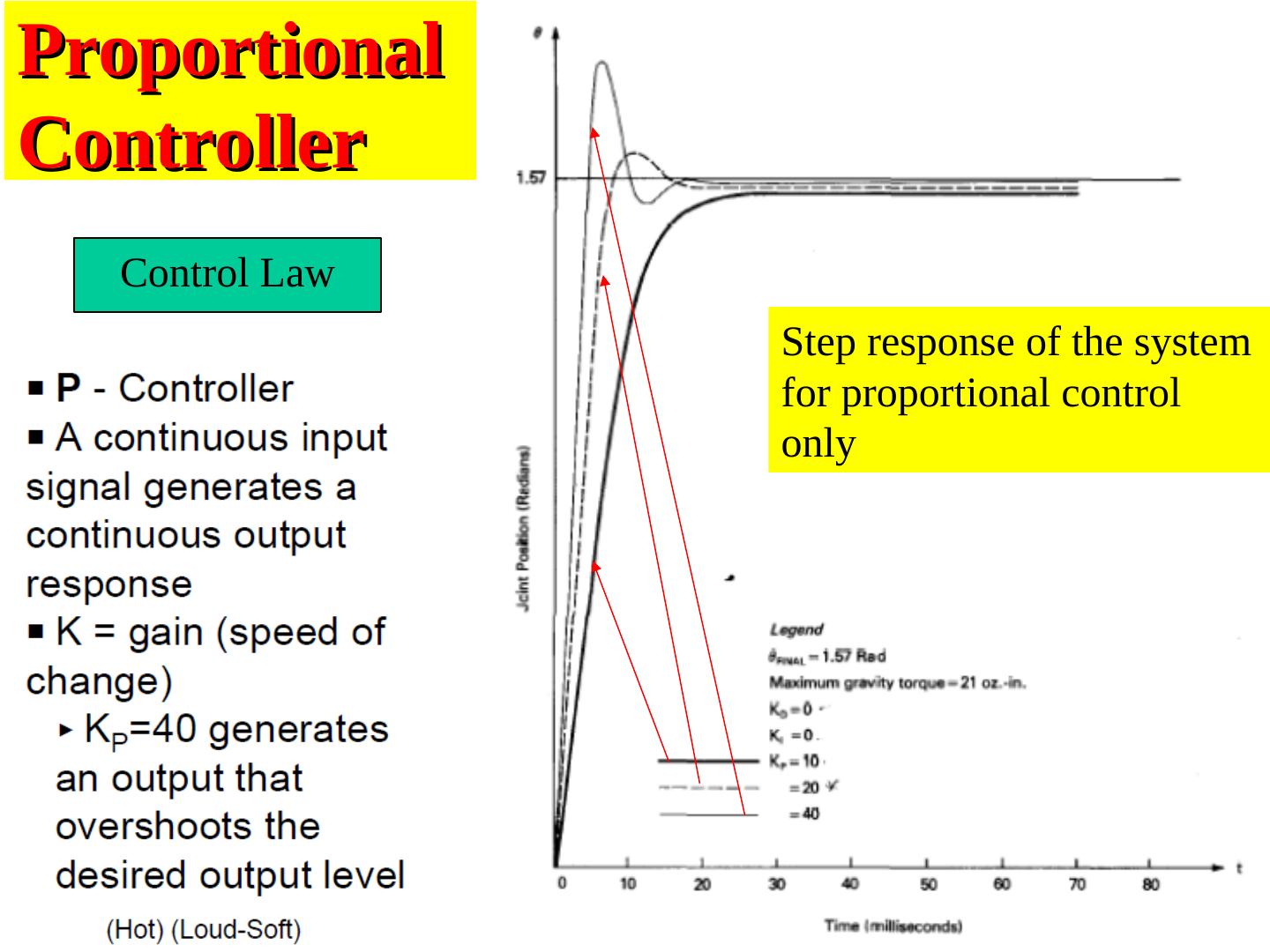
25 .Proportional Controller Control Law Step response of the system for proportional control only 

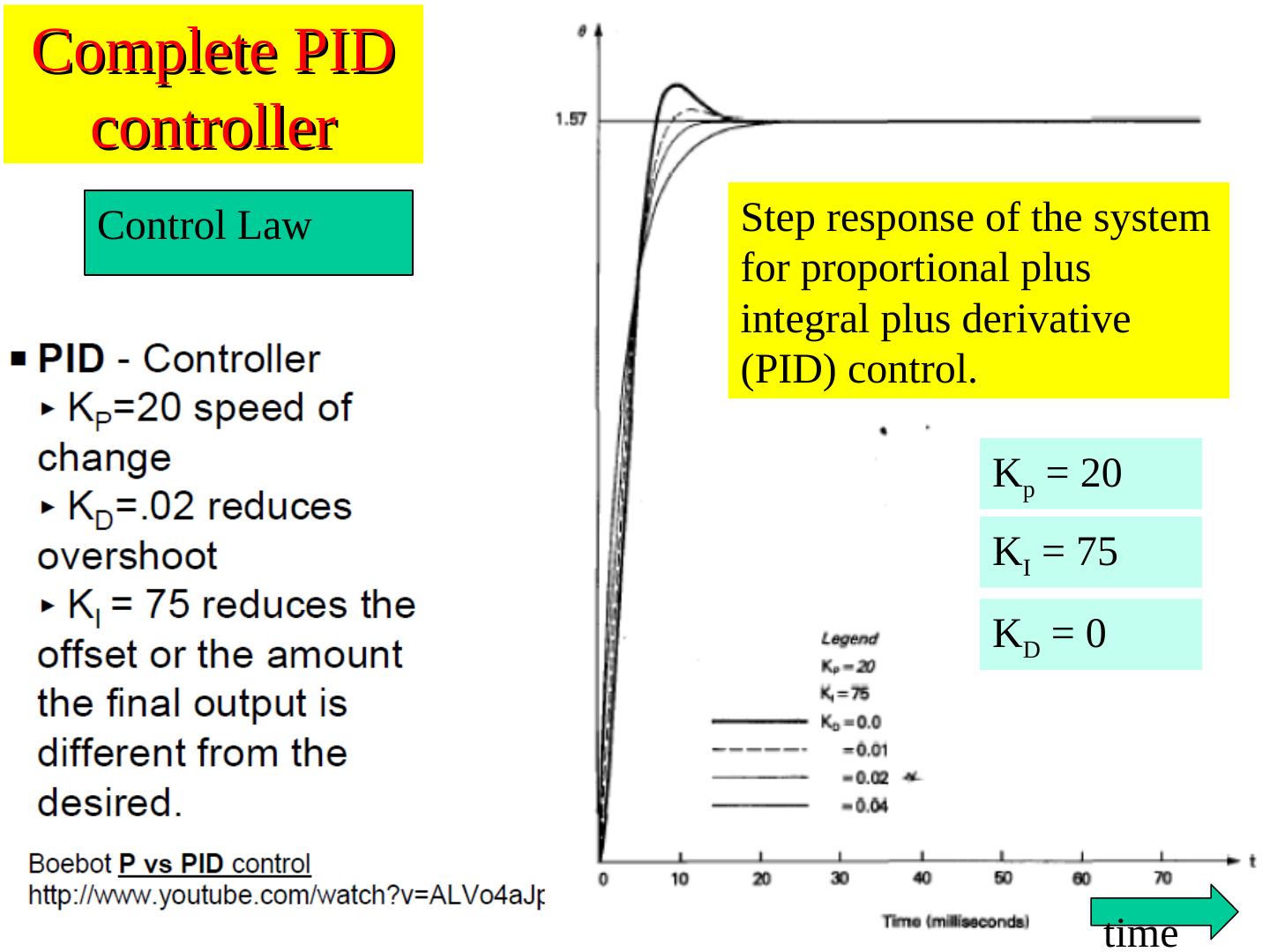
26 .Complete PID controller Control Law Step response of the system for proportional plus integral plus derivative (PID) control. Kp = 20 KI = 75 KD = 0 time 

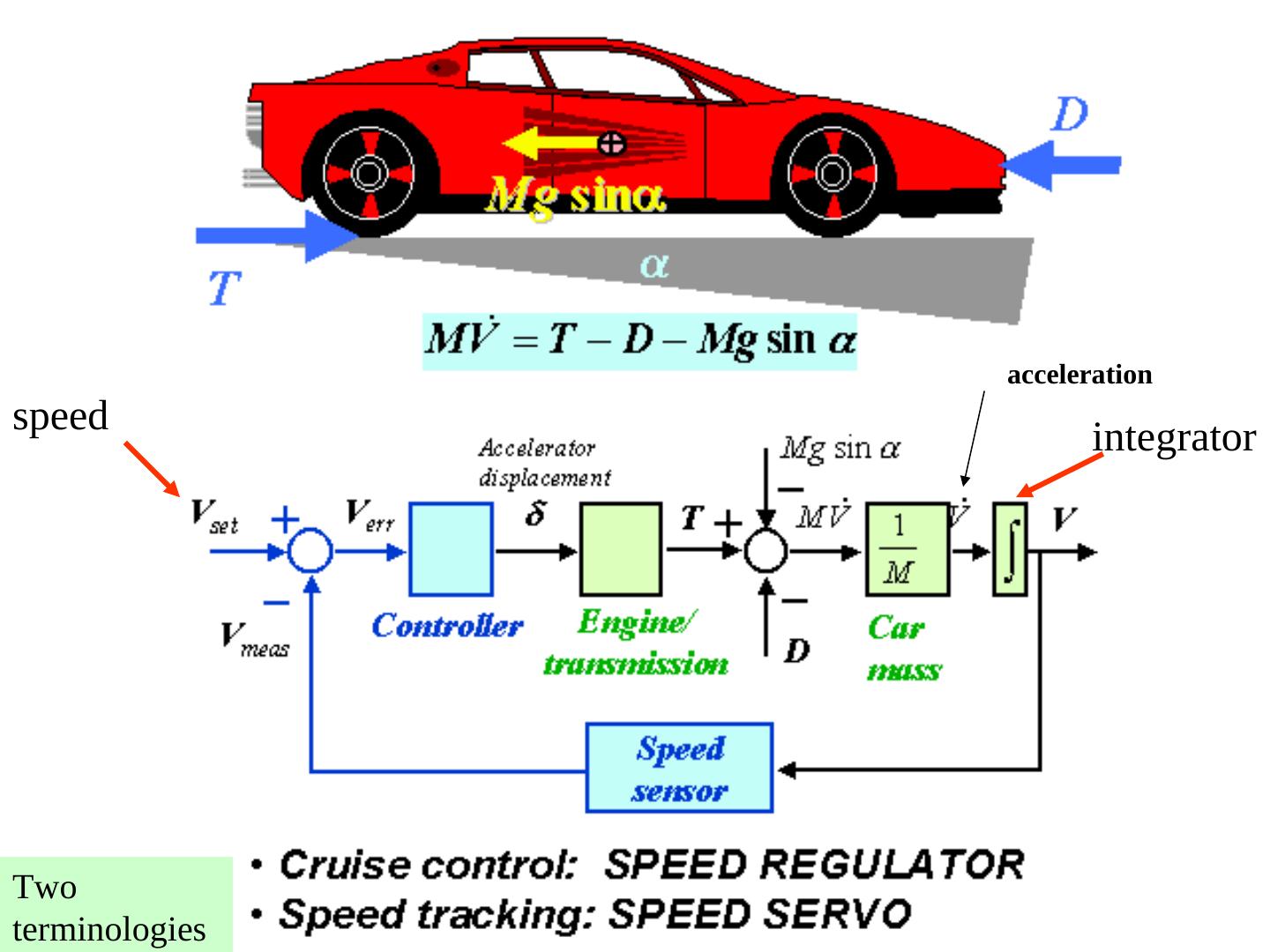
27 .Cruise Control 

28 .Example V = velocity, speed 

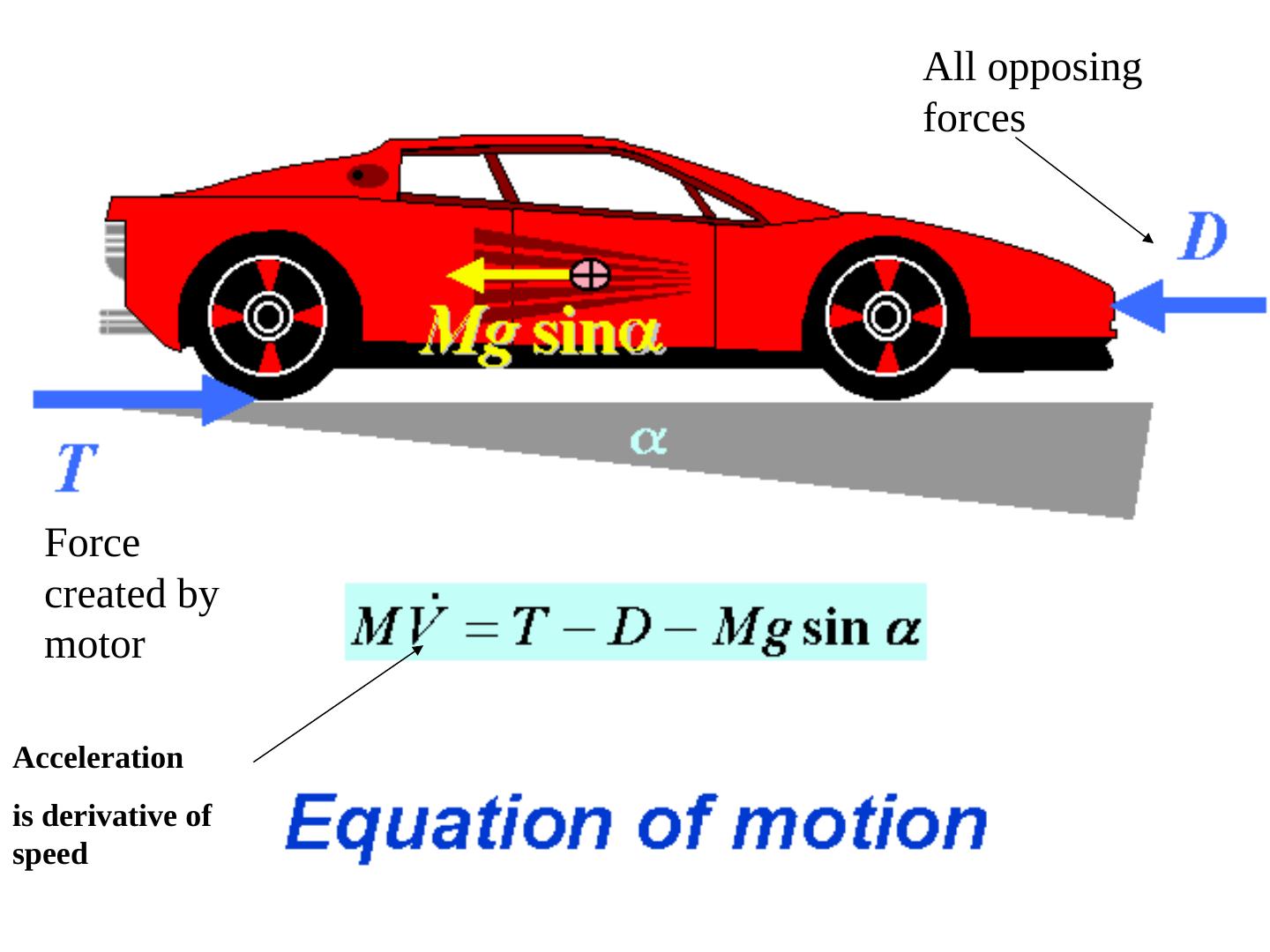
29 . All opposing forces Force created by motor Acceleration is derivative of speed