20_IGA for robot theatre. Part 1.

1 . Artistic Robots through Interactive Genetic Algorithm with ELO rating system Andy Goetz, Camille Huffman, Kevin Riedl, Mathias Sunardi and Marek Perkowski Department of Electrical Engineering, Portland State University 

2 .Portland Cyber Theatre 

3 . Making science out of robot theater? 

4 .How to make a science from robot theatre? 

5 .

6 .

7 .evaluate sound, shape, motion, color,etc. 

8 . Verification Interactive Human Genetic evaluators Algorithm Behavior expressio n robot Probabilistic Automaton behavior Generator and verifier Behavior Automaton 

9 . Main Idea of this work • A new approach to create fitness function for Interactive Genetic Algorithm in which (possibly) many humans evaluate robot motions via Internet page. • Based on ELO rating system known from chess. • The robots use: 1. a genetic algorithm, 2. fuzzy logic, 3. probabilistic state machines, 4. a small set of functions for creating picture components, 5. and a user interface which allows the Internet users to rate individual sequences. 

10 .Previous work on IEC systems 1. Human-based genetic algorithm. 2. Interactive evolution strategy, 3. Interactive genetic programming, 4. Interactive genetic algorithm. Mostly for music composition and graphics Usually weighted functions were used 

11 . Ranking Systems in Sports Rating systems for many sports award points in accordance with subjective evaluations of the 'greatness' of certain achievements. For example, winning an important golf tournament might be worth an arbitrarily chosen five times as many points as winning a lesser tournament. A statistical endeavor, by contrast, uses a model that relates the game results to underlying variables representing the ability of each player. 

12 . Elo rating system • The Elo rating system is a method for calculating the relative skill levels of players in two-player games such as chess. • It is named after its creator Arpad Elo, a Hungarian-born American physics professor. • The Elo system was invented as an improved chess rating system, but today it is also used in many other games. • It is also used as a rating system for multiplayer competition in a number of video games. • It has been adapted to team sports including association football, American college football, basketball, and Major League Baseball. 

13 . Previous works You have many candidates, you want to select the best. 1. You can compare individually each with each 2. You cannot compare individually each with each 

14 . Pairwise Compariso n 

15 .Pairwise Comparison Method: Compare each two candidates (players) head-to-head. Award each candidate one point for each head-to-head victory. The candidate with the most points wins. N(N-1)/2 comparisons. 

16 .Pairwise Comparison - Example Selection of best robot facial expression: expression # of Voters 4 candidates: {A,B,C,D} and 4 rankings of them Rank 14 10 8 4 1 37 voters 1st A C D B C 5 trials (columns) 2nd B B C D D Table shows the rankings of the candidates (rows) and the number of voters 3rd C D B C B (columns) that ranked the candidates that way 4th D A A A A 

17 .Pairwise Comparison - Example Compare candidates A & B: # of Voters 14 voters ranked A Rank 14 10 8 4 1 higher than B 1st A C D B C 10+8+4+1=23 2nd B B C D D voters ranked B higher than A 3rd C D B C B So, B wins against A 4th D A A A A 

18 .Pairwise Comparison - Example Next, compare candidates A & C: 14 voters ranked A higher than C # of Voters 10+8+4+1=23 voters ranked C higher than A Rank 14 10 8 4 1 So, C wins against A 1st A C D B C Continue for next pairs: A vs. D, B vs. C, B vs. D, C vs. D 2nd B B C D D Exclude: permutations (e.g. C vs. A = A vs. 3rd C D B C B C) comparison with itself (e.g. A vs. A) 4th D A A A A 

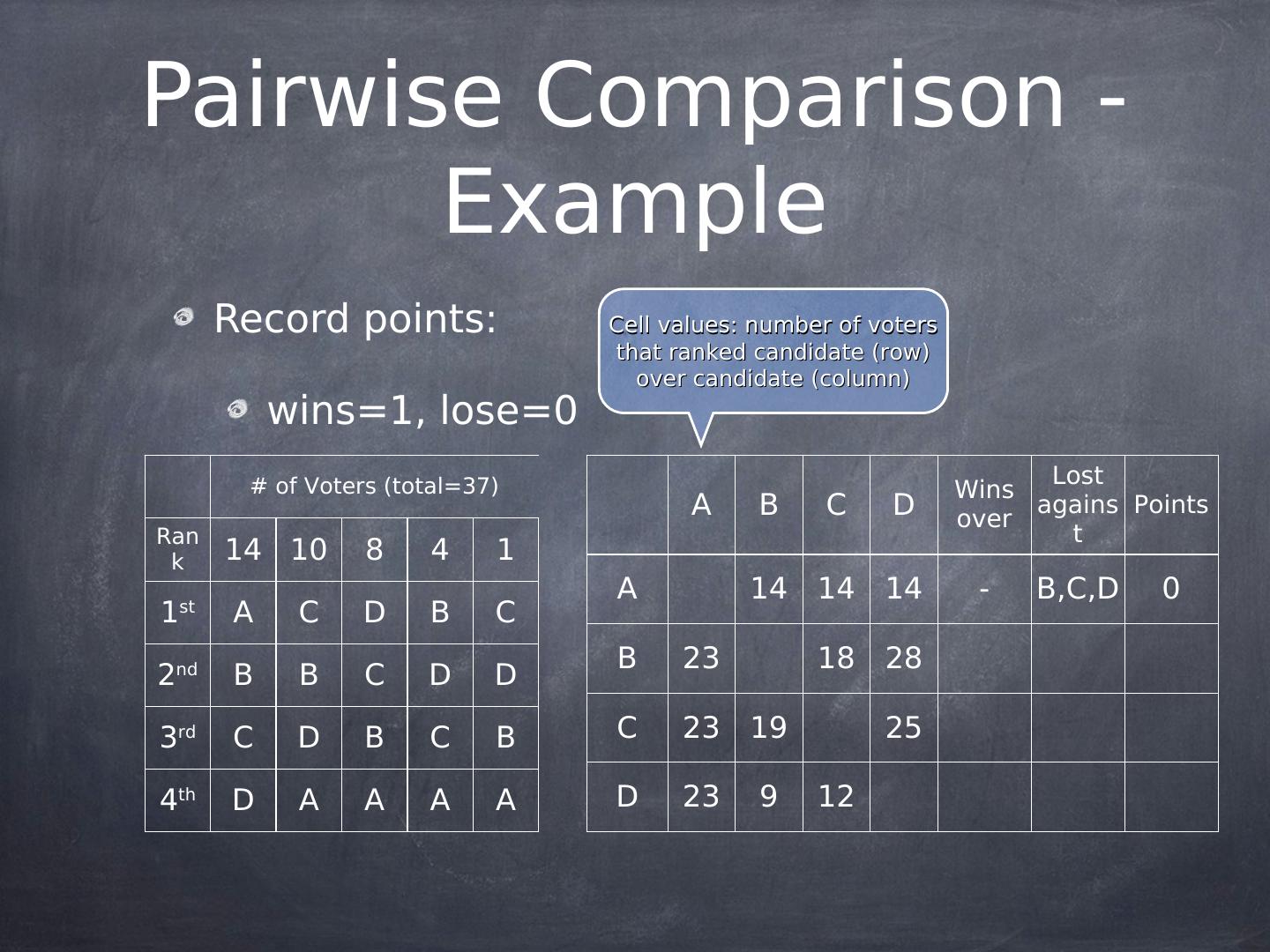
19 .Pairwise Comparison - Example Record points: Cell values: number of voters that ranked candidate (row) over candidate (column) wins=1, lose=0 # of Voters (total=37) Lost Wins A B C D over agains Points Ran t k 14 10 8 4 1 A 14 14 14 1 st A C D B C B 23 18 28 2nd B B C D D 3rd C D B C B C 23 19 25 4th D A A A A D 23 9 12 

20 .Pairwise Comparison - Example Record points: Cell values: number of voters that ranked candidate (row) over candidate (column) wins=1, lose=0 # of Voters (total=37) Lost Wins A B C D over agains Points Ran t k 14 10 8 4 1 A 14 14 14 - B,C,D 0 1 st A C D B C B 23 18 28 2nd B B C D D 3rd C D B C B C 23 19 25 4th D A A A A D 23 9 12 

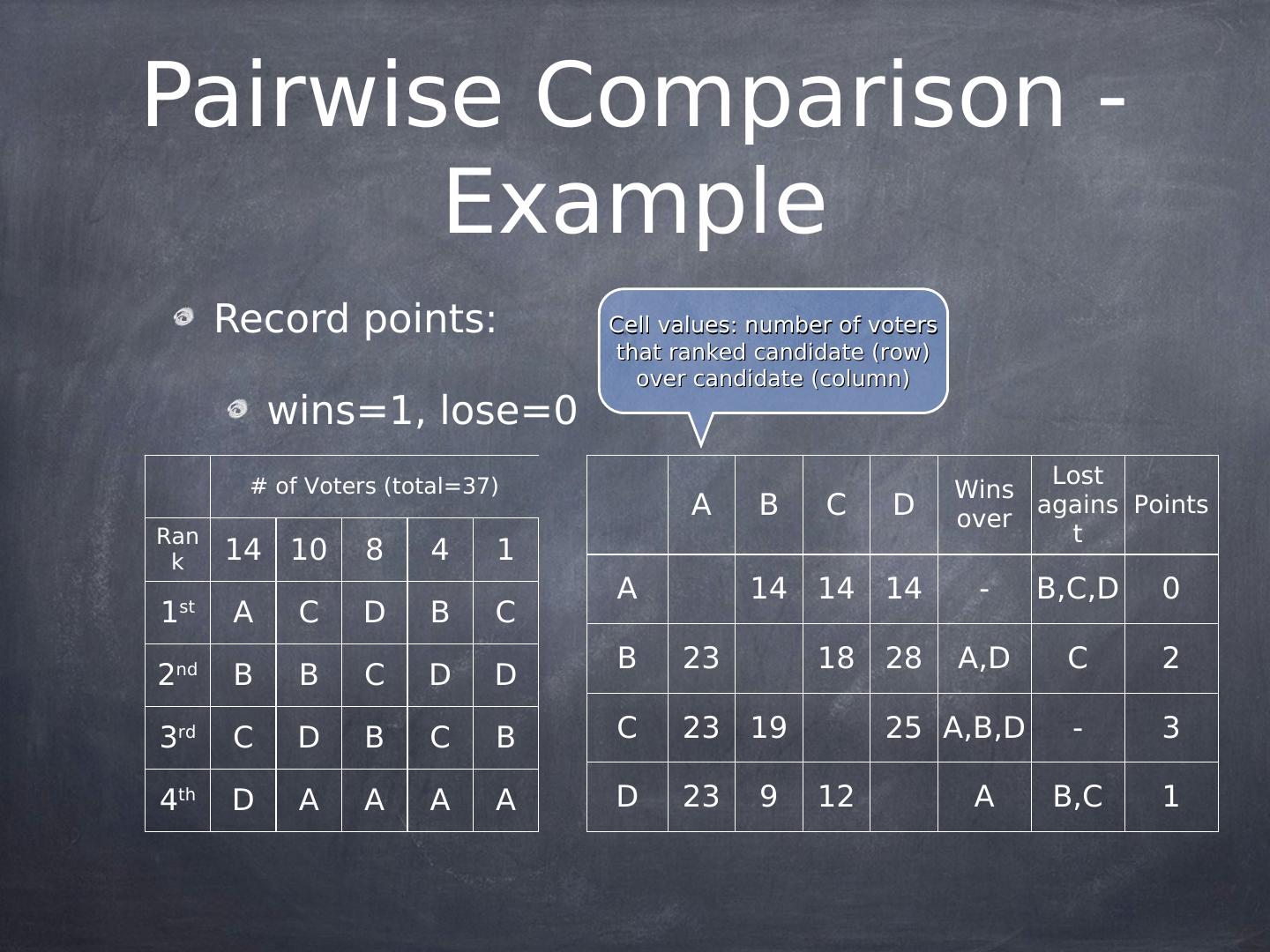
21 .Pairwise Comparison - Example Record points: Cell values: number of voters that ranked candidate (row) over candidate (column) wins=1, lose=0 # of Voters (total=37) Lost Wins A B C D over agains Points Ran t k 14 10 8 4 1 A 14 14 14 - B,C,D 0 1 st A C D B C B 23 18 28 A,D C 2 2nd B B C D D 3rd C D B C B C 23 19 25 A,B,D - 3 4th D A A A A D 23 9 12 A B,C 1 

22 .Pairwise Comparison - Example Record points: Cell values: number of voters that ranked candidate (row) over candidate (column) wins=1, lose=0 # of Voters (total=37) Lost Wins A B C D over agains Points Ran t k 14 10 8 4 1 A 14 14 14 - B,C,D 0 1 st A C D B C B 23 18 28 A,D C 2 2nd B B C D D C wins! 3rd C D B C B C 23 19 25 A,B,D - 3 4th D A A A A D 23 9 12 A B,C 1 

23 .Pairwise Comparison - Example Record points: Another way to calculate the winner: use half the table triangle, mark the winner, and count the number of times the player appears wins=1, lose=0 # of Voters (total=37) Lost Wins A B C D over agains Points Ran t k 14 10 8 4 1 A - B C D - B,C,D 0 1 st A C D B C B - - C B A,D C 2 2nd B B C D D C wins! 3rd C D B C B C - - - C A,B,D - 3 4th D A A A A D - - - - A B,C 1 

24 . Other possible scenario A three-way tie: A B C A - A C B - - B C - - - Inconsistency: A wins over B, B wins over C, C wins over A 

25 . ELO Rating System 

26 . Overview of ELO A player’s skill is assumed to be a normal distribution: True skill is around the mean Elo System gives two things: A players expected chance of winning A method to update a player’s Elo Rating 

27 . Basic Ideas of ELO • One cannot look at a sequence of moves and say, "That performance is 2039." • Performance can only be inferred from wins, draws and losses. • Therefore, if a player wins a game, he is assumed to have performed at a higher level than his opponent for that game. • Conversely if he loses, he is assumed to have performed at a lower level. • If the game is a draw, the two players are assumed to have performed at nearly the same level. 

28 .Scores and ranking of players A player’s ranking is updated based on its: Expected value of winning (E) Which depends on the ranking difference with the opponent Outcome of the match (S for ‘score’) 1 = win 0 = lose 0.5 = draw 

29 . Expected scores in Elo Rating rating Expected score (E) score Where: EA, EB = expected score for player A and B, respectively RA, RB = Rating of player A and B, respectively Remember: 1=win, 0=lose, 0.5=draw http://en.chessbase.com/home/TabId/211/PostId/4007114