18_Search_Crossover_Mutation

1 . Classes of Search Techniques S e a rc h te c h n iq u e s C a lc u lu s - b a s e d t e c h n iq u e s G u id e d ra n d o m s e a rc h te c h n iq u e s E n u m e r a t iv e t e c h n iq u e s D ir e c t m e t h o d s I n d ir e c t m e t h o d s E v o lu tio n a ry a lg o rith m s S im u la t e d a n n e a lin g D y n a m ic p r o g r a m m in g F in o n a c c i N e w to n E v o lu t io n a r y s t r a t e g ie s G e n e tic a lg o rith m s P a ra lle l S e q u e n tia l C e n tra liz e d D is trib u te d S te a d y -s ta te G e n e ra tio n a l 

2 . Dictionary 1 • Gene – smallest unit with genetic information • Genotype – collectivity of all genes • Phenotype – expression of genotype in environment • Individual – single member of a population with genotype and phenotype • Population – set of several individuals • Generation – one iteration of evaluation, selection and reproduction with variation 

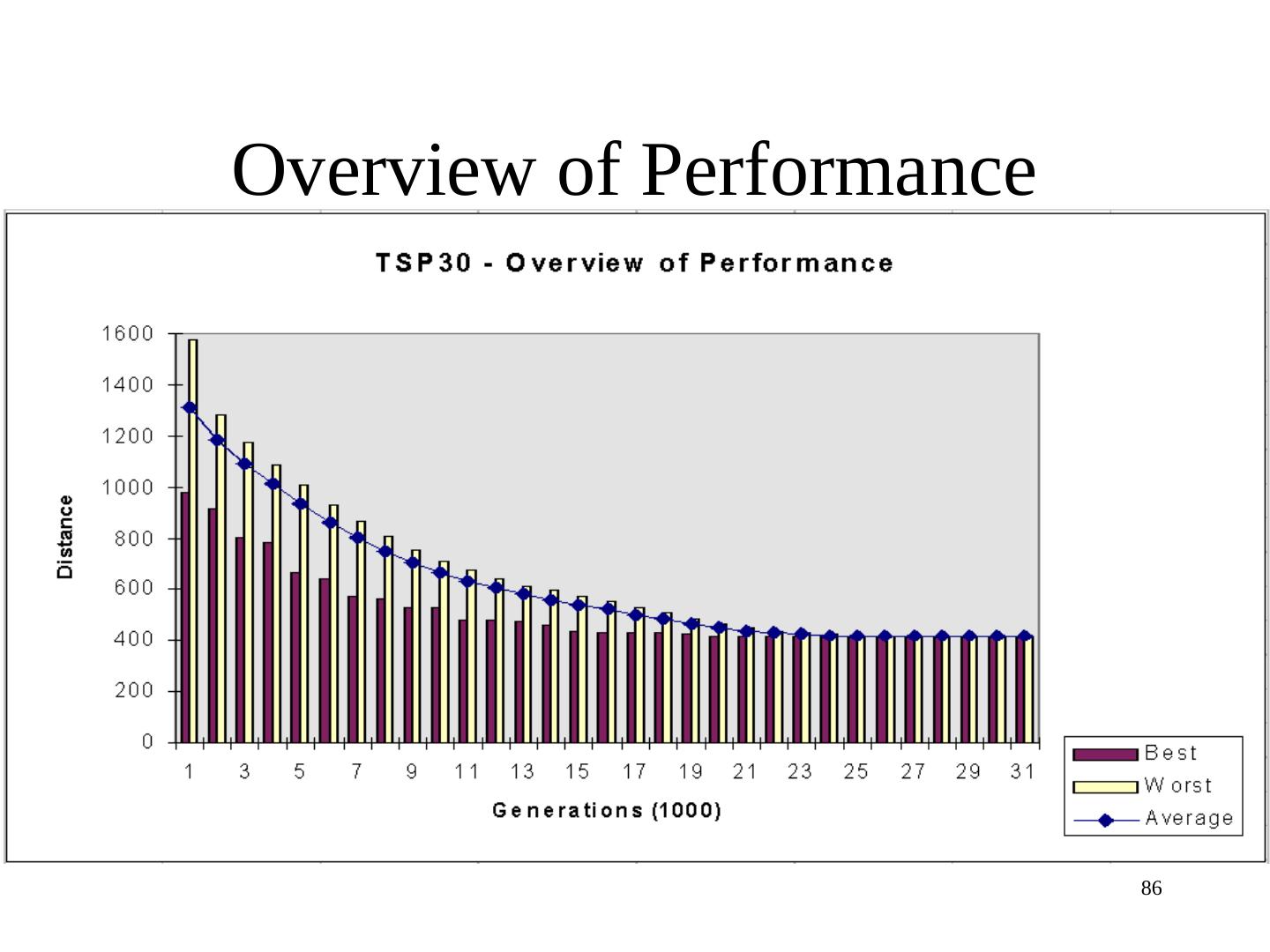
3 .Searching 

4 . Searching • search space defined by all possible encodings of solutions • selection, crossover, and mutation perform ‘pseudo-random’ walk through search space • operations are non-deterministic yet directed • Non-deterministic since random crossover point or mutation prob. Directed by fitness fn 

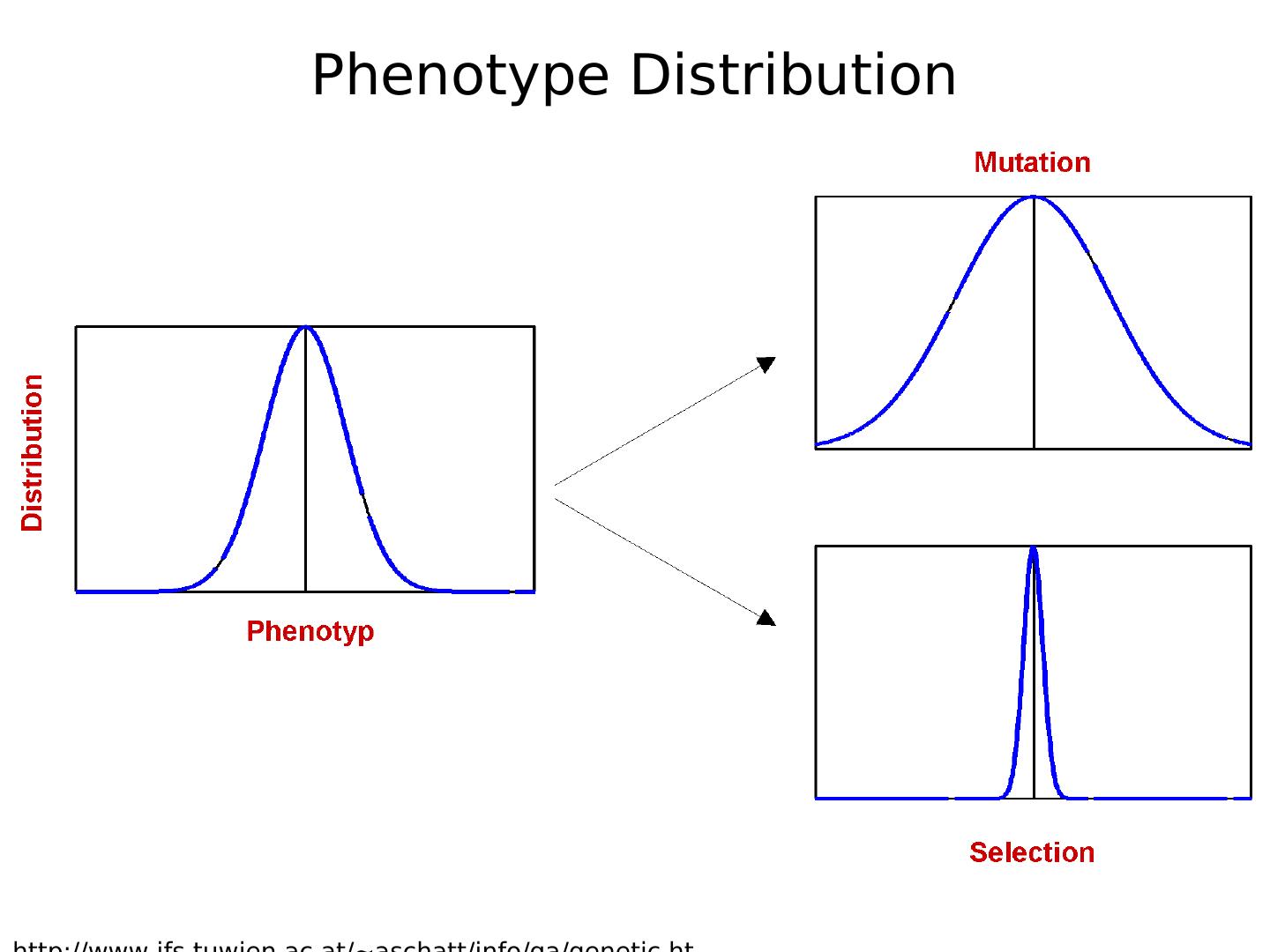
5 .Phenotype Distribution 

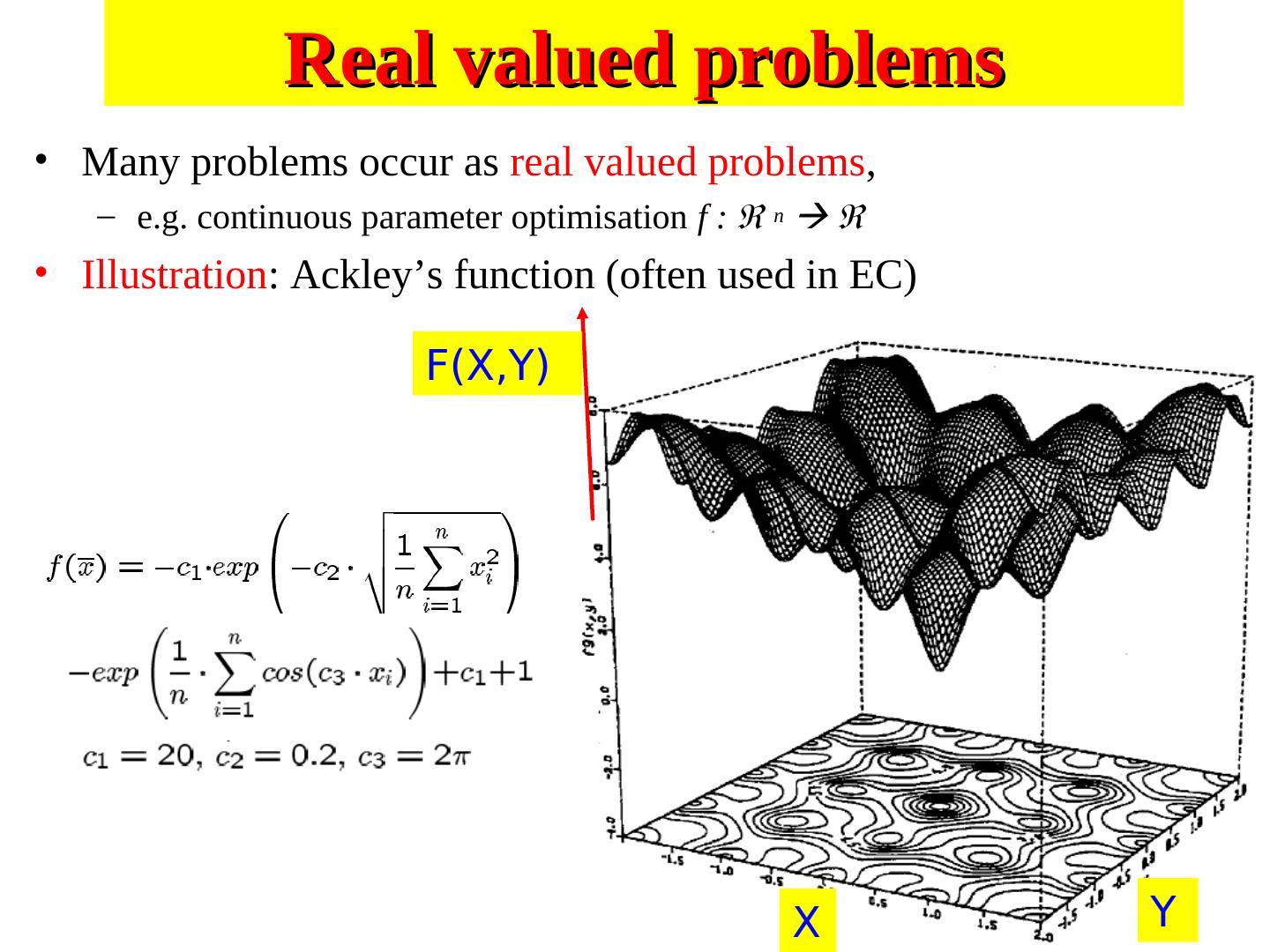
6 . Search Space • For a simple function f(x) the search space is one dimensional. • But by encoding several values into the chromosome many dimensions can be searched e.g. two dimensions f(x,y) • Search space an be visualised as a surface or fitness landscape in which fitness dictates height • Each possible genotype is a point in the space • A GA tries to move the points to better places (higher fitness) in the space 

7 .Fitness landscapes 

8 . Search Space 1. Obviously, the nature of the search space dictates how a GA will perform 2. A completely random space would be bad for a GA 3. Also GA’s can get stuck in local maxima if search spaces contain lots of these 4. Generally, spaces in which small improvements get closer to the global optimum are good 

9 .Optimizatio n 

10 . Optimization • Finding the best solution to a problem • Mathematically: finding the minimum or maximum of a function (optimum) Maximum Minimum 

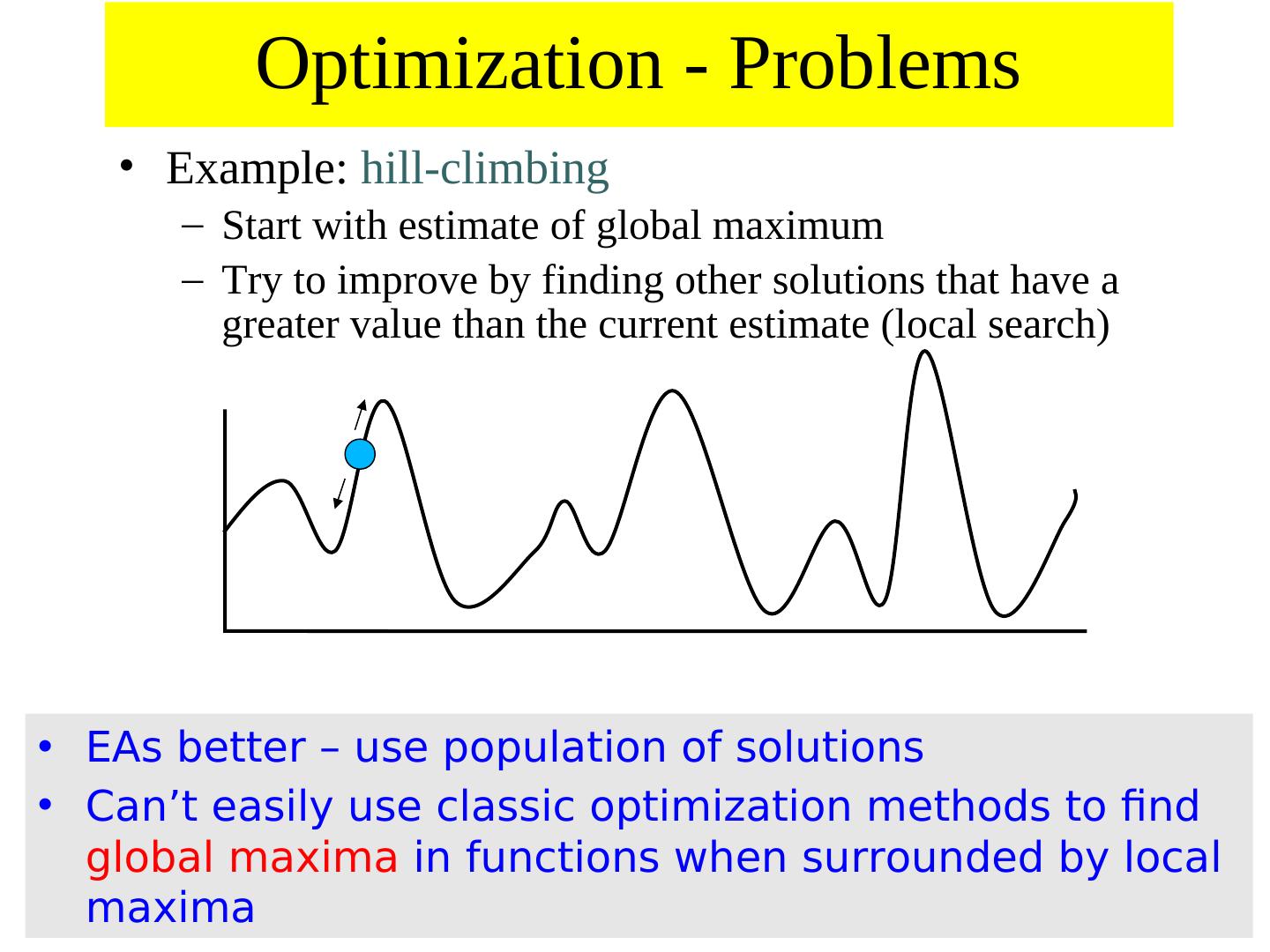
11 . Optimization - Problems • Example: hill-climbing – Start with estimate of global maximum – Try to improve by finding other solutions that have a greater value than the current estimate (local search) • EAs better – use population of solutions • Can’t easily use classic optimization methods to find global maxima in functions when surrounded by local maxima 

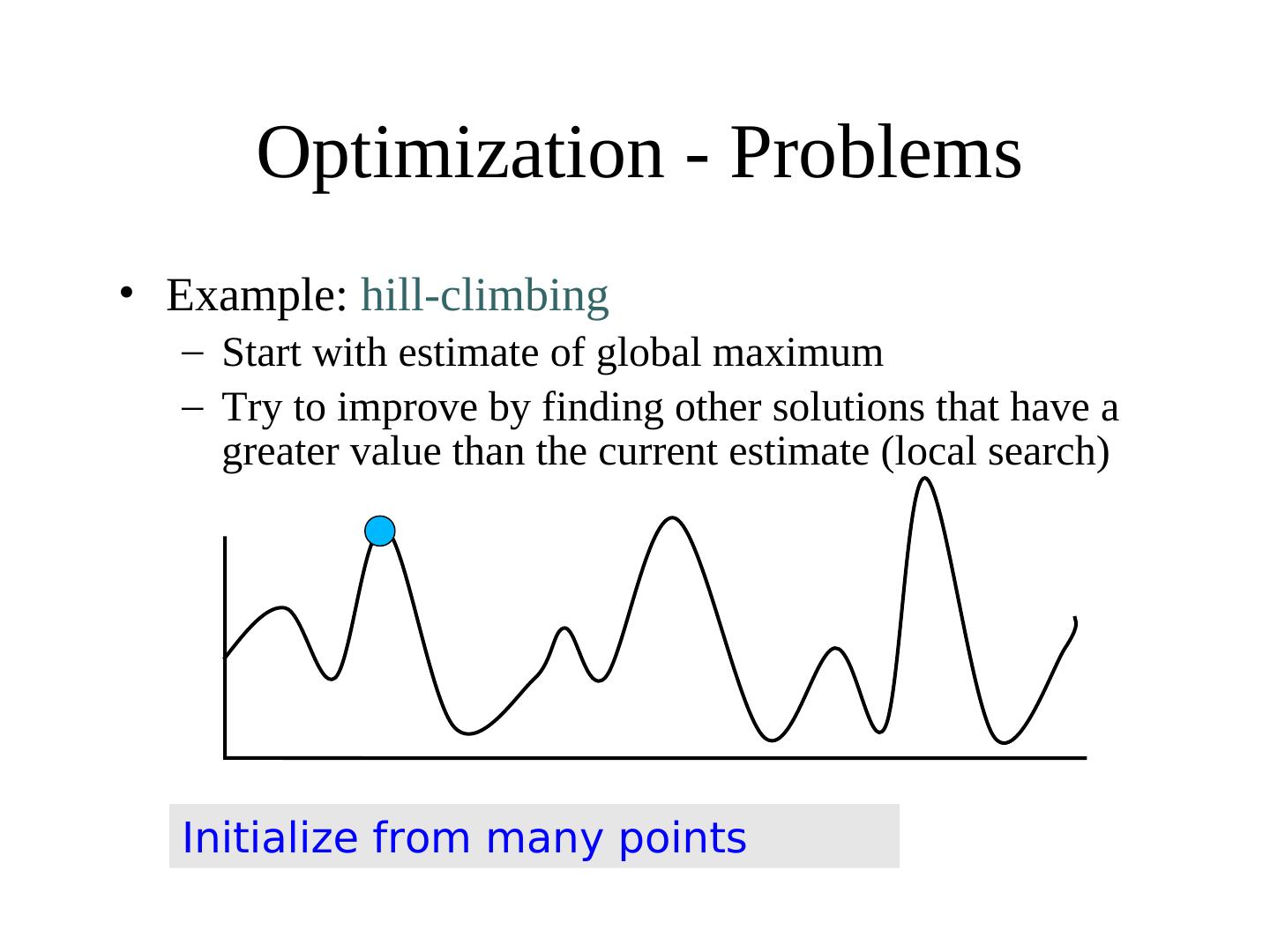
12 . Optimization - Problems • Example: hill-climbing – Start with estimate of global maximum – Try to improve by finding other solutions that have a greater value than the current estimate (local search) Initialize from many points 

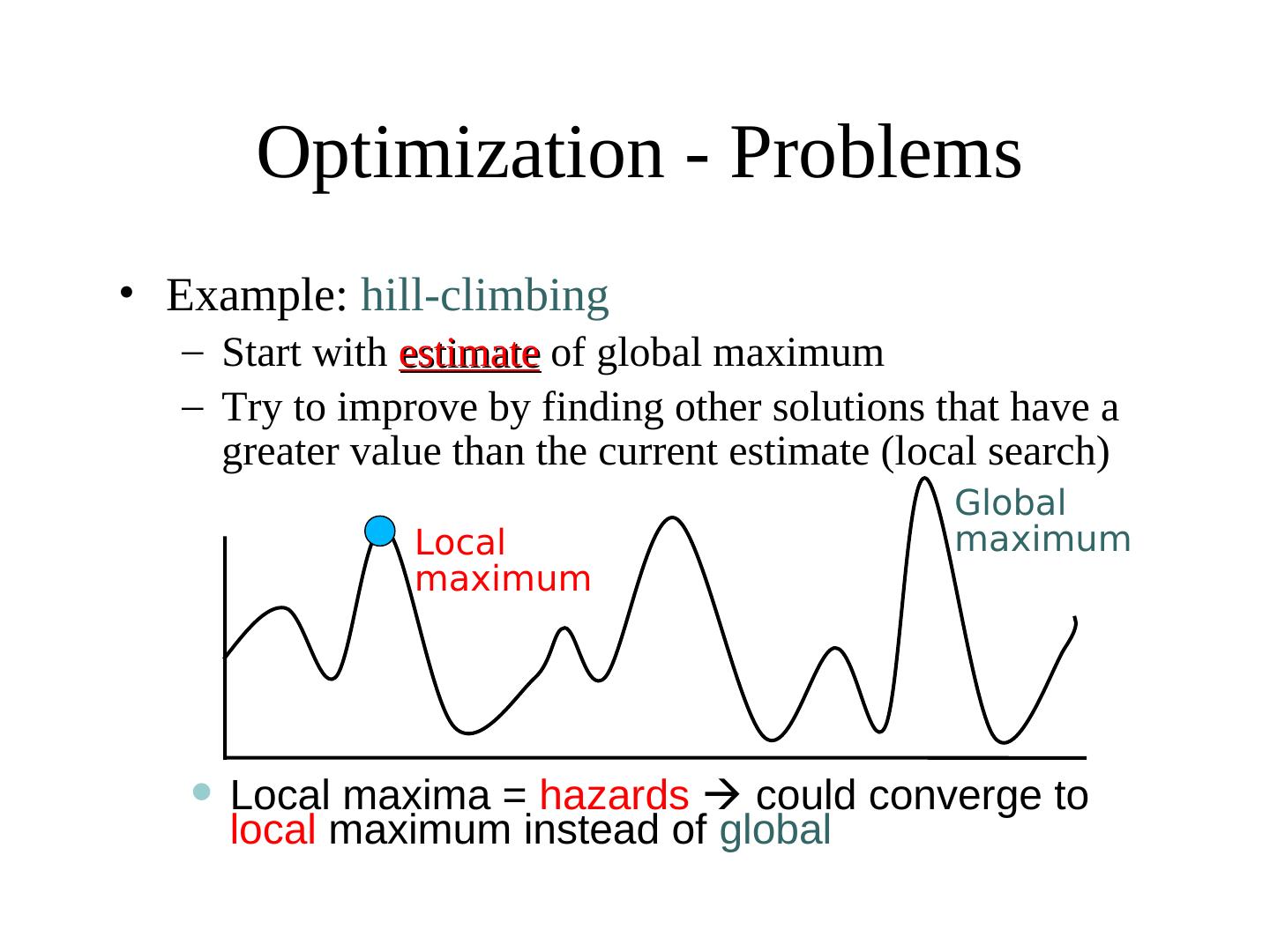
13 . Optimization - Problems • Example: hill-climbing – Start with estimate of global maximum – Try to improve by finding other solutions that have a greater value than the current estimate (local search) Global Local maximum maximum • Local maxima = hazards  could converge to local maximum instead of global 

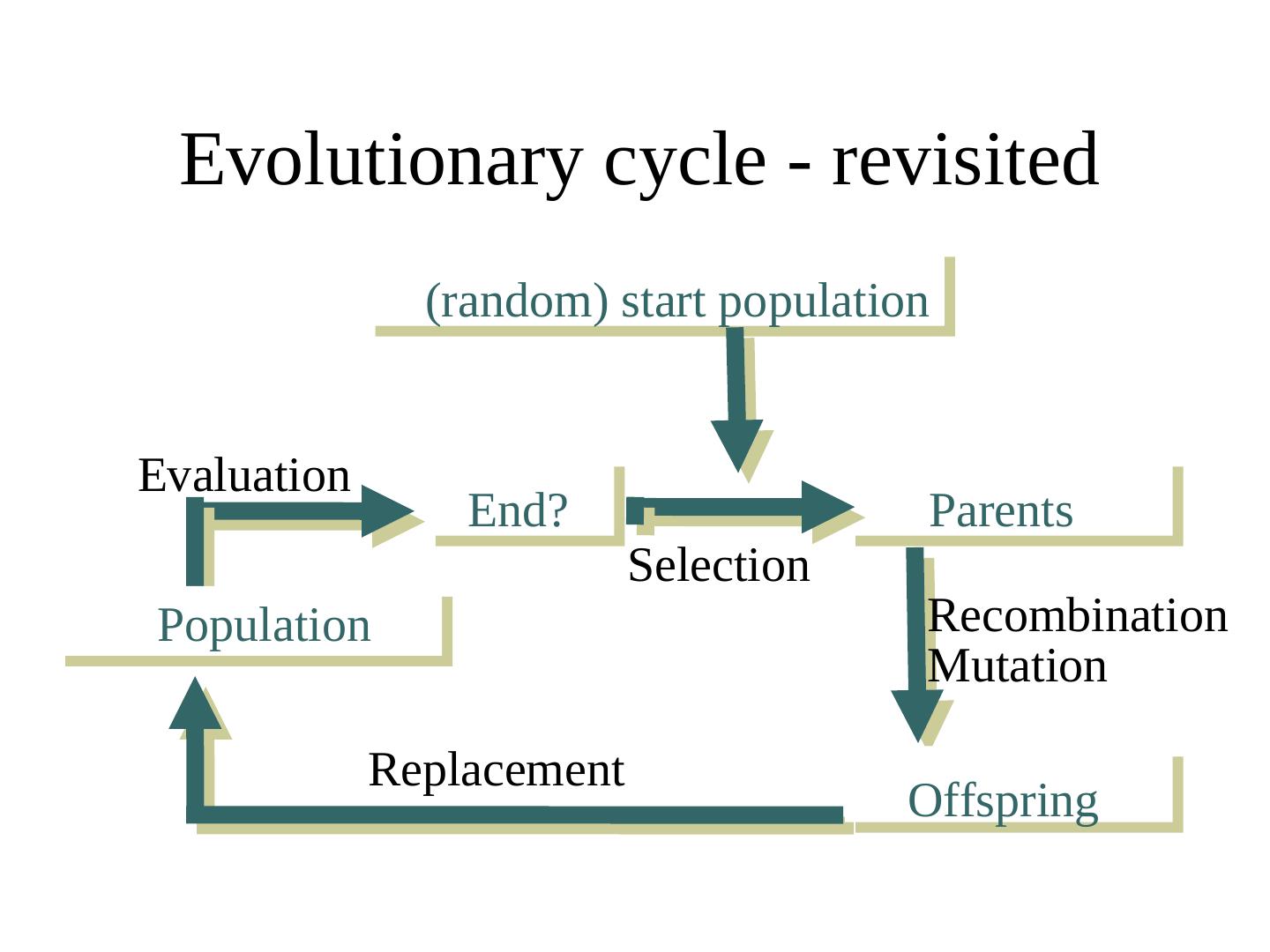
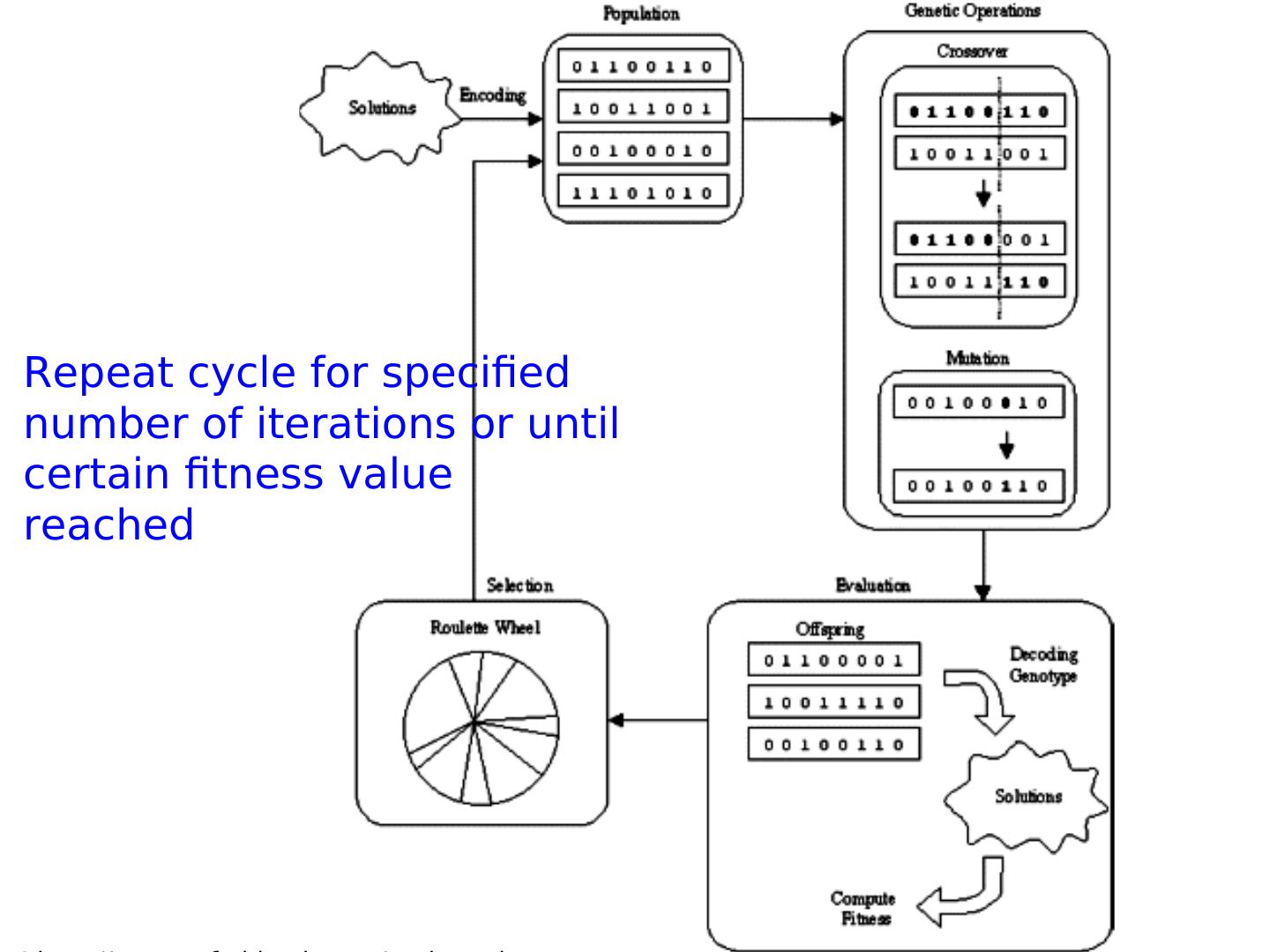
14 . Evolutionary cycle - revisited (random) start population Evaluation End? Parents Selection Population Recombination Mutation Replacement Offspring 

15 . Compared to biological Evolution: - Main concepts (population, reproduction with heredity and variation, pressure of selection) adapted - Natural effects mostly not causally explainable but GAs use: - Randomized, clear defined functions - Functions are arbitrary (chosen by user) and determine success of outcome - Fitness in nature not directly measurable, in GAs fitness clear defined - In contrast to nature GAs need a start and an end point 

16 . Dictionary 2 • Mapping - decodes the phenotype • Mutation - variability operator that modifies a genotype • Recombination/Crossover - variability operator mixing genotypes • Fitness - performance of a phenotype with regard to objective • Iteration - Generation 

17 .Coding and Mapping for Chromosom 

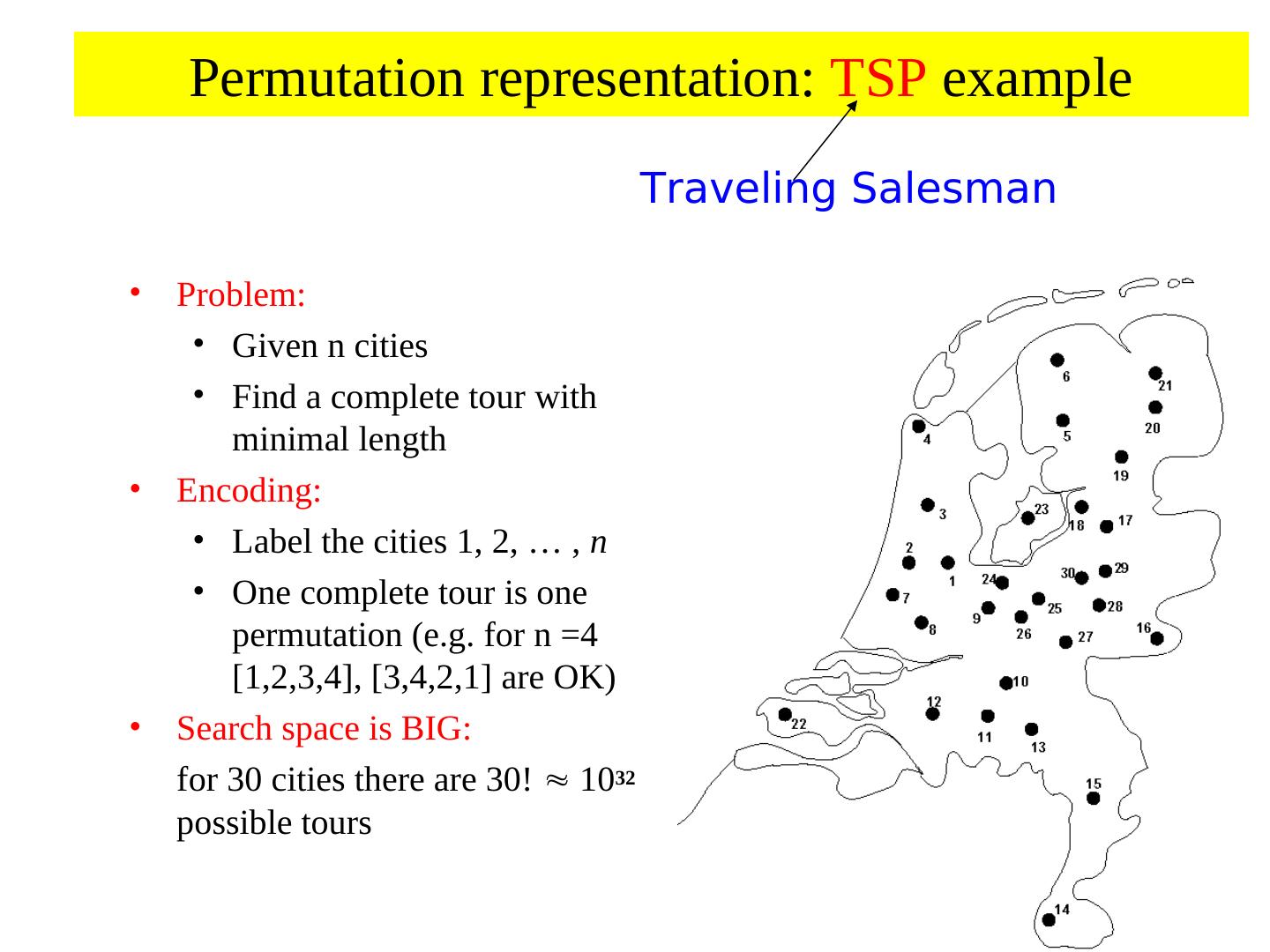
18 . Genetic coding • Finite strings (= genome, represents genotype) • Strings consists of units with information (unit = gene) • One string ( individual) = one possible solution of the problem • Genotype often real numbers or bit string: 1.853 0.492 0 1 0 1 0 1 

19 . Genetic coding and mapping • What should the phenotype look like? • How to encode phenotype as a genotype? • How does one map from genotype to phenotype, considering the sources of variation (mutation and recombination)? – Highly problem dependent! – Hint: small changes to genotype should often result in small changes to phenotype, i.e. similar performance: heritability of traits! – heritability of traits is important  otherwise GA becomes only random search 

20 . Mapping – Example • Binary coding versus Gray coding of a number • Hamming distance: – Number of bits that have to be changed to map one string into another one – E.g. 000 and 001  distance = 1 • Remember: Remember small changes in genotype should cause small changes in phenotype 

21 . Mapping – Example cont‘d • Binary coding of 0-7 (phenotype): 0 000 1 001 2 010 3 011 Long distance complicate 4 100 optimisation because 5 101 neighbouring phenotypes 6 110 are not close together 7 111 

22 . Mapping – Example cont‘d • Binary coding of 0-7 (phenotype): 0 000 1 001 • Hamming distance, e.g.: 2 010 3 011 – 000 (0) and 001 (1) 4 100 • Distance = 1 (optimal) 5 101 – 011 (3) and 100 (4) 6 110 • Distance = 3 (max possible) 7 111 Some close data have high distance! 

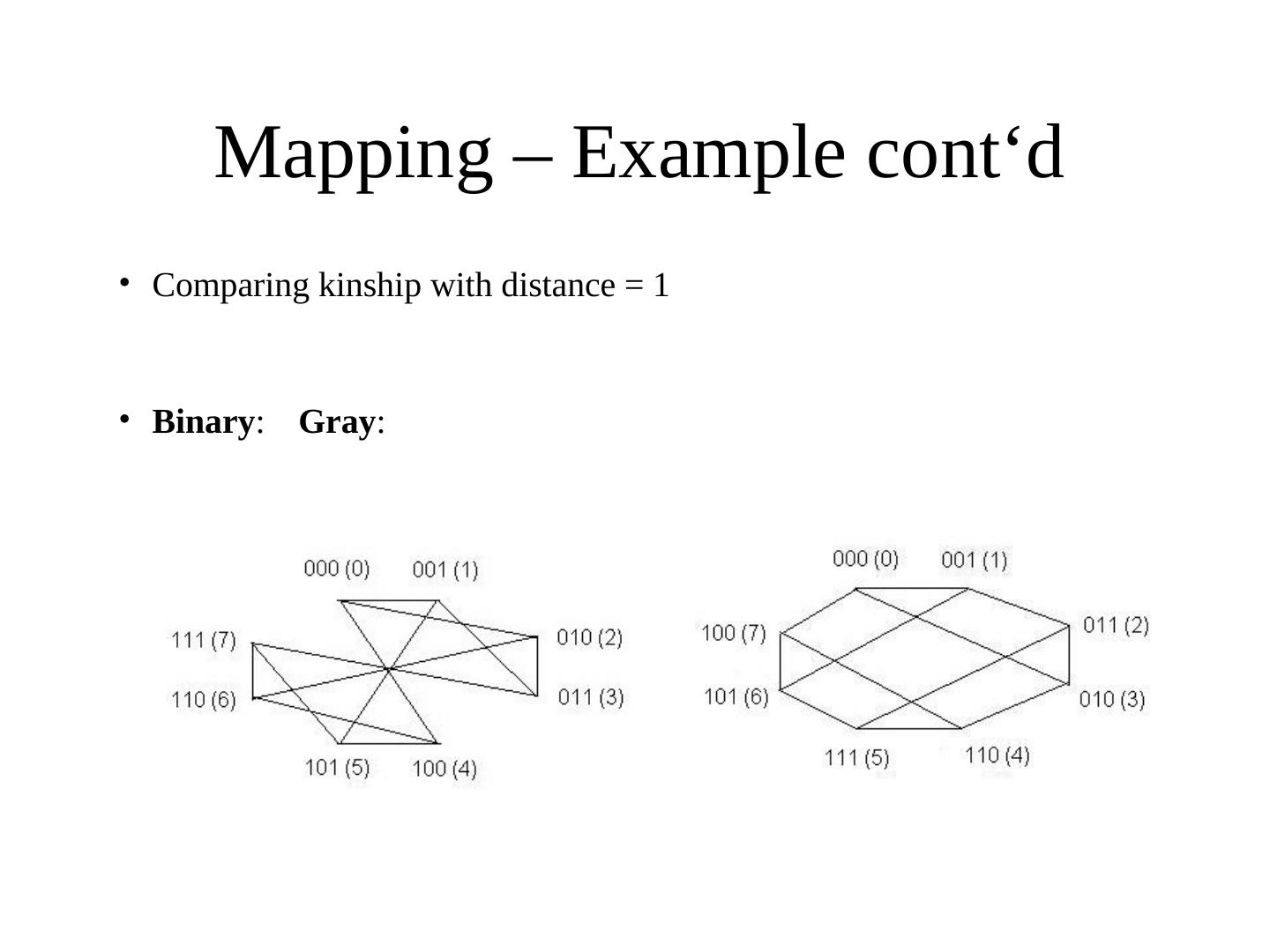
23 . Mapping – Example cont‘d • Gray coding of 0-7: 0 000 1 001 2 011 3 010 4 110 5 111 6 101 7 100 

24 . Mapping – Example cont‘d • Gray coding of 0-7: 0 000 1 001 • Hamming distance: 2 011 – Two neighboring numbers 3 010 (phenotypes) have always a 4 110 genotype distance of 1 (all differ only by one bit flip) – OPTIMAL mapping 5 111 6 101 7 100 

25 . Mapping – Example cont‘d • Comparing kinship with distance = 1 • Binary: Gray: 

26 .CROSSOVER 

27 .poland.virtualave.net/ee/genetic1/3geneticalgorithms.htm Non-Standard Rule-Based Crossover We calculate for every allele separately, using only genes available for this allele http://ib- 

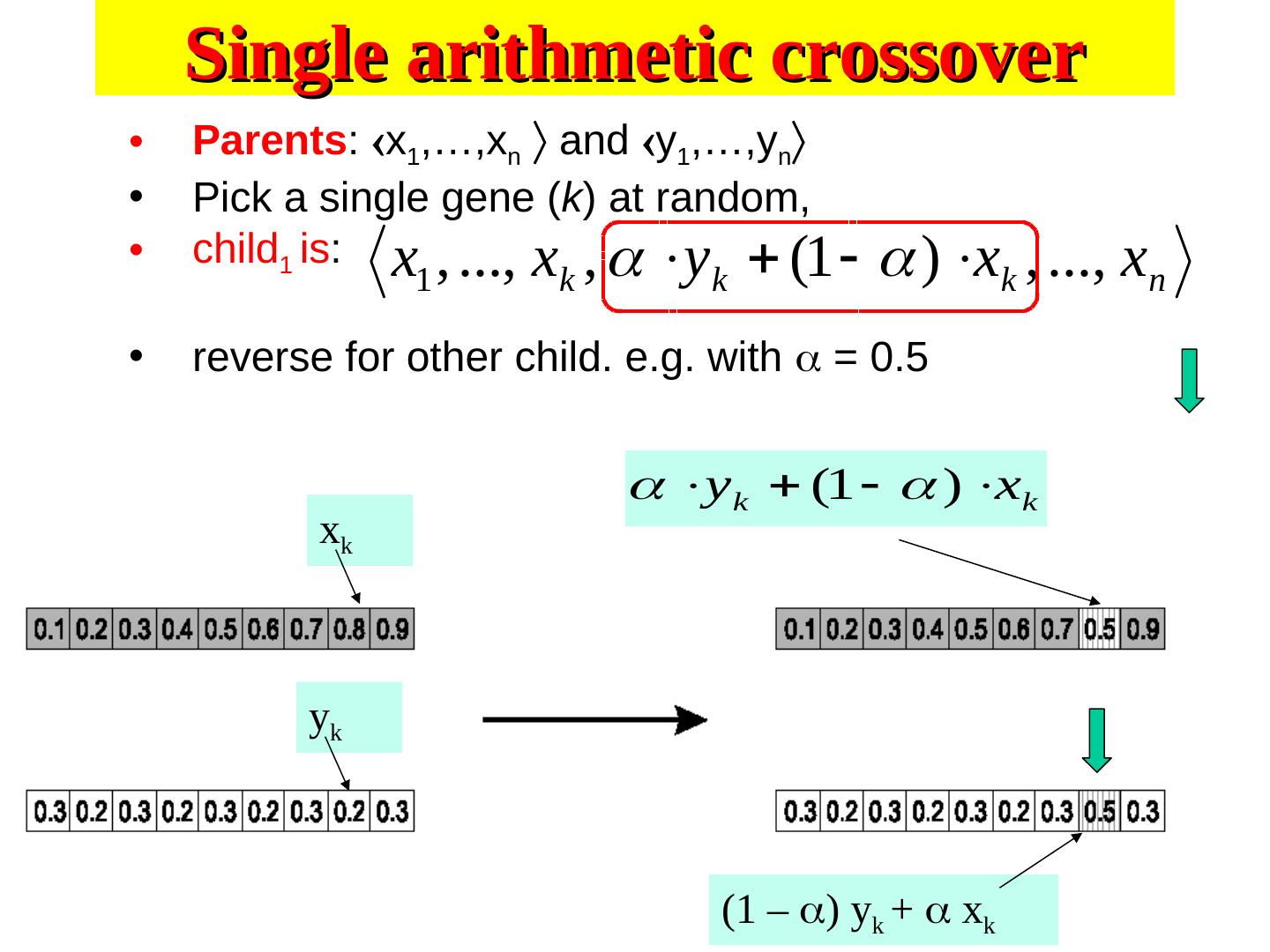
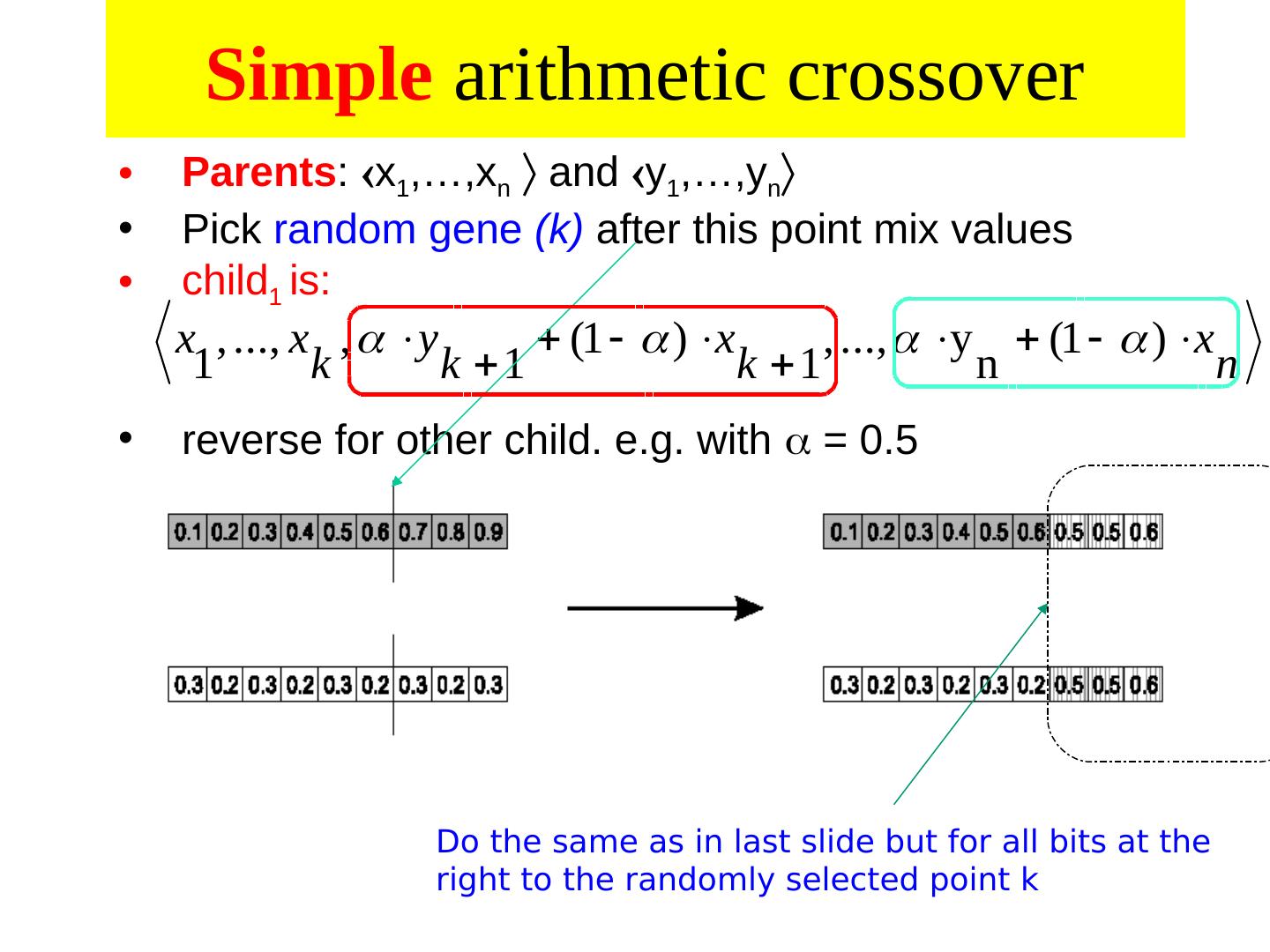
28 .Alternative Crossover Operators • Performance with 1 Point Crossover depends on the order in which the variables occur in the representation – more likely to keep together genes that are near each other – Can never keep together genes from opposite ends of string – This is known as Positional Bias • In some cases the positional bias can be exploited if we know about the structure of our problem, but this is not usually the case 

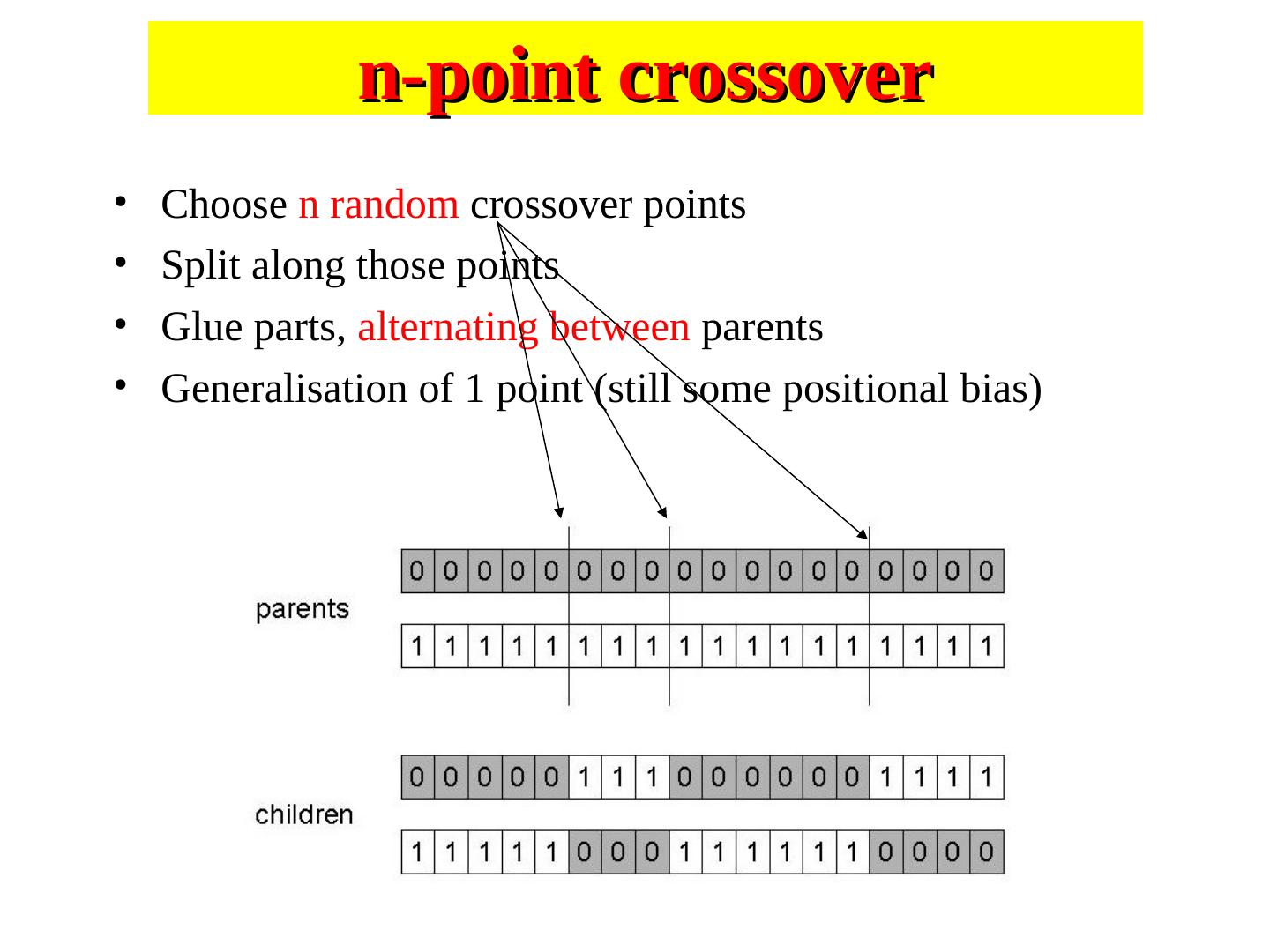
29 . n-point crossover • Choose n random crossover points • Split along those points • Glue parts, alternating between parents • Generalisation of 1 point (still some positional bias)