16_Fuzzy_advanced_SYSTEMS

1 .Misconceptions about Fuzzy concepts 

2 . Fuzziness is not Vague • we shall have a look at some propositions. • Dimitris is six feet tall – The first proposition (traditional) has a crisp truth value of either TRUE or FALSE. • He is tall – The second proposition is vague. – It does not provide sufficient information for us to make a decision, either fuzzy or crisp. – We do not know the value of the pronoun. – Is it Dimitris, John or someone else? 

3 . Fuzziness is not Vague • Andrei is tall – This proposition is a fuzzy proposition. – It is true to some degree depending in the context, i.e., the universe of discourse. – It might be SomeWhat True if we are referring to basketball players or it might be Very True if we are referring to horse-jockeys. 

4 .Fuzziness is not Multi-valued logic – The limitations of two-valued logic were recognised very early. – A number of different logic theories based on multiple values of truth have been formulated through the years. – For example, in three-valued logic three truth values have been employed. – These are TRUTH, FALSE, and UNKNOWN represented by 1, 0 and 0.5 respectively. – In 1921 the first N-valued logic was introduced. – The set of truth values Tn were assumed to be evenly divided over the closed interval [0,1]. – Fuzzy logic may be considered as an extension of multi- valued logic but they are somewhat different. – Multi-valued logic is still based on exact reasoning whereas fuzzy logic is approximate reasoning. 

5 .Fuzziness is not Probability!! ! 

6 . Fuzziness is not Probability • Let X be the set of all liquids (i.e., the universe of discourse) . • Let L be a subset of X which includes all suitable for drinking liquids. A Bottle A label is marked as B The label of bottle B is marked probability of L is 0.9. membership of L is 0.9. Which one would you drink? 

7 . Fuzziness is not Probability • This is better explained using an example. • Let X be the set of all liquids (i.e., the universe of discourse) . • Let L be a subset of X which includes all suitable for drinking liquids. • Suppose now that you find two bottles, A and B. • The labels do not provide any clues about the contents. • Bottle A label is marked as membership of L is 0.9. • The label of bottle B is marked as probability of L is 0.9. • Given that you have to drink from the one you choose, the problem is of how to interpret the labels. 

8 . Fuzziness is not Probability • Well, membership of 0.9 means that the contents of A are fairly similar to perfectly potable liquids. • If, for example, a perfectly liquid is pure water then bottle A might contain, say, tonic water. • Probability of 0.9 means something completely different. • You have a 90% chance that the contents are potable and 10% chance that the contents will be unsavoury, some kind of acid maybe. • Hence, with bottle A you might drink something that is not pure but with bottle B you might drink something deadly. So choose bottle A. 

9 . Fuzziness is not Probability • Opening both bottles you observe beer (bottle A) and hydrochloric acid (bottle B). • The outcome of this observation is that the membership stays the same whereas the probability drops to zero. • All in all: – probability measures the likelihood that a future event will occur, – fuzzy logic measures the ambiguity of events that have already occurred. • In fact, fuzzy sets and probability exist as parts of a greater Generalized Information Theory. • This theory also includes: – Dempster-Shafer evidence theory, – possibility theory, – and so on. 

10 .Applications of Fuzzy concepts 

11 . Fuzzy inference for practical control by Mamdani The most commonly used fuzzy inference technique is the so-called Mamdani method. In 1975, Professor Ebrahim Mamdani of London University built one of the first fuzzy systems to control a steam engine and boiler combination. He applied a set of fuzzy rules supplied by experienced human operators. 

12 . Mamdani versus Sugeno Models • Most of our examples were for Mamdani Model. • Another famous model comes from Sugeno. • We will discuss and compare both models.Mo 

13 .3/18 and Soft ng 9 Sugeno fuzzy inference  Mamdani-style inference, as we have just seen, requires us to find the centroid of a two-dimensional shape by integrating across a continuously varying function. In general, this process is not computationally efficient.  Michio Sugeno suggested to use a single spike, a singleton, as the membership function of the rule consequent. A singleton, or more precisely a fuzzy singleton, is a fuzzy set with a membership function that is unity at a single particular point on the universe of discourse and zero everywhere else. 

14 .4/18 and Soft ng 9 Sugeno-style fuzzy inference is very similar to the Mamdani method. Sugeno changed only a rule consequent. Instead of a fuzzy set, he used a mathematical function of the input variable. The format of the Sugeno-style fuzzy rule is IF x is A AND y is B THEN z is f (x, y) where x, y and z are linguistic variables; A and B are fuzzy sets on universe of discourses X and Y, respectively; and f (x, y) is a mathematical function. 

15 .5/18 and Soft ng 9 The most commonly used zero-order Sugeno fuzzy model applies fuzzy rules in the following form: IF x is A AND y is B THEN z is k where k is a constant. In this case, the output of each fuzzy rule is constant. All consequent membership functions are represented by singleton spikes. 

16 .Sugeno-style rule evaluation 1 1 1 A3 B1 0.1 OR 0.1 0.0 (max) 0 x1 X 0 y1 Y 0 k1 Z Rule 1: IF x is A3 (0.0) OR yis B1 (0.1) THEN z is k1 (0.1) 1 1 1 0.7 A2 0.2 B2 AND 0.2 (min) 0 x1 X 0 y1 Y 0 k2 Z Rule 2: IF xis A2 (0.2) AND yis B2 (0.7) THEN z is k2 (0.2) 1 1 A1 0.5 0.5 0 x1 X 0 k3 Z Rule 3: IF xis A1 (0.5) THEN z is k3 (0.5) 

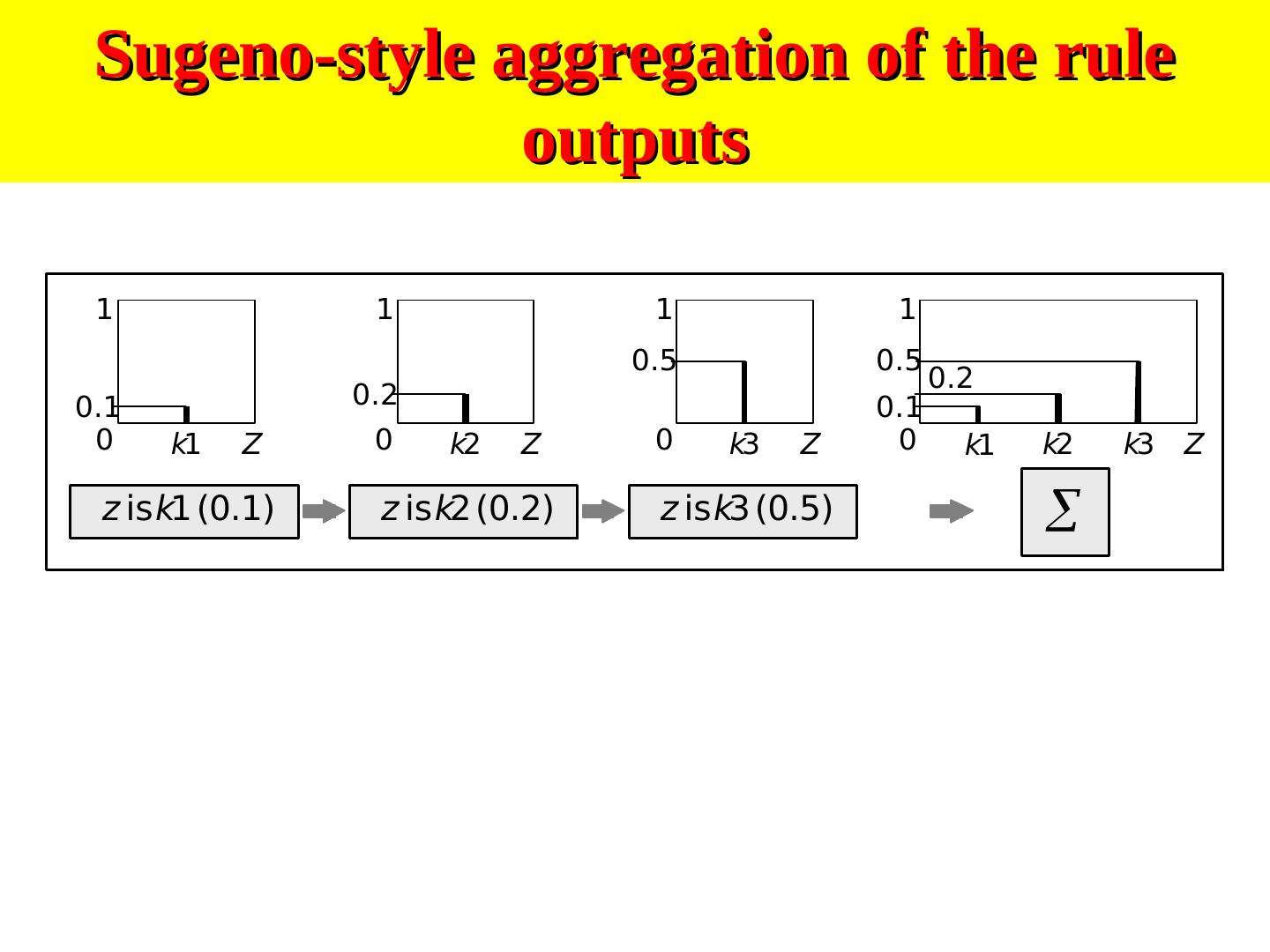
17 .7/18 and Soft ng 9 Sugeno-style aggregation of the rule outputs 1 1 1 1 0.5 0.5 0.2 0.1 0.2 0.1 0 k1 Z 0 k2 Z 0 k3 Z 0 k1 k2 k3 Z z isk1 (0.1) z isk2 (0.2) z isk3 (0.5)  

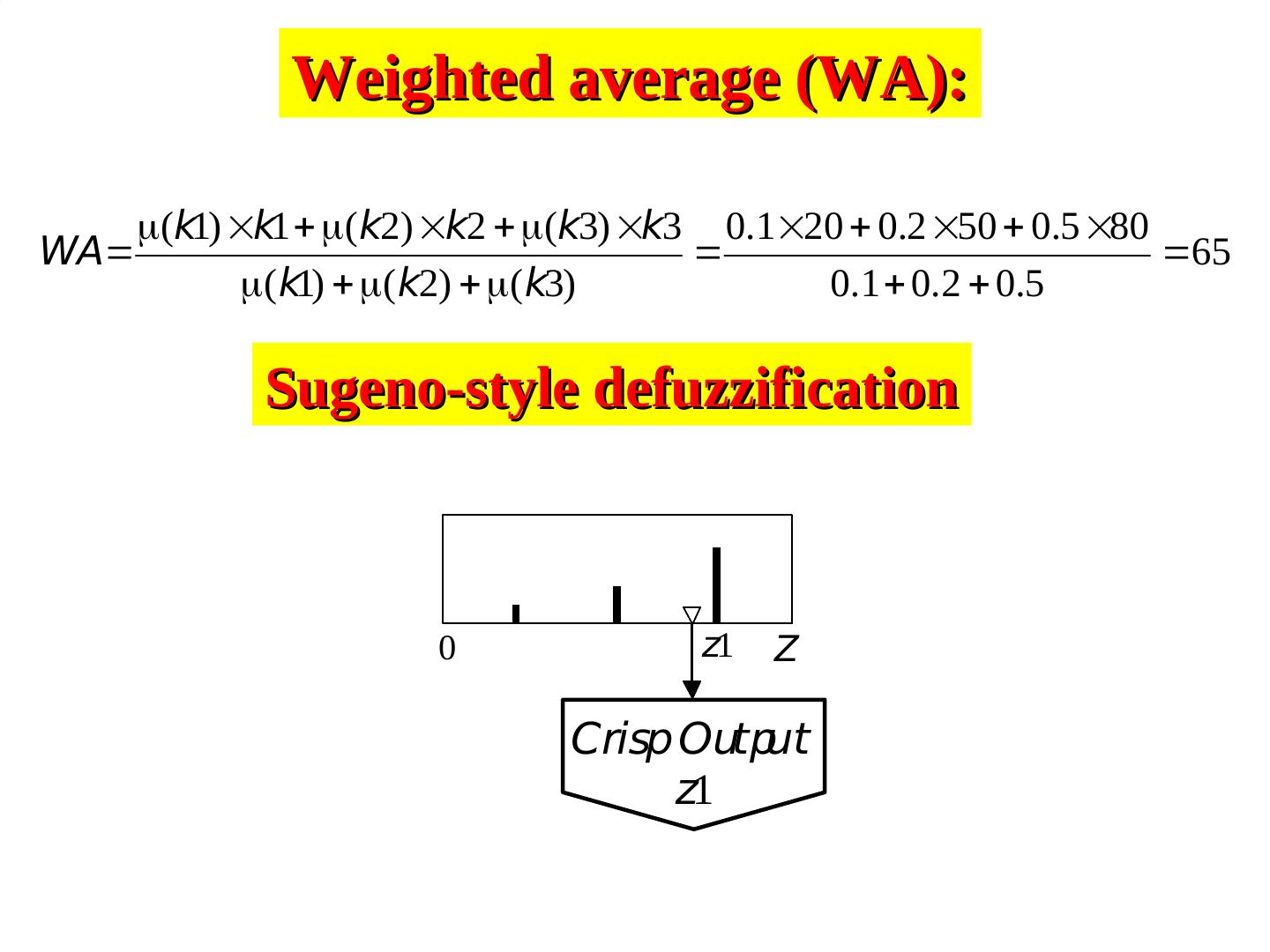
18 .8/18 and Soft ng 9 Weighted average (WA): (k1) k1  ( k2) k2  (k3) k3 0.120  0.2 50  0.5 80 WA  65 ( k1)  ( k2)  ( k3) 0.1  0.2  0.5 Sugeno-style defuzzification 0 z1 Z Crisp Output z1 

19 .9/18 and Soft ng 9 How to make a decision on which method to apply – Mamdani or Sugeno?  Mamdani method is widely accepted for capturing expert knowledge. It allows us to describe the expertise in more intuitive, more human-like manner. However, Mamdani-type fuzzy inference entails a substantial computational burden.  On the other hand, Sugeno method is computationally effective and works well with optimisation and adaptive techniques, which makes it very attractive in control problems, particularly for dynamic nonlinear systems. 

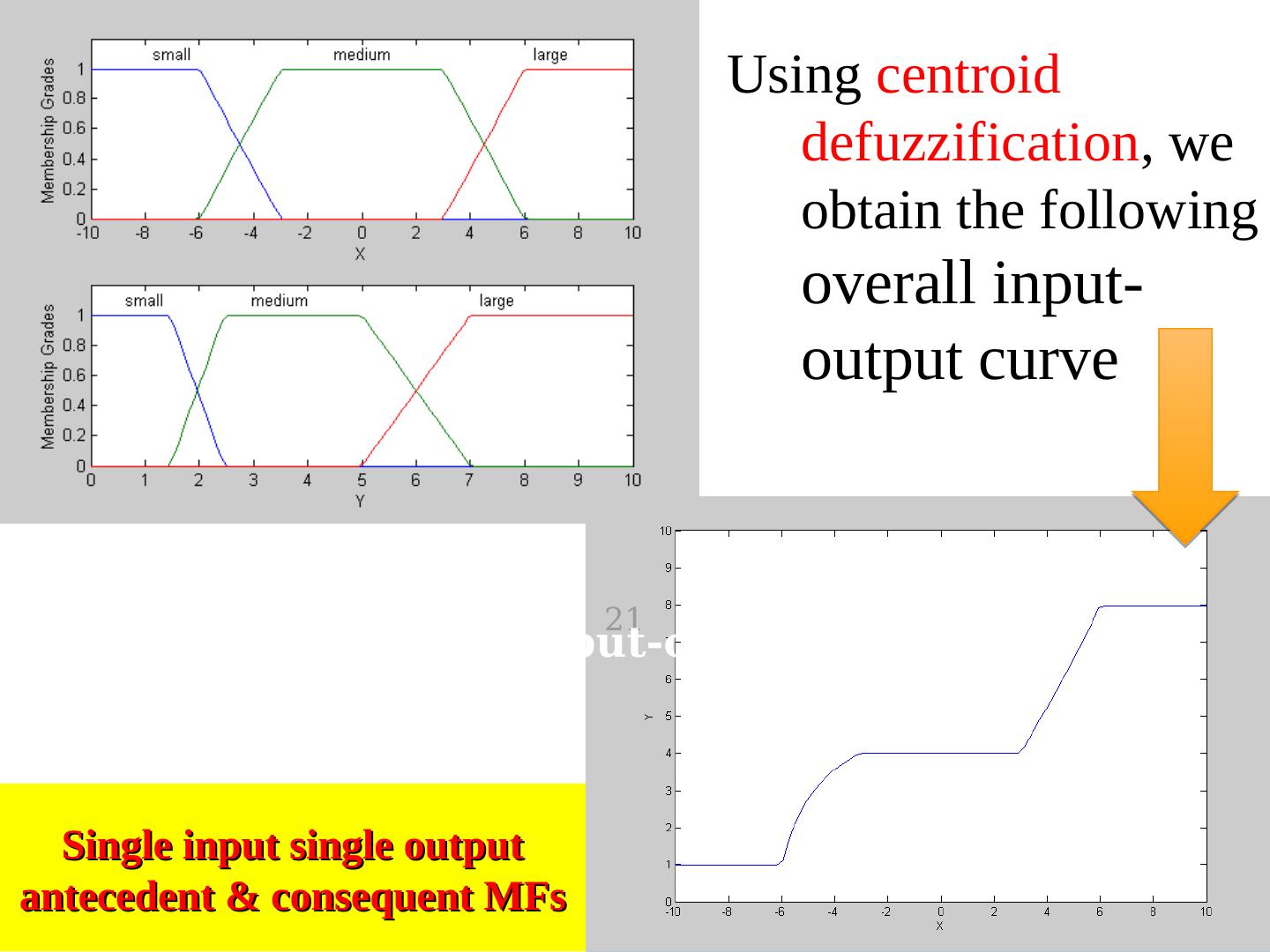
20 .Example 4 (Mamdani Fuzzy Model) Single input single output Mamdani fuzzy model with 3 rules: If X is small then Y is small  R1 If X is medium then Y is medium  R2 Is X is large then Y is large  R3 X = input [-10, 10] Y = output [0,10] 

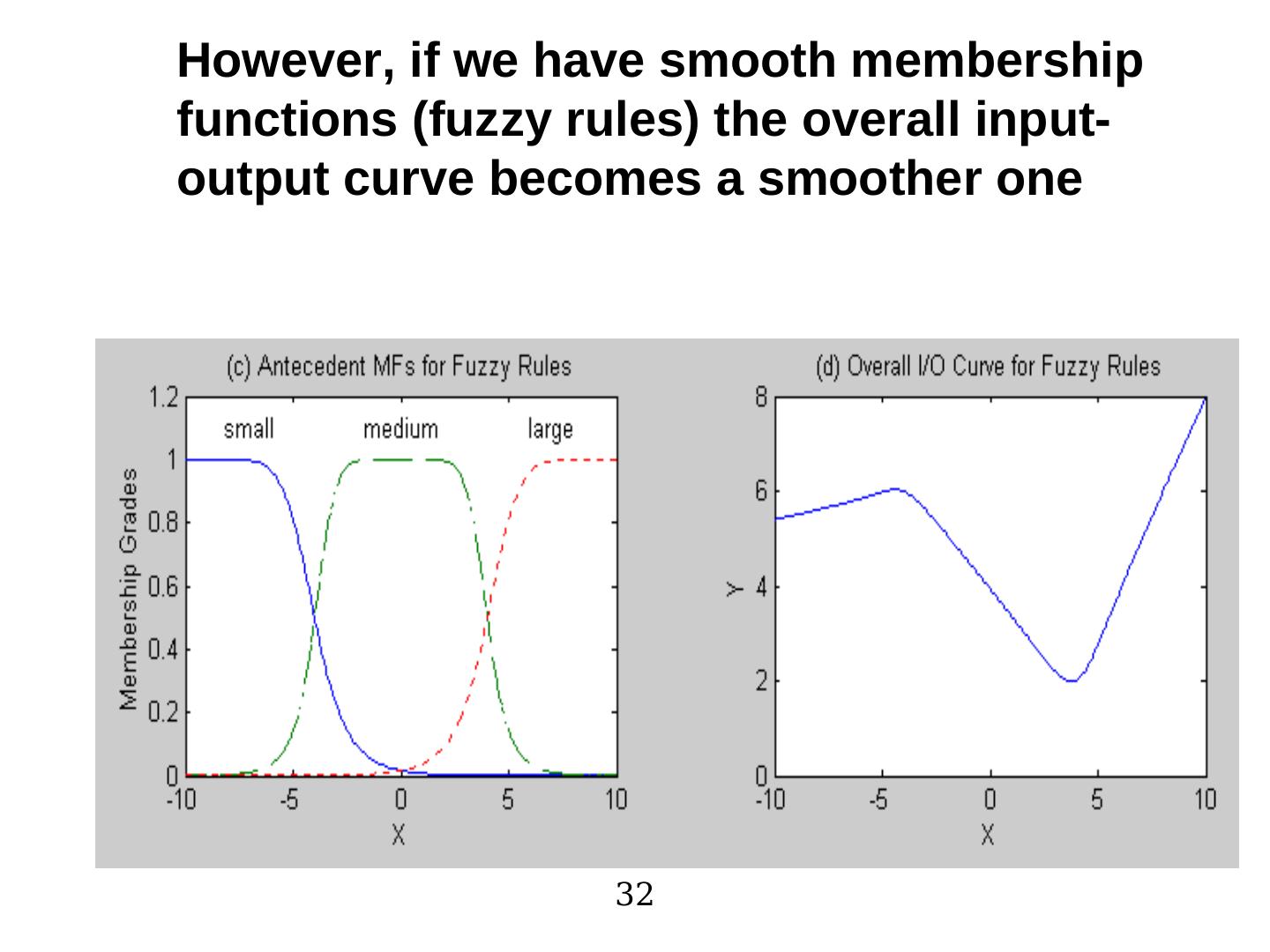
21 . Using centroid defuzzification, we obtain the following overall input- output curve 21 Overall input-output curve Single input single output antecedent & consequent MFs 

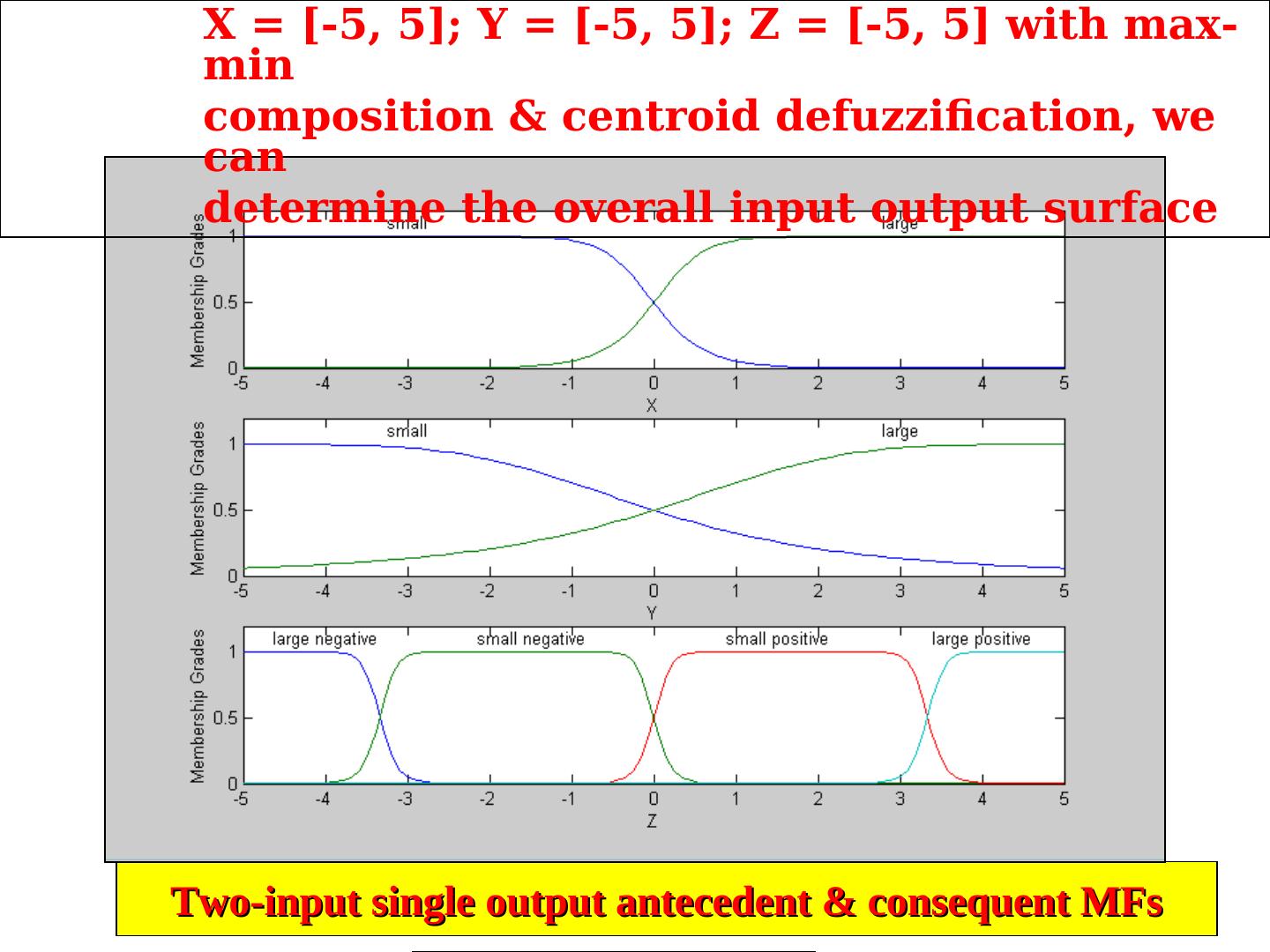
22 ./18 Example 5 and Soft ng 9 (Mamdani Fuzzy model) Two input single-output Mamdani fuzzy model with 4 rules: If X is small & Y is small then Z is negative large If X is small & Y is large then Z is negative small If X is large & Y is small then Z is positive small If X is large & Y is large then Z is positive large 

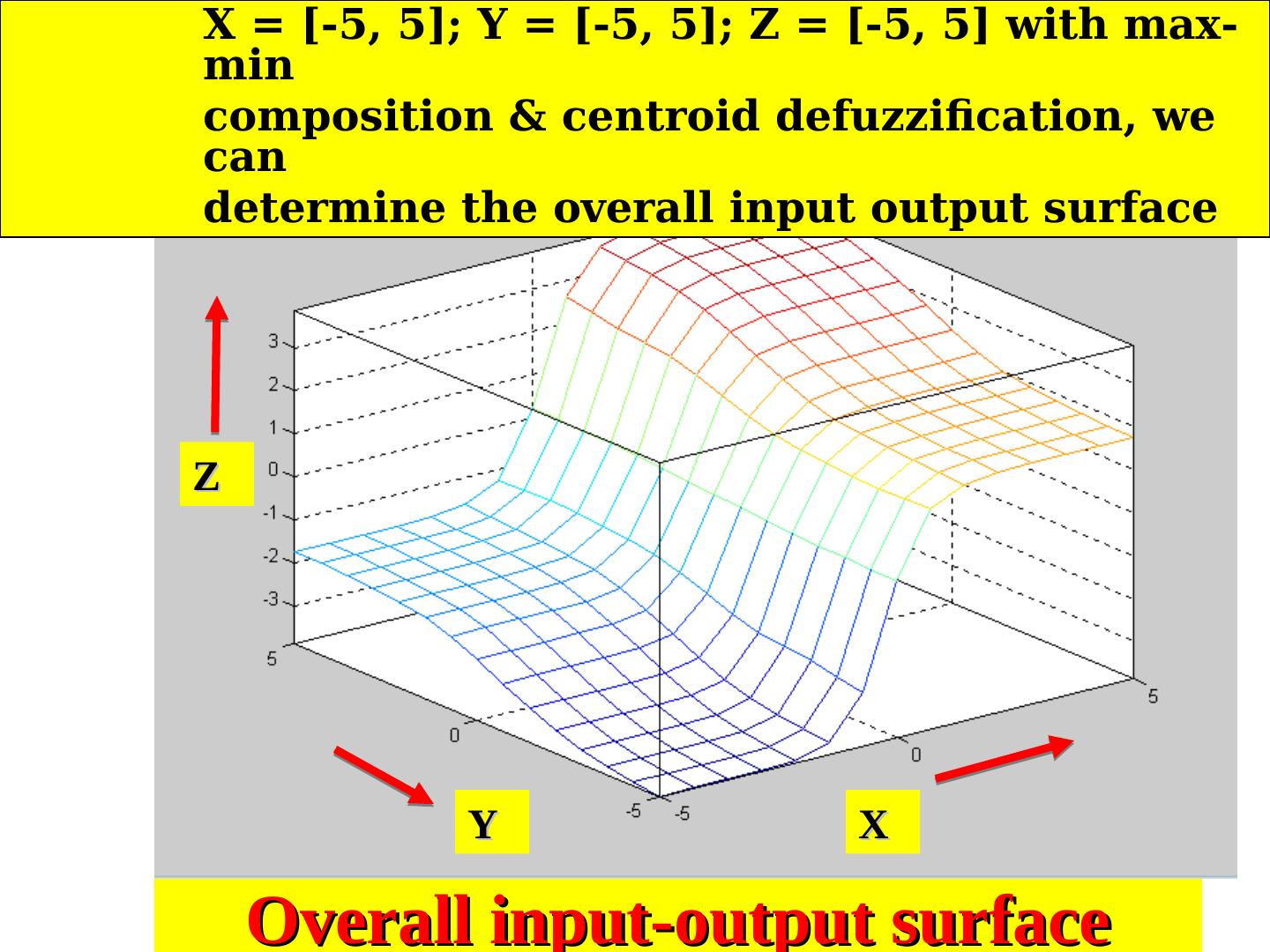
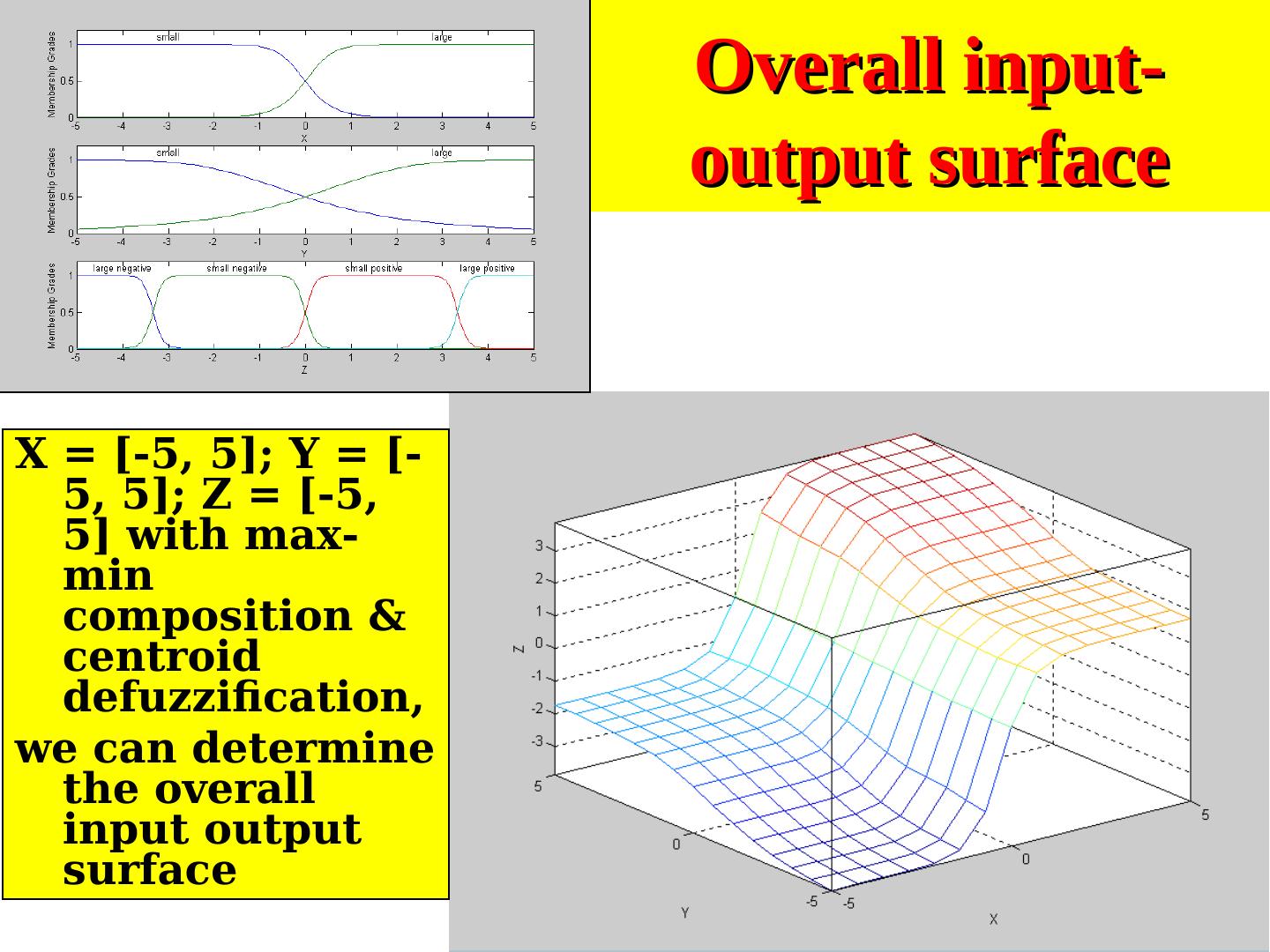
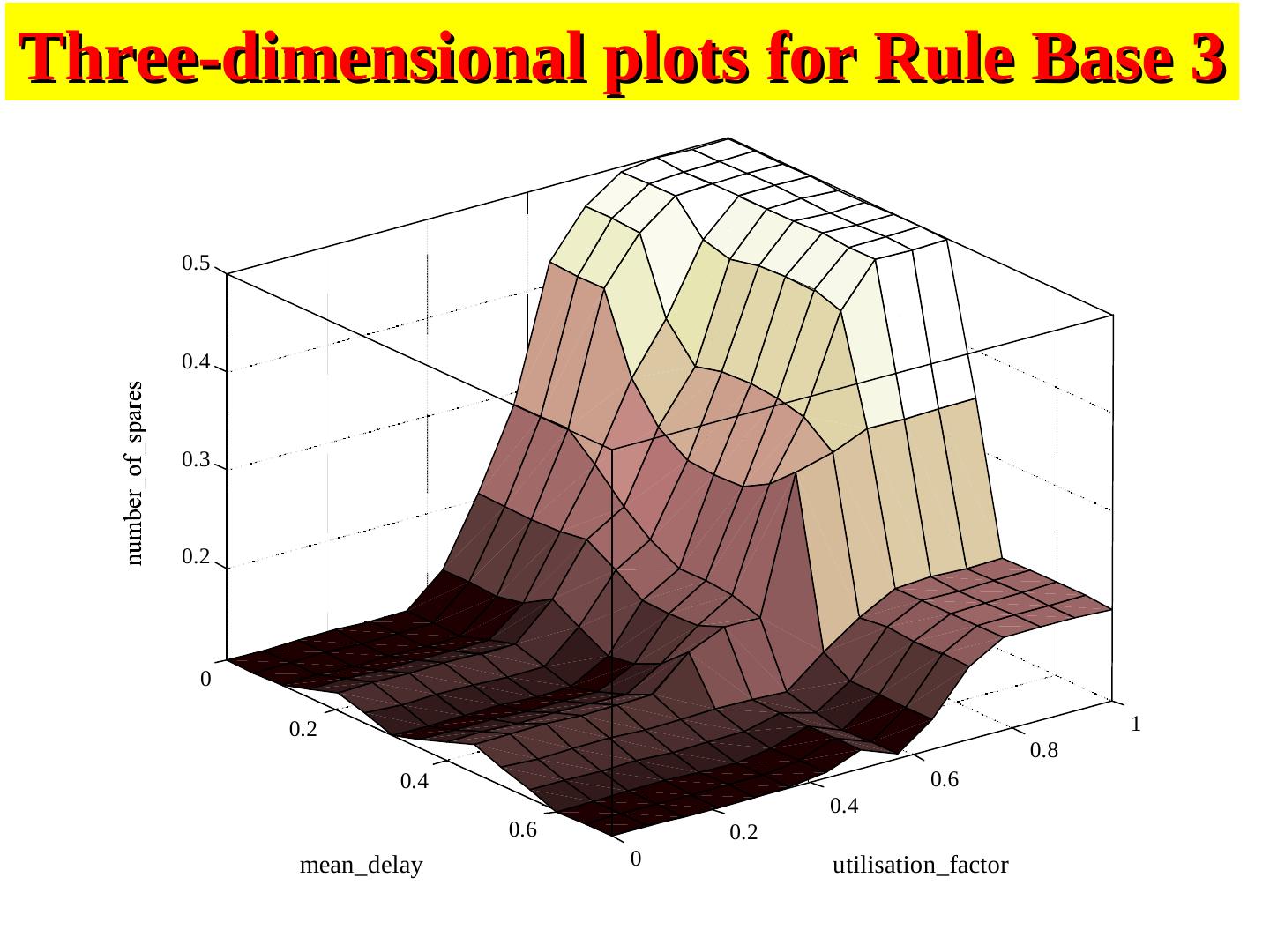
23 . X = [-5, 5]; Y = [-5, 5]; Z = [-5, 5] with max- min composition & centroid defuzzification, we can determine the overall input output surface Two-input single output antecedent & consequent MFs 

24 ./18 and Soft X = [-5, 5]; Y = [-5, 5]; Z = [-5, 5] with max- ng 9 min composition & centroid defuzzification, we can determine the overall input output surface Z Y X Overall input-output surface 

25 ./18 and Soft ng 9 Overall input- output surface X = [-5, 5]; Y = [- 5, 5]; Z = [-5, 5] with max- min composition & centroid defuzzification, we can determine the overall input output surface 

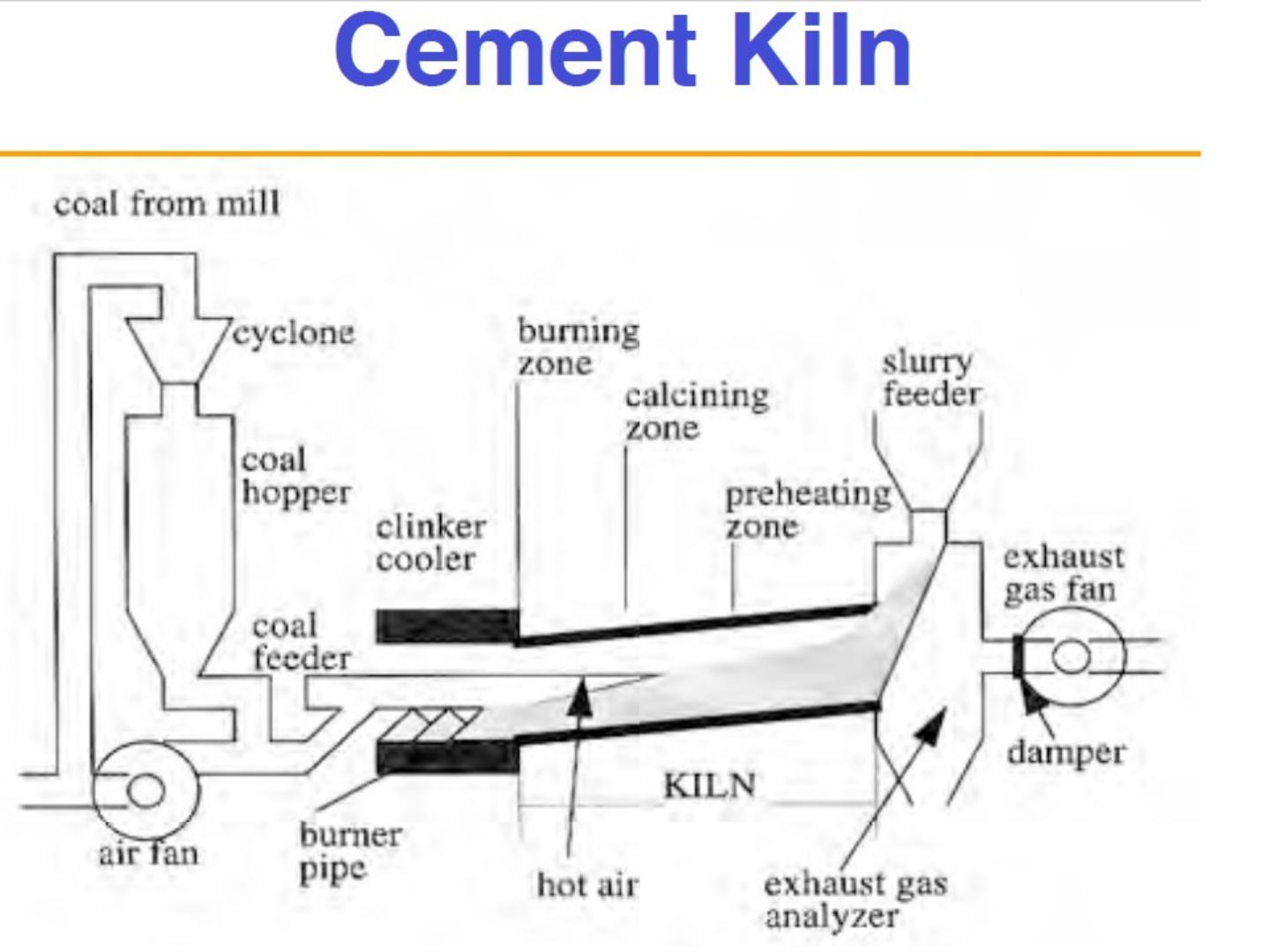
26 .EXAMPLE 6 Example of Mamdani: Cement Kiln Example 

27 .

28 .

29 .