- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
13_Fuzzy_Logic_direct approach-examples
展开查看详情
1 .
2 . A great man who created a complete new mathematics with many practical applications.
3 . Practical examples of Linguistic variables
4 . Linguistic variables in Expert Systems • Expert Systems are based on hundreds of “If the Else rules that combine inputs , logic and outputs • Similar to binary logic and state machines. • We can create similar Fuzzy Expert Systems • Looking at the production rules of either a expert system or a fuzzy expert system one can not see any differences – except that the fuzzy system is employing linguistic descriptors rather than absolute numerical values. – However, both parts of fuzzy rules have associated `levels of belief' something lacking in traditional production rules.
5 . What is good about fuzzy expert systems • Observe that in traditional production rules even when more than one rule applies only one executes. – With fuzzy rules all applicable rules contribute in calculating the resulting output. •All in all, fuzzy expert systems require fewer production rules since fuzzy rules embody more information.
6 .Linguistic variables in Fuzzy Expert Systems • A major reason behind using fuzzy logic is the use of linguistic expressions. expressions • A linguistic variable consists of: – the name of the variable (u), – the term set of the variable (T(u)), – its universe of discourse (U) in which the fuzzy sets are defined, – a syntactic rule for generating the names of values of u, and – a semantic rule for associating with each value its meaning.
7 . More FUZZY LOGIC SYSTEMS APPLICATIONS • 1. Discuss a Fuzzy Logic Control System • 2. Steps in Designing a Fuzzy Logic Control System • 3. Design of a Fuzzy Logic Control System: – Input membership function, – Fuzzy logic rules table, – Output membership function.
8 .Components of Fuzzy system: • The components of a conventional expert system and a fuzzy system are the same. • Fuzzy systems though contain `fuzzifiers’. – Fuzzifiers convert crisp numbers into fuzzy numbers, • Fuzzy systems contain `defuzzifiers', – Defuzzifiers convert fuzzy numbers into crisp numbers.
9 . Fuzzification • The function of the fuzzification component is to convert crisp numbers to equivalent fuzzy sets. • Please notice that the inputs might require some pre-processing in order to fit the range of the fuzzy system.
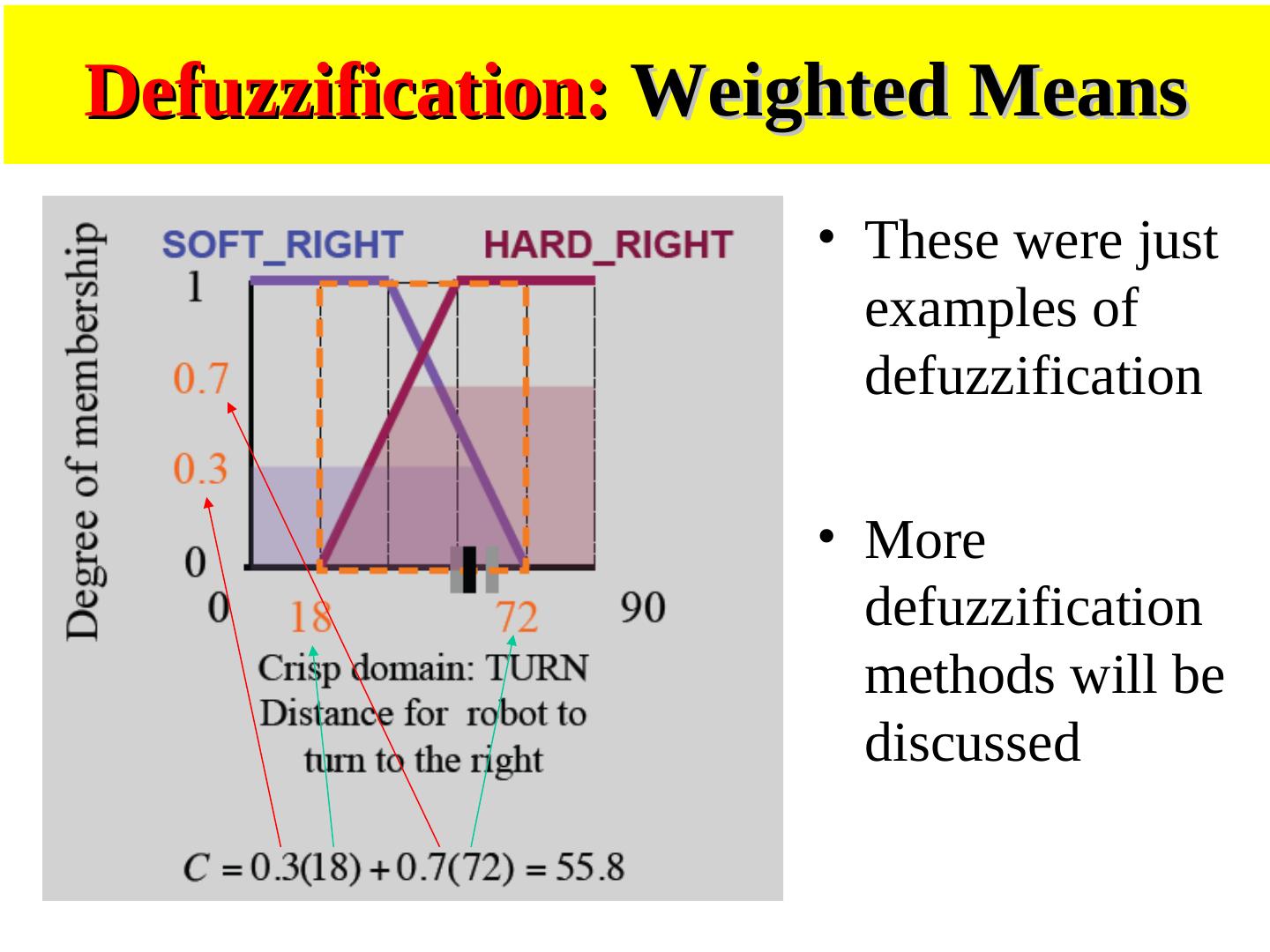
10 . Defuzzification • The output of the combined operation is defuzzified before being broadcast to the external world. • This implies the conversion of a fuzzy set to a crisp number. • There are several techniques of defuzzification.
11 . Conventional vs Fuzzy system Components of a ... conventional expert fuzzy system system precisevalue physical physical device device fuzzy fuzzifier value precise precise precise value value value fuzzy model knowledge model fuzzy defuzzifier value
12 . For example: •if u is temperature, •then its term set T(temperature) could be: – T(temperature)={cold, cool, cool warm, hot} over a universe of discourse U=[0,300]. linguistic Temperature variable Cold Cool Warm Hot term set fuzzy set representation
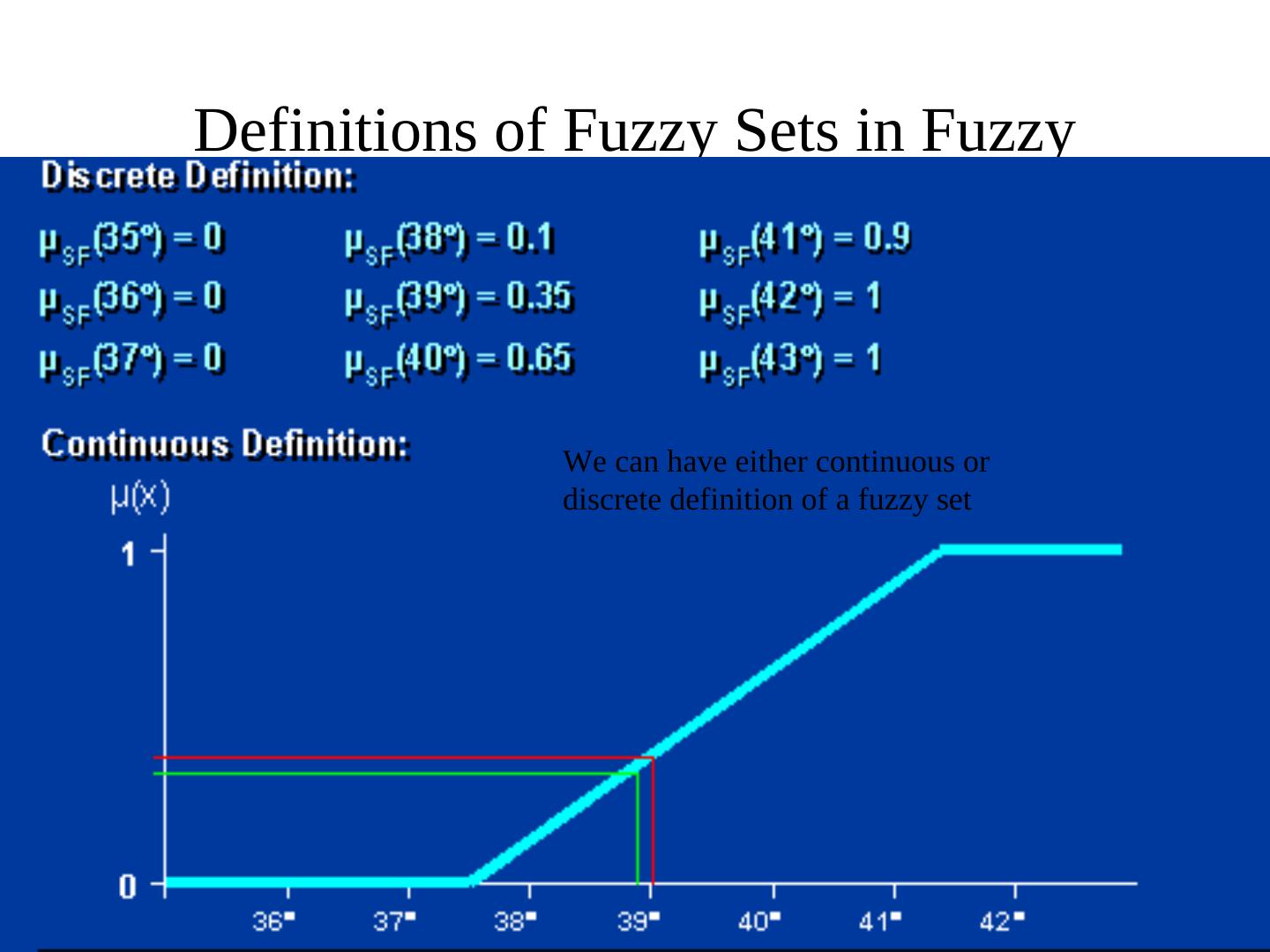
13 .Definitions of Fuzzy Sets in Fuzzy Expert Systems We can have either continuous or discrete definition of a fuzzy set
14 . Example of a Linguistic Variable • …. Terms, Degree of Membership, Membership Function, Base Variable…..
15 . Fuzzy Logic Principles and Learning
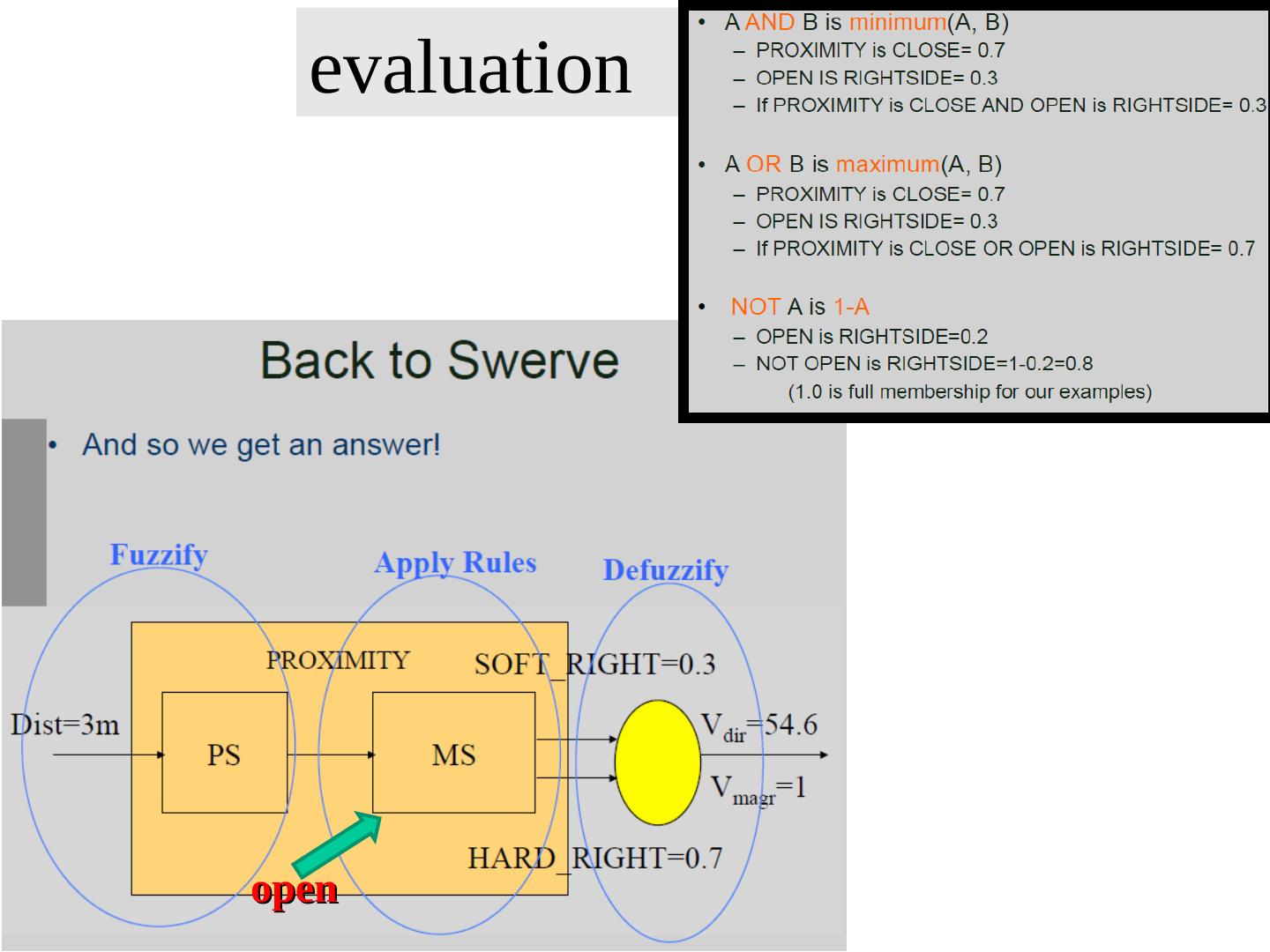
16 . Fuzzy Logic Principles • Fuzzy control produces actions using a set of fuzzy rules based on fuzzy logic Fuzzy controller involves: fuzzifying: mapping sensor readings into a set of fuzzy inputs fuzzy rule base: a set of IF-THEN rules fuzzy inference: maps fuzzy sets onto other fuzzy sets using membership fncts. defuzzifying: mapping a set of fuzzy outputs onto a set of crisp output commands
17 .Fuzzy Control
18 . Fuzzy Control • Fuzzy logic allows for specifying behaviors as fuzzy rules Such behaviors can be smoothly blended together (e.g., Flakey robot) Fuzzy rules can be learned Any learning method can be used
19 .Industrial Application of Fuzzy Logic Control
20 .History, State of the Art, and Future Development of fuzzy logic systems
21 .Uncertainty
22 .Types of Uncertainty and the Modeling of Uncertainty • Stochastic Uncertainty: – The Probability of Hitting the Target is 0.8 Three Examples of Lexical Uncertainty:
23 . Methods of inference under uncertainty • inference under uncertainty is very important to consider when using expert systems since sometimes data is uncertain (i.e., ambiguous, incomplete, noisy etc.). • A number of theories have been devised to deal with uncertainty. – These include : • classical probability, • Bayesian probability, • Shannon theory, • Dempster-Shafer theory, • other. – A popular method of dealing with uncertainty uses certainty factors
24 . Methods of inference under uncertainty • The certainty factor indicates the net belief in the conclusion and premises of a rule based on some evidence. • Certainty factors are hand-crafted by asking potential users questions such as `How much do you believe that opening valve x will start a flooding' and `How much do you disbelieve that opening valve x will start a flooding'. • The degree of certainty is the difference between the two responses.
25 . Fuzzy Logic practical easy examples
26 . Controller Structure • Fuzzification – Scales and maps input variables to fuzzy sets – Linear or not – Single input single output • Inference Mechanism – Approximate reasoning – Deduces the control action – Various shapes of membership functions – Various operators, not only MIN, MAX and NOT. • Defuzzification – Convert fuzzy output values to control signals – Defuzzification can be a single output linear or nonlinear function with fuzzy input and crisp output – Defuzzification can be built-into the “output sum” which can be other function than MAX or SUM or TRUNCATED SUM.
27 . Linguistic • How to combine various, even conflicting pieces of advise?
28 .Examples of Operations on the same variable A B AB AB A
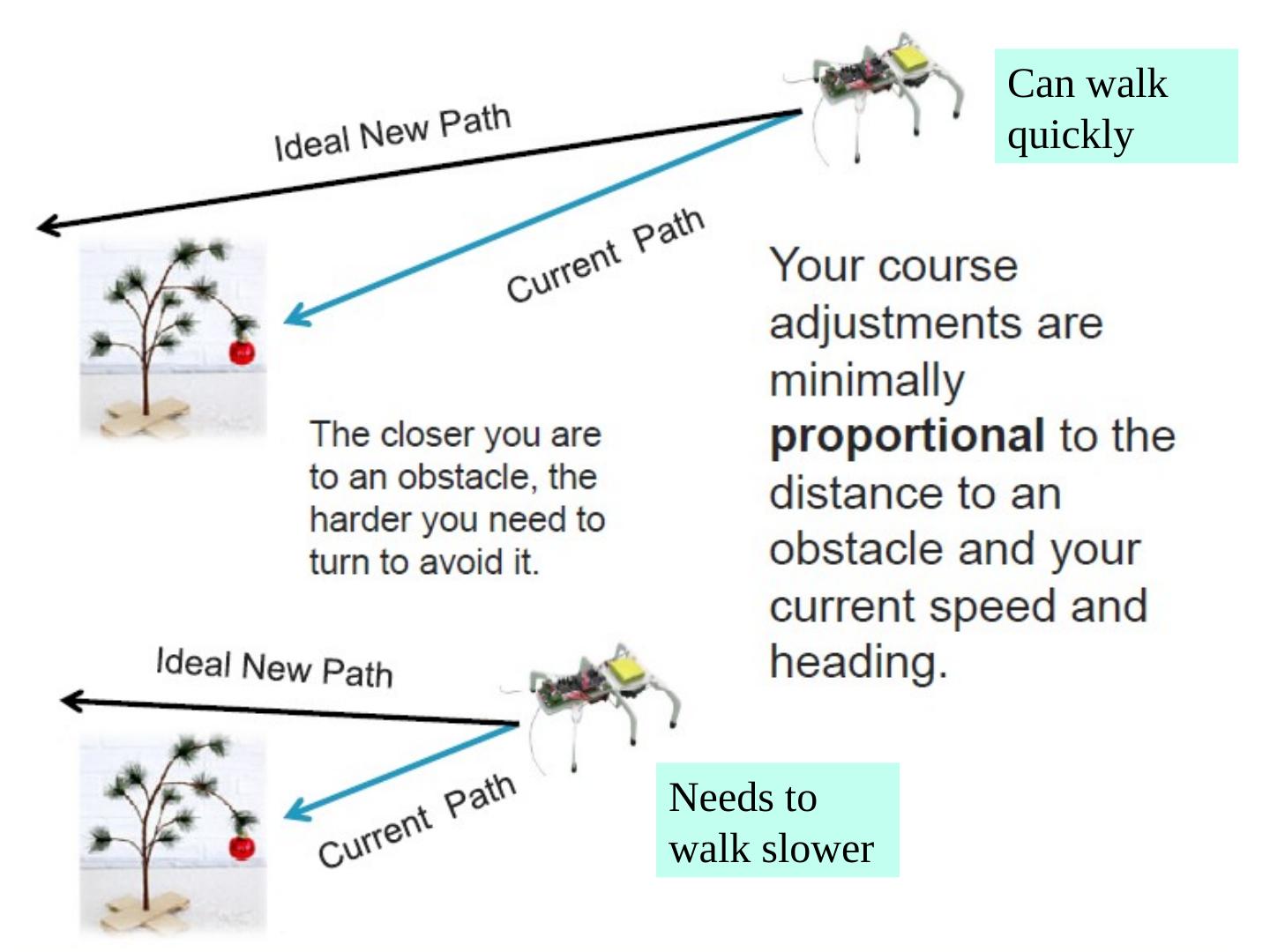
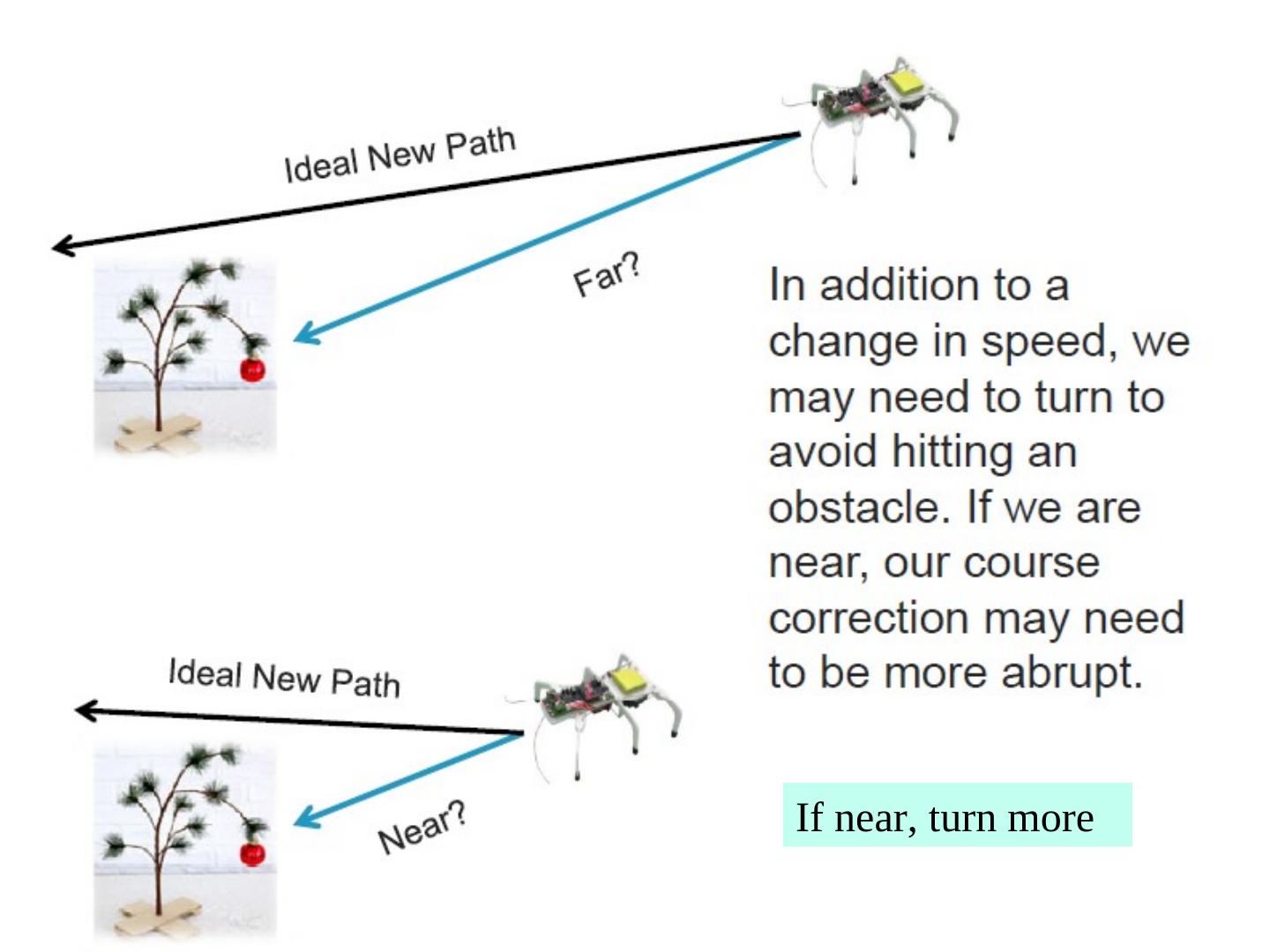
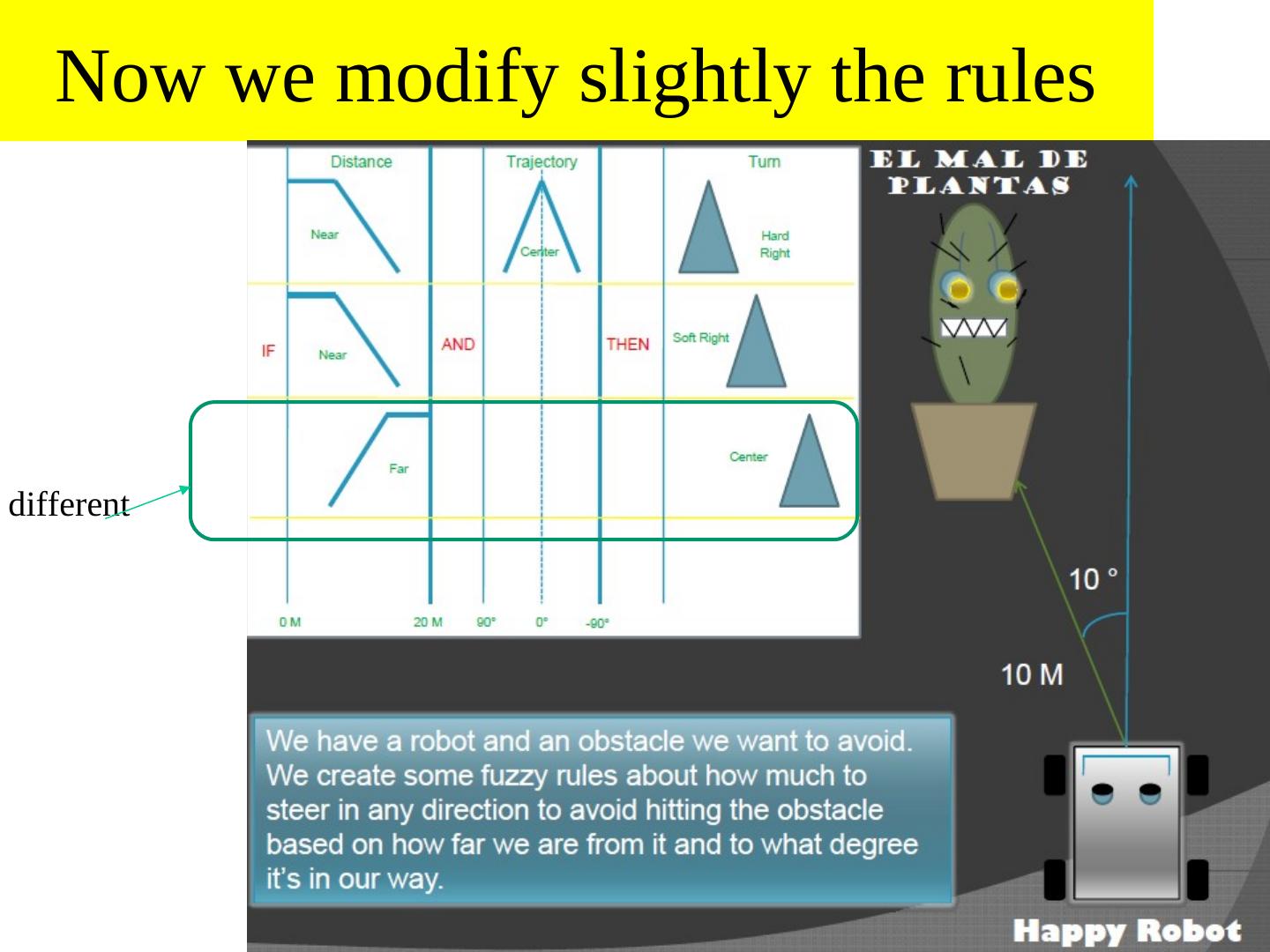
29 . Example 1: Using Fuzzy Logic for a Line Following Robot