06_RobotTheatre_Editors_Event Diagrams.

1 .Languages and tools to create theatre scripts for ROBOT THEATRE

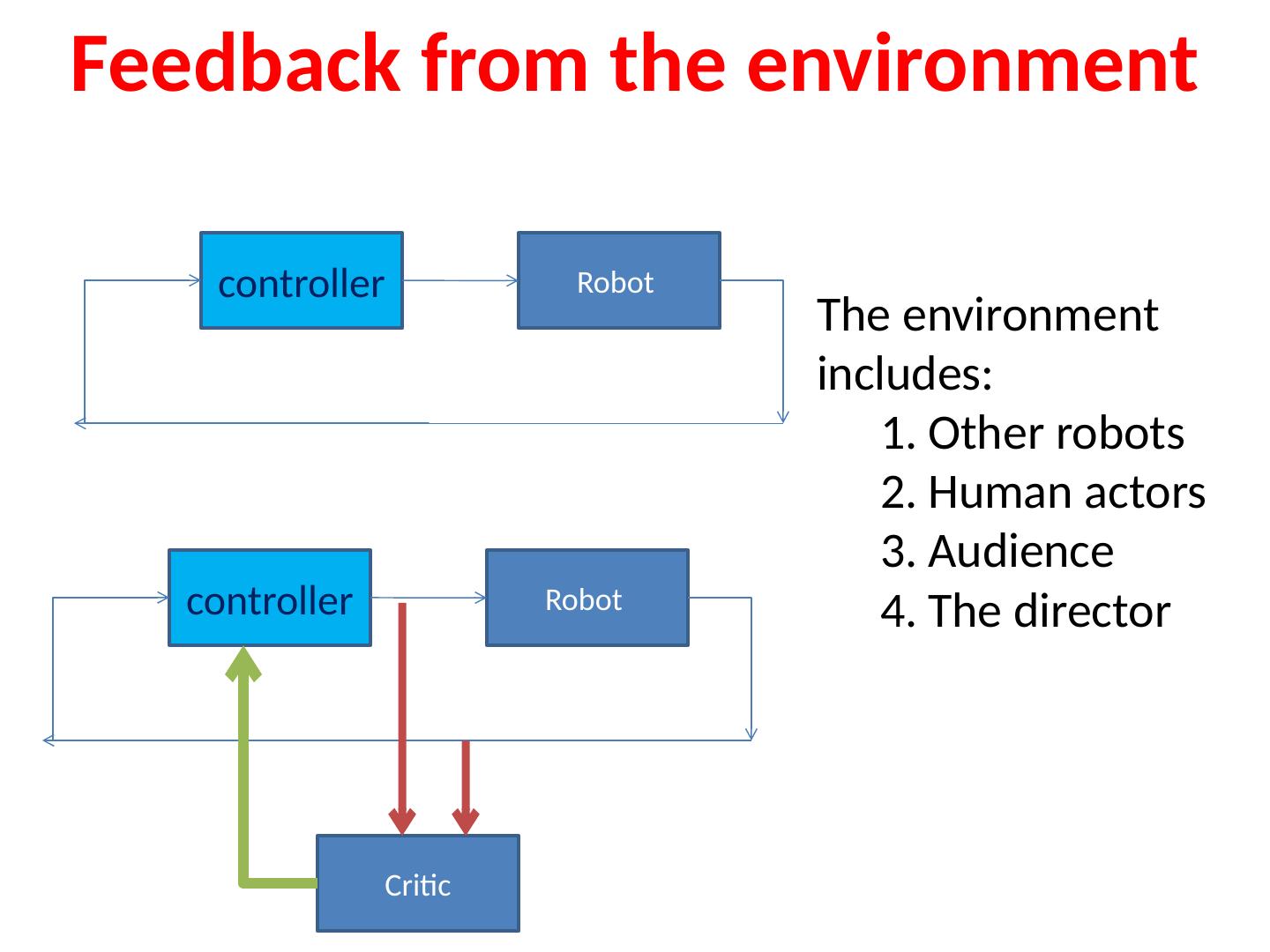
2 .Theory of Robot Theatre?

3 .Professor Einstein Schr ö dinger Cat On Synthesis and Verification from Event Diagrams in a Robot Theatre Marek Perkowski , Aditya Bhutada , Martin Lukac + , and Mathias Sunardi Portland State University, Department of Electrical and Computer Engineering, + Tohoku University, Kameyama Laboratory, Sendai, Japan Physics Debate Theatre of puppet robots Dr. Niels Bohr

4 .The stage of Portland Cyber Theatre in FAB building

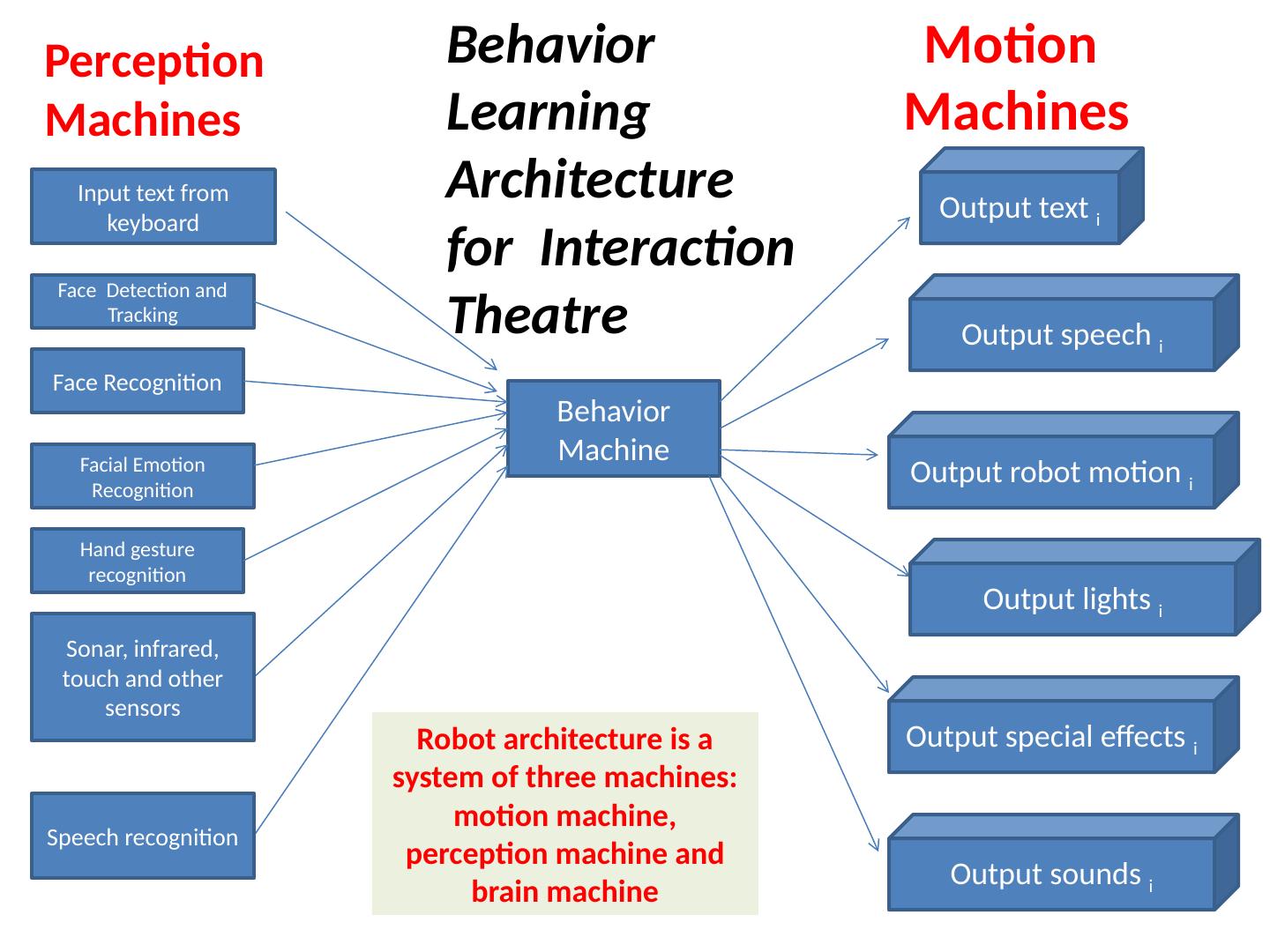
5 .\ Perception = Input Motion = Output Behavior = Input/Output Terminology

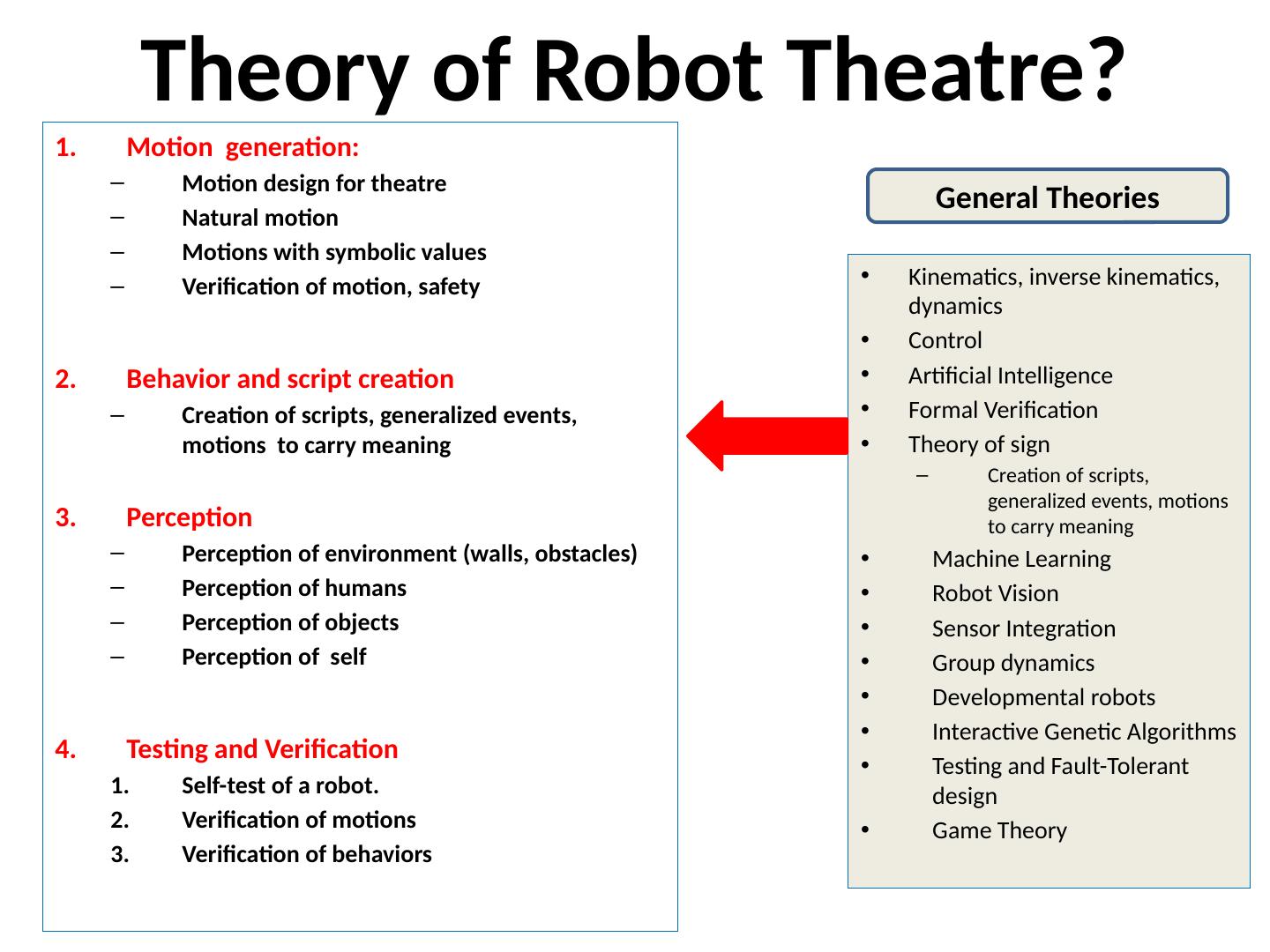
6 .Theory of Robot Theatre? Motion generation: Motion design for theatre Natural motion Motions with symbolic values Verification of motion, safety Behavior and script creation Creation of scripts, generalized events, motions to carry meaning Perception Perception of environment (walls, obstacles) Perception of humans Perception of objects Perception of self Testing and Verification Self-test of a robot. Verification of motions Verification of behaviors K inematics, inverse kinematics, dynamics Control Artificial Intelligence Formal Verification Theory of sign Creation of scripts, generalized events, motions to carry meaning Machine Learning Robot Vision Sensor Integration Group dynamics Developmental robots Interactive Genetic Algorithms Testing and Fault-Tolerant design Game Theory General Theories

7 .Types of motion editors

8 .Languages to describe all kinds of motions and events Labanotation DAP (Disney Animation Principles) and CRL (Common Robot Language)

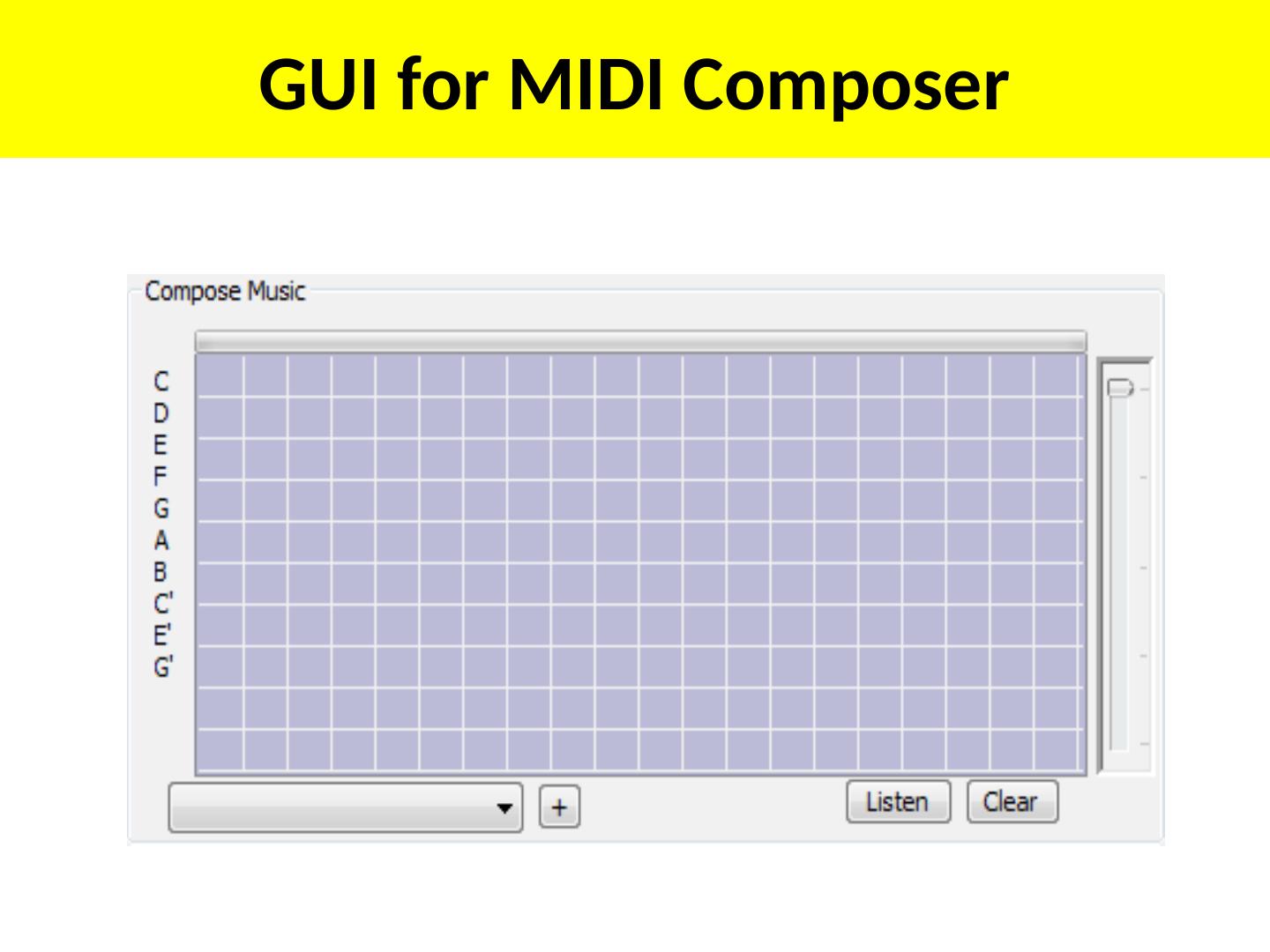
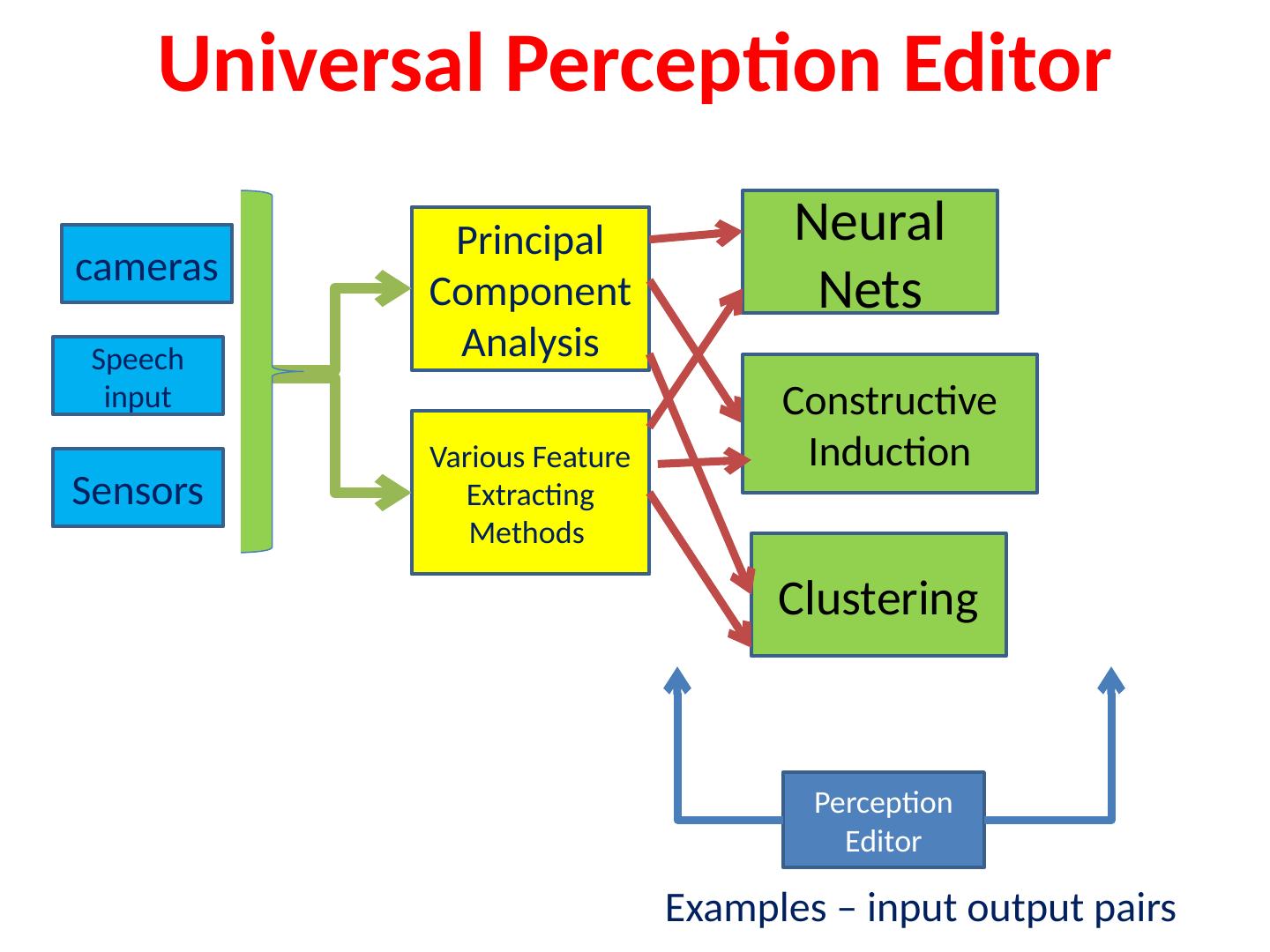
9 .The concept of generalized motions and universal event editor to edit: robot motions, behaviors, lightings and automated events

10 .Mouth Motion text Hexapod walking Distance evaluation Biped walking Number of falls evaluation Biped Gestures Comparison to video evaluation Hand gestures Subjective human evaluation Learning problems in Human-Robot Interaction – Motion Generation problems Motion Problems = examples of correct motions – generalize and modify, interpolate Motion, evaluation, learning

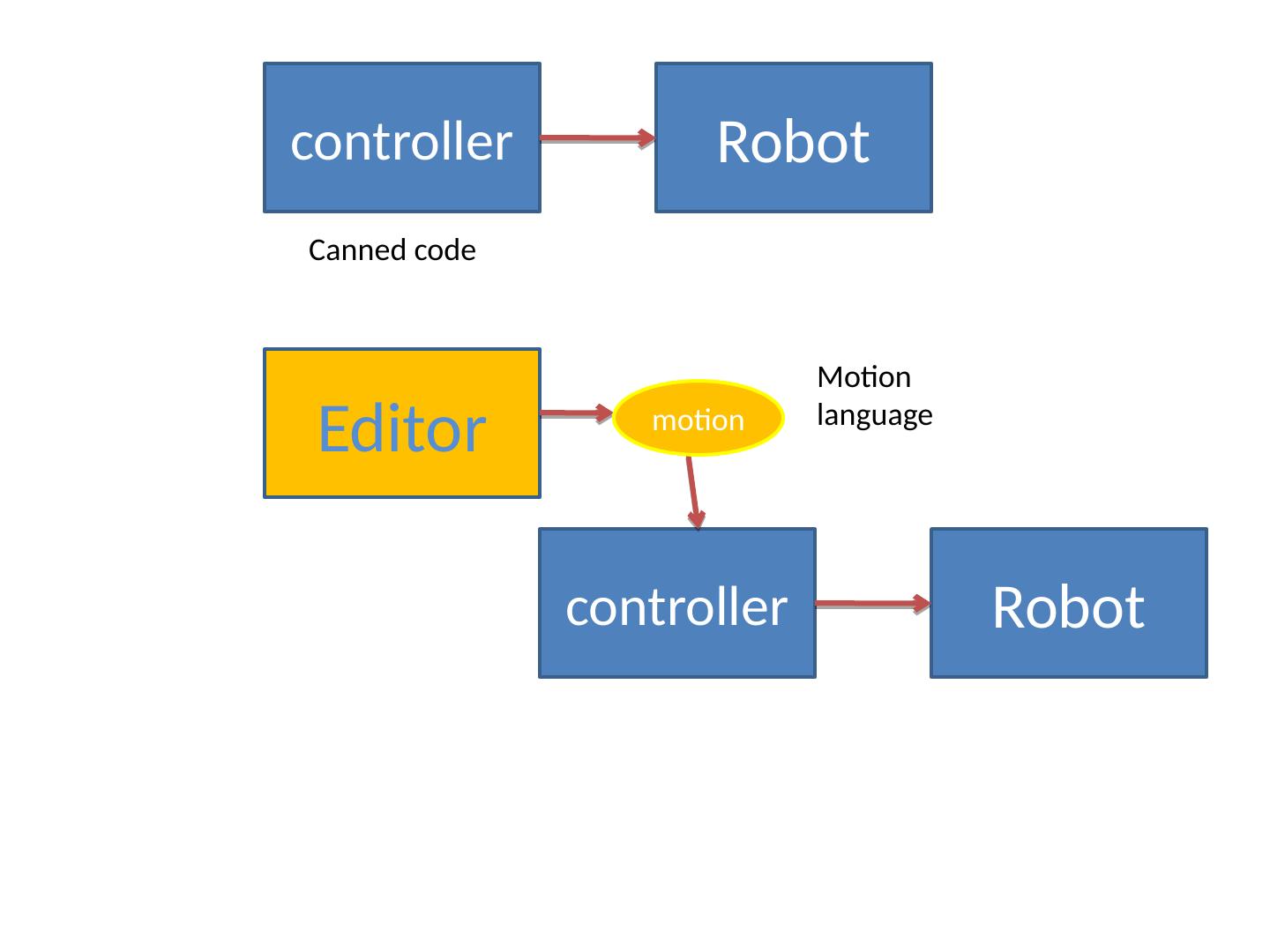
11 .Robot controller Canned code Robot controller Motion language Editor motion

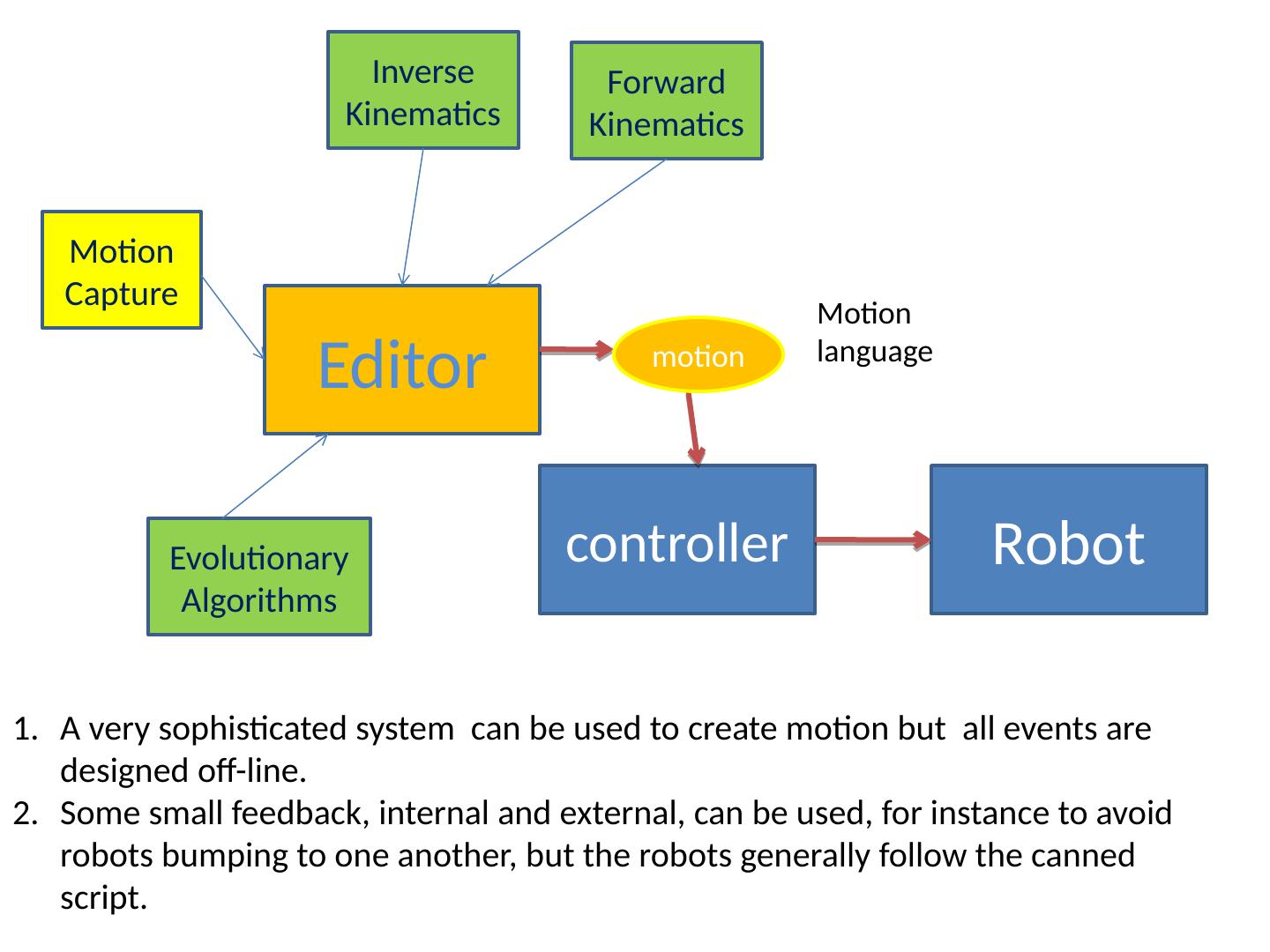
12 .Robot controller Motion language Editor motion Motion Capture Inverse Kinematics Forward Kinematics A very sophisticated system can be used to create motion but all events are designed off-line. Some small feedback, internal and external, can be used, for instance to avoid robots bumping to one another, but the robots generally follow the canned script. Evolutionary Algorithms

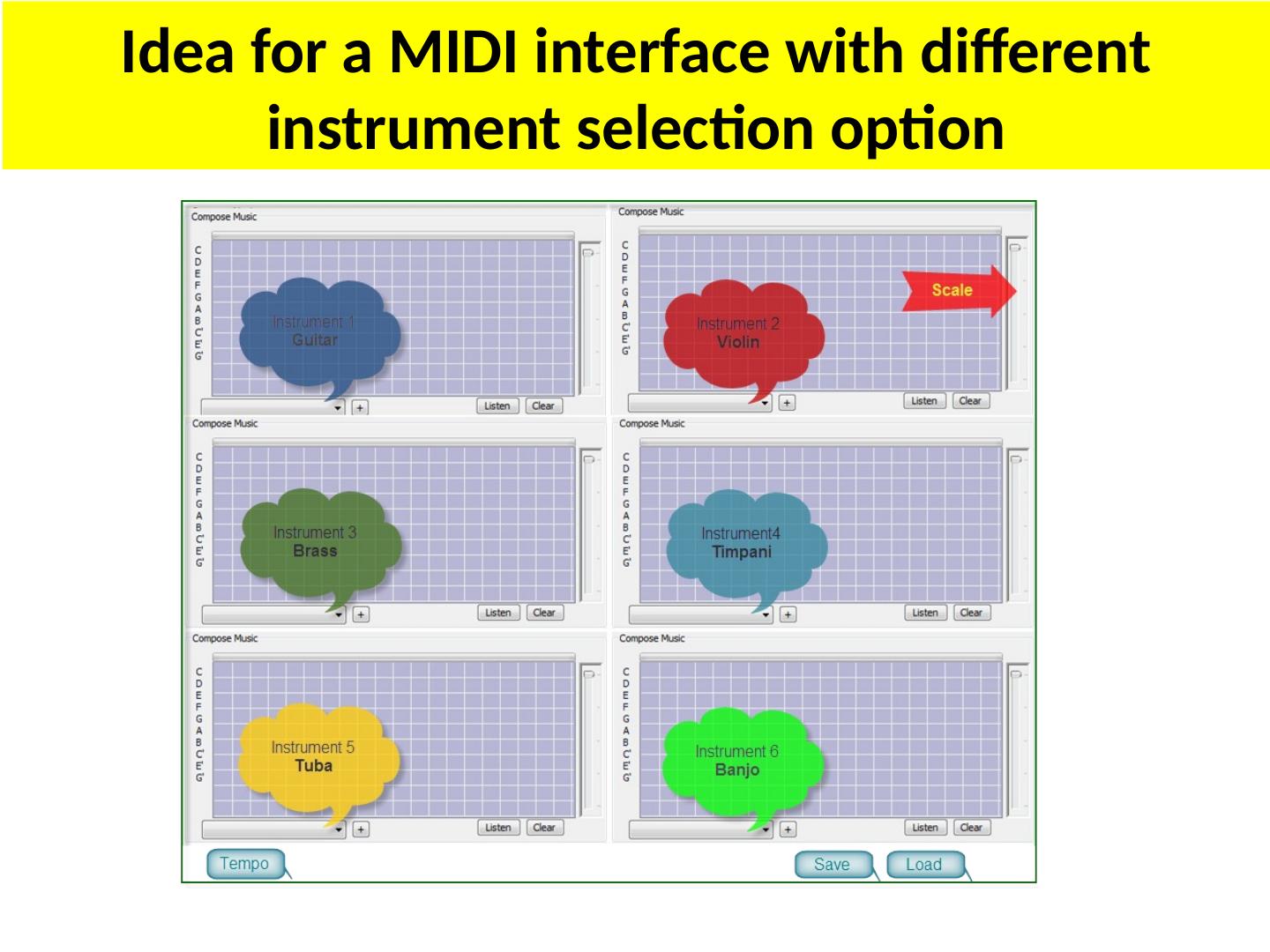
13 .Robots controller Events language Universal Event Editor events Motion Capture Inverse Kinematics Forward Kinematics Lighting System Sound System Curtain and all equipment script Universal Event Editor Initial events

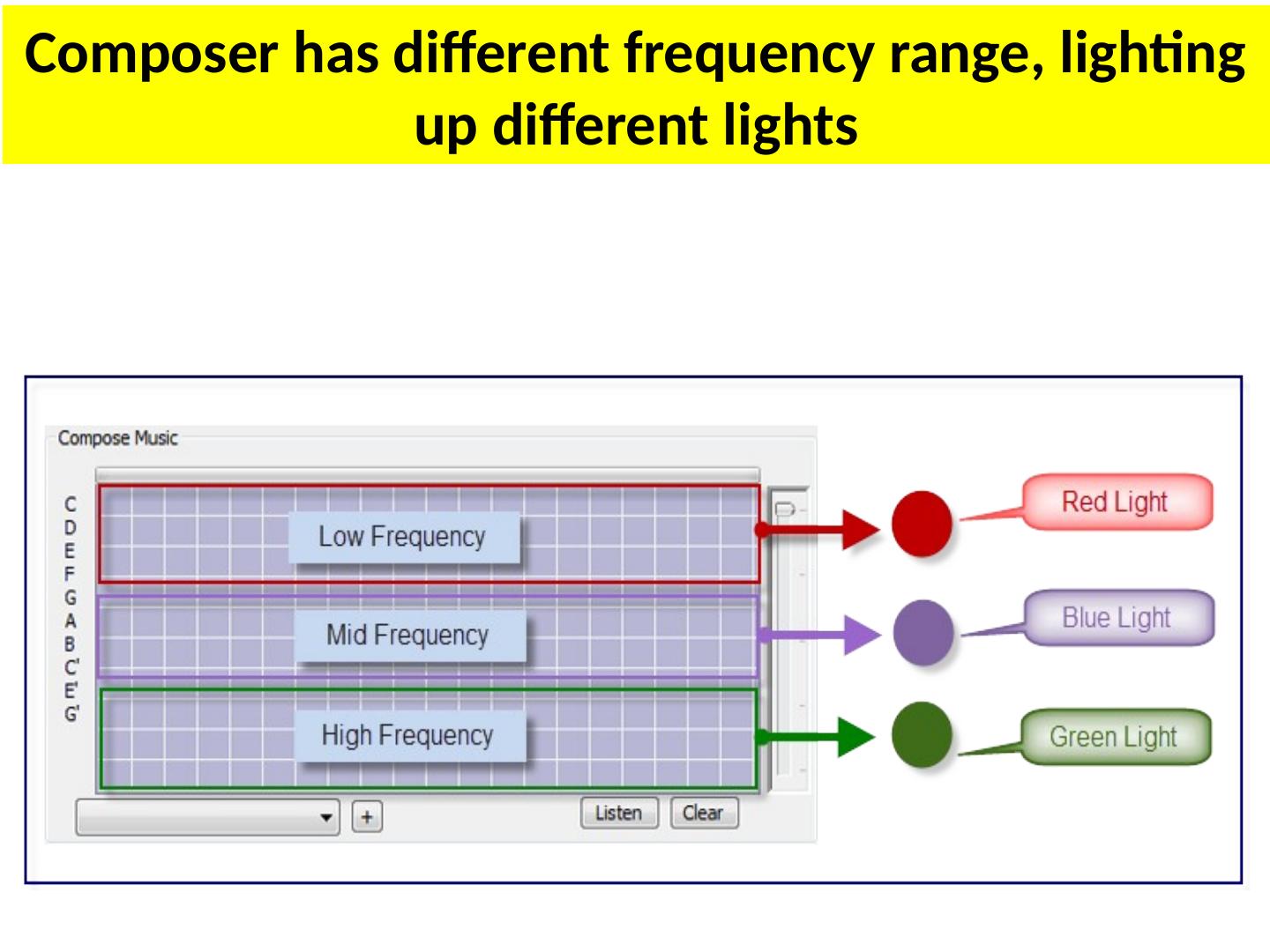
14 .Chameleon box converts sound to light and controls Universal motion editor MIDI Lights and controlled events

15 .Regular Expressions

16 .Language of Regular Expressions We create a formal model for robot behavior. “behavior” = input-output mapping (a relation) This is called Event Diagram Input is a sequence of symbols , output is a sequence symbols Symbols are abstractions. They are grouped into sets Thus, sequences of symbols are the language L* of the symbol set S Symbols for input (input set) I = { a_person , persons, raise_left_hand , head_turn_left , morning, day, evening, car, …} Symbols for output (output set) O = { shake_head , wave_right_arm , waltz_box_step , waltz_travel , lights_blue_on , lights_blue_off , …}

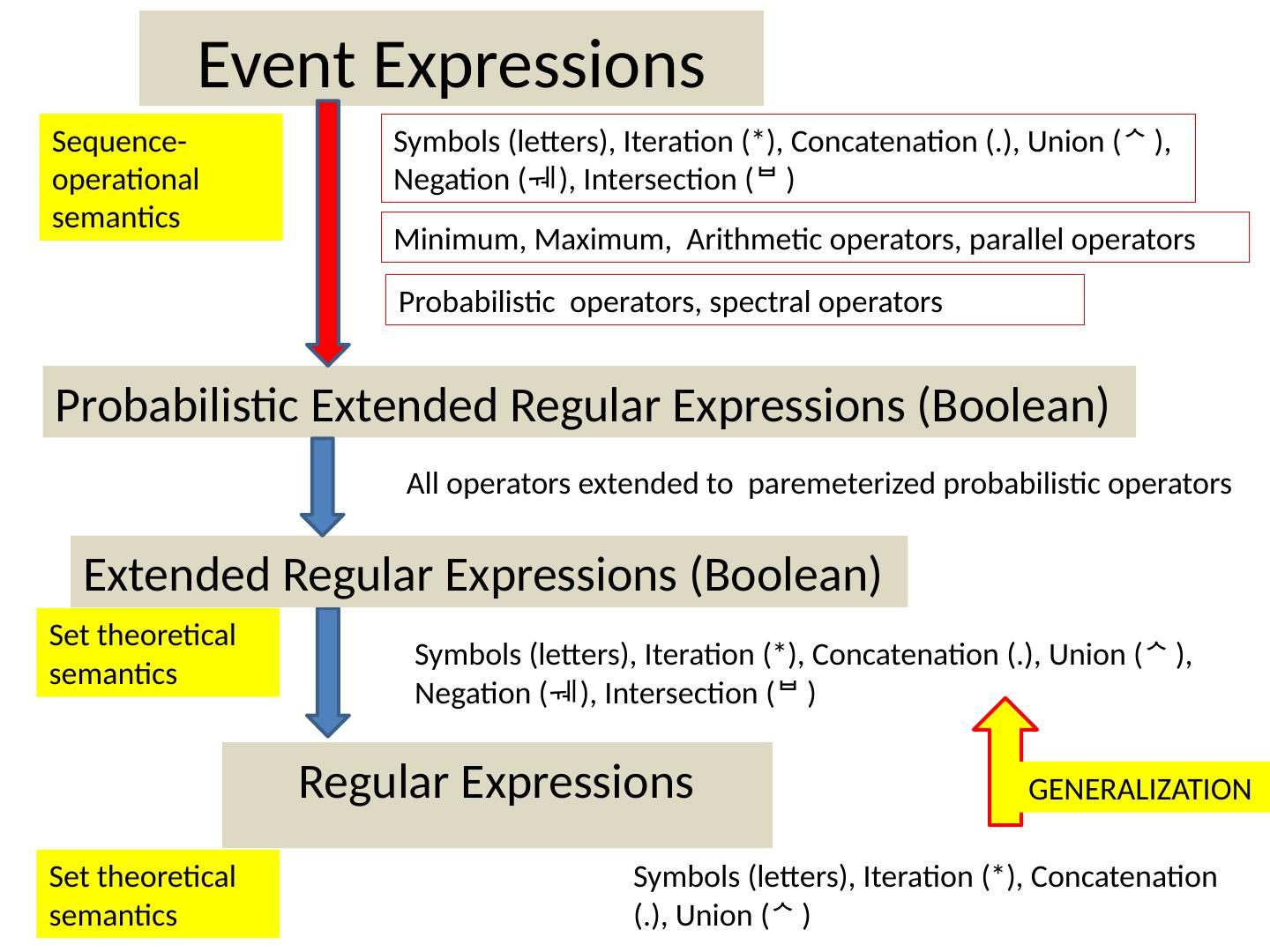
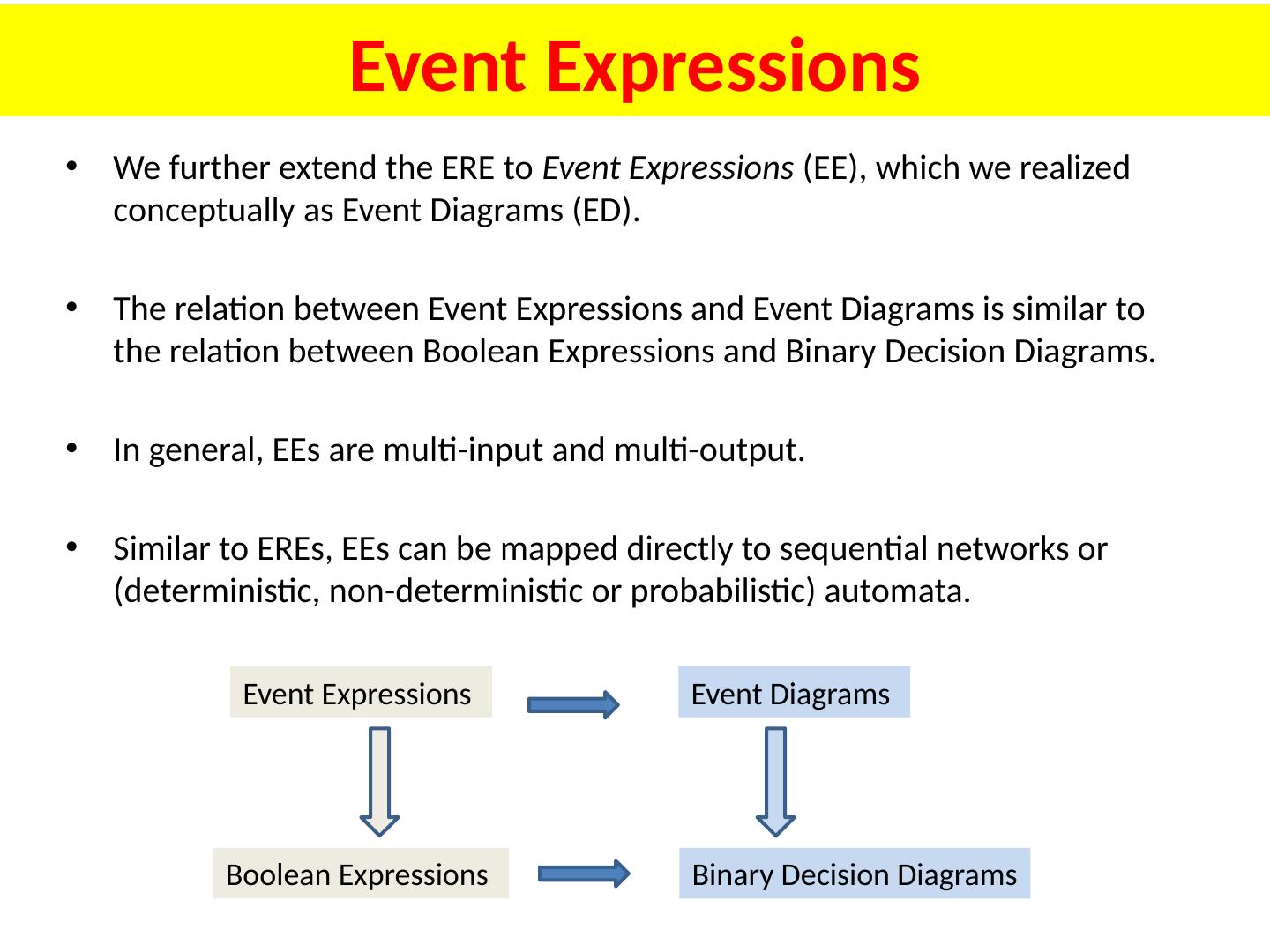
17 .Event Expressions Regular Expressions Probabilistic Extended Regular Expressions (Boolean) Symbols (letters), Iteration (*), Concatenation (.), Union ( ) Symbols (letters), Iteration (*), Concatenation (.), Union ( ), Negation (), Intersection () Set theoretical semantics Set theoretical semantics Sequence-operational semantics Symbols (letters), Iteration (*), Concatenation (.), Union ( ), Negation (), Intersection () Minimum, Maximum, Arithmetic operators, parallel operators Probabilistic operators, spectral operators Extended Regular Expressions (Boolean) All operators extended to paremeterized probabilistic operators GENERALIZATION

18 .Difference between Set-theoretical and Sequence-operational semantics (A · B · A · B)  (B · B · A · B ) = (A B) · (B  B) · (A  A) · (B  B) =  · B · A · B =  In Set-theoretical semantics single difference creates empty set and there is no result of intersection of two motions (A · B · A · B)  (B · B · A · B ) = (A B) · (B  B) · (A  A) · (B  B) =  · B · A · B In Sequence-operational semantics intersection of two symbols is not empty Interpreted as “do nothing”, next execute B, next execute A, next execute B

19 .Regular Expressions to specify languages of motions and behaviors A regular expression is a pattern that matches one or more strings of characters from a finite alphabet. Individual characters are considered regular expressions that match themselves. Original regular expressions used union, concatenation and iteration operators. Regular expressions were next extended by adding negation and intersection to a Boolean Algebra. Observe that X 1 ∩ X 2 is an empty set for atoms X 1  X 2 , as the meaning of intersection operator is set-theoretical. Similarly the interpretation of  operator is set-theoretical in regular expressions, thus new symbols are not being created.

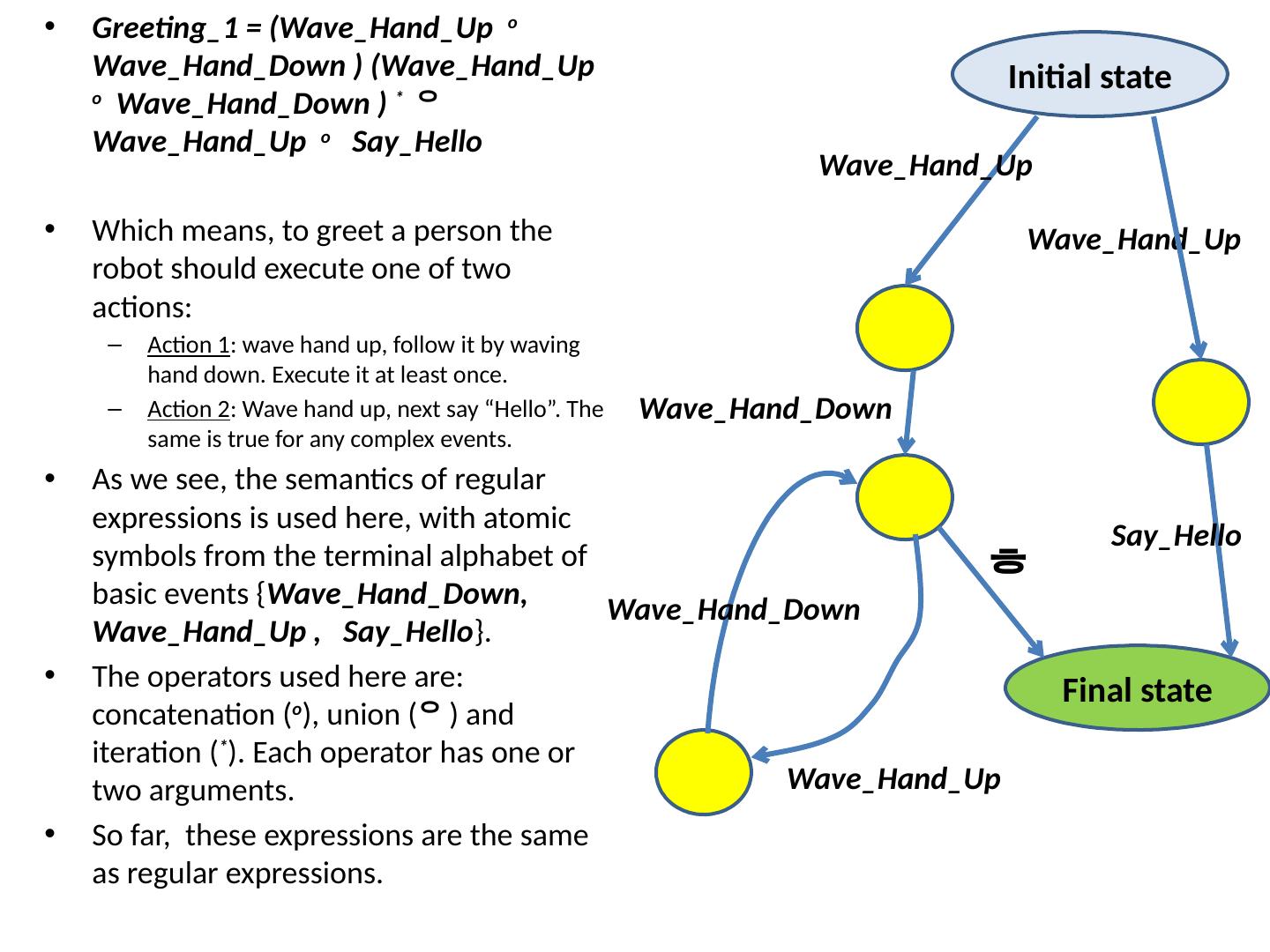
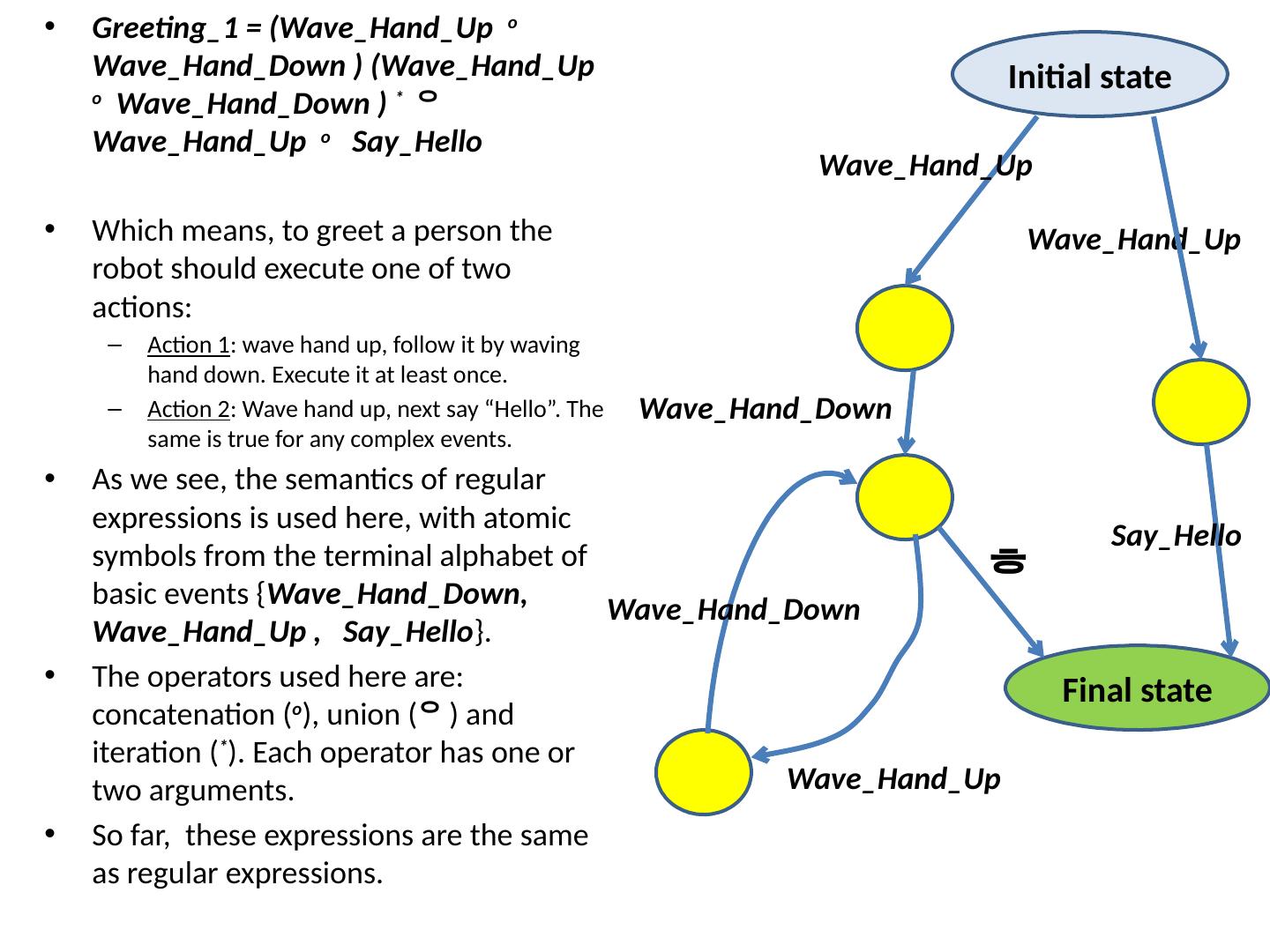
20 .Greeting_1 = ( Wave_Hand_Up o Wave_Hand_Down ) ( Wave_Hand_Up o Wave_Hand_Down ) *  Wave_Hand_Up o Say_Hello Which means, to greet a person the robot should execute one of two actions: Action 1 : wave hand up, follow it by waving hand down. Execute it at least once. Action 2 : Wave hand up, next say “Hello”. The same is true for any complex events. As we see, the semantics of regular expressions is used here, with atomic symbols from the terminal alphabet of basic events { Wave_Hand_Down , Wave_Hand_Up , Say_Hello }. The operators used here are: concatenation ( o ), union (  ) and iteration ( * ). Each operator has one or two arguments. So far, these expressions are the same as regular expressions. Initial state Final state Wave_Hand_Up Say_Hello Wave_Hand_Up Wave_Hand_Down  Wave_Hand_Up Wave_Hand_Down

21 .REVIEW OF REGULAR EXPRESSIONS

22 .REVIEW OF REGULAR EXPRESSIONS A regular expression is a pattern that matches one or more strings of characters (symbols) from a finite alphabet. A regular expression is composed from operators and atomic symbols/characters (e.g. letters). A regular expression corresponds to a language with certain grammar that generates this language. A language is a set of words (i.e. strings/sequences of symbols that are generated by the grammar). Individual characters are considered regular expressions that match themselves. The original regular expressions used three operators: union (  ), concatenation (symbol Ÿ or nothing. e.g : a Ÿ b and ab are equivalent), and iteration (*).

23 .Extension of regular expressions to probabilistic regular expressions For instance, assuming that concatenation is a deterministic operator and union is a probabilistic operator with equal probabilities of both arguments, there is a probability of ½ that the robot will greet with motion Wave_Hand_Up o Say_Hello . Assuming that all operators are probabilistic operators with equal probabilities of both arguments, for event expression Wave_Hand_Up o Say_Hello there is a probability of ½ that the robot will greet with one of the following four motions, each with the same probability: ( 1) Wave_Hand_Up o Say_Hello , ( 2) Wave_Hand_Up , ( 3) Say_Hello , (4) Nothing will happen.

24 .CONVERTING REGULAR EXPRESSIONS TO AUTOMATA

25 .Synthesis with Brzozowski’s Method Brzozowski’s derivatives of REs serve as a sound method for transformation of regular expressions to DFA/NFA. This method not only directly converts regular expressions to DFA/NFA, but also elegantly handles extended regular expressions and works for sets of event expressions. Given E , a regular language over alphabet X , a DFA is derived that accepts all words from the language, and only those words. All words of E , starting from letter X j є X. If the letter is removed from the front of each word from the set, a new language is created, referred to as left-side-derivative of language E by letter X j . This new language is now denoted by E/ X j .

26 . Brzozowski’s derivatives All words of E , starting from letter X j є X. If the letter is removed from the front of each word from the set, a new language is created, referred to as left-side-derivative of language E by letter X j . This new language is now denoted by E/ X j . A derivative for word s = X i1 , X i2 … X in is defined as follows: E/ X j = {s є X* : X j s є E}. As inherent laws of Brzozowski’s derivative method, the following properties P i always hold true .

27 .Recursive Rules for Brzozowski derivatives P1 . X i / X j = e for i = j = ø for i ≠ j P2. (E 1 ∪ E 2 )/X i = E 1 /X i ∪ E 2 /X i P3. ∈(E) = e when e ∈ E = ø when e ∉ E P4. E 1 E 2 /X i =(E 1 /X i )E 2 ∪∈ (E 1 )(E 2 /X i ) P5. E/s=E 1 /X i1 X i2 … X in =[[E/X i1 ]/X i2 ]…]/ Xi n P6. E * /Xi = (E/X i )E * P7. E/e = E P8. (E 1 ∩ E 2 )/X i = (E 1 /X i ) ∩ (E 2 /X i ) P9. (-E)/X i = -(E/X i )

28 .Synthesis example for language ( X 2 X 1 * ∪ X 1 X 2 ). Applying the left-side-derivative with respect to first character in string, X 1 E 1 /X 1 = (X 2 X 1 * ∪ X 1 X 2 )/X 1 = (X 2 X 1 * )/X 1 ∪ (X 1 X 2 )/ X 1 by P2 = (X 2 /X 1 )X 1 * ∪ ∈ (X 2 )X 1 * ∪ (X 1 /X 1 )/X 2 ∪ ∈ (X 1 )(X 2 /X 1 ) by P4 = ø X 1 ∪ ø(X 1 /X 2 ) ∪ eX 2 ∪ ø ø by P1 = X 2 Graph for regular language E 1 = (X 2 X 1 * ∪ X 1 X 2 ). This graph can be interpreted as PMG, EEAM or BM depending on meaning of symbols X i and nodes (states)

29 .Languages to describe motions of humanoid robots