4 Boolean Algebra Z

1 .Lecture 4 Topics Boolean Algebra Huntington’s Postulates Truth Tables Graphic Symbols Boolean Algebra Theorems 1

2 .Boolean Algebra 2

3 .Boolean Algebra A fire sprinkler system should spray water if high heat is sensed and the system is set to enabled Let Boolean variable h represent “high heat is sensed,” e represent “enabled,” and F represent “spraying water.” Then an equation is: F = h AND e A car alarm should sound if the alarm is enabled, and either the car is shaken or the door is opened Let a represent “alarm is enabled,” s represent “car is shaken,” d represent “door is opened,” and F represent “alarm sounds.” Then an equation is: F = a AND (s OR d ) A ssuming that our door sensor d represents “door is closed” instead of open (meaning d=1 when the door is closed, 0 when open), we obtain the following equation: F = a AND (s OR NOT(d)) 3

4 .Boolean Algebra (History) 384-322 BC: Aristotle, foundations of logic 1854: George Boole, An Investigation of the Laws of Thought (mathematical methods for two-valued logic) 1904: H.E. Huntington, Sets of Independent Postulates for the Algebra of Logic 1938: Claude Shannon, A Symbolic Analysis of Relay Switching Circuits 4

5 .Boolean Algebra Postulates (Axioms) Accepted as true; Foundation for further proofs Values B = {0, 1} Variables A,B,C X,Y,Z Ready, Green, OverWeightLimit Operators + ×  Additional Operators () = 5

6 .Huntington’s Postulates (I) 6

7 .Literals Variable or Complement of Variable X ,DoorOpen , Green, Green Expressions Constants (0,1), Literals, Operators (X + Y × Z), A + B Precedence Complement ( ) , AND ( × ), OR (+) () Can be used to modify order Boolean Algebra 7

8 .Operators Complement (NOT) A’ /A !A Ø A ~A A OR A + B A | B A Ú B AND A * B A & B A × B A Ù B 8 For typographical convenience, you’ll see many variations on the symbols used to represent these operations.

9 .Truth Tables (NOT) 9

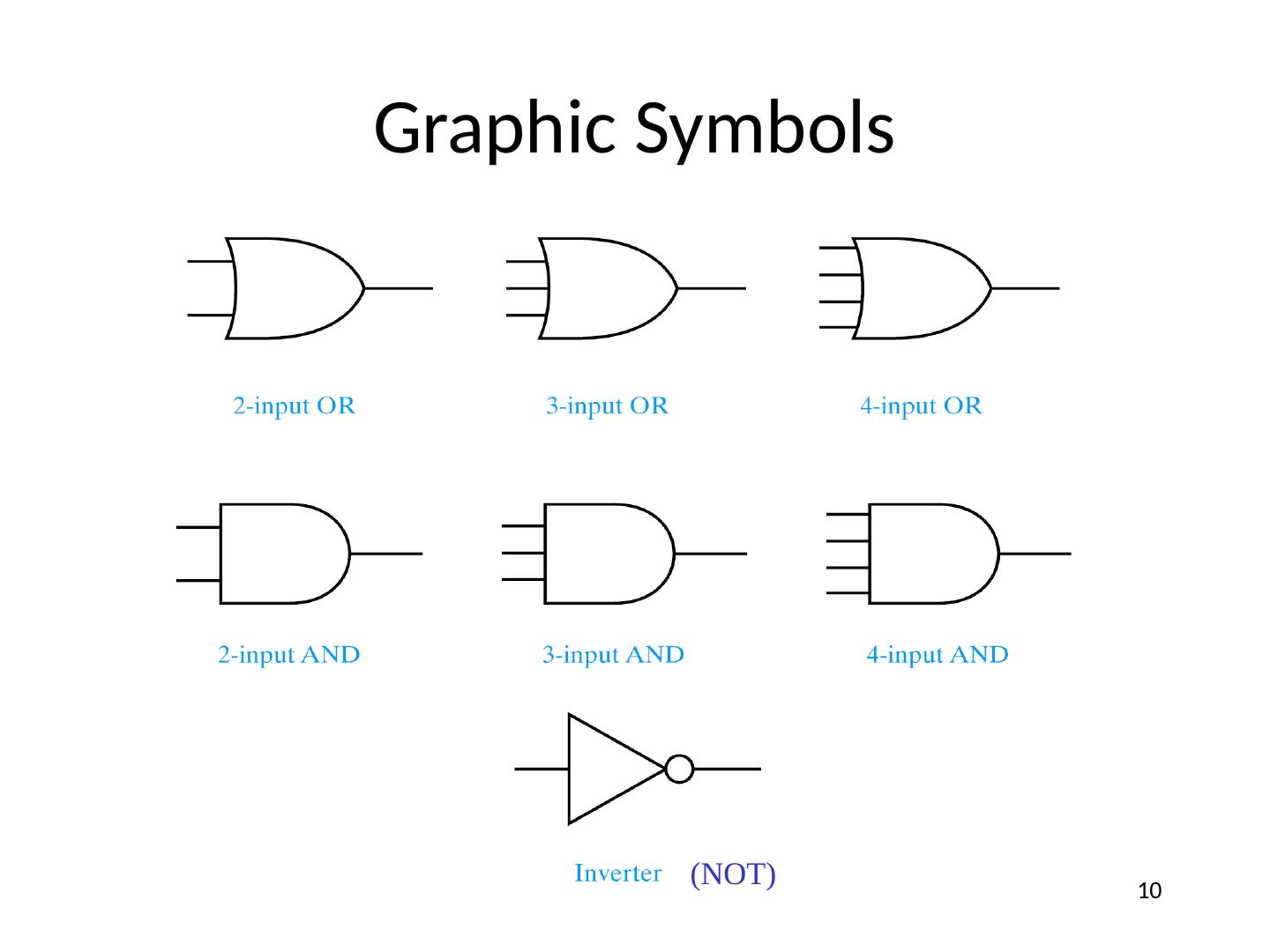
10 .Graphic Symbols (NOT) 10

11 .Additional Operators NOR A + B A | B A Ú B NAND A * B A & B A × B A Ù B 11

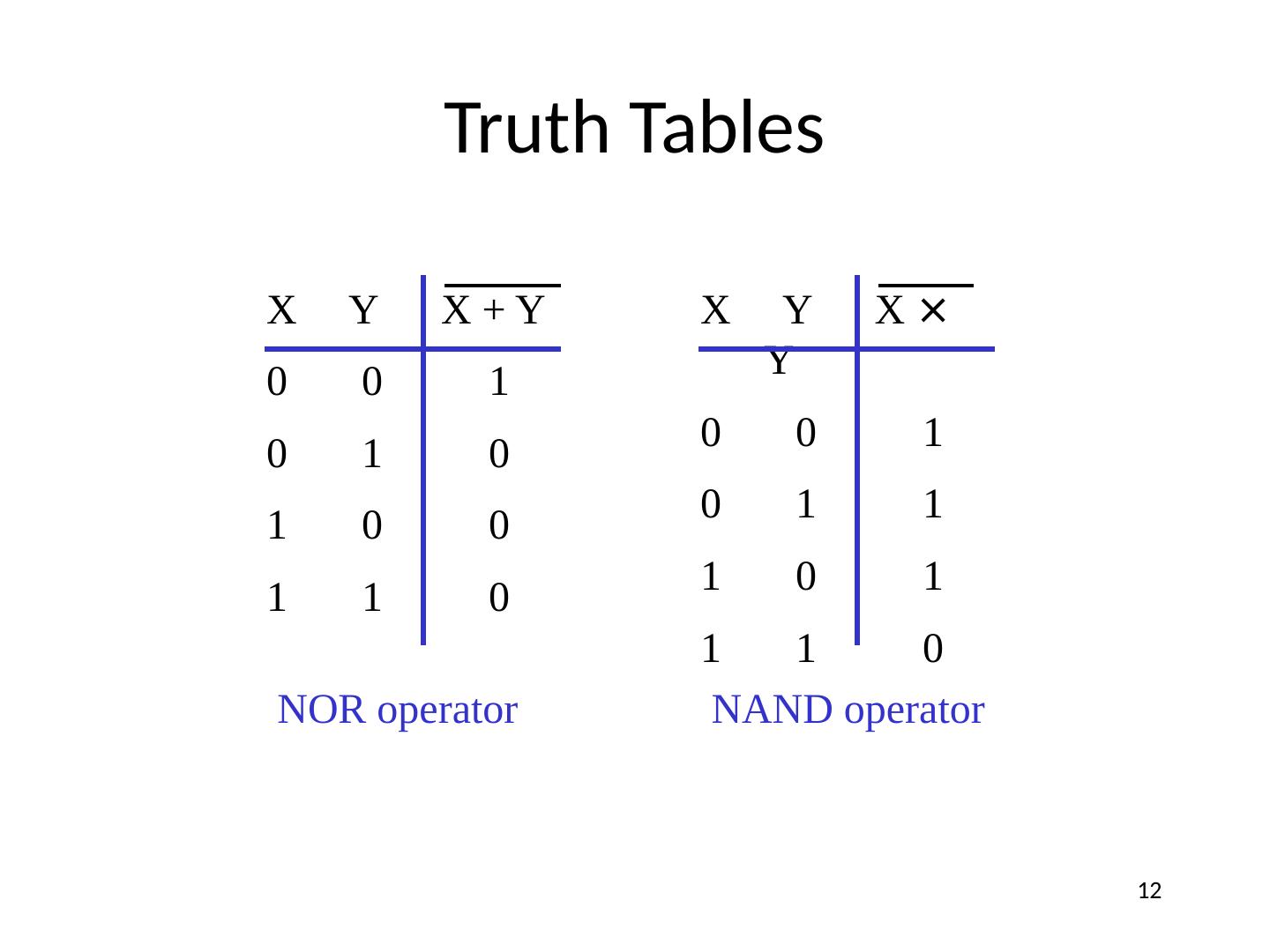
12 .Truth Tables NOR operator NAND operator X Y X + Y 0 0 1 0 1 0 1 0 0 1 1 0 X Y X × Y 0 0 1 0 1 1 1 0 1 1 1 0 12

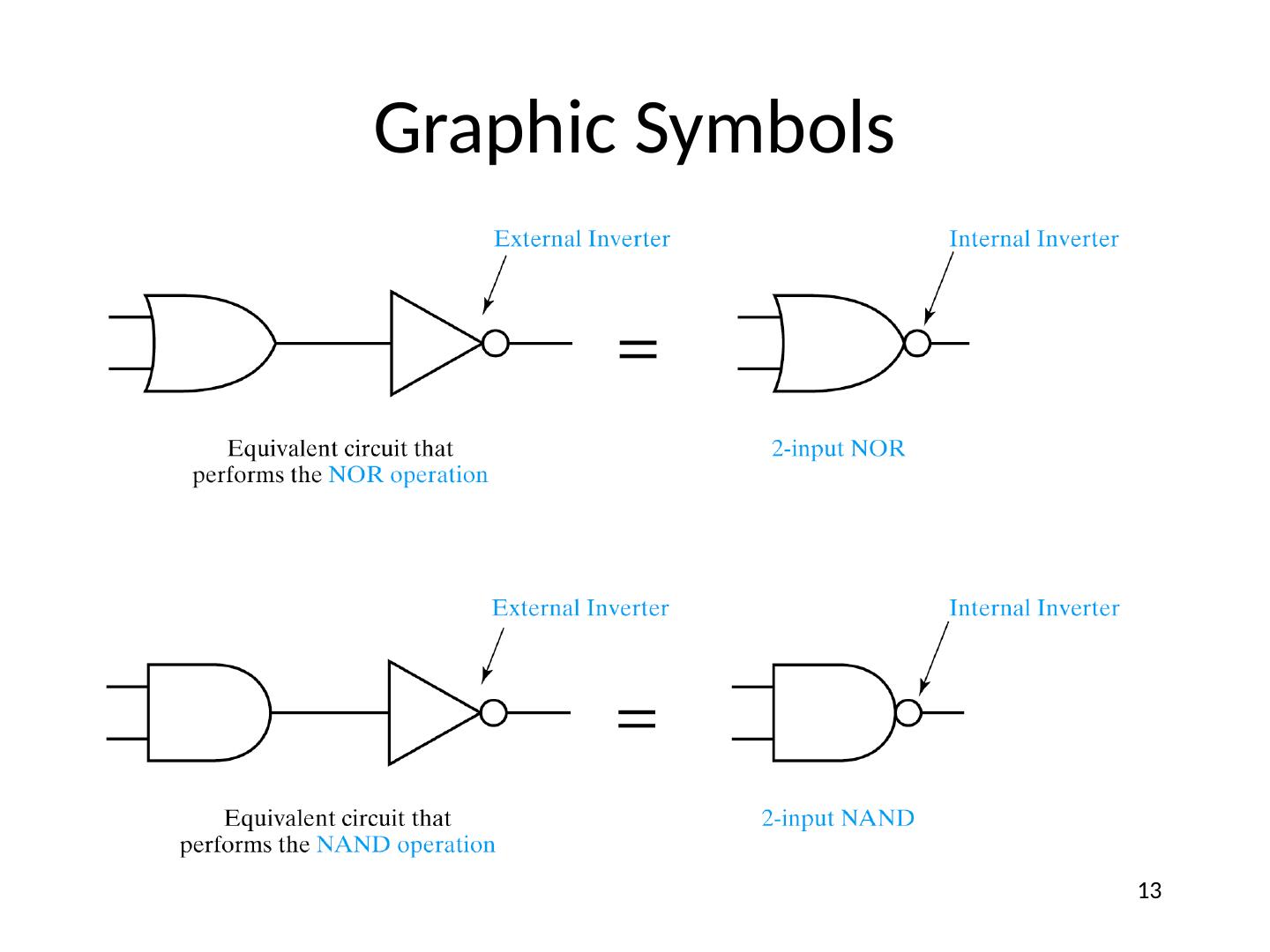
13 .Graphic Symbols 13

14 .Additional Operators: XOR and XNOR XOR (Exclusive OR, Modulo 2) A Å B XNOR (Exclusive NOR, Equivalence) A Å B 14

15 .Truth Tables XOR operator XNOR operator X Y X Å Y 0 0 0 0 1 1 1 0 1 1 1 0 X Y X Å Y 0 0 1 0 1 0 1 0 0 1 1 1 15

16 .Graphic Symbols 16 Observe that this is sum of products of literals

17 .Boolean Functions Product Terms Comprised of literals (including complements), AND X × Y × Z A × B × C Sum Terms Comprised of literals (including complements), OR X + Y + Z A + B + C Sum of Products (SOP) X × Y + X × Z -- note: parentheses not needed Product of Sums (POS) (X + Y) × (X + Z) F(X,Y,Z) = Boolean function of 3 variables : X,Y,Z 17

18 .Truth Tables B 5 B 4 B 3 B 2 B 1 B 0 F 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 0 . . . 1 1 1 1 1 1 1 0 1 2 3 . . . 63 2 6 = 64 Question: How many rows are there in a truth table for n variables? As many rows as unique combinations of inputs Enumerate by counting in binary 2 n 18

19 .Boolean Algebra -- Manipulation Simplify Literal Count Reduction Reduce Number of Terms Transform: Put in Preferred Form AND/OR NAND/NOR 19 Can apply Huntington’s Postulates and Theorems to Simplify or Transform Boolean equations

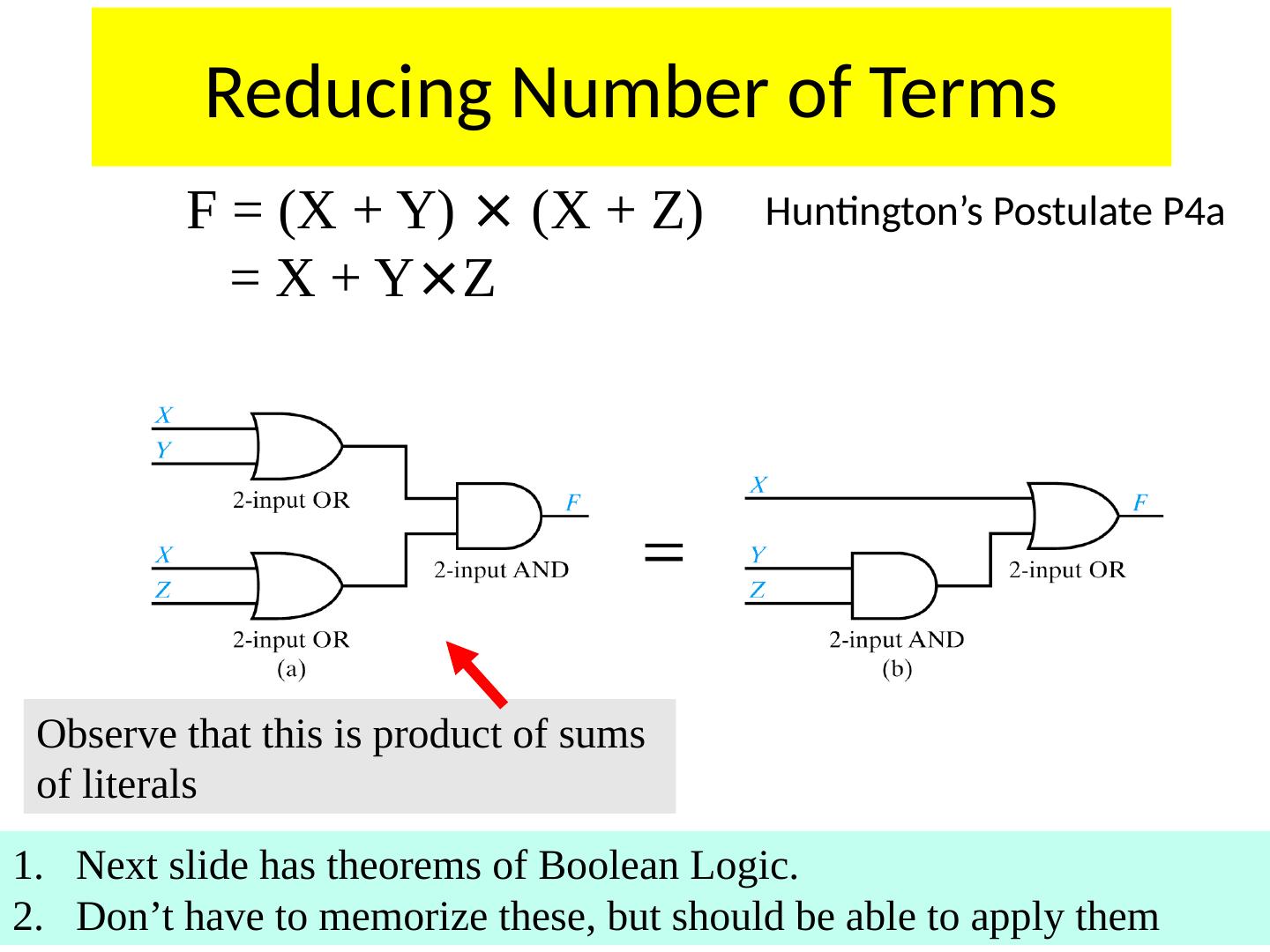
20 .Reducing Number of Terms F = (X + Y) × (X + Z) = X + Y × Z Huntington’s Postulate P4a 20 Next slide has theorems of Boolean Logic. Don’t have to memorize these, but should be able to apply them Observe that this is product of sums of literals

21 .Boolean Theorems 21

22 .Boolean Theorems: let us discuss each of them 22

23 .Boolean Theorems ( cont ) 23

24 .Literal Count Reduction F = X × Y + X + Y × Z = Y + X + Y × Z = Y + X Simplification Theorem Absorption Theorem Simplification Theorem Absorption Theorem X × Y + X = Y + X Y + Y × Z = Y 24 Y + Y × Z= Y(1+Z) = Y × 1 = Y

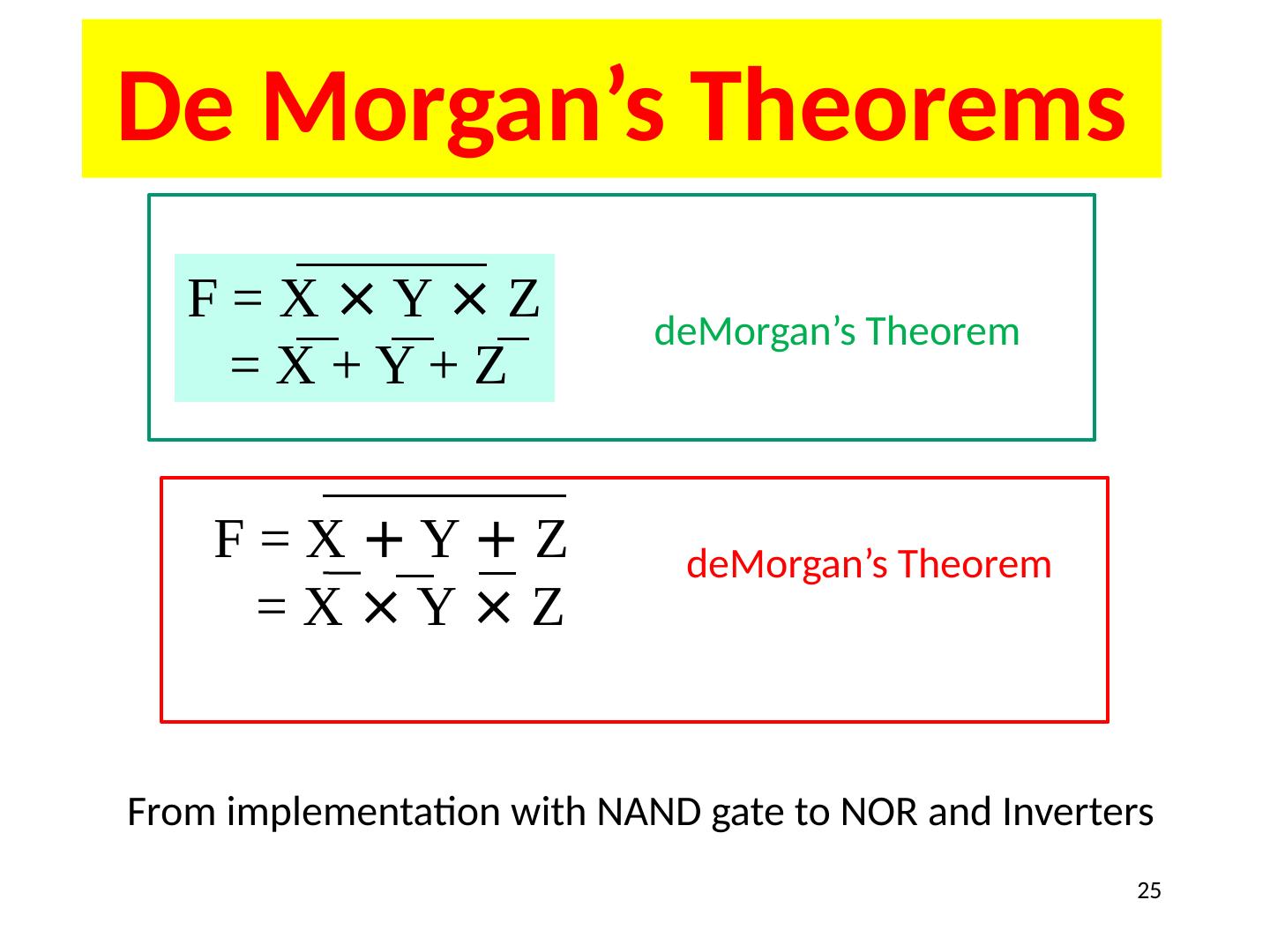
25 .De Morgan’s Theorems F = X × Y × Z = X + Y + Z deMorgan’s Theorem From implementation with NAND gate to NOR and Inverters 25 F = X + Y + Z = X × Y × Z deMorgan’s Theorem

26 .Proofs Using Boolean Algebra Prove: X + X = X X + X = (X + X) × 1 Huntington P2b: X × 1 = X = (X + X) × (X + X) Huntington P5a: X + X = 1 = X + X × X Huntington P4a: X + YZ = (X + Y) × (X + Z) = X + 0 Huntington P5b: X × X = 0 = X Huntington P2a: X + 0 = X Using Principle of Perfect Induction Truth Tables! Q.E.D. 26

27 .Principle of Perfect Induction Prove: X × Y + X × Z + Y × Z = X × Y + X × Z X Y Z X × Y X × Z Y × Z X × Y X × Z 0 0 0 0 + 0 + 0 = 0 0 + 0 = 0 0 0 1 0 + 1 + 0 = 1 0 + 1 = 1 0 1 0 0 + 0 + 0 = 0 0 + 0 = 0 0 1 1 0 + 1 + 1 = 1 0 + 1 = 1 1 0 0 0 + 0 + 0 = 0 0 + 0 = 0 1 0 1 0 + 0 + 0 = 0 0 + 0 = 0 1 1 0 1 + 0 + 0 = 1 1 + 0 = 1 1 1 1 1 + 0 + 1 = 1 1 + 0 = 1 27

28 .Questions, Problems and Exam Problems Give examples of axioms in Boolean Algebra. Create a truth table of function f = a  b. Create a truth table of function f = (a *b)’. Create a truth table of function f = NOR( a, b ). Show graphic symbols for all Boolean Gates. Using truth table prove that NOT( a +b ) = NOT(a) * NOT( b ). Using truth table prove that ( a b ) = NOT(a  b). Explain De Morgan Theorems using graphic symbols. Draw schematic of the circuit for function f = (ab)’ + c’ d’ ( e+g ). Use gates AND, OR and NOT. Draw schematic of the circuit for function f = (ab)’ + c’ d’ ( e+g ). Use gates NAND only. Draw schematic of the circuit for function f = (ab)’ + c’ d’ ( e+g ). Use gates NOR only . Using perfect induction prove DeMorgan’s Laws. Use DeMorgan’s Laws to prove a’b+ab ’=a(ab)’+b(ab)’ = ( a+b )(ab )’. Prove a  0=a, a  a’=1, a 1=a’. Prove that a+b = a b  (ab)= a+a’b = a  a’b Prove that if ab=0 then a+b = a b Draw circuit equivalents of 5 selected Boolean Laws. 28

29 .Sources Prof. Mark G. Faust John Wakerly