12 Quantum Robot

1 .Example of simple Braitenberg Vehicle type of robot in Robot C with quantum logic

2 .Quantum Logic Boolean Logic EXOR/AND Logic Reversible Logic Quantum Logic Quantum Logic Uses matrices and vectors State of a system is a vector Basic vectors – system is in one state Superposed vectors – system is in many states at the same time Entanglement – system is in many states in such a way that it cannot be factorized. 1 0 0 0 1 1 0 0 1/ 2 0 1 0 0 0 0 1 0 0 0 0 1 Basic vectors A superposed state that can be factorized (separable) 00 01 10 11 1 0 0 1 1/ 2 A superposed state that is entangled (cannot be separated)

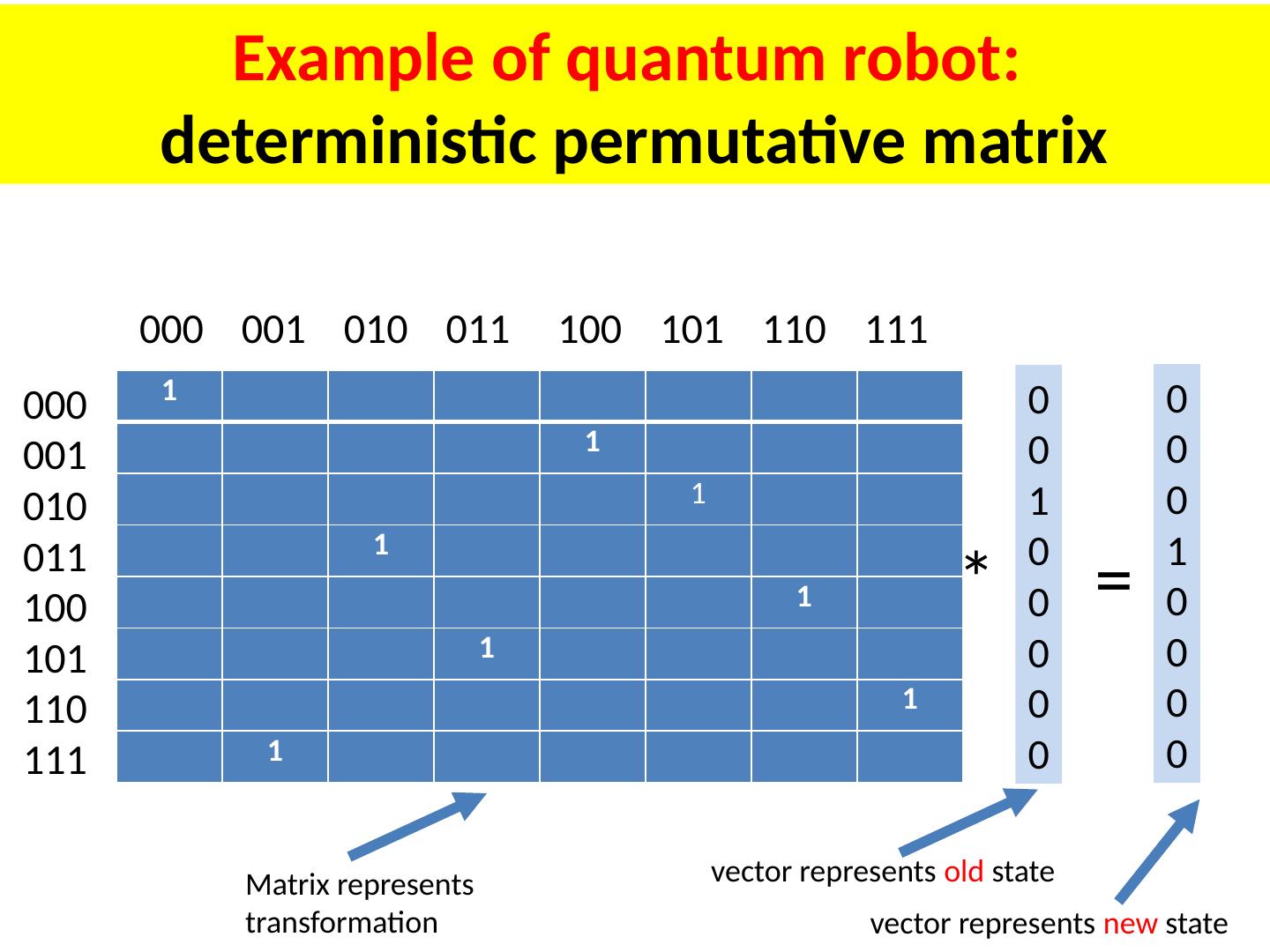
3 .Example of quantum robot: deterministic permutative matrix 1 1 1 1 1 1 1 1 000 001 010 011 100 101 110 111 000 001 010 011 100 101 110 111 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 = * Matrix represents transformation vector represents old state vector represents new state

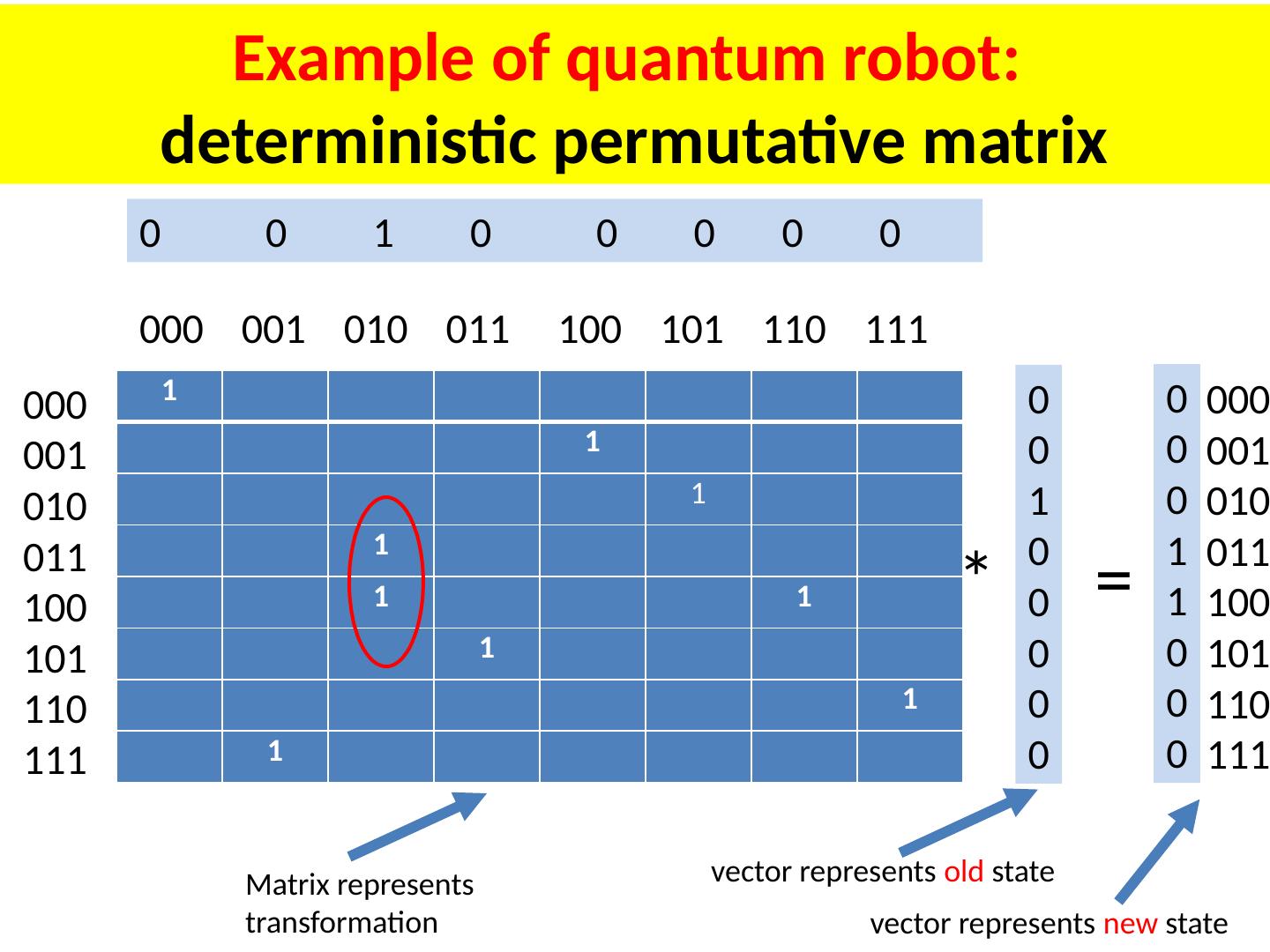
4 .Example of quantum robot: deterministic permutative matrix 1 1 1 1 1 1 1 1 000 001 010 011 100 101 110 111 000 001 010 011 100 101 110 111 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 = * Matrix represents transformation vector represents old state vector represents new state 0 0 1 0 0 0 0 0 000 001 010 011 100 101 110 111

5 .Example of quantum robot: deterministic non- permutative matrix 4 7 1 4 5 6 5 1 4 1 000 001 010 011 100 101 110 111 000 001 010 011 100 101 110 111 Total state of inputs and internal states Total state of outputs and internal states 0 0 3 0 4 0 0 0 = * Different interpretation of results

6 .Example of quantum robot: non-deterministic matrix, probabilistic intepretation 1 1 1 1 1 1 1 1 1 1 000 001 010 011 100 101 110 111 000 001 010 011 100 101 110 111 Total state of inputs and internal states Total state of outputs and internal states This is not a permutative matrix

7 .Example of quantum robot: deterministic permutative matrix 1 1 1 1 1 1 1 1 1 000 001 010 011 100 101 110 111 000 001 010 011 100 101 110 111 0 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 = * Matrix represents transformation vector represents old state vector represents new state 0 0 1 0 0 0 0 0 000 001 010 011 100 101 110 111

8 .Example of quantum robot: deterministic permutative matrix 0 0 0 1 1 0 0 0 vector represents new state 000 001 010 011 100 101 110 111 System is in two states at the same time, 011 and 100 System is in two states at the same time, 011 and 100 But after “measurement” system goes to one state with probability of ½ to be measured in state 011 and probability ½ to be measured in state 100

9 .State representation Easy to calculate new states Has many applications in various types of systems (linear) Use in image processing, vision, control, prediction, quantum computing, reversible computing. Relation to probabilistic systems. Can use Boolean, integer, complex values, etc. Easy to calculate in Matlab .

10 .Robot C language It will take you about one hour to learn if you know C. It is implemented on many computers It is used in high school competitions It is on Lego and VEX, Tetrix etc. It helps with sensors and motors, you do not worry about the details, has PID etc. Unfortunately you have to pay. You can get license for few months for free. My high school kids have done great software.

11 .Example of programming a quantum robot This program can be easily changed to the following types of control: Boolean Logic Fuzzy logic Probabilistic logic Ternary logic Mixed logic Your own control for any algebra you may want

12 .A fourteen years old girl wrote it in few hours! We declare one touch sensor and two light sensors

13 .Review matrices and vectors Review how to multiply matrix by vector Review how to multiply matrix by matrix We declare the matrix of transformation, in this case permutative We link the Boolean inputs to state of the input of our linear system I hope you remember!

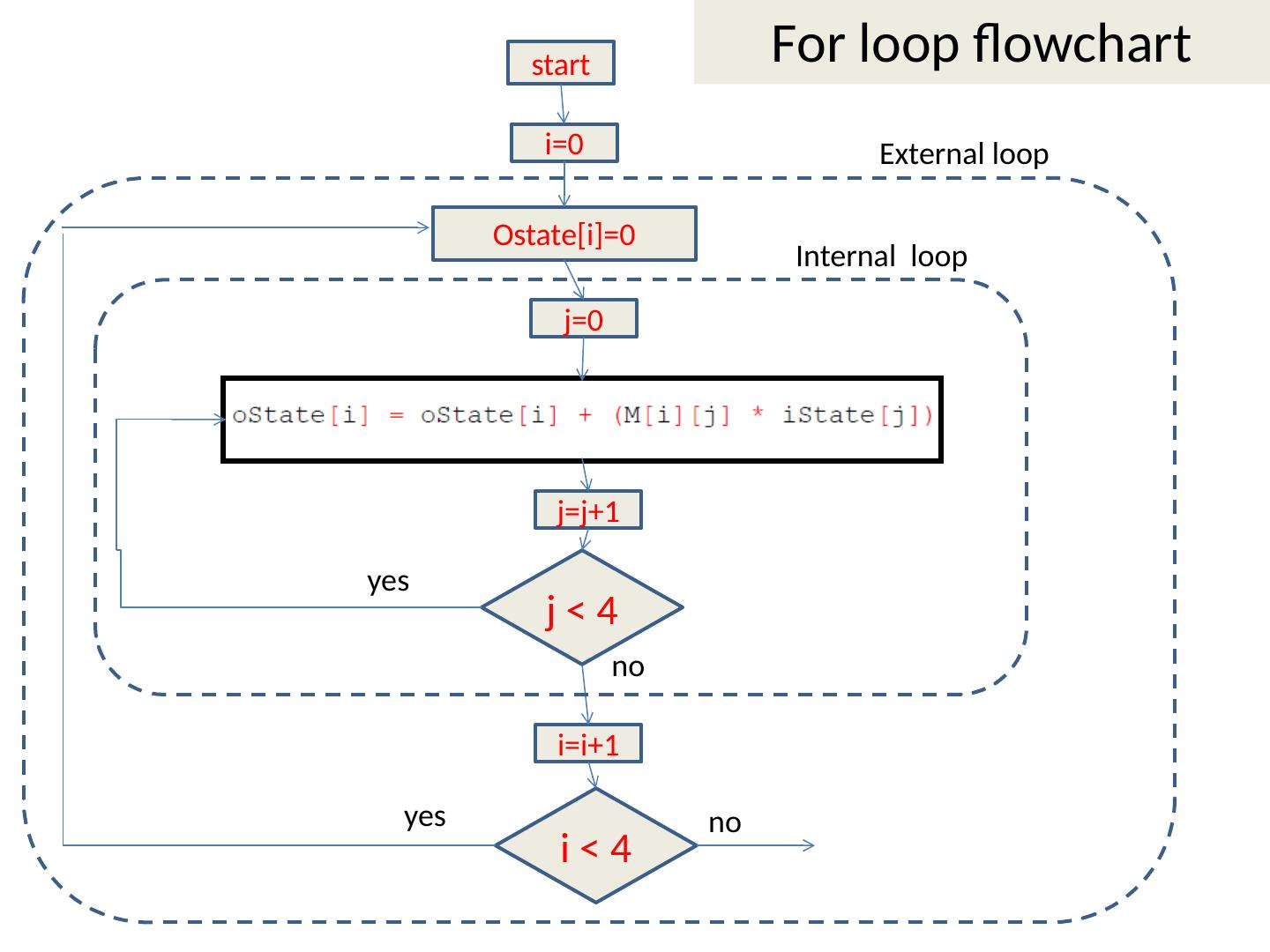
14 .For loop flowchart } } } We calculate the new state of the linear system based on its old state and the transformation matrix

15 .start i =0 Ostate [ i ]=0 j=0 j=j+1 j < 4 i < 4 i =i+1 External loop Internal loop For loop flowchart yes yes no no

16 .Review quantum measurement Review probability I hope you remember!

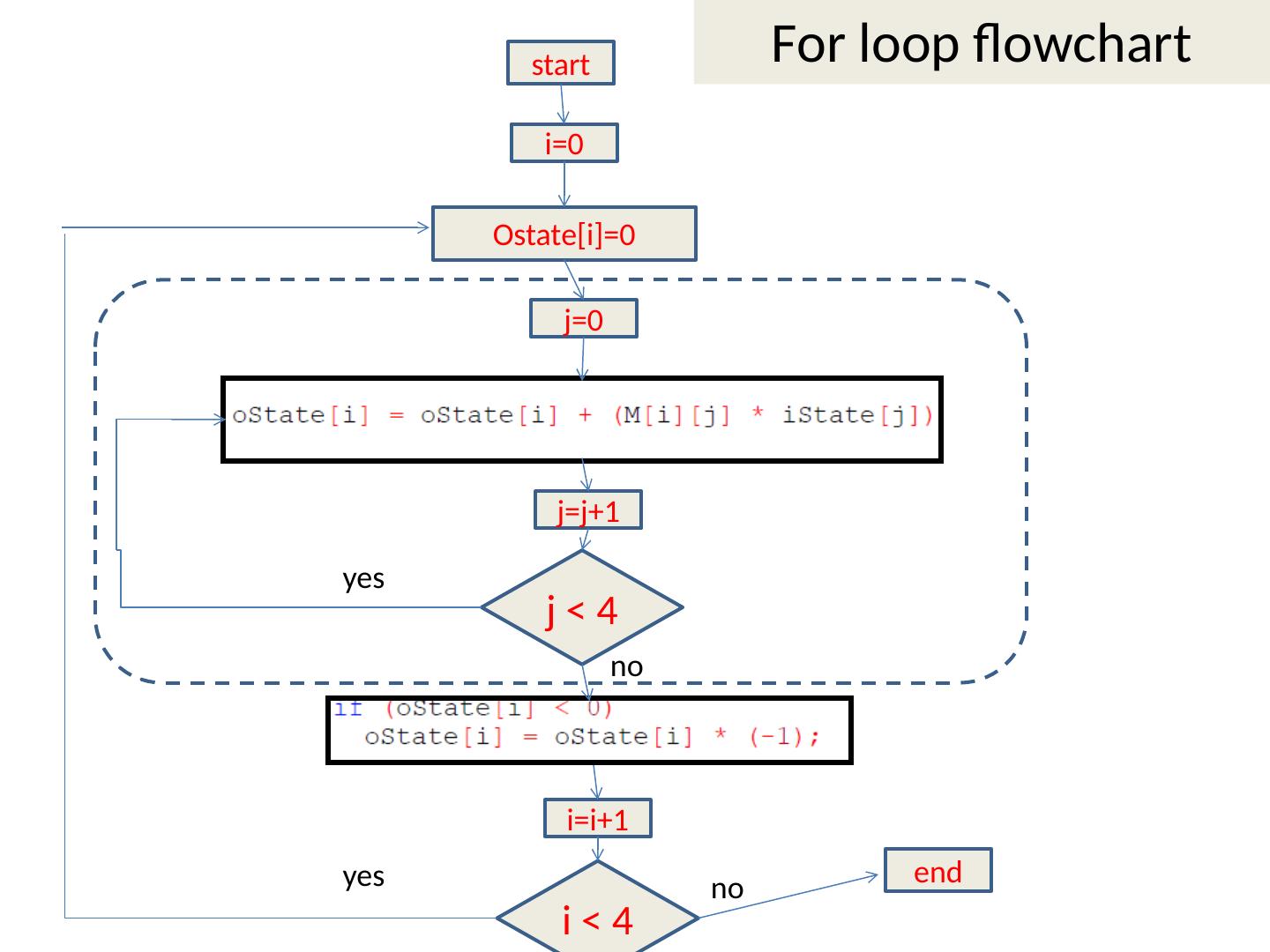
17 .start i =0 Ostate [ i ]=0 j=0 j=j+1 j < 4 i < 4 i =i+1 For loop flowchart yes yes no no end

18 .Initialize total Calculate new value of total Calculate value of output oneCounter counts ones

19 .Calculate deterministic values of control variables P and Q Continue of subroutine of interpreting the output state Loop for oneCounter

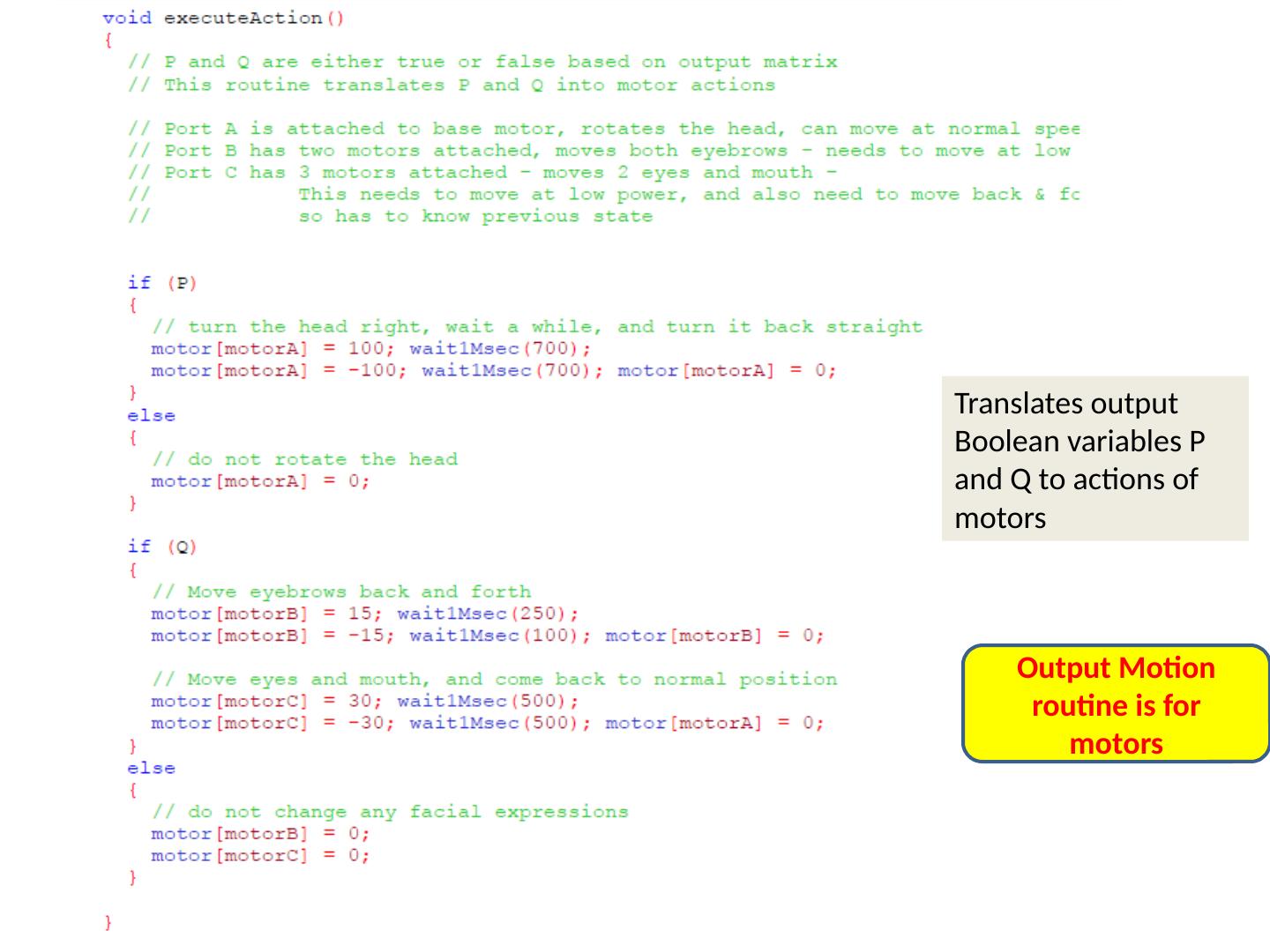
20 .Translates output Boolean variables P and Q to actions of motors Output Motion routine is for motors

21 .Converts sensor reading to input variables a and b Two light sensors and touch sensor Two light sensors and touch sensor Input routine is for sensors

22 .Main program links inputs, outputs and brain (behavior) input brain output Intialize all

23 .Typical Problems for homeworks , quizzes and projects Create shy Braitenberg Vehicle based on principles explained in this set of slides. Create shy Braitenberg Vehicle that you can control its “shyness” C reate aggressive Braitenberg Vehicle with probabilistic behaviors, based on “pseudo-quantum” logic from this set of slides. Create a Braitenberg Vehicle that with clasping your hands you can change the behavior from shy to aggressive and vice versa. The robot should have probabilistic behavior and behave differently in every moment of time, with high probability. Create a Braitenberg Vehicle (mobile robot) with lights on top of head, observe two robots interaction. Change robots’ behaviors using parameters. Create a humanoid robot based on the principles discussed in this set of slides. Combine the logic from this set of slides with fuzzy logic to describe behavior of some robot.