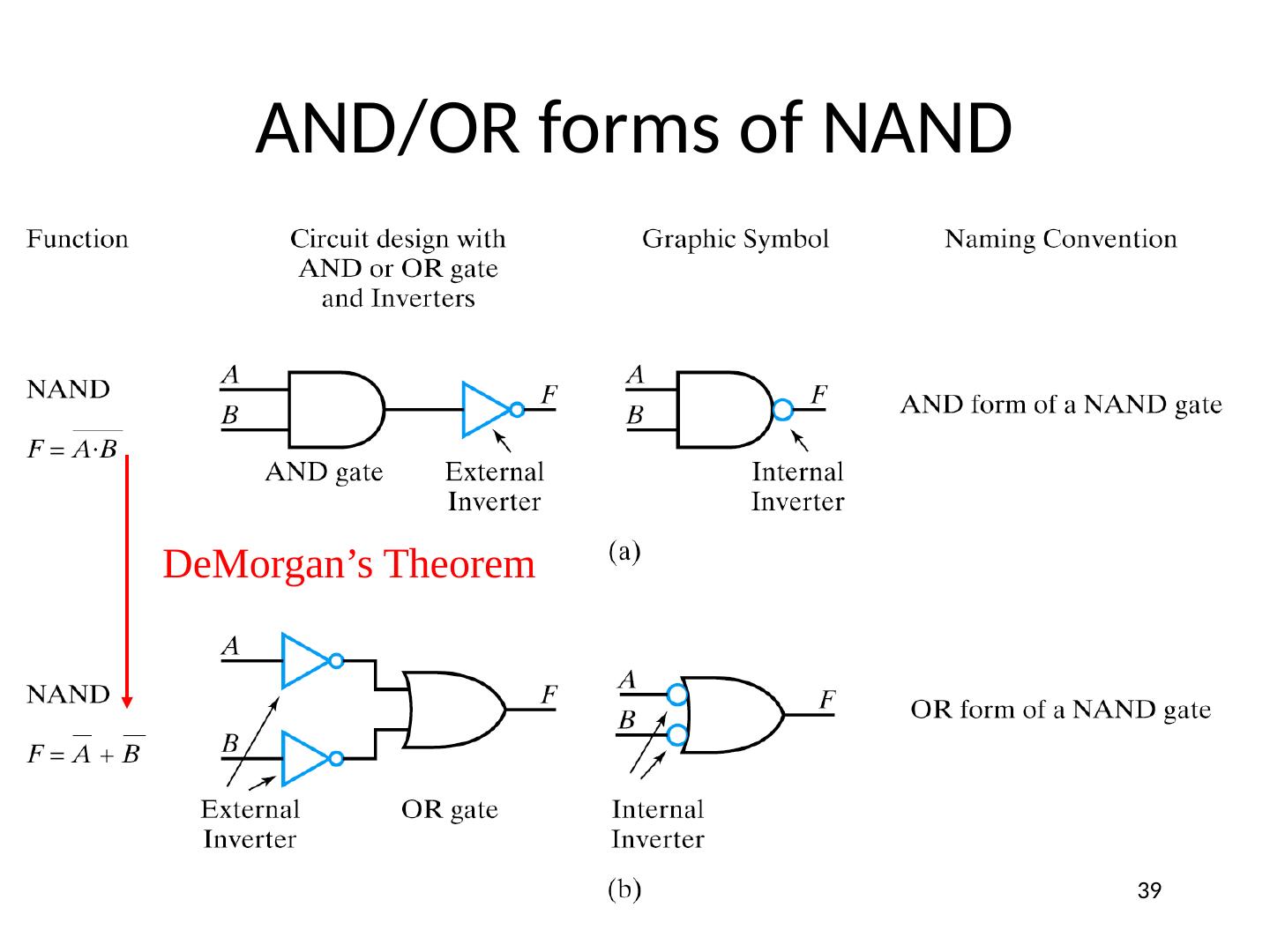
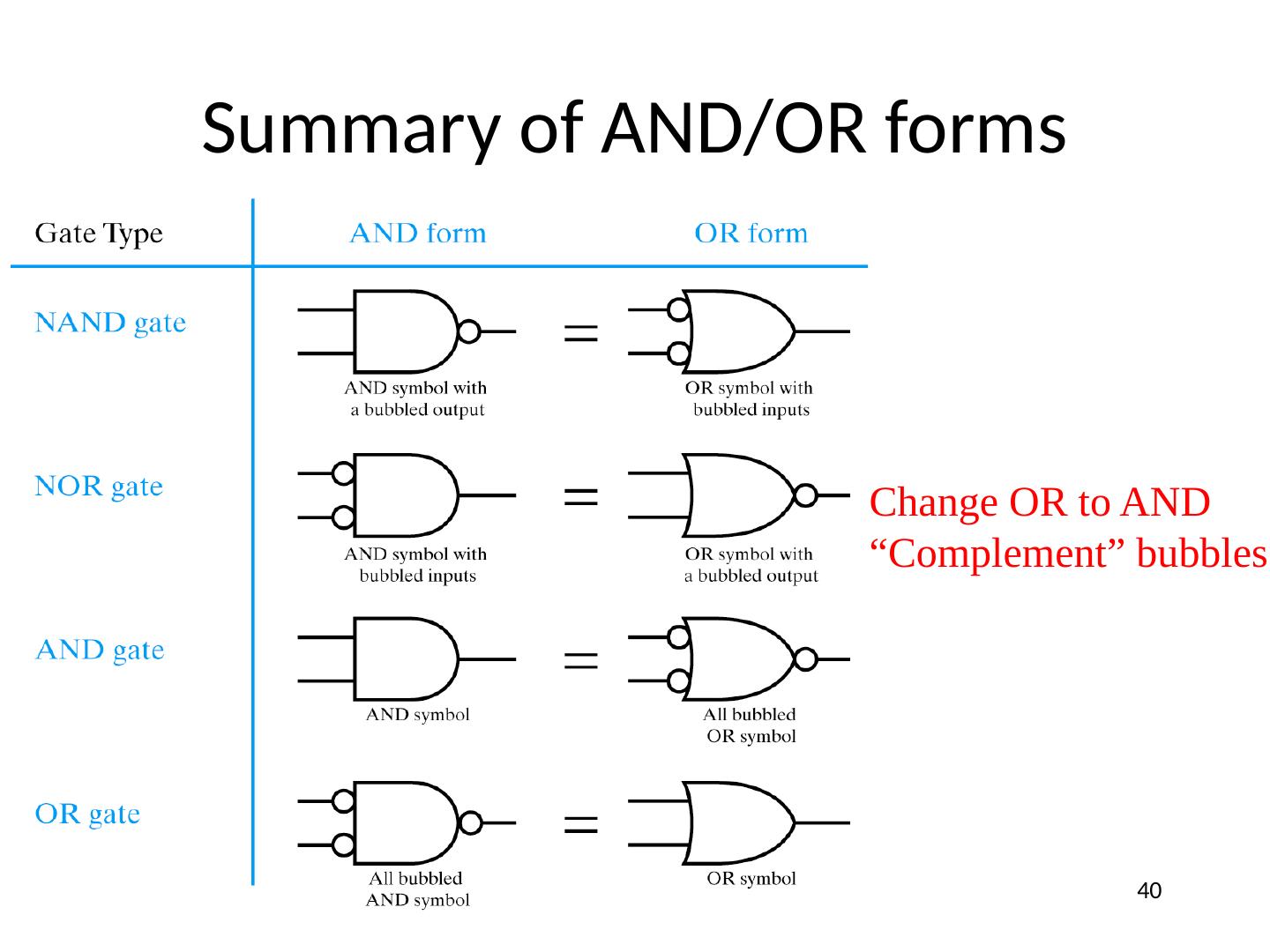
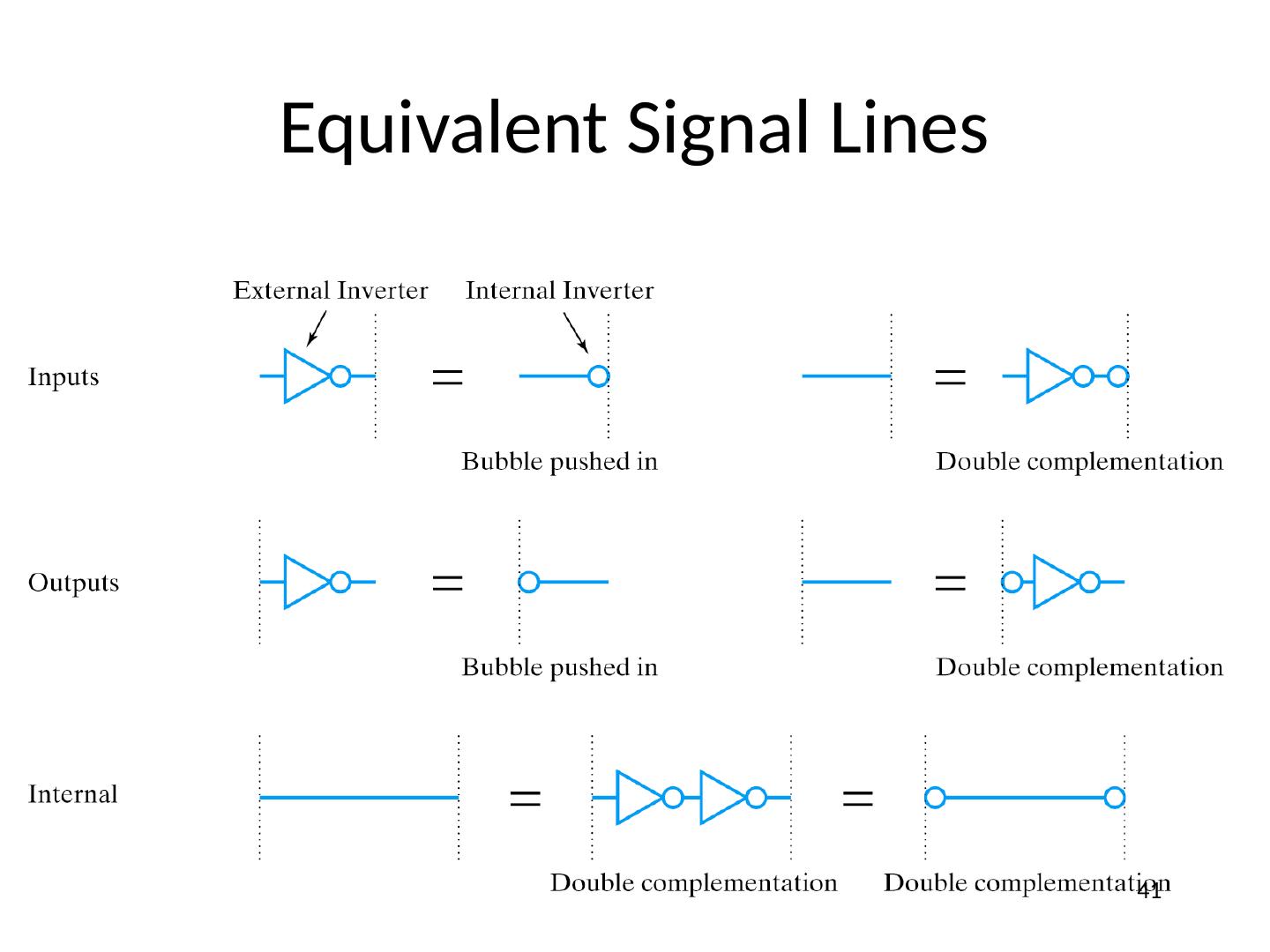
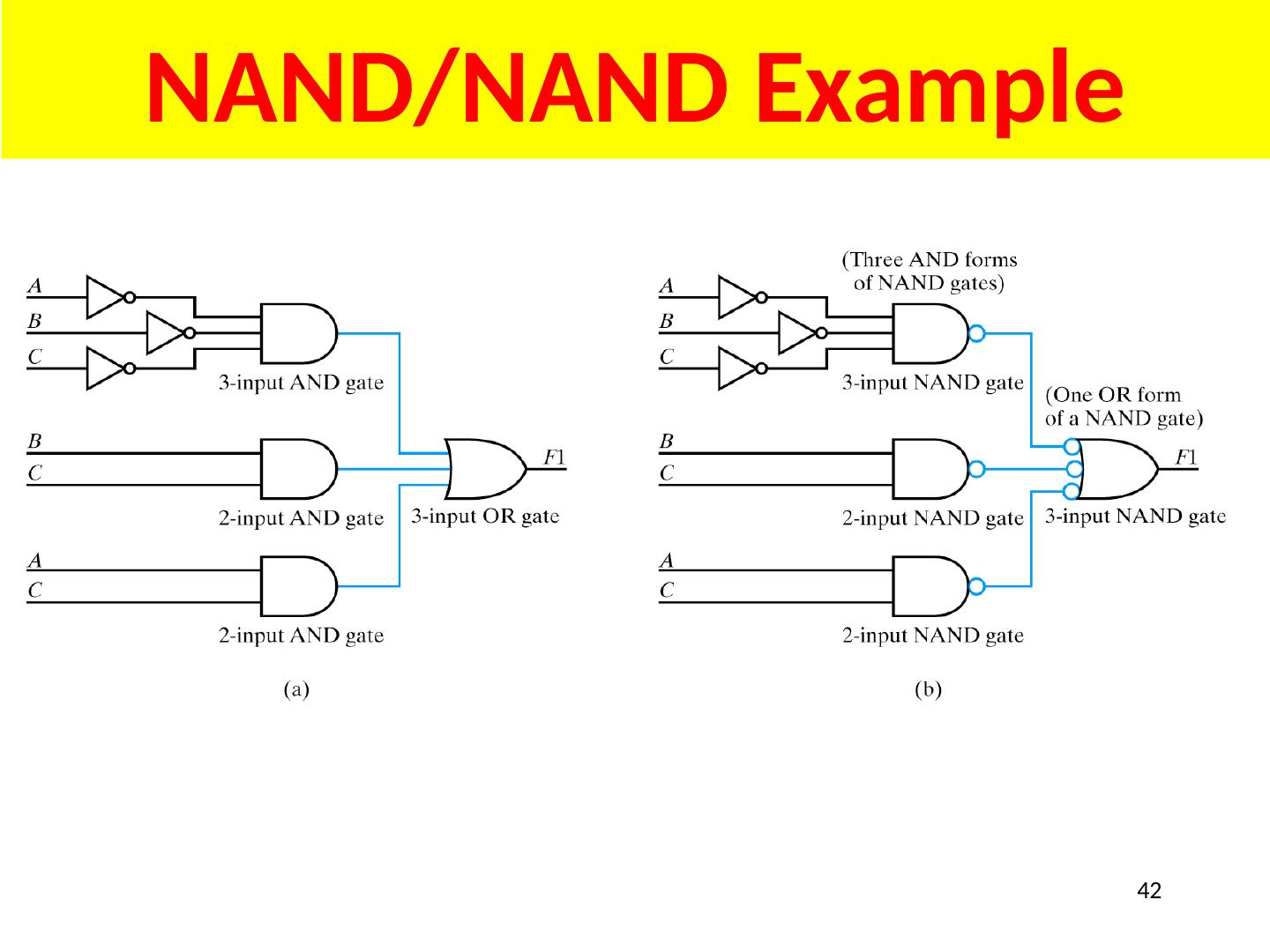
06 Symbols, Analysis, Design, NANDs NN

1 .Lecture 6 Topics Combinational Logic Circuits Graphic Symbols (IEEE and IEC) Switching Circuits Analyzing IC Logic Circuits Designing IC Logic Circuits Detailed Schematic Diagrams Using Equivalent Symbols 1

2 .Combinational Logic Circuits Combinational Logic Outputs depend only upon the current inputs (not previous “state”) Positive Logic High voltage ( H ) represents logic 1 (“True”) “Signal BusGrant is asserted High” Negative Logic Low voltage ( L ) represents logic 1 (“True”) “Signal BusRequest # is asserted Low” 2

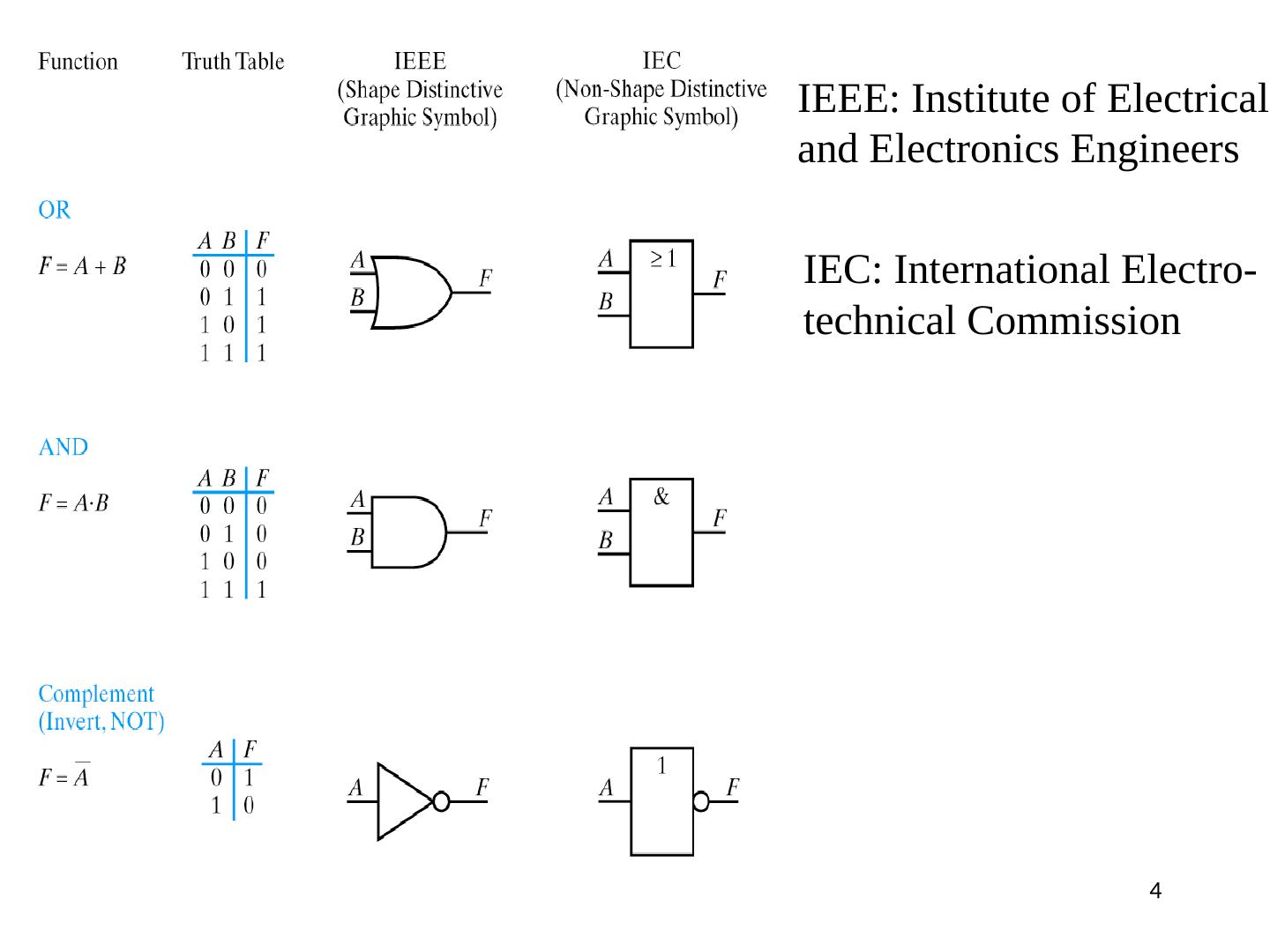
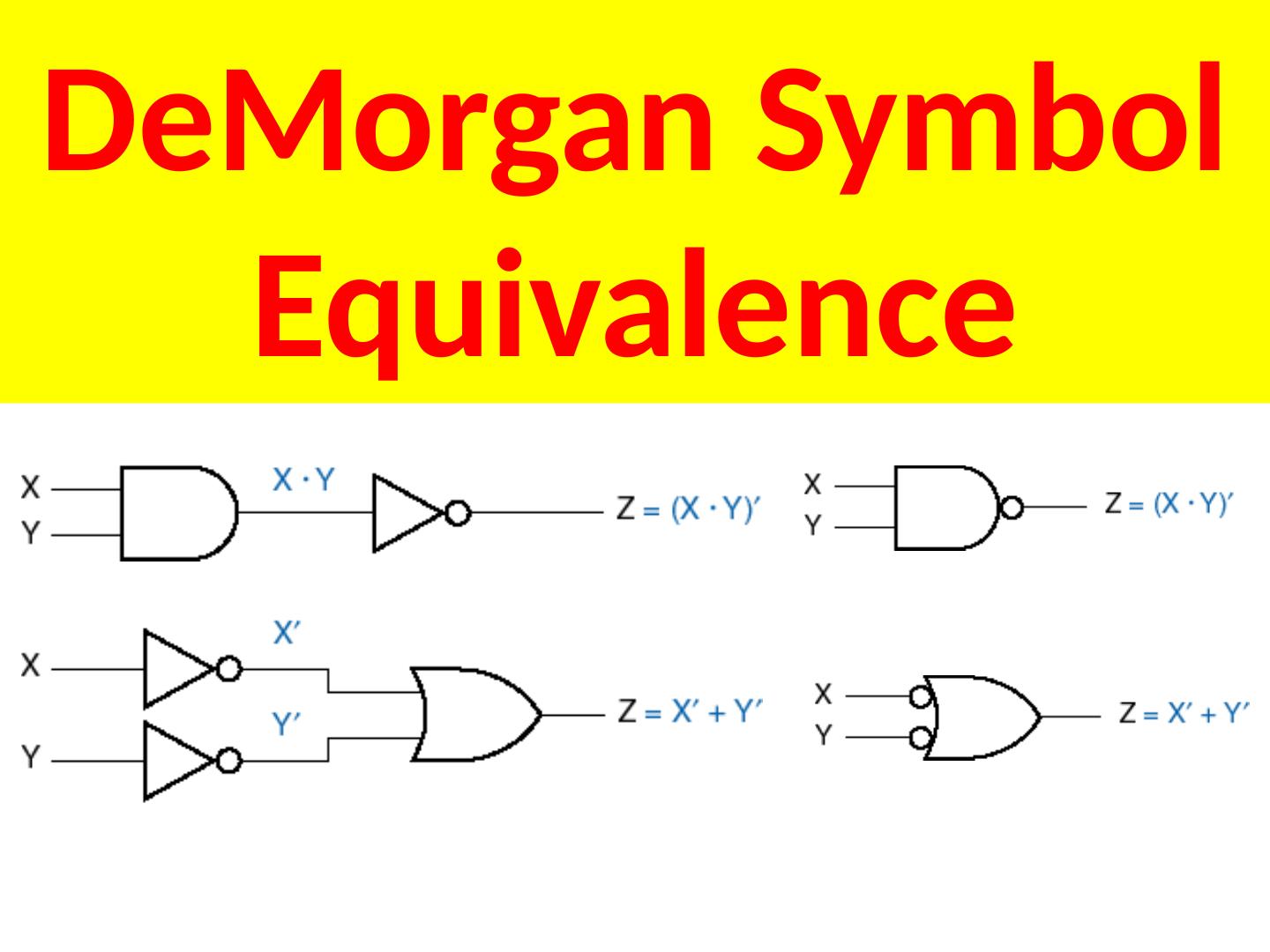
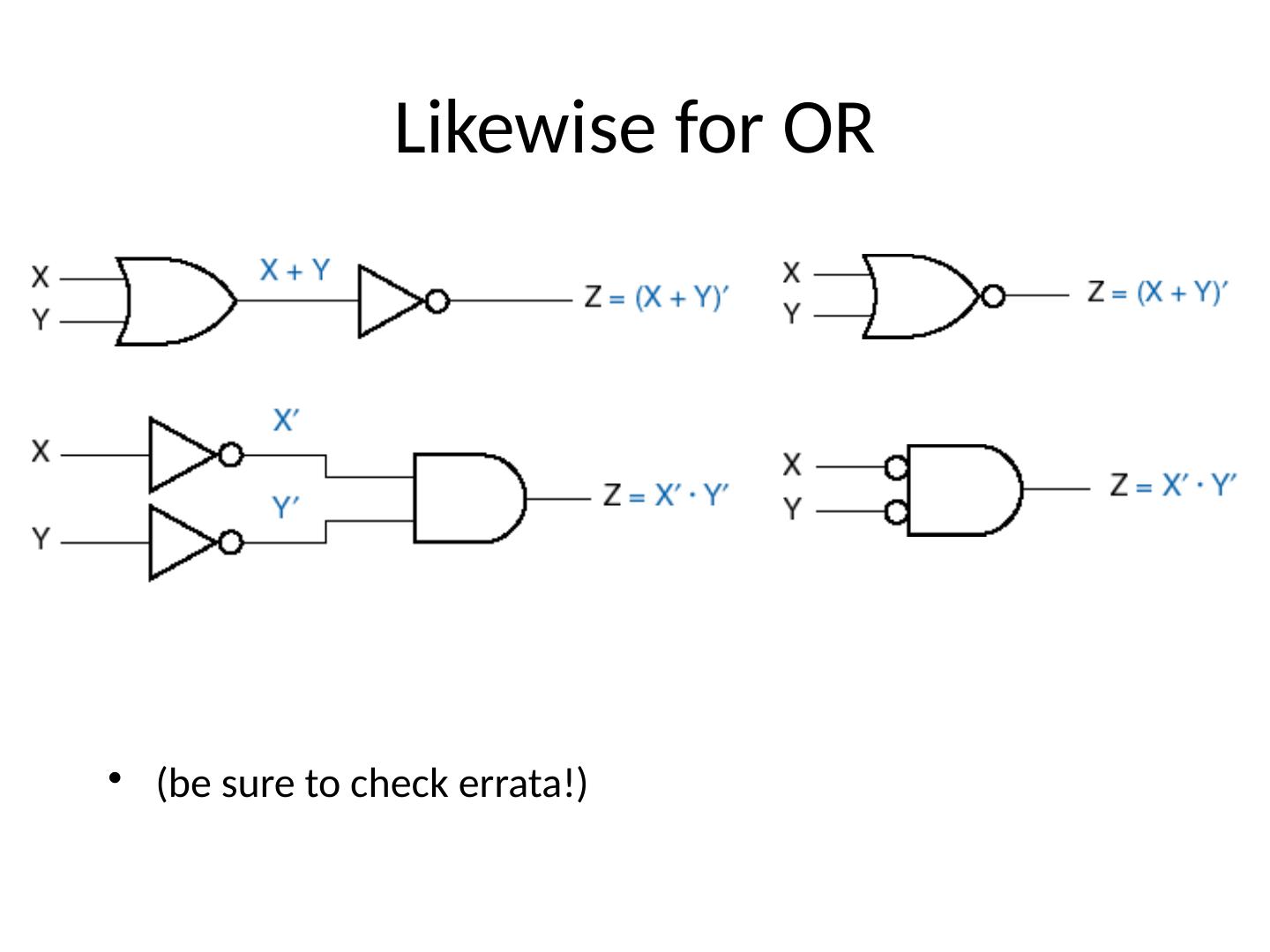
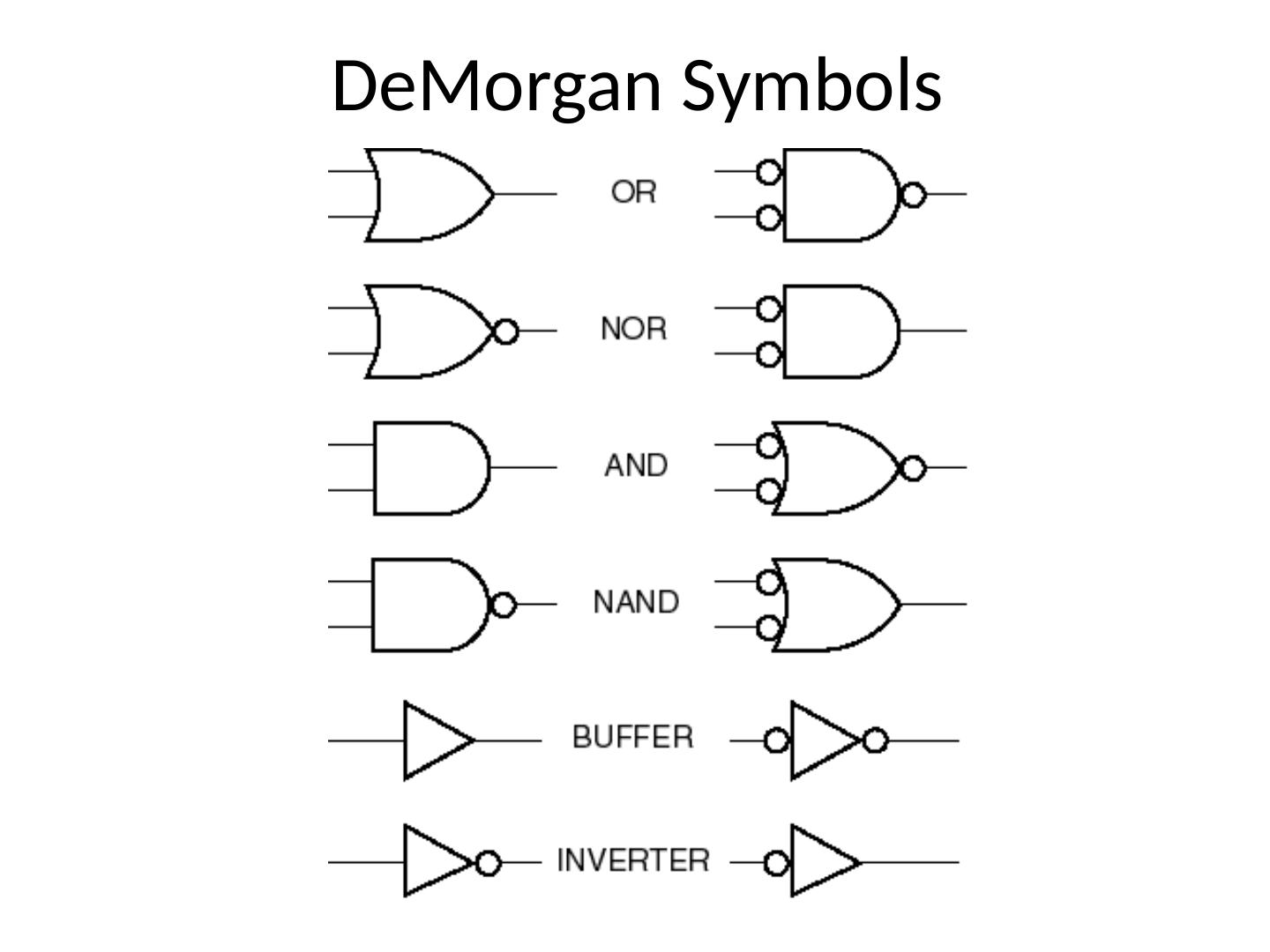
3 .Graphic Symbols

4 .IEEE: Institute of Electrical and Electronics Engineers IEC: International Electro- technical Commission 4

5 .5

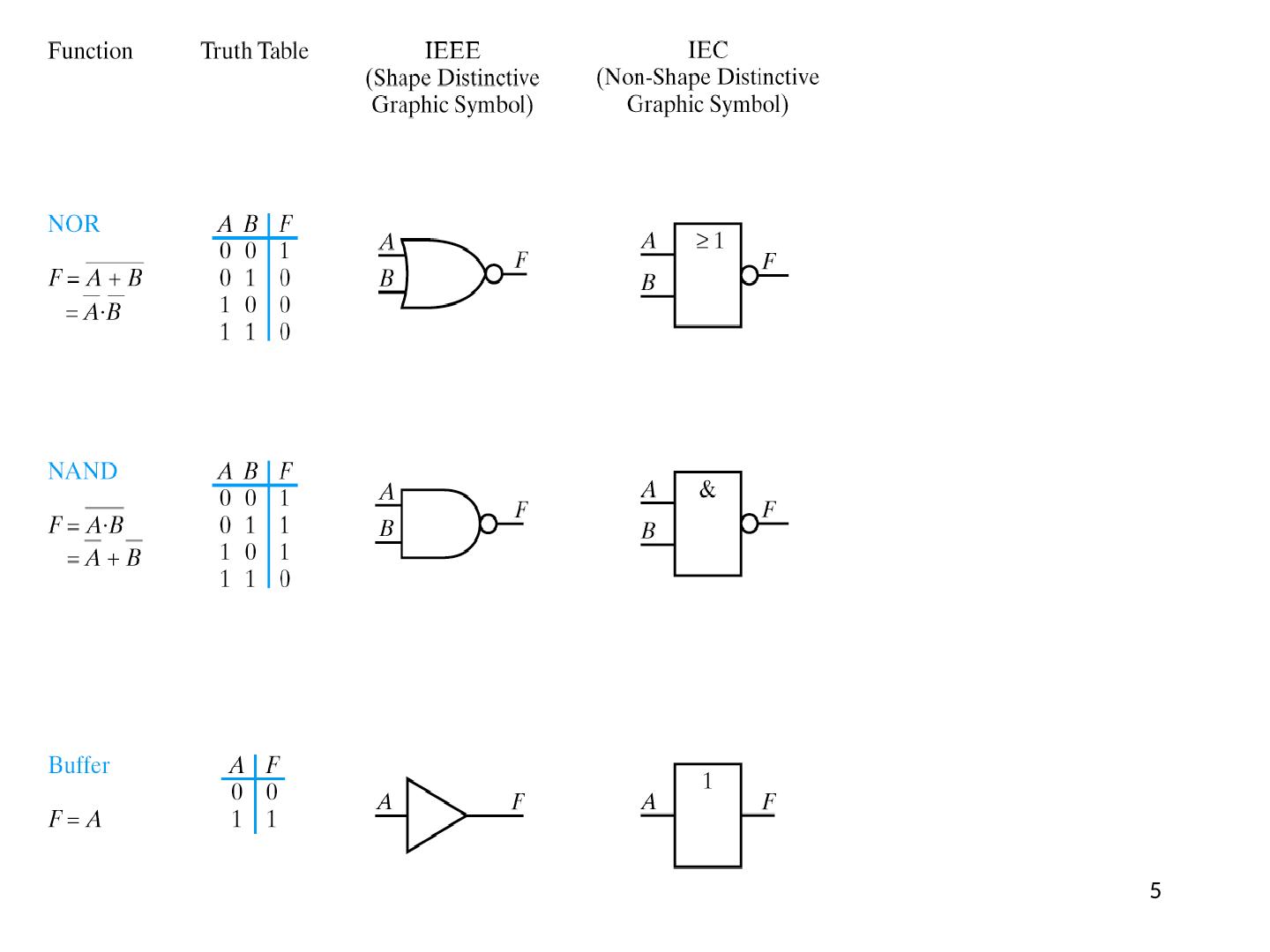
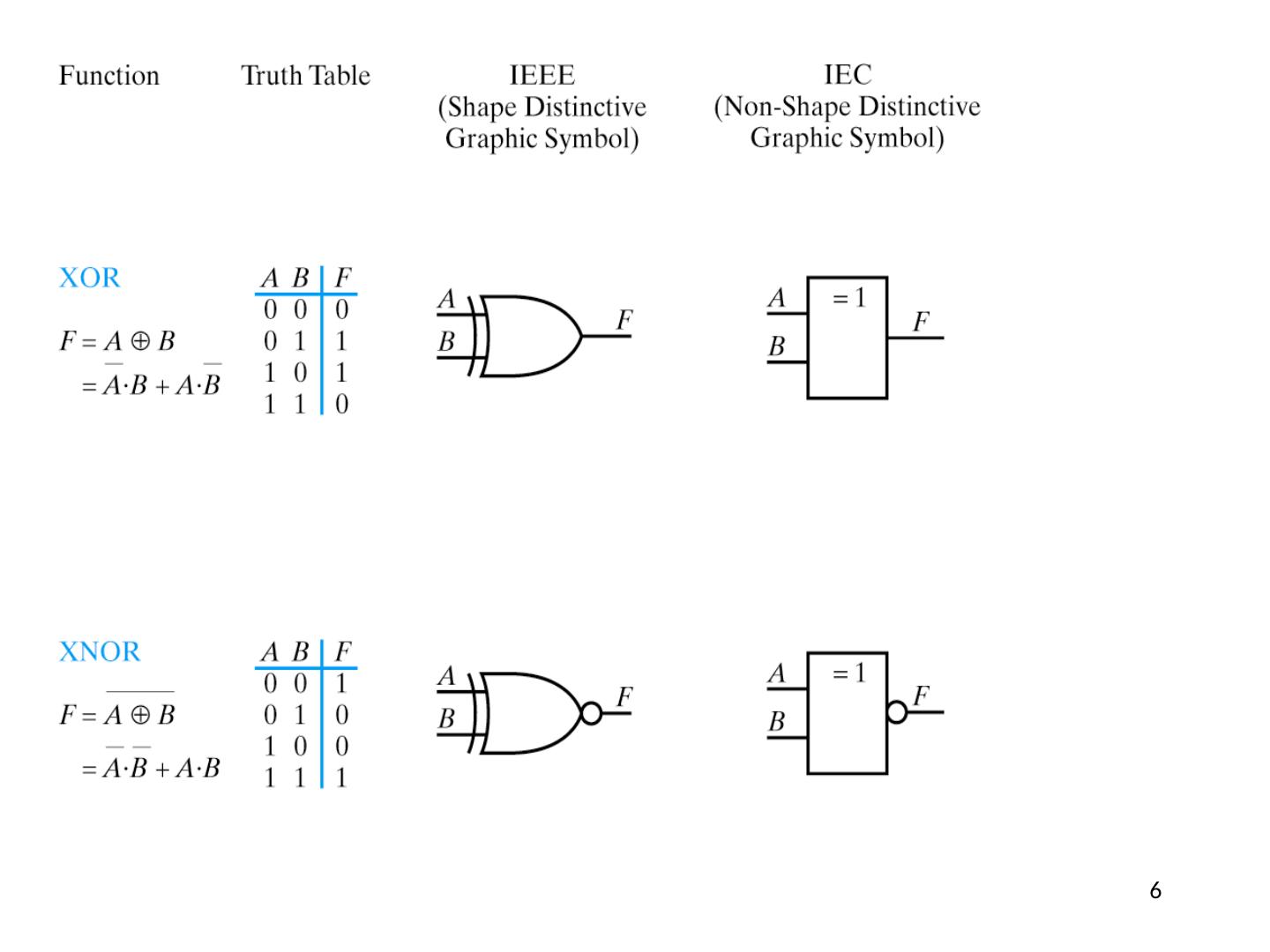
6 .6

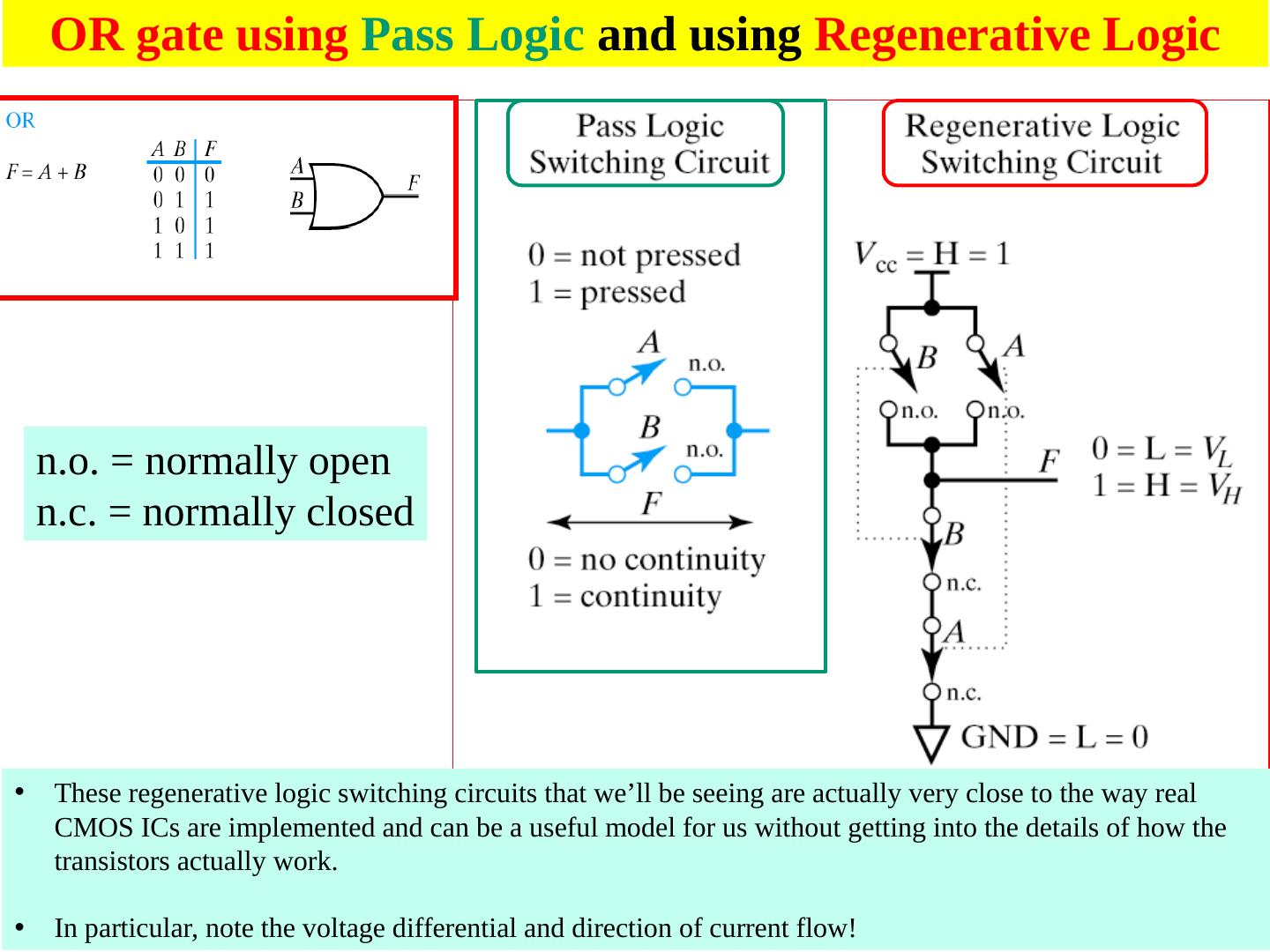
7 .Pass Logic versus Regenerative Logic

8 .n.o . = normally open n.c. = normally closed 8 These regenerative logic switching circuits that we’ll be seeing are actually very close to the way real CMOS ICs are implemented and can be a useful model for us without getting into the details of how the transistors actually work. In particular, note the voltage differential and direction of current flow! OR gate using Pass Logic and using Regenerative Logic

9 .9 AND gate using Pass Logic and using Regenerative Logic n.o . = normally open n.c. = normally closed

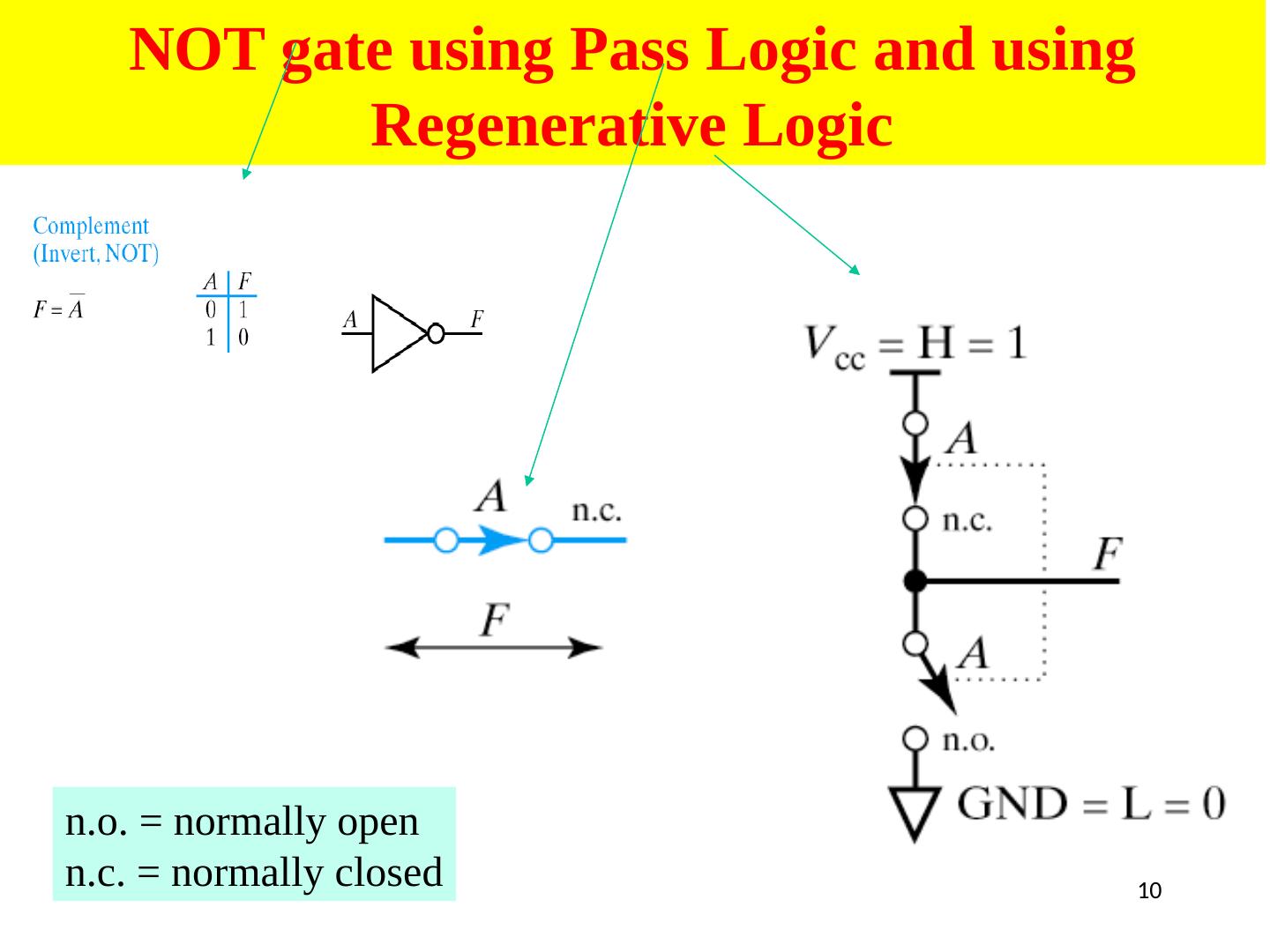
10 .10 NOT gate using Pass Logic and using Regenerative Logic n.o . = normally open n.c. = normally closed

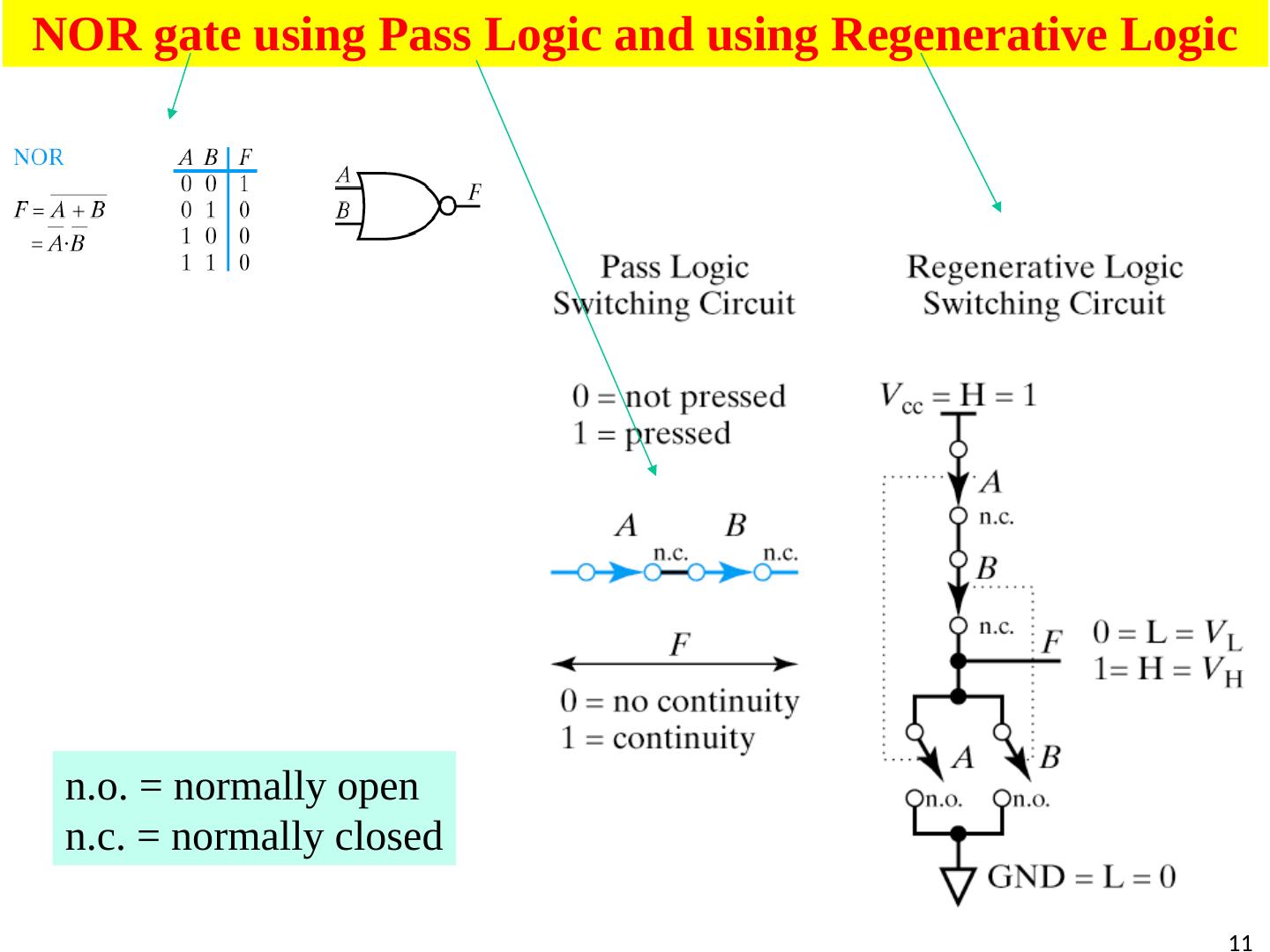
11 .11 NOR gate using Pass Logic and using Regenerative Logic n.o . = normally open n.c. = normally closed

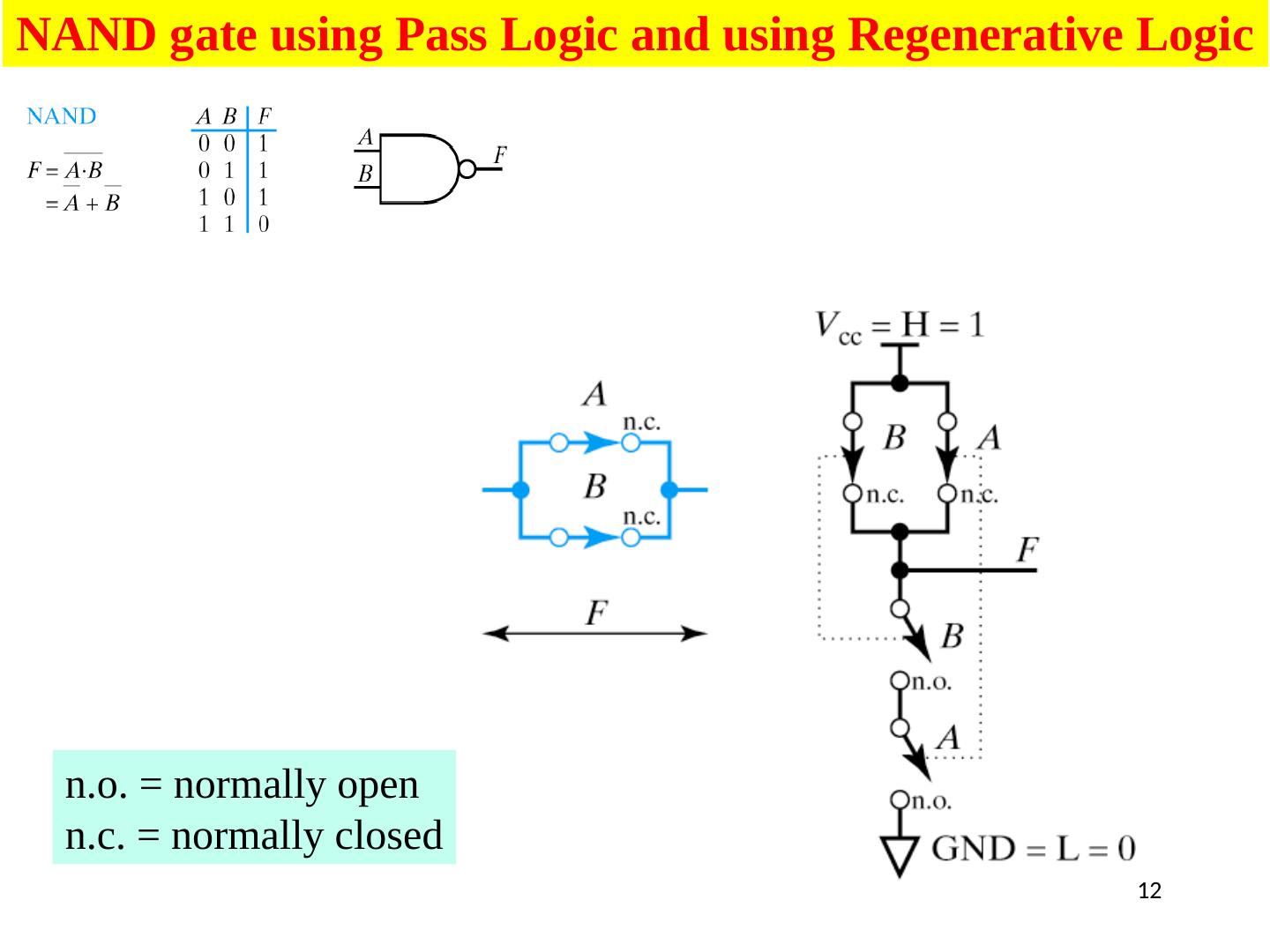
12 .12 NAND gate using Pass Logic and using Regenerative Logic n.o . = normally open n.c. = normally closed

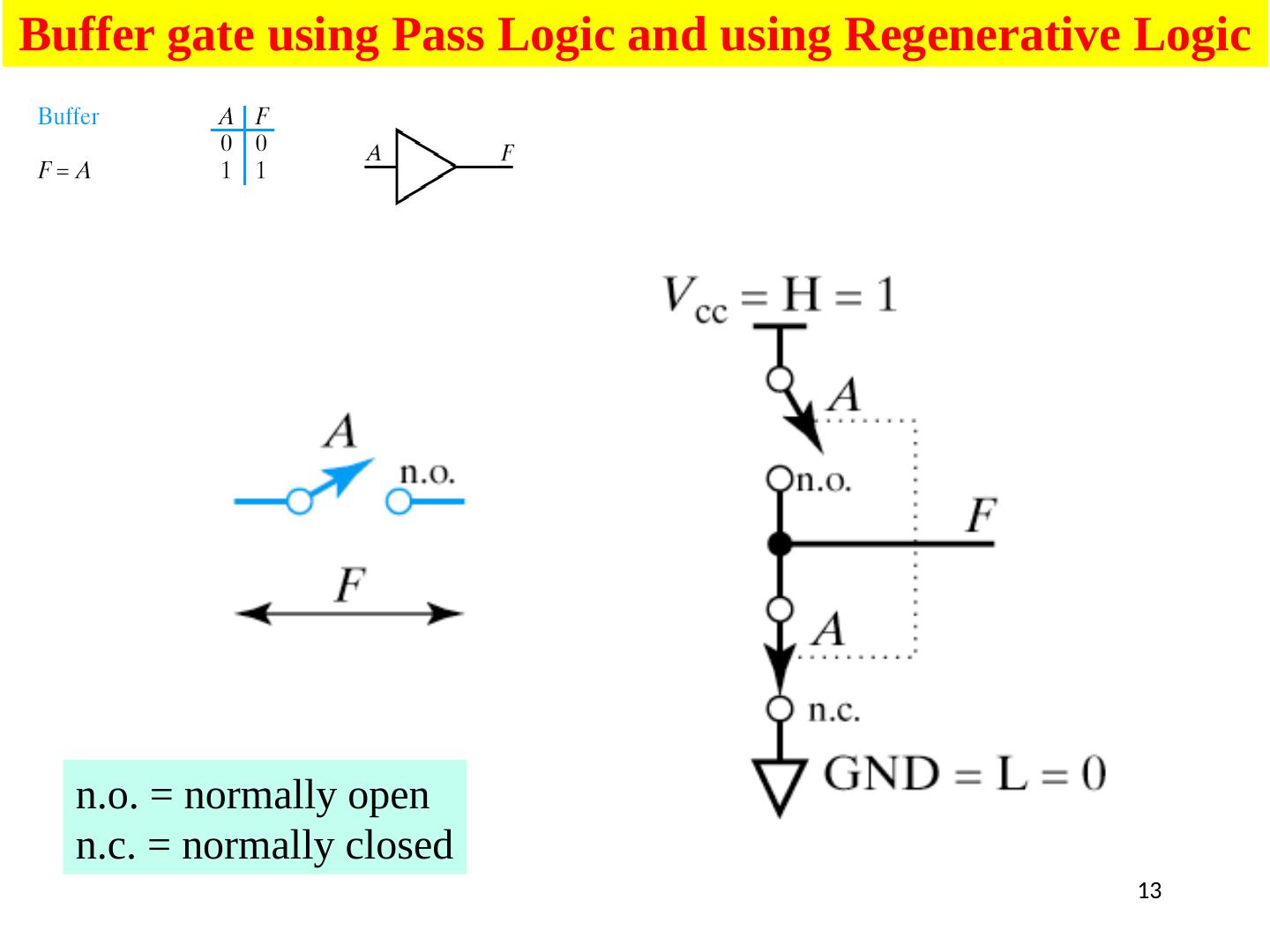
13 .13 Buffer gate using Pass Logic and using Regenerative Logic n.o . = normally open n.c. = normally closed

14 .14 XOR gate using Pass Logic and using Regenerative Logic n.o . = normally open n.c. = normally closed

15 .15 XNOR gate using Pass Logic and using Regenerative Logic n.o . = normally open n.c. = normally closed

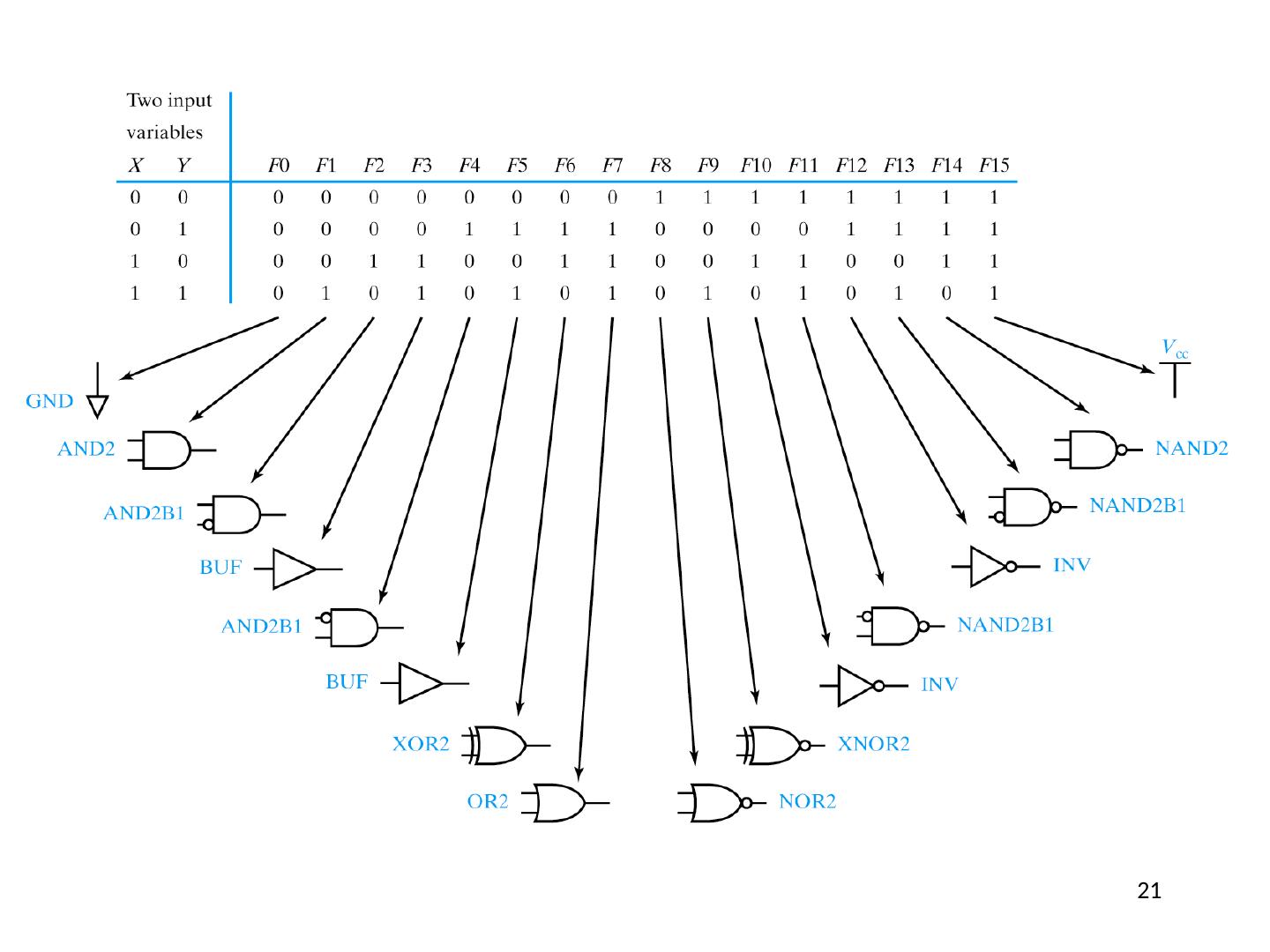
16 .All Possible Two-Variable Functions

17 .All Possible Two Variable Functions Question: How many unique functions of two variables are there? Recall earlier question… 17

18 .Truth Tables B 5 B 4 B 3 B 2 B 1 B 0 F 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 0 . . . 1 1 1 1 1 1 1 0 1 2 3 . . . 63 2 6 = 64 Question: How many rows are there in a truth table for n variables? As many rows as unique combinations of inputs Enumerate by counting in binary 2 n 18

19 .Two Variable Functions Question: How many unique combinations of 2 n bits? Enumerate by counting in binary 2 2 n 2 64 19 B 5 B 4 B 3 B 2 B 1 B 0 F 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 0 . . . 1 1 1 1 1 1 1 0 1 2 3 . . . 63 2 6 = 64

20 .All Possible Two Variable Functions Question: How many unique functions of two variables are there? B 1 B 0 F 0 0 0 0 1 1 1 0 1 1 1 0 2 2 = 4 rows 4 bits Number of unique 4 bit words = 2 4 = 16 20

21 .21

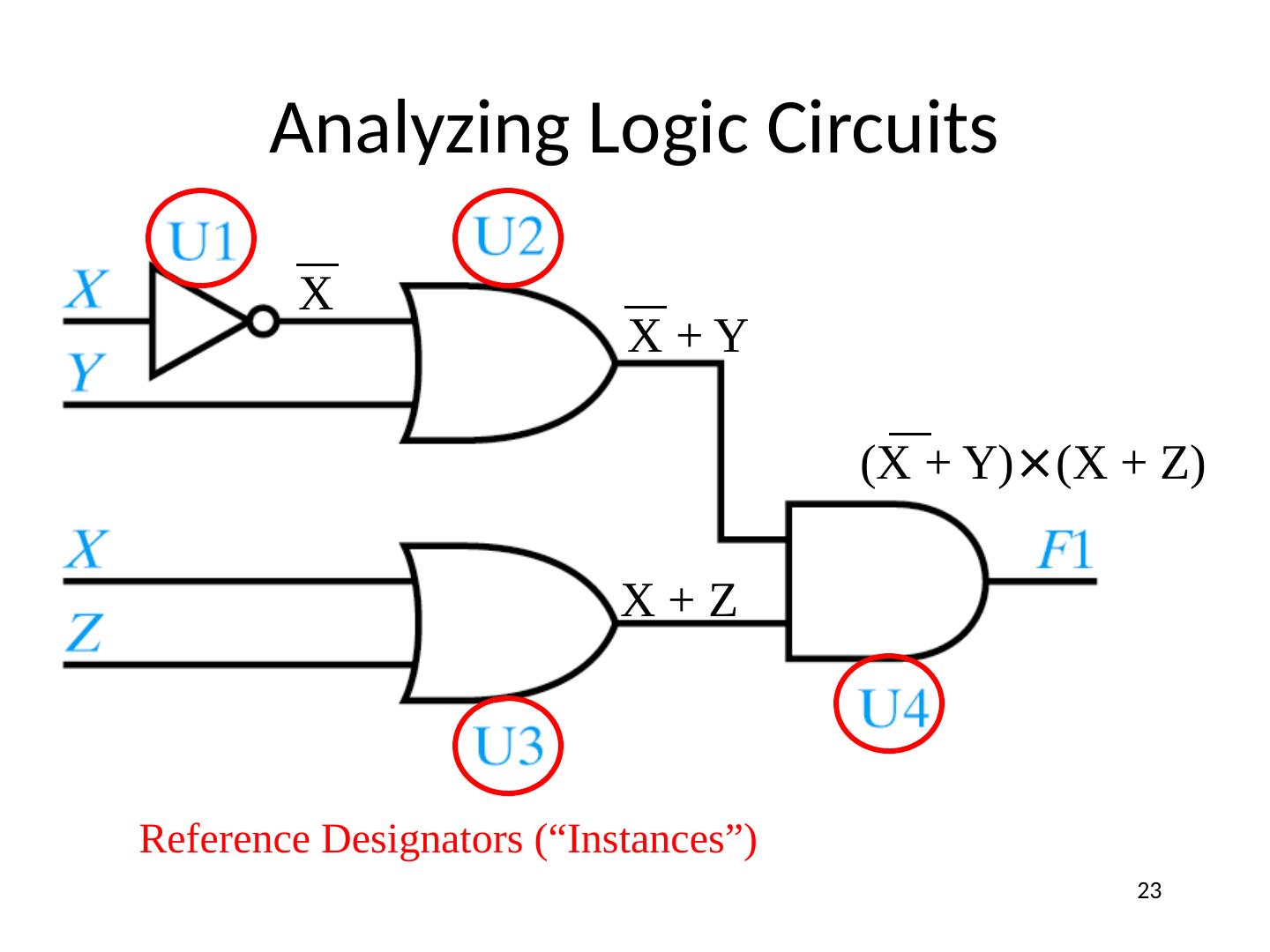
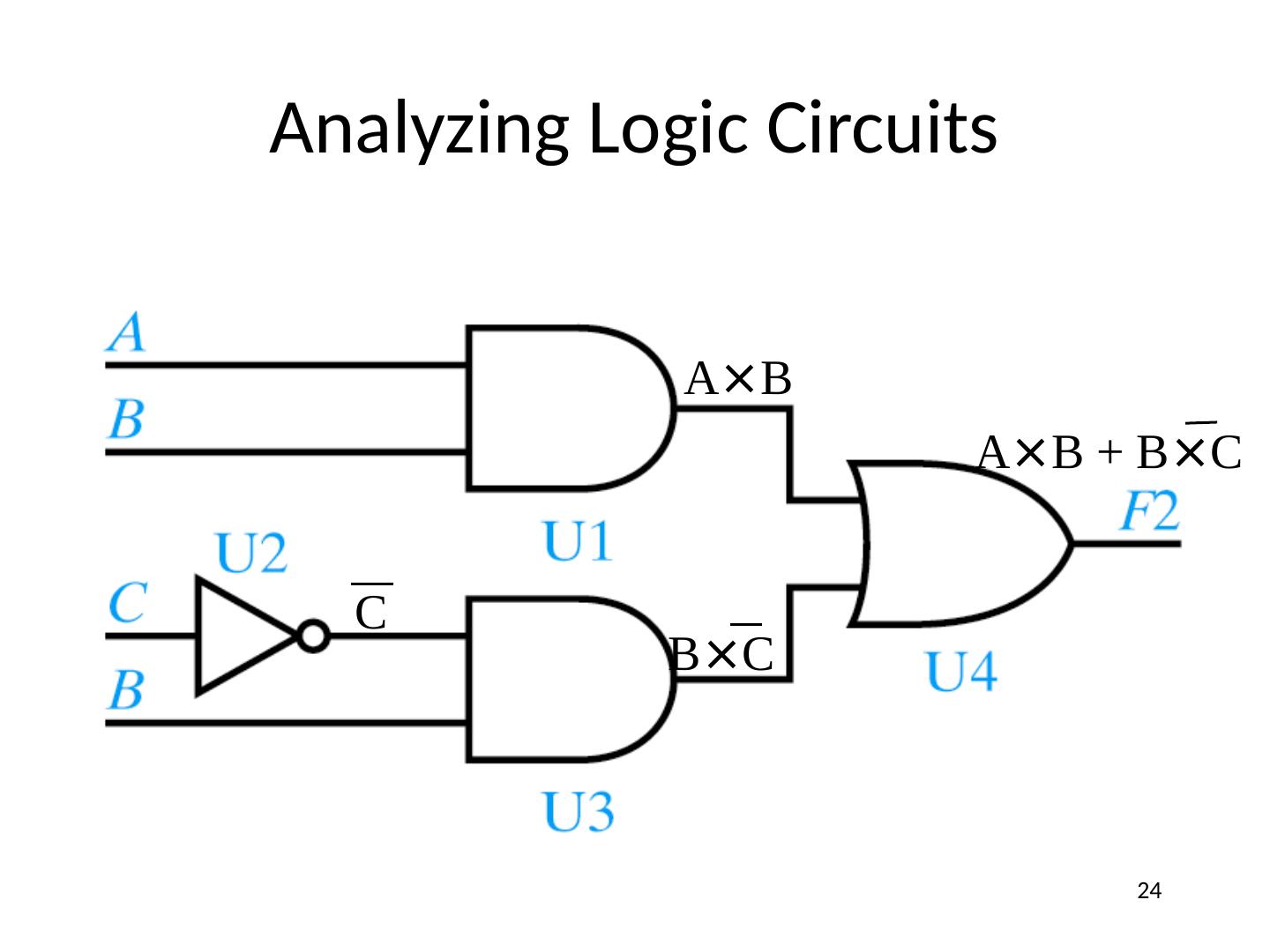
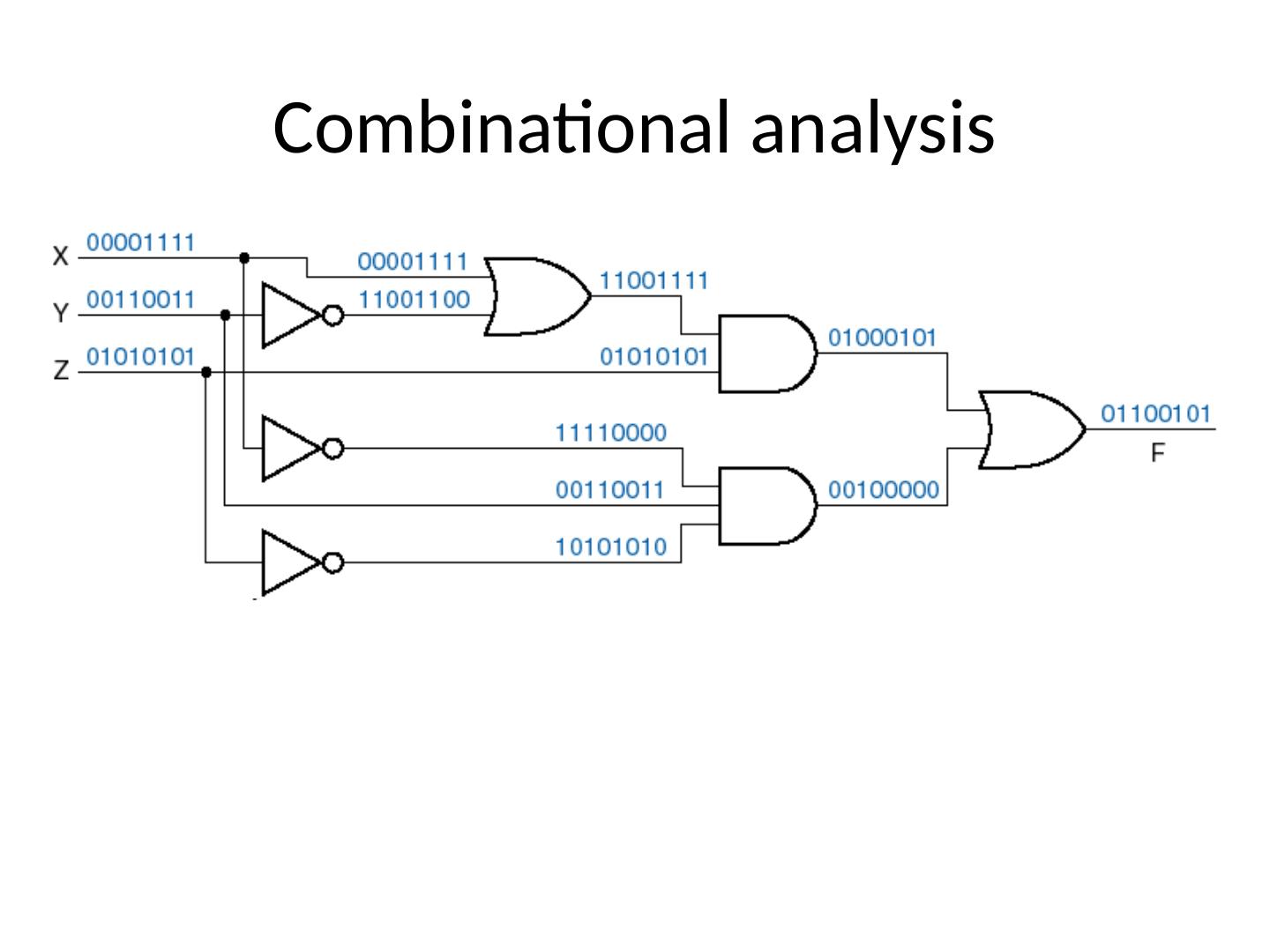
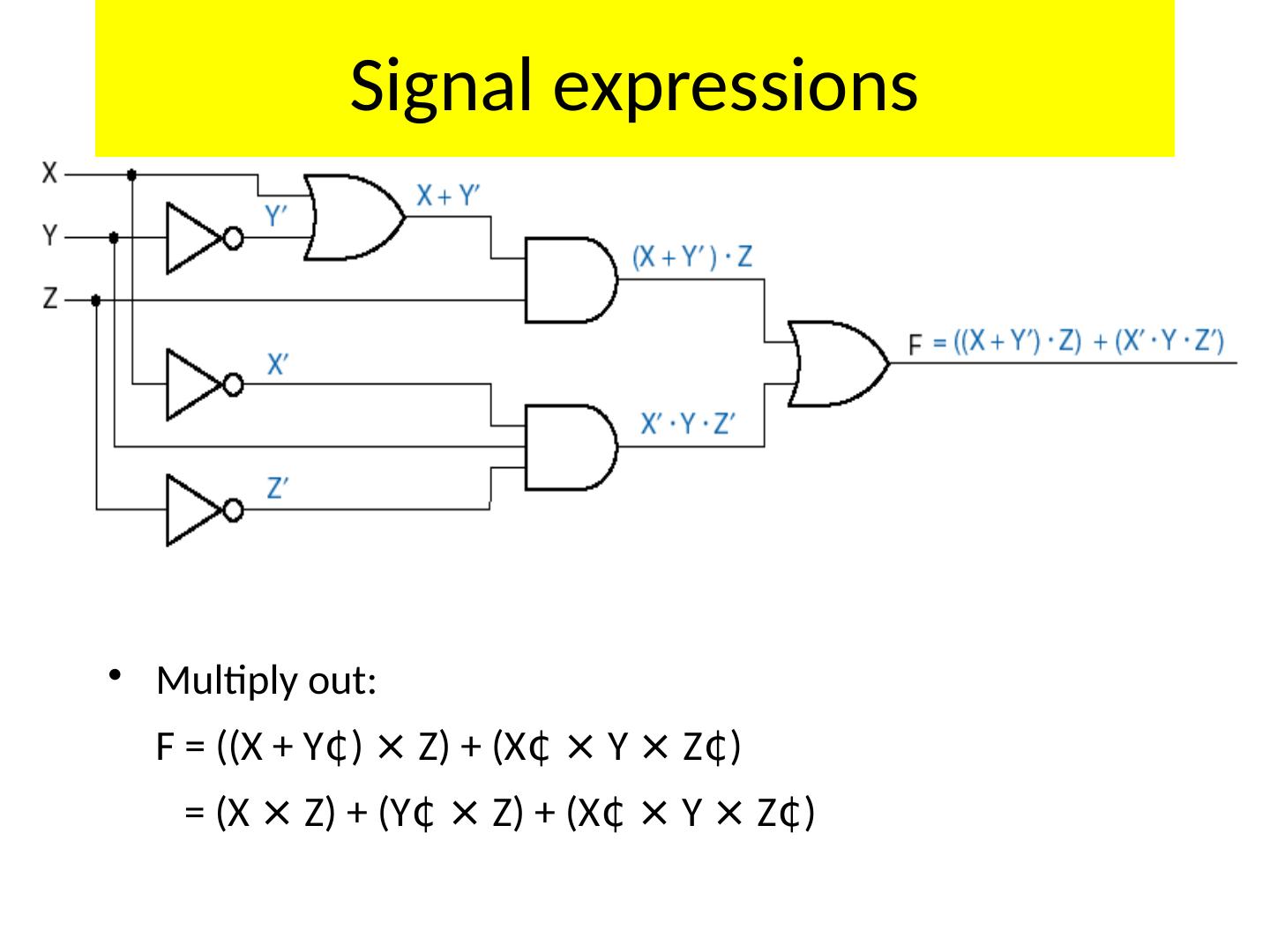
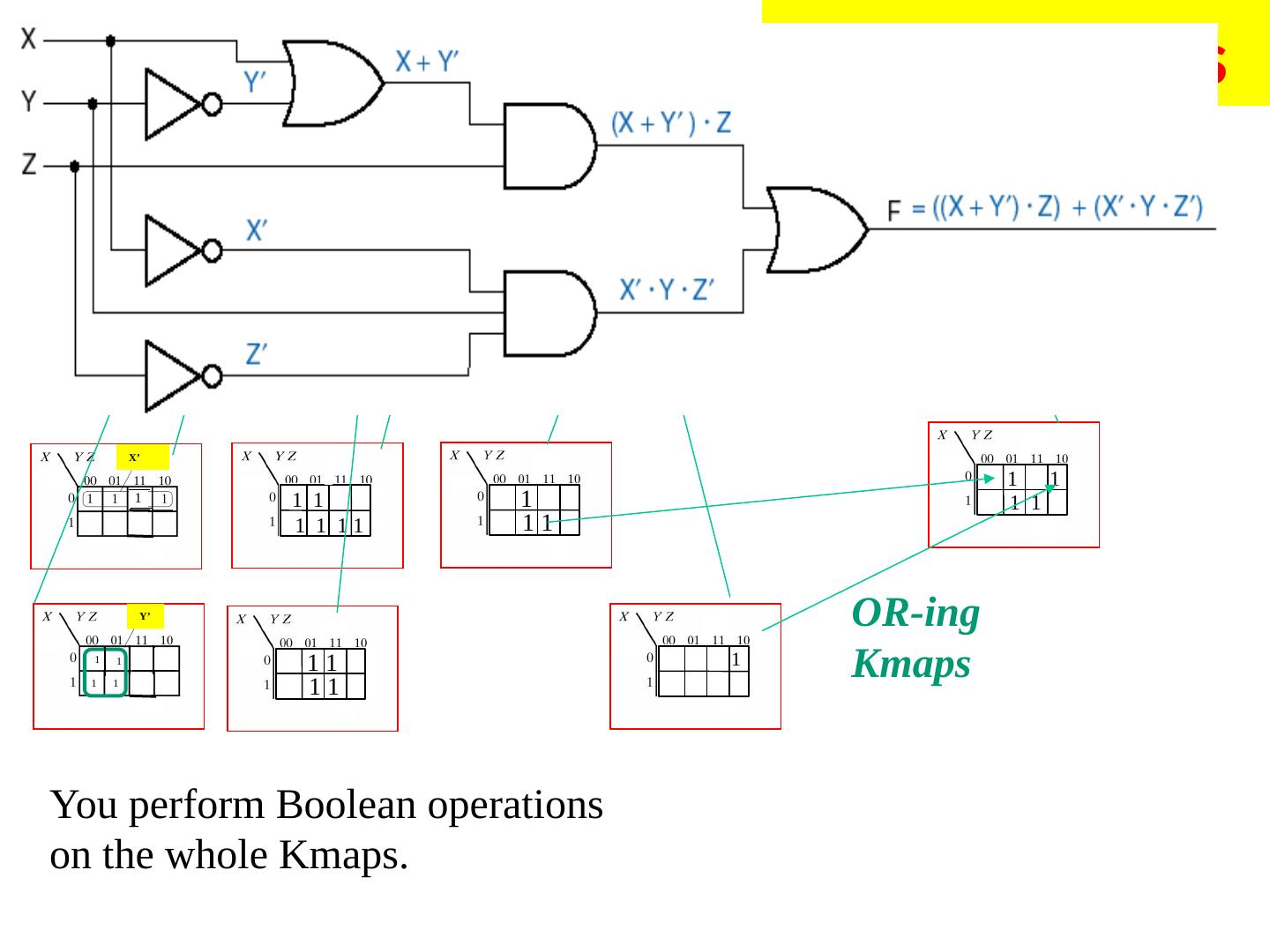
22 .Analyzing Logic Circuits

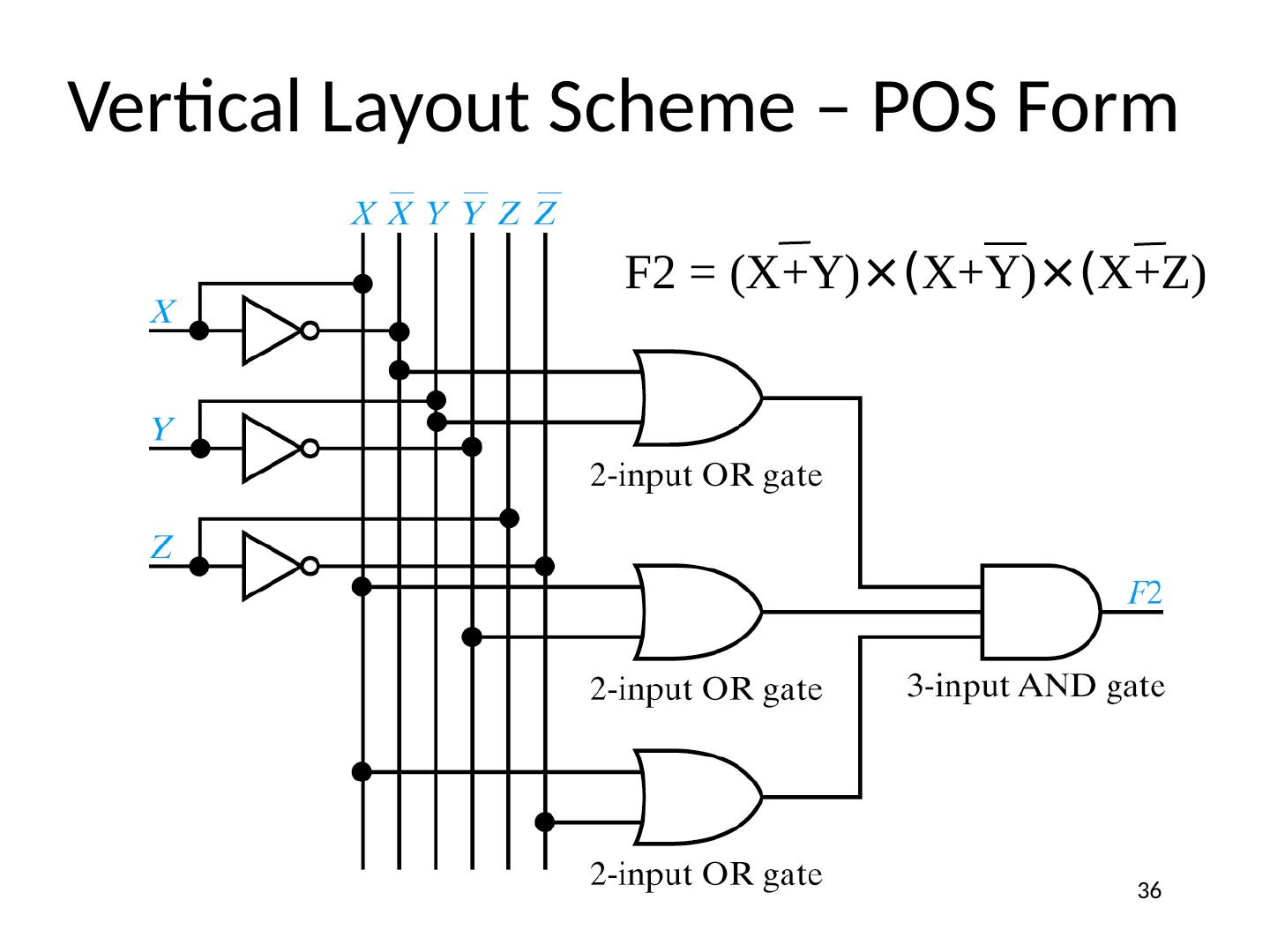
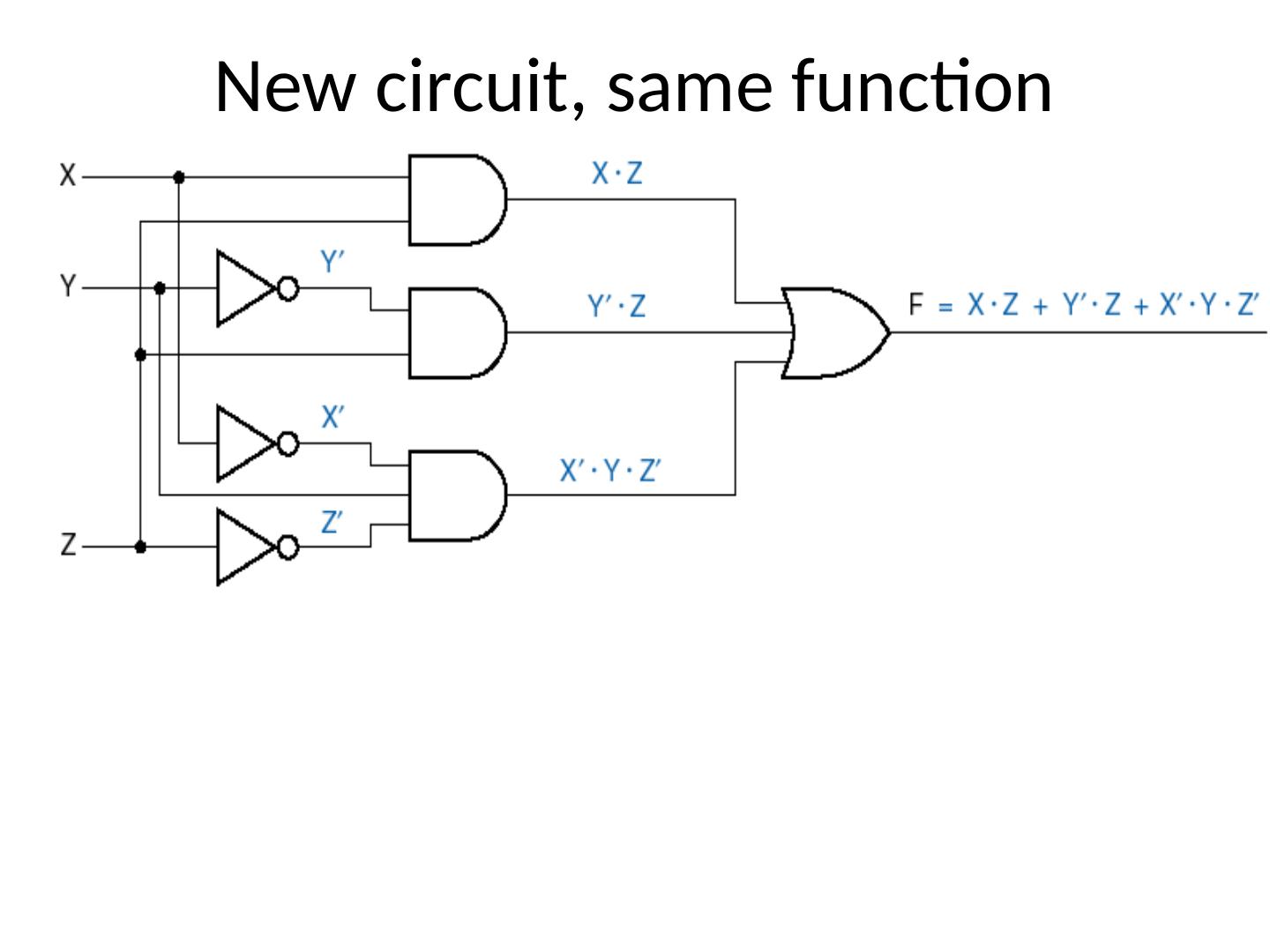
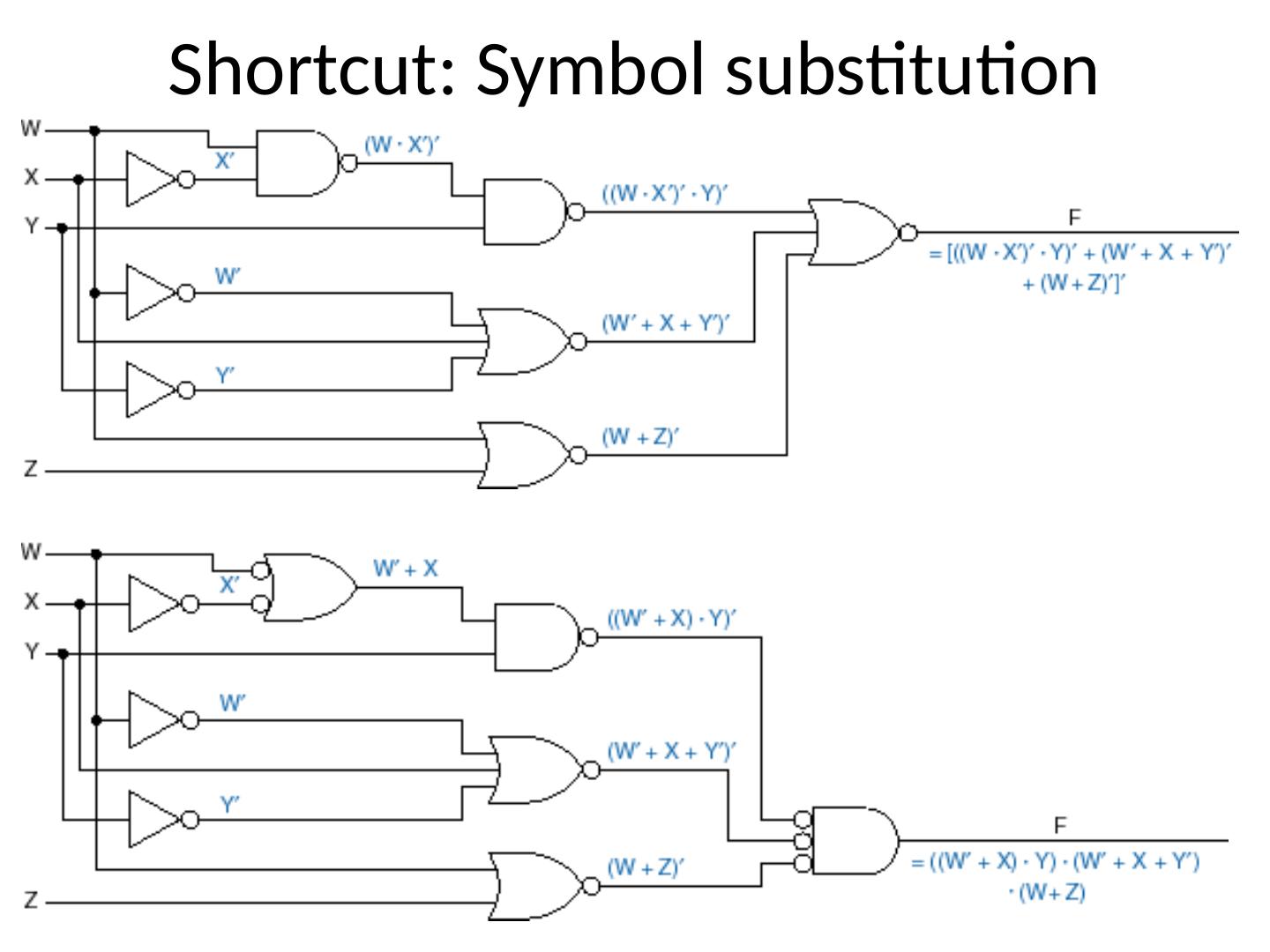
23 .Analyzing Logic Circuits Reference Designators (“Instances”) X + Z X X + Y (X + Y) × (X + Z) 23

24 .Analyzing Logic Circuits C A × B B × C A × B + B × C 24

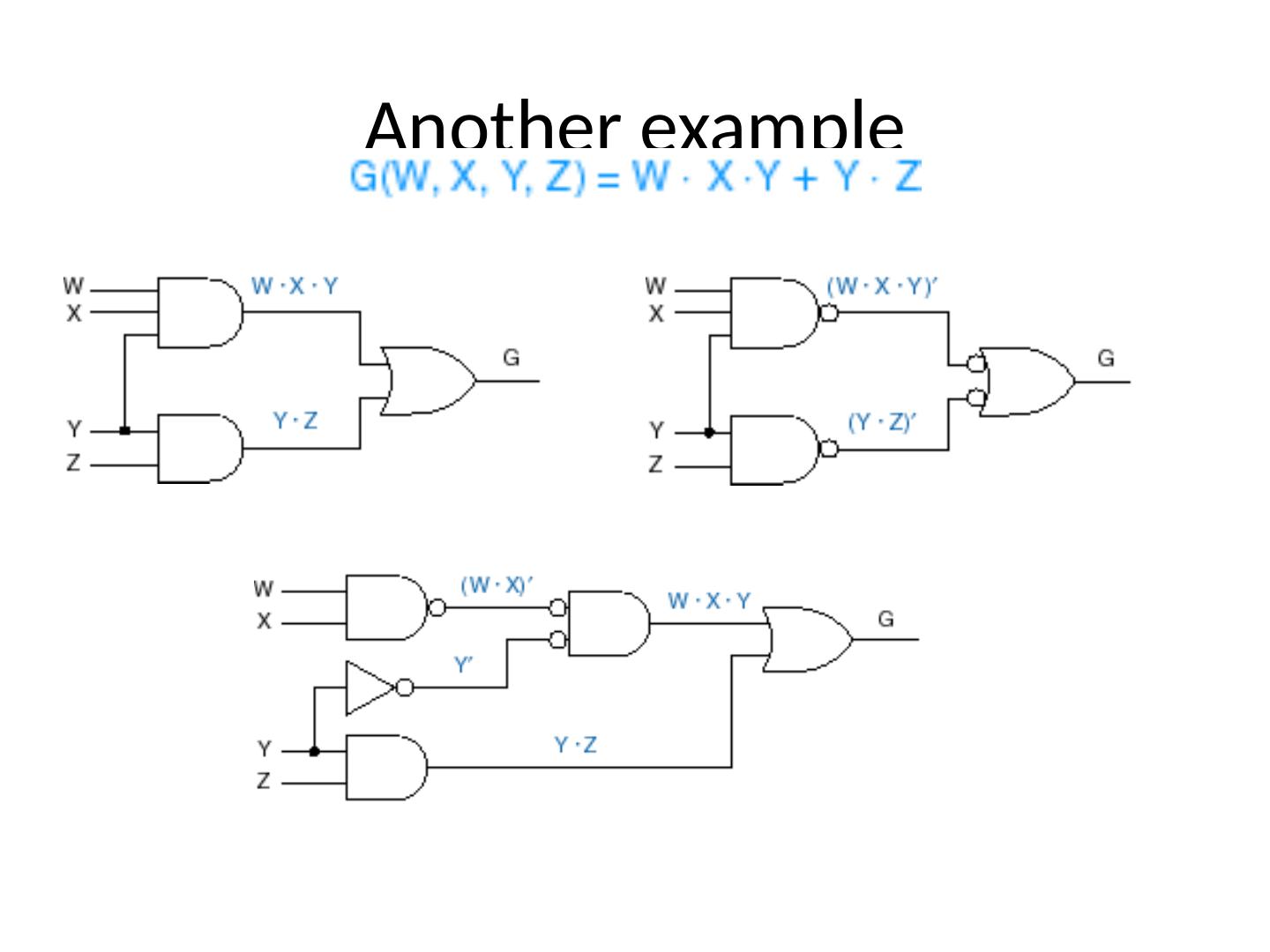
25 .Another example

26 .Designing Logic Circuits

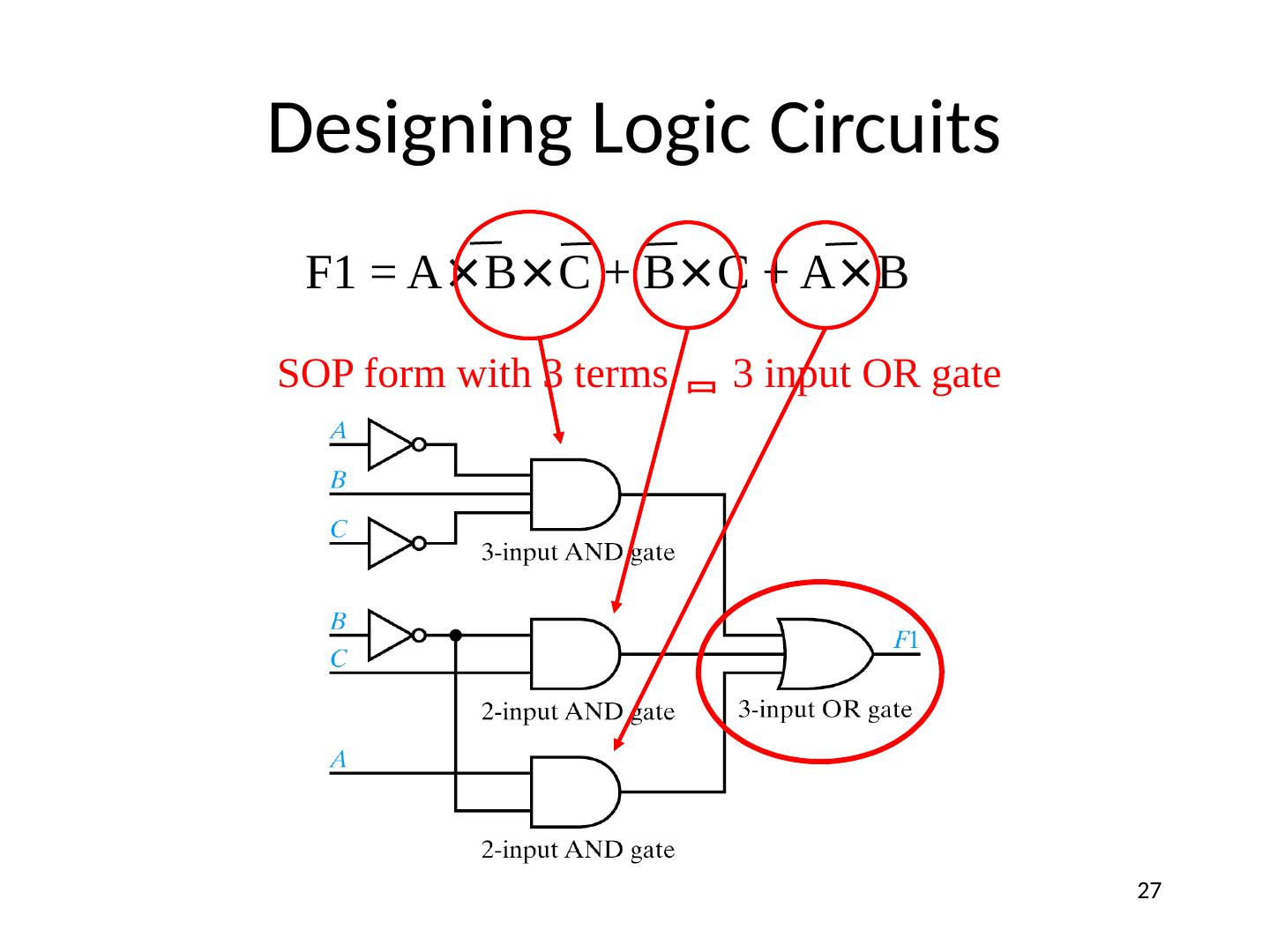
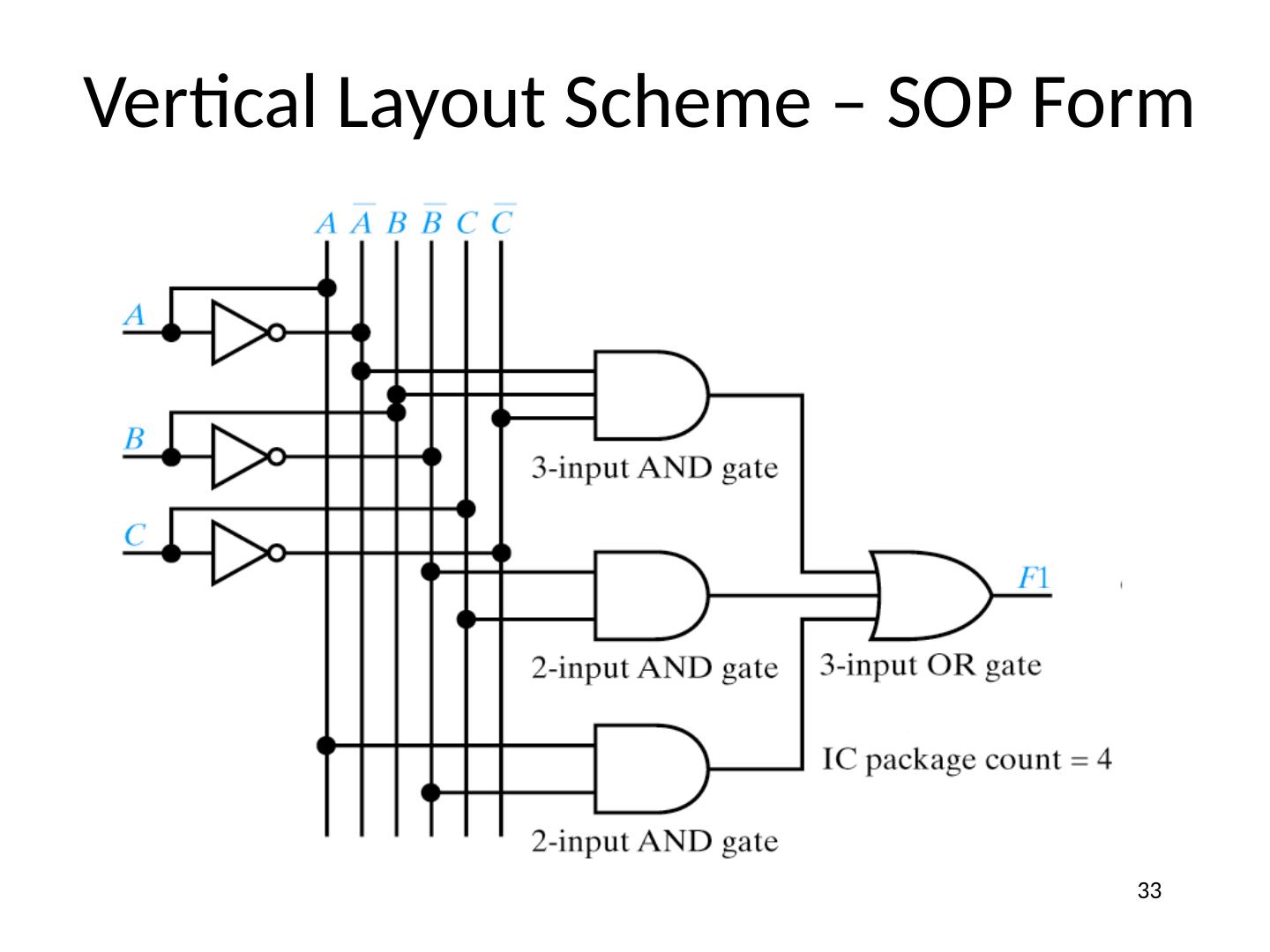
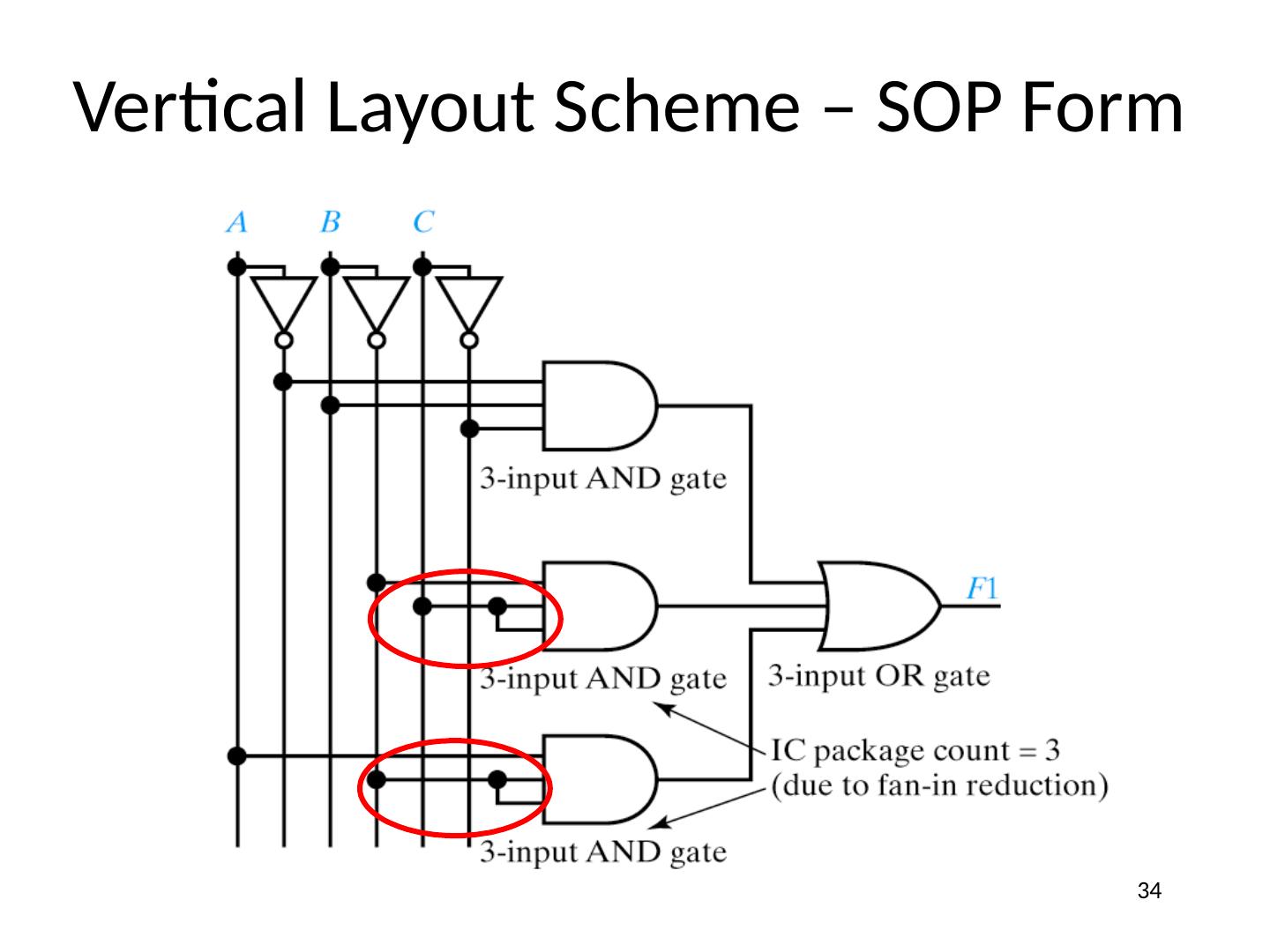
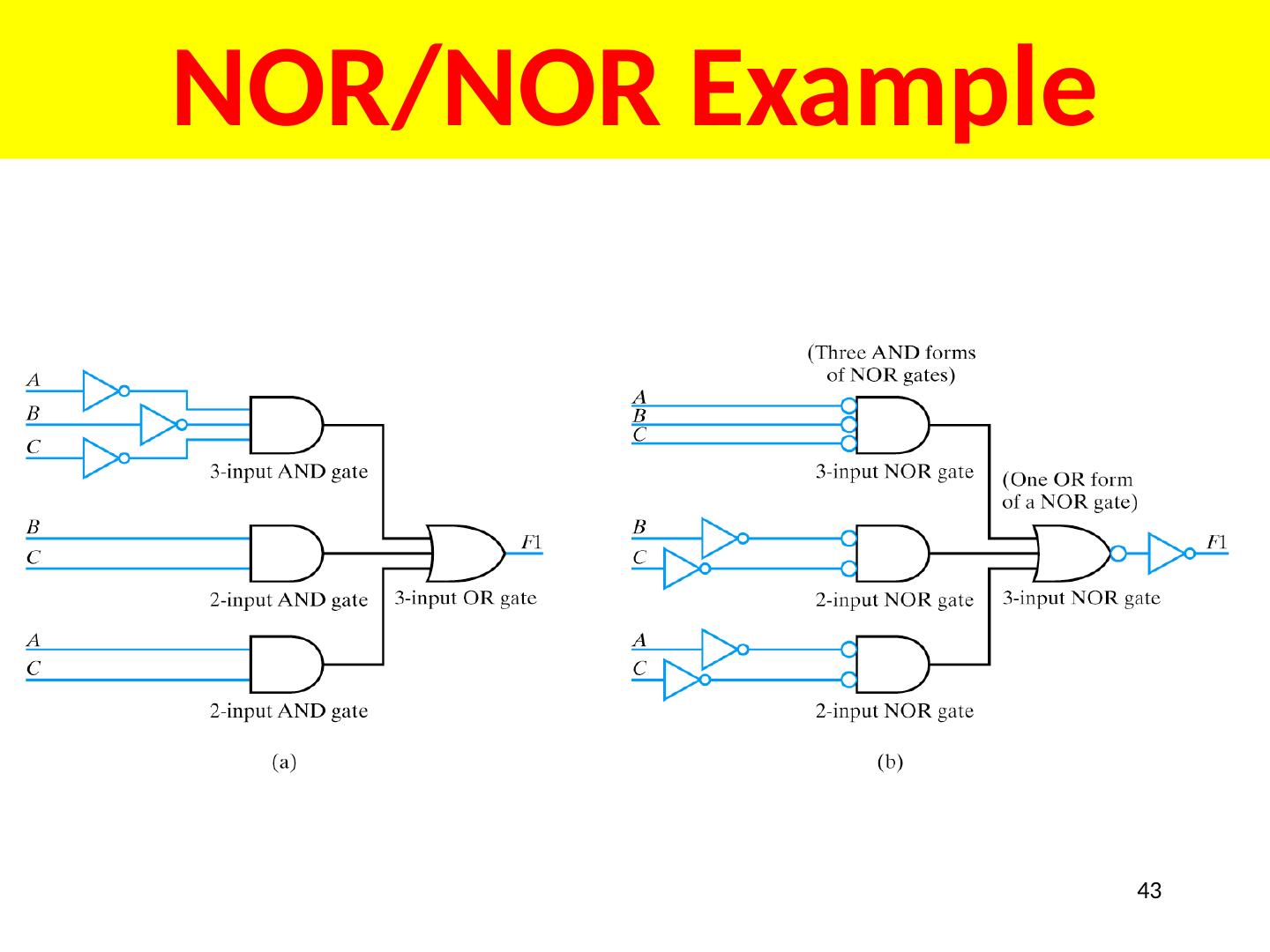
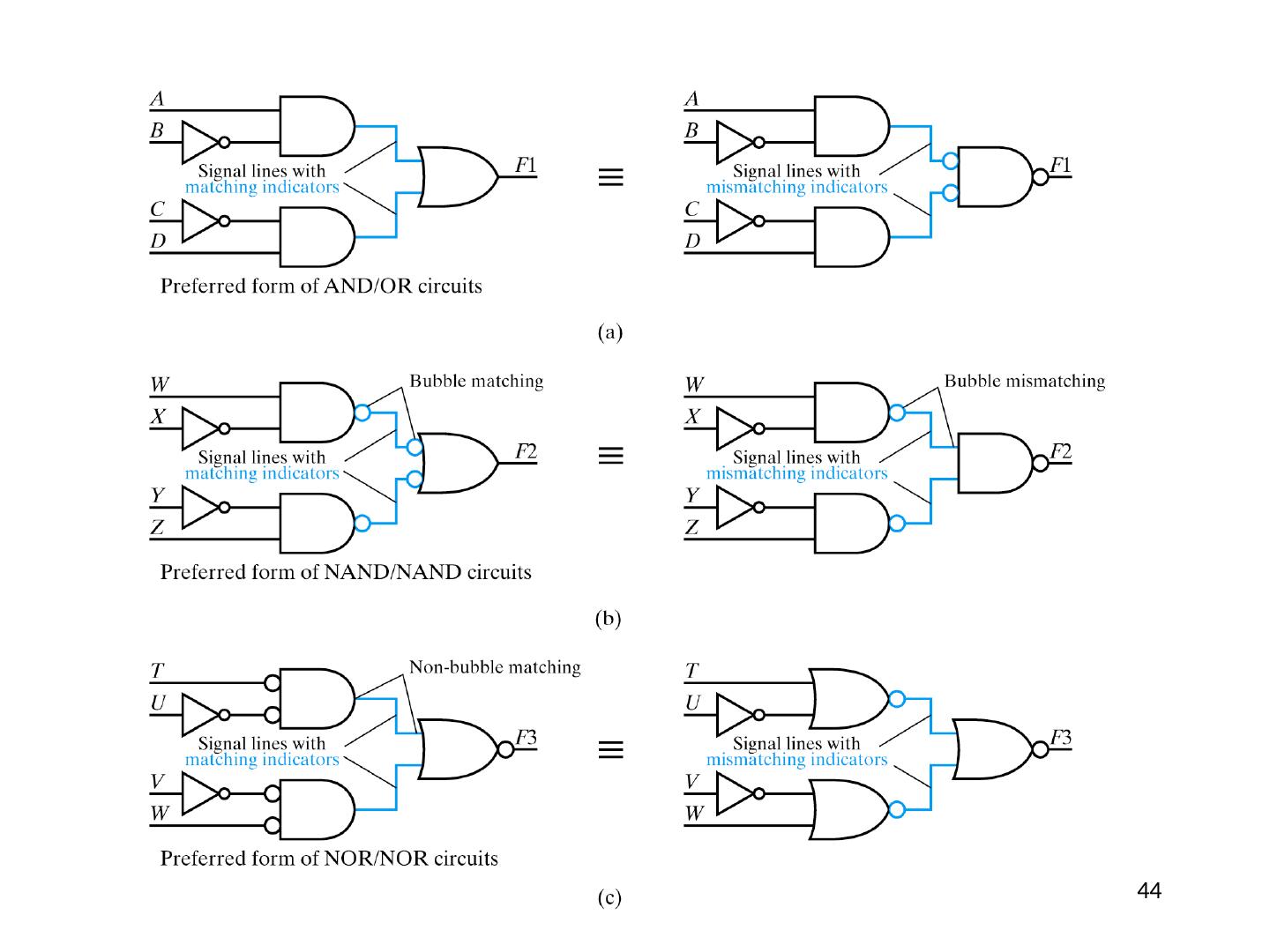
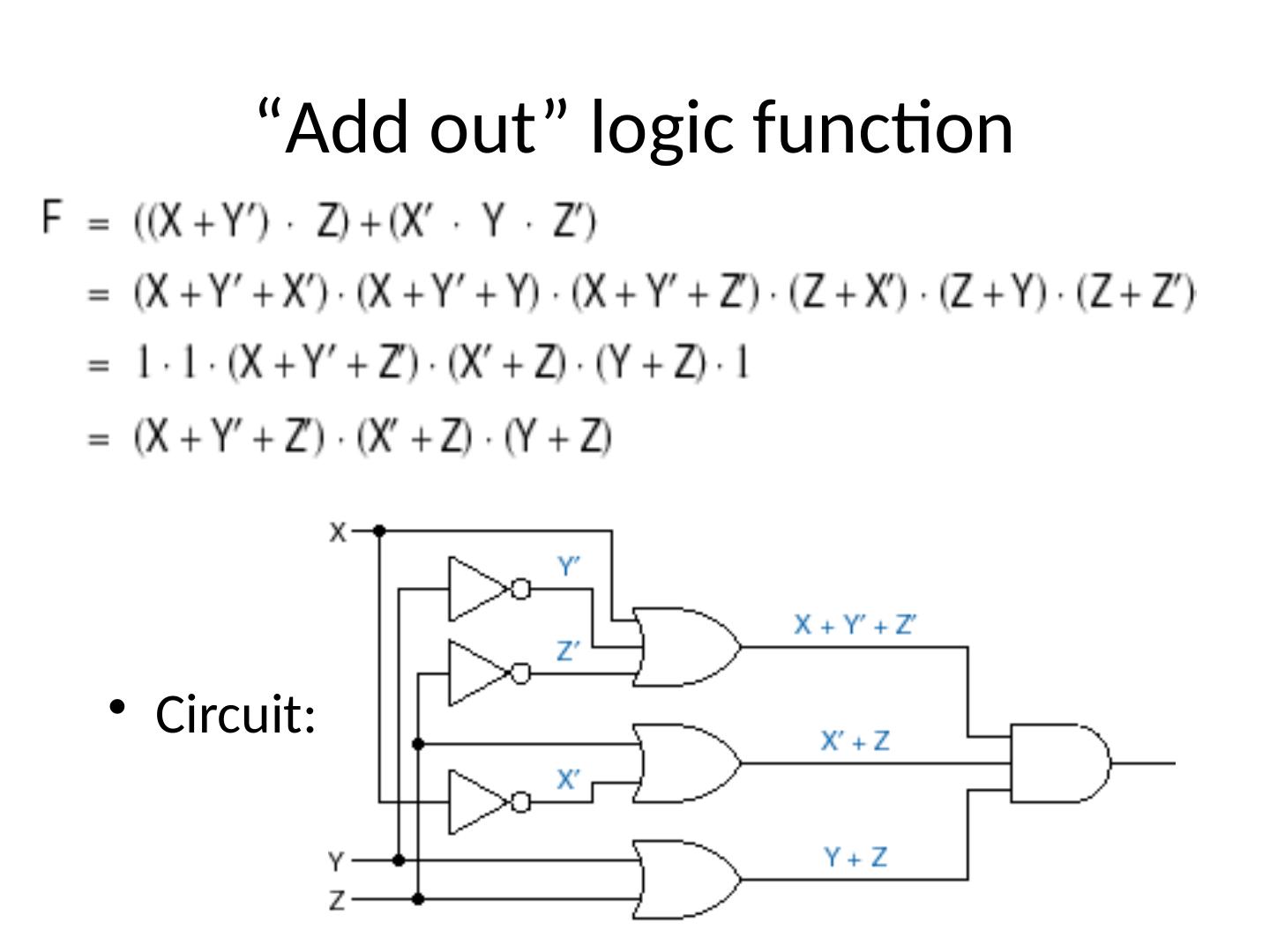
27 .Designing Logic Circuits F1 = A × B × C + B × C + A × B SOP form with 3 terms  3 input OR gate 27

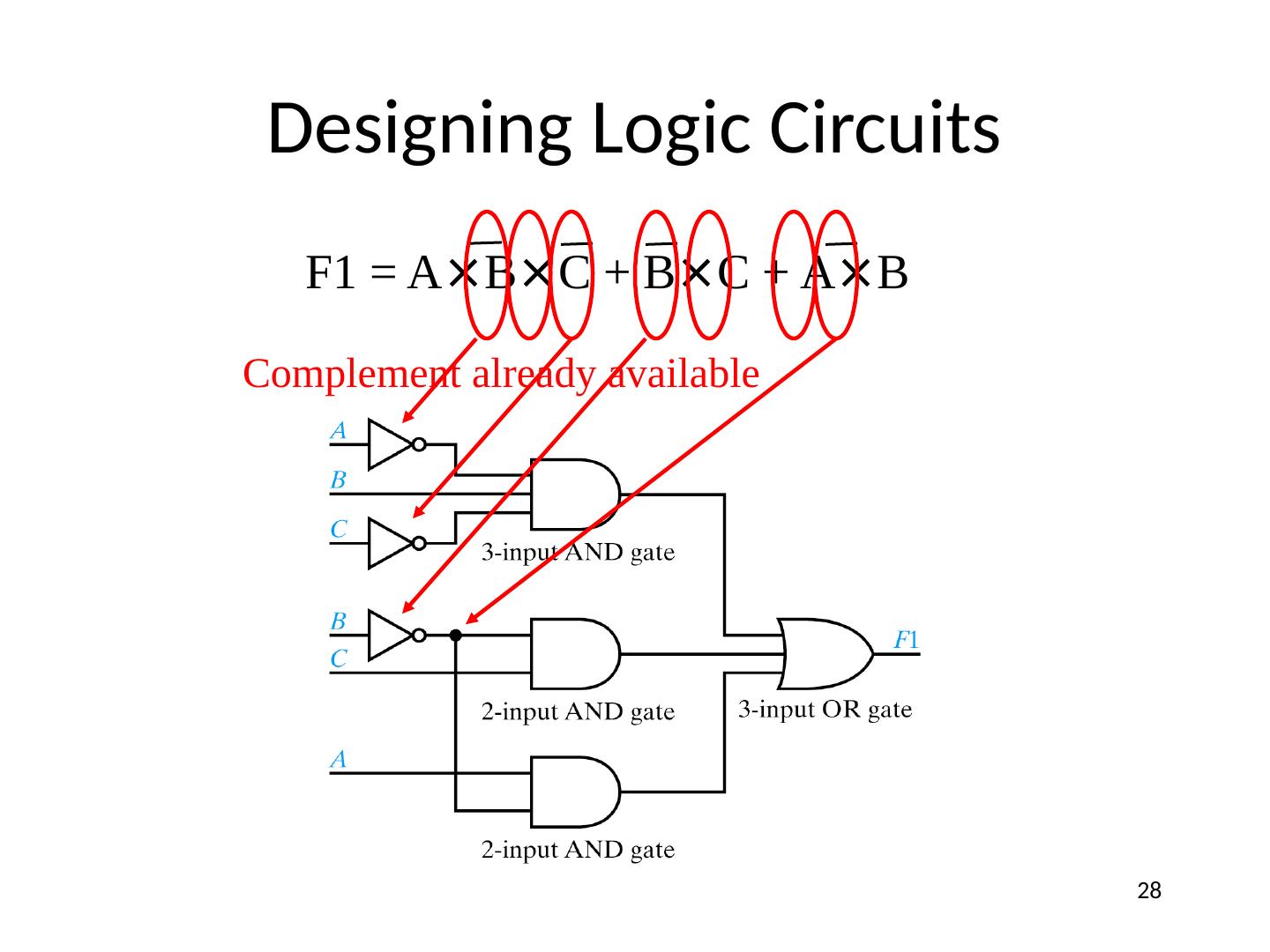
28 .Designing Logic Circuits F1 = A × B × C + B × C + A × B Complement already available 28

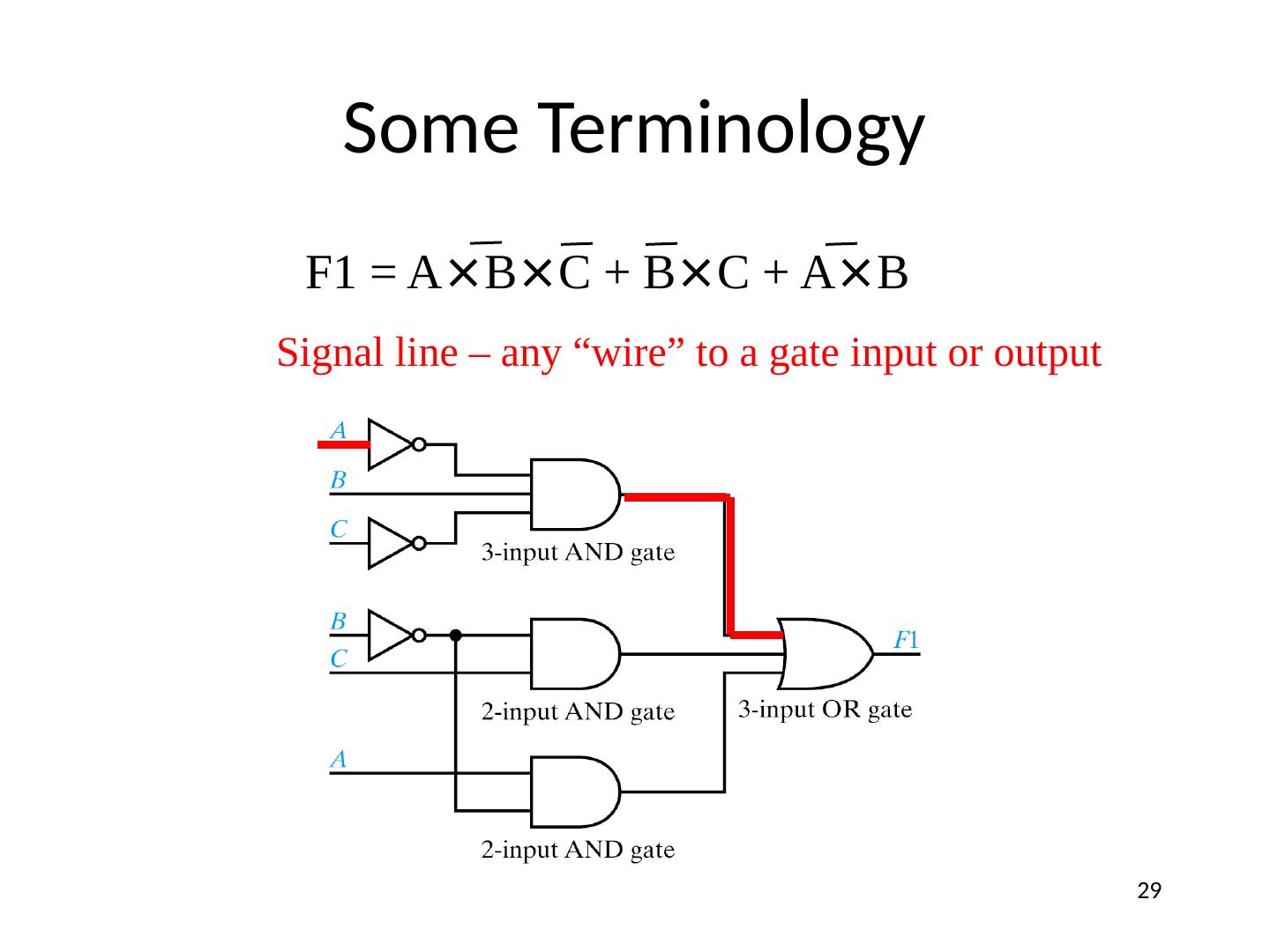
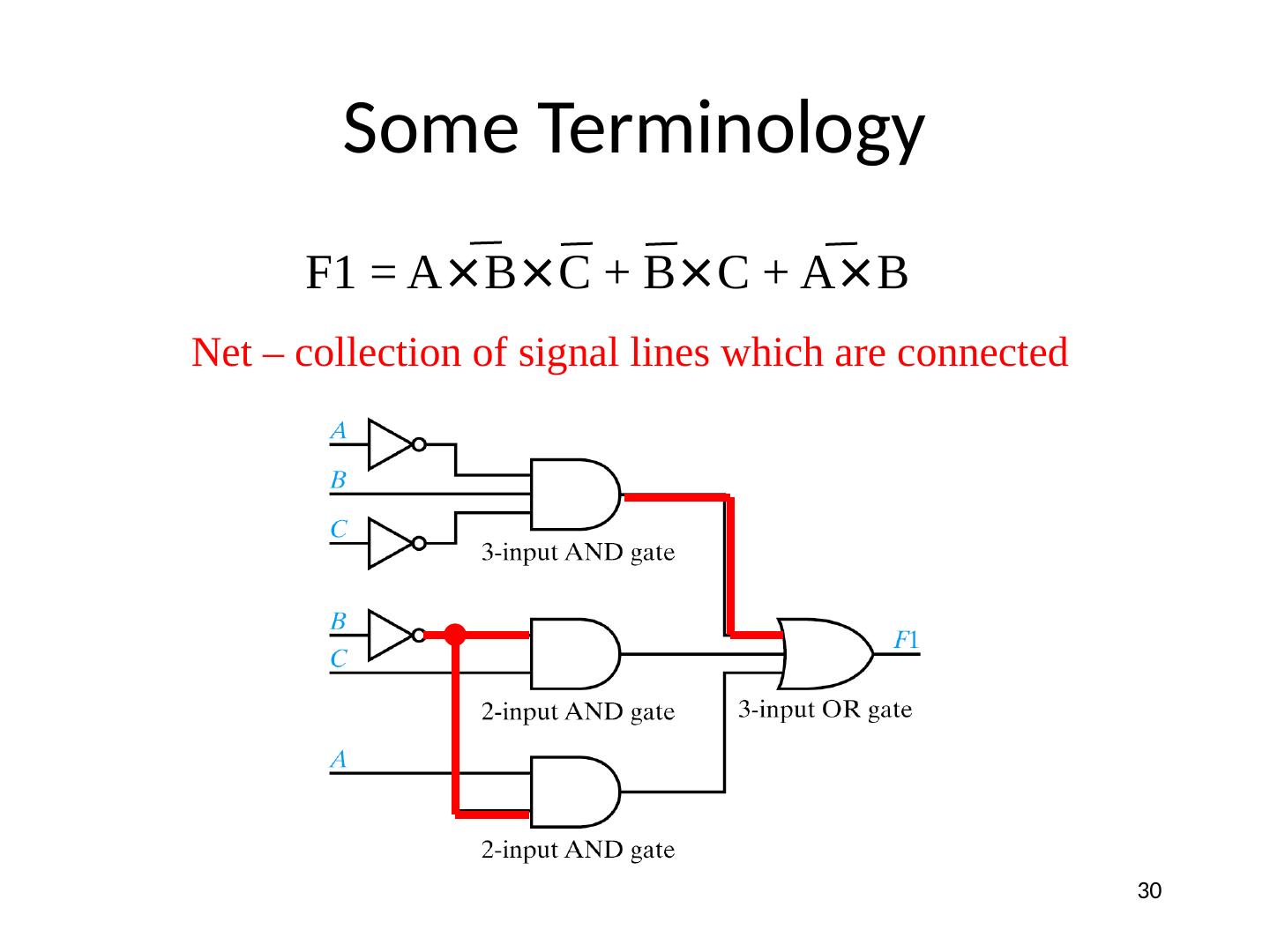
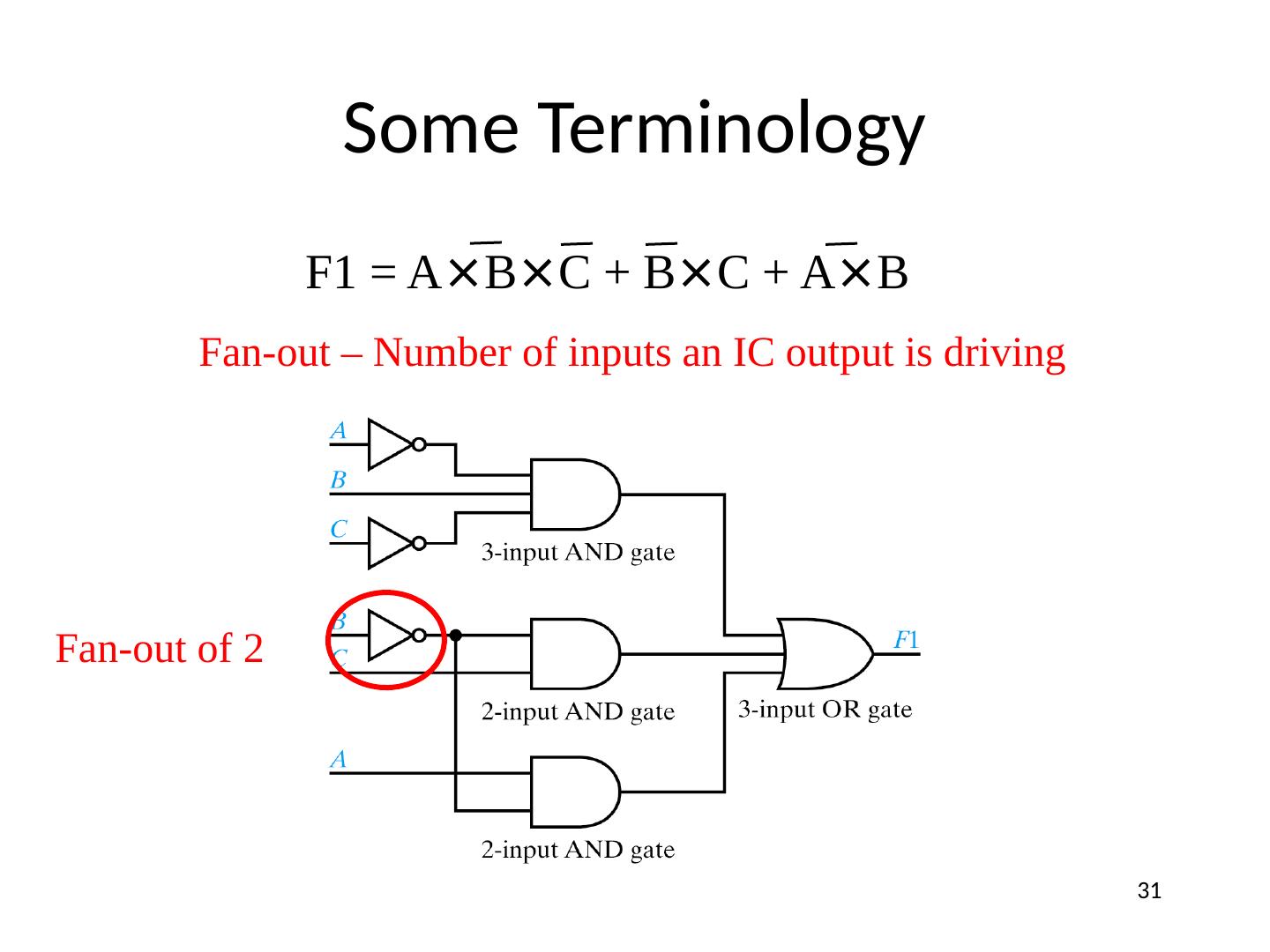
29 .Some Terminology F1 = A × B × C + B × C + A × B Signal line – any “wire” to a gate input or output 29