1 .Lecture 3 Topics IEEE 754 Floating Point Binary Codes BCD ASCII, Unicode Gray Code 7-Segment Code M-out-of-n codes Serial line codes 1

2 .Floating Point Numbers

3 .Floating Point Need to represent “ real ” numbers Fixed point too restrictive for precision and range Not unlike familiar “ scientific notation ” + 6.022 x 10 23 Sign Mantissa Exponent Normalized mantissa – single digit to left of decimal point 3

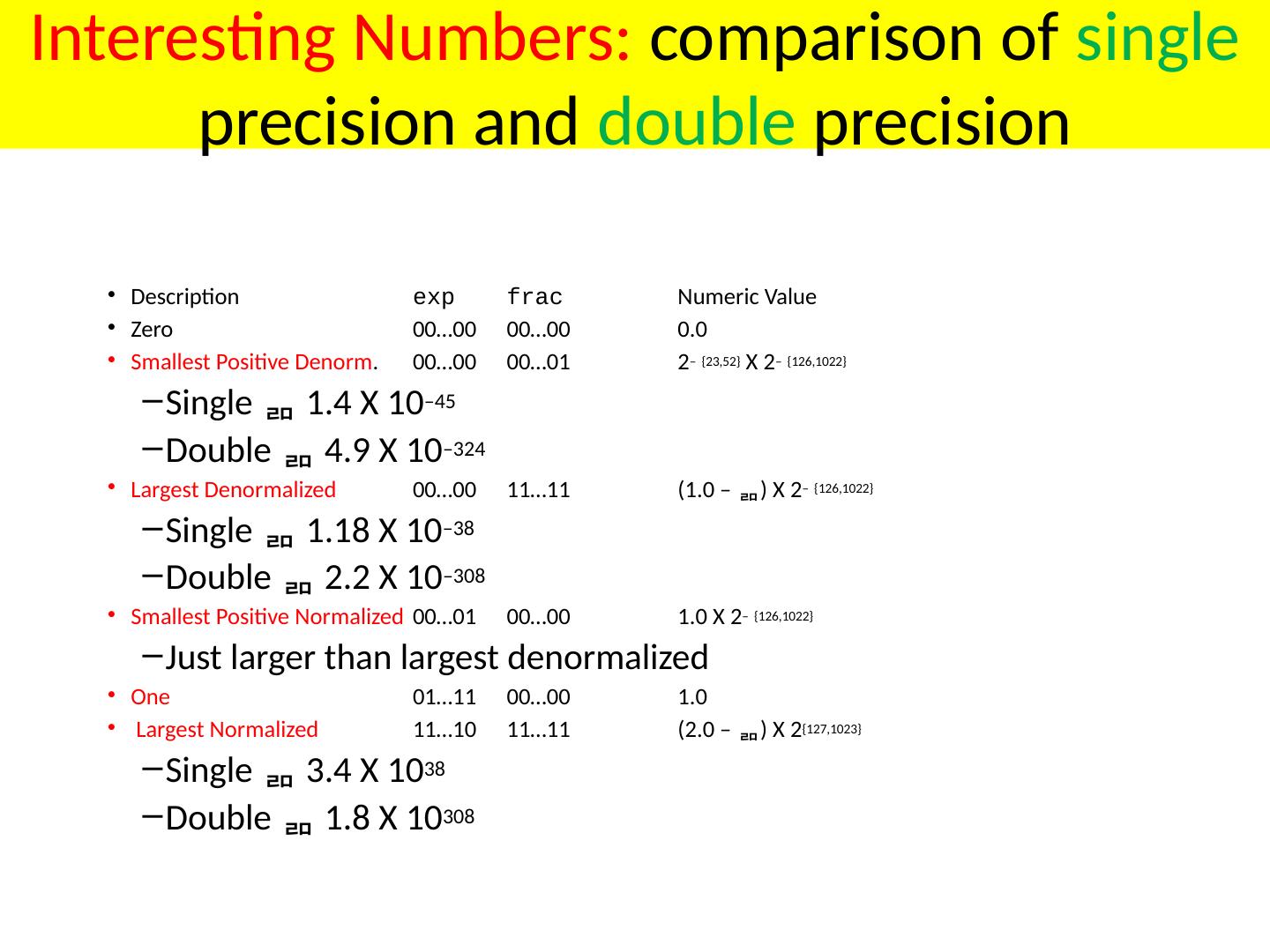
4 .IEEE 754 Floating Point Standard + 1.101011 x 2 12 Sign Mantissa Exponent Binary A normalized (binary) mantissa will always have a leading 1 so we can assume it and get an extra bit of precision instead Sign Exponent Significand Fraction 1 Exponents are stored with a bias which is added to the exponent before being stored (allows fast magnitude compare) Universally used on virtually all computers Several levels of precision/range : Single, Double, Double-Extended 4

5 .The IEEE has established a standard for floating-point numbers The IEEE-754 single precision floating point standard uses an 8-bit exponent ( with a bias of 127 ) and a 23-bit significand . The IEEE-754 double precision standard uses an 11-bit exponent ( with a bias of 1023 ) and a 52-bit significand. Floating-Point Standards

6 .IEEE 754 Single Precision Floating Point Standard

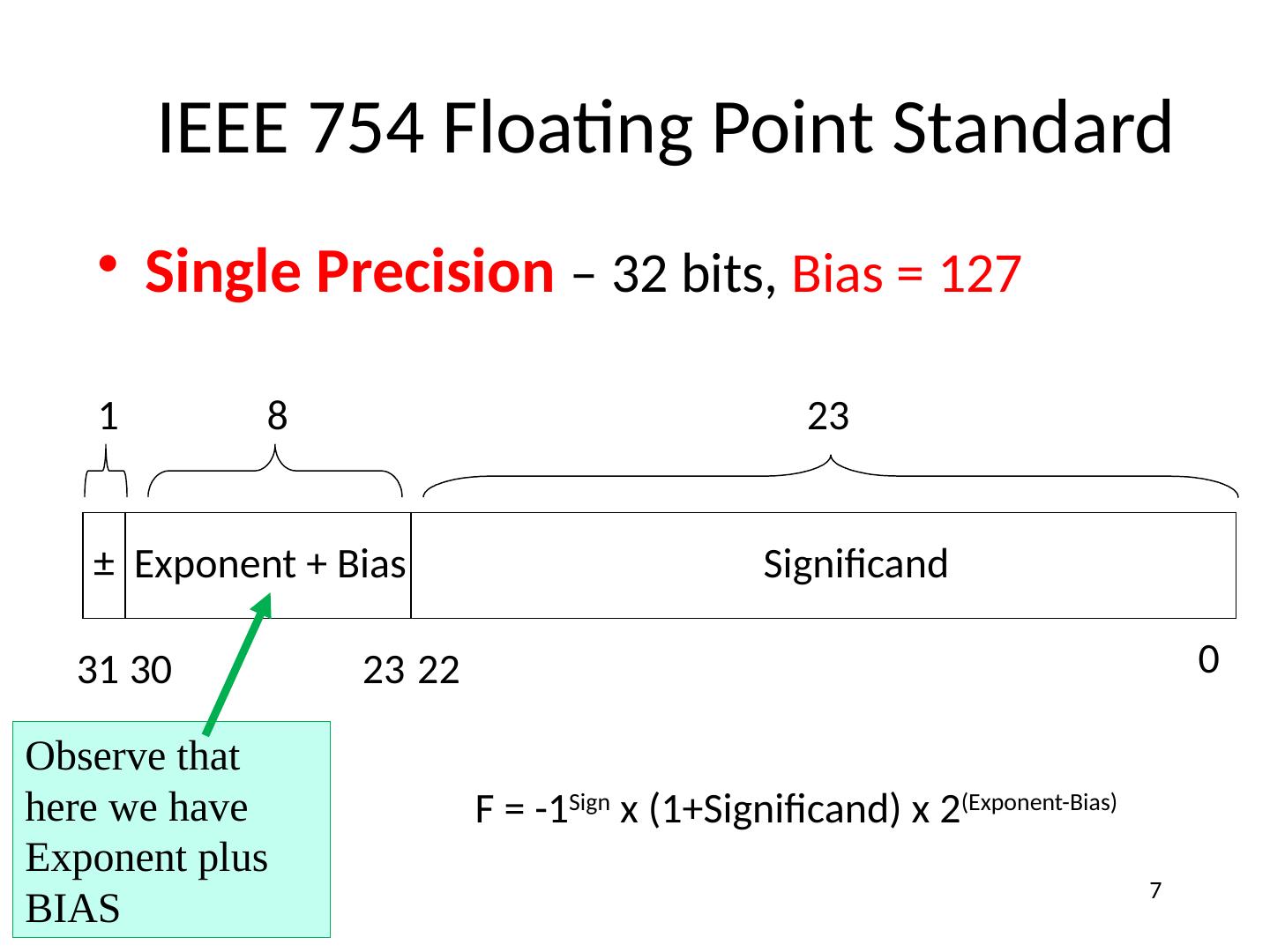
7 .IEEE 754 Floating Point Standard Single Precision – 32 bits, Bias = 127 31 30 23 22 0 ± Exponent + Bias Significand 1 8 23 F = -1 Sign x (1+Significand) x 2 (Exponent-Bias) 7 Observe that here we have Exponent plus BIAS

8 .IEEE 754 Floating Point Standard Example 31 30 23 22 0 1 10000001 01000000000000000000000 1 8 23 F = -1 Sign x ( 1 + Significand ) x 2 (Exponent- Bias ) - 129 = 0.25 10 = - 1 . 01 2 x 2 (129- 127 ) = - 1.25 x 2 (129-127) = - 1.25 x 2 2 = - 1.25 x 4 = - 5.0 = - 1.01 2 x 2 (129-127) = - 1.01 2 x 2 2 = - 101 2 = - 5.0 8 Remember to add 1 Hidden 1

9 .IEEE 754 Floating Point Standard Will commonly see these expressed as hex 31 30 23 22 0 1 10000001 01000000000000000000000 1 8 23 C0A00000 10 = A 11 = B 12 = C 13 = D 14 = E 15 = F 1010 A 1011 B 1100 C 8+4 8+2

10 .Example: Express -3.75 as a floating point number using IEEE single precision . First, let’s normalize according to IEEE rules: 3.75 = -11.11 2 = -1.111 x 2 1 The bias is 127 , so we add 127 + 1 = 128 (this is our final exponent+bias ) The first 1 in the significand is implied, so we have: Since we have an implied 1 in the significand, this equates to -(1).111 2 x 2 (128 – 127) = -1.111 2 x 2 1 = -11.11 2 = -3.75. (implied) Example of calculation of Floating-Point Representation F = -1 Sign x (1+Significand) x 2 (Exponent-Bias) verification

11 .FP Ranges For a 32 bit number 8 bit exponent +/- 2 256  1.5 x 10 77 Accuracy The effect of changing lsb of significand 23 bit significand 2 -23  1.2 x 10 -7 About 6 decimal places

12 .IEEE 754 Floating Point Standard: SPECIAL CASES: Zeros, Infinities, Denormalized

13 .Expressible Numbers in two typical 32-bit formats

14 .Representation of Floating Point Numbers IEEE 754 single precision 31 30 23 22 0 Sign Biased exponent Normalized Mantissa ( fraction, significand ) (implicit 24th bit = 1) (-1) s  fraction  2 E-127 Zero Not a Number 1+Significand

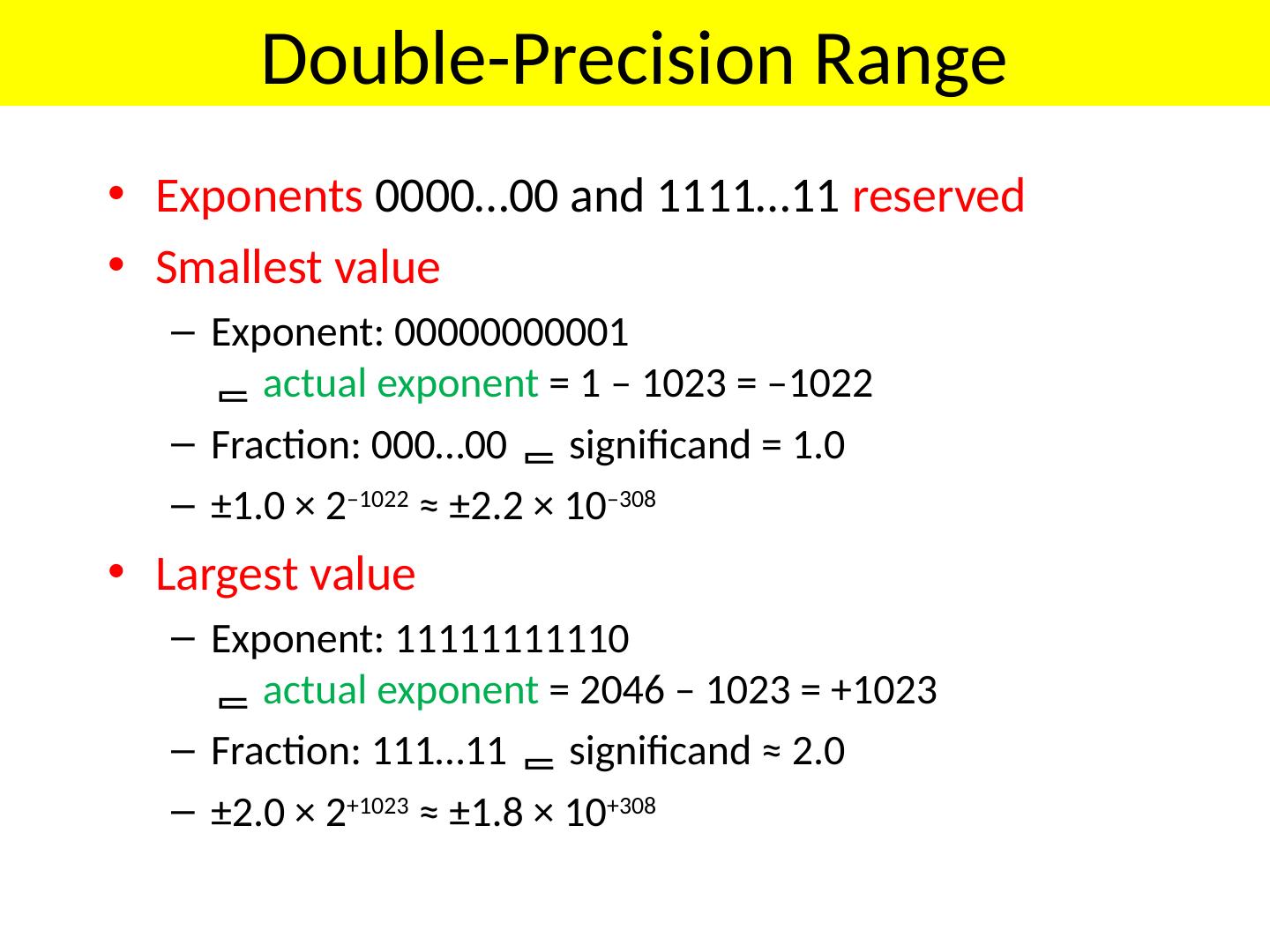
15 .IEEE 754 Floating Point Standard Some Special Cases Zero (no assumed leading 1) Exponent = 0, Significand = 0 NaN (Not a Number), e.g. ¥ Exponent = 255 Denormalized ( Subnormal ) numbers Exponent = 0, Significand ¹ 0 F = -1 Sign x (1+Significand) x 2 (Exponent-Bias) Bias = 127 Remember to subtract bias Standard FP number X = -1 S 2 -126 ( 0 .fraction )

16 .Special-case numbers: Zeros and Infinities Zeroes:  +0  -0 Infinities:  + ∞  - ∞ 0 00…0 00…0 1 00…0 00…0 0 00…0 11…1 1 00…0 11…1

17 .Zeros How do you represent 0? Sign = ?, Exponent = ?, Significand = ? Here’s where the hidden “1” comes back to bite you Hint: Zero is small. What’s the smallest number you can generate? Exponent = -127, Significand = 1.0 -1 0 (1.0) x 2 -127 = 5.87747 x 10 -39 IEEE Convention When E = 0 (Exponent = -127), we’ll interpret numbers differently… 0 00000000 00000000000000000000000 = 0 not 1.0 x 2 -127 1 00000000 00000000000000000000000 = -0 not -1.0 x 2 -127 Yes, there are “2” zeros. Setting E=0 is also used to represent a few other small numbers besides 0. In all of these numbers there is no “hidden” one assumed in F, and they are called the “ unnormalized ( denormalized ) numbers ”. WARNING: be careful !

18 .Positive Infinity, Negative Infinity and Not a Number IEEE floating point also reserves the largest possible exponent to represent “ unrepresentable ” large numbers Positive Infinity : S = 0, E = 255, F = 0 0 11111111 00000000000000000000000 = +∞ 0x7f800000 Negative Infinity : S = 1, E = 255, F = 0 1 11111111 00000000000000000000000 = -∞ 0xff800000 Other numbers with E = 255 (F ≠ 0) are used to represent exceptions or Not-A-Number (NAN) It does, however, attempt to handle a few special cases .

19 .Special Values Condition for infinity and NaN   exp = 111 … 1 Cases INFINITY exp = 111 … 1 , frac = 000 … 0 Represents value  ( infinity ) Operation that overflows Both positive and negative E.g., 1.0/0.0 =  1.0/  0.0 = +  , 1.0/  0.0 = , log(0 ) = - ∞ NOT A NUMBER ( NaN ) exp = 111 … 1 , frac  000 … 0 Represents case when no numeric value can be determined E.g., sqrt (–1), , √ -1, -∞ x 42, 0/0, ∞/∞, log(-5) Not a Number ( NaN ): E = 11…1; F != 00…0 Infinities and NANs

20 .IEEE 754 Floating Point Standard: subnormal ( denormalized ) numbers

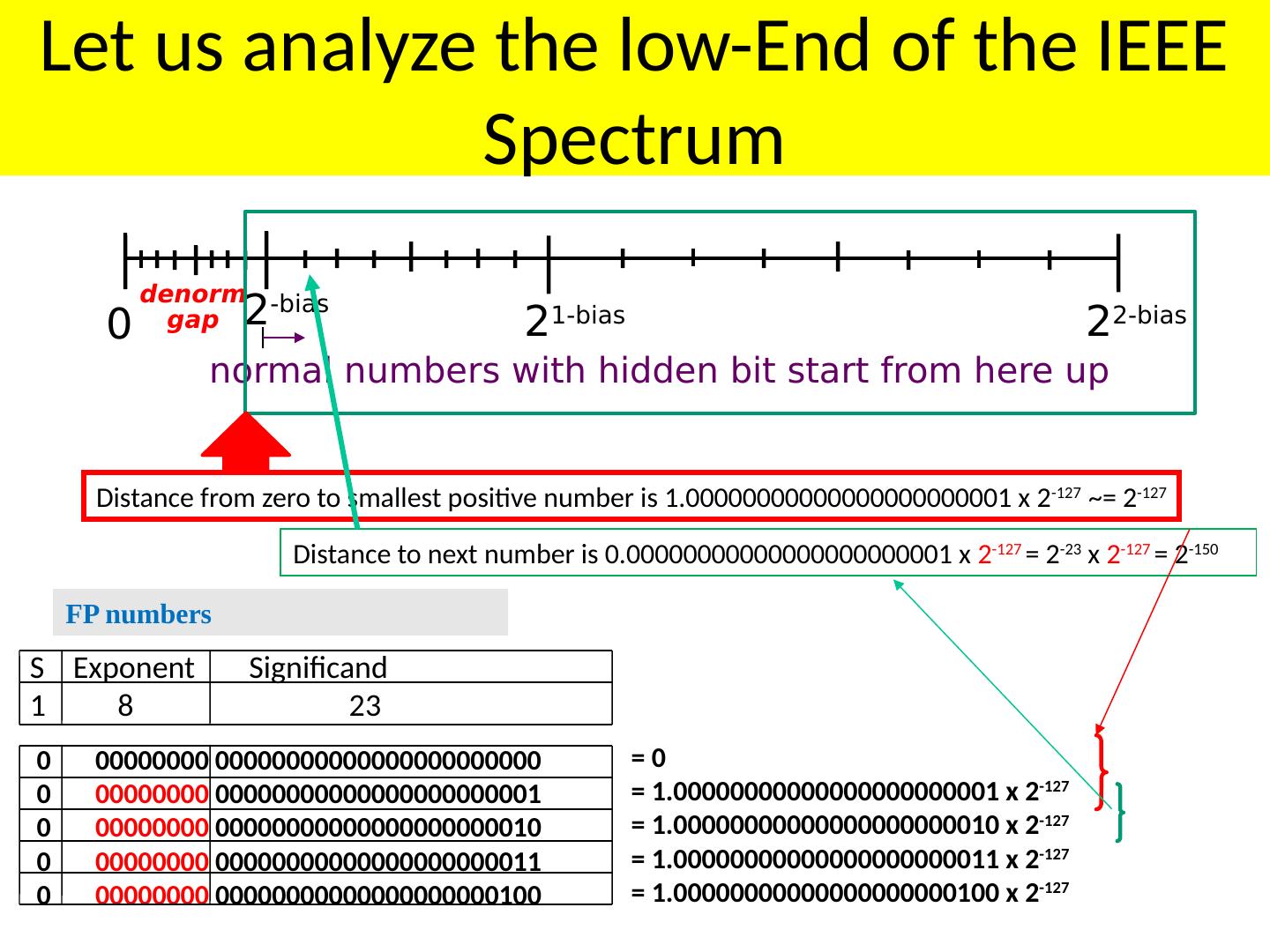
21 .Property of IEEE 754 Floating Point Standard: 0 00000000 00000000000000000000000 0 00000000 00000000000000000000001 0 00000000 00000000000000000000010 0 00000000 00000000000000000000011 0 00000000 00000000000000000000100 = 0 = 1.00000000000000000000001 x 2 -127 = 1.00000000000000000000010 x 2 -127 = 1.00000000000000000000011 x 2 -127 = 1.00000000000000000000100 x 2 -127 S Exponent Significand 1 8 23 Distance to next number is 0.00000000000000000000001 x 2 -127 = 2 -23 x 2 -127 = 2 -150 FP numbers denorm gap Let us analyze the low-End of the IEEE Spectrum 0 2 -bias 2 1-bias 2 2-bias normal numbers with hidden bit start from here up Distance from zero to smallest positive number is 1.00000000000000000000001 x 2 -127 ~= 2 -127

22 .denorm gap The Denormalized Gap in the IEEE Spectrum “ Denormalized Gap” As we see above, the gap between 0 and the next representable normalized number is much larger than the gaps between nearby representable numbers Addresses gap caused by implicit leading 1 IEEE standard uses denormalized numbers to fill in the gap, making the distances between numbers near 0 more alike Denormalized numbers have a hidden “0” and… … a fixed exponent of -126 X = -1 S 2 -126 ( 0 .fraction) 0 2 -bias 2 1-bias 2 2-bias normal numbers with hidden bit start from here up Zero is represented using 0 for the exponent and 0 for the mantissa (fraction). Either , +0 or -0 can be represented, based on the sign bit. Denormalized number

23 .Denormalized numbers to represent very small numbers Fraction or mantissa X = -1 S 2 -126 ( 0 .fraction) Subnormal Numbers - properties Implicit Exponent of -126 F = -1 Sign x (Significand) x 2 (-126) Smallest positive number in subnormal is (a) = 0.000…001 x 2 -126 = 2 -149 Next smallest number in subnormal is (b) = 0.000…010 x 2 -126 = 2 -148 For standard FP Smallest positive number in FP standard (a) is 1.000…000 x 2 -126 Next number in FP standard (b) is 1.000…001 x 2 -126 = (2 -126 + 2 -149 ) E = 00…0  Different interpretation applies  denormalized numbers

24 .Denormalized (subnormal) numbers to represent very small numbers Denormalized numbers have no hidden 1 Denormalized numbers allow numbers very close to 0 Denormalization rule: number represented is (-1) S ×0.fraction×2 -126 (single-precision) (-1) S ×0.fraction×2 -1022 (double-precision) Note : zeroes follow this rule Fraction or mantissa X = -1 S 2 -126 ( 0 .fraction) Subnormal Numbers - properties Implicit Exponent of -126 F = -1 Sign x (Significand) x 2 (-126) Smallest positive number in subnormal is (a) = 0.000…001 x 2 -126 = 2 -149 Next smallest number in subnormal is (b) = 0.000…010 x 2 -126 = 2 -148

25 .Denormalized Values Condition   exp = 000 … 0 Value Exponent value E = – Bias + 1 Significand value M = 0.xxx … x 2 xxx … x : bits of frac Cases exp = 000 … 0 , frac = 000 … 0 Represents value 0 Note that have distinct values +0 and –0 exp = 000 … 0 , frac  000 … 0 Numbers very close to 0.0 Lose precision as get smaller “Gradual underflow” (- 1) S ×0.fraction×2 -127+1= -126 (single-precision) Object Represented

26 .Subnormal Numbers - properties Implicit Exponent of -126 F = -1 Sign x ( Significand ) x 2 (-126) Smallest positive number (a) = 0.000…001 x 2 -126 = 2 -149 Next smallest number (b) = 0.000…010 x 2 -126 = 2 -148 26 F = -1 Sign x ( 1+Significand ) x 2 (Exponent-Bias) Bias = 127 For comparison for FP number Exponent always zero 2 -23

27 .Summary of Floating Point Real Number Encodings NaN NaN +     0 +Denorm +Normalized -Denorm -Normalized +0

28 .Tiny examples for better explanation

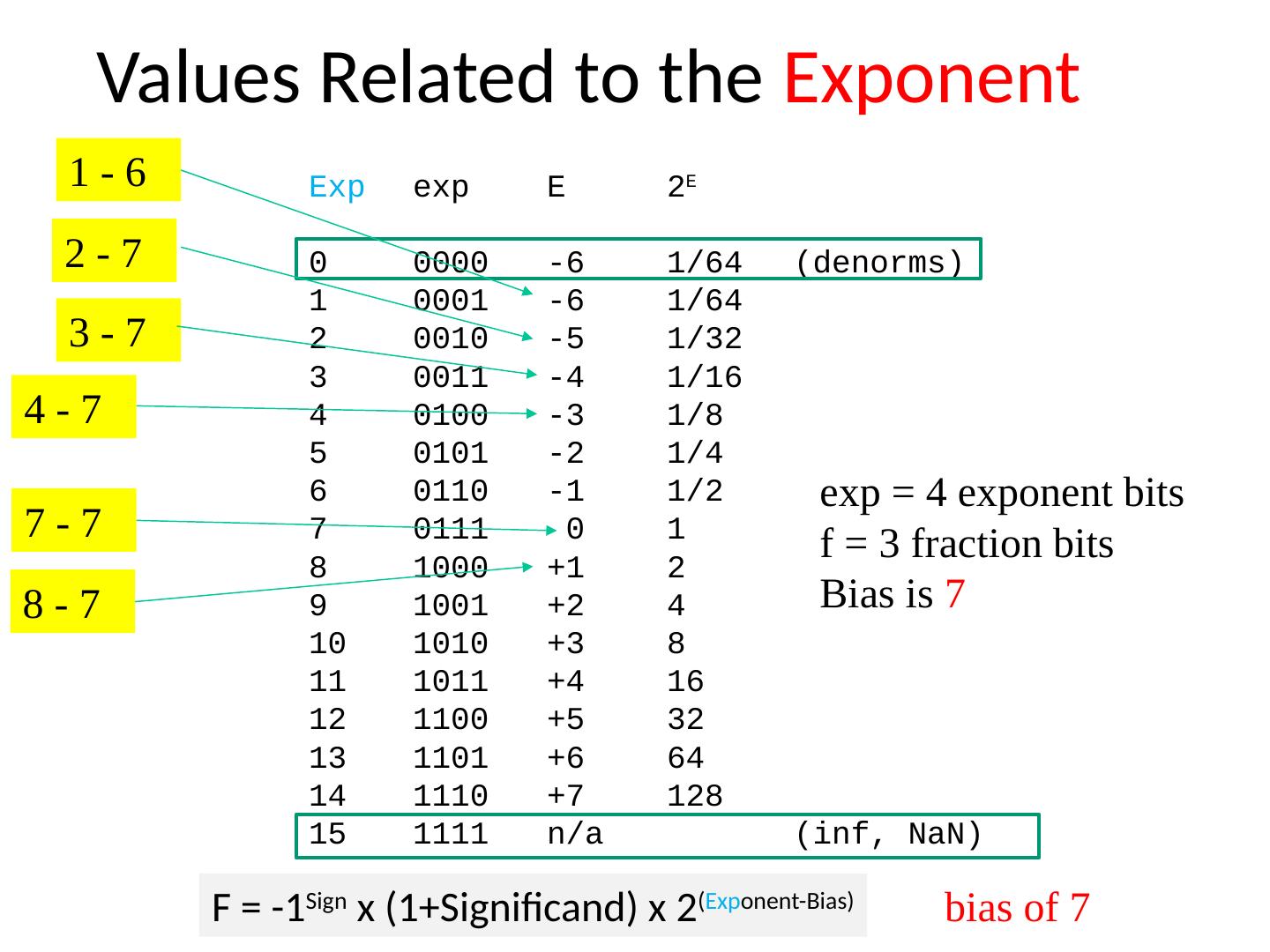
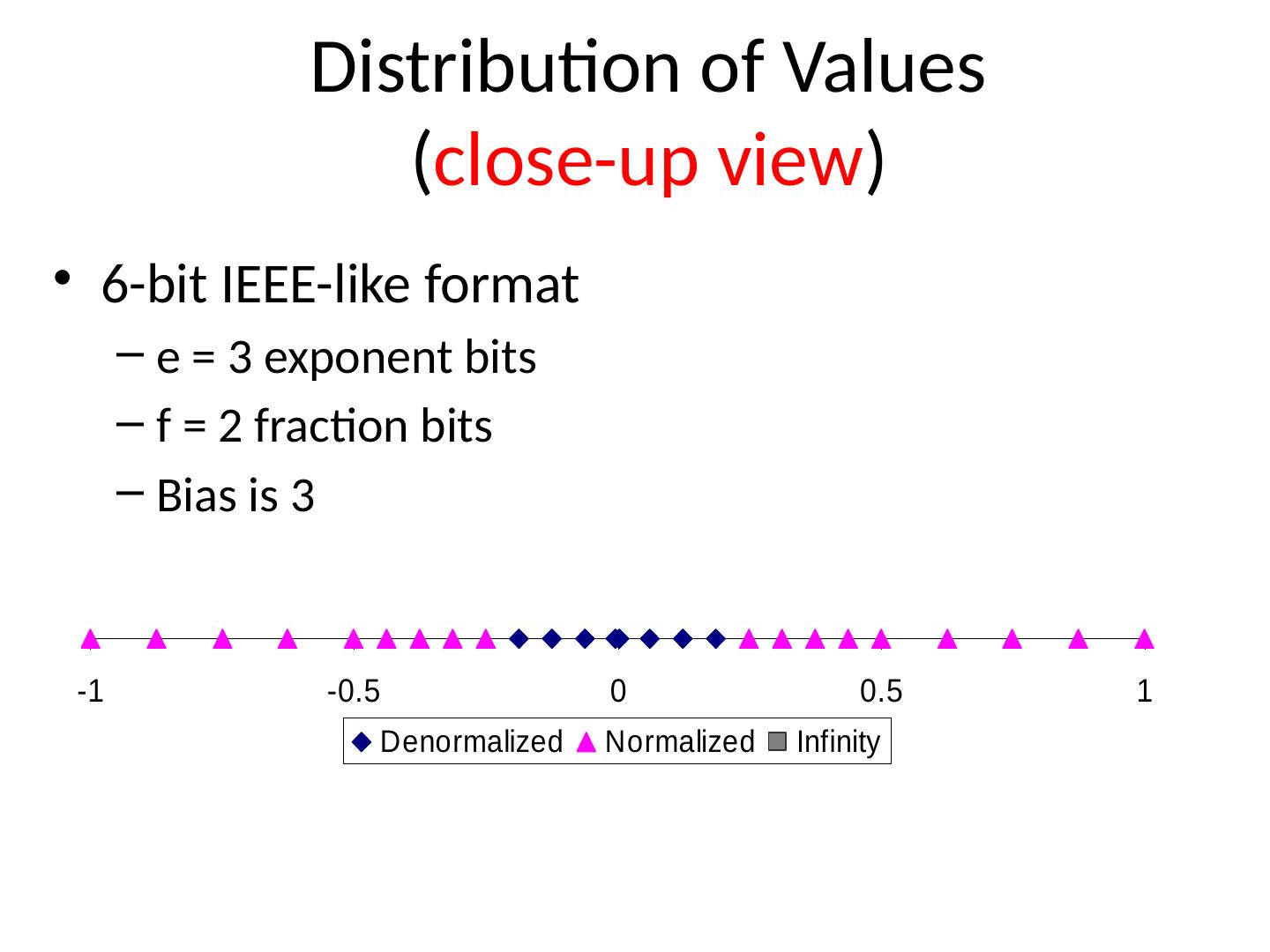
29 .Tiny Floating Point Example in IEEE Format 8-bit Floating Point Representation the sign bit is in the most significant bit. the next four bits are the exponent, with a bias of 7 . the last three bits are the frac Same General Form as IEEE Format normalized, denormalized representation of 0, NaN , infinity s exp frac 0 2 3 6 7