02 Binary Arithmetics Z

1 .Lecture 2 Topics Binary Arithmetic (Unsigned binary operands) Signed number representations Signed Magnitude Diminished Radix Complement (Ones Complement) Radix Complement (Twos Complement) Binary Arithmetic Revisited and Overflow Sign Extension 1

2 .Binary Arithmetic Rules for “ carry ” same as in decimal 0 0 0 + 0 1 1 + 1 0 1 + 1 1 1 0 + 1 carry 2 Here are the rules for adding of each bit carry

3 .Unsigned Binary (UB) Addition Examples (4-bit word) 1011 0110 + 1 1 1 10001 0010 0110 + 1 1 1000 Overflow 2 + 6 2 + 6 8 11 + 6 17 11 + 6 17 > 2 4 -1 3

4 .Overflow (Underflow) 10101101 01101100 Definition: Result of an arithmetic operation is too large (or small) to be represented in number of bits available Detection: Varies with the representation. For unsigned binary, it’s determined by a carry out of the MSB + 1 1 1 1 1 1 0001 1001 8 bit operands 4

5 .Signed Numbers Have been assuming non-negative numbers Unsigned Binary (UB) Several representations for signed numbers Sign Magnitude (SM) Diminished Radix Complement (DRC) 1s Complement Radix Complement (RC) 2s Complement 5

6 .Sign Magnitude MSB functions as sign bit 0 = positive 1 = negative Range of numbers: -(2 n-1 – 1) to +(2 n-1 – 1) n = 6 Two representations for 0 Negative formed by complementing sign bit 15 10 = 001111 SM -15 10 = 101111 SM 010100 SM = 20 10 110100 SM = -20 10 6

7 .Diminished Radix Complement (DRC) Called “ Ones Complement ” MSB indicates sign 0 = positive 1 = negative (but not a sign bit!) Range of numbers: -(2 n-1 – 1) to +(2 n-1 – 1) Two representations for 0 Negative formed by complementing entire word (called “taking the ones complement”) 15 10 = 001111 DRC -15 10 = 110000 DRC 010100 DRC = 20 10 101011 DRC = -20 10 7

8 .Radix Complement (RC) Called “ Twos Complement ” MSB indicates sign 0 = positive 1 = negative (but not a sign bit) Range of numbers: -(2 n-1 ) to +(2 n-1 – 1) Only one representation for 0 Negative formed by complementing entire word and adding 1 (called “taking the twos complement”) 15 10 = 001111 RC -15 10 = 110001 RC 010100 RC = 20 10 101100 RC = -20 10 8

9 .Radix Complement (RC) Called “ Twos Complement ” MSB indicates sign 0 = positive 1 = negative (but not a sign bit) Range of numbers: -(2 n-1 ) to +(2 n-1 – 1) Only one representation for 0 Negative formed by complementing entire word and adding 1 (called “taking the twos complement”) 15 10 = 001111 RC -15 10 = 110001 RC 010100 RC = 20 10 101100 RC = -20 10 9 1 1 1 1 0 1 -3 000 011 =3 111 100 = neg 111101=-3

10 .Twos Complement – Special Cases

11 .Twos Complement – Special Cases Example: Take Twos Complement (RC) of 0000 ( 0 10 ) 0000 1111 + 1 0000 Complement Add One 1 1 1 Ignore carry out of MSB 11 Note: Discard carry out of sign bit position! Only one representation for 0

12 .Twos Complement – Special Cases Example: Take Twos Complement (RC) of 1000 (-8 10 ) ( most negative ) 1000 0111 + 1 1000 Complement Add One 1 1 1 Can’t represent Complement of the most negative number 12 1000 (-8 10 ) is the most negative number -8 10 +8 10 is not represented

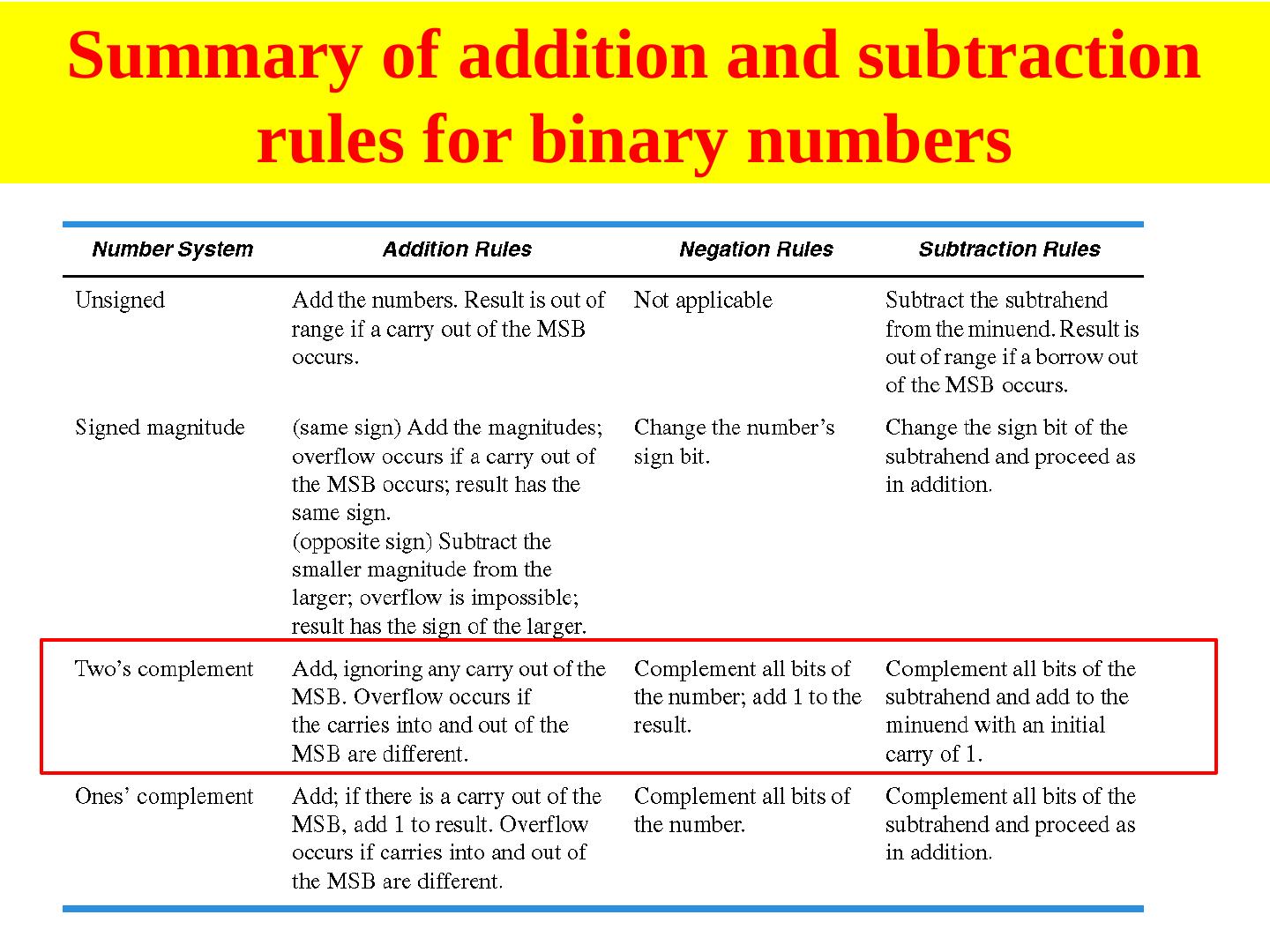
13 .BCD (which we’ll see shortly) was used in very early 4-bit microprocessors, but 2s complement is universally used now Why do we use RC (Twos Complement)? Only one representation for zero Simplified Addition in Twos Complement! Sign Magnitude Addition has complicated algorithm below: Must consider two operands without sign bits If sign bits same: perform add, check overflow If sign bits different: subtract (two cases) +A and – B  A – B – A and + B  B – A Generate correct sign bit for sum Radix Complement (Twos Complement) Addition Just add! Simple Subtraction Done via addition A + B A – B = A + (-B) Caution: Can’t take negative of most negative number 13

14 .Conversions of Signed Representations

15 .Conversions of Signed Representations From Decimal Conversion from decimal Represent the absolute value of the number in unsigned binary (UB) Use the correct number of bits (add leading 0s) If the decimal number is negative , use the appropriate rule to negate the representation Sing/Magnitude (S/M) – complement the sign bit DRC ( ones complement ) – complement every bit RC ( twos complement ) – complement every bit, add 1

16 .Conversions of Signed Representations to Decimal Conversion to decimal if number is + convert from unsigned binary to decimal (done!) Conversion to decimal if number is - use appropriate rule to negate it (obtain its absolute value) Sign/Magnitude – complement the sign bit Ones complement – complement every bit Twos complement – complement every bit, add 1 Convert this (positive) number as though unsigned binary to decimal Add a negative sign 16

17 .Binary Arithmetic Unsigned Binary (UB) Signed Binary (SB) Diminished Radix Complement (DRC) 1s complement Radix Complement (RC) 2s complement Rarely used 17

18 .Radix Complement (RC) or Twos Complement Addition – Subtraction and Negative Numbers Examples (4-bit word) 0101 1001 + 1 1110 Ignore carry out of MSB 7 + (-2) 5 + (-7) 7 + (-2) 5 5 + (-7) (-2) 0111 1110 + 1 1 10101 1 18 No overflow

19 .Radix Complement (RC) or Twos Complement Addition Examples (4-bit word) Ignore carry out of MSB -7 + (-2) -7 + (-2) -9 1001 1110 + 10111 1 -9 < - (2 3 ) We added two negative numbers and got a positive result! Overflow!! 19

20 .Carry and Overflow

21 .Carry and Overflow Is this an overflow condition? If this is an unsigned binary (UB) number – Yes ! 10101101 01101100 + 1 1 1 1 1 100011001 0 0 0 21 Overflow in UB

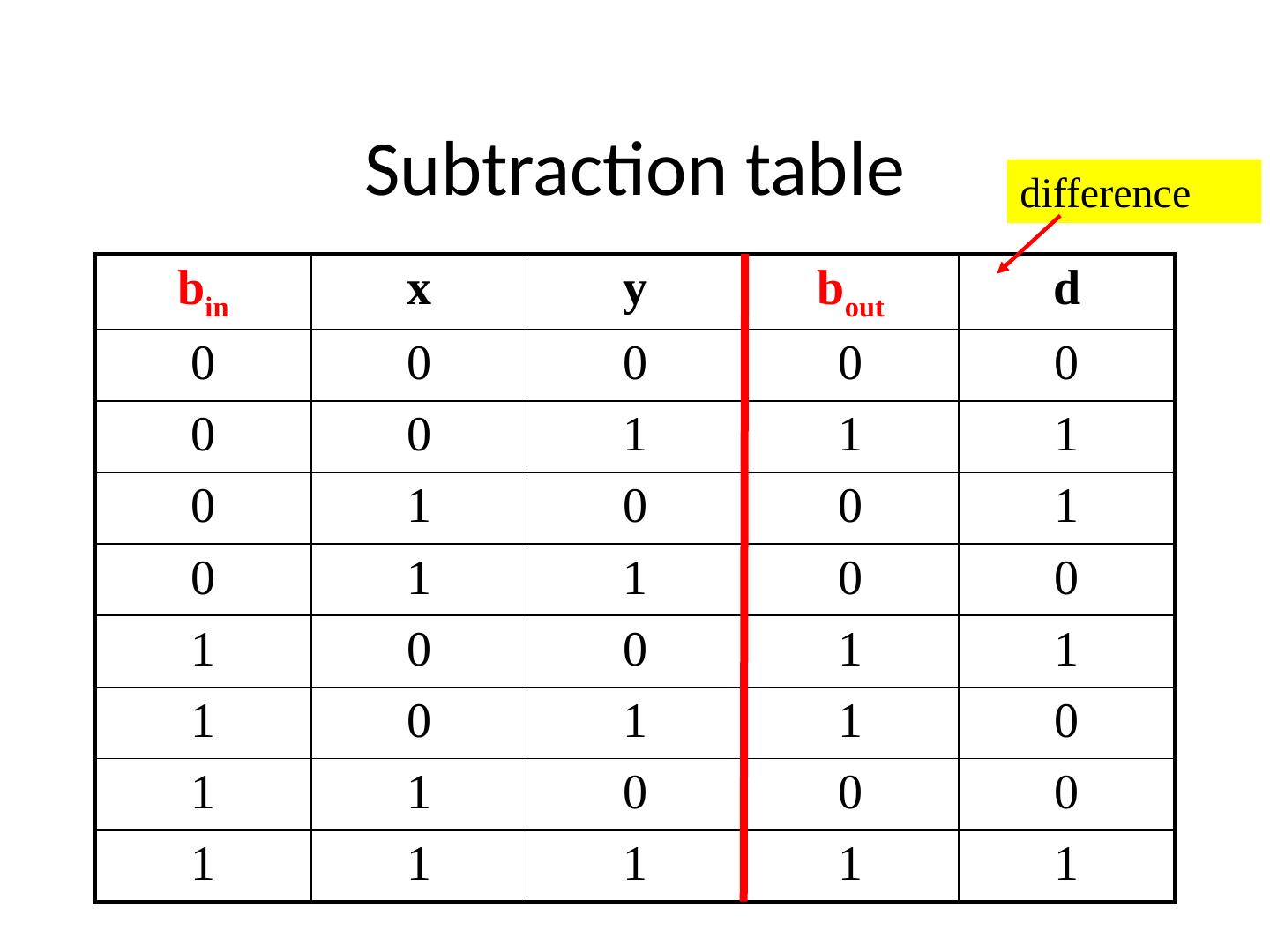
22 .Carry and Overflow Is this an overflow condition? If this is a radix complement (RC) number – No ! 10101101 01101100 + 1 1 1 1 1 100011001 0 0 0 A negative number plus a positive number cannot produce an overflow 22 No overflow in Twos Complement

23 .Carry and Overflow Radix Complement ( 2s Complement ) Consider : Positive + Negative  Never overflow Negative + Negative  Overflow possible Positive + Positive  Overflow possible Detecting Overflow : If signs of addends are same and sign of sum is different Equivalent to C SBP ¹ C SBP+1 23 C – Carry SBP – Sign Bit Position

24 .Carry and Overflow in Twos Complement 10101101 01101100 + 1 1 1 1 1 100011001 C SBP+1 C SBP C – Carry SBP – Sign Bit Position 0 0 0 24 C SBP = C SBP+1 A negative number plus a positive number cannot produce an overflow No overflow in Twos Complement

25 .Addition in Twos Complement Examples (4-bit word) 1001 1110 + 10111 -7 + (-2) -7 + (-2) -9 1 -9 < - (2 3 ) We added two negative numbers and got a positive result! 0 0 0 C SBP+1 C SBP C SBP+1 ¹ C SBP Overflow! 25 Conclusion on Overflow in 2s Complement : There is an overflow if signs of addends are same and sign of sum is different Equivalent to C SBP ¹ C SBP+1 In this case there is an overflow

26 .Sign Extension What happens when you move a number from a smaller word size to a larger one? 00000011 0000000000000011 (3) (3) 11111101 0000000011111101 (253) (253) UB 0 0000011 0 000000000000011 (3) (3) 1 1111101 1 000000001111101 (-125) (-125) S/M 0 0000011 000000000 0000011 (3) (3) 11111101 00000000 11111101 (-3) (+253!) RC (2s complement) 11111101 1111111111111101 (-3) (-3) “extend” the sign bit left through the new MSB Unsigned Binary is no problem, fill with zeros Sign Magnitude is no problem, sign goes to MSB 26 bad good

27 .Subtraction in Two’s -Complement

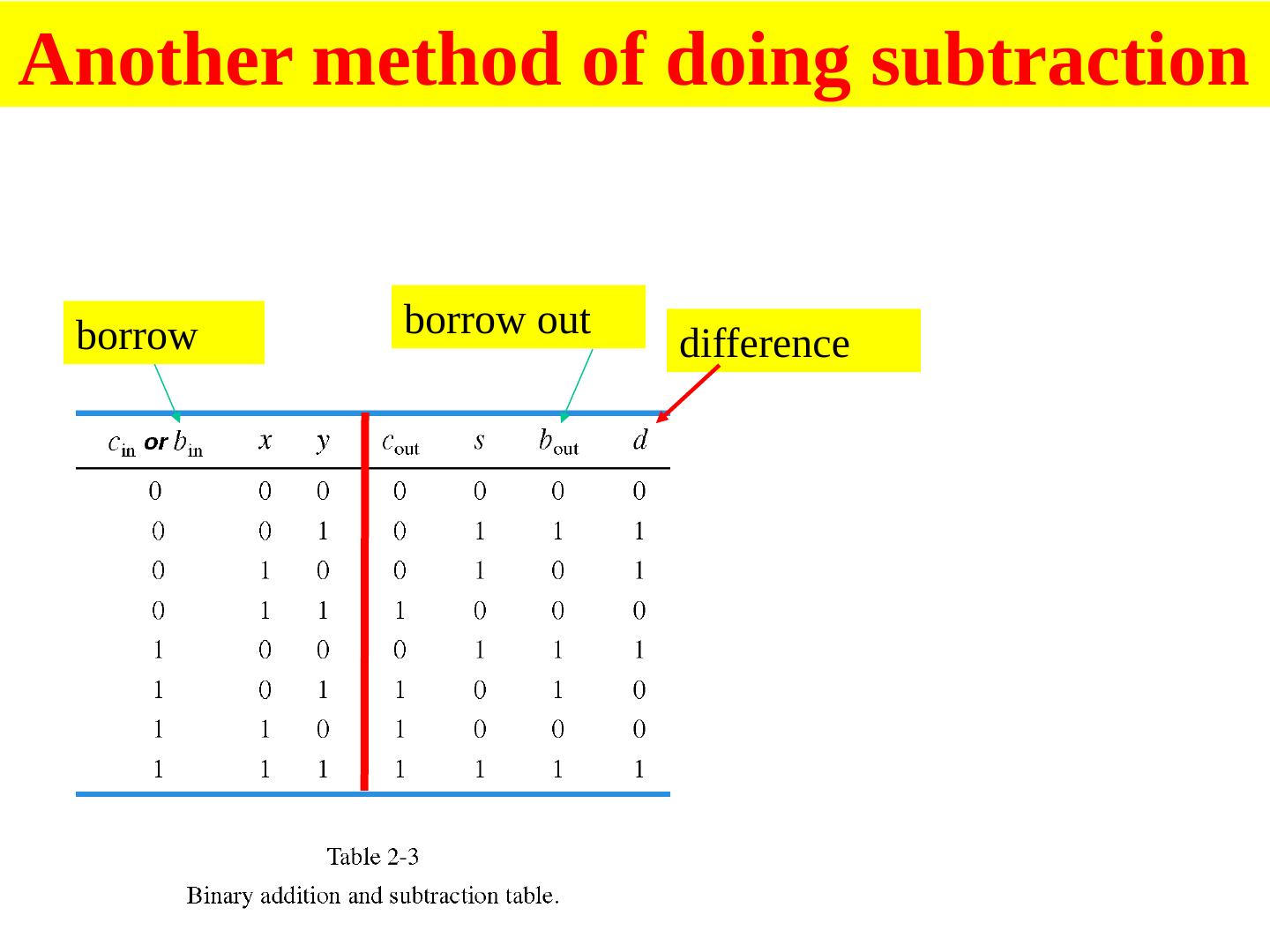
28 .Addition versus Subtraction Use same technique as decimal Except that the addition and subtraction tables are different Already seen addition table Truth table for Sum and Cout function

29 .Subtraction table b in x y b out d 0 0 0 0 0 0 0 1 1 1 0 1 0 0 1 0 1 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 1 1 1 1 1 difference