- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
01 Digital Circuits
展开查看详情
1 .ECE 171 Digital Circuits Prof. Marek Perkowski Maseeh College of Engineering and Computer Science
2 .Marek Perkowski obtained his M.S. degree in Electronics and Ph.D. Degree in automatic control from Institute of Automatic Control, Department of Electronics, Technical University of Warsaw, Warsaw, Poland. He studied also pure mathematics at University of Warsaw. In years 1981-1983 he was a Visiting Assistant Professor at University of Minnesota in Minneapolis. Since 1983 Dr. Perkowski works for Department of Electrical and Computer Engineering at Portland State University where he is a full professor and director of Intelligent Robotics Laboratory. He worked for Cypress Semiconductor (co-author of WARP, the first FPGA compiler of VHDL), Intel Supercomputer, Sharp Microelectronics, GTE and other companies in areas of computer architecture, CAD tools for logic synthesis and image processing. Dr. Perkowski invented Kronecker Decision Diagrams and lattices and contributed to logic synthesis software that is used in US industry. In 1994 he worked for Machine Learning group in Wright Laboratories of U.S. Air Force applying logic decomposition as a machine learning approach to pattern recognition and continued this work on several grants. He is an author of more than 340 papers in CAD, logic synthesis, multiple-valued logic, machine learning, robotics and quantum computing and his research is highly cited. His h-index is 41 and there are more than 6300 citations to his work on Google Scholar. His “ Erd Ö s Number” is 4 and his ”Publication Distance” to Einstein and many famous researchers is also 4 or 3. He had visiting professor and visiting scientist positions in the Netherlands, France, Japan and Korea. In years 2002-2004 he was professor in KAIST – Korean Advanced Institute of Science and Technology where he participated in research on humanoid robotics and quantum computing. He chaired the IEEE Technical Committee on Multiple-Valued Logic in years 2003-2005 and was a chair of IEEE Computational Intelligence Society Task Force on Quantum Computing 2006 - 2007. His main current interests are in quantum circuits and algorithms, humanoid bipeds, emotional quantum robots, robotics for teenagers, Grover algorithm, memristor logic and system design and logic synthesis for other nano -technologies such as QCA and STO. He collaborates with many groups worldwide. Dr. Perkowski works with very talented middle-school and high-school students on projects related to quantum computing, intelligent robotics and image processing. Since 2001, the students that he supervised obtained more than 40 awards in US national and international science fairs and competitions. His main research area is quantum computing – how to build a new generations of computers based on principles of quantum mechanics. These computers will be significantly more powerful than all contemporary standard computers. Who is this old guy?
3 .I teach this class since 1970 3 1996 1981-1983 1983-2017 1970-1981 1996 2010 2002-2005 2002 And it has been exciting
4 .Year 1967 4 Polish Computer UMC-1 Me in your age Flip-flops and logic gates
5 .Why Study Digital Systems Because you’ll probably Design them Use them Interface with them Program them They’re ubiquitous Obvious: PCs, Consumer Electronics Audio, Video, Cameras, Phones, Cable Set-top Boxes, Games Also: Appliances, Automobiles, Medical Devices 5
6 .The old days… Only electronics – car radio (analog) 6
7 .Now… Hybrid vehicle >150 motors, solenoids to control >15 microcontrollers (MCUs) >100 sensors to be checked Airbags and belt pretensioners to be fired/pre-fired 60kW of electrical power to control 7
8 .Features Digital satellite radio GPS guidance systems ABS brakes Fuel injection Anti-collision systems Video camera Cell phone Entertainment systems (DVD, CD, MP3) Anti-theft system 8
9 .To the “pedestrian” 9
10 .Our Robots 10
11 .Digital Systems Two Valued (Binary) System On/Off High/Low Voltage Open/Closed Switch (vs. “Dimmer” Switch) Magnetized/Unmagnetized 1/0 11
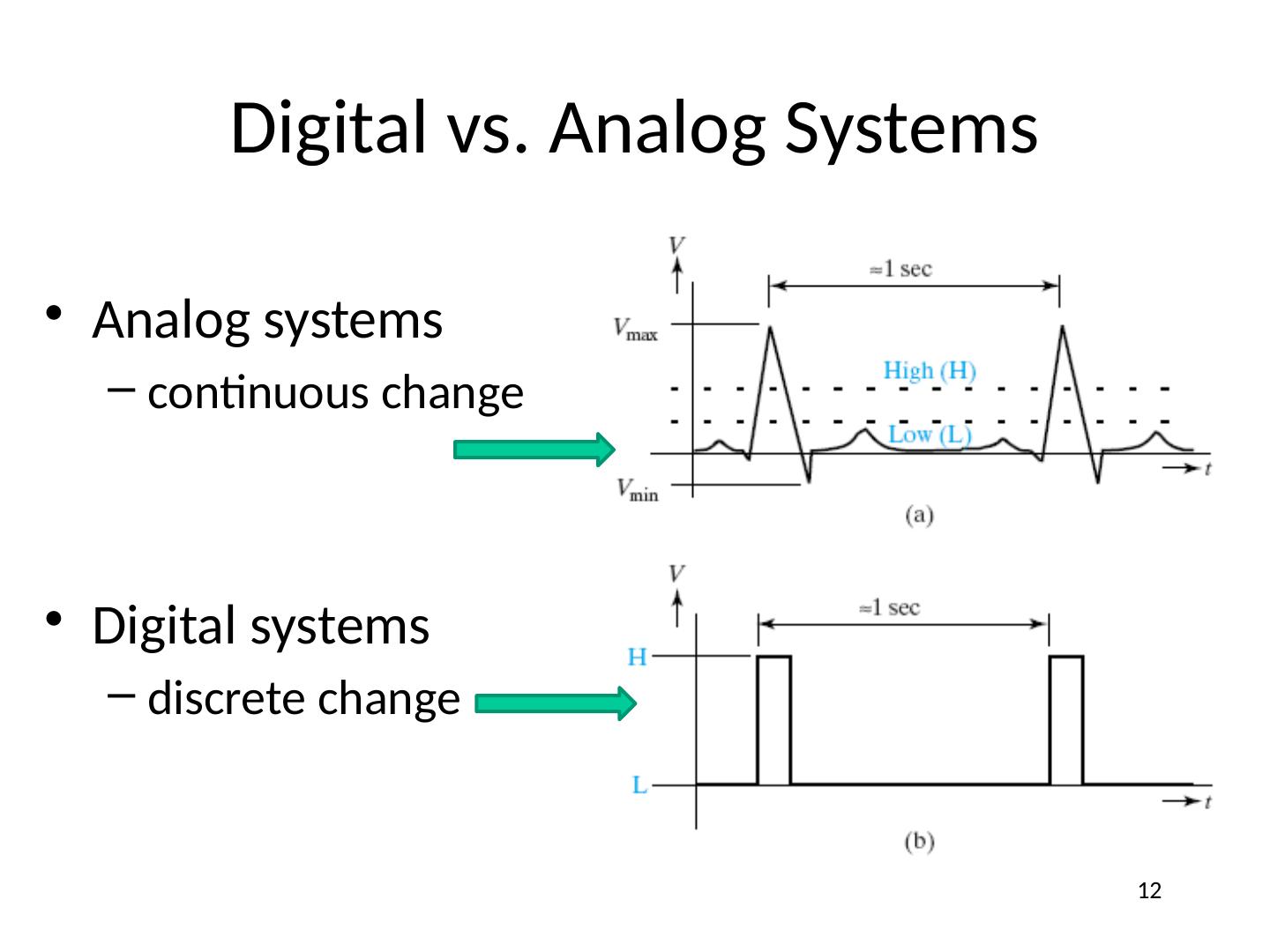
12 .Digital vs. Analog Systems Analog systems continuous change Digital systems discrete change 12
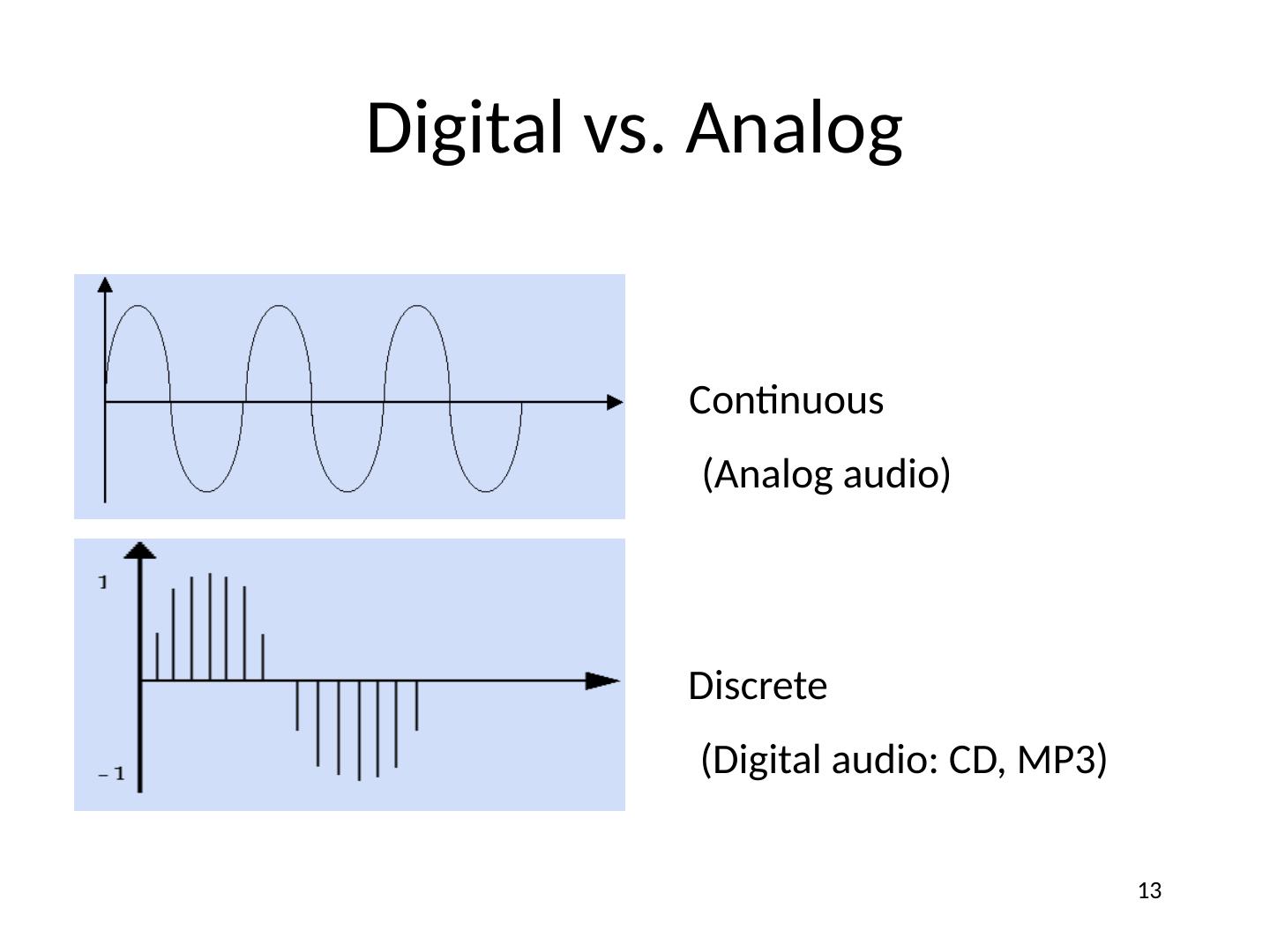
13 .Digital vs. Analog Continuous Discrete (Analog audio) (Digital audio: CD, MP3) 13
14 .Lecture 1 Topics Radix number representations Decimal, Binary, Octal, Hexadecimal Conversions Decimal to Binary, Octal, Hexadecimal Binary, Octal, Hexadecimal to Decimal Group of 3 for Octal Group of 4 for Hexadecimal 14
15 .Decimal and Binary Numbers
16 .Decimal 6234 10 100 10 1 10 3 10 2 10 1 10 0 6 2 3 4 d n d n-1 …d 1 d 0 = d n x 10 n + d n-1 x 10 n-1 + … d 1 x 10 1 + d 0 x 10 0 where: 0 £ d £ 9 6234 10 = 6 x 10 3 + 2 x 10 2 + 3 x 10 1 + 4 x 10 0 MSD LSD Radix or Base 10 (Why?) Zero referencing 16 MSD = most significant digit LSD = least significant digit
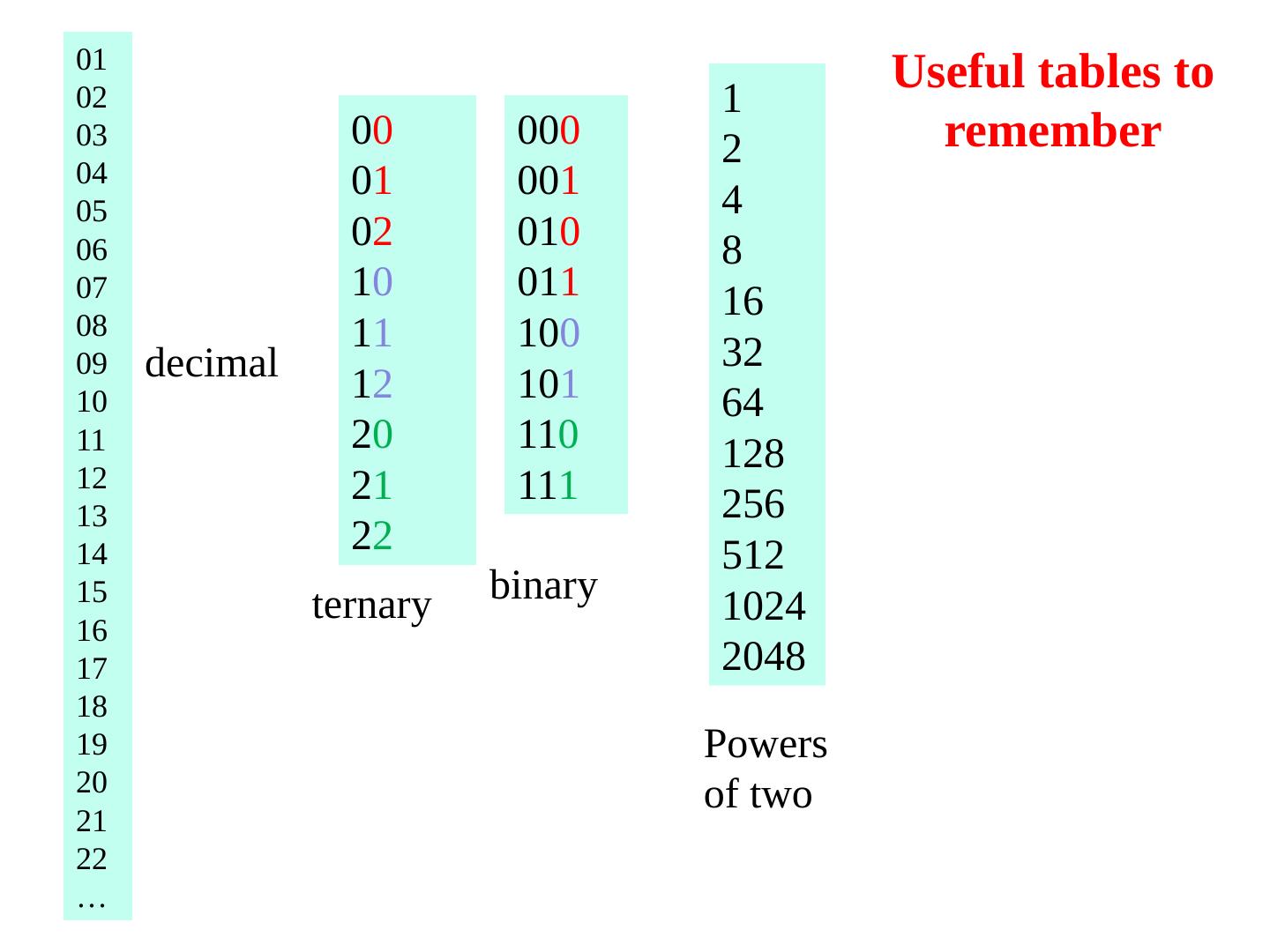
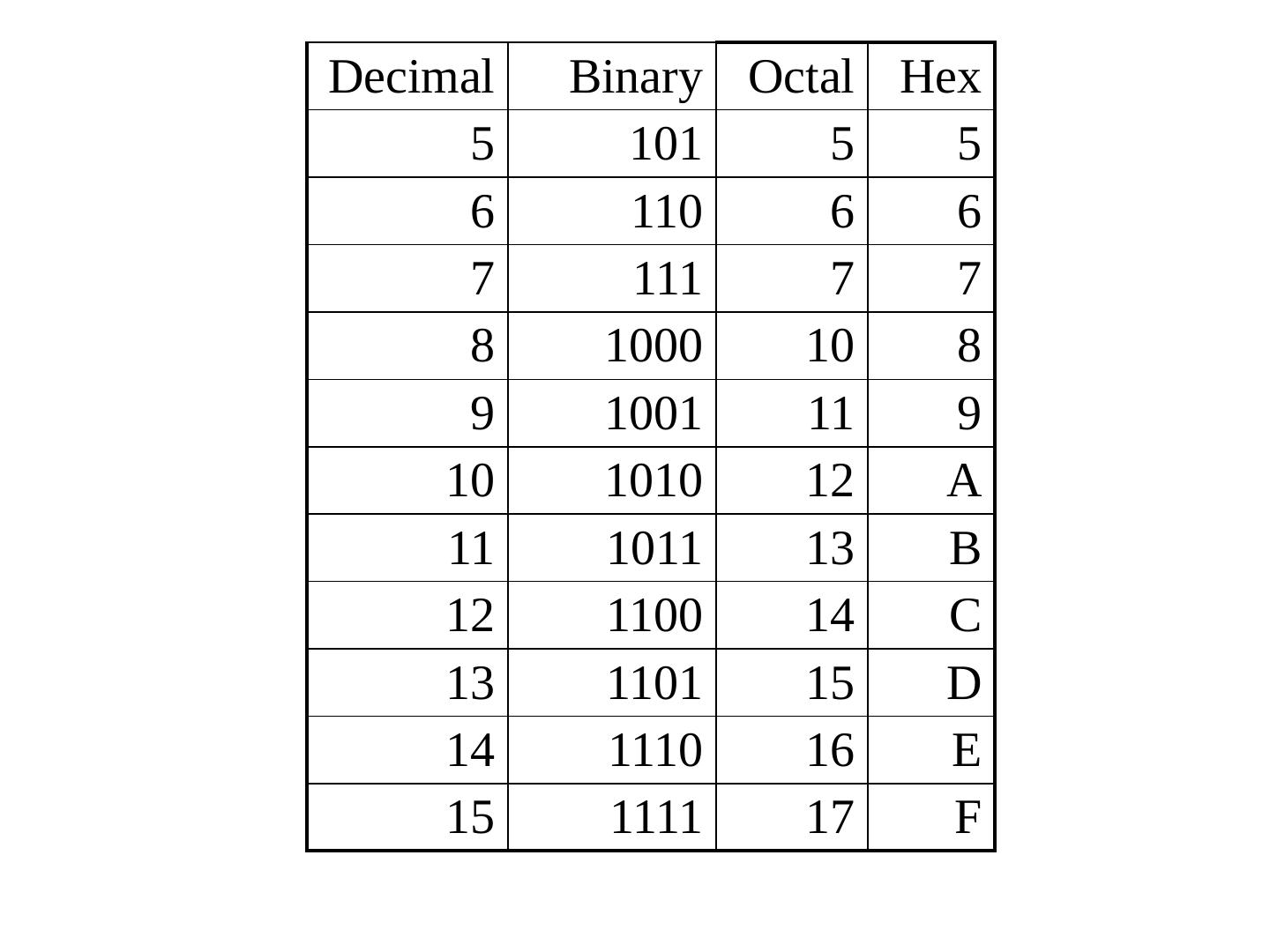
17 .01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 … 0 0 0 1 0 2 1 0 1 1 1 2 2 0 2 1 2 2 decimal ternary 00 0 00 1 01 0 01 1 10 0 10 1 11 0 11 1 1 2 4 8 16 32 64 128 256 512 1024 2048 binary Powers of two Useful tables to remember
18 .Decimal Question : How many unique (non-negative) n digit decimal numbers are there? 10 n 1 digit: 0-9, 10 (10 1 ) 2 digits: 00-99, 100 (10 2 ) 3 digits: 000-999, 1000 (10 3 ) Question: What’s the largest n digit decimal number? 10 n -1 18 For n=2 it is 10 2 -1 = 99
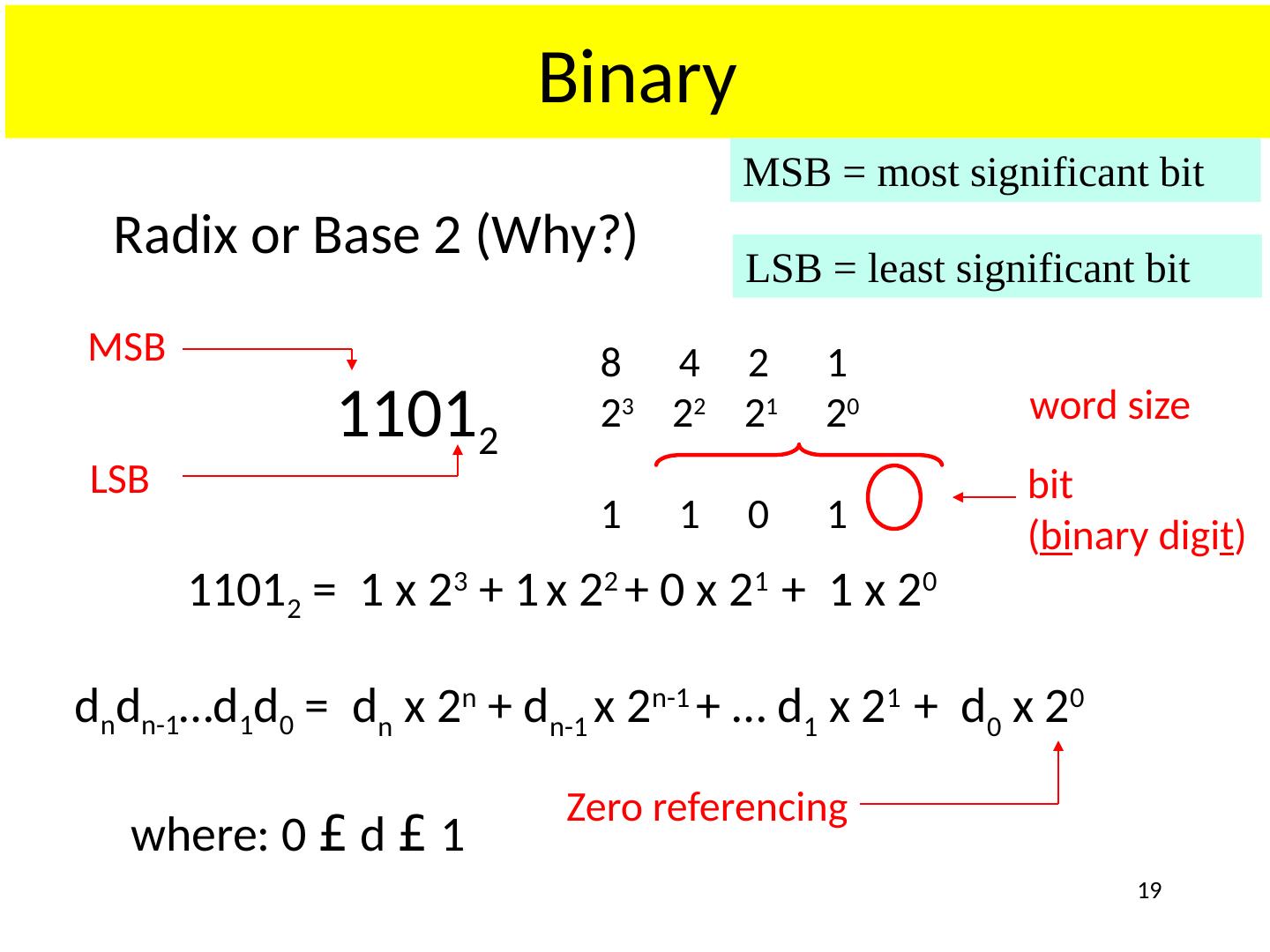
19 .Binary 1101 2 8 4 2 1 2 3 2 2 2 1 2 0 1 1 0 1 d n d n-1 …d 1 d 0 = d n x 2 n + d n-1 x 2 n-1 + … d 1 x 2 1 + d 0 x 2 0 where: 0 £ d £ 1 1101 2 = 1 x 2 3 + 1 x 2 2 + 0 x 2 1 + 1 x 2 0 MSB LSB Zero referencing Radix or Base 2 (Why?) bit ( bi nary digi t ) word size 19 MSB = most significant bit LSB = least significant bit
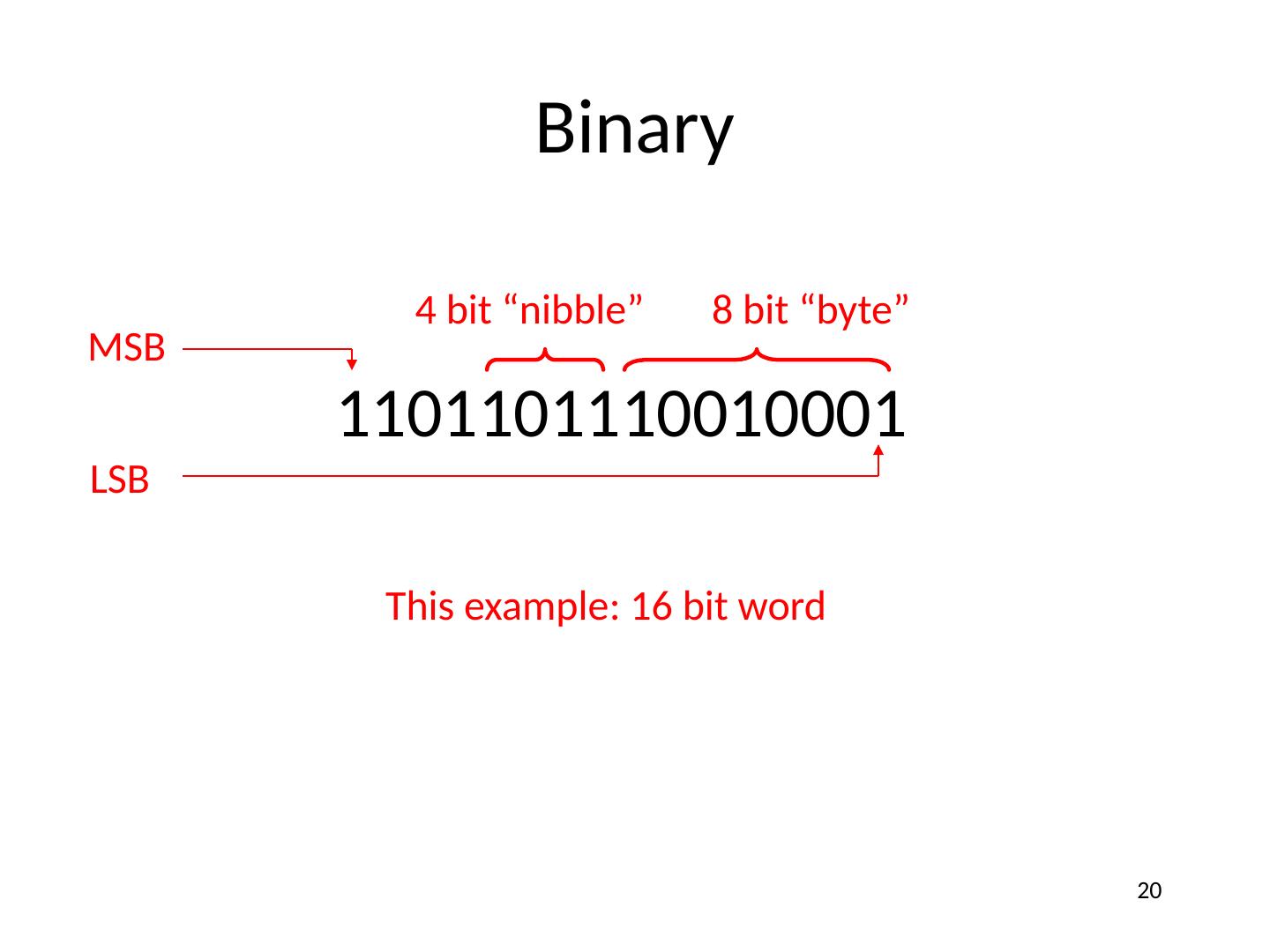
20 .Binary 1101101110010001 MSB LSB 4 bit “nibble” 8 bit “byte” This example: 16 bit word 20
21 .Binary Question: How many different (non-negative) n bit binary numbers are there? 2 n 1 bit: {0,1} 2 (2 1 ) 2 bits: {00, 01, 10, 11}, 4 (2 2 ) 3 bits: {000, 001, 010, 011, 100, 101, 110, 111}, 8 (2 3 ) Question: What’s the largest n bit binary number (what’s the largest number you can represent in an n bit word)? 2 n -1 21
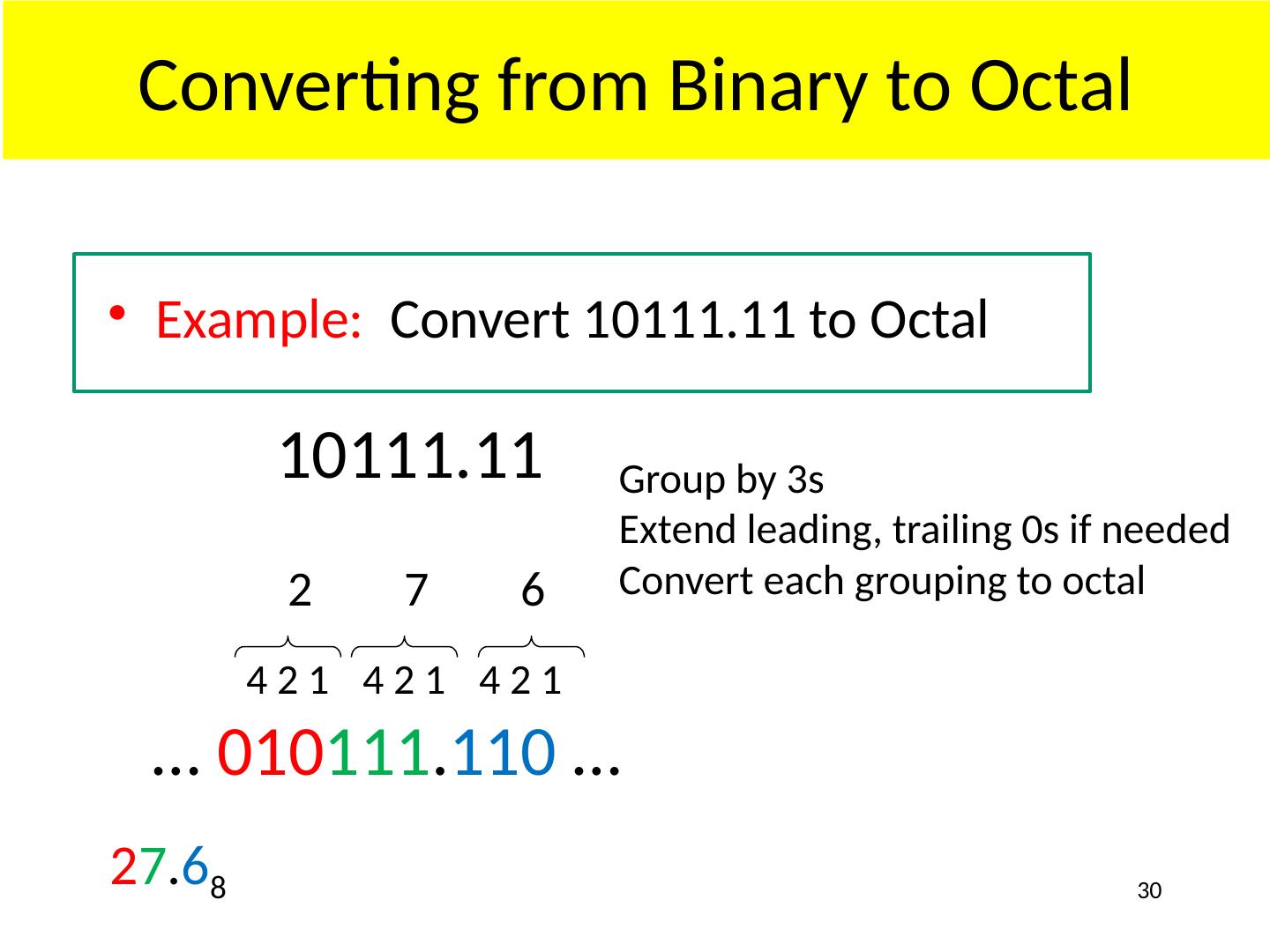
22 .Binary Question: How many bits (what word size) do you need to represent a number n in binary? Let’s first ask : How many bits do you need to represent n different binary numbers? é log 2 n ù 1 bit: n = (2 1 ) numbers 2 bits: n = (2 2 ) numbers 3 bits: n = (2 3 ) numbers m bits: n = 2 m numbers Ceiling function because we need an integer number of bits Now, to represent number n , how many different numbers? n+1 , so é log 2 (n+1) ù 22 0 and 1 00, 01, 10 and 11 n=4, then é log (4+1) ù = 3 100
23 .Example: Disk Drives Early ATA specification for hard disk drives Identified sectors of 512 (2 9 ) bytes each Cylinder (16 bits), numbered [0..2 16 -1] Head (4 bits), numbered [0..2 4 -1] Sector (8 bits), numbered [1..2 8 -1] Limited hard disk capacity 2 16 x 2 4 x (2 8 -1) x 2 9 bytes = 127.5 x 2 30 = 127.5 GB = 136902082560 ≈ 137 x 10 9 bytes (137 GB) 23
24 .Decimal Fractions
25 .Decimal Fractions 6234 .125 10 100 10 1 1/10 1/100 1/1000 10 3 10 2 10 1 10 0 10 -1 10 -2 10 -3 6 2 3 4 . 1 2 5 d n d n-1 …d 1 d 0 . d -1… d -m = d n x 10 n + d n-1 x 10 n-1 + … d 1 x 10 1 + d 0 x 10 0 + d -1 x 10 -1 + … d -m x 10 -m where: 0 £ d £ 9 6234 .125 10 = 6 x 10 3 + 2 x 10 2 + 3 x 10 1 + 4 x 10 0 + 1 x 10 -1 + 2 x 10 -2 + 5 x 10 -3 25
26 .Binary Fractions (“Fixed Point”) 1101 . 101 2 8 4 2 1 1/2 1/4 1/8 2 3 2 2 2 1 2 0 2 -1 2 -2 2 -3 1 1 0 1 . 1 0 1 d n d n-1 …d 1 d 0 . d -1… d -m = d n x 2 n + d n-1 x 2 n-1 + … d 1 x 2 1 + d 0 x 2 0 + d -1 x 2 -1 + … d -m x 2 -m where: 0 £ d £ 1 1101 . 101 2 = 1 x 2 3 + 1 x 2 2 + 0 x 2 1 + 1 x 2 0 + 1 x 2 -1 + 0 x 2 -2 + 1 x 2 -3 26
27 .Octal Numbers
28 .Octal 2736 8 512 64 8 1 8 3 8 2 8 1 8 0 2 7 3 6 d n d n-1 …d 1 d 0 = d n x 8 n + d n-1 x 8 n-1 + … d 1 x 8 1 + d 0 x 8 0 where: 0 £ d £ 7 2736 8 = 2 x 8 3 + 7 x 8 2 + 3 x 8 1 + 6 x 8 0 Radix or Base 8 (Why?) Why: binary quickly becomes cumbersome for larger numbers, octal has advantage of requiring fewer digits but easily convertible to binary
29 .Octal Radix or Base 8 (Why?) Groups of 3 bits (8 = 2 3) 2736 8 = 010 111 011 110 2 2 7 3 6 2736 8 = 010 111 011 110 2 4 2 1 4 2 1 4 2 1 4 2 1 29 Why: binary quickly becomes cumbersome for larger numbers, octal has advantage of requiring fewer digits but easily convertible to binary