12-Introduction to Parallel Algorithms and Parallel Program Design

1 .Introduction to Parallel Algorithms and Parallel Program Design Parallel Computing CIS 410/510 Department of Computer and Information Science Lecture 12 – Introduction to Parallel Algorithms 

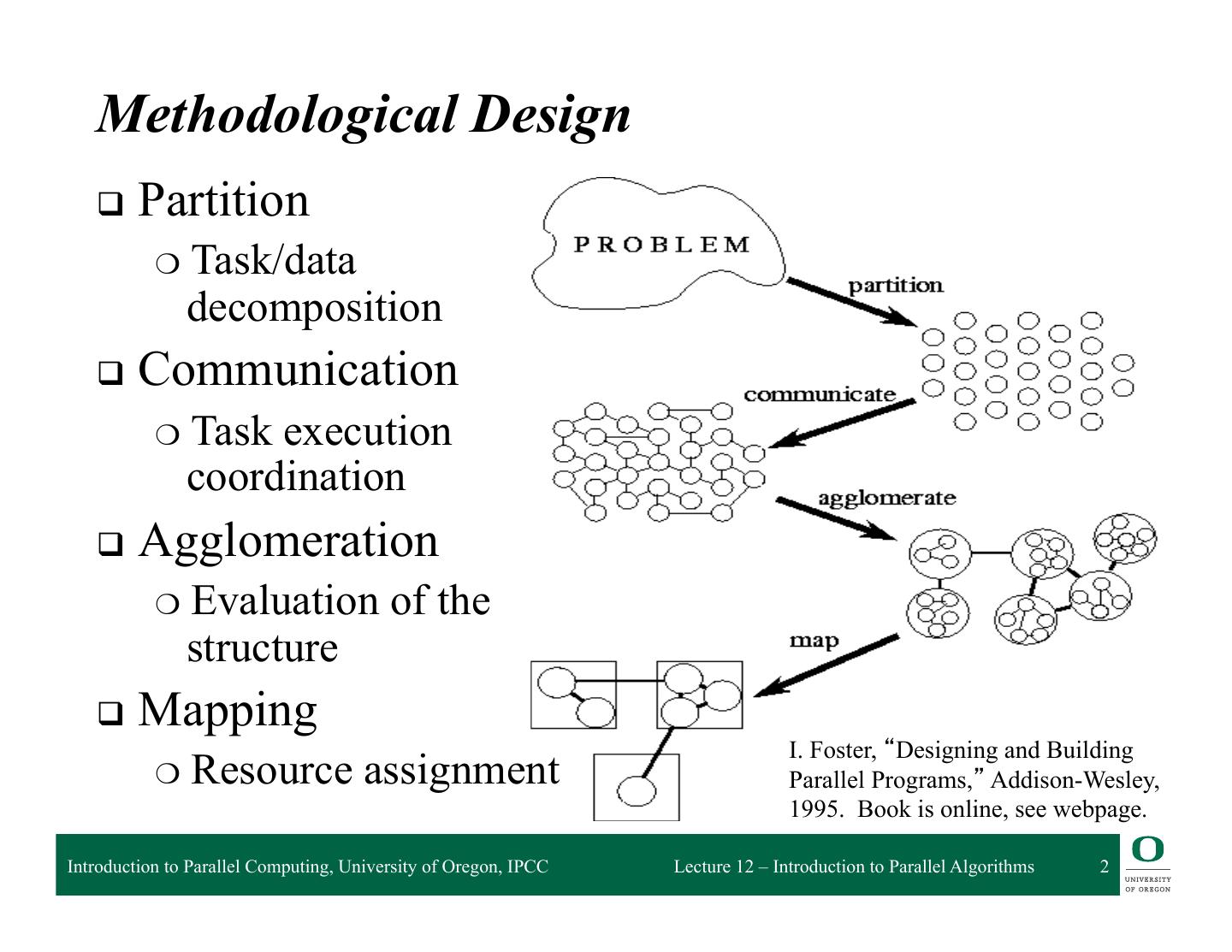
2 . Methodological Design q  Partition ❍  Task/data decomposition q  Communication ❍  Task execution coordination q  Agglomeration ❍  Evaluation of the structure q  Mapping I. Foster, “Designing and Building ❍  Resource assignment Parallel Programs,” Addison-Wesley, 1995. Book is online, see webpage. Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 2 

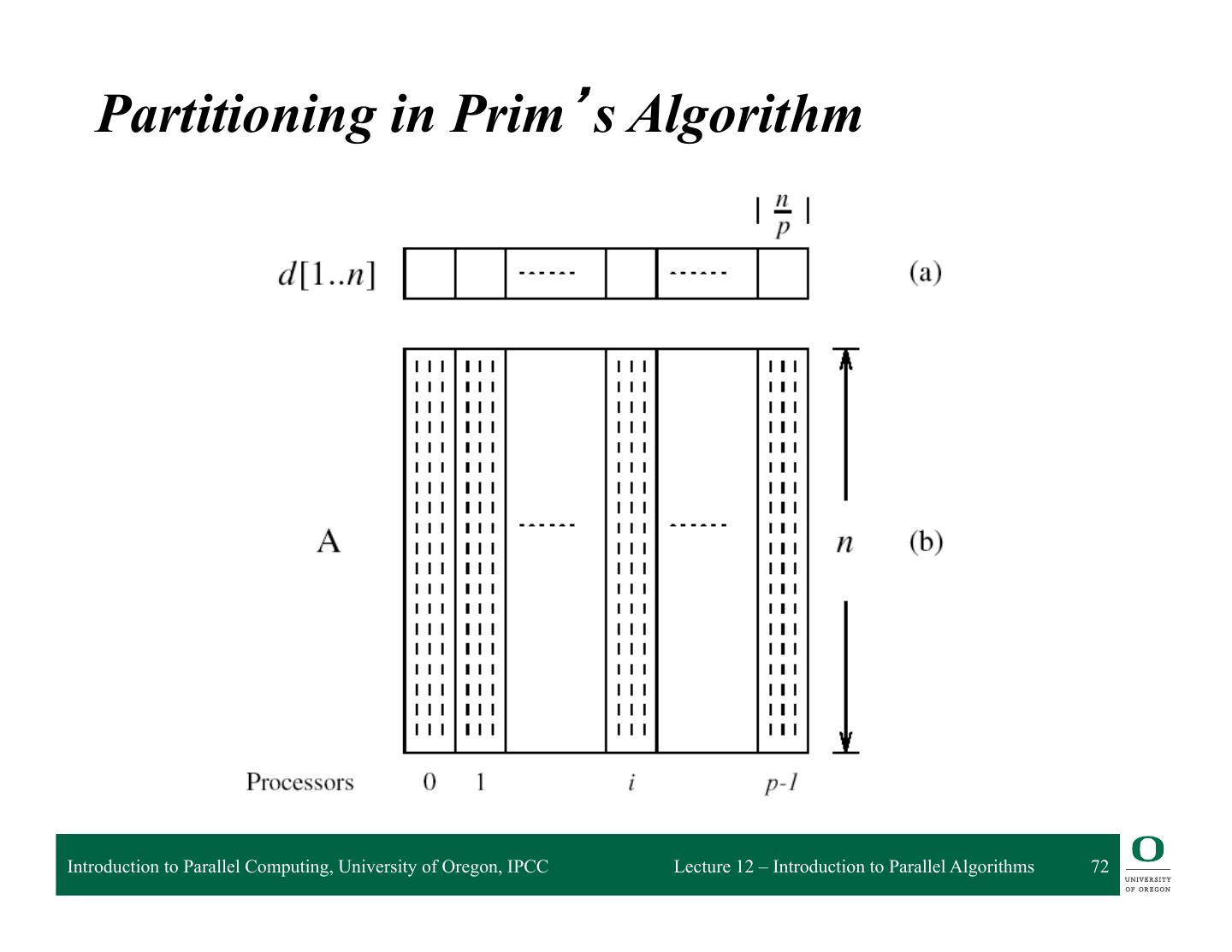
3 . Partitioning q  Partitioning stage is intended to expose opportunities for parallel execution q  Focus on defining large number of small task to yield a fine-grained decomposition of the problem q  A good partition divides into small pieces both the computational tasks associated with a problem and the data on which the tasks operates q  Domain decomposition focuses on computation data q  Functional decomposition focuses on computation tasks q  Mixing domain/functional decomposition is possible Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 3 

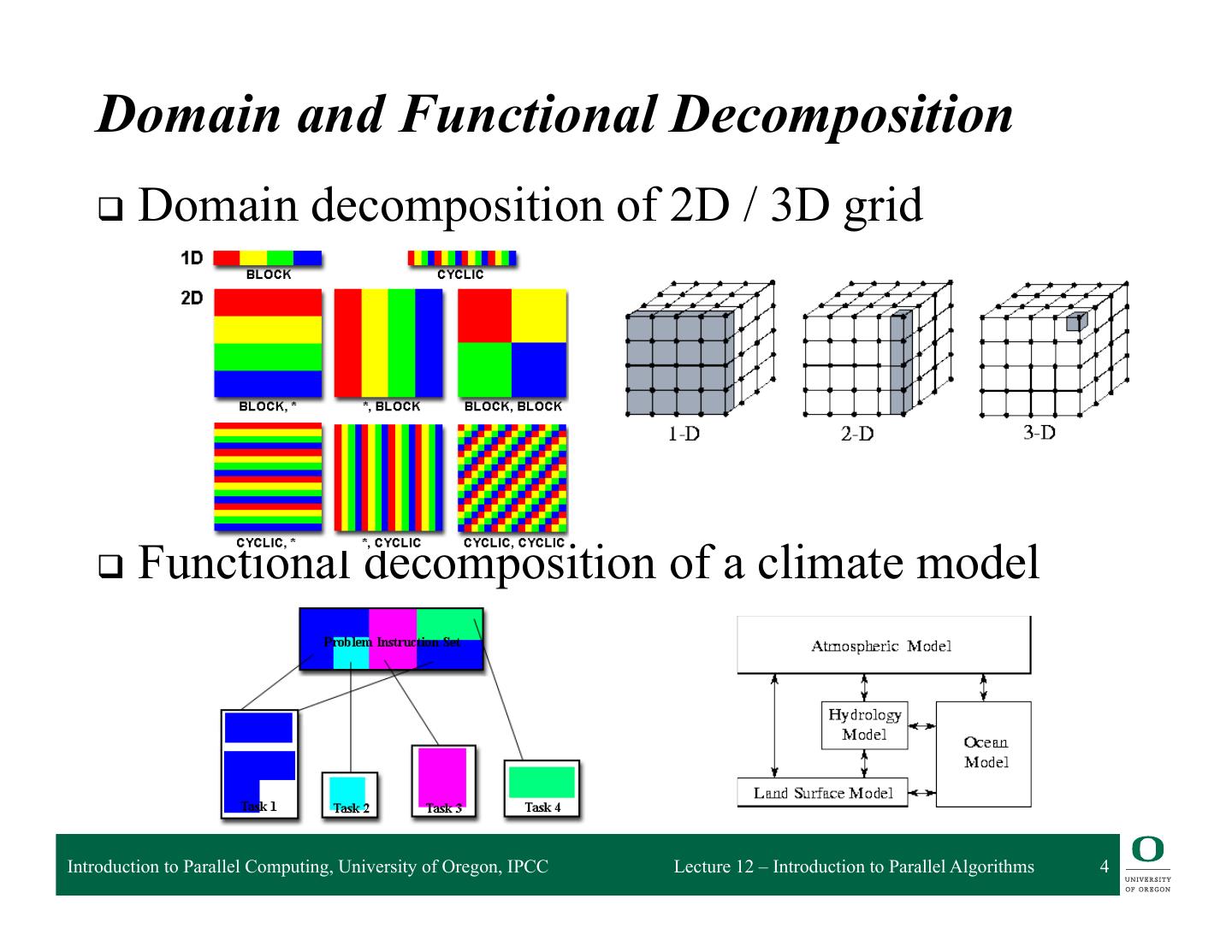
4 . Domain and Functional Decomposition q  Domain decomposition of 2D / 3D grid q  Functional decomposition of a climate model Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 4 

5 . Partitioning Checklist q  Does your partition define at least an order of magnitude more tasks than there are processors in your target computer? If not, may loose design flexibility. q  Does your partition avoid redundant computation and storage requirements? If not, may not be scalable. q  Are tasks of comparable size? If not, it may be hard to allocate each processor equal amounts of work. q  Does the number of tasks scale with problem size? If not may not be able to solve larger problems with more processors q  Have you identified several alternative partitions? Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 5 

6 . Communication (Interaction) q  Tasks generated by a partition must interact to allow the computation to proceed ❍  Information flow: data and control q  Types of communication ❍  Local vs. Global: locality of communication ❍  Structured vs. Unstructured: communication patterns ❍  Static vs. Dynamic: determined by runtime conditions ❍  Synchronous vs. Asynchronous: coordination degree q  Granularity and frequency of communication ❍  Size of data exchange q  Think of communication as interaction and control ❍  Applicable to both shared and distributed memory parallelism Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 6 

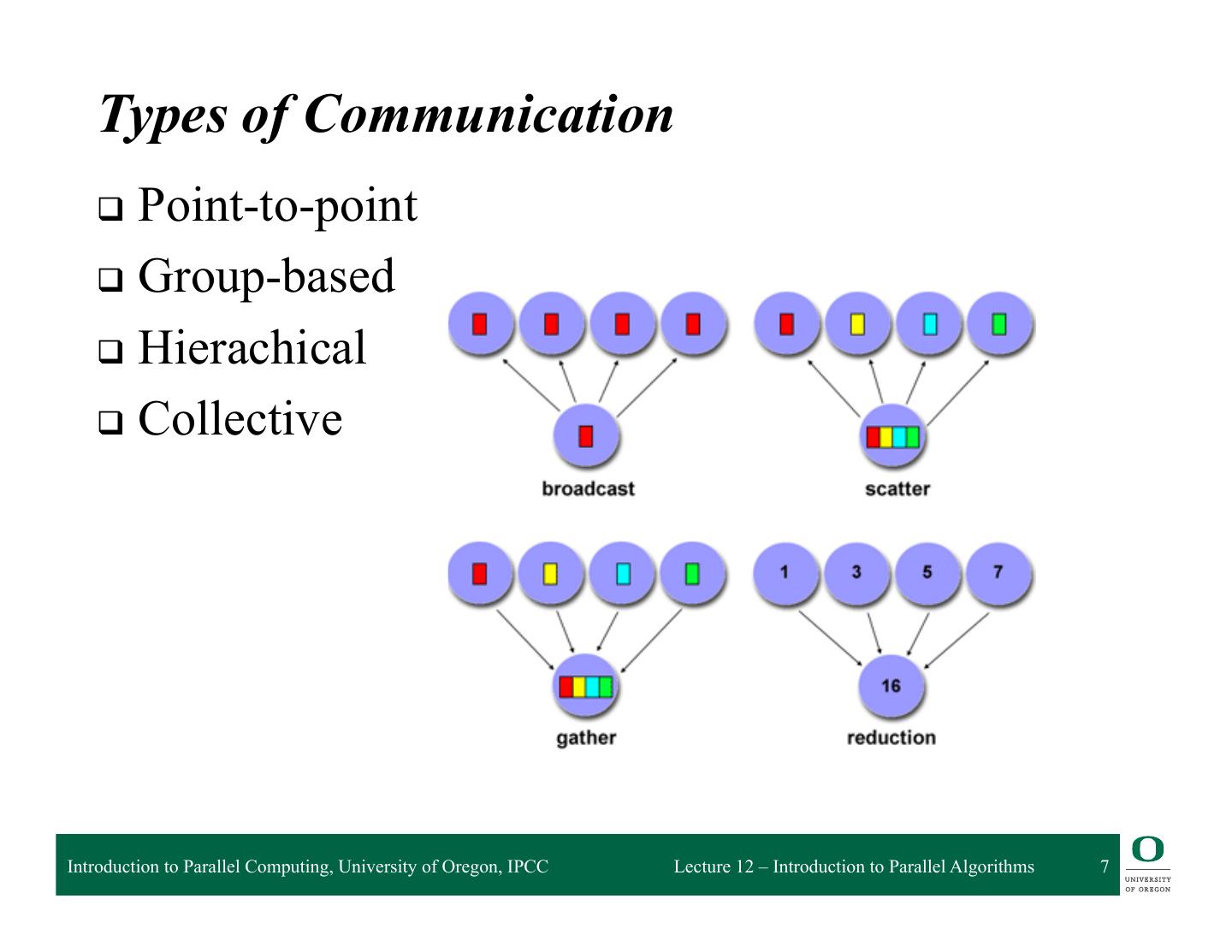
7 . Types of Communication q  Point-to-point q  Group-based q  Hierachical q  Collective Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 7 

8 . Communication Design Checklist q  Is the distribution of communications equal? ❍  Unbalanced communication may limit scalability q  What is the communication locality? ❍  Wider communication locales are more expensive q  What is the degree of communication concurrency? ❍  Communication operations may be parallelized q  Is computation associated with different tasks able to proceed concurrently? Can communication be overlapped with computation? ❍  Try to reorder computation and communication to expose opportunities for parallelism Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 8 

9 . Agglomeration q  Move from parallel abstractions to real implementation q  Revisit partitioning and communication ❍  View to efficient algorithm execution q  Is it useful to agglomerate? ❍  What happens when tasks are combined? q  Is it useful to replicate data and/or computation? q  Changes important algorithm and performance ratios ❍  Surface-to-volume: reduction in communication at the expense of decreasing parallelism ❍  Communication/computation: which cost dominates q  Replication may allow reduction in communication q  Maintain flexibility to allow overlap Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 9 

10 . Types of Agglomeration q  Element to column q  Element to block ❍  Better surface to volume q  Task merging q  Task reduction ❍  Reduces communication Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 10 

11 . Agglomeration Design Checklist q  Has increased locality reduced communication costs? q  Is replicated computation worth it? q  Does data replication compromise scalability? q  Is the computation still balanced? q  Is scalability in problem size still possible? q  Is there still sufficient concurrency? q  Is there room for more agglomeration? q  Fine-grained vs. coarse-grained? Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 11 

12 . Mapping q  Specify where each task is to execute ❍  Less of a concern on shared-memory systems q  Attempt to minimize execution time ❍  Place concurrent tasks on different processors to enhance physical concurrency ❍  Place communicating tasks on same processor, or on processors close to each other, to increase locality ❍  Strategies can conflict! q  Mapping problem is NP-complete ❍  Use problem classifications and heuristics q  Static and dynamic load balancing Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 12 

13 . Mapping Algorithms q  Load balancing (partitioning) algorithms q  Data-based algorithms ❍  Think of computational load with respect to amount of data being operated on ❍  Assign data (i.e., work) in some known manner to balance ❍  Take into account data interactions q  Task-based (task scheduling) algorithms ❍  Used when functional decomposition yields many tasks with weak locality requirements ❍  Use task assignment to keep processors busy computing ❍  Consider centralized and decentralize schemes Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 13 

14 . Mapping Design Checklist q  Is static mapping too restrictive and non- responsive? q  Is dynamic mapping too costly in overhead? q  Does centralized scheduling lead to bottlenecks? q  Do dynamic load-balancing schemes require too much coordination to re-balance the load? q  What is the tradeoff of dynamic scheduling complexity versus performance improvement? q  Are there enough tasks to achieve high levels of concurrency? If not, processors may idle. Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 14 

15 . Types of Parallel Programs q  Flavors of parallelism ❍  Data parallelism ◆ all processors do same thing on different data ❍  Task parallelism ◆ processors are assigned tasks that do different things q  Parallel execution models ❍  Data parallel ❍  Pipelining (Producer-Consumer) ❍  Task graph ❍  Work pool ❍  Master-Worker Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 15 

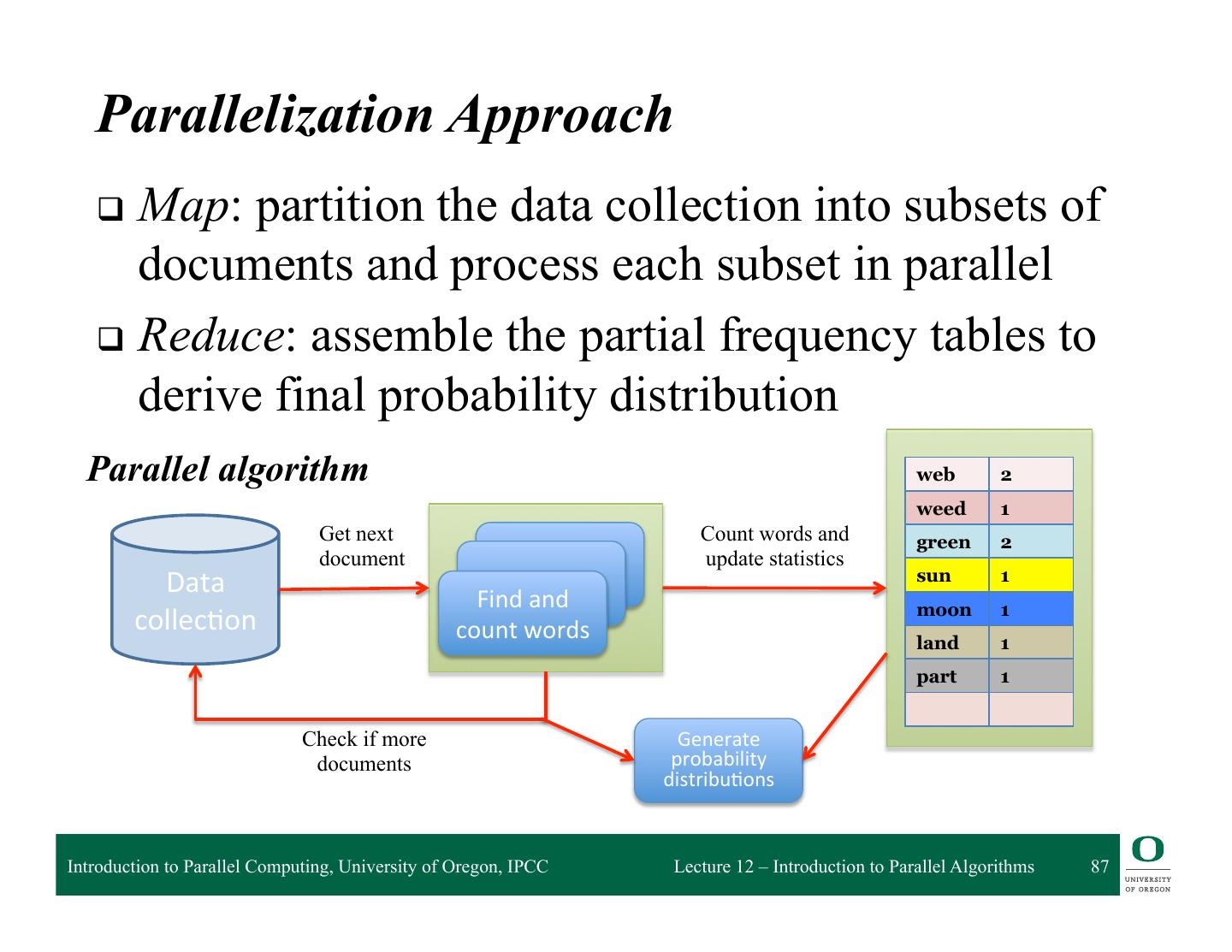
16 . Data Parallel q  Data is decomposed (mapped) onto processors q  Processors performance similar (identical) tasks on data q  Tasks are applied concurrently q  Load balance is obtained through data partitioning ❍  Equal amounts of work assigned q  Certainly may have interactions between processors q  Data parallelism scalability ❍  Degree of parallelism tends to increase with problem size ❍  Makes data parallel algorithms more efficient q  Single Program Multiple Data (SPMD) ❍  Convenient way to implement data parallel computation ❍  More associated with distributed memory parallel execution Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 16 

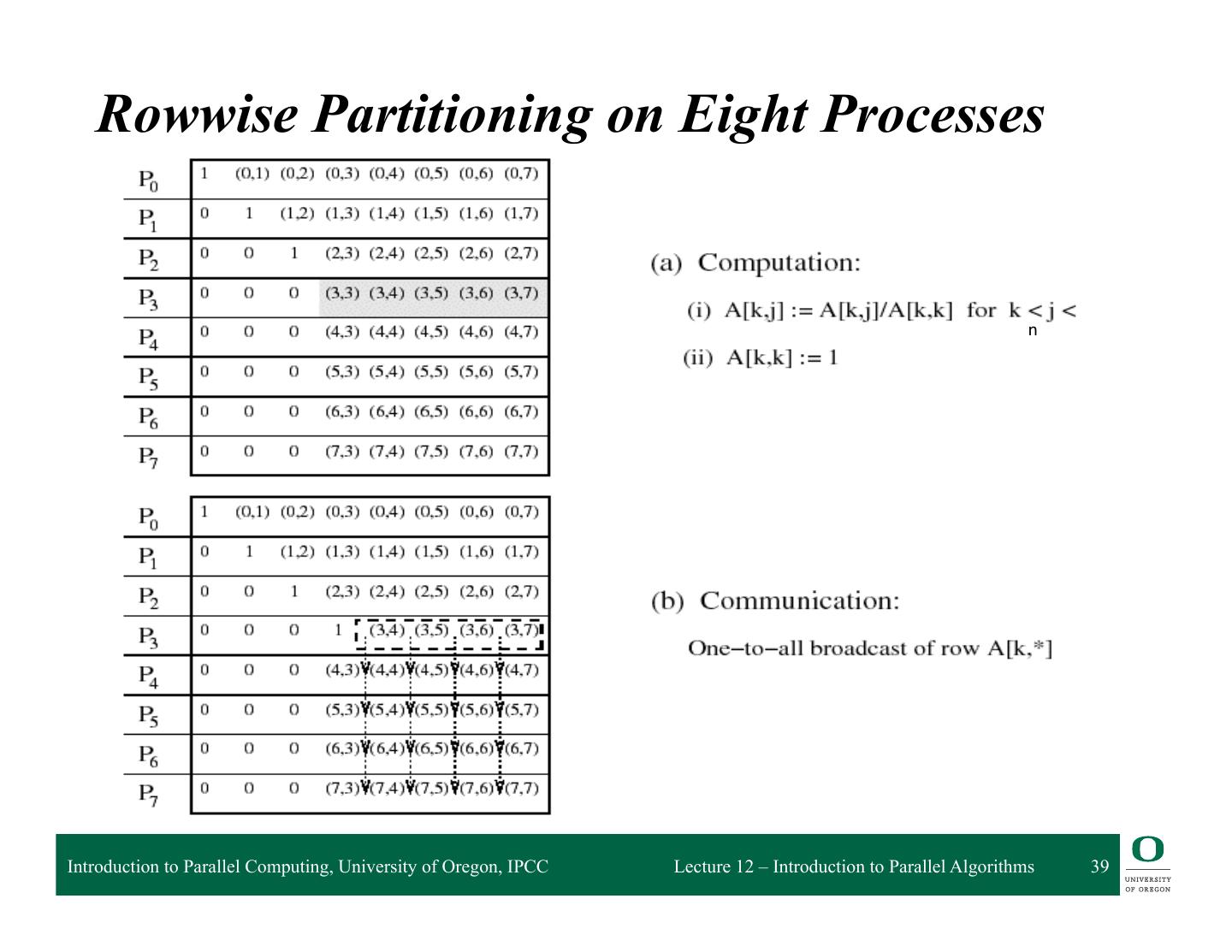
17 . Matrix - Vector Multiplication q  A xb=y q  Allocate tasks to rows of A y[i] = ∑A[i,j]*b[j] j   q  Dependencies? q  Speedup? q  Computing each element of y can be done independently Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 17 

18 . Matrix-Vector Multiplication (Limited Tasks) q  Supposewe only have 4 tasks q  Dependencies? q  Speedup? Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 18 

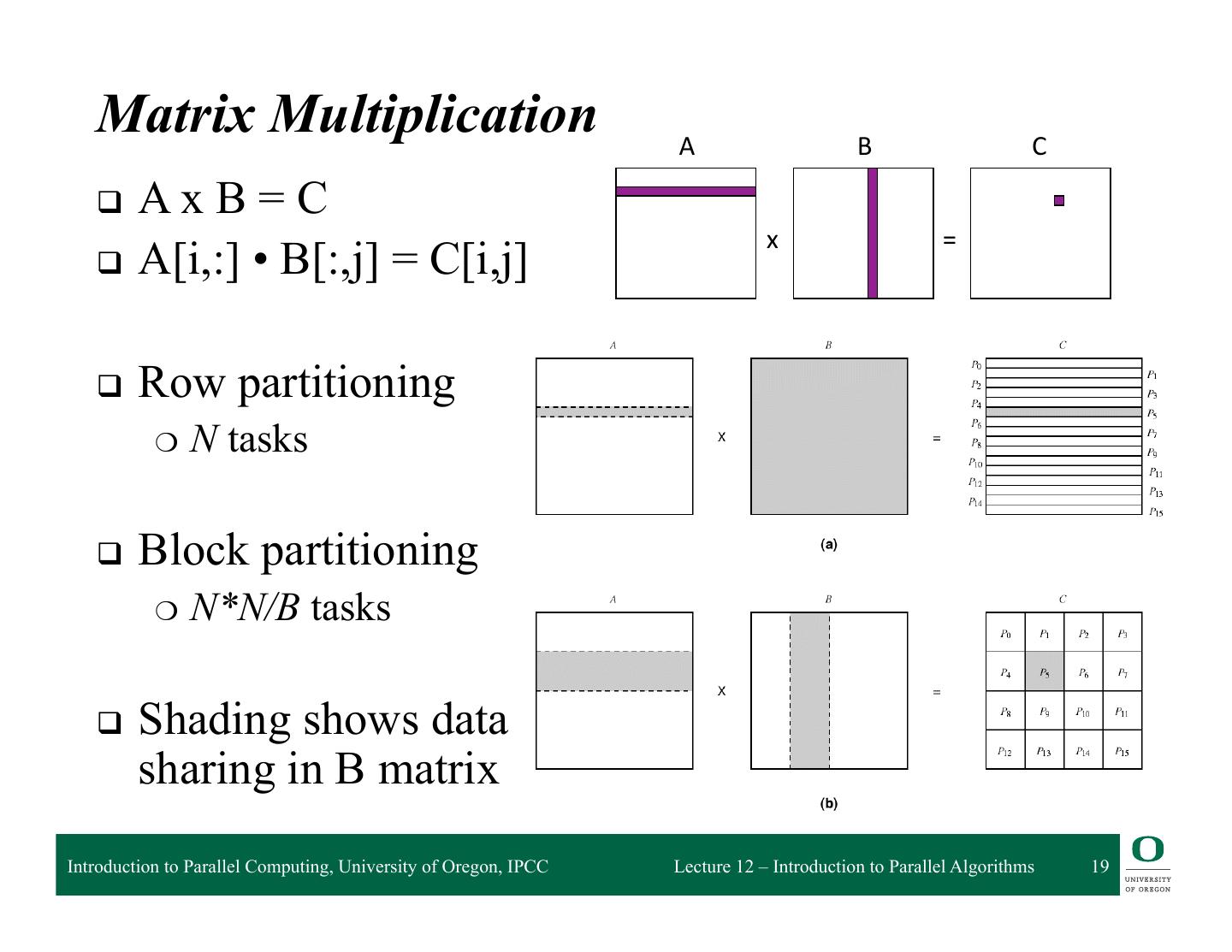
19 . Matrix Multiplication A   B   C   q  AxB=C x   =   q  A[i,:] • B[:,j] = C[i,j] q  Row partitioning ❍  N tasks q  Block partitioning ❍  N*N/B tasks q  Shading shows data sharing in B matrix Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 19 

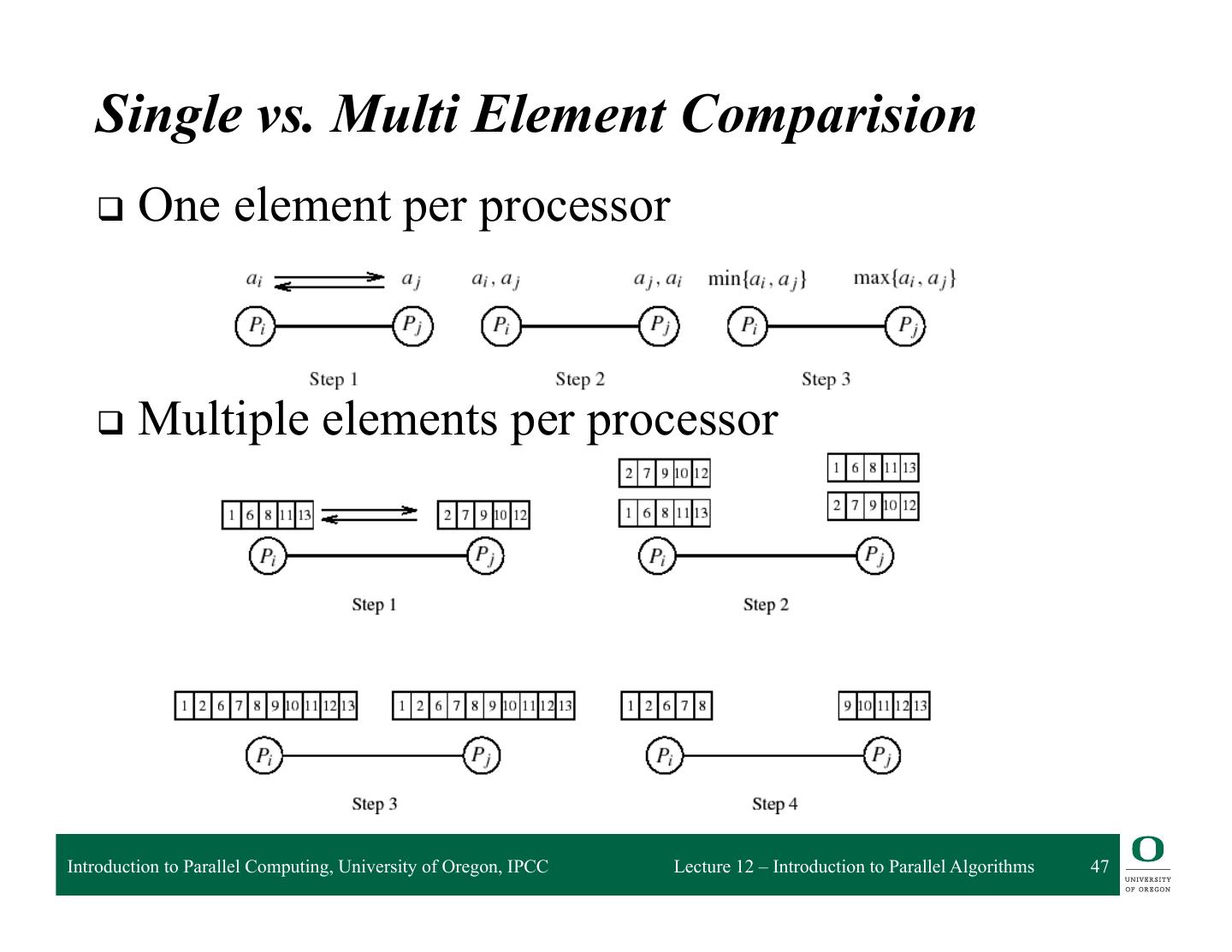
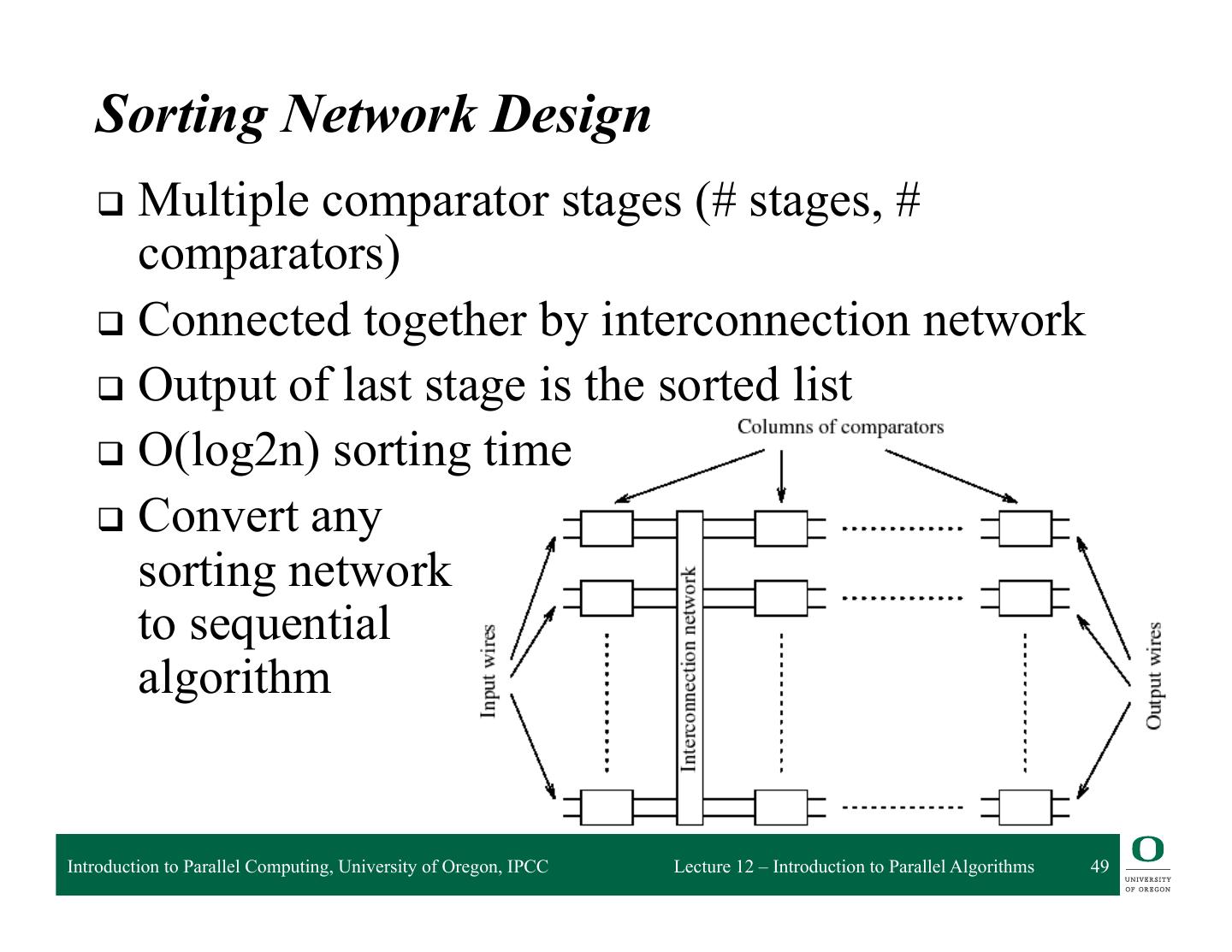
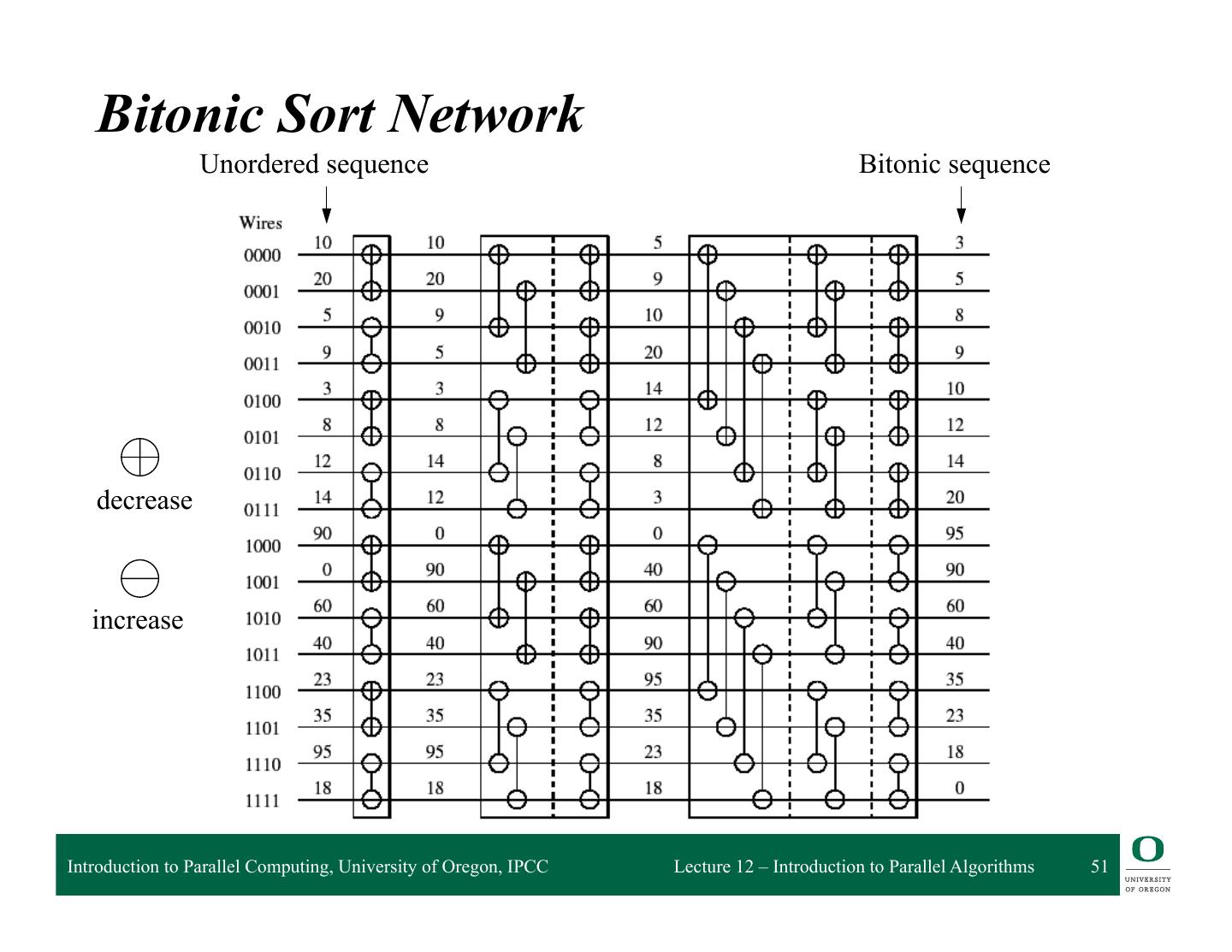
20 . Granularity of Task and Data Decompositions q  Granularity can be with respect to tasks and data q  Task granularity ❍  Equivalent to choosing the number of tasks ❍  Fine-grained decomposition results in large # tasks ❍  Large-grained decomposition has smaller # tasks ❍  Translates to data granularity after # tasks chosen ◆  consider matrix multiplication q  Data granularity ❍  Think of in terms of amount of data needed in operation ❍  Relative to data as a whole ❍  Decomposition decisions based on input, output, input- output, or intermediate data Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 20 

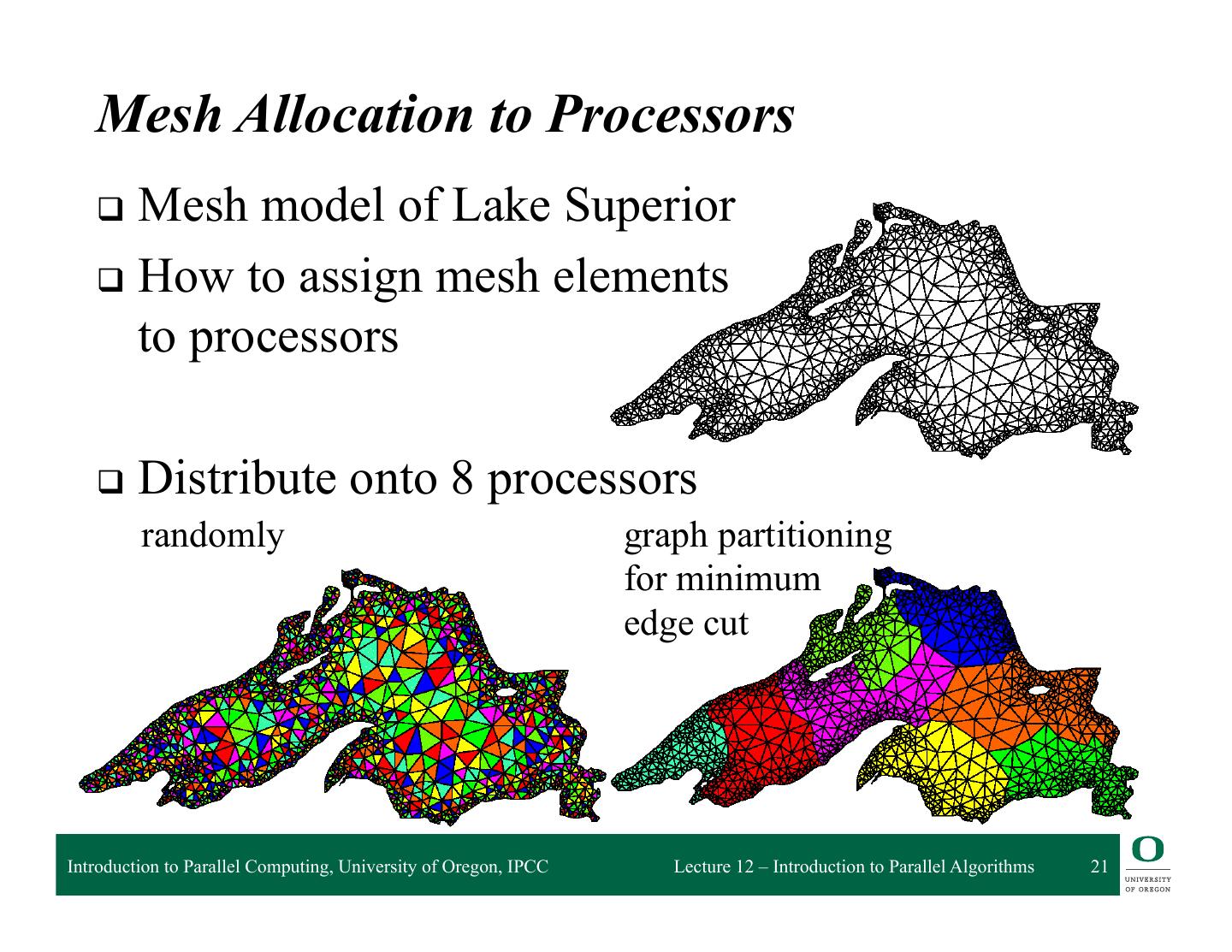
21 . Mesh Allocation to Processors q  Mesh model of Lake Superior q  How to assign mesh elements to processors q  Distribute onto 8 processors randomly graph partitioning for minimum edge cut Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 21 

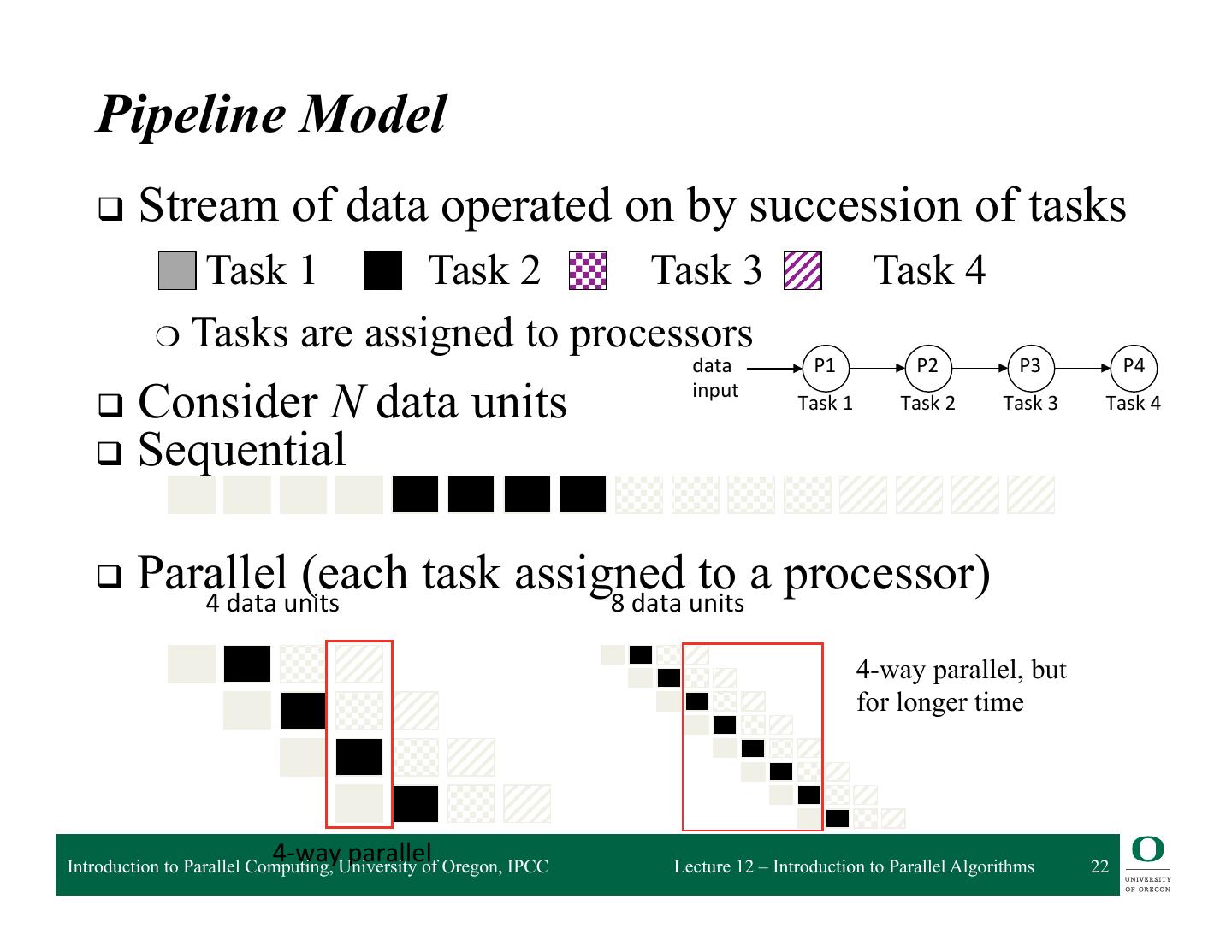
22 . Pipeline Model q  Stream of data operated on by succession of tasks Task 1 Task 2 Task 3 Task 4 ❍  Tasks are assigned to processors data   P1   P2   P3   P4   q  Consider N data units input   Task  1   Task  2   Task  3   Task  4   q  Sequential q  Parallel (each task assigned to a processor) 4  data  units   8  data  units     4-way parallel, but for longer time   4-­‐way  parallel   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 22 

23 . Pipeline Performance q  N data and T tasks q  Each task takes unit time t q  Sequential time = N*T*t q  Parallel pipeline time = start + finish + (N-2T)/T * t = O(N/T) (for N>>T) q  Try to find a lot of data to pipeline q  Try to divide computation in a lot of pipeline tasks ❍  More tasks to do (longer pipelines) ❍  Shorter tasks to do q  Pipeline computation is a special form of producer-consumer parallelism ❍  Producer tasks output data input by consumer tasks Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 23 

24 . Tasks Graphs q  Computations in any parallel algorithms can be viewed as a task dependency graph q  Task dependency graphs can be non-trivial Task  1   Task  2   Task  3   Task  4   ❍  Pipeline ❍  Arbitrary (represents the algorithm dependencies) Numbers are time taken to perform task Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 24 

25 . Task Graph Performance q  Determined by the critical path (span) ❍  Sequence of dependent tasks that takes the longest time Min time = 27 Min time = 34 ❍  Critical path length bounds parallel execution time Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 25 

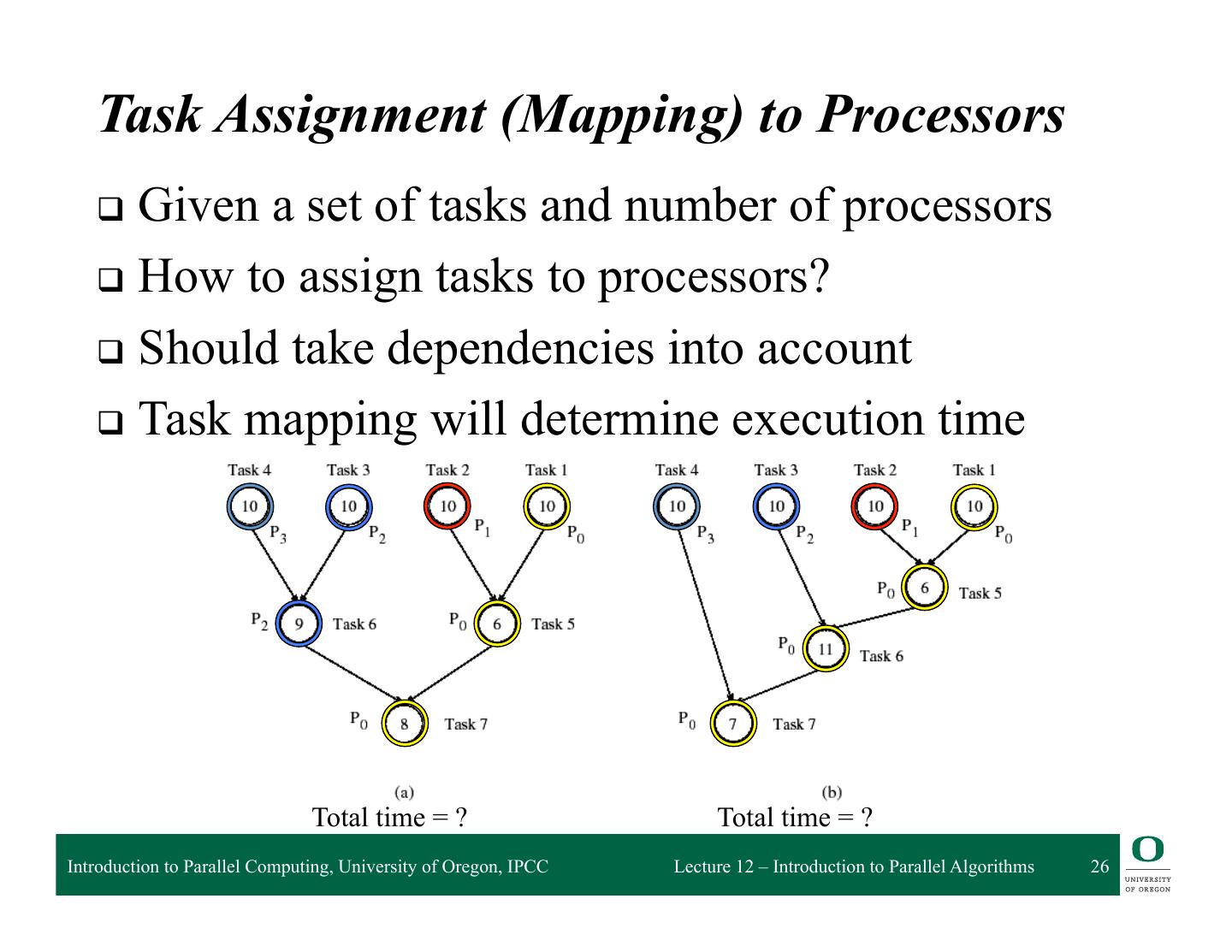
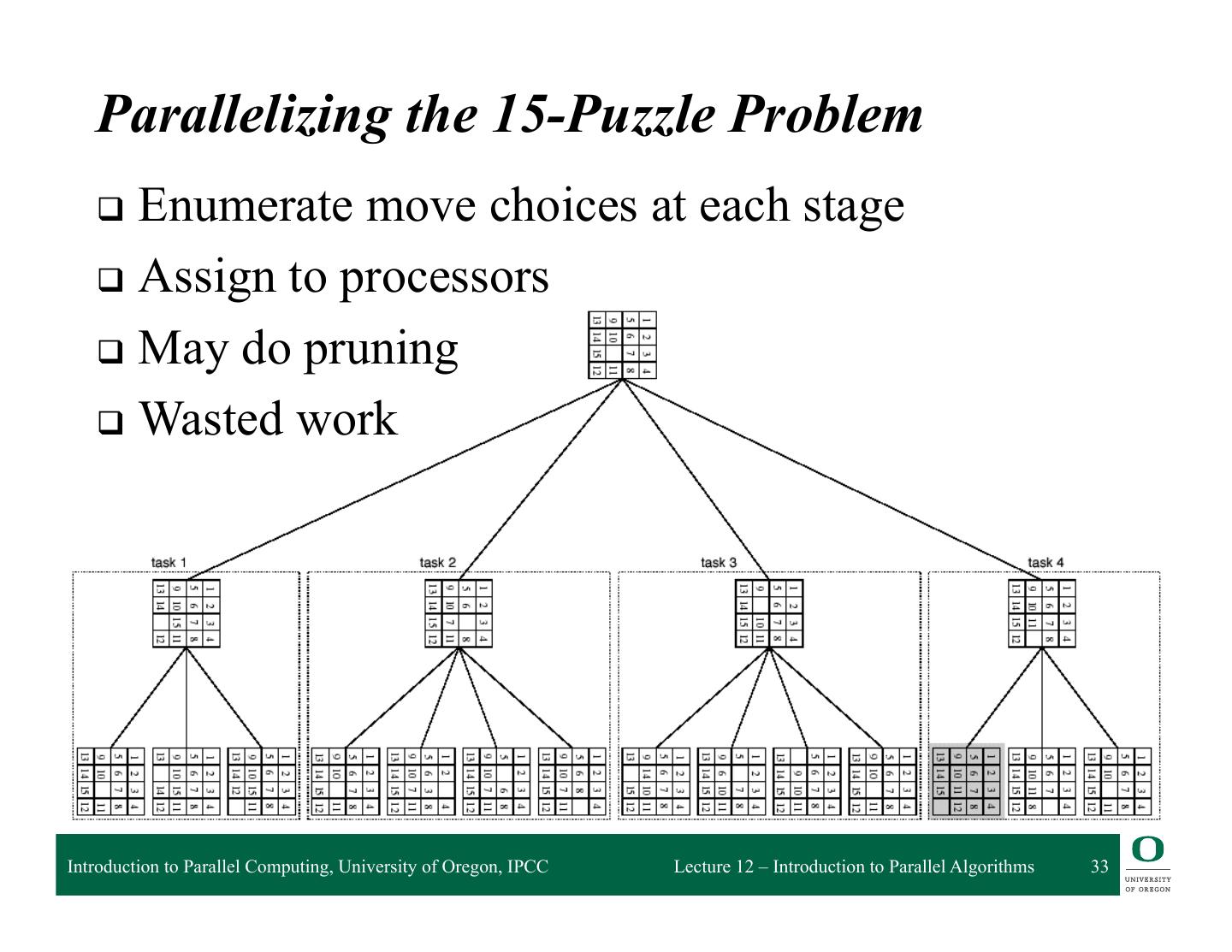
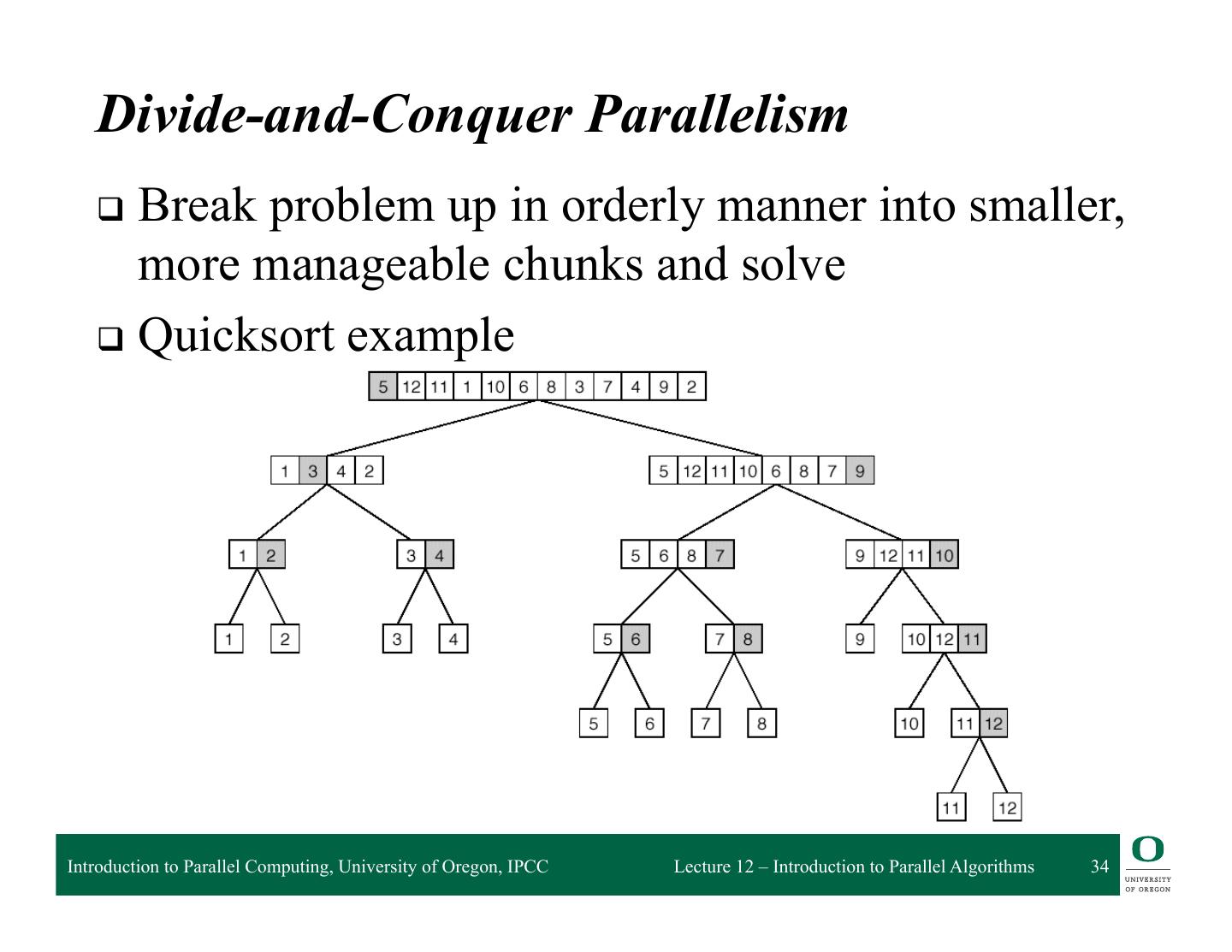
26 . Task Assignment (Mapping) to Processors q  Given a set of tasks and number of processors q  How to assign tasks to processors? q  Should take dependencies into account q  Task mapping will determine execution time Total time = ? Total time = ? Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 26 

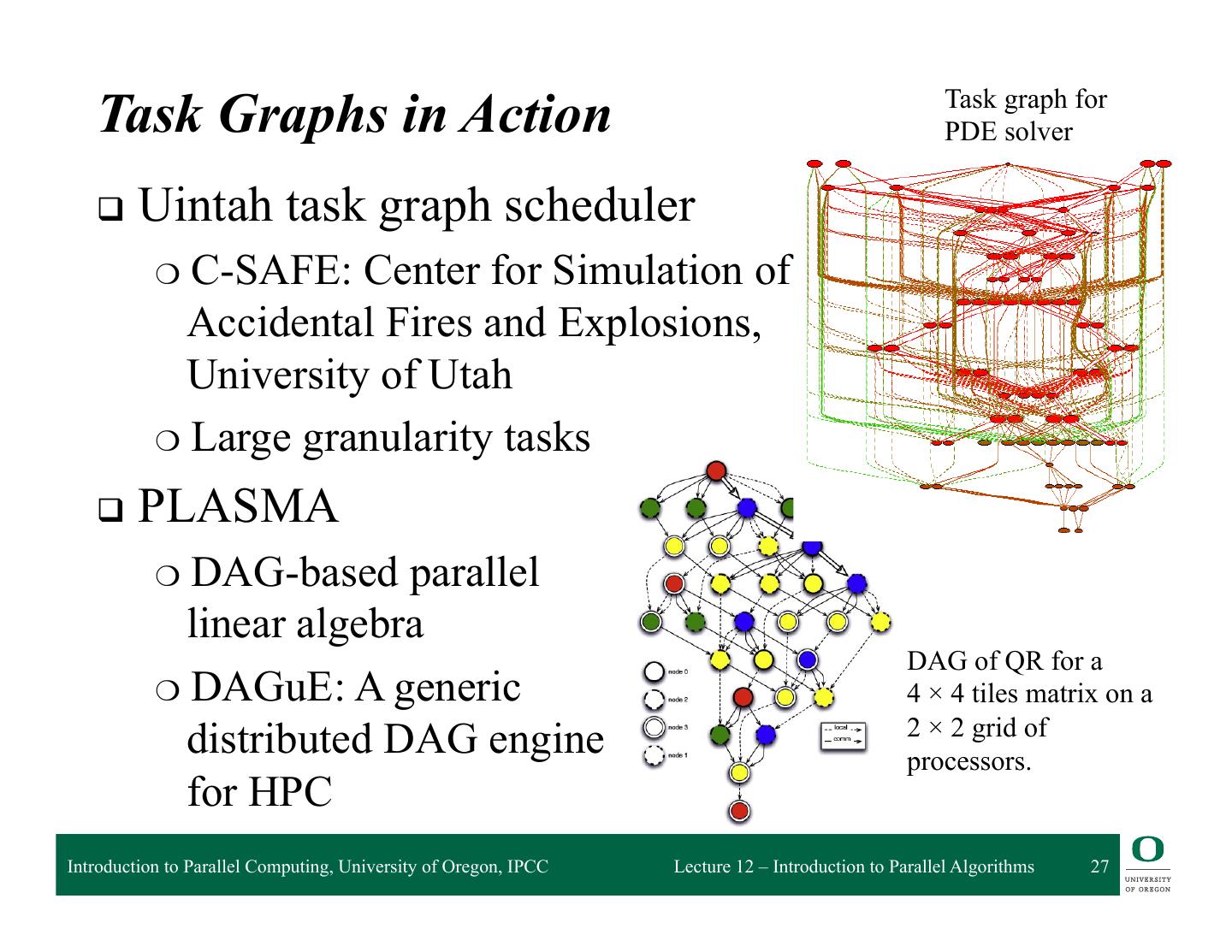
27 . Uintah Taskgraph basedTask PDE Solver Task Graphs in Action graph for PDE solver q  Uintah task graph scheduler V. ❍  C-SAFE: Center for Simulation of L. Accidental Fires and Explosions, S University of Utah K. ❍  Large granularity tasks J. An q  PLASMA ❍  DAG-based parallel Wasatch Taskgraph linear algebra DAG of QR for a ❍  DAGuE: A generic 4 × 4 tiles matrix on a 2 × 2 grid of distributed DAG engine processors. for HPC Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 27 

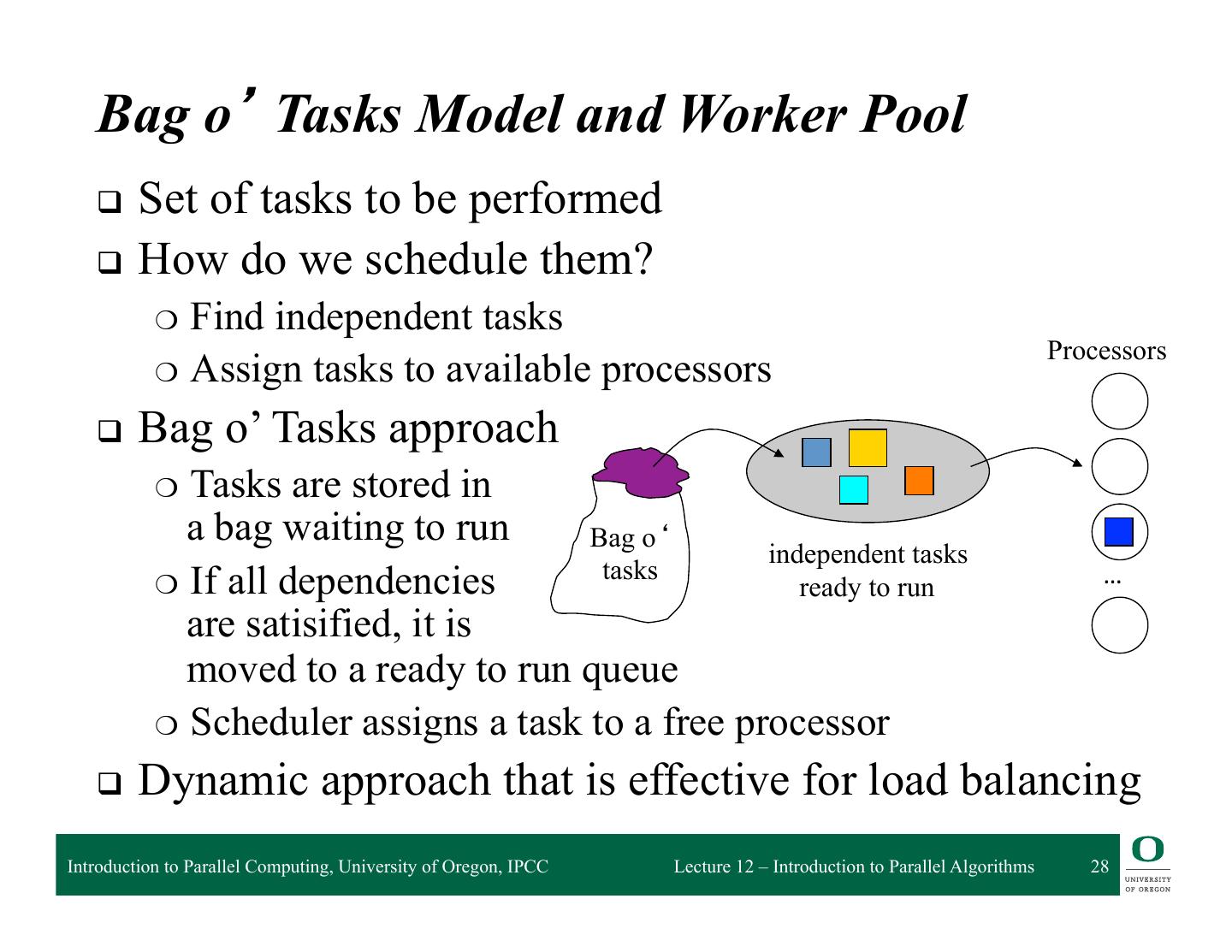
28 . Bag o’ Tasks Model and Worker Pool q  Set of tasks to be performed q  How do we schedule them? ❍  Find independent tasks Processors ❍  Assign tasks to available processors q  Bag o’ Tasks approach ❍  Tasks are stored in a bag waiting to run Bag o‘ independent tasks tasks …   ❍  If all dependencies ready to run are satisified, it is moved to a ready to run queue ❍  Scheduler assigns a task to a free processor q  Dynamic approach that is effective for load balancing Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 28 

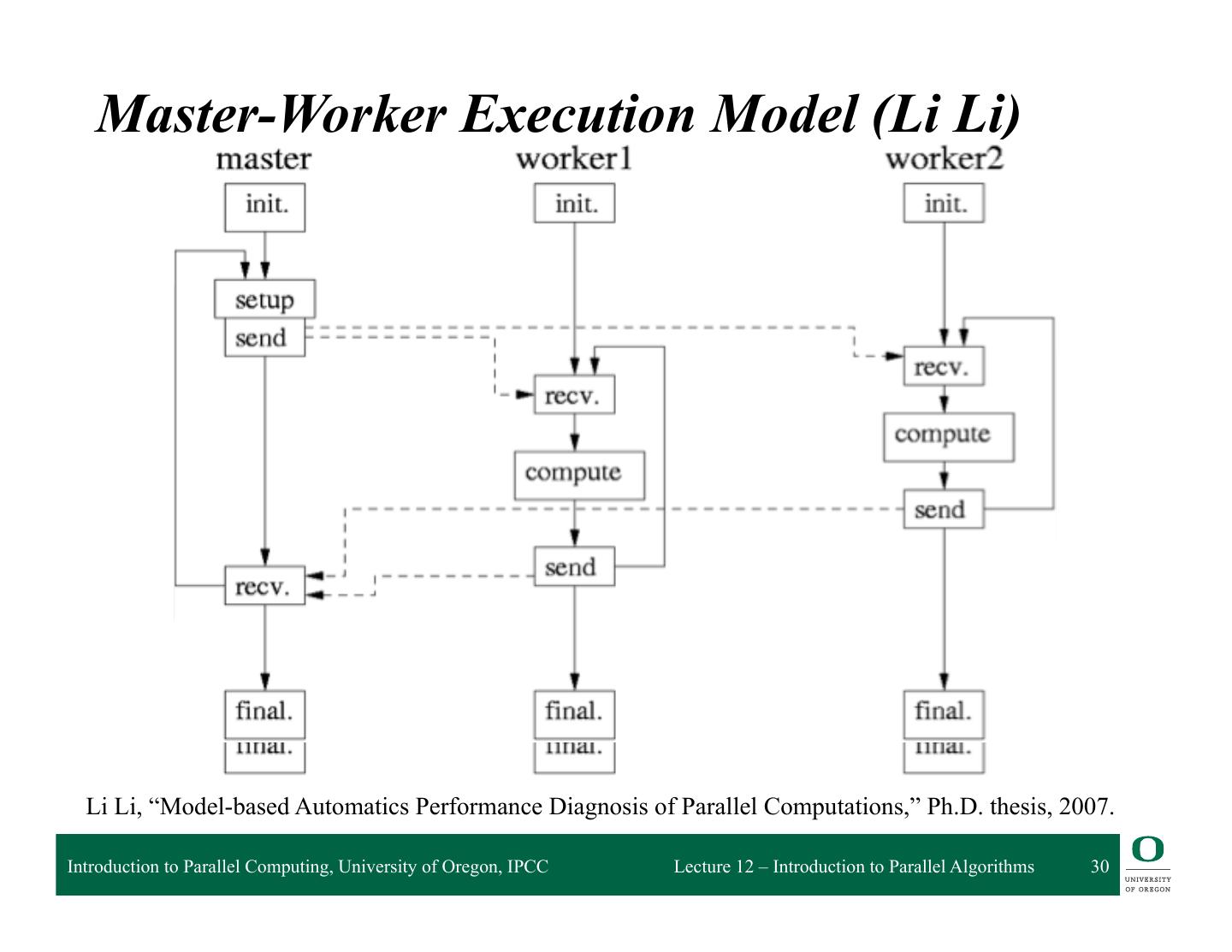
29 . Master-Worker Parallelism q  One or more master processes generate work q  Masters allocate work to worker processes q  Workers idle if have nothing to do q  Workers are mostly stupid and must be told what to do ❍  Execute independently ❍  May need to synchronize, but most be told to do so q  Master may become the bottleneck if not careful q  What are the performance factors and expected performance behavior ❍  Consider task granularity and asynchrony ❍  How do they interact? Introduction to Parallel Computing, University of Oregon, IPCC Lecture 12 – Introduction to Parallel Algorithms 29