8-Stencil Pattern

1 . Stencil Pattern Parallel Computing CIS 410/510 Department of Computer and Information Science Lecture 8 – Stencil Pattern 

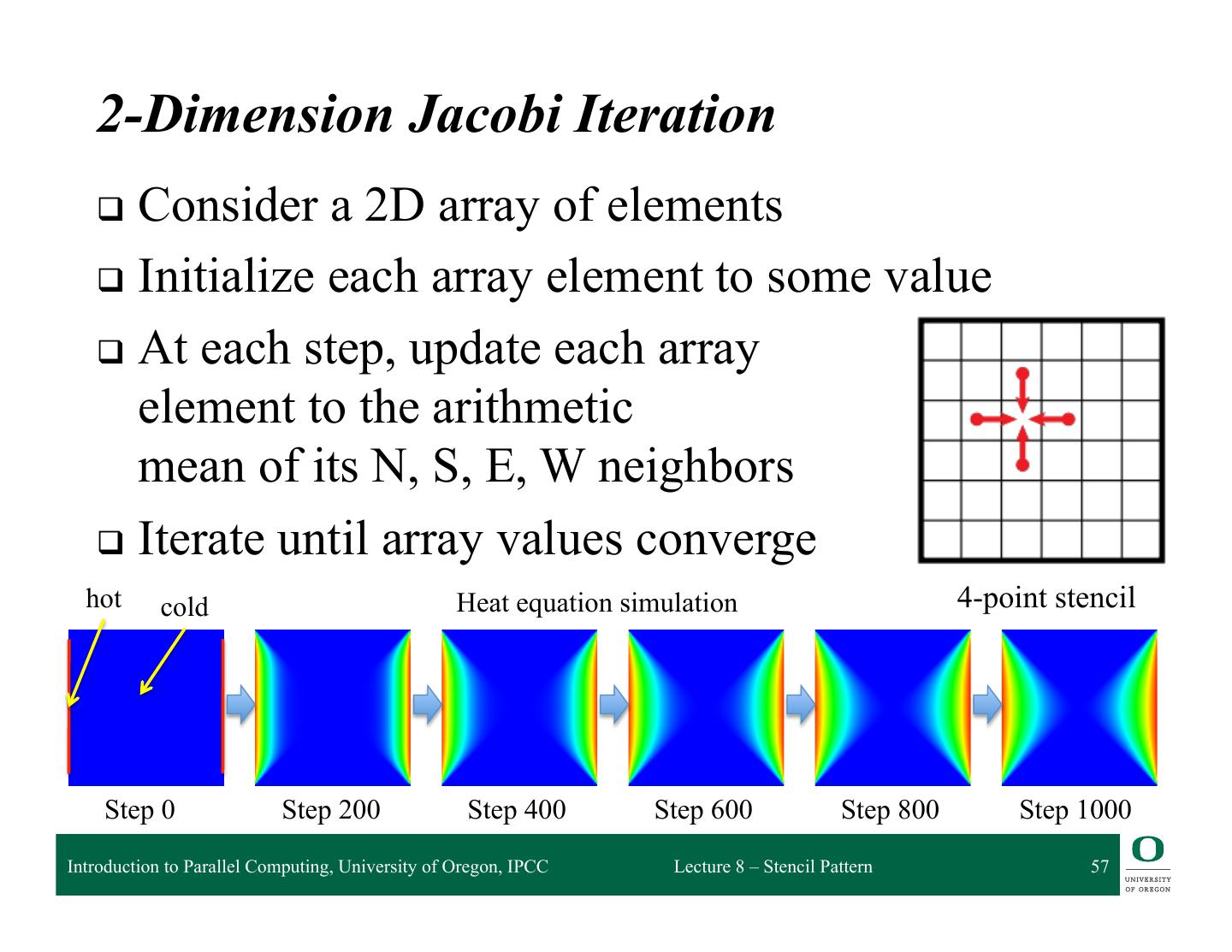
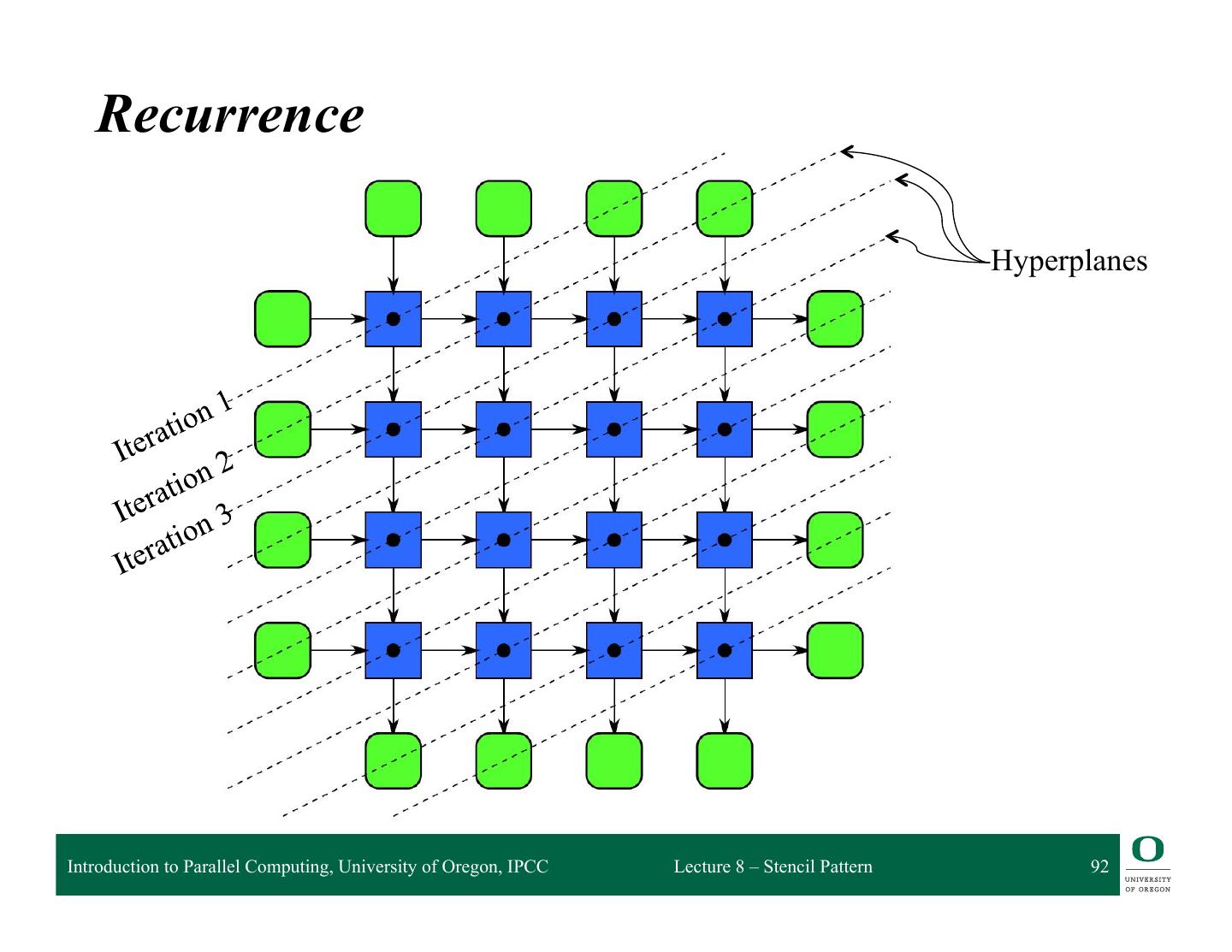
2 . Outline q  Partitioning q  What is the stencil pattern? ❍  Update alternatives ❍  2D Jacobi iteration ❍  SOR and Red/Black SOR q  Implementing stencil with shift q  Stencil and cache optimizations q  Stencil and communication optimizations q  Recurrence Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 2 

3 . we ensure that the instance has exclusive access to that section, then within the partition serial scatter patterns, such as random writes, can be used without problems with race conditions. It is also possible torights ect the applyof thethe pattern author(s) recursively, and publisher we inform yousubdividing a section that this PDF is an uncorrected into proof subsections for internal forbynested business use only parallelism. the author(s), editor(s), er(s), Elsevier and typesetter diacriTech. It is not allowed to publish this proof online or in print. This proof copy is the copyright property of the publisher This can Partitioning be a until good way to map a problem onto hierarchically organized parallel hardware. confidential formal publication. McCool — e9780124159938 — 2012/6/6 — 23:09 — Page 192 — #192 192 q CHAPTER 6 Data Reorganization 1D FIGURE 6.16 Partitioning. Data is divided into non-overlapping, equal-sized regions. 2D FIGURE 6.17 q  Data is divided into Partitioning in 2D. The partition pattern can be extended to multiple dimensions. non-overlapping regions (avoid write conflicts, race conditions) ❍  ❍  equal-sized regions (improve load balancing) These diagrams show only the simplest case, where the sections of the partition fit exactly into the domain. In practice, there may be boundary conditions where partial sections are required along the edges. These may need to be treated with special-purpose code, but even in this case the majority of Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 3 the sections will be regular, which lends itself to vectorization. Ideally, to get good memory behavior and to allow efficient vectorization, we also normally want to partition data, especially for writes, so that it aligns with cache line and vectorization boundaries. You should be aware of how data is actually 

4 . we ensure that the instance has exclusive access to that section, then within the partition serial scatter patterns, such as random writes, can be used without problems with race conditions. It is also possible torights ect the applyof thethe pattern author(s) recursively, and publisher we inform yousubdividing a section that this PDF is an uncorrected into proof subsections for internal forbynested business use only parallelism. the author(s), editor(s), er(s), Elsevier and typesetter diacriTech. It is not allowed to publish this proof online or in print. This proof copy is the copyright property of the publisher This can Partitioning be a until good way to map a problem onto hierarchically organized parallel hardware. confidential formal publication. McCool — e9780124159938 — 2012/6/6 — 23:09 — Page 192 — #192 192 q CHAPTER 6 Data Reorganization 1D FIGURE 6.16 Partitioning. Data is divided into non-overlapping, equal-sized regions. 2D 3D FIGURE 6.17 q  Data is divided into Partitioning in 2D. The partition pattern can be extended to multiple dimensions. non-overlapping regions (avoid write conflicts, race conditions) ❍  ❍  equal-sized regions (improve load balancing) These diagrams show only the simplest case, where the sections of the partition fit exactly into the domain. In practice, there may be boundary conditions where partial sections are required along the edges. These may need to be treated with special-purpose code, but even in this case the majority of Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 4 the sections will be regular, which lends itself to vectorization. Ideally, to get good memory behavior and to allow efficient vectorization, we also normally want to partition data, especially for writes, so that it aligns with cache line and vectorization boundaries. You should be aware of how data is actually 

5 . Outline q  Partitioning q  What is the stencil pattern? ❍  Update alternatives ❍  2D Jacobi iteration ❍  SOR and Red/Black SOR q  Implementing stencil with shift q  Stencil and cache optimizations q  Stencil and communication optimizations q  Recurrence Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 5 

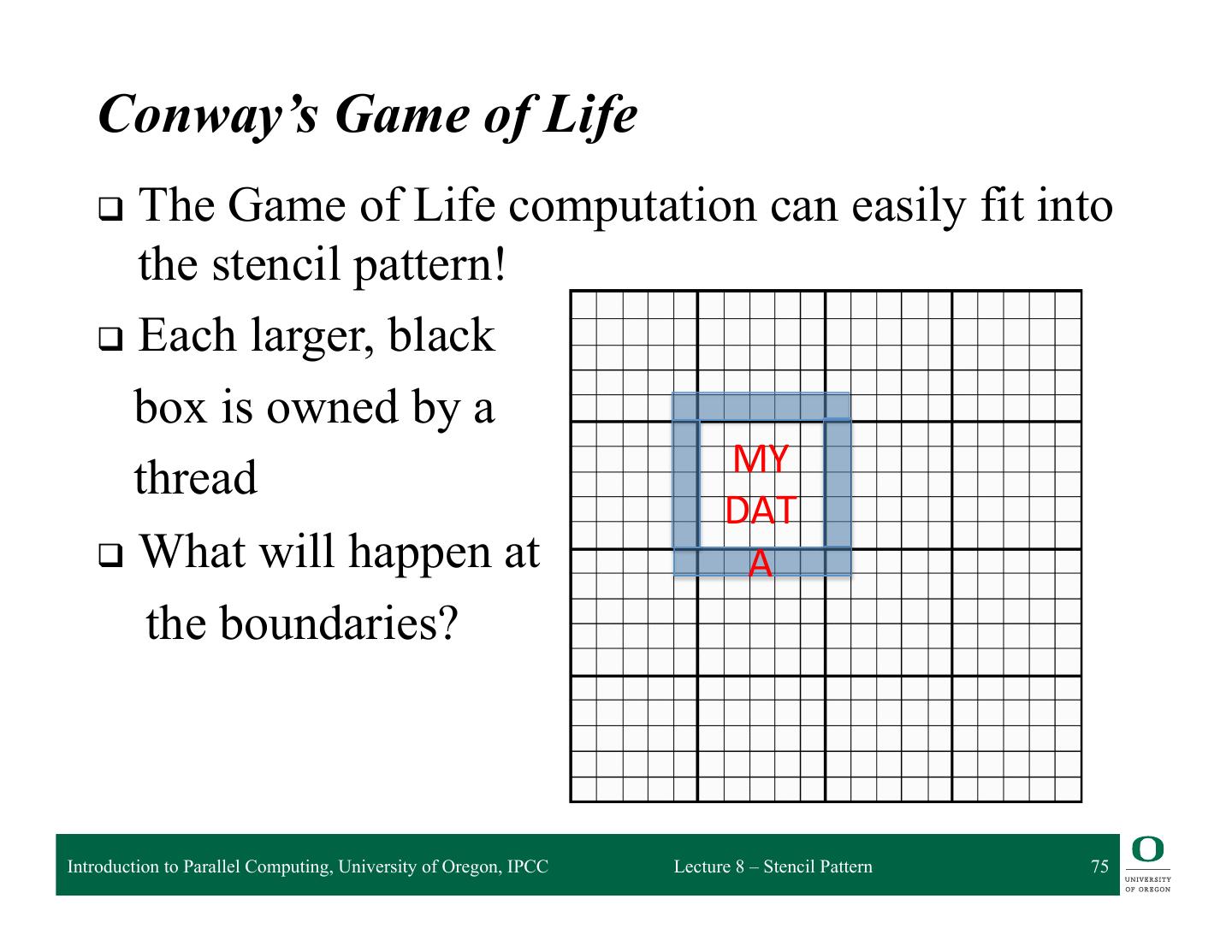
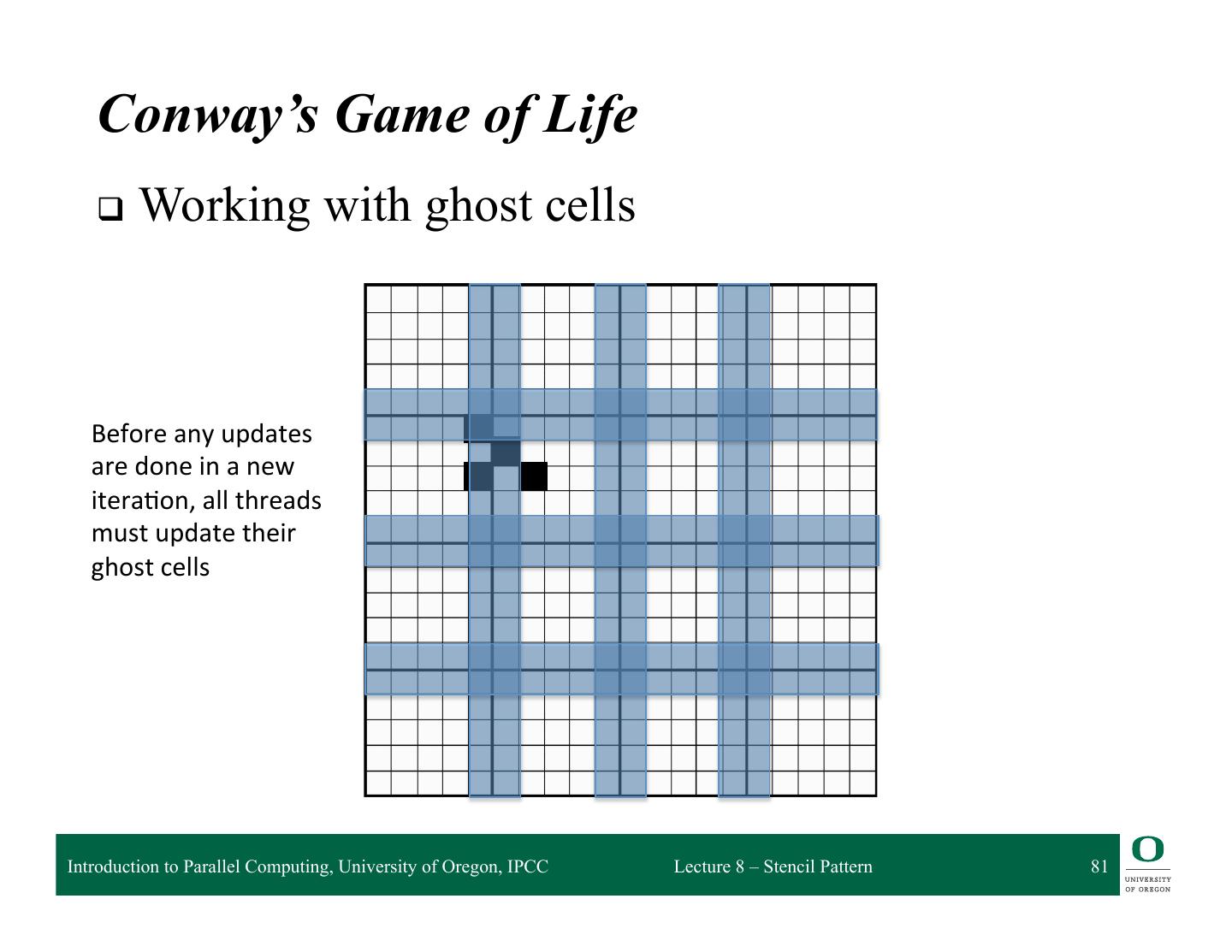
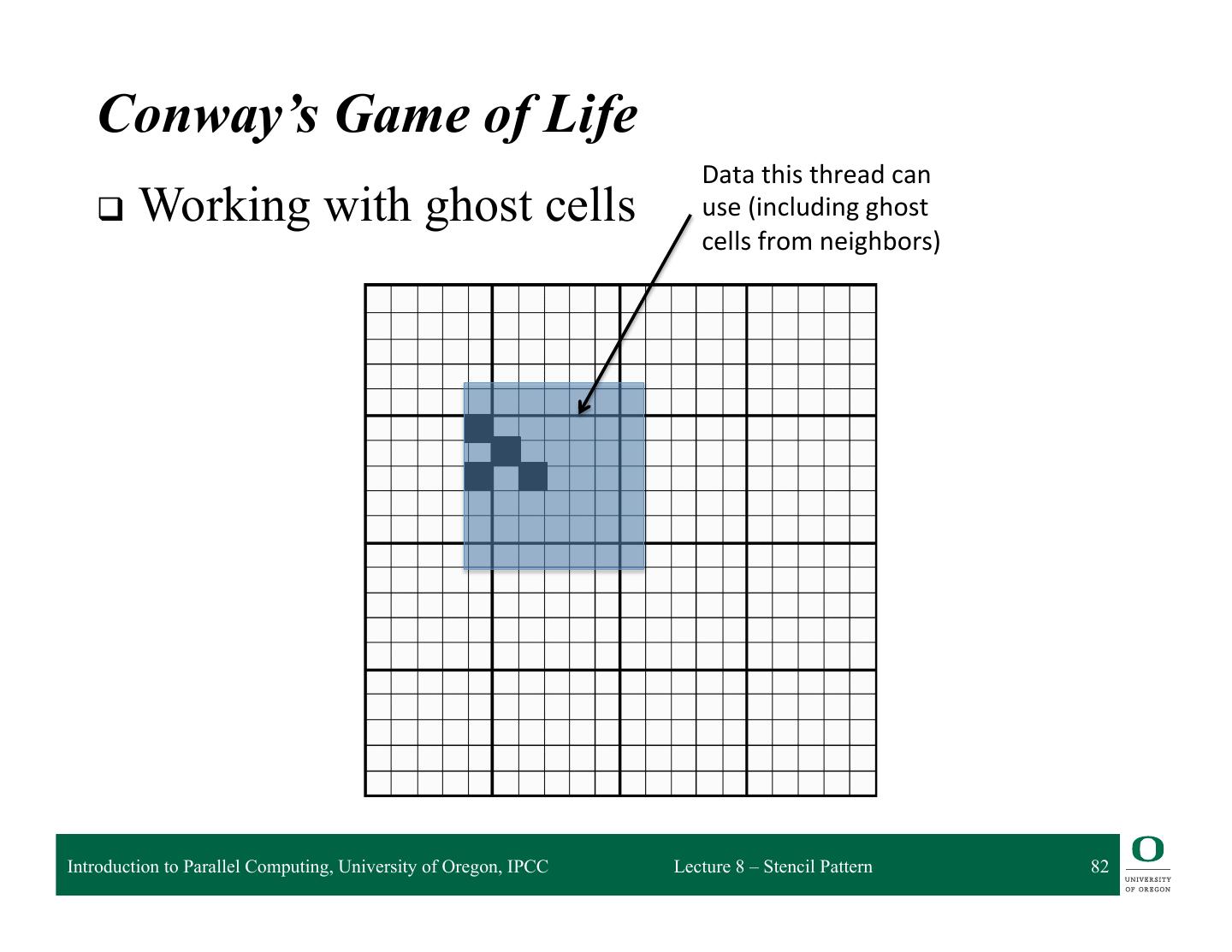
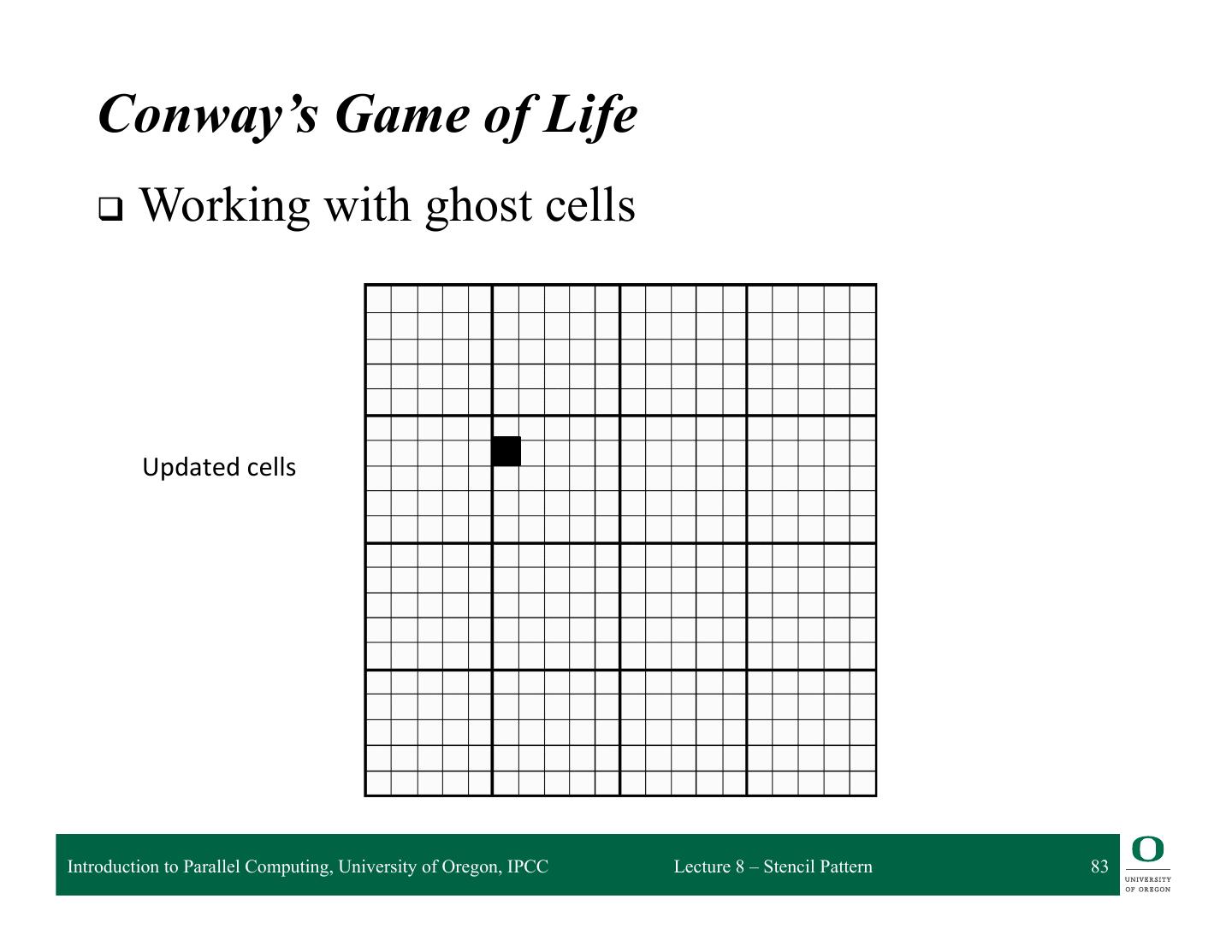
6 . Stencil Pattern q  A stencil pattern is a map where each output depends on a “neighborhood” of inputs q  These inputs are a set of fixed offsets relative to the output position q  A stencil output is a function of a “neighborhood” of elements in an input collection ❍  Applies the stencil to select the inputs q  Data access patterns of stencils are regular ❍  Stencil is the “shape” of “neighborhood” ❍  Stencil remains the same Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 6 

7 . Serial Stencil Example (part 1) Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 7 

8 . Serial Stencil Example (part 2) How would we parallelize this? Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 8 

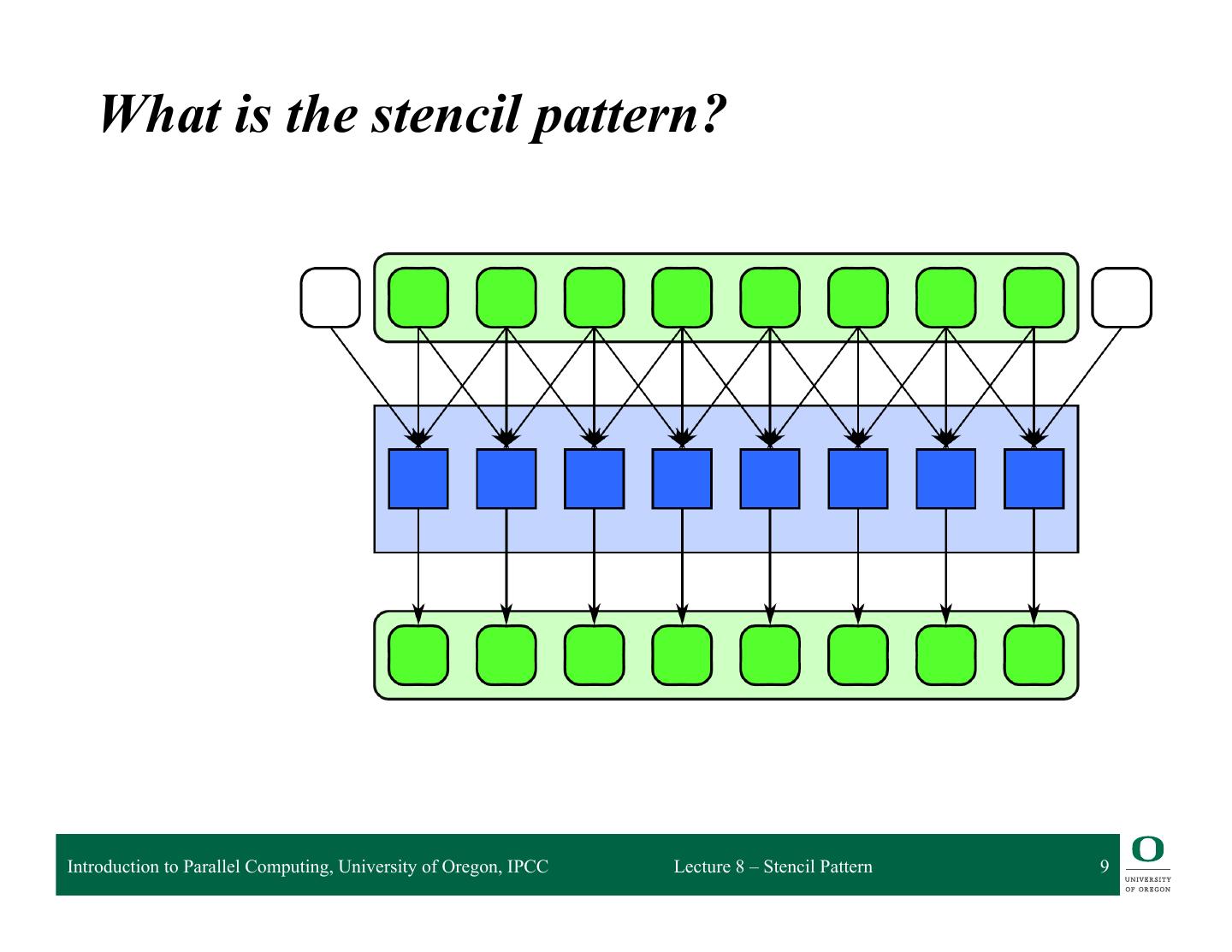
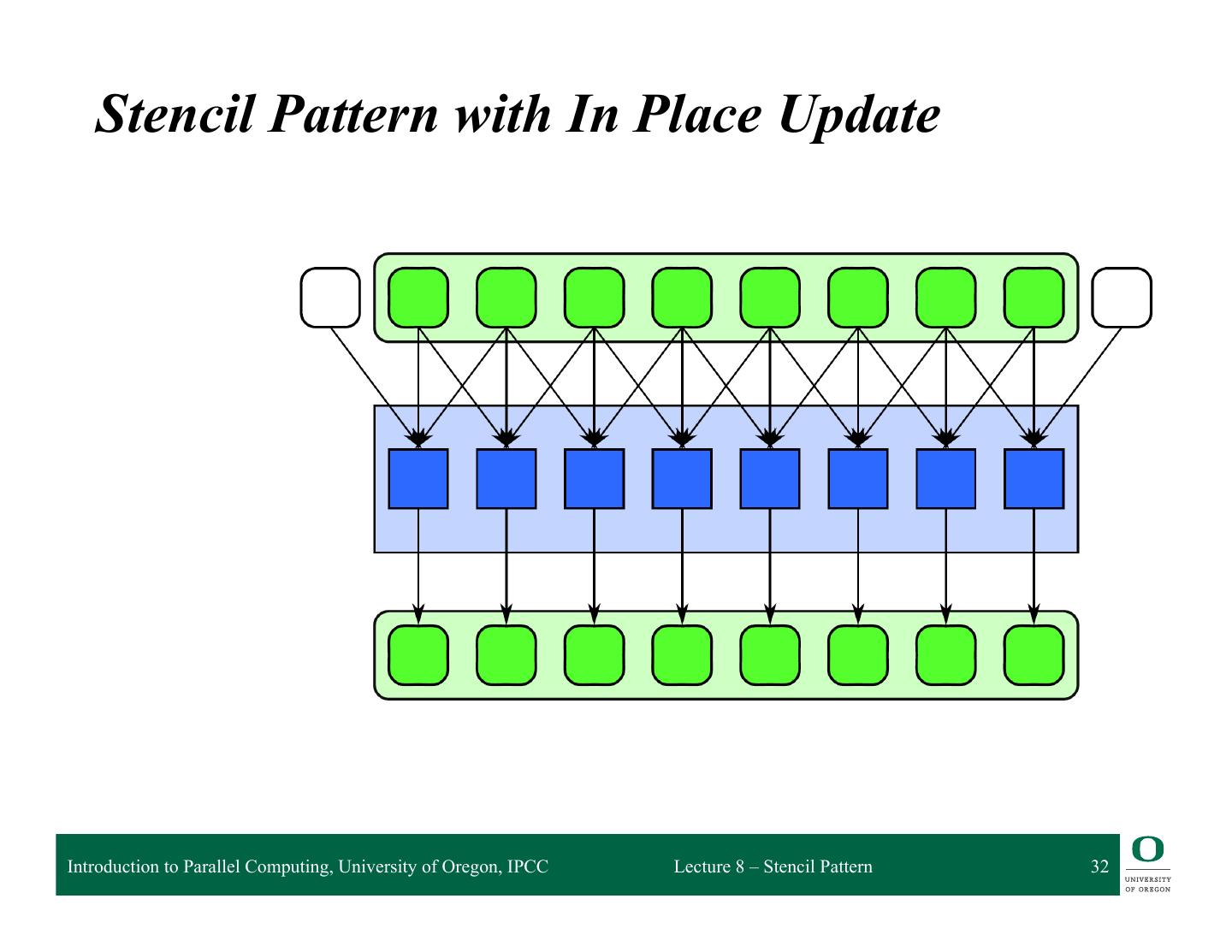
9 . What is the stencil pattern? Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 9 

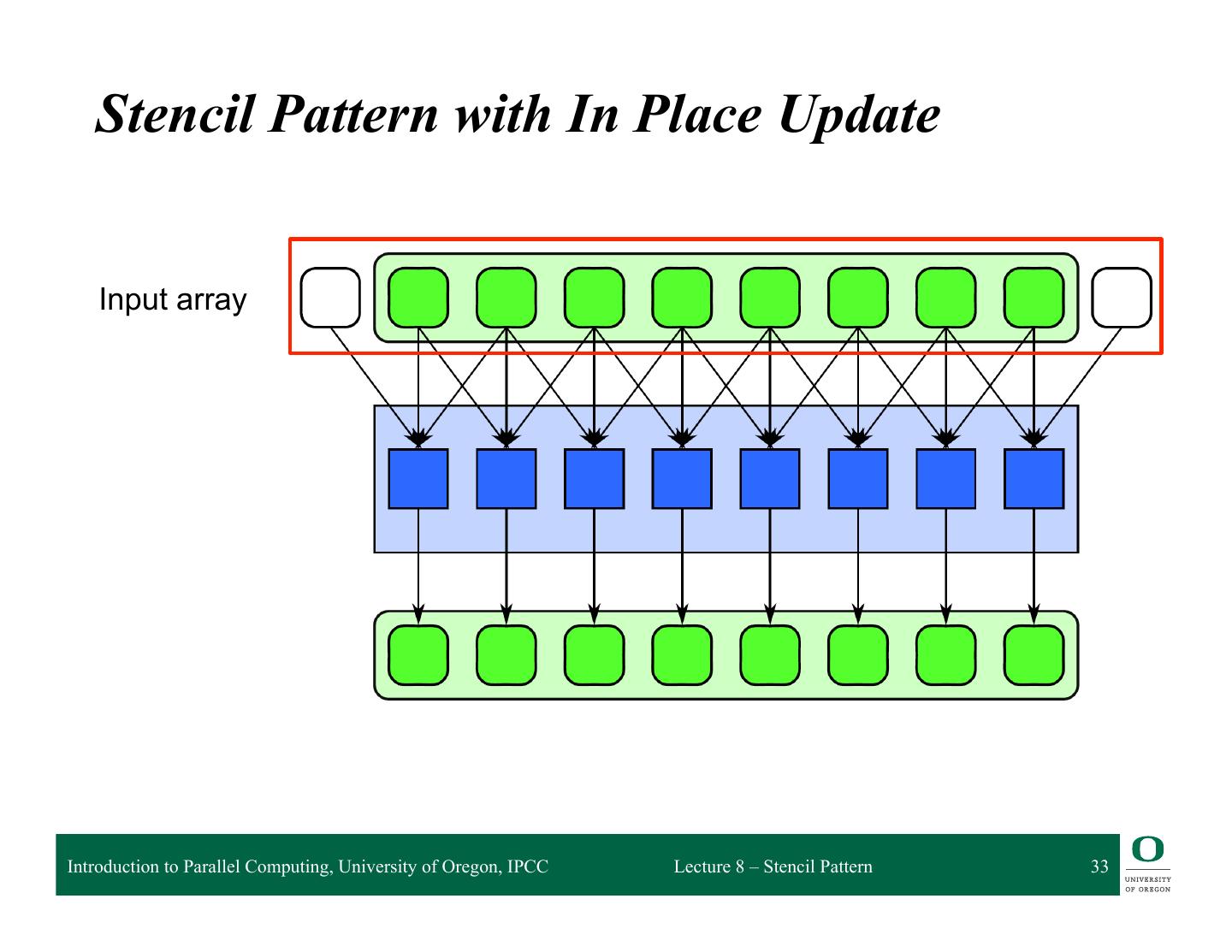
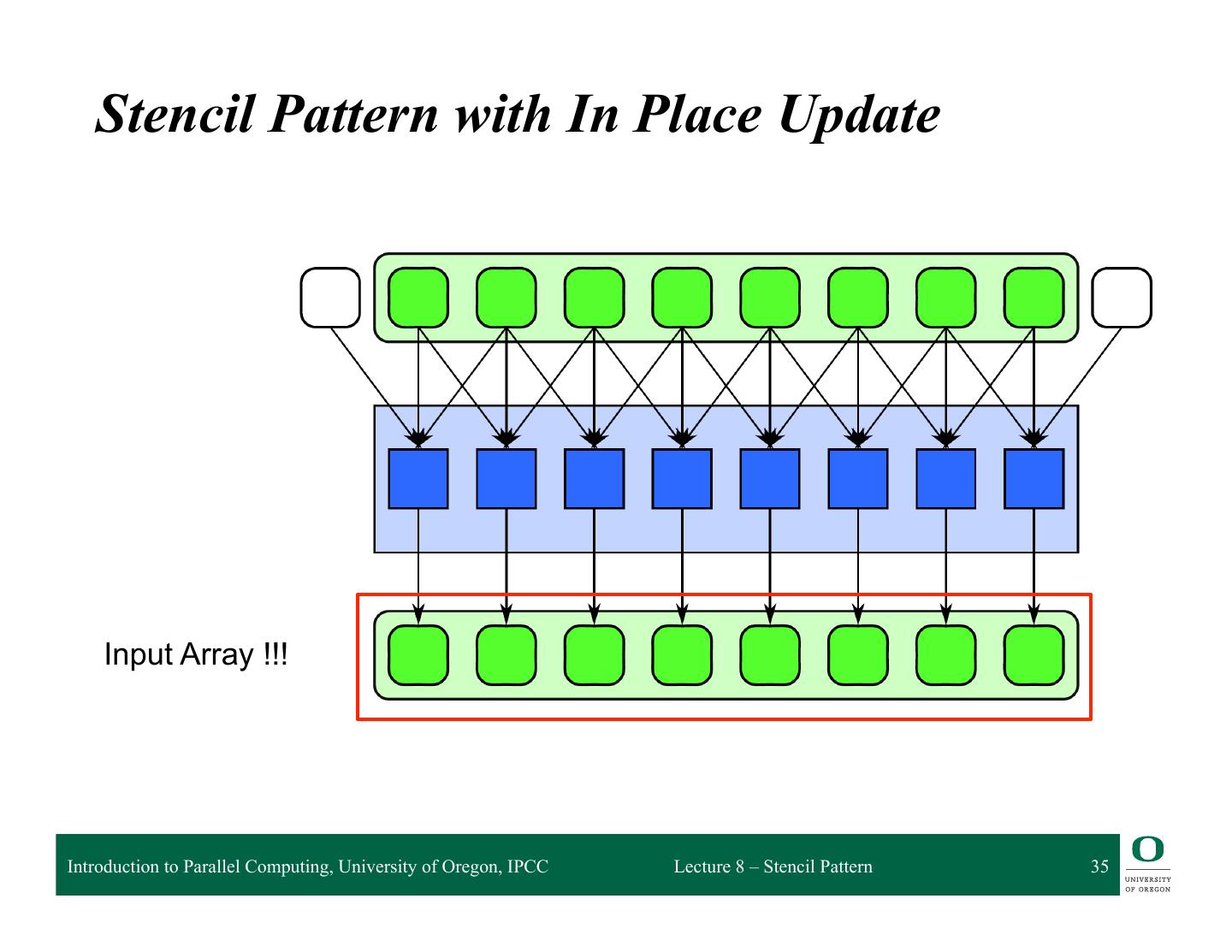
10 . What is the stencil pattern? Input array Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 10 

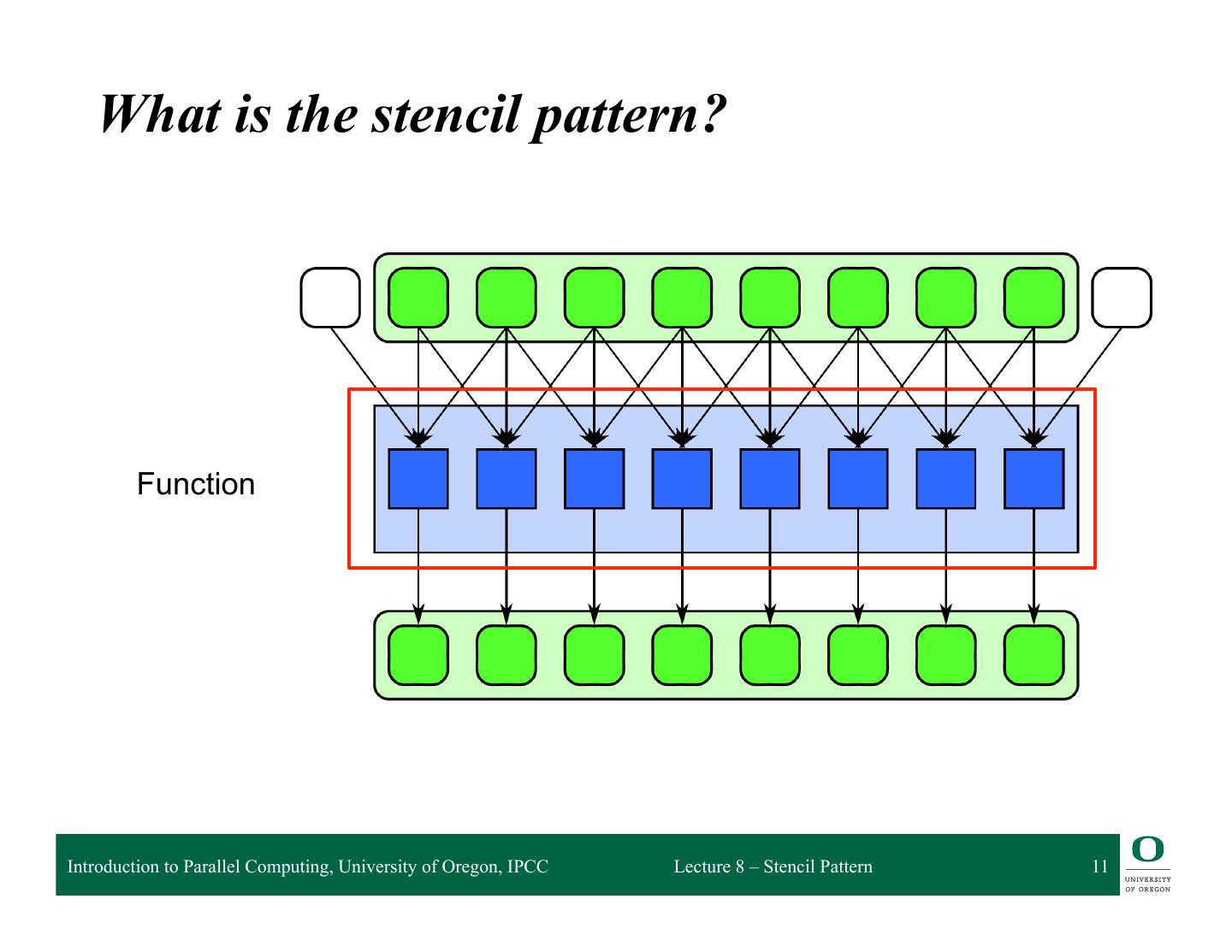
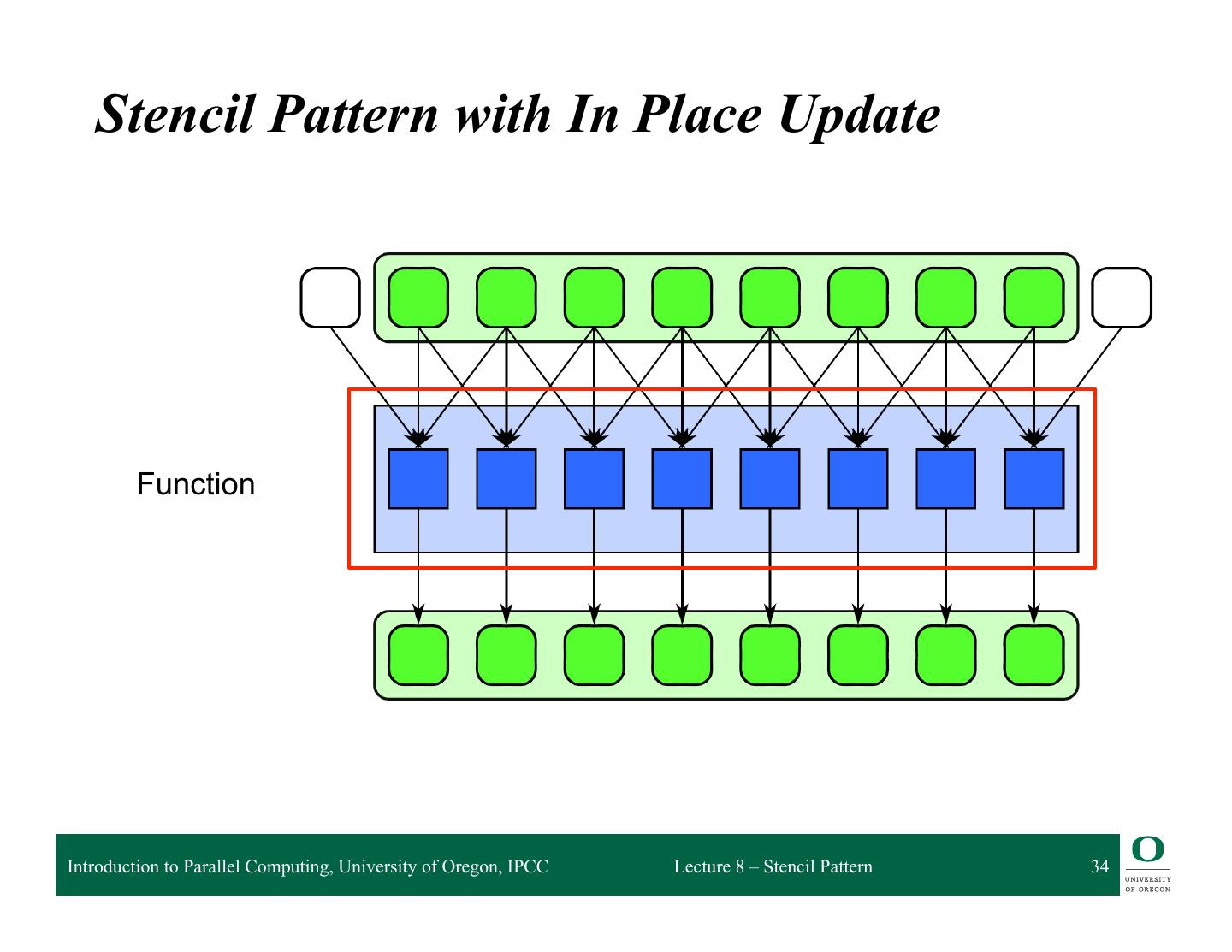
11 . What is the stencil pattern? Function Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 11 

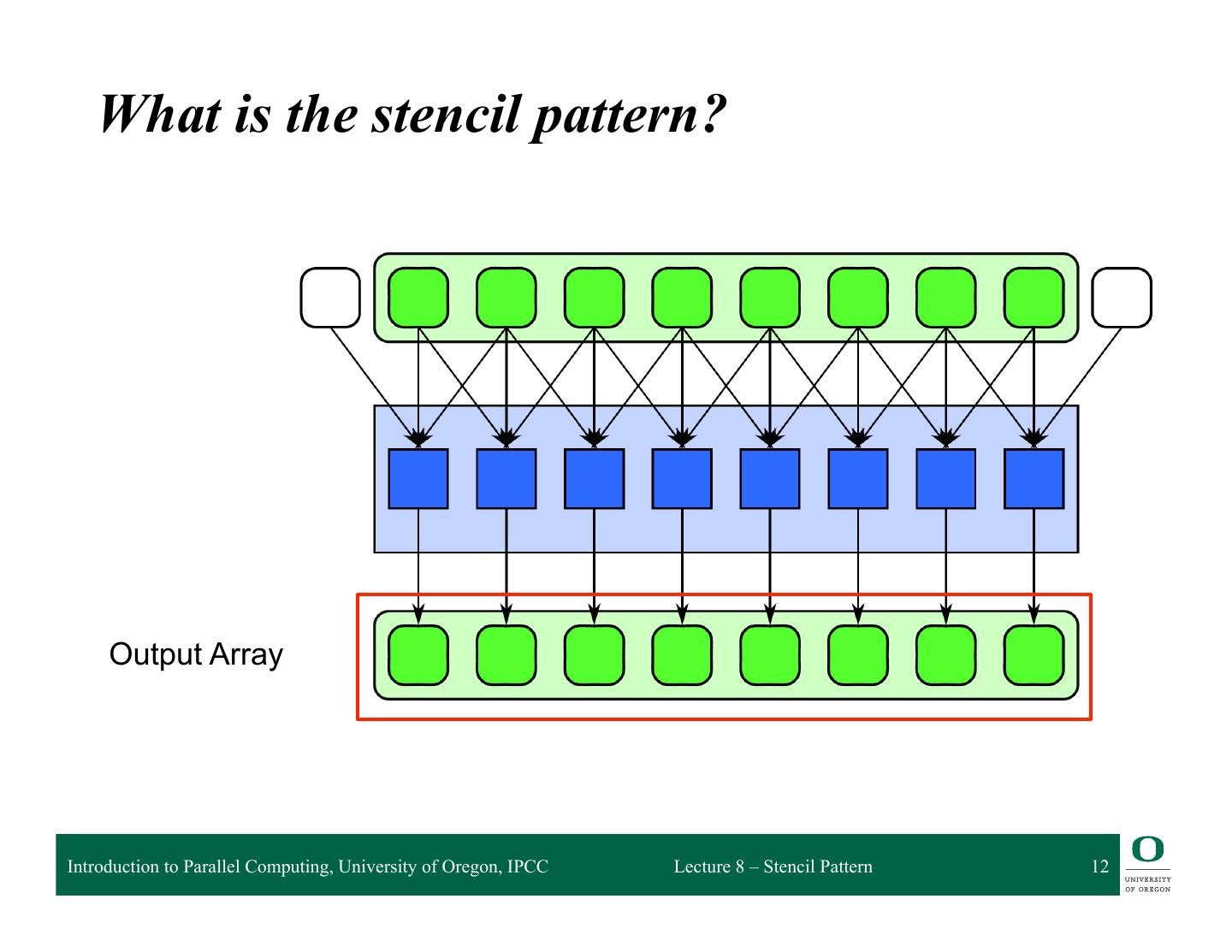
12 . What is the stencil pattern? Output Array Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 12 

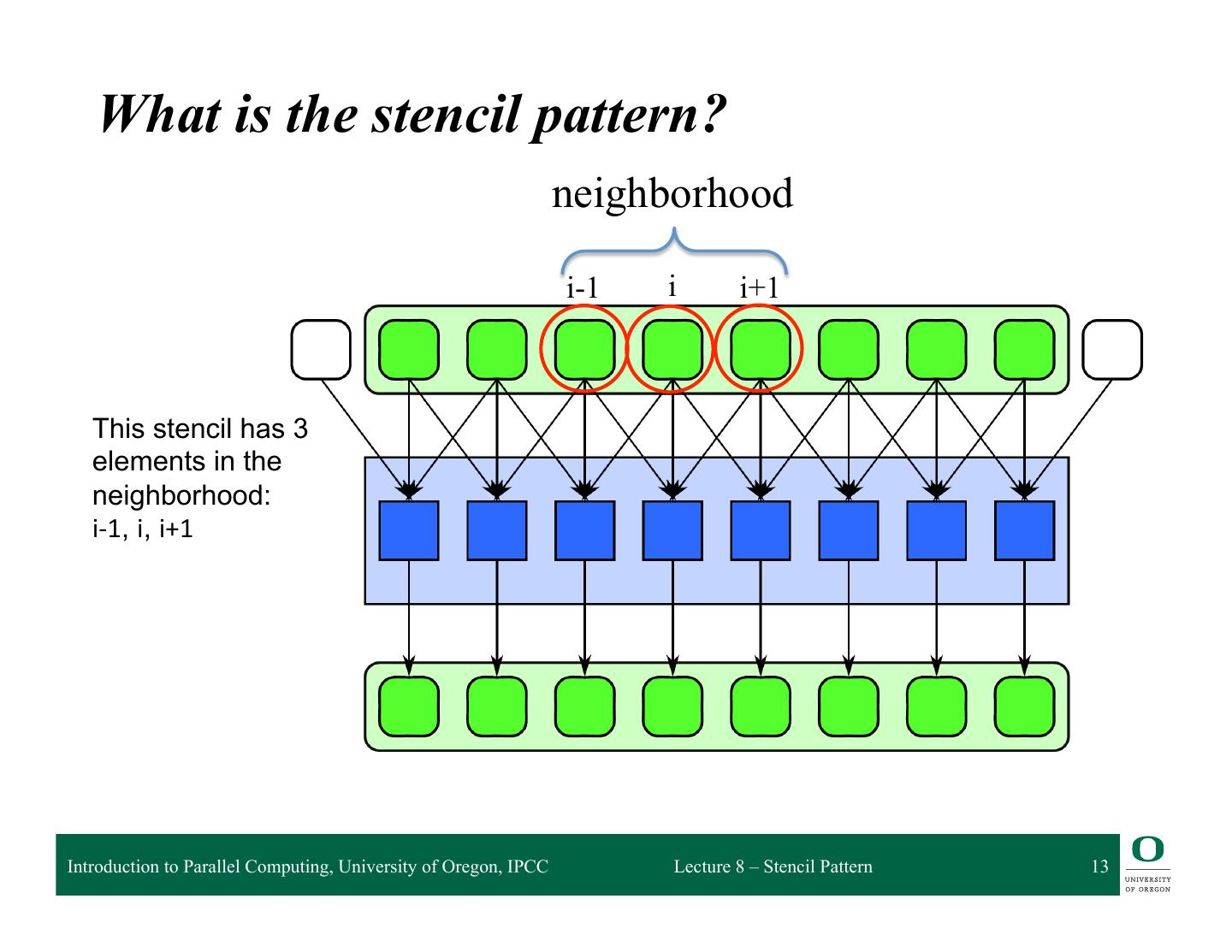
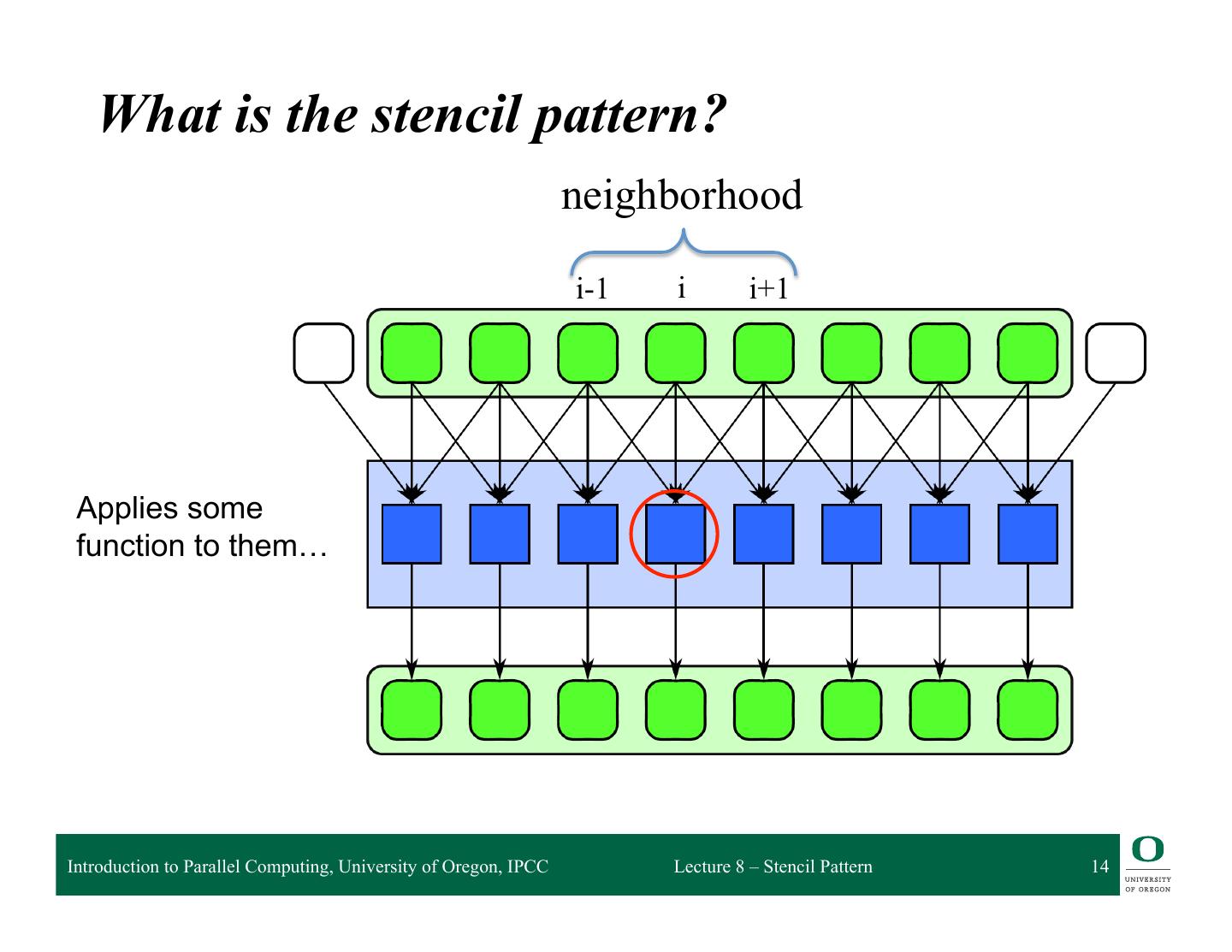
13 . What is the stencil pattern? neighborhood i-1 i i+1 This stencil has 3 elements in the neighborhood: i-­‐1, i, i+1 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 13 

14 . What is the stencil pattern? neighborhood i-1 i i+1 Applies some function to them… Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 14 

15 . What is the stencil pattern? And outputs to the ith position of the output array Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 15 

16 . Stencil Patterns q  Stencils can operate on one dimensional and multidimensional data q  Stencil neighborhoods can range from compact to sparse, square to cube, and anything else! q  It is the pattern of the stencil that determines how the stencil operates in an application Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 16 

17 . 2-Dimensional Stencils 4-point stencil 5-point stencil 9-point stencil Center cell (P) Center cell (P) Center cell (C) is not used is used as well is used as well Source:  h.p://en.wikipedia.org/wiki/Stencil_code   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 17 

18 . 3-Dimensional Stencils 6-point stencil (7-point stencil) 24-point stencil (25-point stencil) Source:  h.p://en.wikipedia.org/wiki/Stencil_code   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 18 

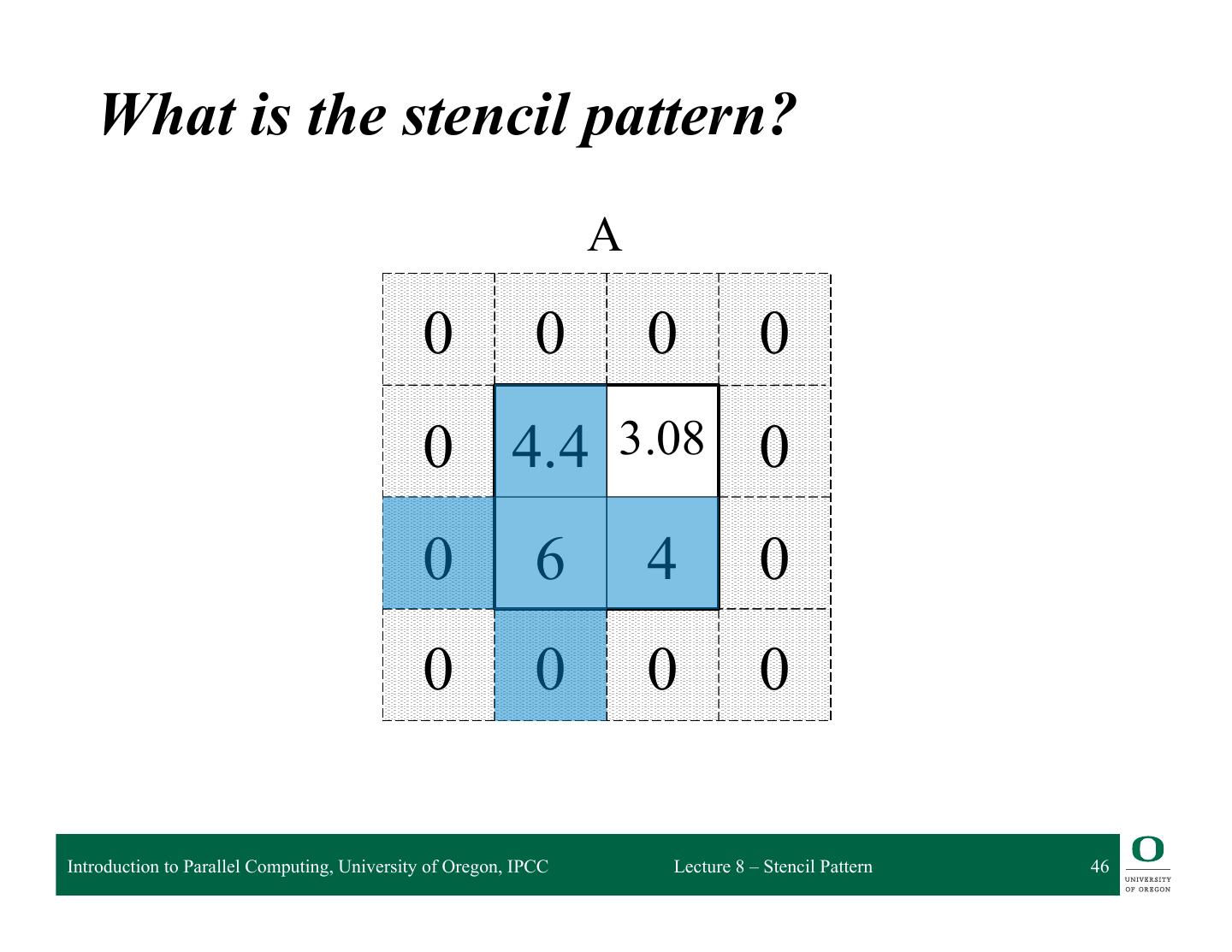
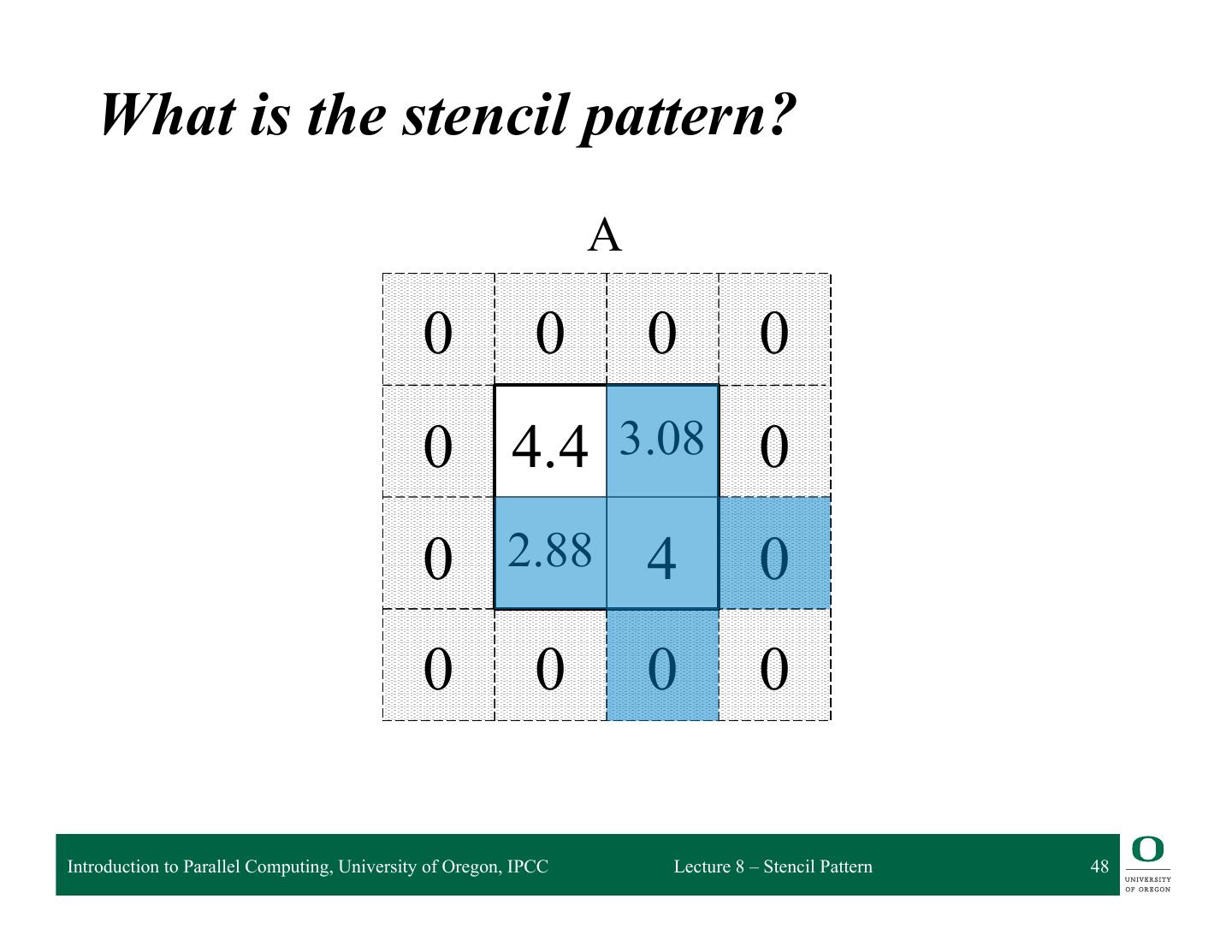
19 . Stencil Example A •  Here is our array, A 0 0 0 0 0 9 7 0 0 6 4 0 0 0 0 0 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 19 

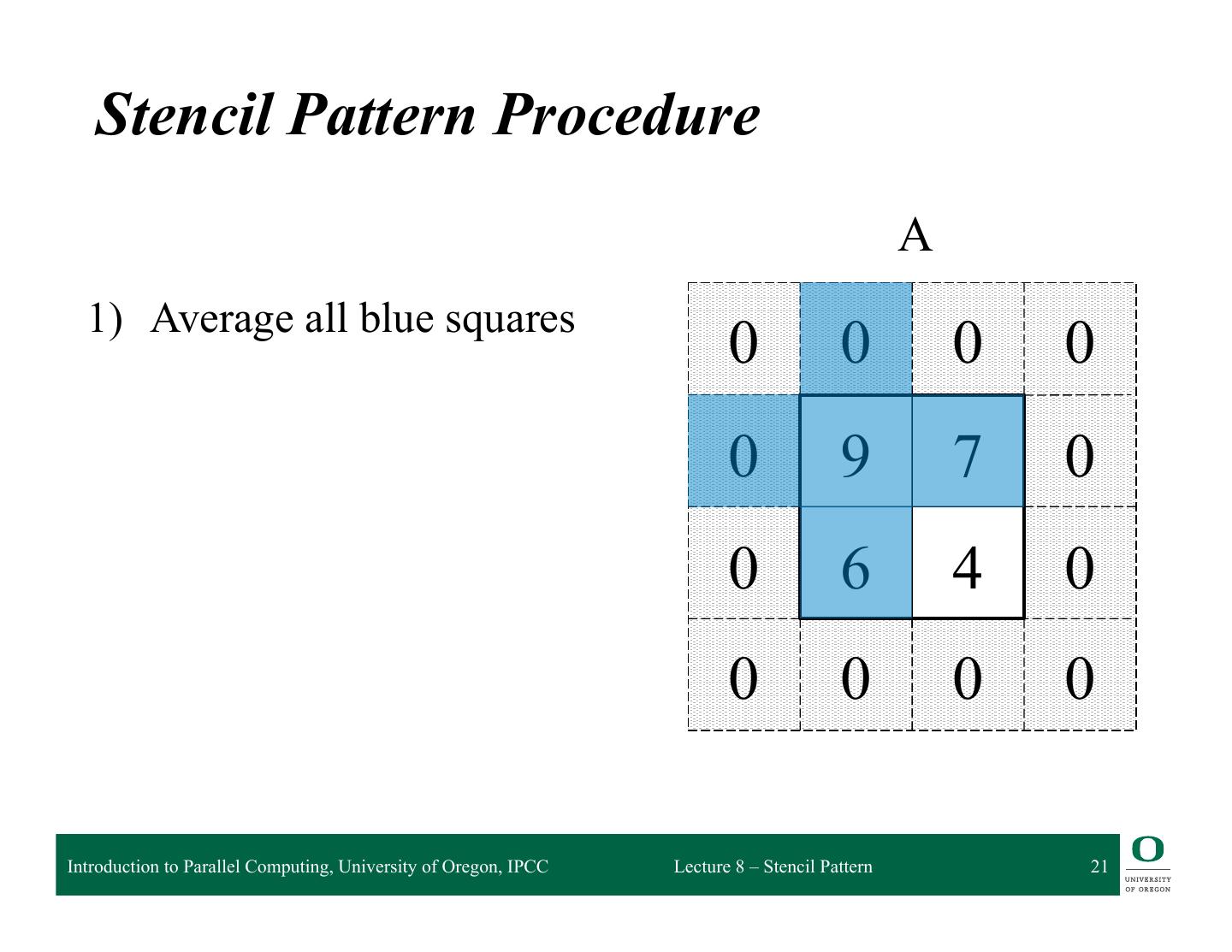
20 . Stencil Example A •  Here is our array A •  B is the output array 0 0 0 0 –  Initialize to all 0 0 9 7 0 •  Apply a stencil operation to the inner square of the form: 0 6 4 0 B(i,j) = avg( A(i,j), A(i-1,j), A(i+1,j), A(i,j-1), A(i,j+1) 0 0 0 0 ) What is the stencil? Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 20 

21 . Stencil Pattern Procedure A 1)  Average all blue squares 0 0 0 0 0 9 7 0 0 6 4 0 0 0 0 0 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 21 

22 . Stencil Pattern Procedure B 1)  Average all blue squares 2)  Store result in B 0 0 0 0 0 4.4 0 0 0 0 0 0 0 0 0 0 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 22 

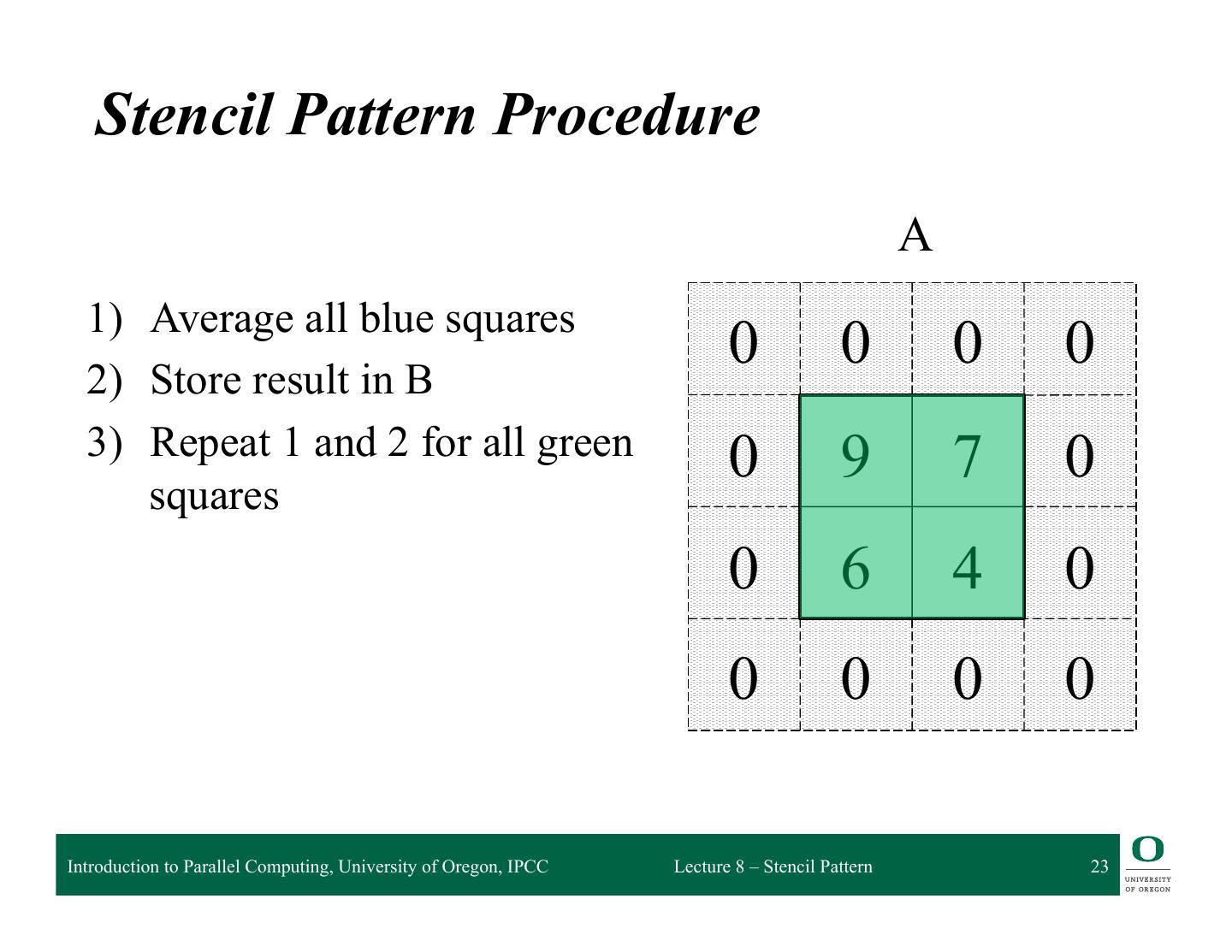
23 . Stencil Pattern Procedure A 1)  Average all blue squares 2)  Store result in B 0 0 0 0 3)  Repeat 1 and 2 for all green 0 9 7 0 squares 0 6 4 0 0 0 0 0 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 23 

24 . Practice! Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 24 

25 . Stencil Pattern Practice A B 0 0 0 0 0 0 0 0 0 9 7 0 0 4.4 0 0 0 6 4 0 0 0 0 0 0 0 0 0 0 0 0 0 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 25 

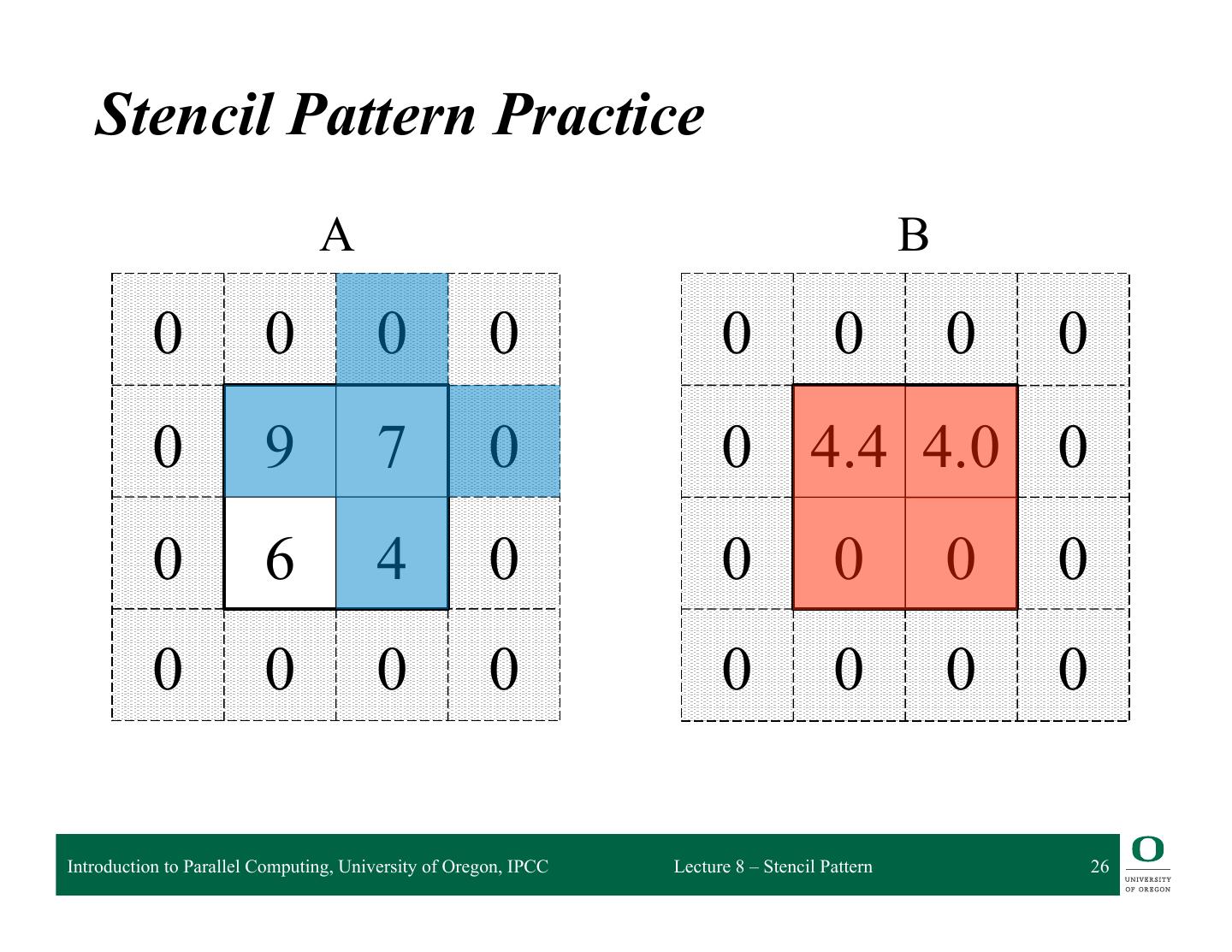
26 . Stencil Pattern Practice A B 0 0 0 0 0 0 0 0 0 9 7 0 0 4.4 4.0 0 0 6 4 0 0 0 0 0 0 0 0 0 0 0 0 0 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 26 

27 . Stencil Pattern Practice A B 0 0 0 0 0 0 0 0 0 9 7 0 0 4.4 4.0 0 0 6 4 0 0 3.8 0 0 0 0 0 0 0 0 0 0 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 27 

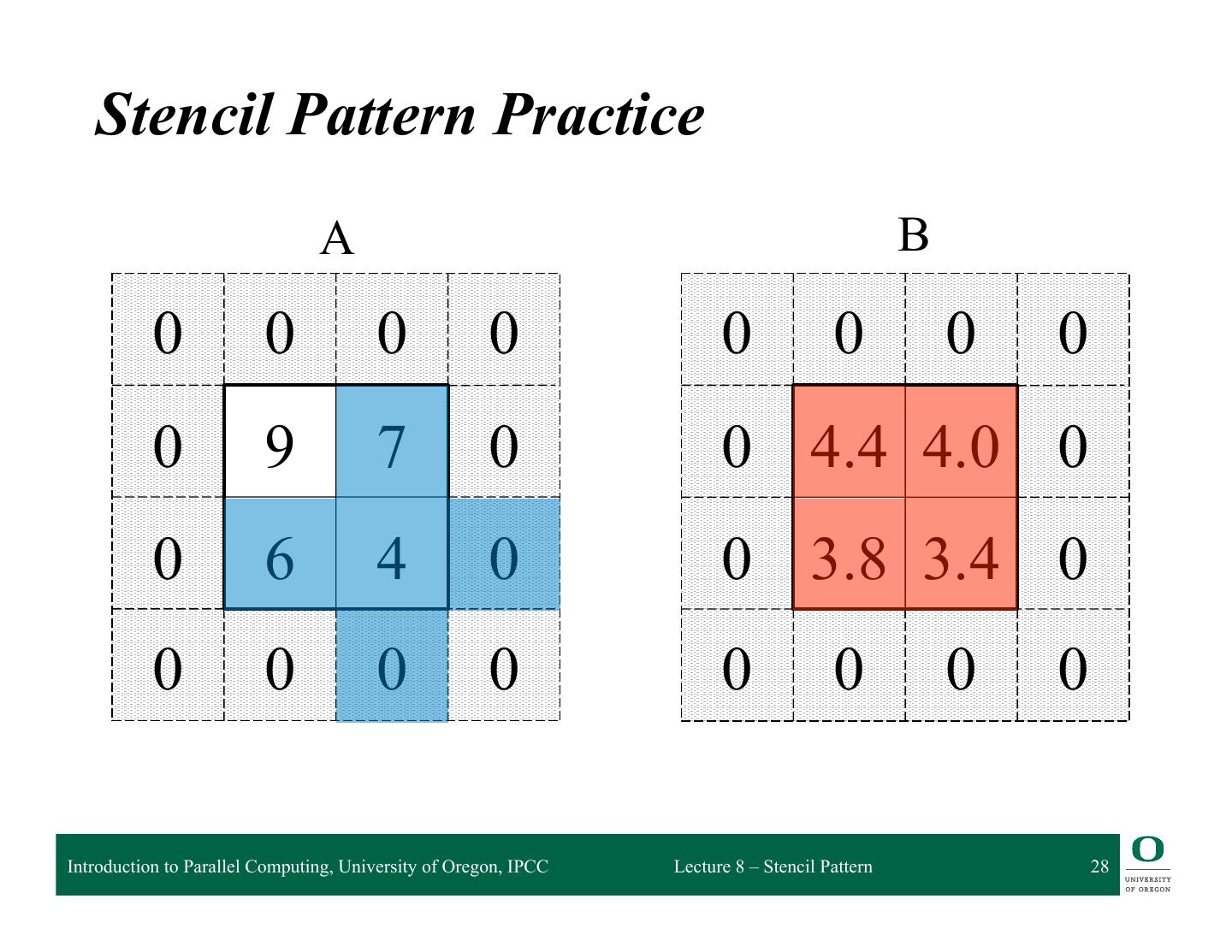
28 . Stencil Pattern Practice A B 0 0 0 0 0 0 0 0 0 9 7 0 0 4.4 4.0 0 0 6 4 0 0 3.8 3.4 0 0 0 0 0 0 0 0 0 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 28 

29 . Outline q  Partitioning q  What is the stencil pattern? ❍  Update alternatives ❍  2D Jacobi iteration ❍  SOR and Red/Black SOR q  Implementing stencil with shift q  Stencil and cache optimizations q  Stencil and communication optimizations q  Recurrence Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Stencil Pattern 29