6-Collectives Pattern

1 . Collectives Pattern Parallel Computing CIS 410/510 Department of Computer and Information Science Lecture 8 – Collective Pattern 

2 . Outline q  What are Collectives? q  Reduce Pattern q  Scan Pattern q  Sorting Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 2 

3 . Collectives q  Collective operations deal with a collection of data as a whole, rather than as separate elements q  Collective patterns include: ❍  Reduce ❍  Scan ❍  Partition ❍  Scatter ❍  Gather Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 3 

4 . Collectives q  Collective operations deal with a collection of data as a whole, rather than as separate elements q  Collective patterns include: ❍  Reduce ❍  Scan ❍  Partition Reduce  and  Scan  will  be   ❍  Scatter covered  in  this  lecture   ❍  Gather Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 4 

5 . Reduce q  Reduce is used to combine a collection of elements into one summary value q  A combiner function combines elements pairwise q  A combiner function only needs to be associative to be parallelizable q  Example combiner functions: ❍  Addition ❍  Multiplication ❍  Maximum / Minimum Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 5 

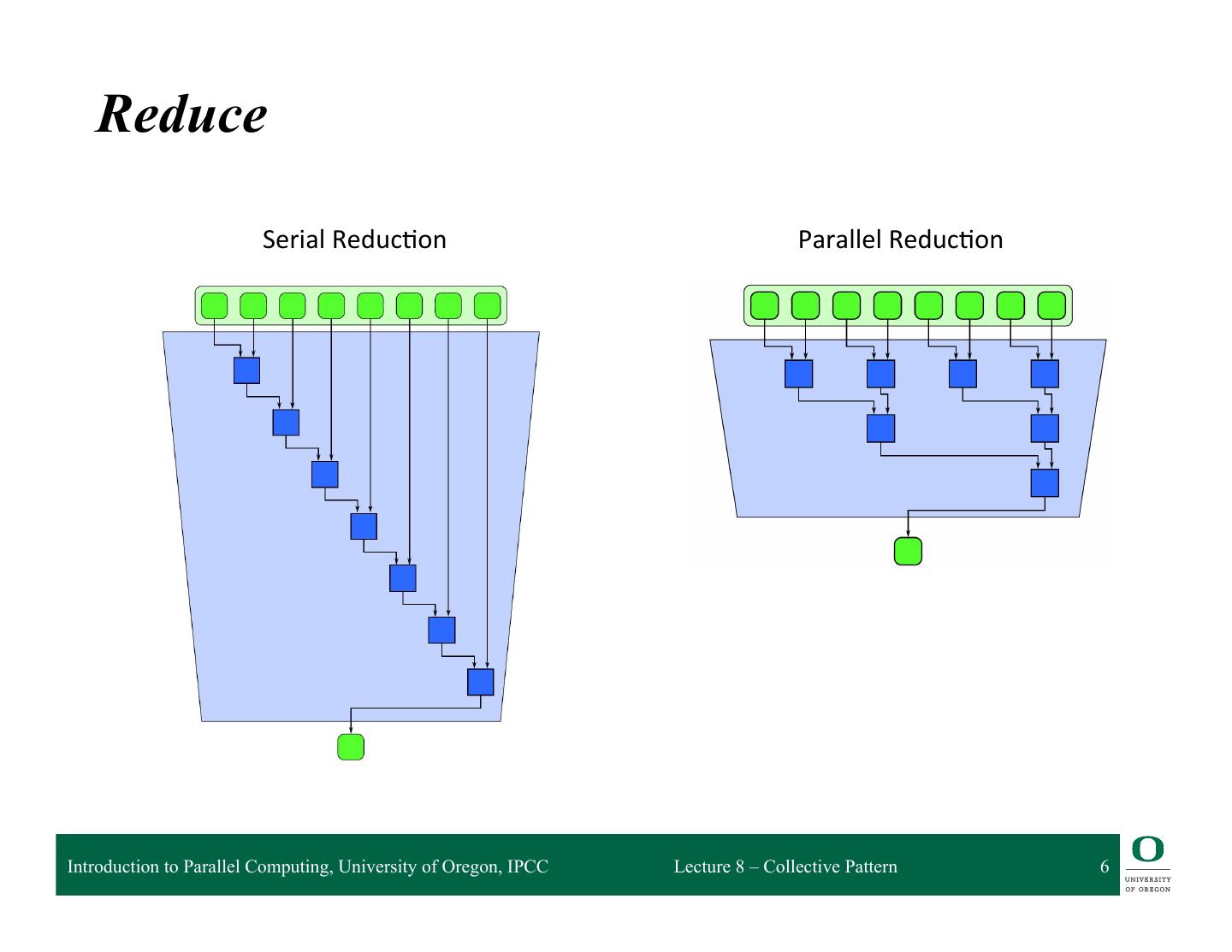
6 . Reduce Serial  Reduc4on   Parallel  Reduc4on   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 6 

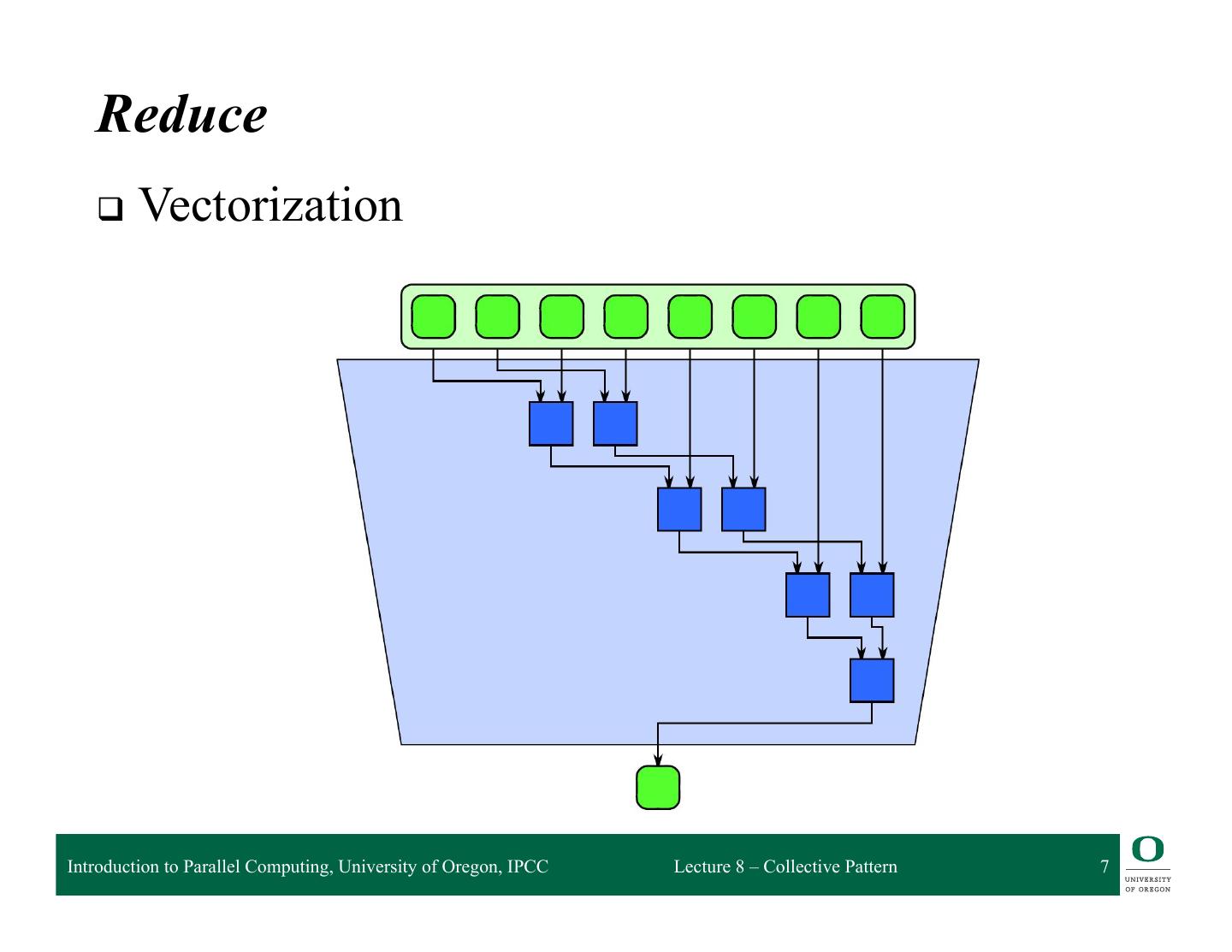
7 . Reduce q  Vectorization Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 7 

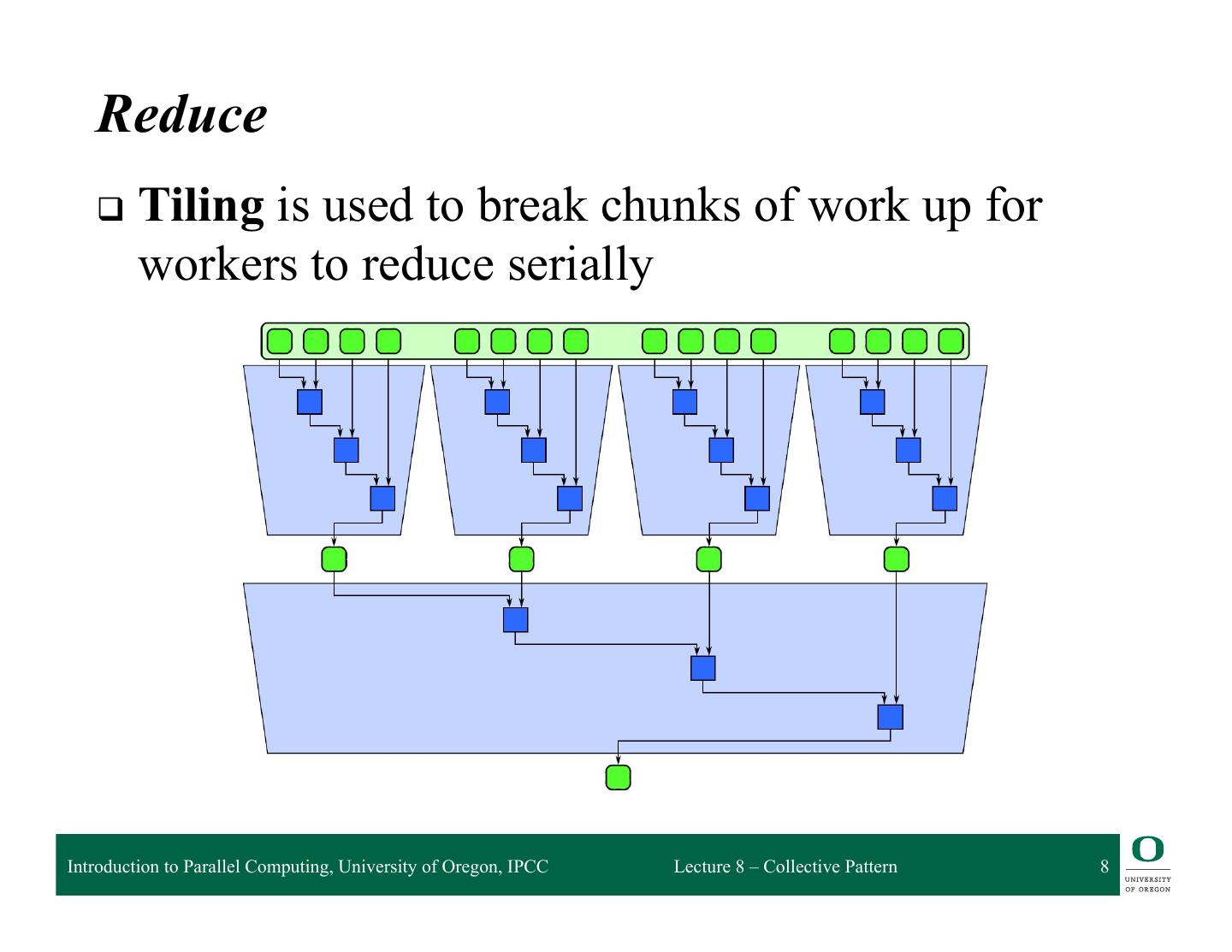
8 . Reduce q  Tiling is used to break chunks of work up for workers to reduce serially Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 8 

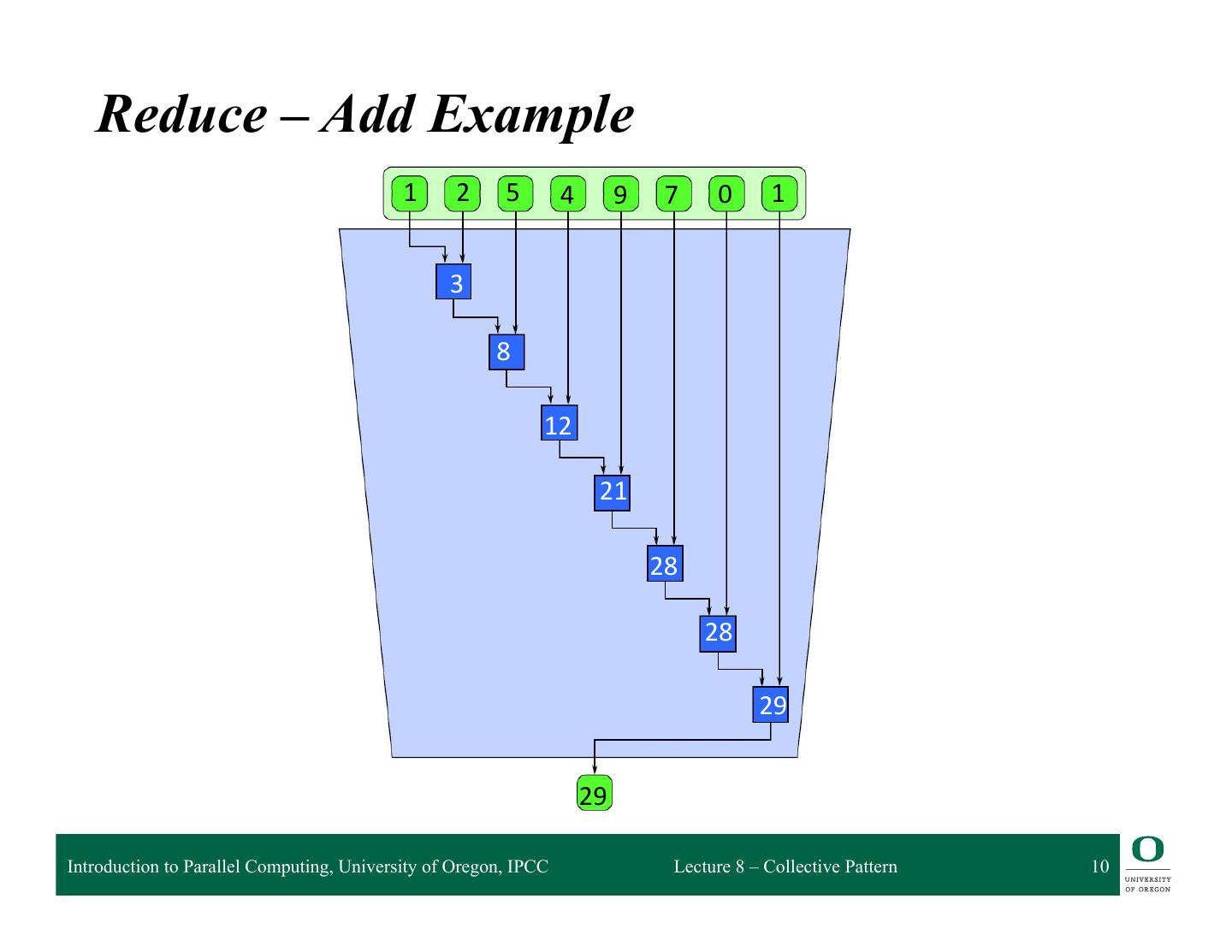
9 . Reduce – Add Example 1   2   5   4   9   7   0   1   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 9 

10 . Reduce – Add Example 1   2   5   4   9   7   0   1   3   8   12   21   28   28   29   29   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 10 

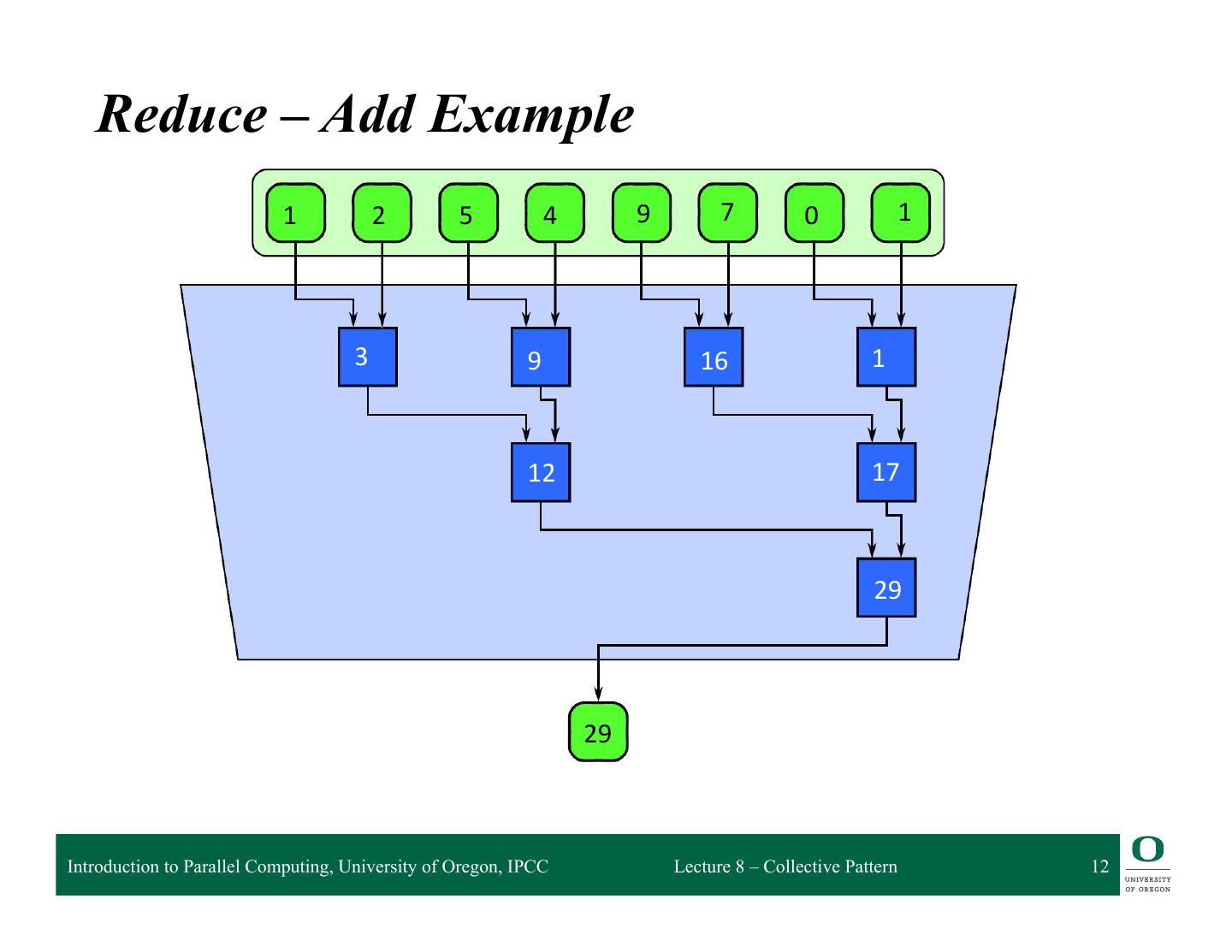
11 . Reduce – Add Example 1   2   5   4   9   7   0   1   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 11 

12 . Reduce – Add Example 1   2   5   4   9   7   0   1   3   9   16   1   12   17   29   29   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 12 

13 . Reduce q  We can “fuse” the map and reduce patterns Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 13 

14 . Reduce q  Precision can become a problem with reductions on floating point data q  Different orderings of floating point data can change the reduction value Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 14 

15 . Reduce Example: Dot Product q  2vectors of same length q  Map (*) to multiply the components q  Then reduce with (+) to get the final answer Also:     Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 15 

16 . Dot Product – Example Uses q  Essential operation in physics, graphics, video games,… q  Gaming analogy: in Mario Kart, there are “boost pads” on the ground that increase your speed ❍  red vector is your speed (x and y direction) ❍  blue vector is the orientation of the boost pad (x and y direction). Larger numbers are more power. How  much  boost  will  you  get?  For  the   analogy,  imagine  the  pad  mul4plies  your   speed:   •  If  you  come  in  going  0,  you’ll  get  nothing   •  If  you  cross  the  pad  perpendicularly,  you’ll   get  0  [just  like  the  banana  oblitera4on,  it   will  give  you  0x  boost  in  the  perpendicular   direc4on]   Photo  source     Ref:  hRp://beRerexplained.com/ar4cles/vector-­‐calculus-­‐understanding-­‐the-­‐dot-­‐product/   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 16 

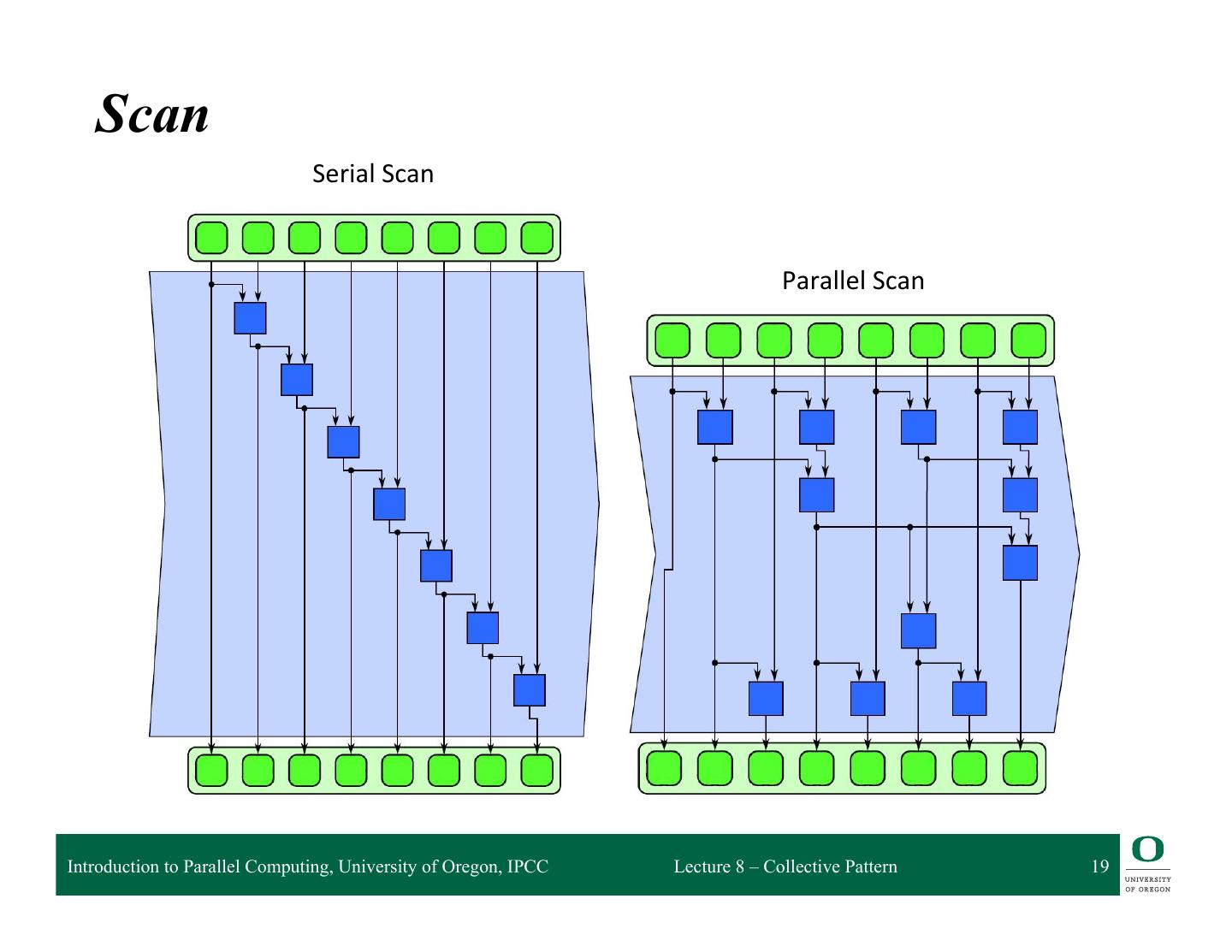
17 . Scan q  The scan pattern produces partial reductions of input sequence, generates new sequence q  Trickier to parallelize than reduce q  Inclusive scan vs. exclusive scan ❍  Inclusive scan: includes current element in partial reduction ❍  Exclusive scan: excludes current element in partial reduction, partial reduction is of all prior elements prior to current element Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 17 

18 . Scan – Example Uses q  Lexical comparison of strings – e.g., determine that “strategy” should appear before “stratification” in a dictionary q  Add multi-precision numbers (those that cannot be represented in a single machine word) q  Evaluate polynomials q  Implement radix sort or quicksort q  Delete marked elements in an array q  Dynamically allocate processors q  Lexical analysis – parsing programs into tokens q  Searching for regular expressions q  Labeling components in 2-D images q  Some tree algorithms – e.g., finding the depth of every vertex in a tree Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 18 

19 . Scan Serial  Scan   Parallel  Scan   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 19 

20 . Scan q  One algorithm for parallelizing scan is to perform an “up sweep” and a “down sweep” q  Reduce the input on the up sweep q  The down sweep produces the intermediate results Up  sweep  –  compute  reduc4on   Down  sweep  –  compute  intermediate  values   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 20 

21 . Scan – Maximum Example 1 4 0 2 7 2 4 3 1 4 0 2 7 2 4 3 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 21 

22 . Scan – Maximum Example 1 4 0 2 7 2 4 3 4 1 4 0 2 7 2 4 3 4 4 2 7 4 4 7 4 7 7 7 7 7 7   4 7 7 1 4 4 4 7 7 7 7 1 4 4 4 7 7 7 7 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 22 

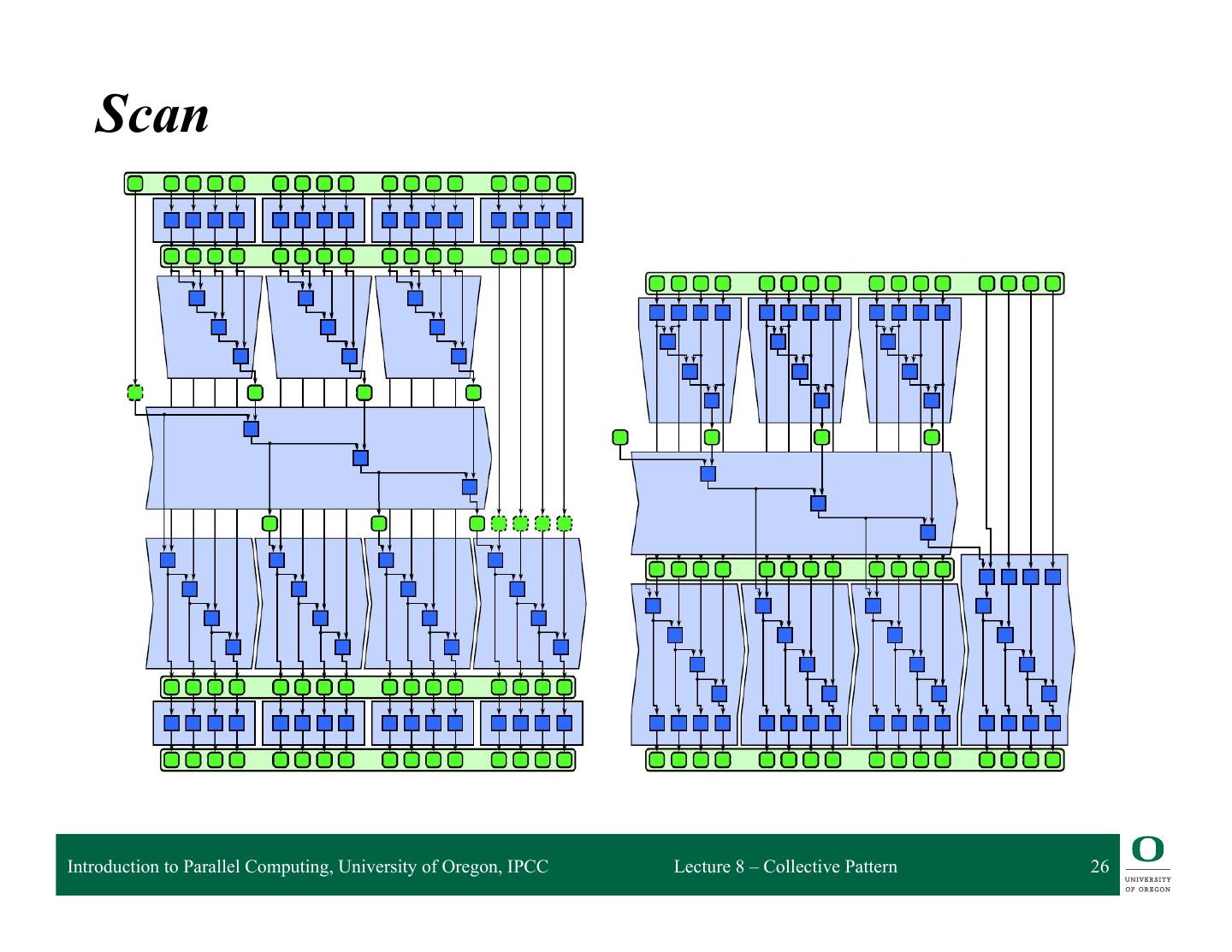
23 . Scan q  Three phase scan with tiling Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 23 

24 . Scan Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 24 

25 . Scan q  Just like reduce, we can also fuse the map pattern with the scan pattern Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 25 

26 . Scan Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 26 

27 . Merge Sort as a reduction q  We can sort an array via a pair of a map and a reduce q  Map each element into a vector containing just that element ❍  <> is the merge operation: [1,3,5,7] <> [2,6,15] = [1,2,3,5,6,7,15] ❍  [] is the empty list q  How fast is this? Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 27 

28 . Right Biased Sort Start with [14,3,4,8,7,52,1] Map to [[14],[3],[4],[8],[7],[52],[1]] Reduce: [14] <> ([3] <> ([4] <> ([8] <> ([7] <> ([52] <> [1]))))) = [14] <> ([3] <> ([4] <> ([8] <> ([7] <> [1,52])))) = [14] <> ([3] <> ([4] <> ([8] <> [1,7,52]))) = [14] <> ([3] <> ([4] <> [1,7,8,52])) = [14] <> ([3] <> [1,4,7,8,52]) = [14] <> [1,3,4,7,8,52] = [1,3,4,7,8,14,52] Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 28 

29 . Right Biased Sort Cont q  How long did that take? q  We did O(n) merges…but each one took O(n) time q  O(n2) q  We wanted merge sort, but instead we got insertion sort! Introduction to Parallel Computing, University of Oregon, IPCC Lecture 8 – Collective Pattern 29