4-Parallel Performance Theory - 2

1 . Parallel Performance Theory - 2 Parallel Computing CIS 410/510 Department of Computer and Information Science Lecture 4 – Parallel Performance Theory - 2 

2 . Outline q  Scalable parallel execution q  Parallel execution models q  Isoefficiency q  Parallel machine models q  Parallel performance engineering Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 2 

3 . Scalable Parallel Computing q  Scalability in parallel architecture ❍  Processor numbers ❍  Memory architecture ❍  Interconnection network ❍  Avoid critical architecture bottlenecks q  Scalability in computational problem ❍  Problemsize ❍  Computational algorithms ◆ Computation to memory access ratio ◆ Computation to communication ratio q  Parallel programming models and tools q  Performance scalability Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 3 

4 . Why Aren’t Parallel Applications Scalable? q  Sequential performance q  Critical Paths ❍  Dependencies between computations spread across processors q  Bottlenecks ❍  One processor holds things up q  Algorithmic overhead ❍  Some things just take more effort to do in parallel q  Communication overhead ❍  Spending increasing proportion of time on communication q  Load Imbalance ❍  Makes all processor wait for the “slowest” one ❍  Dynamic behavior q  Speculative loss ❍  Do A and B in parallel, but B is ultimately not needed Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 4 

5 . Critical Paths q  Long chain of dependence ❍  Main limitation on performance ❍  Resistance to performance improvement q  Diagnostic ❍  Performance stagnates to a (relatively) fixed value ❍  Critical path analysis q  Solution ❍  Eliminate long chains if possible ❍  Shorten chains by removing work from critical path Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 5 

6 . Bottlenecks q  How to detect? ❍  One processor A is busy while others wait ❍  Data dependency on the result produced by A q  Typical situations: ❍  N-to-1 reduction / computation / 1-to-N broadcast ❍  One processor assigning job in response to requests q  Solution techniques: ❍  More efficient communication ❍  Hierarchical schemes for master slave q  Program may not show ill effects for a long time q  Shows up when scaling Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 6 

7 . Algorithmic Overhead q  Different sequential algorithms to solve the same problem q  All parallel algorithms are sequential when run on 1 processor q  All parallel algorithms introduce addition operations (Why?) ❍  Parallel overhead q  Where should be the starting point for a parallel algorithm? ❍  Best sequential algorithm might not parallelize at all ❍  Or, it doesn’t parallelize well (e.g., not scalable) q  What to do? ❍  Choose algorithmic variants that minimize overhead ❍  Use two level algorithms q  Performance is the rub ❍  Are you achieving better parallel performance? ❍  Must compare with the best sequential algorithm Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 7 

8 . What is the maximum parallelism possible? q  Depends on application, algorithm, program ❍  Data dependencies in execution q  Remember MaxPar 512-­‐point  FFT   ❍  Analyzes the earliest possible “time” any data can be computed parallel signature ❍  Assumes a simple model for time it takes to execute instruction or go to memory ❍  Result is the maximum parallelism available q  Parallelism varies! Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 8 

9 . Embarrassingly Parallel Computations r  No or very little communication between processes r  Each process can do its tasks without any interaction with other processes Input  Data   Processes ... r  Examples Results ¦  Numerical integration ¦  Mandelbrot set ¦  Monte Carlo methods Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 9 

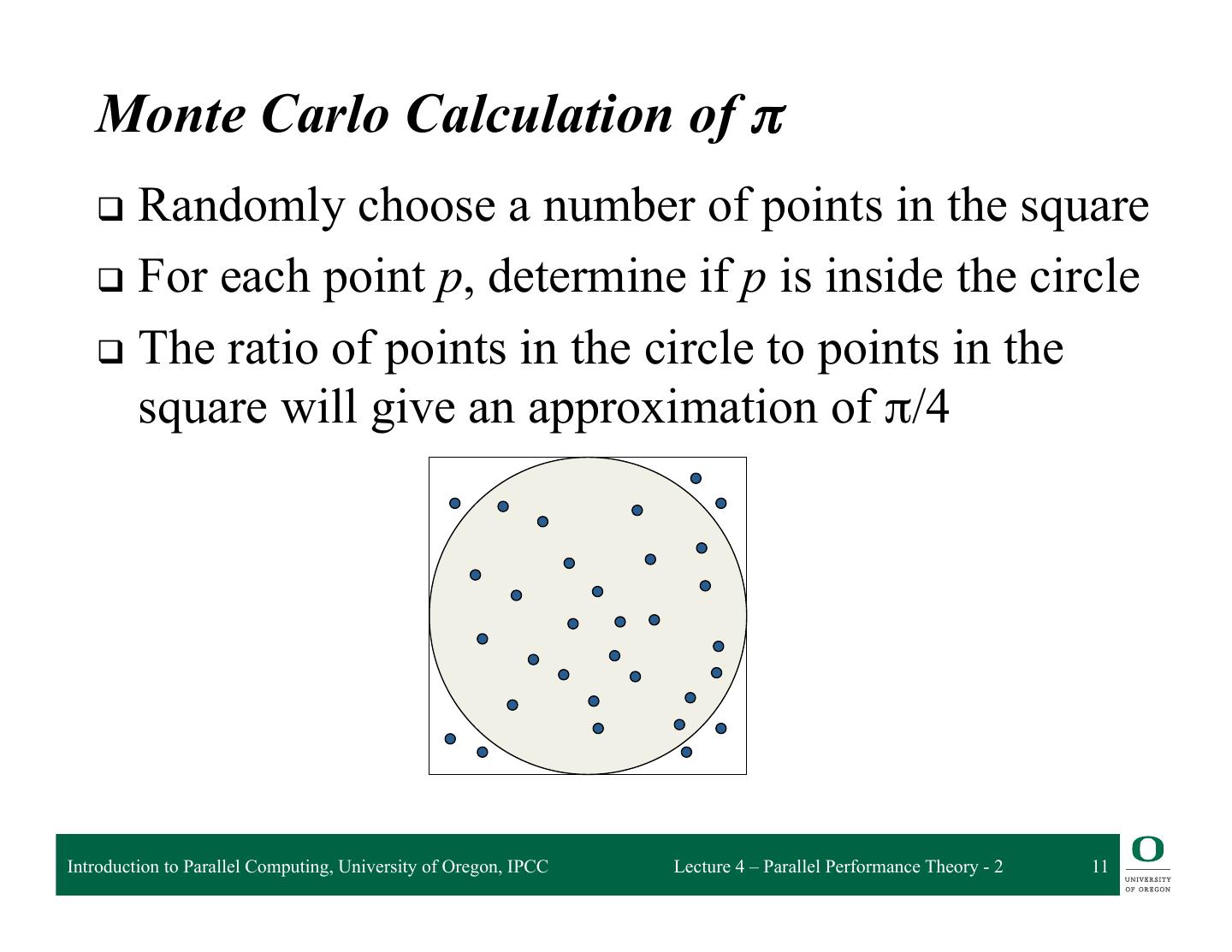
10 . Calculating π with Monte Carlo q  Consider a circle of unit radius q  Place circle inside a square box with side of 2 in 2  in   q  The ratio of the circle area to the square area is: π ∗1 ∗1 π = 2∗2 4 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 10 

11 . Monte Carlo Calculation of π q  Randomly choose a number of points in the square q  For each point p, determine if p is inside the circle q  The ratio of points in the circle to points in the square will give an approximation of π/4 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 11 

12 . Performance Metrics and Formulas q  T1 is the execution time on a single processor q  Tp is the execution time on a p processor system q  S(p) (Sp) is the speedup T1   S(  p)  =   Tp   q  E(p) (Ep) is the efficiency Sp   Efficiency  =   p   q  Cost(p) (Cp) is the cost Cost  =  p  ×  Tp   q  Parallel algorithm is cost-optimal ❍  Parallel time = sequential time (Cp = T1 , Ep = 100%) Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 12 

13 . Analytical / Theoretical Techniques q  Involves simple algebraic formulas and ratios ❍  Typical variables are: ◆ data size (N), number of processors (P), machine constants ❍  Want to model performance of individual operations, components, algorithms in terms of the above ◆ be careful to characterize variations across processors ◆ model them with max operators ❍  Constants are important in practice ◆ Use asymptotic analysis carefully q  Scalability analysis ❍  Isoefficiency (Kumar) Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 13 

14 . Isoefficiency q  Goal is to quantify scalability q  How much increase in problem size is needed to retain the same efficiency on a larger machine? q  Efficiency ❍  T1 / (p * Tp) ❍  Tp = computation + communication + idle Equal  efficiency  curves   q  Isoefficiency Equation for equal-efficiency curves problem  size   ❍  ❍  If no solution ◆  problem is not scalable in the sense defined by isoefficiency processors   q  See original paper by Kumar on webpage Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 14 

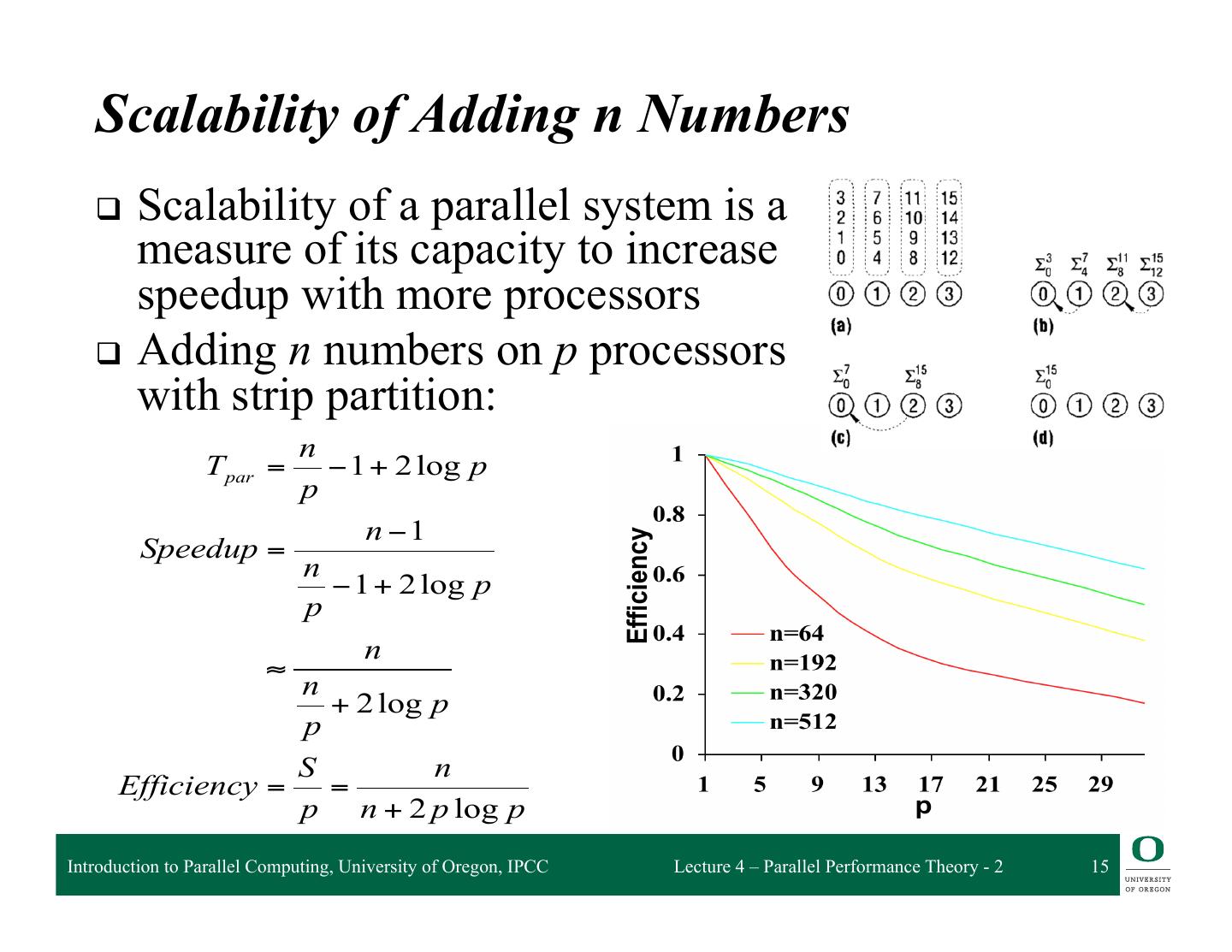
15 . Scalability of Adding n Numbers q  Scalability of a parallel system is a measure of its capacity to increase speedup with more processors q  Adding n numbers on p processors with strip partition: n T par = − 1 + 2 log p p n −1 Speedup = n − 1 + 2 log p p n ≈ n + 2 log p p S n Efficiency = = p n + 2 p log p Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 15 

16 . Problem Size and Overhead q  Informally, problem size is expressed as a parameter of the input size q  A consistent definition of the size of the problem is the total number of basic operations (Tseq ) ❍  Also refer to problem size as “work (W = Tseq ) q  Overhead of a parallel system is defined as the part of the cost not in the best serial algorithm q  Denoted by TO, it is a function of W and p TO(W,p) = pTpar - W (pTpar includes overhead) TO(W,p) + W = pTpar Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 16 

17 . Isoefficiency Function q  With a fixed efficiency, W is as a function of p W + TO (W , p ) Tpar = W  =  Tseq   p W Wp Speedup = = Tpar W + TO (W , p ) S W 1 Efficiency = = = p W + TO (W , p ) 1 + TO (W , p ) W 1 T (W , p ) 1 − E E= → O = TO (W , p ) W E 1+ W E W= TO (W , p ) = KTO (W , p ) Isoefficiency Function 1− E Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 17 

18 . Isoefficiency Function of Adding n Numbers q  Overhead function: …   ❍  TO(W,p) = pTpar – W = 2plog(p) …   q  Isoefficiency function: .   .   .   ❍  W=K*2plog(p) q  Ifp doubles, W needs also to be doubled to roughly maintain the same efficiency q  Isoefficiency functions can be more difficult to express for more complex algorithms Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 18 

19 . More Complex Isoefficiency Functions q  A typical overhead function TO can have several distinct terms of different orders of magnitude with respect to both p and W q  We can balance W against each term of TO and compute the respective isoefficiency functions for individual terms ❍  Keep only the term that requires the highest grow rate with respect to p ❍  This is the asymptotic isoefficiency function Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 19 

20 . Isoefficiency q  Consider a parallel system with an overhead function TO = p 3 / 2 + p 3 / 4W 3 / 4 q  Using only the first term W = Kp 3 / 2 q  Using only the second term W = Kp 3 / 4W 3 / 4 W 1/ 4 = Kp 3 / 4 W = K 4 p3 q  K4p3 is the overall asymptotic isoefficiency function Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 20 

21 . Parallel Computation (Machine) Models q  PRAM (parallel RAM) ❍  Basic parallel machine q  BSP (Bulk Synchronous Parallel) ❍  Isolates regions of computation from communication q  LogP ❍  Used for studying distribute memory systems ❍  Focuses on the interconnection network q  Roofline ❍  Based in analyzing “feeds” and “speeds” Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 21 

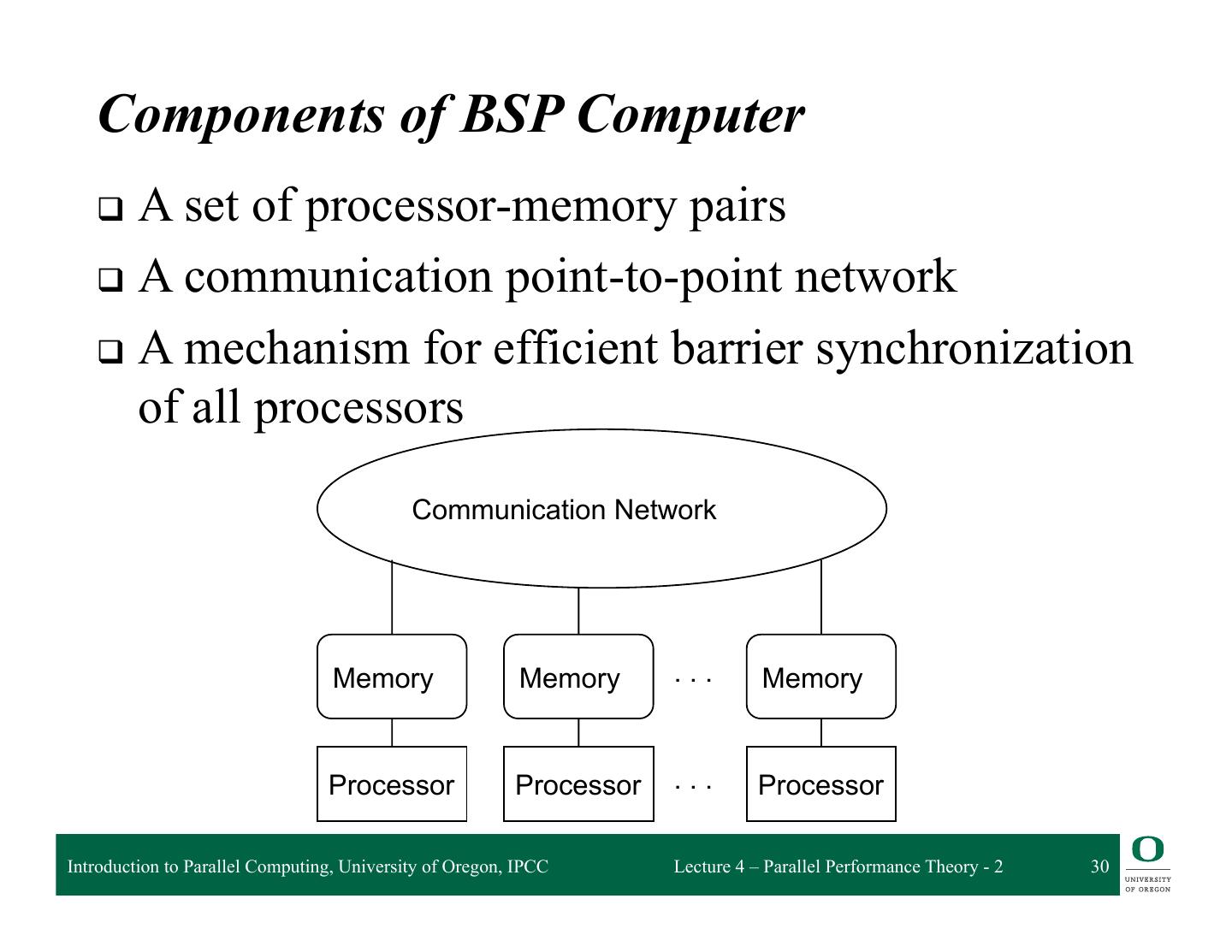
22 . PRAM q  Parallel Random Access Machine (PRAM) q  Shared-memory multiprocessor model q  Unlimited number of processors ❍  Unlimited local memory ❍  Each processor knows its ID q  Unlimited shared memory q  Inputs/outputs are placed in shared memory q  Memory cells can store an arbitrarily large integer q  Each instruction takes unit time q  Instructions are sychronized across processors (SIMD) Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 22 

23 . PRAM Complexity Measures q  For each individual processor ❍  Time:number of instructions executed ❍  Space: number of memory cells accessed q  PRAM machine ❍  Time:time taken by the longest running processor ❍  Hardware: maximum number of active processors q  Technical issues ❍  How processors are activated ❍  How shared memory is accessed Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 23 

24 . Processor Activation q  P0 places the number of processors (p) in the designated shared-memory cell ❍  Each active Pi, where i < p, starts executing ❍  O(1) time to activate ❍  All processors halt when P0 halts q  Active processors explicitly activate additional processors via FORK instructions ❍  Tree-like activation ❍  O(log p) time to activate Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 24 

25 . PRAM is a Theoretical (Unfeasible) Model q  Interconnection network between processors and memory would require a very large amount of area q  The message-routing on the interconnection network would require time proportional to network size q  Algorithm’s designers can forget the communication problems and focus their attention on the parallel computation only q  There exist algorithms simulating any PRAM algorithm on bounded degree networks q  Design general algorithms for the PRAM model and simulate them on a feasible network Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 25 

26 . Classification of PRAM Models q  EREW (Exclusive Read Exclusive Write) ❍  No concurrent read/writes to the same memory location q  CREW (Concurrent Read Exclusive Write) ❍  Multiple processors may read from the same global memory location in the same instruction step q  ERCW (Exclusive Read Concurrent Write) ❍  Concurrent writes allowed q  CRCW (Concurrent Read Concurrent Write) ❍  Concurrent reads and writes allowed q  CRCW > (ERCW,CREW) > EREW Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 26 

27 . CRCW PRAM Models q  COMMON: all processors concurrently writing into the same address must be writing the same value q  ARBITRARY: if multiple processors concurrently write to the address, one of the competing processors is randomly chosen and its value is written into the register q  PRIORITY: if multiple processors concurrently write to the address, the processor with the highest priority succeeds in writing its value to the memory location q  COMBINING: the value stored is some combination of the values written, e.g., sum, min, or max q  COMMON-CRCW model most often used Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 27 

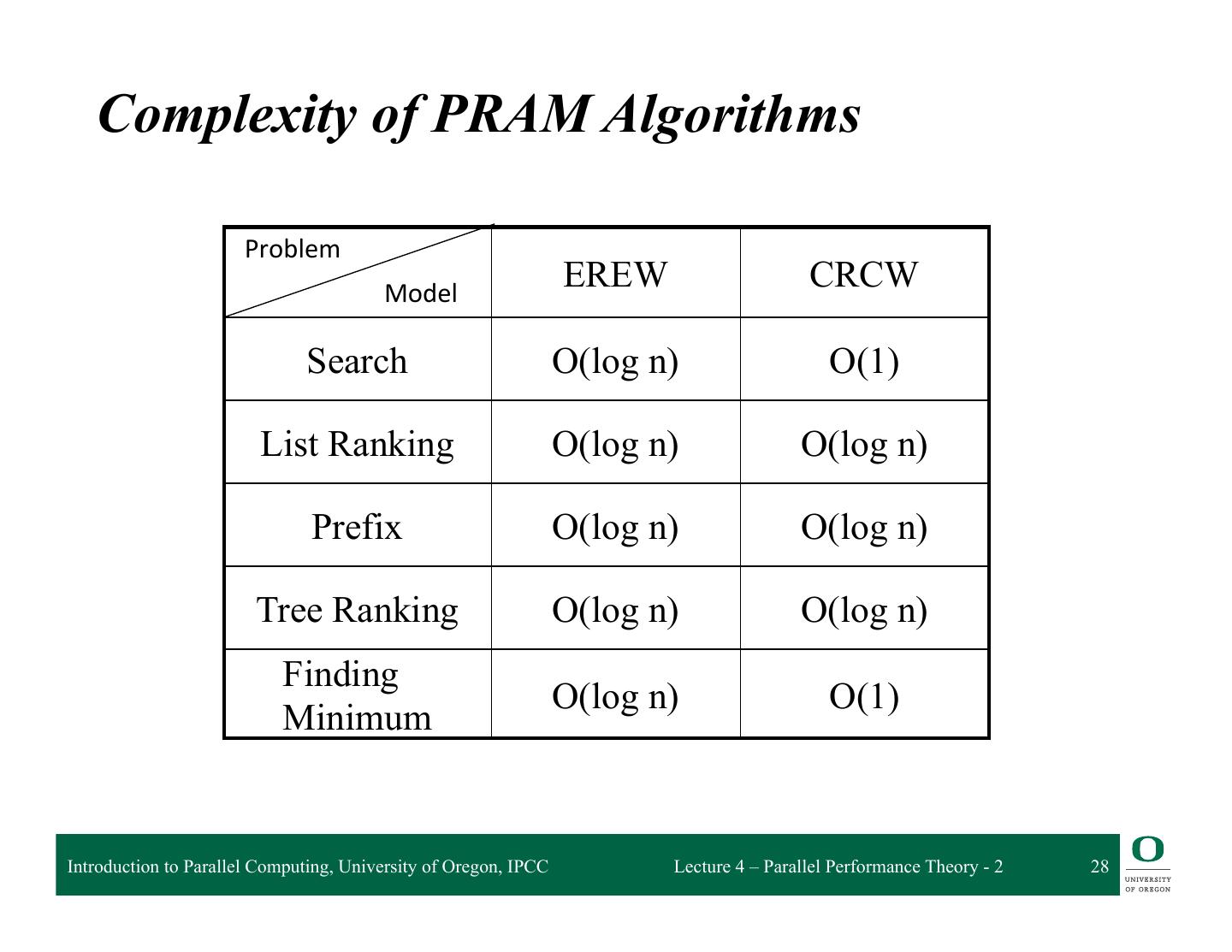
28 . Complexity of PRAM Algorithms Problem   Model   EREW CRCW Search O(log n) O(1) List Ranking O(log n) O(log n) Prefix O(log n) O(log n) Tree Ranking O(log n) O(log n) Finding O(log n) O(1) Minimum Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 28 

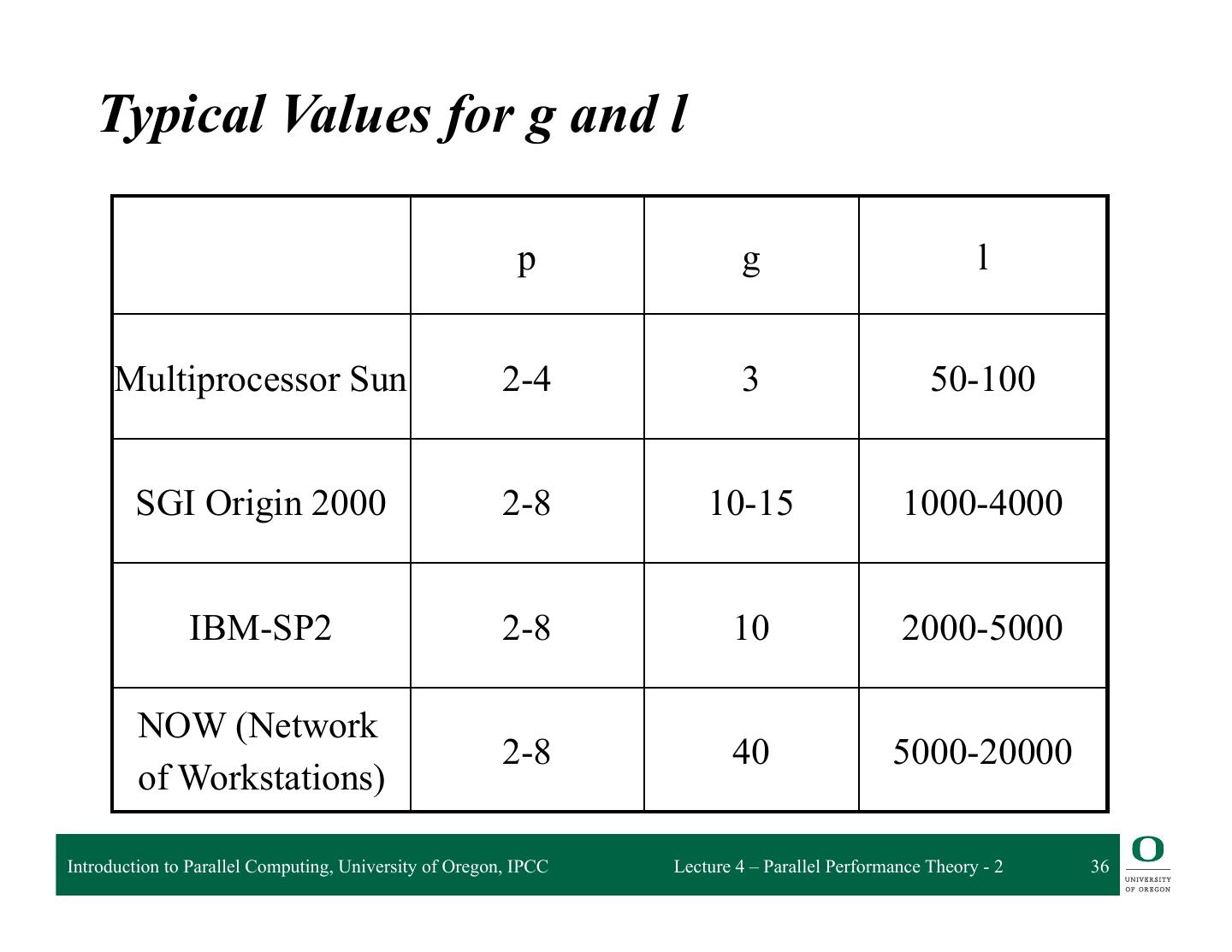
29 . BSP Overview q  Bulk Synchronous Parallelism q  A parallel programming model q  Invented by Leslie Valiant at Harvard q  Enables performance prediction q  SPMD (Single Program Multiple Data) style q  Supports both direct memory access and message passing semantics q  BSPlib is a BSP library implemented at Oxford Introduction to Parallel Computing, University of Oregon, IPCC Lecture 4 – Parallel Performance Theory - 2 29