3-Parallel Performance Theory - 1

1 . Parallel Performance Theory - 1 Parallel Computing CIS 410/510 Department of Computer and Information Science Lecture 3 – Parallel Performance Theory - 1 

2 . Outline q  Performance scalability q  Analytical performance measures q  Amdahl’s law and Gustafson-Barsis’ law Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 2 

3 . What is Performance? q  In computing, performance is defined by 2 factors ❍  Computational requirements (what needs to be done) ❍  Computing resources (what it costs to do it) q  Computational problems translate to requirements q  Computing resources interplay and tradeoff 1 Performance ~ Resources for solution …  and  ul0mately   Hardware   Time   Energy   Money   Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 3 

4 . Why do we care about Performance? q  Performance itself is a measure of how well the computational requirements can be satisfied q  We evaluate performance to understand the relationships between requirements and resources ❍  Decide how to change “solutions” to target objectives q  Performance measures reflect decisions about how and how well “solutions” are able to satisfy the computational requirements “The most constant difficulty in contriving the engine has arisen from the desire to reduce the time in which the calculations were executed to the shortest which is possible.” Charles Babbage, 1791 – 1871 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 4 

5 . What is Parallel Performance? q  Here we are concerned with performance issues when using a parallel computing environment ❍  Performance with respect to parallel computation q  Performance is the raison d’être for parallelism ❍  Parallel performance versus sequential performance ❍  If the “performance” is not better, parallelism is not necessary q  Parallel processing includes techniques and technologies necessary to compute in parallel ❍  Hardware, networks, operating systems, parallel libraries, languages, compilers, algorithms, tools, … q  Parallelism must deliver performance ❍  How? How well? Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 5 

6 . Performance Expectation (Loss) q  If each processor is rated at k MFLOPS and there are p processors, should we see k*p MFLOPS performance? q  If it takes 100 seconds on 1 processor, shouldn’t it take 10 seconds on 10 processors? q  Several causes affect performance ❍  Each must be understood separately ❍  But they interact with each other in complex ways ◆  Solution to one problem may create another ◆  One problem may mask another q  Scaling (system, problem size) can change conditions q  Need to understand performance space Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 6 

7 . Embarrassingly Parallel Computations q  An embarrassingly parallel computation is one that can be obviously divided into completely independent parts that can be executed simultaneously ❍  In a truly embarrassingly parallel computation there is no interaction between separate processes ❍  In a nearly embarrassingly parallel computation results must be distributed and collected/combined in some way q  Embarrassingly parallel computations have potential to achieve maximal speedup on parallel platforms ❍  If it takes T time sequentially, there is the potential to achieve T/P time running in parallel with P processors ❍  What would cause this not to be the case always? Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 7 

8 . Scalability q  A program can scale up to use many processors ❍  What does that mean? q  How do you evaluate scalability? q  How do you evaluate scalability goodness? q  Comparative evaluation ❍  If double the number of processors, what to expect? ❍  Is scalability linear? q  Use parallel efficiency measure ❍  Is efficiency retained as problem size increases? q  Apply performance metrics Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 8 

9 . Performance and Scalability q  Evaluation ❍  Sequential runtime (Tseq) is a function of ◆ problem size and architecture ❍  Parallel runtime (Tpar) is a function of ◆ problem size and parallel architecture ◆ # processors used in the execution ❍  Parallel performance affected by ◆ algorithm + architecture q  Scalability ❍  Ability of parallel algorithm to achieve performance gains proportional to the number of processors and the size of the problem Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 9 

10 . Performance Metrics and Formulas q  T1 is the execution time on a single processor q  Tp is the execution time on a p processor system q  S(p) (Sp) is the speedup T1   S(  p)  =   Tp   q  E(p) (Ep) is the efficiency Sp   Efficiency  =   p   q  Cost(p) (Cp) is the cost Cost  =  p  ×  Tp   q  Parallel algorithm is cost-optimal ❍  Parallel time = sequential time (Cp = T1 , Ep = 100%) Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 10 

11 . Amdahl’s Law (Fixed Size Speedup) q  Let f be the fraction of a program that is sequential ❍  1-f is the fraction that can be parallelized q  Let T1 be the execution time on 1 processor q  Let Tp be the execution time on p processors q  Sp is the speedup Sp = T1 / Tp = T1 / (fT1 +(1-f)T1 /p)) = 1 / (f +(1-f)/p)) q  As p → ∞ Sp = 1 / f Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 11 

12 . Amdahl’s Law and Scalability q  Scalability ❍  Ability of parallel algorithm to achieve performance gains proportional to the number of processors and the size of the problem q  When does Amdahl’s Law apply? ❍  When the problem size is fixed ❍  Strong scaling (p→∞, Sp = S∞ → 1 / f ) ❍  Speedup bound is determined by the degree of sequential execution time in the computation, not # processors!!! ❍  Uhh, this is not good … Why? ❍  Perfect efficiency is hard to achieve q  See original paper by Amdahl on webpage Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 12 

13 . Gustafson-Barsis’ Law (Scaled Speedup) q  Often interested in larger problems when scaling ❍  How big of a problem can be run (HPC Linpack) ❍  Constrain problem size by parallel time q  Assume parallel time is kept constant ❍  Tp = C = (f +(1-f)) * C ❍  fseq is the fraction of Tp spent in sequential execution ❍  fpar is the fraction of Tp spent in parallel execution q  What is the execution time on one processor? ❍  Let C=1, then Ts = fseq + p(1 – fseq ) = 1 + (p-1)fpar q  What is the speedup in this case? ❍  Sp = Ts / Tp = Ts / 1 = fseq + p(1 – fseq) = 1 + (p-1)fpar Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 13 

14 . Gustafson-Barsis’ Law and Scalability q  Scalability ❍  Ability of parallel algorithm to achieve performance gains proportional to the number of processors and the size of the problem q  When does Gustafson’s Law apply? ❍  When the problem size can increase as the number of processors increases ❍  Weak scaling (Sp = 1 + (p-1)fpar ) ❍  Speedup function includes the number of processors!!! ❍  Can maintain or increase parallel efficiency as the problem scales q  See original paper by Gustafson on webpage Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 14 

15 . Amdahl versus Gustafson-Baris Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 15 

16 . Amdahl versus Gustafson-Baris Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 16 

17 . DAG Model of Computation q  Think of a program as a directed acyclic graph (DAG) of tasks ❍  A task can not execute until all the inputs to the tasks are available ❍  These come from outputs of earlier executing tasks ❍  DAG shows explicitly the task dependencies q  Think of the hardware as consisting of workers (processors) q  Consider a greedy scheduler of the DAG tasks to workers ❍  No worker is idle while there are tasks still to execute Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 17 

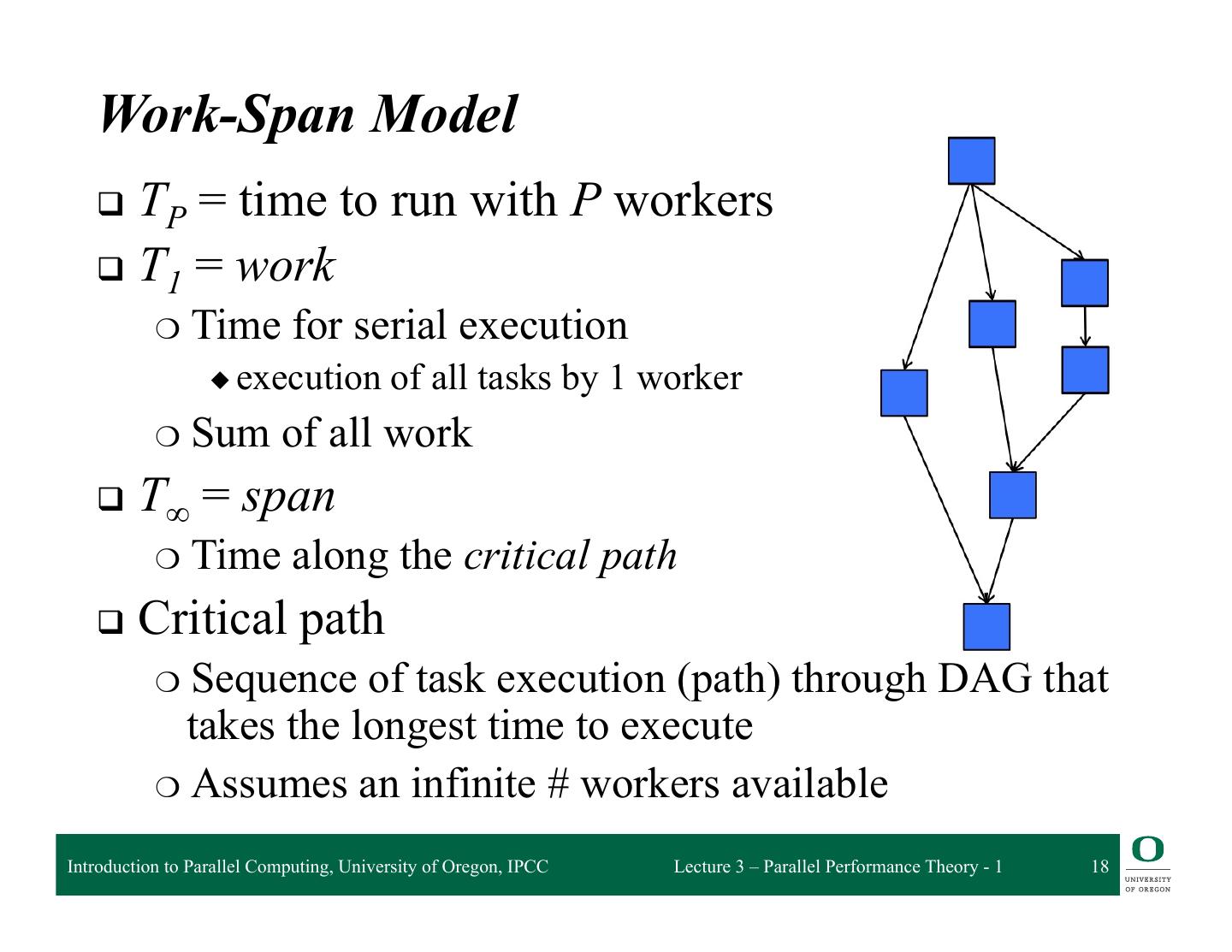
18 . Work-Span Model q  TP = time to run with P workers q  T1 = work ❍  Time for serial execution ◆ execution of all tasks by 1 worker ❍  Sum of all work q  T∞ = span ❍  Time along the critical path q  Critical path ❍  Sequence of task execution (path) through DAG that takes the longest time to execute ❍  Assumes an infinite # workers available Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 18 

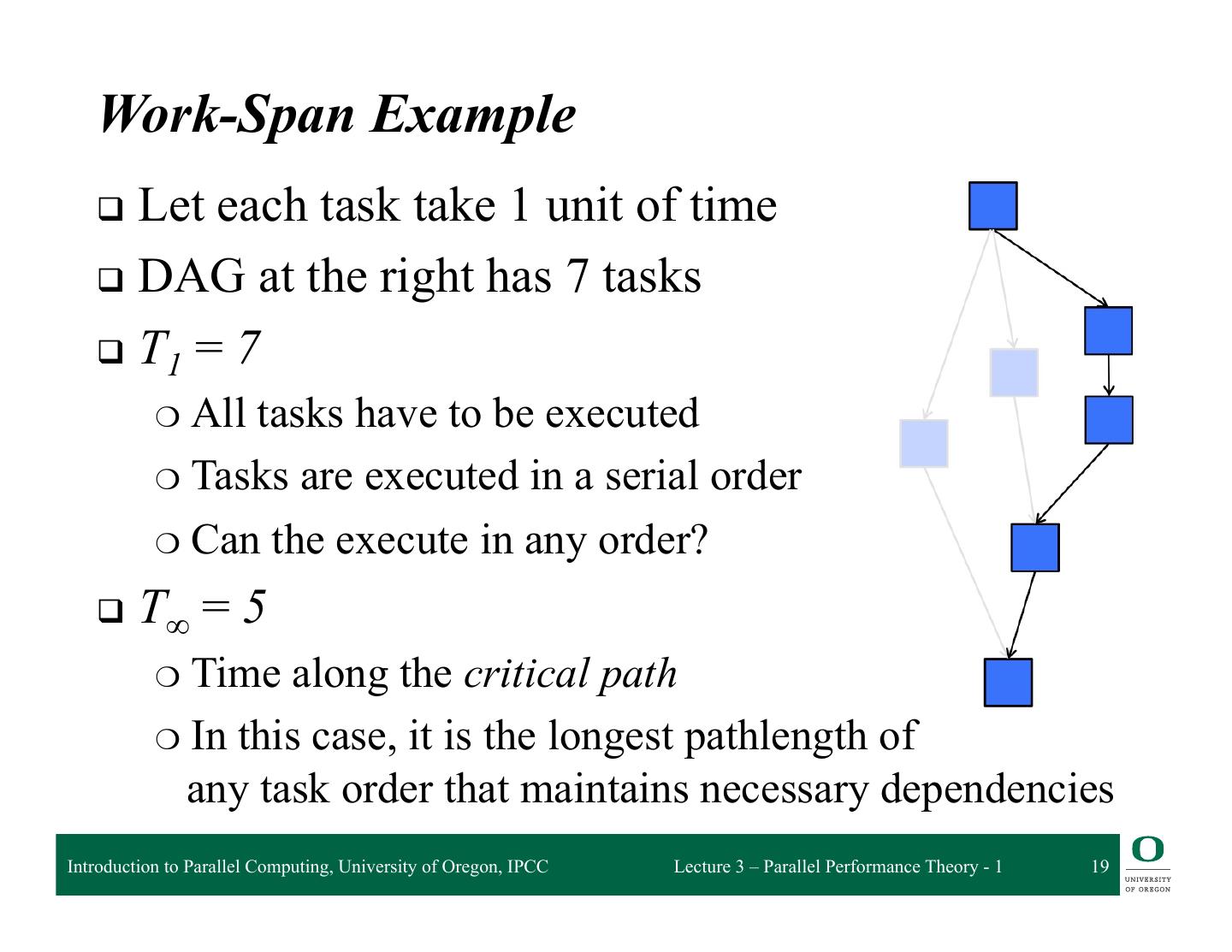
19 . Work-Span Example q  Let each task take 1 unit of time q  DAG at the right has 7 tasks q  T1 = 7 ❍  Alltasks have to be executed ❍  Tasks are executed in a serial order ❍  Can the execute in any order? q  T∞ =5 ❍  Time along the critical path ❍  In this case, it is the longest pathlength of any task order that maintains necessary dependencies Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 19 

20 . Lower/Upper Bound on Greedy Scheduling q  Suppose we only have P workers q  We can write a work-span formula to derive a lower bound on TP ❍  Max(T1 / P , T∞ ) ≤ TP q  T∞ is the best possible execution time q  Brent’s Lemma derives an upper bound ❍  Capture the additional cost executing the other tasks not on the critical path ❍  Assume can do so without overhead ❍  TP ≤ (T1 - T∞ ) / P + T∞ Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 20 

21 . Consider Brent’s Lemma for 2 Processors q  T1=7 q  T∞ = 5 q  T2 ≤ (T1 - T∞ ) / P + T∞ ≤ (7 – 5) / 2 + 5 ≤6 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 21 

22 . Amdahl was an optimist! Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 22 

23 . Estimating Running Time q  Scalability requires that T∞ be dominated by T1 TP ≈ T1 / P + T∞ if T∞ << T1 q  Increasingwork hurts parallel execution proportionately q  The span impacts scalability, even for finite P Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 23 

24 . Parallel Slack q  Sufficient parallelism implies linear speedup Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 24 

25 . Asymptotic Complexity q  Time complexity of an algorithm summarizes how the execution time grows with input size q  Space complexity summarizes how memory requirements grow with input size q  Standard work-span model considers only computation, not communication or memory q  Asymptotic complexity is a strong indicator of performance on large-enough problem sizes and reveals an algorithm’s fundamental limits Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 25 

26 . Definitions for Asymptotic Notation q  LetT(N) mean the execution time of an algorithm q  Big O notation ❍  T(N) is a member of O(f(N)) means that T(N) ≤ cŸf(N) for constant c q  Big Omega notation ❍  T(N) is a member of Ω(f(N)) means that T(N) ≥ cŸf(N) for constant c q  Big Theta notation ❍  T(N) is a member of Θ(f(N)) means that c1Ÿf(n) ≤T(N) < c2Ÿf(N) for constants c1 and c2 Introduction to Parallel Computing, University of Oregon, IPCC Lecture 3 – Parallel Performance Theory - 1 26