10 Transaction Locking and Concurrency #3

1 . Today’s Papers • Time, Clocks, and the Ordering of Events in a Distributed System EECS 262a Leslie Lamport. Appears in Communications of the ACM, Vol 21, No. 7, pp Advanced Topics in Computer Systems 558-565, July 1978 • Efficient Optimistic Concurrency Control Using Loosely Synchronized Lecture 10 Clocks Atul Adya, Robert Gruber, Barbara Liskov, Umesh Maheshwari. Appears in Proceedings of ACM SIGMOD international conference on Management of Data,1995 Lamport Clocks and OCC September 25th, 2018 • Thoughts? John Kubiatowicz Electrical Engineering and Computer Sciences University of California, Berkeley http://www.eecs.berkeley.edu/~kubitron/cs262 9/25/2018 cs262a-F18 Lecture-10 2 Time Distributed System • One dimension. It can not move backward. It can not stop. • It is derived from concept of the order in which events occur. • The concepts “before” and “after” need to • A distributed system consists of collection of distinct be reconsidered in a distributed system. processes which are spatially separated, and which communicate with one another by exchanging messages. • It could be a network of interconnected computers, like Internet, or just a single computer with separate processes. • It is sometimes impossible to say that one of two events occurred first in a distributed system. “happened before” is a partial ordering of the events in the system. 9/25/2018 cs262a-F18 Lecture-10 3 9/25/2018 cs262a-F18 Lecture-10 4 

2 . The Partial Ordering Definition of “happened before” • The system described in paper: • The relation “→” on the set of events of a system is – System is composed of a collection of processes. the smallest relation satisfying the following three – Each process consists of a sequence of events. conditions: – A single process is defined to be a set of events with an a priori total 1. If a and b are events in the same process, and a comes before b, ordering then a→b. • Events: 2. If a is the sending of a message by one process and b is the receipt of the same message by another processes, then a→b. – Program Events 3. If a→b and b→c then a→c. – Message Events • Two distinct events a and b are said to be • Messages carry dependencies between processes concurrent if a —/→b and b —/→ a. • We assume that a —/→ a for any event a. 9/25/2018 cs262a-F18 Lecture-10 5 9/25/2018 cs262a-F18 Lecture-10 6 Space-time diagram Logical Clocks • A clock is just a way of assigning a number to an event – Monotonically increasing except when reset – Not necessarily related to “real time” in any particular frame • Definition of logical clocks: – A clock Ci for each process Pi is a function which assigns a number Ci<a> to any event a in that process. – The entire system of clocks is represented by the function C which assigns to any event b the number C<b> = Cj<b> if b is an event b in process Pj. • p1→r4 since p1 → q2 and q2 → q4 and q4 → r3 and r3 → r4 • p3 and q3 are concurrent. 9/25/2018 cs262a-F18 Lecture-10 7 9/25/2018 cs262a-F18 Lecture-10 8 

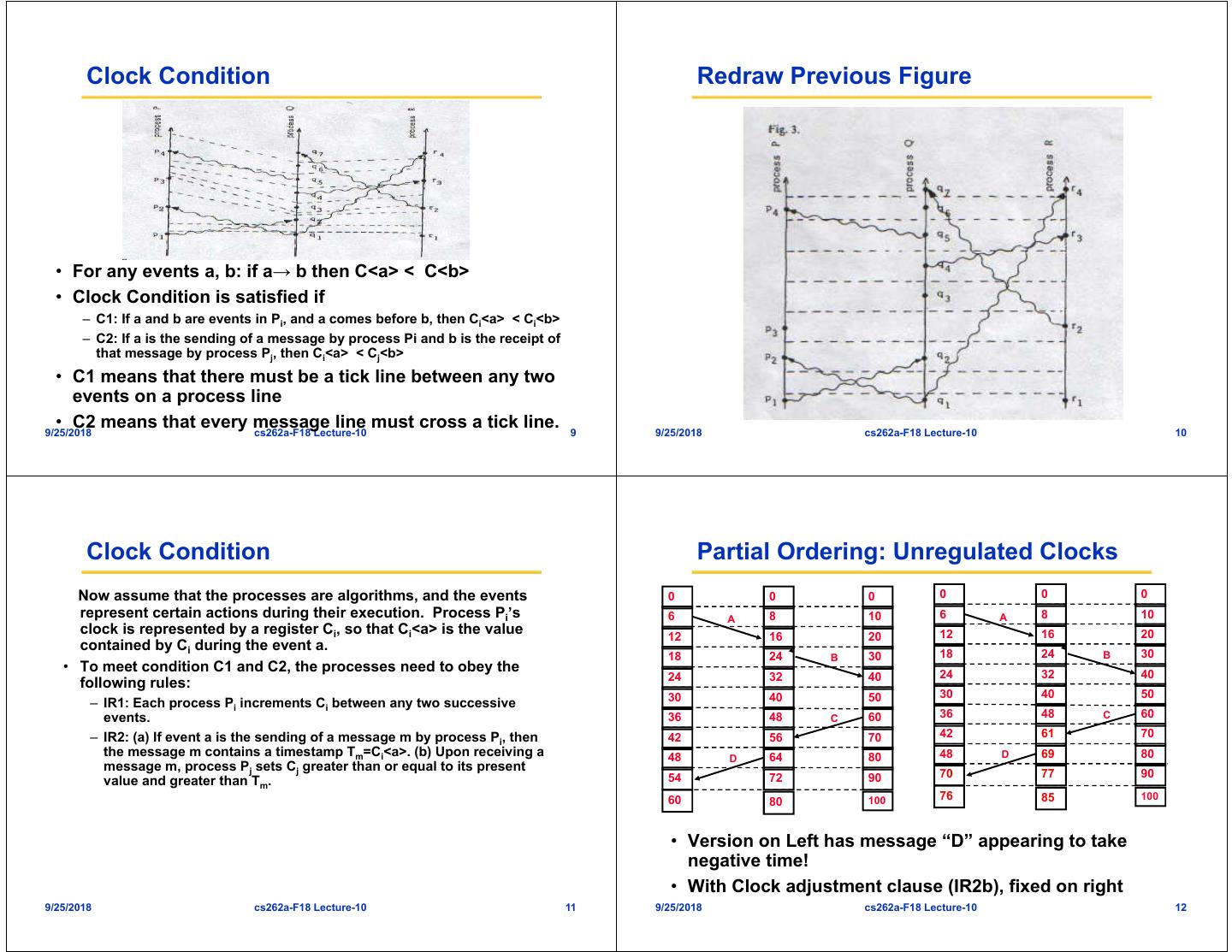
3 . Clock Condition Redraw Previous Figure • For any events a, b: if a→ b then C<a> < C<b> • Clock Condition is satisfied if – C1: If a and b are events in Pi, and a comes before b, then Ci<a> < Ci<b> – C2: If a is the sending of a message by process Pi and b is the receipt of that message by process Pj, then Ci<a> < Cj<b> • C1 means that there must be a tick line between any two events on a process line • C2 means that every message 9/25/2018 line must cross a tick line. cs262a-F18 Lecture-10 9 9/25/2018 cs262a-F18 Lecture-10 10 Clock Condition Partial Ordering: Unregulated Clocks Now assume that the processes are algorithms, and the events 0 0 0 0 0 0 represent certain actions during their execution. Process Pi’s 6 A 8 10 6 A 8 10 clock is represented by a register Ci, so that Ci<a> is the value 12 16 20 12 16 20 contained by Ci during the event a. 18 24 B 30 18 24 B 30 • To meet condition C1 and C2, the processes need to obey the 24 32 40 24 32 40 following rules: 30 40 50 30 40 50 – IR1: Each process Pi increments Ci between any two successive events. 36 48 C 60 36 48 C 60 – IR2: (a) If event a is the sending of a message m by process Pi, then 42 56 70 42 61 70 the message m contains a timestamp Tm=Ci<a>. (b) Upon receiving a 48 D 64 80 48 D 69 80 message m, process Pj sets Cj greater than or equal to its present 54 72 90 70 77 90 value and greater than Tm. 60 100 76 85 100 80 • Version on Left has message “D” appearing to take negative time! • With Clock adjustment clause (IR2b), fixed on right 9/25/2018 cs262a-F18 Lecture-10 11 9/25/2018 cs262a-F18 Lecture-10 12 

4 . Definition of total ordering “” Solving Mutual Exclusion • We can use a system of clocks satisfying the Clock • Mutual exclusion: Only one process can use the resource at a time, the other processes will be excluded from doing the same thing Condition to place a total ordering on the set of all events: – We simply order the events by the times at which they occur • Requirements: 1. A process which has been granted the resource must release it before – To break ties, we use any arbitrary total ordering ~< of the processes. it can be granted to another process. • Definition of total ordering “” 2. Different requests for the resource must be granted in the order in – If a is an event in process Pi and b is an event in process Pj, then ab if which they are made. and only if either 3. If every process which is granted the resource eventually release it, (i) Ci(a)<Cj(b) or (ii) Ci(a) =Cj(b) and Pi ~< Pj. then every request is eventually granted. – Clock Condition implies that if a → b then ab. • How to do it with clocks: Implement Clocks as above, define “” In other words, the relation  is a way of completing the “happened before” partial ordering to a total ordering • Assumptions: 1. For any two processes Pi and Pj, the messages sent from Pi to Pj are • The ordering “” depends upon the clock systems and is received in the same order as they are sent. not unique! 2. Every message is eventually received. – Example: If we have Ci(a) =Cj(b) and choose Pi ~< Pj, then a  b. If we 3. A process can send messages directly to every other process. choose Pj ~< Pi, then b  a 4. Each process maintains its own request queue which is never seen by • The partial ordering “→” is uniquely determined by the any other process. The request queues initially contain the single system of events. message T0:P0 requests resource. 9/25/2018 cs262a-F18 Lecture-10 13 9/25/2018 cs262a-F18 Lecture-10 14 Mutual Exclusion Algorithm Mutual Exclusion Algorithm (Con’t) • To request the resource, process Pi sends the message • When process Pj receives a “Tm:Pi requests resource” “Pi release resource” to every other process, and puts that message on its request message, it removes any Tm:Pi requests resource message queue, where Tm is the timestamp of the message from its request queue. • When process Pj receives the message • Process Pi is granted the resource when the following two “Tm:Pi requests resource” conditions are satisfied: it places it on its request queue and sends a (timestamped) acknowledgment message to Pi. 1. There is a Tm:Pi request resource message in its request queue which is ordered before any other request in its queue • To release the resource, process Pi removes any Tm:Pi request by the relation . resource message from its request queue and sends a 2. Pi has received a message from every other process time- (timestamped) stamped later than Tm. “Pi releases resource” messages to every other process. 9/25/2018 cs262a-F18 Lecture-10 15 9/25/2018 cs262a-F18 Lecture-10 16 

5 . Anomalous Behavior (External Channels) Physical Clocks • Consider a nationwide system of interconnected computers. • We can construct a system of physical clocks which, running quite Suppose a person issues a request A on a computer A, and independently of one another, will satisfy the Strong Clock then telephones a friend in another city to have him issue a Condition. Then we can use physical clocks to eliminate anomalous behavior: request B on a different computer B. It is quite possible for a Ci(t+µ) – Cj(t) > 0, with µ < shortest transmission time request B to receive a lower timestamp and be ordered before request A. • Above condition translates into strong clock condition, since we know that it takes longer than µ to send message, if a b in • Relevant external events may influence the ordering of physical time means that C<a> < C<b> system events! • Properties of clocks: 1. Clock runs continuously. • Two possible solutions: 2. Clock runs at approximately the correct rate. i.e. dCi(t)/dt ≈1 for all t. 1. The user makes sure that the timestamp TB is later than TA 3. Clocks must be synchronized so that Ci(t) ≈ Cj(t) for all i, j, and t. 2. Construct a system of clocks which satisfies the Strong Clock • Two new conditions for physical clocks: Condition: For any event a, b in φ: if a→b then C<a> < C<b> – PC1. There exists a constant ĸ<<1 such that for all i: | dCi(t)/dt -1| < ĸ – PC2. For all i, j: | Ci(t) - Cj(t) | < ε ( ε is a sufficiently small constant ) • Clock Synchronization algorithm: – Send messages so that clocks stay in sync (and always move forward) 9/25/2018 cs262a-F18 Lecture-10 17 9/25/2018 cs262a-F18 Lecture-10 18 General Ideas from Paper Is this a good paper? • Using Virtual Clocks to order events in distributed • What were the authors’ goals? system • What about the evaluation/metrics? • Using Resulting Ordering to build distributed state • Did they convince you that this was a good machines system/approach? • Clock Synchronization with no backtracking • Were there any red-flags? • What mistakes did they make? • Does the system/approach meet the “Test of Time” challenge? • How would you review this paper today? 9/25/2018 cs262a-F18 Lecture-10 19 9/25/2018 cs262a-F18 Lecture-10 20 

6 . Break OCC with Loosely Synchronized Clocks • Basic Idea: Use Loosely Synchronized Clocks to pick ordering of transactions – Ultimately, this is the Serializable order • Slight Twist: Want consistency with real world’s view of transaction order • Two desired consistency properties: – Serializability: The committed transactions can be placed in a total order, called the serialization order, such that the actual effect of running the transactions is the same as running them one at a time in that order – External consistency: The serialization order is such that, if transaction S committed before T began (in real time), S is ordered before T 9/25/2018 cs262a-F18 Lecture-10 21 9/25/2018 cs262a-F18 Lecture-10 22 OCC with Clocks: Basic Sketch Validation during Prepare Phase • Clients perform transactions • This is where the optimism comes in to play Locally on Cached Pages – Set of rules to look at log of previously validated transactions to see if any of them conflict with incoming commit request – Reads and Writes done locally – If rules violated, then “abort”. If rules not violated, the “accept” – When ready to commit, send request to one server which will interact with • Since no locking, it is possible that ongoing all servers which have data in read transactions will conflict and need to be aborted and write set of transaction – Conflicting transactions proceed together – OCC will eventually abort • Receiving server timestamps one of them transaction with local clock, then performs 2-phase – Insufficient information may occasionally cause aborts when commit of transaction unnecessary – Prepare phase: Ask each participating server if it is ok to commit – Validation algorithm is conservative in allowing commit to proceed » Response: server either says “yes” or “no” • Key property: Serializability » If all servers say “yes”, then transaction is committed – In picking serializable order, must make sure that values written by – Commit phase: If all servers say “yes” earlier transactions picked up by later transactions » Note commit in stable log, notify everyone that it is time to commit • Key property: External Consistency » Can be done in background – client can go on immediately – If transaction S committed before T (in real time), then T should not appear before S in final order 9/25/2018 cs262a-F18 Lecture-10 23 9/25/2018 cs262a-F18 Lecture-10 24 

7 . Full Algorithm Simulation Results • Information Flow: • Comparison with Locking Discipline – If using value from uncommitted transaction (because have later timestamp), must fail – If using stale value, must fail • External Consistency: – Make sure that transactions with earlier timestamps that commit later can be reordered to match external appearances • Threshold Truncation – If validation depends on truncated • Overhead of locking involves multiple round-trips, part of log, simply abort while overhead of OCC involves Abort and Retry • Which is better? 9/25/2018 cs262a-F18 Lecture-10 25 9/25/2018 cs262a-F18 Lecture-10 26 Read Only Transactions Is this a good paper? • What about high-percentage of read-only • What were the authors’ goals? transactions? • What about the evaluation/metrics? – ACBL does not need to lock – simply use local state • Did they convince you that this was a good • AOCC Still better for most transaction mixes: system/approach? • Were there any red-flags? • What mistakes did they make? • Does the system/approach meet the “Test of Time” challenge? • How would you review this paper today? 9/25/2018 cs262a-F18 Lecture-10 27 9/25/2018 cs262a-F18 Lecture-10 28