11 Resource Allocation and Scheduling #1

1 . Today’s Papers • Lottery Scheduling: Flexible Proportional-Share Resource Management EECS 262a Carl A. Waldspurger and William E. Weihl. Appears in Proceedings of Advanced Topics in Computer Systems the First USENIX Symposium on Operating Systems Design and Implementation (OSDI), 1994 Lecture 11 • Integrating Multimedia Applications in Hard Real-Time Systems Luca Abeni and Giorgio Buttazzo. Appears in Proceedings of the Real- Time Systems Symposium (RTSS), 1998 Scheduling September 27th, 2018 • Thoughts? John Kubiatowicz Electrical Engineering and Computer Sciences University of California, Berkeley http://www.eecs.berkeley.edu/~kubitron/cs262 9/27/2018 Cs262a-F18 Lecture-11 2 Scheduling Review Multi-Level Feedback Scheduling • Scheduling: selecting a waiting process and allocating a Long-Running resource (e.g., CPU time) to it Compute tasks demoted to low priority • First Come First Serve (FCFS/FIFO) Scheduling: – Run threads to completion in order of submission – Pros: Simple (+) • A scheduling method for exploiting past behavior – Cons: Short jobs get stuck behind long ones (-) – First used in Cambridge Time Sharing System (CTSS) – Multiple queues, each with different priority » Higher priority queues often considered “foreground” tasks • Round-Robin Scheduling: – Each queue has its own scheduling algorithm – Give each thread a small amount of CPU time (quantum) when it » e.g., foreground – Round Robin, background – First Come First Serve executes; cycle between all ready threads » Sometimes multiple RR priorities with quantum increasing exponentially – Pros: Better for short jobs (+) (highest:1ms, next:2ms, next: 4ms, etc.) – Cons: Poor when jobs are same length (-) • Adjust each job’s priority as follows (details vary) – Job starts in highest priority queue – If timeout expires, drop one level – If timeout doesn’t expire, push up one level (or to top) 9/27/2018 Cs262a-F18 Lecture-11 3 9/27/2018 Cs262a-F18 Lecture-11 4 

2 . Lottery Scheduling Lottery Scheduling • Very general, proportional-share scheduling • Give each job some number of lottery tickets algorithm • On each time slice, randomly pick a winning • Problems with traditional schedulers: ticket and give owner the resource – Priority systems are ad hoc at best: highest priority always wins, • On average, resource fraction (CPU time) is starvation risk proportional to number of tickets given to – “Fair share” implemented by adjusting priorities with a feedback each job loop to achieve fairness over the (very) long term (highest priority still wins all the time, but now the Unix priorities are always • Tickets can be used for a wide variety of changing) different resources (uniform) and are – Priority inversion: high-priority jobs can be blocked behind low- priority jobs machine independent (abstract) – Schedulers are complex and difficult to control with hard to understand behaviors 9/27/2018 Cs262a-F18 Lecture-11 5 9/27/2018 Cs262a-F18 Lecture-11 6 How to Assign Tickets? Lottery Scheduling Example • Priority determined by the number of tickets • Assume short jobs get 10 tickets, long jobs get 1 ticket each process has: # short jobs/ % of CPU each % of CPU each – Priority is the relative percentage of all of the tickets short jobs gets long jobs gets # long jobs competing for this resource 1/1 91% 9% • To avoid starvation, every job gets at least 0/2 N/A 50% one ticket (everyone makes progress) 2/0 50% N/A 10/1 9.9% 0.99% 1/10 50% 5% 9/27/2018 Cs262a-F18 Lecture-11 7 9/27/2018 Cs262a-F18 Lecture-11 8 

3 . How Fair is Lottery Scheduling? Ticket Transfer • If client has probability p = (t/T) of winning, then the expected • How to deal with dependencies number of wins (from the binomial distribution) is np – Probabilistically fair • Basic idea: if you are blocked on someone else, – Variance of binomial distribution: σ2 = np(1 – p) give them your tickets – Accuracy improves with √n • Example: client-server • Geometric distribution yields number of tries until first win – Server has no tickets of its own – Clients give server all of their tickets during RPC • Advantage over strict priority scheduling: behaves gracefully – Server’s priority is the sum of the priorities of all of its active clients as load changes – Server can use lottery scheduling to give preferential service to – Adding or deleting a job affects all jobs proportionally, independent of high-priority clients how many tickets each job possesses • Very elegant solution to long-standing problem (not • Big picture answer: mostly accurate, but short-term the first solution however) inaccuracies are possible – See (hidden) Stride Scheduling lecture slides for follow-on solution 9/27/2018 Cs262a-F18 Lecture-11 9 9/27/2018 Cs262a-F18 Lecture-11 10 Ticket Inflation Currencies • Make up your own tickets (print your own money) • Set up an exchange rate with the base currency • Only works among mutually trusting clients • Enables inflation just within a group – Also isolates from other groups • Presumably works best if inflation is temporary • Simplifies mini-lotteries, such as for a mutex • Allows clients to adjust their priority dynamically with zero communication 9/27/2018 Cs262a-F18 Lecture-11 11 9/27/2018 Cs262a-F18 Lecture-11 12 

4 . Compensation Tickets Lottery Scheduling Problems • What happens if a thread is I/O bound and regular • Not as fair as we’d like: blocks before its quantum expires? – mutex comes out 1.8:1 instead of 2:1, while multimedia apps – Without adjustment, this implies that thread gets less than its come out 1.92:1.50:1 instead of 3:2:1 share of the processor • Practice midterm question: • Basic idea: – Are these differences statistically significant? – If you complete fraction f of the quantum, your tickets are inflated by 1/f until the next time you win – Probably are, which would imply that the lottery is biased or that there is a secondary force affecting the relative priority • Example: (e.g., X server) – If B on average uses 1/5 of a quantum, its tickets will be inflated 5x and it will win 5 times as often and get its correct share overall 9/27/2018 Cs262a-F18 Lecture-11 13 9/27/2018 Cs262a-F18 Lecture-11 14 Lottery Scheduling Problems Stride Scheduling • Multimedia app: • Follow on to lottery scheduling (not in paper) – Biased due to X server assuming uniform priority instead of • Basic idea: using tickets – Make a deterministic version to reduce short-term variability – Conclusion: to really work, tickets must be used everywhere – Mark time virtually using “passes” as the unit – every queue is an implicit scheduling decision... every spinlock ignores priority... • A process has a stride, which is the number of passes between executions • Can we force it to be unfair? – Strides are inversely proportional to the number of tickets, – Is there a way to use compensation tickets to get more time, so high priority jobs have low strides and thus run often e.g., quit early to get compensation tickets and then run for the full time next time? • Very regular: a job with priority p will run every 1/p passes • What about kernel cycles? – If a process uses a lot of cycles indirectly, such as through the Ethernet driver, does it get higher priority implicitly? (probably) 9/27/2018 Cs262a-F18 Lecture-11 15 9/27/2018 Cs262a-F18 Lecture-11 16 

5 . Stride Scheduling Algorithm Linux Completely Fair Scheduler (CFS) • Algorithm (roughly): • First appeared in 2.6.23, modified in 2.6.24 – Always pick the job with the lowest pass number • “CFS doesn't track sleeping time and doesn't use – Updates its pass number by adding its stride heuristics to identify interactive tasks—it just makes sure • Similar mechanism to compensation tickets every process gets a fair share of CPU within a set amount of time given the number of runnable processes on the – If a job uses only fraction f, update its pass number by f × stride instead of just using the stride CPU.” • Overall result: • Inspired by Networking “Fair Queueing” – Each process given their fair share of resources – It is far more accurate than lottery scheduling and error can be bounded absolutely instead of probabilistically – Models an “ideal multitasking processor” in which N processes execute simultaneously as if they truly got 1/N of the processor » Tries to give each process an equal fraction of the processor – Priorities reflected by weights such that increasing a task’s priority by 1 always gives the same fractional increase in CPU time – regardless of current priority 9/27/2018 Cs262a-F18 Lecture-11 17 9/27/2018 Cs262a-F18 Lecture-11 18 CFS (Continued) Is this a good paper? • Idea: track amount of “virtual time” received by each process when it is executing • What were the authors’ goals? – Take real execution time, scale by weighting factor • What about the evaluation/metrics? » Higher priority  real time divided by greater weight • Did they convince you that this was a good » Actually – multiply by sum of all weights/current weight – Keep virtual time advancing at same rate system/approach? • Targeted latency (𝑇 ): period of time after which all • Were there any red-flags? processes get to run at least a little • What mistakes did they make? – Each process runs with quantum 𝑊 ⁄∑ 𝑊 𝑇 • Does the system/approach meet the “Test of Time” – Never smaller than “minimum granularity” challenge? • Use of Red-Black tree to hold all runnable processes as sorted on vruntime variable • How would you review this paper today? – O(log n) time to perform insertions/deletions » Cash the item at far left (item with earliest vruntime) – When ready to schedule, grab version with smallest vruntime (which will be item at the far left). 9/27/2018 Cs262a-F18 Lecture-11 19 9/27/2018 Cs262a-F18 Lecture-11 20 

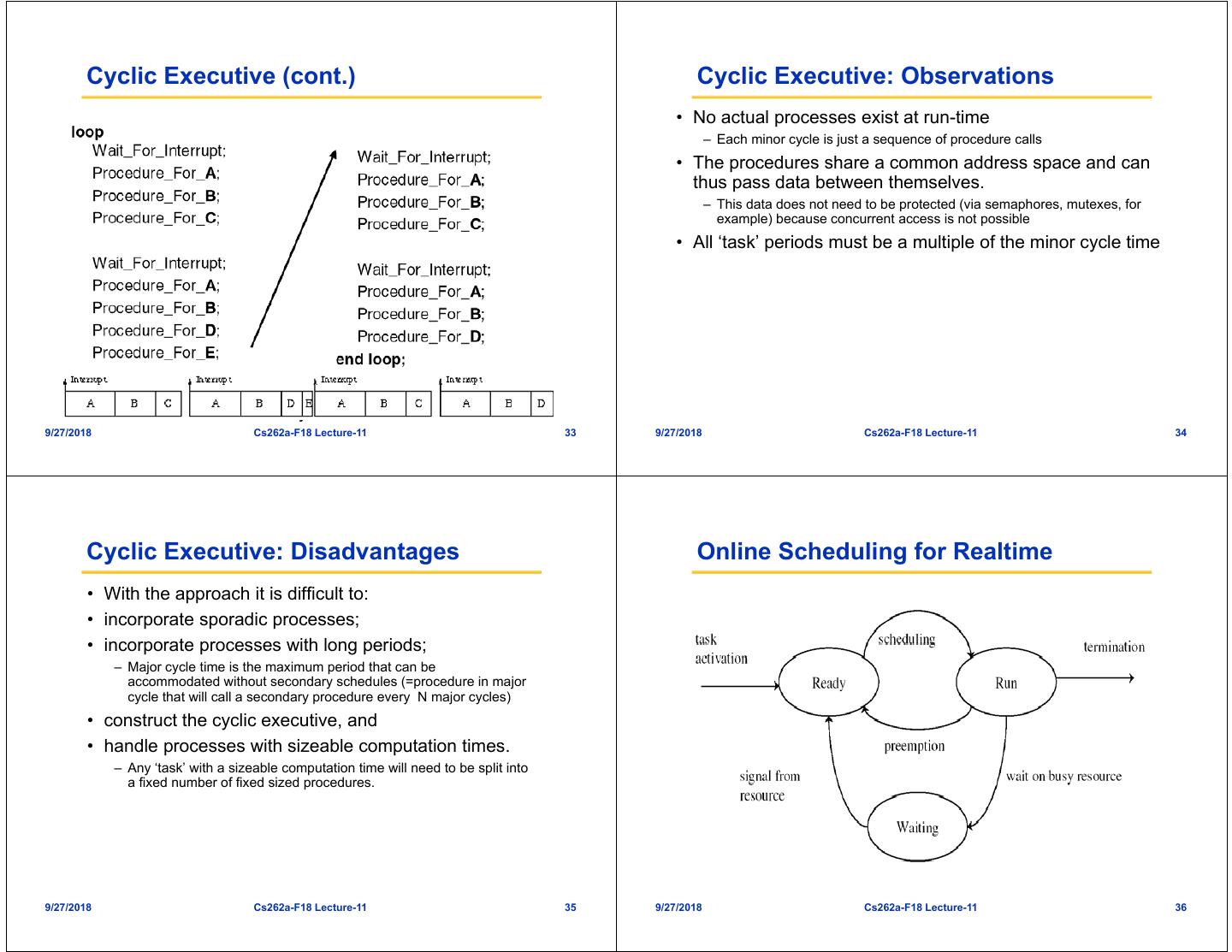
6 . Realtime Sceduling Motivation: Consolidation/Energy Efficiency Recall: Non-Real-Time Scheduling • Primary Goal: maximize performance • Secondary Goal: ensure fairness • Typical metrics: – Minimize response time • Consider current approach with ECUs in cars: – Maximize throughput – Today: 50-100 individual “Engine Control Units” – E.g., FCFS (First-Come-First-Served), RR (Round-Robin) – Trend: Consolidate into smaller number of processors – How to provide guarantees? • Better coordination for hard realtime/streaming media – Save energy rather than “throwing hardware at it” 9/27/2018 Cs262a-F18 Lecture-11 21 9/27/2018 Cs262a-F18 Lecture-11 22 Characteristics of a RTS Typical Realtime Workload Characteristics Slides adapted from Frank Drew • Extreme reliability and safety • Tasks are preemptable, independent with arbitrary arrival – Embedded systems typically control the environment in which they operate (=release) times – Failure to control can result in loss of life, damage to environment or economic loss • Times have deadlines (D) and known computation times (C) • Guaranteed response times – We need to be able to predict with confidence the worst case response times • Tasks execute on a uniprocessor system for systems • Example Setup: – Efficiency is important but predictability is essential » In RTS, performance guarantees are: • Task- and/or class centric • Often ensured a priori » In conventional systems, performance is: • System oriented and often throughput oriented • Post-processing (… wait and see …) • Soft Real-Time – Attempt to meet deadlines with high probability – Important for multimedia applications 9/27/2018 Cs262a-F18 Lecture-11 23 9/27/2018 Cs262a-F18 Lecture-11 24 

7 . Example: Example: Non-preemptive FCFS Scheduling Round-Robin Scheduling 9/27/2018 Cs262a-F18 Lecture-11 25 9/27/2018 Cs262a-F18 Lecture-11 26 Real-Time Scheduling Task Assignment and Scheduling • Primary goal: ensure predictability • Cyclic executive scheduling ( later) • Secondary goal: ensure predictability • Cooperative scheduling • Typical metrics: – scheduler relies on the current process to give up the CPU before it can – Guarantee miss ratio = 0 (hard real-time) start the execution of another process – Guarantee Probability(missed deadline) < X% (firm real- • A static priority-driven scheduler can preempt the current time) process to start a new process. Priorities are set pre- – Minimize miss ratio / maximize completion ration (firm real- execution time) – E.g., Rate-monotonic scheduling (RMS), Deadline Monotonic scheduling – Minimize overall tardiness; maximize overall usefulness (soft (DM) real-time) • E.g., EDF (Earliest Deadline First), LLF (Least Laxity • A dynamic priority-driven scheduler can assign, and First), RMS (Rate-Monotonic Scheduling), DM possibly also redefine, process priorities at run-time. (Deadline Monotonic Scheduling) – Earliest Deadline First (EDF), Least Laxity First (LLF) • Real-time is about enforcing predictability, and does not equal to fast computing!!! 9/27/2018 Cs262a-F18 Lecture-11 27 9/27/2018 Cs262a-F18 Lecture-11 28 

8 . Simple Process Model Performance Metrics • Fixed set of processes (tasks) • Completion ratio / miss ratio • Processes are periodic, with known periods • Maximize total usefulness value (weighted sum) • Processes are independent of each other • Maximize value of a task • System overheads, context switches etc, are ignored • Minimize lateness (zero cost) • Minimize error (imprecise tasks) • Processes have a deadline equal to their period • Feasibility (all tasks meet their deadlines) – i.e., each process must complete before its next release • Processes have fixed worst-case execution time (WCET) 9/27/2018 Cs262a-F18 Lecture-11 29 9/27/2018 Cs262a-F18 Lecture-11 30 Scheduling Approaches (Hard RTS) Cyclic Executive Approach • Off-line scheduling / analysis (static analysis + static scheduling) – All tasks, times and priorities given a priori (before system startup) – Time-driven; schedule computed and hardcoded (before system startup) • Clock-driven (time-driven) Process Period Comp. Time scheduling algorithm – E.g., Cyclic Executives – Inflexible • Off-line algorithm A 25 10 – May be combined with static or dynamic scheduling approaches • Minor Cycle (e.g. 25ms) - • Fixed priority scheduling (static analysis + dynamic scheduling) gcd of all periods B 25 8 – All tasks, times and priorities given a priori (before system startup) • Major Cycle (e.g. 100ms) - – Priority-driven, dynamic(!) scheduling lcm of all periods » The schedule is constructed by the OS scheduler at run time C 50 5 – For hard / safety critical systems Construction of a cyclic executive – E.g., RMA/RMS (Rate Monotonic Analysis / Rate Monotonic Scheduling) is equivalent to bin packing D 50 4 • Dynamic priority scheduling – Tasks times may or may not be known – Assigns priorities based on the current state of the system E 100 2 – For hard / best effort systems – E.g., Least Completion Time (LCT), Earliest Deadline First (EDF), Least Slack Time (LST) 9/27/2018 Cs262a-F18 Lecture-11 31 9/27/2018 Cs262a-F18 Lecture-11 32 

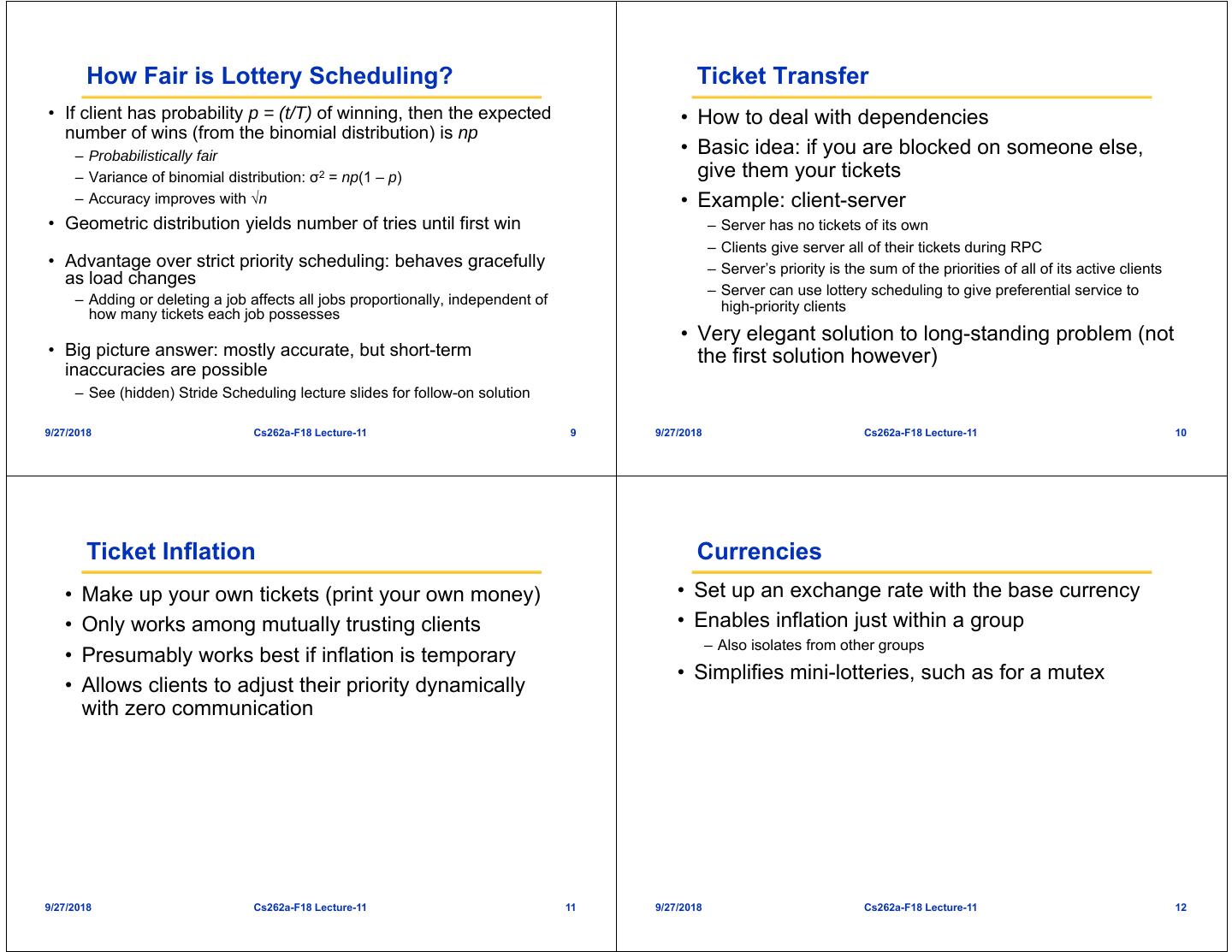
9 . Cyclic Executive (cont.) Cyclic Executive: Observations • No actual processes exist at run-time – Each minor cycle is just a sequence of procedure calls • The procedures share a common address space and can thus pass data between themselves. – This data does not need to be protected (via semaphores, mutexes, for example) because concurrent access is not possible • All ‘task’ periods must be a multiple of the minor cycle time Frank Drews Real-Time Systems 9/27/2018 Cs262a-F18 Lecture-11 33 9/27/2018 Cs262a-F18 Lecture-11 34 Cyclic Executive: Disadvantages Online Scheduling for Realtime • With the approach it is difficult to: • incorporate sporadic processes; • incorporate processes with long periods; – Major cycle time is the maximum period that can be accommodated without secondary schedules (=procedure in major cycle that will call a secondary procedure every N major cycles) • construct the cyclic executive, and • handle processes with sizeable computation times. – Any ‘task’ with a sizeable computation time will need to be split into a fixed number of fixed sized procedures. 9/27/2018 Cs262a-F18 Lecture-11 35 9/27/2018 Cs262a-F18 Lecture-11 36 

10 . Schedulability Test Rate Monotonic Analysis: Assumptions • Test to determine whether a feasible schedule exists A1: Tasks are periodic (activated at a constant rate). • Sufficient Test Period Pi = Interval between two consecutive activations of task Ti – If test is passed, then tasks are definitely schedulable A2: All instances of a periodic task have Ti – If test is not passed, tasks may be schedulable, but not necessarily the same computation time Ci A3: All instances of a periodic task have T the same relative deadline, • Necessary Test i which is equal to the period ( Di  Pi ) – If test is passed, tasks may be schedulable, but not necessarily A4: All tasks are independent – If test is not passed, tasks are definitely not schedulable (i.e., no precedence constraints and no resource constraints) • Exact Test (= Necessary + Sufficient) – The task set is schedulable if and only if it passes the test. Implicit assumptions: A5: Tasks are preemptable A6: No task can suspend itself A7: All tasks are released as soon as they arrive A8: All overhead in the kernel is assumed to be zero (or part of )Ci 9/27/2018 Cs262a-F18 Lecture-11 37 9/27/2018 Cs262a-F18 Lecture-11 38 Rate Monotonic Scheduling: Principle Example: Rate Monotonic Scheduling • Principle: Each process is assigned a (unique) priority • Example instance based on its period (rate); always execute active job with highest priority • The shorter the period the higher the priority Pi  Pj   i   j ( 1 = low priority) • W.l.o.g. number the tasks in reverse order of priority Process Period Priority () Name • RMA - Gant chart A 25 5 T1 B 60 3 T3 C 42 4 T2 D 105 1 T5 E 75 2 T4 9/27/2018 Cs262a-F18 Lecture-11 39 9/27/2018 Cs262a-F18 Lecture-11 40 

11 . Example: Rate Monotonic Scheduling Utilization Ti  ( Pi , Ci ) Pi  period Ci  processing time Ci Ui  Utilization of task Ti Deadline Miss Pi 2 T1  (4,1) Example : U 2   0.4 5 T2  (5,2) T1  (4,1) T3  (7,2) 0 5 10 15 T2  (5,2) response time of job J 3,1 T3  (7,2) 0 5 10 15 9/27/2018 Cs262a-F18 Lecture-11 41 9/27/2018 Cs262a-F18 Lecture-11 42 RMS: Schedulability Test RMS Schedulability Example Theorem (Utilization-based Schedulability Test): • For our failed example earlier: A periodic task set T1 , T2 ,  , Tnwith Di  Pi , 1  i  n, T1  (4,1), T2  (5,2), T3  (7,2) is schedulable by the rate monotonic scheduling algorithm if: C1 C C  1 4  0.25, 2  2 5  0.4, 3  2 7  0.286 P1 P2 P3 n  Ci  • The schedulability test requires:     n(21/ n  1), n  1,2,  i 1  Pi  n  Ci    P   n(2 1/ n  1), n  1,2,  i 1  i  This schedulability test is “sufficient”! Does not satisfy • Hence, we get schedulability condition! • For harmonic periods ( evenly divides ), the utilization bound is 100% 𝑃 𝑃 3  Ci  •   P   0.936  3(2 1/ 3  1)  0.780 n(21/ n  1)  ln 2 for n   i 1  i  9/27/2018 Cs262a-F18 Lecture-11 43 9/27/2018 Cs262a-F18 Lecture-11 44 

12 . EDF: Assumptions EDF Scheduling: Principle A1: Tasks are periodic or aperiodic. • Preemptive priority-based dynamic scheduling Period Pi = Interval between two consequtive activations of task Ti • Each task is assigned a (current) priority based on how A2: All instances of a periodic task have Ti close the absolute deadline is. the same computation time Ci • The scheduler always schedules the active task with the A3: All instances of a periodic task have T the same relative deadline, i which is equal to the period ( Di  Pi ) closest absolute deadline. A4: All tasks are independent (i.e., no precedence constraints and no resource constraints) T1  (4,1) Implicit assumptions: A5: Tasks are preemptable T2  (5,2) A6: No task can suspend itself A7: All tasks are released as soon as they arrive T3  (7,2) A8: All overhead in the kernel is assumed to be zero (or part of )Ci 0 5 10 15 9/27/2018 Cs262a-F18 Lecture-11 45 9/27/2018 Cs262a-F18 Lecture-11 46 EDF: Schedulability Test EDF Optimality Theorem (Utilization-based Schedulability Test): EDF Properties A task set T1 , T2 ,  , Tnwith Di  Pi is schedulable by • EDF is optimal with respect to feasibility (i.e., the earliest deadline first (EDF) scheduling algorithm schedulability) if: • EDF is optimal with respect to minimizing the maximum lateness n  Ci    D   1 i 1  i  Exact schedulability test (necessary + sufficient) Proof: [Liu and Layland, 1973] 9/27/2018 Cs262a-F18 Lecture-11 47 9/27/2018 Cs262a-F18 Lecture-11 48 

13 . EDF Example: Domino Effect Constant Bandwidth Server • Intuition: give fixed share of CPU to certain of jobs – Good for tasks with probabilistic resource requirements • Basic approach: Slots (called “servers”) scheduled with EDF, rather than jobs – CBS Server defined by two parameters: Qs and Ts – Mechanism for tracking processor usage so that no more than Qs CPU seconds used every Ts seconds (or whatever measurement you like) when there is demand. Otherwise get to use processor as you like • Since using EDF, can mix hard-realtime and soft realtime: EDF minimizes lateness of the “most tardy task” [Dertouzos, 1974] 9/27/2018 Cs262a-F18 Lecture-11 49 9/27/2018 Cs262a-F18 Lecture-11 50 Comparison of CBS with EDF in Overload Is this a good paper? • What were the authors’ goals? • What about the evaluation/metrics? • Did they convince you that this was a good system/approach? • Were there any red-flags? • What mistakes did they make? • Does the system/approach meet the “Test of Time” Overload with EDF Overload with CBS challenge? • How would you review this paper today? • If scheduled items do not meet EDF schedulability: – EDF yields unpredictable results when overload starts and stops – CBS servers provide better isolation • Isolation particularly important when deadlines crucial – I.e. hard realtime tasks 9/27/2018 Cs262a-F18 Lecture-11 51 9/27/2018 Cs262a-F18 Lecture-11 52