Wasserstein GAN

1 . Wasserstein GAN Martin Arjovsky1 , Soumith Chintala2 , and L´eon Bottou1,2 arXiv:1701.07875v3 [stat.ML] 6 Dec 2017 1 Courant Institute of Mathematical Sciences 2 Facebook AI Research 1 Introduction The problem this paper is concerned with is that of unsupervised learning. Mainly, what does it mean to learn a probability distribution? The classical answer to this is to learn a probability density. This is often done by defining a parametric family of densities (Pθ )θ∈Rd and finding the one that maximized the likelihood on our data: if we have real data examples {x(i) }mi=1 , we would solve the problem m 1 max log Pθ (x(i) ) θ∈Rd m i=1 If the real data distribution Pr admits a density and Pθ is the distribution of the parametrized density Pθ , then, asymptotically, this amounts to minimizing the Kullback-Leibler divergence KL(Pr Pθ ). For this to make sense, we need the model density Pθ to exist. This is not the case in the rather common situation where we are dealing with distributions supported by low dimensional manifolds. It is then unlikely that the model manifold and the true distribution’s support have a non-negligible intersection (see [1]), and this means that the KL distance is not defined (or simply infinite). The typical remedy is to add a noise term to the model distribution. This is why virtually all generative models described in the classical machine learning literature include a noise component. In the simplest case, one assumes a Gaussian noise with relatively high bandwidth in order to cover all the examples. It is well known, for instance, that in the case of image generation models, this noise degrades the quality of the samples and makes them blurry. For example, we can see in the recent paper [23] that the optimal standard deviation of the noise added to the model when maximizing likelihood is around 0.1 to each pixel in a generated image, when the pixels were already normalized to be in the range [0, 1]. This is a very high amount of noise, so much that when papers report the samples of their models, they don’t add the noise term on which they report likelihood numbers. In other words, the added noise term is clearly incorrect for the problem, but is needed to make the maximum likelihood approach work. 1 

2 . Rather than estimating the density of Pr which may not exist, we can define a random variable Z with a fixed distribution p(z) and pass it through a paramet- ric function gθ : Z → X (typically a neural network of some kind) that directly generates samples following a certain distribution Pθ . By varying θ, we can change this distribution and make it close to the real data distribution Pr . This is useful in two ways. First of all, unlike densities, this approach can represent distribu- tions confined to a low dimensional manifold. Second, the ability to easily generate samples is often more useful than knowing the numerical value of the density (for example in image superresolution or semantic segmentation when considering the conditional distribution of the output image given the input image). In general, it is computationally difficult to generate samples given an arbitrary high dimensional density [16]. Variational Auto-Encoders (VAEs) [9] and Generative Adversarial Networks (GANs) [4] are well known examples of this approach. Because VAEs focus on the approximate likelihood of the examples, they share the limitation of the stan- dard models and need to fiddle with additional noise terms. GANs offer much more flexibility in the definition of the objective function, including Jensen-Shannon [4], and all f -divergences [17] as well as some exotic combinations [6]. On the other hand, training GANs is well known for being delicate and unstable, for reasons theoretically investigated in [1]. In this paper, we direct our attention on the various ways to measure how close the model distribution and the real distribution are, or equivalently, on the various ways to define a distance or divergence ρ(Pθ , Pr ). The most fundamental difference between such distances is their impact on the convergence of sequences of probability distributions. A sequence of distributions (Pt )t∈N converges if and only if there is a distribution P∞ such that ρ(Pt , P∞ ) tends to zero, something that depends on how exactly the distance ρ is defined. Informally, a distance ρ induces a weaker topology when it makes it easier for a sequence of distribution to converge.1 Section 2 clarifies how popular probability distances differ in that respect. In order to optimize the parameter θ, it is of course desirable to define our model distribution Pθ in a manner that makes the mapping θ → Pθ continuous. Continuity means that when a sequence of parameters θt converges to θ, the distributions Pθt also converge to Pθ . However, it is essential to remember that the notion of the convergence of the distributions Pθt depends on the way we compute the distance between distributions. The weaker this distance, the easier it is to define a continuous mapping from θ-space to Pθ -space, since it’s easier for the distributions to converge. The main reason we care about the mapping θ → Pθ to be continuous is as follows. If ρ is our notion of distance between two distributions, we would like to have a loss function θ → ρ(Pθ , Pr ) that is continuous, and this is equivalent to having the mapping θ → Pθ be continuous when using the distance between distributions ρ. 1 More exactly, the topology induced by ρ is weaker than that induced by ρ when the set of convergent sequences under ρ is a superset of that under ρ . 2 

3 . The contributions of this paper are: • In Section 2, we provide a comprehensive theoretical analysis of how the Earth Mover (EM) distance behaves in comparison to popular probability distances and divergences used in the context of learning distributions. • In Section 3, we define a form of GAN called Wasserstein-GAN that mini- mizes a reasonable and efficient approximation of the EM distance, and we theoretically show that the corresponding optimization problem is sound. • In Section 4, we empirically show that WGANs cure the main training prob- lems of GANs. In particular, training WGANs does not require maintaining a careful balance in training of the discriminator and the generator, and does not require a careful design of the network architecture either. The mode dropping phenomenon that is typical in GANs is also drastically reduced. One of the most compelling practical benefits of WGANs is the ability to continuously estimate the EM distance by training the discriminator to op- timality. Plotting these learning curves is not only useful for debugging and hyperparameter searches, but also correlate remarkably well with the observed sample quality. 2 Different Distances We now introduce our notation. Let X be a compact metric set (such as the space of images [0, 1]d ) and let Σ denote the set of all the Borel subsets of X . Let Prob(X ) denote the space of probability measures defined on X . We can now define elementary distances and divergences between two distributions Pr , Pg ∈ Prob(X ): • The Total Variation (TV) distance δ(Pr , Pg ) = sup |Pr (A) − Pg (A)| . A∈Σ • The Kullback-Leibler (KL) divergence Pr (x) KL(Pr Pg ) = log Pr (x)dµ(x) , Pg (x) where both Pr and Pg are assumed to be absolutely continuous, and therefore admit densities, with respect to a same measure µ defined on X .2 The KL divergence is famously assymetric and possibly infinite when there are points such that Pg (x) = 0 and Pr (x) > 0. 2 Recall that a probability distribution P ∈ Prob(X ) admits a density p (x) with respect to µ, r r that is, ∀A ∈ Σ, Pr (A) = A Pr (x)dµ(x), if and only it is absolutely continuous with respect to µ, that is, ∀A ∈ Σ, µ(A) = 0 ⇒ Pr (A) = 0 . 3 

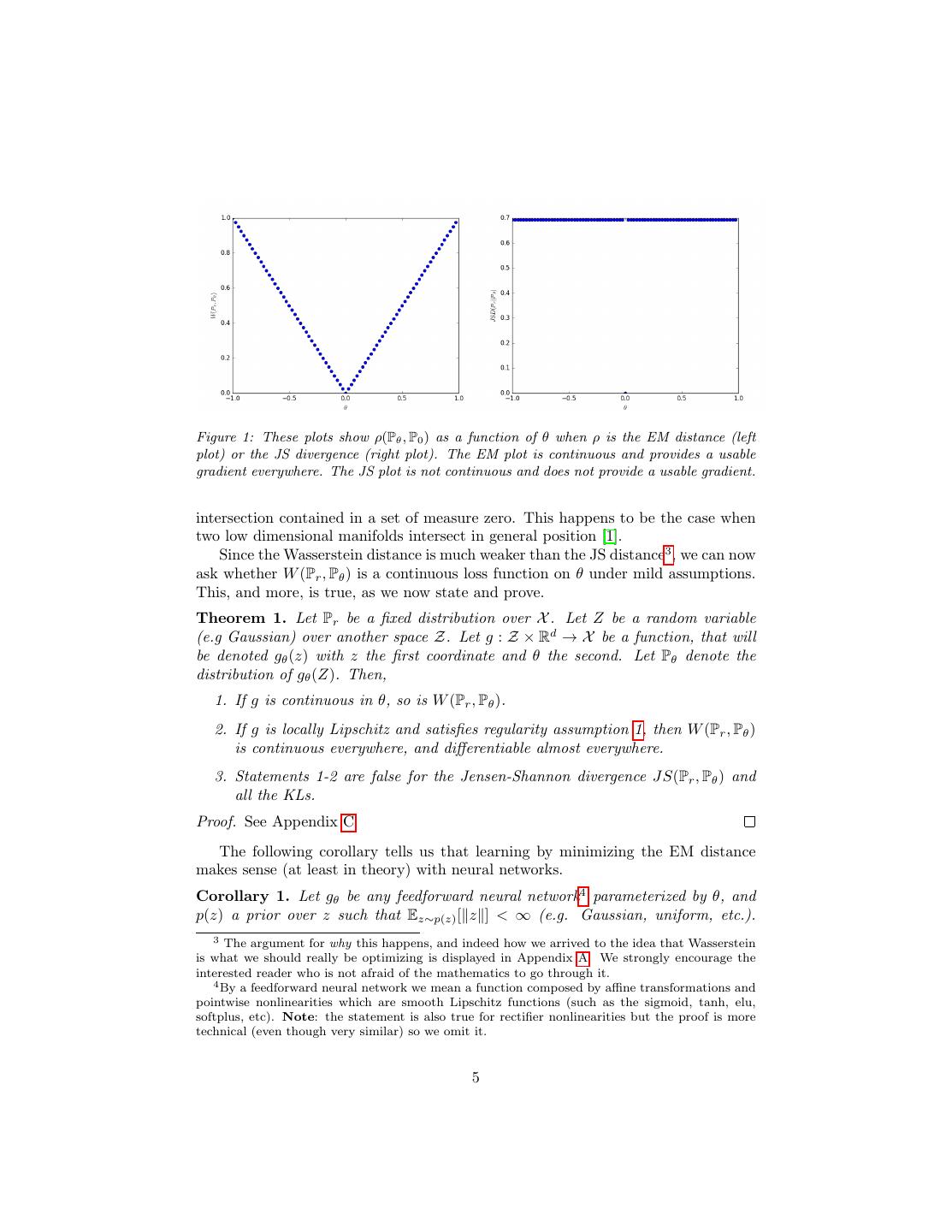
4 . • The Jensen-Shannon (JS) divergence JS(Pr , Pg ) = KL(Pr Pm ) + KL(Pg Pm ) , where Pm is the mixture (Pr + Pg )/2. This divergence is symmetrical and always defined because we can choose µ = Pm . • The Earth-Mover (EM) distance or Wasserstein-1 W (Pr , Pg ) = inf E(x,y)∼γ x−y , (1) γ∈Π(Pr ,Pg ) where Π(Pr , Pg ) denotes the set of all joint distributions γ(x, y) whose marginals are respectively Pr and Pg . Intuitively, γ(x, y) indicates how much “mass” must be transported from x to y in order to transform the distributions Pr into the distribution Pg . The EM distance then is the “cost” of the optimal transport plan. The following example illustrates how apparently simple sequences of probability distributions converge under the EM distance but do not converge under the other distances and divergences defined above. Example 1 (Learning parallel lines). Let Z ∼ U [0, 1] the uniform distribution on the unit interval. Let P0 be the distribution of (0, Z) ∈ R2 (a 0 on the x-axis and the random variable Z on the y-axis), uniform on a straight vertical line passing through the origin. Now let gθ (z) = (θ, z) with θ a single real parameter. It is easy to see that in this case, • W (P0 , Pθ ) = |θ|, log 2 if θ = 0 , • JS(P0 , Pθ ) = 0 if θ = 0 , +∞ if θ = 0 , • KL(Pθ P0 ) = KL(P0 Pθ ) = 0 if θ = 0 , 1 if θ = 0 , • and δ(P0 , Pθ ) = 0 if θ = 0 . When θt → 0, the sequence (Pθt )t∈N converges to P0 under the EM distance, but does not converge at all under either the JS, KL, reverse KL, or TV divergences. Figure 1 illustrates this for the case of the EM and JS distances. Example 1 gives us a case where we can learn a probability distribution over a low dimensional manifold by doing gradient descent on the EM distance. This cannot be done with the other distances and divergences because the resulting loss function is not even continuous. Although this simple example features distributions with disjoint supports, the same conclusion holds when the supports have a non empty 4 

5 .Figure 1: These plots show ρ(Pθ , P0 ) as a function of θ when ρ is the EM distance (left plot) or the JS divergence (right plot). The EM plot is continuous and provides a usable gradient everywhere. The JS plot is not continuous and does not provide a usable gradient. intersection contained in a set of measure zero. This happens to be the case when two low dimensional manifolds intersect in general position [1]. Since the Wasserstein distance is much weaker than the JS distance3 , we can now ask whether W (Pr , Pθ ) is a continuous loss function on θ under mild assumptions. This, and more, is true, as we now state and prove. Theorem 1. Let Pr be a fixed distribution over X . Let Z be a random variable (e.g Gaussian) over another space Z. Let g : Z × Rd → X be a function, that will be denoted gθ (z) with z the first coordinate and θ the second. Let Pθ denote the distribution of gθ (Z). Then, 1. If g is continuous in θ, so is W (Pr , Pθ ). 2. If g is locally Lipschitz and satisfies regularity assumption 1, then W (Pr , Pθ ) is continuous everywhere, and differentiable almost everywhere. 3. Statements 1-2 are false for the Jensen-Shannon divergence JS(Pr , Pθ ) and all the KLs. Proof. See Appendix C The following corollary tells us that learning by minimizing the EM distance makes sense (at least in theory) with neural networks. Corollary 1. Let gθ be any feedforward neural network4 parameterized by θ, and p(z) a prior over z such that Ez∼p(z) [ z ] < ∞ (e.g. Gaussian, uniform, etc.). 3 The argument for why this happens, and indeed how we arrived to the idea that Wasserstein is what we should really be optimizing is displayed in Appendix A. We strongly encourage the interested reader who is not afraid of the mathematics to go through it. 4 By a feedforward neural network we mean a function composed by affine transformations and pointwise nonlinearities which are smooth Lipschitz functions (such as the sigmoid, tanh, elu, softplus, etc). Note: the statement is also true for rectifier nonlinearities but the proof is more technical (even though very similar) so we omit it. 5 

6 .Then assumption 1 is satisfied and therefore W (Pr , Pθ ) is continuous everywhere and differentiable almost everywhere. Proof. See Appendix C All this shows that EM is a much more sensible cost function for our problem than at least the Jensen-Shannon divergence. The following theorem describes the relative strength of the topologies induced by these distances and divergences, with KL the strongest, followed by JS and TV, and EM the weakest. Theorem 2. Let P be a distribution on a compact space X and (Pn )n∈N be a sequence of distributions on X . Then, considering all limits as n → ∞, 1. The following statements are equivalent • δ(Pn , P) → 0 with δ the total variation distance. • JS(Pn , P) → 0 with JS the Jensen-Shannon divergence. 2. The following statements are equivalent • W (Pn , P) → 0. D D • Pn −→ P where −→ represents convergence in distribution for random variables. 3. KL(Pn P) → 0 or KL(P Pn ) → 0 imply the statements in (1). 4. The statements in (1) imply the statements in (2). Proof. See Appendix C This highlights the fact that the KL, JS, and TV distances are not sensible cost functions when learning distributions supported by low dimensional manifolds. However the EM distance is sensible in that setup. This obviously leads us to the next section where we introduce a practical approximation of optimizing the EM distance. 3 Wasserstein GAN Again, Theorem 2 points to the fact that W (Pr , Pθ ) might have nicer properties when optimized than JS(Pr , Pθ ). However, the infimum in (1) is highly intractable. On the other hand, the Kantorovich-Rubinstein duality [22] tells us that W (Pr , Pθ ) = sup Ex∼Pr [f (x)] − Ex∼Pθ [f (x)] (2) f L ≤1 where the supremum is over all the 1-Lipschitz functions f : X → R. Note that if we replace f L ≤ 1 for f L ≤ K (consider K-Lipschitz for some constant K), then we end up with K · W (Pr , Pg ). Therefore, if we have a parameterized family of 6 

7 .functions {fw }w∈W that are all K-Lipschitz for some K, we could consider solving the problem max Ex∼Pr [fw (x)] − Ez∼p(z) [fw (gθ (z)] (3) w∈W and if the supremum in (2) is attained for some w ∈ W (a pretty strong assumption akin to what’s assumed when proving consistency of an estimator), this process would yield a calculation of W (Pr , Pθ ) up to a multiplicative constant. Further- more, we could consider differentiating W (Pr , Pθ ) (again, up to a constant) by back-proping through equation (2) via estimating Ez∼p(z) [∇θ fw (gθ (z))]. While this is all intuition, we now prove that this process is principled under the optimality assumption. Theorem 3. Let Pr be any distribution. Let Pθ be the distribution of gθ (Z) with Z a random variable with density p and gθ a function satisfying assumption 1. Then, there is a solution f : X → R to the problem max Ex∼Pr [f (x)] − Ex∼Pθ [f (x)] f L ≤1 and we have ∇θ W (Pr , Pθ ) = −Ez∼p(z) [∇θ f (gθ (z))] when both terms are well-defined. Proof. See Appendix C Now comes the question of finding the function f that solves the maximization problem in equation (2). To roughly approximate this, something that we can do is train a neural network parameterized with weights w lying in a compact space W and then backprop through Ez∼p(z) [∇θ fw (gθ (z))], as we would do with a typical GAN. Note that the fact that W is compact implies that all the functions fw will be K-Lipschitz for some K that only depends on W and not the individual weights, therefore approximating (2) up to an irrelevant scaling factor and the capacity of the ‘critic’ fw . In order to have parameters w lie in a compact space, something simple we can do is clamp the weights to a fixed box (say W = [−0.01, 0.01]l ) after each gradient update. The Wasserstein Generative Adversarial Network (WGAN) procedure is described in Algorithm 1. Weight clipping is a clearly terrible way to enforce a Lipschitz constraint. If the clipping parameter is large, then it can take a long time for any weights to reach their limit, thereby making it harder to train the critic till optimality. If the clipping is small, this can easily lead to vanishing gradients when the number of layers is big, or batch normalization is not used (such as in RNNs). We experimented with simple variants (such as projecting the weights to a sphere) with little difference, and we stuck with weight clipping due to its simplicity and already good performance. However, we do leave the topic of enforcing Lipschitz constraints in a neural network setting for further investigation, and we actively encourage interested researchers to improve on this method. 7 

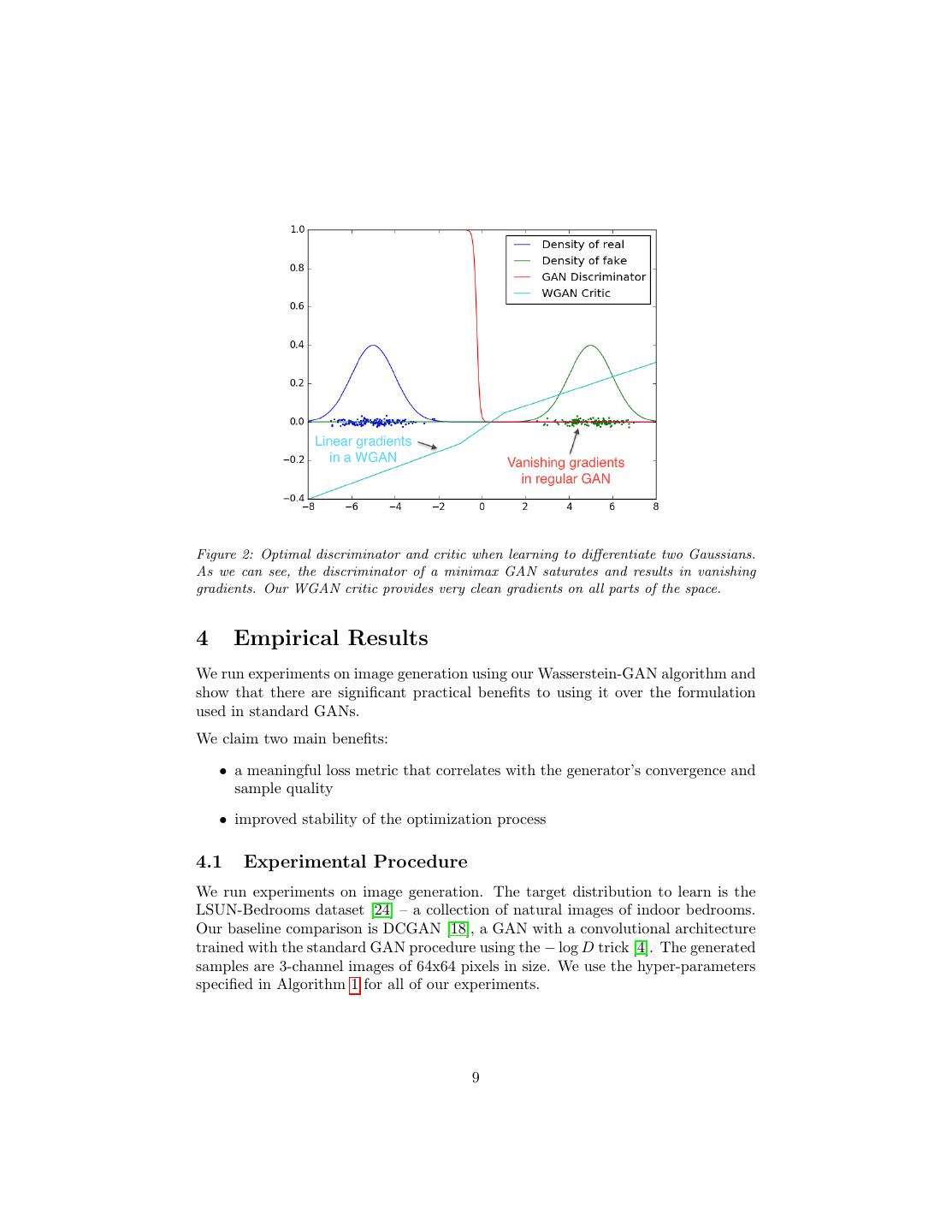
8 .Algorithm 1 WGAN, our proposed algorithm. All experiments in the paper used the default values α = 0.00005, c = 0.01, m = 64, ncritic = 5. Require: : α, the learning rate. c, the clipping parameter. m, the batch size. ncritic , the number of iterations of the critic per generator iteration. Require: : w0 , initial critic parameters. θ0 , initial generator’s parameters. 1: while θ has not converged do 2: for t = 0, ..., ncritic do 3: Sample {x(i) }mi=1 ∼ Pr a batch from the real data. 4: Sample {z (i) }m i=1 ∼ p(z) a batch of prior samples. 1 m (i) 1 m (i) 5: gw ← ∇w m i=1 fw (x ) − m i=1 fw (gθ (z )) 6: w ← w + α · RMSProp(w, gw ) 7: w ← clip(w, −c, c) 8: end for 9: Sample {z (i) }m i=1 ∼ p(z) a batch of prior samples. 1 m (i) 10: gθ ← −∇θ m i=1 fw (gθ (z )) 11: θ ← θ − α · RMSProp(θ, gθ ) 12: end while The fact that the EM distance is continuous and differentiable a.e. means that we can (and should) train the critic till optimality. The argument is simple, the more we train the critic, the more reliable gradient of the Wasserstein we get, which is actually useful by the fact that Wasserstein is differentiable almost everywhere. For the JS, as the discriminator gets better the gradients get more reliable but the true gradient is 0 since the JS is locally saturated and we get vanishing gradients, as can be seen in Figure 1 of this paper and Theorem 2.4 of [1]. In Figure 2 we show a proof of concept of this, where we train a GAN discriminator and a WGAN critic till optimality. The discriminator learns very quickly to distinguish between fake and real, and as expected provides no reliable gradient information. The critic, however, can’t saturate, and converges to a linear function that gives remarkably clean gradients everywhere. The fact that we constrain the weights limits the possible growth of the function to be at most linear in different parts of the space, forcing the optimal critic to have this behaviour. Perhaps more importantly, the fact that we can train the critic till optimality makes it impossible to collapse modes when we do. This is due to the fact that mode collapse comes from the fact that the optimal generator for a fixed discriminator is a sum of deltas on the points the discriminator assigns the highest values, as observed by [4] and highlighted in [11]. In the following section we display the practical benefits of our new algorithm, and we provide an in-depth comparison of its behaviour and that of traditional GANs. 8 

9 .Figure 2: Optimal discriminator and critic when learning to differentiate two Gaussians. As we can see, the discriminator of a minimax GAN saturates and results in vanishing gradients. Our WGAN critic provides very clean gradients on all parts of the space. 4 Empirical Results We run experiments on image generation using our Wasserstein-GAN algorithm and show that there are significant practical benefits to using it over the formulation used in standard GANs. We claim two main benefits: • a meaningful loss metric that correlates with the generator’s convergence and sample quality • improved stability of the optimization process 4.1 Experimental Procedure We run experiments on image generation. The target distribution to learn is the LSUN-Bedrooms dataset [24] – a collection of natural images of indoor bedrooms. Our baseline comparison is DCGAN [18], a GAN with a convolutional architecture trained with the standard GAN procedure using the − log D trick [4]. The generated samples are 3-channel images of 64x64 pixels in size. We use the hyper-parameters specified in Algorithm 1 for all of our experiments. 9 

10 .Figure 3: Training curves and samples at different stages of training. We can see a clear correlation between lower error and better sample quality. Upper left: the generator is an MLP with 4 hidden layers and 512 units at each layer. The loss decreases constistently as training progresses and sample quality increases. Upper right: the generator is a standard DCGAN. The loss decreases quickly and sample quality increases as well. In both upper plots the critic is a DCGAN without the sigmoid so losses can be subjected to comparison. Lower half: both the generator and the discriminator are MLPs with substantially high learning rates (so training failed). Loss is constant and samples are constant as well. The training curves were passed through a median filter for visualization purposes. 4.2 Meaningful loss metric Because the WGAN algorithm attempts to train the critic f (lines 2–8 in Algo- rithm 1) relatively well before each generator update (line 10 in Algorithm 1), the loss function at this point is an estimate of the EM distance, up to constant factors related to the way we constrain the Lipschitz constant of f . Our first experiment illustrates how this estimate correlates well with the quality of the generated samples. Besides the convolutional DCGAN architecture, we also ran experiments where we replace the generator or both the generator and the critic by 4-layer ReLU-MLP with 512 hidden units. Figure 3 plots the evolution of the WGAN estimate (3) of the EM distance during WGAN training for all three architectures. The plots clearly show that these curves correlate well with the visual quality of the generated samples. To our knowledge, this is the first time in GAN literature that such a property is shown, where the loss of the GAN shows properties of convergence. This property is extremely useful when doing research in adversarial networks as one does not need 10 

11 .Figure 4: JS estimates for an MLP generator (upper left) and a DCGAN generator (upper right) trained with the standard GAN procedure. Both had a DCGAN discriminator. Both curves have increasing error. Samples get better for the DCGAN but the JS estimate increases or stays constant, pointing towards no significant correlation between sample quality and loss. Bottom: M LP with both generator and discriminator. The curve goes up and down regardless of sample quality. All training curves were passed through the same median filter as in Figure 3. to stare at the generated samples to figure out failure modes and to gain information on which models are doing better over others. However, we do not claim that this is a new method to quantitatively evaluate generative models yet. The constant scaling factor that depends on the critic’s architecture means it’s hard to compare models with different critics. Even more, in practice the fact that the critic doesn’t have infinite capacity makes it hard to know just how close to the EM distance our estimate really is. This being said, we have succesfully used the loss metric to validate our experiments repeatedly and without failure, and we see this as a huge improvement in training GANs which previously had no such facility. In contrast, Figure 4 plots the evolution of the GAN estimate of the JS distance during GAN training. More precisely, during GAN training, the discriminator is trained to maximize L(D, gθ ) = Ex∼Pr [log D(x)] + Ex∼Pθ [log(1 − D(x))] which is is a lower bound of 2JS(Pr , Pθ )−2 log 2. In the figure, we plot the quantity 1 2 L(D, gθ ) + log 2, which is a lower bound of the JS distance. This quantity clearly correlates poorly the sample quality. Note also that the 11 

12 .JS estimate usually stays constant or goes up instead of going down. In fact it often remains very close to log 2 ≈ 0.69 which is the highest value taken by the JS distance. In other words, the JS distance saturates, the discriminator has zero loss, and the generated samples are in some cases meaningful (DCGAN generator, top right plot) and in other cases collapse to a single nonsensical image [4]. This last phenomenon has been theoretically explained in [1] and highlighted in [11]. When using the − log D trick [4], the discriminator loss and the generator loss are different. Figure 8 in Appendix E reports the same plots for GAN training, but using the generator loss instead of the discriminator loss. This does not change the conclusions. Finally, as a negative result, we report that WGAN training becomes unstable at times when one uses a momentum based optimizer such as Adam [8] (with β1 > 0) on the critic, or when one uses high learning rates. Since the loss for the critic is nonstationary, momentum based methods seemed to perform worse. We identified momentum as a potential cause because, as the loss blew up and samples got worse, the cosine between the Adam step and the gradient usually turned negative. The only places where this cosine was negative was in these situations of instability. We therefore switched to RMSProp [21] which is known to perform well even on very nonstationary problems [13]. 4.3 Improved stability One of the benefits of WGAN is that it allows us to train the critic till optimality. When the critic is trained to completion, it simply provides a loss to the generator that we can train as any other neural network. This tells us that we no longer need to balance generator and discriminator’s capacity properly. The better the critic, the higher quality the gradients we use to train the generator. We observe that WGANs are much more robust than GANs when one varies the architectural choices for the generator. We illustrate this by running experi- ments on three generator architectures: (1) a convolutional DCGAN generator, (2) a convolutional DCGAN generator without batch normalization and with a con- stant number of filters, and (3) a 4-layer ReLU-MLP with 512 hidden units. The last two are known to perform very poorly with GANs. We keep the convolutional DCGAN architecture for the WGAN critic or the GAN discriminator. Figures 5, 6, and 7 show samples generated for these three architectures using both the WGAN and GAN algorithms. We refer the reader to Appendix F for full sheets of generated samples. Samples were not cherry-picked. In no experiment did we see evidence of mode collapse for the WGAN algorithm. 12 

13 .Figure 5: Algorithms trained with a DCGAN generator. Left: WGAN algorithm. Right: standard GAN formulation. Both algorithms produce high quality samples. Figure 6: Algorithms trained with a generator without batch normalization and constant number of filters at every layer (as opposed to duplicating them every time as in [18]). Aside from taking out batch normalization, the number of parameters is therefore reduced by a bit more than an order of magnitude. Left: WGAN algorithm. Right: standard GAN formulation. As we can see the standard GAN failed to learn while the WGAN still was able to produce samples. Figure 7: Algorithms trained with an MLP generator with 4 layers and 512 units with ReLU nonlinearities. The number of parameters is similar to that of a DCGAN, but it lacks a strong inductive bias for image generation. Left: WGAN algorithm. Right: standard GAN formulation. The WGAN method still was able to produce samples, lower quality than the DCGAN, and of higher quality than the MLP of the standard GAN. Note the significant degree of mode collapse in the GAN MLP. 5 Related Work There’s been a number of works on the so called Integral Probability Metrics (IPMs) [15]. Given F a set of functions from X to R, we can define dF (Pr , Pθ ) = sup Ex∼Pr [f (x)] − Ex∼Pθ [f (x)] (4) f ∈F as an integral probability metric associated with the function class F. It is easily verified that if for every f ∈ F we have −f ∈ F (such as all examples we’ll consider), then dF is nonnegative, satisfies the triangular inequality, and is symmetric. Thus, dF is a pseudometric over Prob(X ). While IPMs might seem to share a similar formula, as we will see different classes of functions can yeald to radically different metrics. • By the Kantorovich-Rubinstein duality [22], we know that W (Pr , Pθ ) = dF (Pr , Pθ ) 13 

14 . when F is the set of 1-Lipschitz functions. Furthermore, if F is the set of K- Lipschitz functions, we get K · W (Pr , Pθ ) = dF (Pr , Pθ ). • When F is the set of all measurable functions bounded between -1 and 1 (or all continuous functions between -1 and 1), we retrieve dF (Pr , Pθ ) = δ(Pr , Pθ ) the total variation distance [15]. This already tells us that going from 1-Lipschitz to 1-Bounded functions drastically changes the topology of the space, and the regularity of dF (Pr , Pθ ) as a loss function (as by Theorems 1 and 2). • Energy-based GANs (EBGANs) [25] can be thought of as the generative ap- proach to the total variation distance. This connection is stated and proven in depth in Appendix D. At the core of the connection is that the discriminator will play the role of f maximizing equation (4) while its only restriction is be- ing between 0 and m for some constant m. This will yeald the same behaviour as being restricted to be between −1 and 1 up to a constant scaling factor irrelevant to optimization. Thus, when the discriminator approaches opti- mality the cost for the generator will aproximate the total variation distance δ(Pr , Pθ ). Since the total variation distance displays the same regularity as the JS, it can be seen that EBGANs will suffer from the same problems of classical GANs regarding not being able to train the discriminator till optimality and thus limiting itself to very imperfect gradients. • Maximum Mean Discrepancy (MMD) [5] is a specific case of integral proba- bility metrics when F = {f ∈ H : f ∞ ≤ 1} for H some Reproducing Kernel Hilbert Space (RKHS) associated with a given kernel k : X × X → R. As proved on [5] we know that MMD is a proper metric and not only a pseudomet- ric when the kernel is universal. In the specific case where H = L2 (X , m) for m the normalized Lebesgue measure on X , we know that {f ∈ Cb (X ), f ∞ ≤ 1} will be contained in F, and therefore dF (Pr , Pθ ) ≤ δ(Pr , Pθ ) so the regularity of the MMD distance as a loss function will be at least as bad as the one of the total variation. Nevertheless this is a very extreme case, since we would need a very powerful kernel to approximate the whole L2 . However, even Gaus- sian kernels are able to detect tiny noise patterns as recently evidenced by [20]. This points to the fact that especially with low bandwidth kernels, the distance might be close to a saturating regime similar as with total variation or the JS. This obviously doesn’t need to be the case for every kernel, and figuring out how and which different MMDs are closer to Wasserstein or total variation distances is an interesting topic of research. The great aspect of MMD is that via the kernel trick there is no need to train a separate network to maximize equation (4) for the ball of a RKHS. However, this has the disadvantage that evaluating the MMD distance has computational cost that grows quadratically with the amount of samples used to estimate the expectations in (4). This last point makes MMD have limited scalability, and is sometimes inapplicable to many real life applications be- cause of it. There are estimates with linear computational cost for the MMD 14 

15 . [5] which in a lot of cases makes MMD very useful, but they also have worse sample complexity. • Generative Moment Matching Networks (GMMNs) [10, 2] are the genera- tive counterpart of MMD. By backproping through the kernelized formula for equation (4), they directly optimize dM M D (Pr , Pθ ) (the IPM when F is as in the previous item). As mentioned, this has the advantage of not requiring a separate network to approximately maximize equation (4). However, GMMNs have enjoyed limited applicability. Partial explanations for their unsuccess are the quadratic cost as a function of the number of samples and vanishing gra- dients for low-bandwidth kernels. Furthermore, it may be possible that some kernels used in practice are unsuitable for capturing very complex distances in high dimensional sample spaces such as natural images. This is properly justified by the fact that [19] shows that for the typical Gaussian MMD test to be reliable (as in it’s power as a statistical test approaching 1), we need the number of samples to grow linearly with the number of dimensions. Since the MMD computational cost grows quadratically with the number of samples in the batch used to estimate equation (4), this makes the cost of having a reliable estimator grow quadratically with the number of dimensions, which makes it very inapplicable for high dimensional problems. Indeed, for some- thing as standard as 64x64 images, we would need minibatches of size at least 4096 (without taking into account the constants in the bounds of [19] which would make this number substantially larger) and a total cost per iteration of 40962 , over 5 orders of magnitude more than a GAN iteration when using the standard batch size of 64. That being said, these numbers can be a bit unfair to the MMD, in the sense that we are comparing empirical sample complexity of GANs with the theoretical sample complexity of MMDs, which tends to be worse. However, in the original GMMN paper [10] they indeed used a minibatch of size 1000, much larger than the standard 32 or 64 (even when this incurred in quadratic computational cost). While estimates that have linear computational cost as a function of the number of samples exist [5], they have worse sample complexity, and to the best of our knowledge they haven’t been yet applied in a generative context such as in GMMNs. On another great line of research, the recent work of [14] has explored the use of Wasserstein distances in the context of learning for Restricted Boltzmann Machines for discrete spaces. The motivations at a first glance might seem quite different, since the manifold setting is restricted to continuous spaces and in finite discrete spaces the weak and strong topologies (the ones of W and JS respectively) coincide. However, in the end there is more in commmon than not about our motivations. We both want to compare distributions in a way that leverages the geometry of the underlying space, and Wasserstein allows us to do exactly that. Finally, the work of [3] shows new algorithms for calculating Wasserstein dis- tances between different distributions. We believe this direction is quite important, and perhaps could lead to new ways of evaluating generative models. 15 

16 .6 Conclusion We introduced an algorithm that we deemed WGAN, an alternative to traditional GAN training. In this new model, we showed that we can improve the stability of learning, get rid of problems like mode collapse, and provide meaningful learn- ing curves useful for debugging and hyperparameter searches. Furthermore, we showed that the corresponding optimization problem is sound, and provided exten- sive theoretical work highlighting the deep connections to other distances between distributions. Acknowledgments We would like to thank Mohamed Ishmael Belghazi, Emily Denton, Ian Goodfel- low, Ishaan Gulrajani, Alex Lamb, David Lopez-Paz, Eric Martin, Maxime Oquab, Aditya Ramesh, Ronan Riochet, Uri Shalit, Pablo Sprechmann, Arthur Szlam, Ruo- han Wang, for helpful comments and advice. References [1] Martin Arjovsky and L´eon Bottou. Towards principled methods for training generative adversarial networks. In International Conference on Learning Rep- resentations, 2017. Under review. [2] Gintare Karolina Dziugaite, Daniel M. Roy, and Zoubin Ghahramani. Train- ing generative neural networks via maximum mean discrepancy optimization. CoRR, abs/1505.03906, 2015. [3] Aude Genevay, Marco Cuturi, Gabriel Peyr´e, and Francis Bach. Stochastic op- timization for large-scale optimal transport. In D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, editors, Advances in Neural Information Processing Systems 29, pages 3440–3448. Curran Associates, Inc., 2016. [4] Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde- Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adver- sarial nets. In Advances in Neural Information Processing Systems 27, pages 2672–2680. Curran Associates, Inc., 2014. [5] Arthur Gretton, Karsten M. Borgwardt, Malte J. Rasch, Bernhard Sch¨olkopf, and Alexander Smola. A kernel two-sample test. J. Mach. Learn. Res., 13:723– 773, 2012. [6] Ferenc Huszar. How (not) to train your generative model: Scheduled sampling, likelihood, adversary? CoRR, abs/1511.05101, 2015. [7] Shizuo Kakutani. Concrete representation of abstract (m)-spaces (a characteri- zation of the space of continuous functions). Annals of Mathematics, 42(4):994– 1024, 1941. 16 

17 . [8] Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimiza- tion. CoRR, abs/1412.6980, 2014. [9] Diederik P. Kingma and Max Welling. Auto-encoding variational bayes. CoRR, abs/1312.6114, 2013. [10] Yujia Li, Kevin Swersky, and Rich Zemel. Generative moment matching net- works. In Proceedings of the 32nd International Conference on Machine Learn- ing (ICML-15), pages 1718–1727. JMLR Workshop and Conference Proceed- ings, 2015. [11] Luke Metz, Ben Poole, David Pfau, and Jascha Sohl-Dickstein. Unrolled gen- erative adversarial networks. Corr, abs/1611.02163, 2016. [12] Paul Milgrom and Ilya Segal. Envelope theorems for arbitrary choice sets. Econometrica, 70(2):583–601, 2002. [13] Volodymyr Mnih, Adri` a Puigdom`enech Badia, Mehdi Mirza, Alex Graves, Tim- othy P. Lillicrap, Tim Harley, David Silver, and Koray Kavukcuoglu. Asyn- chronous methods for deep reinforcement learning. In Proceedings of the 33nd International Conference on Machine Learning, ICML 2016, New York City, NY, USA, June 19-24, 2016, pages 1928–1937, 2016. [14] Gr´egoire Montavon, Klaus-Robert M¨ uller, and Marco Cuturi. Wasserstein training of restricted boltzmann machines. In D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, editors, Advances in Neural Information Processing Systems 29, pages 3718–3726. Curran Associates, Inc., 2016. [15] Alfred M¨uller. Integral probability metrics and their generating classes of func- tions. Advances in Applied Probability, 29(2):429–443, 1997. [16] Radford M. Neal. Annealed importance sampling. Statistics and Computing, 11(2):125–139, April 2001. [17] Sebastian Nowozin, Botond Cseke, and Ryota Tomioka. f-gan: Training genera- tive neural samplers using variational divergence minimization. pages 271–279, 2016. [18] Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representa- tion learning with deep convolutional generative adversarial networks. CoRR, abs/1511.06434, 2015. [19] Aaditya Ramdas, Sashank J. Reddi, Barnabas Poczos, Aarti Singh, and Larry Wasserman. On the high-dimensional power of linear-time kernel two-sample testing under mean-difference alternatives. Corr, abs/1411.6314, 2014. [20] Dougal J Sutherland, Hsiao-Yu Tung, Heiko Strathmann, Soumyajit De, Aa- ditya Ramdas, Alex Smola, and Arthur Gretton. Generative models and model criticism via optimized maximum mean discrepancy. In International Confer- ence on Learning Representations, 2017. Under review. 17 

18 .[21] T. Tieleman and G. Hinton. Lecture 6.5—RmsProp: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Networks for Machine Learning, 2012. [22] C´edric Villani. Optimal Transport: Old and New. Grundlehren der mathema- tischen Wissenschaften. Springer, Berlin, 2009. [23] Yuhuai Wu, Yuri Burda, Ruslan Salakhutdinov, and Roger B. Grosse. On the quantitative analysis of decoder-based generative models. CoRR, abs/1611.04273, 2016. [24] Fisher Yu, Yinda Zhang, Shuran Song, Ari Seff, and Jianxiong Xiao. LSUN: Construction of a large-scale image dataset using deep learning with humans in the loop. Corr, abs/1506.03365, 2015. [25] Junbo Zhao, Michael Mathieu, and Yann LeCun. Energy-based generative adversarial network. Corr, abs/1609.03126, 2016. 18 

19 .A Why Wasserstein is indeed weak We now introduce our notation. Let X ⊆ Rd be a compact set (such as [0, 1]d the space of images). We define Prob(X ) to be the space of probability measures over X . We note Cb (X ) = {f : X → R, f is continuous and bounded} Note that if f ∈ Cb (X ), we can define f ∞ = maxx∈X |f (x)|, since f is bounded. With this norm, the space (Cb (X ), · ∞ ) is a normed vector space. As for any normed vector space, we can define its dual Cb (X )∗ = {φ : Cb (X ) → R, φ is linear and continuous} and give it the dual norm φ = supf ∈Cb (X ), f ∞ ≤1 |φ(f )|. With this definitions, (Cb (X )∗ , · ) is another normed space. Now let µ be a signed measure over X , and let us define the total variation distance µ TV = sup |µ(A)| A⊆X where the supremum is taken all Borel sets in X . Since the total variation is a norm, then if we have Pr and Pθ two probability distributions over X , δ(Pr , Pθ ) := Pr − Pθ TV is a distance in Prob(X ) (called the total variation distance). We can consider Φ : (Prob(X ), δ) → (Cb (X )∗ , · ) where Φ(P)(f ) := Ex∼P [f (x)] is a linear function over Cb (X ). The Riesz Represen- tation theorem ([7], Theorem 10) tells us that Φ is an isometric immersion. This tells us that we can effectively consider Prob(X ) with the total variation distance as a subset of Cb (X )∗ with the norm distance. Thus, just to accentuate it one more time, the total variation over Prob(X ) is exactly the norm distance over Cb (X )∗ . Let us stop for a second and analyze what all this technicality meant. The main thing to carry is that we introduced a distance δ over probability distributions. When looked as a distance over a subset of Cb (X )∗ , this distance gives the norm topology. The norm topology is very strong. Therefore, we can expect that not many functions θ → Pθ will be continuous when measuring distances between dis- tributions with δ. As we will show later in Theorem 2, δ gives the same topology as the Jensen-Shannon divergence, pointing to the fact that the JS is a very strong distance, and is thus more propense to give a discontinuous loss function. Now, all dual spaces (such as Cb (X )∗ and thus Prob(X )) have a strong topology (induced by the norm), and a weak* topology. As the name suggests, the weak* topology is much weaker than the strong topology. In the case of Prob(X ), the strong topology is given by the total variation distance, and the weak* topology is given by the Wasserstein distance (among others) [22]. 19 

20 .B Assumption definitions Assumption 1. Let g : Z × Rd → X be locally Lipschitz between finite dimensional vector spaces. We will denote gθ (z) it’s evaluation on coordinates (z, θ). We say that g satisfies assumption 1 for a certain probability distribution p over Z if there are local Lipschitz constants L(θ, z) such that Ez∼p [L(θ, z)] < +∞ C Proofs of things Proof of Theorem 1. Let θ and θ be two parameter vectors in Rd . Then, we will first attempt to bound W (Pθ , Pθ ), from where the theorem will come easily. The main element of the proof is the use of the coupling γ, the distribution of the joint (gθ (Z), gθ (Z)), which clearly has γ ∈ Π(Pθ , Pθ ). By the definition of the Wasserstein distance, we have W (Pθ , Pθ ) ≤ x − y dγ X ×X = E(x,y)∼γ [ x − y ] = Ez [ gθ (z) − gθ (z) ] If g is continuous in θ, then gθ (z) →θ→θ gθ (z), so gθ − gθ → 0 pointwise as functions of z. Since X is compact, the distance of any two elements in it has to be uniformly bounded by some constant M , and therefore gθ (z) − gθ (z) ≤ M for all θ and z uniformly. By the bounded convergence theorem, we therefore have W (Pθ , Pθ ) ≤ Ez [ gθ (z) − gθ (z) ] →θ→θ 0 Finally, we have that |W (Pr , Pθ ) − W (Pr , Pθ )| ≤ W (Pθ , Pθ ) →θ→θ 0 proving the continuity of W (Pr , Pθ ). Now let g be locally Lipschitz. Then, for a given pair (θ, z) there is a constant L(θ, z) and an open set U such that (θ, z) ∈ U , such that for every (θ , z ) ∈ U we have gθ (z) − gθ (z ) ≤ L(θ, z)( θ − θ + z − z ) By taking expectations and z = z we Ez [ gθ (z) − gθ (z) ] ≤ θ − θ Ez [L(θ, z)] whenever (θ , z) ∈ U . Therefore, we can define Uθ = {θ |(θ , z) ∈ U }. It’s easy to see that since U was open, Uθ is as well. Furthermore, by assumption 1, we can define L(θ) = Ez [L(θ, z)] and achieve |W (Pr , Pθ ) − W (Pr , Pθ )| ≤ W (Pθ , Pθ ) ≤ L(θ) θ − θ 20 

21 .for all θ ∈ Uθ , meaning that W (Pr , Pθ ) is locally Lipschitz. This obviously implies that W (Pr , Pθ ) is everywhere continuous, and by Radamacher’s theorem we know it has to be differentiable almost everywhere. The counterexample for item 3 of the Theorem is indeed Example 1. Proof of Corollary 1. We begin with the case of smooth nonlinearities. Since g is C 1 as a function of (θ, z) then for any fixed (θ, z) we have L(θ, Z) ≤ ∇θ,x gθ (z) + is an acceptable local Lipschitz constant for all > 0. Therefore, it suffices to prove Ez∼p(z) [ ∇θ,z gθ (z) ] < +∞ H If H is the number of layers we know that ∇z gθ (z) = k=1 Wk Dk where Wk are the weight matrices and Dk is are the diagonal Jacobians of the nonlinearities. Let fi:j be the application of layers i to j inclusively (e.g. gθ = f1:H ). Then, H ∇Wk gθ (z) = i=k+1 Wi Di Dk f1:k−1 (z). We recall that if L is the Lipschitz k−1 constant of the nonlinearity, then Di ≤ L and f1:k−1 (z) ≤ z Lk−1 i=1 Wi . Putting this together, H H H ∇z,θ gθ (z) ≤ Wi Di + Wi Di Dk f1:k−1 (z) i=1 k=1 i=k+1 K H k−1 H ≤ LH Wi + z LH Wi Wi i=H k=1 i=1 i=k+1 H H k−1 H If C1 (θ) = LH i=1 Wi and C2 (θ) = k=1 LH i=1 Wi i=k+1 Wi then Ez∼p(z) [ ∇θ,z gθ (z) ] ≤ C1 (θ) + C2 (θ)Ez∼p(z) [ z ] < +∞ finishing the proof Proof of Theorem 2. 1. • (δ(Pn , P) → 0 ⇒ JS(Pn , P) → 0) — Let Pm be the mixture dis- tribution Pm = 21 Pn + 21 P (note that Pm depends on n). It is easily verified that δ(Pm , Pn ) ≤ δ(Pn , P), and in particular this tends to 0 (as does δ(Pm , P)). We now show this for completeness. Let µ be a signed measure, we define µ T V = supA⊆X |µ(A)|. for all Borel sets A. In this case, δ(Pm , Pn ) = Pm − Pn T V 1 1 = P + Pn − Pn T V 2 2 1 = P − Pn T V 2 1 = δ(Pn , P) ≤ δ(Pn , P) 2 21 

22 . dPn Let fn = dP m be the Radon-Nykodim derivative between Pn and the mixture. Note that by construction for every Borel set A we have Pn (A) ≤ 2Pm (A). If A = {fn > 3} then we get Pn (A) = fn dPm ≥ 3Pm (A) A which implies Pm (A) = 0. This means that fn is bounded by 3 Pm (and therefore Pn and P)-almost everywhere. We could have done this for any constant larger than 2 but for our purposes 3 will sufice. Let > 0 fixed, and An = {fn > 1 + }. Then, Pn (An ) = fn dPm ≥ (1 + )Pm (An ) An Therefore, Pm (An ) ≤ Pn (An ) − Pm (An ) ≤ |Pn (An ) − Pm (An )| ≤ δ(Pn , Pm ) ≤ δ(Pn , P). Which implies Pm (Am ) ≤ 1 δ(Pn , P). Furthermore, Pn (An ) ≤ Pm (An ) + |Pn (An ) − Pm (An )| 1 ≤ δ(Pn , P) + δ(Pn , Pm ) 1 ≤ δ(Pn , P) + δ(Pn , P) 1 ≤ + 1 δ(Pn , P) We now can see that KL(Pn Pm ) = log(fn ) dPn ≤ log(1 + ) + log(fn ) dPn An ≤ log(1 + ) + log(3)Pn (An ) 1 ≤ log(1 + ) + log(3) + 1 δ(Pn , P) Taking limsup we get 0 ≤ lim sup KL(Pn Pm ) ≤ log(1 + ) for all > 0, which means KL(Pn Pm ) → 0. dP In the same way, we can define gn = dP m , and 2Pm ({gn > 3}) ≥ P({gn > 3}) ≥ 3Pm ({gn > 3}) 22 

23 . meaning that Pm ({gn > 3}) = 0 and therefore gn is bounded by 3 almost everywhere for Pn , Pm and P. With the same calculation, Bn = {gn > 1 + } and P(Bn ) = gn dPm ≥ (1 + )Pm (Bn ) Bn 1 so Pm (Bn ) ≤ δ(P, Pm ) → 0, and therefore P(Bn ) → 0. We can now show KL(P Pm ) = log(gn ) dP ≤ log(1 + ) + log(gn ) dP Bn ≤ log(1 + ) + log(3)P(Bn ) so we achieve 0 ≤ lim sup KL(P Pm ) ≤ log(1+ ) and then KL(P Pm ) → 0. Finally, we conclude 1 1 JS(Pn , P) = KL(Pn Pm ) + KL(P Pm ) → 0 2 2 • (JS(Pn , P) → 0 ⇒ δ(Pn , P) → 0) — by a simple application of the triangular and Pinsker’s inequalities we get δ(Pn , P) ≤ δ(Pn , Pm ) + δ(P, Pm ) 1 1 ≤ KL(Pn Pm ) + KL(P Pm ) 2 2 ≤ 2 JS(Pn , P) → 0 2. This is a long known fact that W metrizes the weak* topology of (C(X ), · ∞ ) on Prob(X ), and by definition this is the topology of convergence in distribution. A proof of this can be found (for example) in [22]. 3. This is a straightforward application of Pinsker’s inequality 1 δ(Pn , P) ≤ KL(Pn P) → 0 2 1 δ(P, Pn ) ≤ KL(P Pn ) → 0 2 4. This is trivial by recalling the fact that δ and W give the strong and weak* topologies on the dual of (C(X ), · ∞ ) when restricted to Prob(X ). 23 

24 .Proof of Theorem 3. Let us define V (f˜, θ) = Ex∼Pr [f˜(x)] − Ex∼Pθ [f˜(x)] = Ex∼P [f˜(x)] − Ez∼p(z) [f˜(gθ (z))] r where f˜ lies in F = {f˜ : X → R , f˜ ∈ Cb (X ), f˜ L ≤ 1} and θ ∈ Rd . Since X is compact, we know by the Kantorovich-Rubenstein duality [22] that there is an f ∈ F that attains the value W (Pr , Pθ ) = sup V (f˜, θ) = V (f, θ) f˜∈F Let us define X ∗ (θ) = {f ∈ F : V (f, θ) = W (Pr , Pθ )}. By the above point we know then that X ∗ (θ) is non-empty. We know that by a simple envelope theorem ([12], Theorem 1) that ∇θ W (Pr , Pθ ) = ∇θ V (f, θ) for any f ∈ X ∗ (θ) when both terms are well-defined. Let f ∈ X ∗ (θ), which we knows exists since X ∗ (θ) is non-empty for all θ. Then, we get ∇θ W (Pr , Pθ ) = ∇θ V (f, θ) = ∇θ [Ex∼Pr [f (x)] − Ez∼p(z) [f (gθ (z))] = −∇θ Ez∼p(z) [f (gθ (z))] under the condition that the first and last terms are well-defined. The rest of the proof will be dedicated to show that −∇θ Ez∼p(z) [f (gθ (z))] = −Ez∼p(z) [∇θ f (gθ (z))] (5) when the right hand side is defined. For the reader who is not interested in such technicalities, he or she can skip the rest of the proof. Since f ∈ F, we know that it is 1-Lipschitz. Furthermore, gθ (z) is locally Lipschitz as a function of (θ, z). Therefore, f (gθ (z)) is locally Lipschitz on (θ, z) with constants L(θ, z) (the same ones as g). By Radamacher’s Theorem, f (gθ (z)) has to be differentiable almost everywhere for (θ, z) jointly. Rewriting this, the set A = {(θ, z) : f ◦ g is not differentiable} has measure 0. By Fubini’s Theorem, this implies that for almost every θ the section Aθ = {z : (θ, z) ∈ A} has measure 0. Let’s now fix a θ0 such that the measure of Aθ0 is null (such as when the right hand side of equation (5) is well defined). For this θ0 we have ∇θ f (gθ (z))|θ0 is well-defined for almost any z, and since p(z) has a density, it is defined p(z)-a.e. By assumption 1 we know that Ez∼p(z) [ ∇θ f (gθ (z))|θ0 ] ≤ Ez∼p(z) [L(θ0 , z)] < +∞ so Ez∼p(z) [∇θ f (gθ (z))|θ0 ] is well-defined for almost every θ0 . Now, we can see Ez∼p(z) [f (gθ (z))] − Ez∼p(z) [f (gθ0 (z))] − (θ − θ0 ), Ez∼p(z) [∇θ f (gθ (z))|θ0 ] (6) θ − θ0 24 

25 . f (gθ (z)) − f (gθ0 (z)) − (θ − θ0 ), ∇θ f (gθ (z))|θ0 = Ez∼p(z) θ − θ0 By differentiability, the term inside the integral converges p(z)-a.e. to 0 as θ → θ0 . Furthermore, f (gθ (z)) − f (gθ0 (z)) − (θ − θ0 ), ∇θ f (gθ (z))|θ0 θ − θ0 θ − θ0 L(θ0 , z) + θ − θ0 ∇θ f (gθ (z))|θ0 ≤ θ − θ0 ≤ 2L(θ0 , z) and since Ez∼p(z) [2L(θ0 , z)] < +∞ by assumption 1, we get by dominated conver- gence that Equation 6 converges to 0 as θ → θ0 so ∇θ Ez∼p(z) [f (gθ (z))] = Ez∼p(z) [∇θ f (gθ (z))] for almost every θ, and in particular when the right hand side is well defined. Note that the mere existance of the left hand side (meaning the differentiability a.e. of Ez∼p(z) [f (gθ (z))]) had to be proven, which we just did. 25 

26 .D Energy-based GANs optimize total variation In this appendix we show that under an optimal discriminator, energy-based GANs (EBGANs) [25] optimize the total variation distance between the real and generated distributions. Energy-based GANs are trained in a similar fashion to GANs, only under a different loss function. They have a discriminator D who tries to minimize LD (D, gθ ) = Ex∼Pr [D(x)] + Ez∼p(z) [[m − D(gθ (z))]+ ] for some m > 0 and [x]+ = max(0, x) and a generator network gθ that’s trained to minimize LG (D, gθ ) = Ez∼p(z) [D(gθ (z))] − Ex∼Pr [D(x)] Very importantly, D is constrained to be non-negative, since otherwise the trivial solution for D would be to set everything to arbitrarily low values. The original EBGAN paper used only Ez∼p(z) [D(gθ (z))] for the loss of the generator, but this is obviously equivalent to our definition since the term Ex∼Pr [D(x)] does not depen- dent on θ for a fixed discriminator (such as when backproping to the generator in EBGAN training) and thus minimizing one or the other is equivalent. We say that a measurable function D∗ : X → [0, +∞) is optimal for gθ (or Pθ ) if LD (D∗ , gθ ) ≤ LD (D, gθ ) for all other measurable functions D. We show that such a discriminator always exists for any two distributions Pr and Pθ , and that under such a discriminator, LG (D∗ , gθ ) is proportional to δ(Pr , Pθ ). As a simple corollary, we get the fact that LG (D∗ , gθ ) attains its minimum value if and only if δ(Pr , Pθ ) is at its minimum value, which is 0, and Pr = Pθ (Theorems 1-2 of [25]). Theorem 4. Let Pr be a the real data distribution over a compact space X . Let gθ : Z → X be a measurable function (such as any neural network). Then, an optimal discriminator D∗ exists for Pr and Pθ , and m LG (D∗ , gθ ) = δ(Pr , Pθ ) 2 Proof. First, we prove that there exists an optimal discriminator. Let D : X → [0, +∞) be a measurable function, then D (x) := min(D(x), m) is also a measurable function, and LD (D , gθ ) ≤ LD (D, gθ ). Therefore, a function D∗ : X → [0, +∞) is optimal if and only if D∗ is. Furthermore, it is optimal if and only if LD (D∗ , gθ ) ≤ LD (D, gθ ) for all D : X → [0, m]. We are then interested to see if there’s an optimal discriminator for the problem min0≤D(x)≤m LD (D, gθ ). Note now that if 0 ≤ D(x) ≤ m we have LD (D, gθ ) = Ex∼Pr [D(x)] + Ez∼p(z) [[m − D(gθ (z))]+ ] = Ex∼Pr [D(x)] + Ez∼p(z) [m − D(gθ (z))] = m + Ex∼Pr [D(x)] − Ez∼p(z) [D(gθ (z))] = m + Ex∼Pr [D(x)] − Ex∼Pθ [D(x)] 26 

27 .Therefore, we know that inf LD (D, gθ ) = m + inf Ex∼Pr [D(x)] − Ex∼Pθ [D(x)] 0≤D(x)≤m 0≤D(x)≤m =m+ inf Ex∼Pr [D(x)] − Ex∼Pθ [D(x)] −m m 2 ≤D(x)≤ 2 m =m+ inf Ex∼Pr [f (x)] − Ex∼Pθ [f (x)] 2 −1≤f (x)≤1 The interesting part is that inf Ex∼Pr [f (x)] − Ex∼Pθ [f (x)] = −δ(Pr , Pθ ) (7) −1≤f (x)≤1 and there is an f ∗ : X → [−1, 1] such that Ex∼Pr [f ∗ (x)]−Ex∼Pθ [f ∗ (x)] = −δ(Pr , Pθ ). This is a long known fact, found for example in [22], but we prove it later for completeness. In that case, we define D∗ (x) = m ∗ m 2 f (x) + 2 . We then have 0 ≤ D(x) ≤ m and LD (D∗ , gθ ) = m + Ex∼Pr [D∗ (x)] − Ex∼Pθ [D∗ (x)] m = m + Ex∼Pr [D∗ (x)] − Ex∼Pθ [f ∗ (x)] 2 m = m − δ(Pr , Pθ ) 2 = inf LD (D, gθ ) 0≤D(x)≤m This shows that D∗ is optimal and LD (D∗ , gθ ) = m − m 2 δ(Pr , Pθ ). Furthermore, LG (D∗ , gθ ) = Ez∼p(z) [D∗ (gθ (z))] − Ex∼Pr [D∗ (x)] = −LD (D∗ , gθ ) + m m = δ(Pr , Pg ) 2 concluding the proof. For completeness, we now show a proof for equation (7) and the existence of said f ∗ that attains the value of the infimum. Take µ = Pr − Pθ , which is a signed measure, and (P, Q) its Hahn decomposition. Then, we can define f ∗ := ✶Q − ✶P . By construction, then EEx∼Pr [f ∗ (x)] − Ex∼Pθ [f ∗ (x)] = f ∗ dµ = µ(Q) − µ(P ) = −(µ(P ) − µ(Q)) = − µ TV = − Pr − Pθ TV = −δ(Pr , Pθ ) 27 

28 .Furthermore, if f is bounded between -1 and 1, we get |Ex∼Pr [f (x)] − Ex∼Pθ [f (x)]| = | f dPr − f dPθ | =| f dµ| ≤ |f | d|µ| ≤ 1 d|µ| = |µ|(X ) = µ TV = δ(Pr , Pθ ) Since δ is positive, we can conclude Ex∼Pr [f (x)] − Ex∼Pθ [f (x)] ≥ −δ(Pr , Pθ ). 28 

29 .E Generator’s cost during normal GAN training Figure 8: Cost of the generator during normal GAN training, for an MLP generator (upper left) and a DCGAN generator (upper right). Both had a DCGAN discriminator. Both curves have increasing error. Samples get better for the DCGAN but the cost of the generator increases, pointing towards no significant correlation between sample quality and loss. Bottom: M LP with both generator and discriminator. The curve goes up and down regardless of sample quality. All training curves were passed through the same median filter as in Figure 3. F Sheets of samples 29