Deep Single-View 3D Object Reconstruction with Visual Hull Embedding

1 . Deep Single-View 3D Object Reconstruction with Visual Hull Embedding Hanqing Wang∗1 Jiaolong Yang2 Wei Liang1 Xin Tong2 1 2 Beijing Institute of Technology Microsoft Research {hanqingwang,liangwei}@bit.edu.cn {jiaoyan,xtong}@microsoft.com arXiv:1809.03451v1 [cs.CV] 10 Sep 2018 Abstract 3D object reconstruction is a fundamental task of many robotics and AI problems. With the aid of deep convolutional Synthetic neural networks (CNNs), 3D object reconstruction has wit- Data nessed a significant progress in recent years. However, possi- bly due to the prohibitively high dimension of the 3D object space, the results from deep CNNs are often prone to miss- Input 3D-R2N2 Marrnet Ours GT ing some shape details. In this paper, we present an approach which aims to preserve more shape details and improve the reconstruction quality. The key idea of our method is to lever- age object mask and pose estimation from CNNs to assist the 3D shape learning by constructing a probabilistic single- Real Data view visual hull inside of the network. Our method works by first predicting a coarse shape as well as the object pose and silhouette using CNNs, followed by a novel 3D refinement CNN which refines the coarse shapes using the constructed Input 3D-R2N2 Marrnet Ours Pseudo GT probabilistic visual hulls. Experiment on both synthetic data and real images show that embedding a single-view visual Figure 1: Some results reconstructed from synthetic data and hull for shape refinement can significantly improve the re- real data by the baseline approach (Choy et al. 2016), Marr- construction quality by recovering more shapes details and Net (Wu et al. 2017) and our approach on the chair category. improving shape consistency with the input image. Note the inconsistency with input images and missing parts in the results of the former two methods. Introduction Although promising results have been shown by these CNN-based methods, single-view 3D reconstruction is still Recovering the dense 3D shapes of objects from 2D im- a challenging problem and the results are far from being per- ageries is a fundamental AI problem which has many ap- fect. One of the main difficulties lies in the object shape plications such as robot-environment interaction, 3D-based variations which can be very large even in a same object object retrieval and recognition, etc. Given a single image of category. The appearance variations in the input images an object, a human can reason the 3D structure of the object caused by pose differences make this task even harder. Con- reliably. However, single-view 3D object reconstruction is sequently, the results from CNN-based methods are prone to very challenging for computer algorithms. missing some shape details and sometimes generate plausi- Recently, a significant progress of single-view 3D recon- ble shapes which, however, are inconsistent with input im- struction has been achieved by using deep convolutional ages, as shown in Figure 1. neural networks (CNNs) (Choy et al. 2016; Girdhar et al. 2016; Wu et al. 2016; Yan et al. 2016; Fan, Su, and Guibas In this paper, we propose an approach to improve the fi- 2017; Tulsiani et al. 2017b; Zhu et al. 2017; Wu et al. 2017; delity of the reconstructed shapes by CNNs. Our method Tulsiani, Efros, and Malik 2018). Most CNN-based meth- combined traditional wisdom into the network architecture. ods reconstruct the object shapes using 2D and 3D convo- It is motivated by two observations: 1) while directly recov- lutions in a 2D encoder-3D decoder structure with the volu- ering all the shape details in 3D is difficult, extracting the metric 3D representation. The input to these CNNs are ob- projected shape silhouette on the 2D plane, i.e. segmenting ject images taken under unknown viewpoints, while the out- out the object from background in a relatively easy task us- put shapes are often aligned with the canonical viewpoint in ing CNNs; 2) for some common objects such as chairs and a single, pre-defined 3D coordinate system such that shape cars whose 3D coordinate systems are well defined with- regression is more tractable. out ambiguity, the object pose (or equivalently, the view- point) can also be well estimated by a CNN (Su et al. 2015; ∗ Part of this work was done when HW was an intern at MSR. Massa, Marlet, and Aubry 2016). As such, we propose to 

2 . Deep learning for 3D reconstruction. Deep learning based CNN CNN methods directly learn the mapping from 2D image to a dense 3D shape from training data. For example, (Choy et Input Image Coarse Shape Final Shape al. 2016) directly trained a network with 3D shape loss. (Yan et al. 2016) trained a network by minimizing the difference CNN between the silhouette of the predicted 3D shape and ground truth silhouette on multiple views. A ray consistency loss is PSVH Layer Silhouette (R,T) proposed in (Tulsiani et al. 2017b) which uses other types CNN of multi-view observations for training such as depth, color Single-view Visual and semantics. (Wu et al. 2017) applied CNNs to first pre- Pose Hull dict the 2.5D sketches including normal, depth and silhou- Figure 2: An overview of the proposed method. Given an ette, then reconstruct the 3D shape. A reprojection consis- input image, we first use CNNs to predict a coarse 3D vol- tency constraint between the 3D shape and 2.5D sketches umetric shape, the silhouette and the object pose. The latter is used to finetune the network on real images. (Zhu et al. two are used to construct a single-view visual hull, which is 2017) jointly trained a pose regressor with a 3D reconstruc- used to refine the coarse shape using another CNN. tion network so that the object images with annotated masks yet unknown poses can be used for training. Many existing leverage the object silhouettes to assist the 3D learning by methods have explored using pose and silhouette (or other lifting them to 3D using pose estimates. 2D/2.5D observations) to supervise the 3D shape predic- Figure 2 is a schematic description of our method, which tion (Yan et al. 2016; Tulsiani et al. 2017b; Gwak et al. 2017; is a pure GPU-friendly neural network solution. Specifically, Zhu et al. 2017; Wu et al. 2017; Tulsiani, Efros, and Malik we embed into the network a single-view visual hull us- 2018). However, our goal is to refine the 3D shape inside ing the estimated object silhouettes and poses. Embedding of the network using an estimated visual hull, and our vi- a visual hull can help recover more shape details by consid- sual hull construction is an inverse process of their shape-to- ering the projection relationship between the reconstructed image projection scheme. More discussions can be found in 3D shape and the 2D silhouette. Since both the pose and the supplementary material. segmentation are subject to estimation error, we opted for a “soft” visual-hull embedding strategy: we first predict a Generative models for 3D shape. Some efforts are devoted coarse 3D shape using a CNN, then employ another CNN to to modeling the 3D shape space using generative models refine the coarse shape with the constructed visual hull. We such as GAN (Goodfellow et al. 2014) and VAE (Kingma propose a probabilistic single-view visual hull (PSVH) con- and Welling 2013). In (Wu et al. 2016), a 3D-GAN method struction layer which is differentiable such that the whole is proposed for learning the latent space of 3D shapes and network can be trained end-to-end. a 3D-VAE-GAN is also presented for mapping image space In summary, we present a novel CNN-based approach to shape space. A fully convolutional 3D autoencoder for which uses a single-view visual hull to improve the qual- learning shape representation from noisy data is proposed in ity of shape predictions. Through our method, the perspec- (Sharma, Grau, and Fritz 2016). A weakly-supervised GAN tive geometry is seamlessly embedded into a deep network. for 3D reconstruction with the weak supervision from sil- We evaluate our method on synthetic data and real images, houettes can be found in (Gwak et al. 2017). and demonstrate that using a single-view visual hull can sig- 3D shape representation. Most deep object reconstruction nificantly improve the reconstruction quality by recovering methods use the voxel grid representation (Choy et al. 2016; more shape details and improving shape consistency with Girdhar et al. 2016; Yan et al. 2016; Tulsiani et al. 2017b; input images. Zhu et al. 2017; Wu et al. 2017; 2016; Gwak et al. 2017), i.e., the output is a voxelized occupancy map. Recently, Related Work memory-efficient representations such as point clouds (Qi et al. 2017), voxel octree (H¨ane, Tulsiani, and Malik 2017; Traditional methods. Reconstructing a dense 3D object Tatarchenko, Dosovitskiy, and Brox 2017) and shape primi- shape from a single image is an ill-posed problem. Tradi- tives (Zou et al. 2017) are investigated. tional methods resort to geometry priors for the otherwise prohibitively challenging task. For example, some meth- Visual hull for deep multi-view 3D reconstruction. Some re- ods leveraged pre-defined CAD models (Sun et al. 2013). cent works use visual hulls of color (Ji et al. 2017) or learned Category-specific reconstruction methods (Vicente et al. feature (Kar, H¨ane, and Malik 2017) for multi-view stereo 2014; Kar et al. 2015; Tulsiani et al. 2017a) reconstruct a with CNNs. Our method is different from theirs in several 3D shape template from images of the objects in the same ways. First, the motivations of using visual hulls differ: they category as shape prior. Given an input image, these meth- use visual hulls as input to their multi-view stereo matching ods estimate silhouette and viewpoint from the input image networks in order to reconstruct the object shape, whereas and then reconstruct 3D object shape by fitting the shape our goal is to leverage a visual hull to refine a coarse single- template to the estimated visual hull. Our method integrates view shape prediction. Second, the object poses are given in the single-view visual hull with deep neural network for re- their methods, while in ours the object pose is estimated by constructing 3D shape from single image. a CNN. Related to the above, our novel visual hull construc- 

3 .tion layer is made differentiable, and object segmentation, V-Net: The V-Net for voxel occupancy prediction consists pose estimation and 3D reconstruction are jointly trained in of a 2D encoder and a 3D decoder, as depicted in Fig. 3 (a). It one framework. is adapted from the network structure of (Choy et al. 2016), and the main difference is we replaced their LSTM layer Our Approach designed for multi-view reconstruction with a simple fully In this section, we detail our method which takes as input connected (FC) layer. We denote the 3D voxel occupation a single image of a common object such as car, chair and probability map produced by the V-Net as V. coach, and predicts its 3D shape. We assume the objects are P-Net: The P-Net for pose estimation is a simple regres- roughly centered (e.g. those in bounding boxes given by an sor outputting 6-dimensional pose vector denoted as p, as object detector). shown in Fig. 3 (b). We construct the P-Net structure sim- ply by appending two FC layers to the encoder structure of Shape representation. We use voxel grid for shape repre- V-Net, one with 512 neurons and the other with 6 neurons. sentation similar to previous works (Wu et al. 2015; Yan et al. 2016; Wu et al. 2016; Zhu et al. 2017; Wu et al. 2017), S-Net: The S-Net for object segmentation has a 2D i.e., the output of our network is a voxelized occupancy map encoder-decoder structure, as shown in Fig. 3 (c). We use in the 3D space. This representation is very suitable for vi- the same encoder structure of V-Net for S-Net encoder, and sual hull construction and processing, and it is also possible apply a mirrored decoder structure consisting of deconv and to extend our method to use tree-structured voxel grids for uppooling layers. The S-Net generates an object probability more fine-grained details (H¨ane, Tulsiani, and Malik 2017; map of 2D pixels, which we denote as S. Tatarchenko, Dosovitskiy, and Brox 2017) PSVH Layer for Probabilistic Visual Hull Camera model. We choose the perspective camera model for Given the estimated pose p and the object probability map the 3D-2D projection geometry, and reconstruct the object in S on the image plane, we construct inside of our neural net- a unit-length cube located in front of the camera (i.e., with work a Probabilistic Single-view Visual Hull (PSVH) in the cube center near the positive Z-axis in the camera coordinate 3D voxel grid. To achieve this, we project each voxel loca- frame). Under a perspective camera model, the relationship tion X onto the image plane by the perspective transforma- between a 3D point (X, Y, Z) and its projected pixel loca- tion in Eq. 1 to obtain its corresponding pixel x. Then we tion (u, v) on the image is assign H(X) = S(x), where H denotes the generated prob- Z[u, v, 1]T = K R[X, Y, Z]T + t (1) abilistic visual hull. This process is illustrated in Fig. 3 (d). The PSVH layer is differentiable, which means that the f 0 u0 gradients backpropagated to H can be backpropagated to S where K = 0 f v0 is the camera intrinsic matrix and pose P , hence further to S-Net and P-Net. The gradi- 0 0 1 ent of H with respect to S is easy to discern: we have built with f being the focal length and (u0 , v0 ) the principle point. correspondences from H to S and simply copied the val- We assume that the principal points coincide with image ues. Propagating gradients to p is somewhat tricky. Accord- center (or otherwise given), and focal lengths are known. ∂l ∂l ∂H(X) ∂X Note that when the exact focal length is not available, a ing to the chain rule, we have ∂p = X ∂H(X) ∂X ∂p ∂l rough estimate or an approximation may still suffice. When where l is the network loss. Obtaining ∂p necessitates com- the object is reasonably distant from the camera, one can use puting ∂H(X) ∂X , i.e., the spatial gradients of H, which can be a large focal length to strike a balance between perspective numerically computed by three convolution operations with and weak-perspective models. pre-defined kernels along X-, Y- and Z-axis respectively. ∂X ∂p Pose parametrization. The object pose is characterized by can be derived analytically. a rotation matrix R ∈ SO(3) and a translation vector t = [tX , tY , tZ ]T ∈ R3 in Eq. 1. We parameterize rota- Refinement Network for Final Shape tion simply with Euler angles θi , i = 1, 2, 3. For translation With a coarse voxel occupancy probability V from V-Net we estimate tZ and a 2D vector [tu , tv ] which centralizes the and the visual hull H from the PSVH layer, we use a 3D object on image plane, and obtain t via [ tfu ∗tZ , tfv ∗tZ , tZ ]T . CNN to refine V and obtain a final prediction, denoted by In summary, we parameterize the pose as a 6-D vector V + . We refer to this refinement CNN as R-Net. The basic p = [θ1 , θ2 , θ3 , tu , tv , tZ ]T . structure of our R-Net is shown in Fig. 3 (e). It consists of five 3D conv layers in the encoder and 14 3D conv layers in Sub-nets for Pose, Silhouette and Coarse Shape the decoder. Given a single image as input, we first apply a CNN to di- A straightforward way for R-Net to process V and H is rectly regress a 3D volumetric reconstruction similar to pre- concatenating V and H to form a 2-channel 3D voxel grid vious works such as (Choy et al. 2016). We call this network as input then generating a new V as output. Nevertheless, the V-Net. Additionally, we apply another two CNNs for we have some domain knowledge on this specific problem. pose estimation and segmentation, referred to as P-Net and For example, if a voxel predicted as occupied falls out of the S-Net respectively. In the following we describe the main visual hull, it’s likely to be a false alarm; if the prediction structure of these sub-networks; more details can be found does not have any occupied voxel in a viewing ray of the in the supplementary material. visual hull, some voxels may have been missed. This domain 

4 . (R,T) (a) (b) (c) 2D Encoder 3D Decoder 2D Encoder 2D Decoder Regressor (d) (e) + 3D Encoder 3D Decoder Figure 3: Network structure illustration. Our network consists of (a) a coarse shape estimation subnet V-Net, (b) an object pose estimation subnet P-Net , (c) an object segmentation subnet, (d) a probabilistic single-view visual hull (PSVH) layer, and finally (e) a shape refinement network R-Net. knowledge prompted us to design the R-Net in the following for S-Net. The P-Net produces a 6-D pose estimate p = manners. [θ1 , θ2 , θ3 , tu , tv , tZ ]T as described before. We use the L1 First, in addition to V and H, we feed into R-Net two more regression loss to train the network: occupancy probability maps: V (1 − H) and H (1 − V) where denotes element-wise product. These two probabil- l= α|θi −θi∗ | + β|tj −t∗j | + γ|tZ −t∗Z |, (3) ity maps characterize voxels in V but not in H, and voxels i=1,2,3 j=u,v in H but not in V 1 , respectively. Second, we add a resid- ual connection between the input voxel prediction V and the where the Euler angles are normalized into [0, 1]. We found output of the last layer. This way, we guide R-Net to gen- in our experiments the L1 loss produces better results than erate an effective shape deformation to refine V rather than an L2 loss. directly predicting a new V, as the predicted V from V-Net is often mostly reasonable (as found in our experiments). Experiments Network Training Implementation details. Our network is implemented in TensorFlow. The input image size is 128 × 128 and the out- We now present our training strategies, including the train- put voxel grid size is 32×32×32. Batch size of 24 and the ing pipeline for the sub-networks and their training losses. ADAM solver are used throughout the training. We use a Training pipeline. We employ a three-step network train- learning rate of 1e−4 for S-Net, V-Net and R-Net and divide ing algorithm to train the proposed network. Specifically, it by 10 at the 20K-th and 60K-th iterations. The learning we first train V-Net, S-Net and R-Net separately, with in- rate for P-Net is 1e−5 and is dropped by 10 at the 60K-th put training images and their ground-truth shapes, silhou- iteration. When finetuning all the subnets together the learn- ettes and poses. After V-Net converges, we train R-Net in- ing rate is 1e−5 and dropped by 10 at the 20K-th iteration. dependently, with the predicted voxel occupancy probability Training and testing data. In this paper, we test our method V from V-Net and the ground-truth visual hull, which is con- on four common object categories: car and airplane as the structed by ground-truth silhouettes and poses via the PSVH representative vehicle objects, and chair and couch as furni- layer. The goal is to let R-Net learn how to refine coarse ture classes. Real images that come with precise 3D shapes shape predictions with ideal, error-free visual hulls. In the are difficult to obtain, so we first resort to the CAD models last stage, we finetune the whole network, granting the sub- from the ShapeNet repository (Chang et al. 2015). We use nets more opportunity to cooperate accordingly. Notably, the the ShapeNet object images rendered by (Choy et al. 2016) R-Net will adapt to input visual hulls that are subject to es- to train and test our method. We then use the PASCAL 3D+ timation error from S-Net and P-Net. dataset (Xiang, Mottaghi, and Savarese 2014) to evaluate our Training loss. We use the binary cross-entropy loss to train method on real images with pseudo ground truth shapes. V-Net, S-Net and R-Net. Concretely, let pn be the estimated probability at location n in either V, S or V + , then the loss Results on Rendered ShapeNet Objects is defined as The numbers of 3D models for the four categories are 7,496 1 for car, 4,045 for airplane, 6,778 for chair and 3,173 for ta- l=− p∗n log pn + (1 − p∗n )log(1 − pn ) (2) N n ble, respectively. In the rendering process of (Choy et al. 2016), the objects were normalized to fit in a radius-0.5 where p∗n is the target probability (0 or 1). n traverses over sphere, rotated with random azimuth and elevation angles, the 3D voxels for V-Net and R-Net, and over 2D pixels and placed in front of a 50-degree FOV camera. Each object 1 A better alternative for H (1 − V) would be constructing has 24 images rendered with random poses and lighting. another visual hull using V and p then compute its difference from Following (Choy et al. 2016), we use 80% of the 3D mod- H. We choose H (1 − V) here for simplicity. els for training and the rest 20% for testing. We train one 

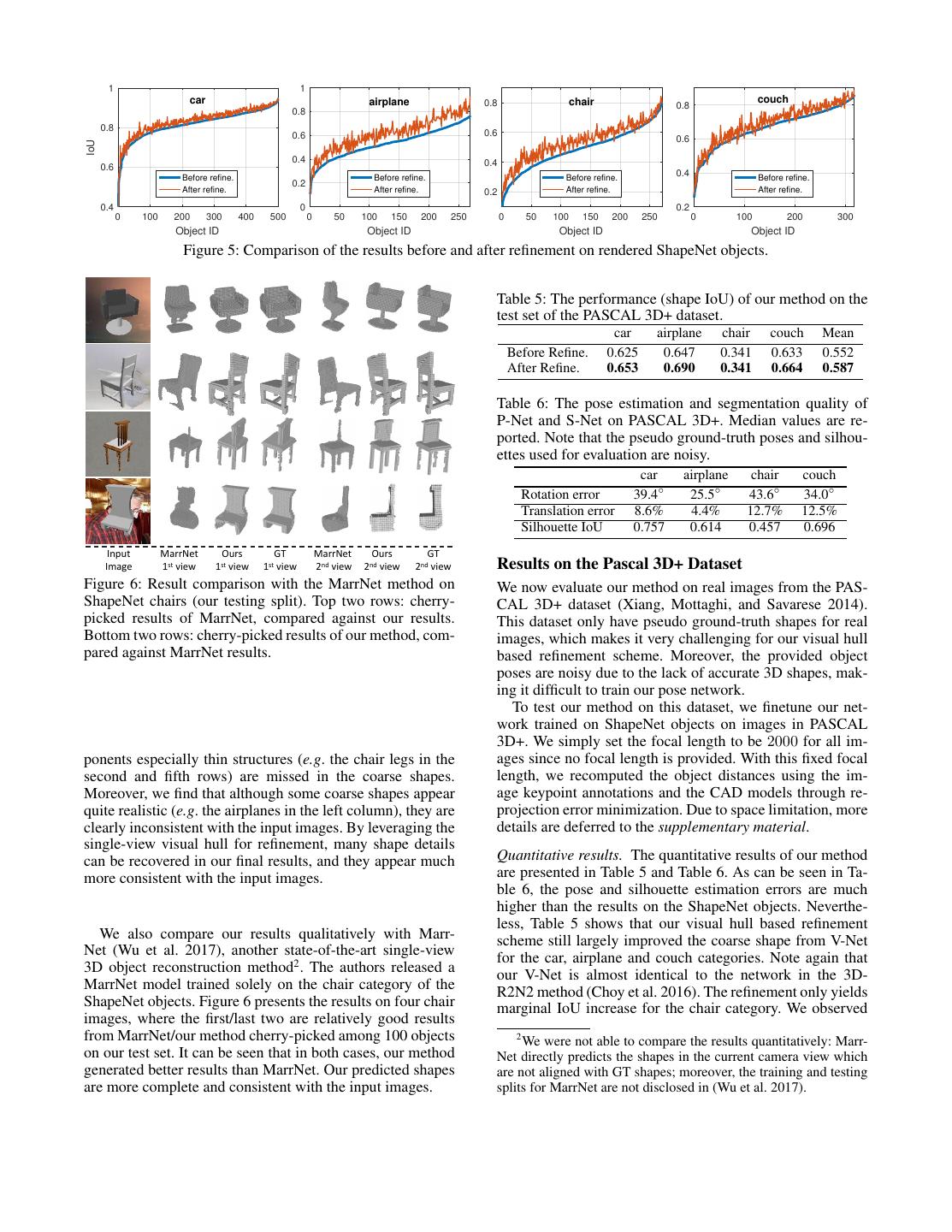
5 . IoU 0.955 IoU 0.157 IoU 0.682 IoU 0.975 IoU 0.694 IoU 0.837 IoU 0.906 IoU 0.119 IoU 0.508 IoU 0.978 IoU 0.362 IoU 0.718 IoU 0.951 IoU 0.401 IoU 0.674 IoU 0.964 IoU 0.422 IoU 0.650 IoU 0.979 IoU 0.275 IoU 0.654 IoU 0.959 IoU 0.398 IoU 0.610 Input Estimated Visual Coarse Refined GT Input Estimated Visual Coarse Refined GT Image Silhouette Hull Shape Shape Shape Image Silhouette Hull Shape Shape Shape Figure 4: Qualitative results on the test set of the rendered ShapeNet objects. The top two rows and bottom two rows show some results on images with a clean background and real-image background, respectively. The color of the voxels indicates the predicted probability (red/yellow for high/low probability). While the coarse shapes may miss some shape details or be inconsistent with the image, our final shapes refined with single-view visual hulls are of high fidelity. Table 1: The performance (shape IoU) of our method on the Table 4: The pose estimation and segmentation quality of test set of the rendered ShapeNet objects. H denotes visual our P-Net and S-Net on the rendered ShapeNet objects. hull and GT indicates ground truth. Mean values are shown for each category. car airplane chair couch Mean car airplane chair couch Mean Before Refine. 0.819 0.537 0.499 0.667 0.631 Rotation error 7.96◦ 4.72◦ 6.59◦ 10.41◦ 7.42◦ After Refine. 0.839 0.631 0.552 0.698 0.680 Translation error 3.33% 2.60% 3.26% 3.41% 3.15% Refine. w/o H 0.824 0.541 0.505 0.675 0.636 Silhouette IoU 0.923 0.978 0.954 0.982 0.959 Refine. w. GT H 0.869 0.701 0.592 0.741 0.726 Refine. w/o 2 prob.maps 0.840 0.610 0.549 0.701 0.675 our V-Net is adapted from (Choy et al. 2016) as mentioned Refine. w/o end-to-end 0.822 0.593 0.542 0.677 0.658 previously, the results before refinement can be viewed as the 3D-R2N2 method of (Choy et al. 2016) trained by us. Table 2: The performance (shape IoU) of our method and To better understand the performance gain from our visual PointOutNet (Fan, Su, and Guibas 2017). hull based refinement, we compute the IoU of the coarse car airplane chair couch Mean and refined shapes for each object from the four categories. (Fan, Su, and Guibas 2017) 0.831 0.601 0.544 0.708 0.671 Figure 5 presents the comparisons, where the object IDs are Ours 0.839 0.631 0.552 0.698 0.680 uniformly sampled and sorted by the IoUs of coarse shapes. The efficacy of our refinement scheme can be clearly seen. Table 3: The performance (shape IoU) of our method on the It consistently benefits the shape reconstruction for most of test set of the rendered ShapeNet objects with clean back- the objects, despite none of them is seen before. ground and background from natural image crops. We further compare the numerical results with PointOut- Background car airplane chair couch Mean Net (Fan, Su, and Guibas 2017) which was also evaluated Clean 0.839 0.631 0.552 0.698 0.680 on this rendered dataset and used the same training/testing Image crop. 0.837 0.617 0.541 0.700 0.674 lists as ours. Table 1 shows that our method outperformed it on the three of the four categories (car, airplane and chair) network for all the four shape categories until the network and obtained a higher mean IoU over the four categories. converge. The rendered images are with clean background Note that the results of (Fan, Su, and Guibas 2017) were ob- (uniform colors). During training, we blend half of the train- tained by first generating point clouds using their PointOut- ing images with random crops of natural images from the Net, then converting them to volumetric shapes and applying SUN database (Xiao et al. 2010). We binarize the output another 3D CNN to refine them. voxel probability with threshold 0.4 and report Intersection- Table 3 compares the results of our method on test images over-Union (IoU). with clean background and those blended with random real images. It shows that with random real image as background Quantitative results. The performance of our method eval- the results are only slightly worse. Table 4 shows the quality uated by IoU is shown in Table 1. It shows that the results of the pose and silhouette estimated by P-Net and S-Net. after refinement (i.e., our final results) are significantly bet- ter, especially for airplane and chair where the IoUs are im- Qualitative results. Figure 4 presents some visual results proved by about 16% and 10%, respectively. Note that since from our method. It can be observed that some object com- 

6 . 1 1 car airplane 0.8 chair couch 0.8 0.8 0.8 0.6 0.6 0.6 IoU 0.4 0.4 0.6 Before refine. Before refine. Before refine. 0.4 Before refine. 0.2 After refine. After refine. 0.2 After refine. After refine. 0.4 0 0.2 0 100 200 300 400 500 0 50 100 150 200 250 0 50 100 150 200 250 0 100 200 300 Object ID Object ID Object ID Object ID Figure 5: Comparison of the results before and after refinement on rendered ShapeNet objects. Table 5: The performance (shape IoU) of our method on the test set of the PASCAL 3D+ dataset. car airplane chair couch Mean Before Refine. 0.625 0.647 0.341 0.633 0.552 After Refine. 0.653 0.690 0.341 0.664 0.587 Table 6: The pose estimation and segmentation quality of P-Net and S-Net on PASCAL 3D+. Median values are re- ported. Note that the pseudo ground-truth poses and silhou- ettes used for evaluation are noisy. car airplane chair couch Rotation error 39.4◦ 25.5◦ 43.6◦ 34.0◦ Translation error 8.6% 4.4% 12.7% 12.5% Silhouette IoU 0.757 0.614 0.457 0.696 Input MarrNet Ours GT MarrNet Ours GT Image 1st view 1st view 1st view 2nd view 2nd view 2nd view Results on the Pascal 3D+ Dataset Figure 6: Result comparison with the MarrNet method on We now evaluate our method on real images from the PAS- ShapeNet chairs (our testing split). Top two rows: cherry- CAL 3D+ dataset (Xiang, Mottaghi, and Savarese 2014). picked results of MarrNet, compared against our results. This dataset only have pseudo ground-truth shapes for real Bottom two rows: cherry-picked results of our method, com- images, which makes it very challenging for our visual hull pared against MarrNet results. based refinement scheme. Moreover, the provided object poses are noisy due to the lack of accurate 3D shapes, mak- ing it difficult to train our pose network. To test our method on this dataset, we finetune our net- work trained on ShapeNet objects on images in PASCAL 3D+. We simply set the focal length to be 2000 for all im- ponents especially thin structures (e.g. the chair legs in the ages since no focal length is provided. With this fixed focal second and fifth rows) are missed in the coarse shapes. length, we recomputed the object distances using the im- Moreover, we find that although some coarse shapes appear age keypoint annotations and the CAD models through re- quite realistic (e.g. the airplanes in the left column), they are projection error minimization. Due to space limitation, more clearly inconsistent with the input images. By leveraging the details are deferred to the supplementary material. single-view visual hull for refinement, many shape details can be recovered in our final results, and they appear much Quantitative results. The quantitative results of our method more consistent with the input images. are presented in Table 5 and Table 6. As can be seen in Ta- ble 6, the pose and silhouette estimation errors are much higher than the results on the ShapeNet objects. Neverthe- less, Table 5 shows that our visual hull based refinement We also compare our results qualitatively with Marr- scheme still largely improved the coarse shape from V-Net Net (Wu et al. 2017), another state-of-the-art single-view for the car, airplane and couch categories. Note again that 3D object reconstruction method2 . The authors released a our V-Net is almost identical to the network in the 3D- MarrNet model trained solely on the chair category of the R2N2 method (Choy et al. 2016). The refinement only yields ShapeNet objects. Figure 6 presents the results on four chair marginal IoU increase for the chair category. We observed images, where the first/last two are relatively good results from MarrNet/our method cherry-picked among 100 objects 2 We were not able to compare the results quantitatively: Marr- on our test set. It can be seen that in both cases, our method Net directly predicts the shapes in the current camera view which generated better results than MarrNet. Our predicted shapes are not aligned with GT shapes; moreover, the training and testing are more complete and consistent with the input images. splits for MarrNet are not disclosed in (Wu et al. 2017). 

7 . 0.14 0.12 0.1 IoU Gain 0.08 0.06 IoU 0.533 IoU 0.739 IoU 0.902 0.04 0.02 0 5 10 0.85 0.9 0.95 0 100 200 300 Rotation error Silhouette IoU Azimuth angle Figure 8: Performance of the shape refinement (IoU gain IoU 0.808 IoU 0.555 IoU 0.899 compared to coarse shape) w.r.t. pose and silhouette estima- tion quality and rotation angle. The airplane category of the rendered ShapeNet objects is used IoU 0417 IoU 0.373 IoU 0.645 result without end-to-end training. The clear performance drop demonstrates the necessity of our end-to-end finetun- ing which grants the subnets the opportunity to better adapt to each other (notably, R-Net will adapt to input visual hulls IoU 0.738 IoU 0.710 IoU 0.724 that are subject to estimation error from S-Net and P-Net). Input Estimated Visual Coarse Refined Pseudo Performance w.r.t. pose and silhouette estimation qual- Image Silhouette Hull Shape Shape GT ity. We find that the performance gain from refinement de- Figure 7: Qualitative results on the test set of PASCAL 3D+ creases gracefully w.r.t. rotation estimation error, as shown in Fig. 8 (left). One interesting phenomenon is that, as shown that the chair category on this dataset contains large intra- in Fig. 8 (middle), the best performance gain is not from best class shape variations (yet only 10 CAD shapes as pseudo silhouette estimates. This is because larger and fuzzier sil- ground truth) and many instances with occlusion; see the houette estimates may compensate the 2D-to-3D correspon- suppl. material for more details. dence errors arisen due to noisy pose estimates. Qualitative results. Figure 7 shows some visual results of Performance w.r.t. rotation angle. Figure 8 (right) shows our method on the test data. It can be seen that the coarse that the performance gain from refinement is high at 30 shapes are noisy or contain erroneous components. For ex- and 330 degrees while low near 0 and 180 degrees. This is ample, possibly due to the low input image quality, the easy to discern as frontal and real views exhibit more self- coarse shape prediction of the car image in the second row of occlusion thus the visual hulls are less informative. the left column has a mixed car and chair structure. Never- Sensitivity w.r.t. focal length. We conducted another experi- theless, the final results after the refinement are much better. ment to further test our method under wrong focal lengths Figure 1 shows some results from both our method and and distorted visual hulls. The results indicate that our MarrNet (Wu et al. 2017). Visually inspected, our method method still works well with some weak-perspective ap- produces better reconstruction results again. proximations and the results are insensitive to the real focal lengths especially for reasonably-distant objects. The details More Ablation Study and Performance Analysis can be found in the suppl. material. Performance of refinement without visual hull. In this ex- periment, we remove the probabilistic visual hull and train Running Time R-Net to directly process the coarse shape. As shown in Ta- For a batch of 24 input images, the forward pass of our ble 1, the results are slightly better than the coarse shapes, whole network takes 0.44 seconds on an NVIDIA Tesla M40 but lag far behind the results refined with visual hull. GPU, i.e., our network processes one image with 18 mil- Performance of refinement with GT visual hull. We also liseconds on average. trained R-Net with visual hulls constructed by ground-truth poses and silhouettes. Table 1 shows that the performance Conclusions is dramatically increased: the shape IoU is increased by up We have presented a novel framework for single-view 3D to 30% from the coarse shape for the four object categories. object reconstruction, where we embed the perspective ge- The above two experiments indicate that our R-Net not only ometry into a deep neural network to solve the challenging leveraged the visual hull to refine shape, but also can work problem. Our key innovations include an in-network visual remarkably well if given a quality visual hull. hull construction scheme which connects the 2D space and Effect of two additional occupancy probability maps V pose space to the 3D space, and a refinement 3D CNN which (1 − H) and H (1 − V). The results in Table 1 shows learns shape refinement with visual hulls. The experiments that, if these two additional maps are removed from the input demonstrate that our method achieves very promising results of R-Net, the mean IoU drops slightly from 0.680 to 0.675, on both synthetic data and real images. indicating our explicit knowledge embedding helps. Limitations and future work. Since our method involves Effect of end-to-end training. Table 1 also presents the pose estimation, objects with ambiguous pose (symmetric 

8 .shapes) or even do not have a well-defined pose system (ir- European Conference on Computer Vision Workshop on Ge- regular shapes) will be challenging. For the former cases, ometry Meets Deep Learning, 236–250. using a classification loss to train the pose network would Su, H.; Qi, C. R.; Li, Y.; and Guibas, L. J. 2015. Render be a good remedy (Su et al. 2015), although this may render for CNN: Viewpoint estimation in images using cnns trained the gradient backpropagation problematic. For the latter, one with rendered 3D model views. In ICCV, 2686–2694. possible solution is resorting to multi-view inputs and train Sun, M.; Kumar, S. S.; Bradski, G.; and Savarese, S. 2013. the pose network to estimate relative poses. Object detection, shape recovery, and 3d modelling by depth-encoded hough voting. Computer Vision and Image References Understanding (CVIU) 117(9):1190–1202. Chang, A. X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Tatarchenko, M.; Dosovitskiy, A.; and Brox, T. 2017. Oc- Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; tree generating networks: Efficient convolutional architec- Xiao, J.; Yi, L.; and Yu, F. 2015. ShapeNet: An information- tures for high-resolution 3d outputs. In ICCV, 2088–2096. rich 3D model repository. arXiv:1512.03012. Tulsiani, S.; Kar, A.; Carreira, J.; and Malik, J. 2017a. Choy, C. B.; Xu, D.; Gwak, J.; Chen, K.; and Savarese, S. Learning category-specific deformable 3d models for object 2016. 3D-R2N2: A unified approach for single and multi- reconstruction. IEEE Transactions on Pattern Analysis and view 3D object reconstruction. In ECCV, 628–644. Machine Intelligence (TPAMI) 39(4):719–731. Fan, H.; Su, H.; and Guibas, L. 2017. A point set generation Tulsiani, S.; Zhou, T.; Efros, A. A.; and Malik, J. 2017b. network for 3d object reconstruction from a single image. In Multi-view supervision for single-view reconstruction via CVPR, 605–613. differentiable ray consistency. In CVPR, 2626–2633. Girdhar, R.; Fouhey, D. F.; Rodriguez, M.; and Gupta, A. Tulsiani, S.; Efros, A. A.; and Malik, J. 2018. Multi- 2016. Learning a predictable and generative vector repre- view consistency as supervisory signal for learning shape sentation for objects. In ECCV, 484–499. and pose prediction. In CVPR, 2897–2905. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Vicente, S.; Carreira, J.; Agapito, L.; and Batista, J. 2014. Warde-Farley, D.; Ozair, S.; Courville, A.; and Bengio, Y. Reconstructing pascal voc. In CVPR, 41–48. 2014. Generative adversarial nets. In Advances in Neural Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Information Processing Systems (NIPS), 2672–2680. and Xiao, J. 2015. 3D ShapeNets: A deep representation for Gwak, J.; Choy, C. B.; Garg, A.; Chandraker, M.; and volumetric shapes. In CVPR, 1912–1920. Savarese, S. 2017. Weakly supervised generative adversarial Wu, J.; Zhang, C.; Xue, T.; Freeman, B.; and Tenenbaum, J. networks for 3D reconstruction. arXiv:1705.10904. 2016. Learning a probabilistic latent space of object shapes H¨ane, C.; Tulsiani, S.; and Malik, J. 2017. Hierarchical sur- via 3D generative-adversarial modeling. In NIPS, 82–90. face prediction for 3d object reconstruction. In International Wu, J.; Wang, Y.; Xue, T.; Sun, X.; Freeman, W. T.; and Conference on 3D Vision (3DV). Tenenbaum, J. B. 2017. MarrNet: 3d shape reconstruction Ji, M.; Gall, J.; Zheng, H.; Liu, Y.; and Fang, L. 2017. via 2.5D sketches. In NIPS, 540–550. SurfaceNet: an end-to-end 3d neural network for multiview Xiang, Y.; Mottaghi, R.; and Savarese, S. 2014. Beyond stereopsis. In ICCV, 2307–2315. pascal: A benchmark for 3d object detection in the wild. In Kar, A.; Tulsiani, S.; Carreira, J.; and Malik, J. 2015. IEEE Winter Conference on Applications of Computer Vi- Category-specific object reconstruction from a single image. sion (WACV), 75–82. In CVPR, 1966–1974. Xiao, J.; Hays, J.; Ehinger, K. A.; Oliva, A.; and Torralba, Kar, A.; H¨ane, C.; and Malik, J. 2017. Learning a multi-view A. 2010. Sun database: Large-scale scene recognition from stereo machine. In NIPS, 364–375. abbey to zoo. In CVPR, 3485–3492. Kingma, D. P., and Welling, M. 2013. Auto-encoding vari- Yan, X.; Yang, J.; Yumer, E.; Guo, Y.; and Lee, H. 2016. ational bayes. arXiv:1312.6114. Perspective transformer nets: Learning single-view 3D ob- Massa, F.; Marlet, R.; and Aubry, M. 2016. Crafting a multi- ject reconstruction without 3D supervision. In NIPS, 1696– task cnn for viewpoint estimation. The British Machine Vi- 1704. sion Conference (BMVC). Zhu, R.; Galoogahi, H. K.; Wang, C.; and Lucey, S. 2017. Qi, C. R.; Su, H.; Mo, K.; and Guibas, L. J. 2017. Pointnet: Rethinking reprojection: Closing the loop for pose-aware Deep learning on point sets for 3d classification and segmen- shape reconstruction from a single image. In ICCV, 57–64. tation. In CVPR, 652–659. Zou, C.; Yumer, E.; Yang, J.; Ceylan, D.; and Hoiem, D. Sharma, A.; Grau, O.; and Fritz, M. 2016. VConv-DAE: 2017. 3D-PRNN: generating shape primitives with recurrent Deep volumetric shape learning without object labels. In neural networks. In ICCV, 900–909.