Neural Autoregressive Distribution Estimation

1 . Journal of Machine Learning Research 1 (2000) 1-48 Submitted 4/00; Published 10/00 Neural Autoregressive Distribution Estimation Benigno Uria benigno.uria@gmail.com Google DeepMind London, UK Marc-Alexandre Cˆ ot´ e marc-alexandre.cote@usherbrooke.ca Department of Computer Science Universit´e de Sherbrooke arXiv:1605.02226v3 [cs.LG] 27 May 2016 Sherbrooke, QC, Canada Karol Gregor karol.gregor@gmail.com Google DeepMind London, UK Iain Murray i.murray@ed.ac.uk School of Informatics University of Edinburgh Edinburgh, UK Hugo Larochelle hlarochelle@twitter.com Twitter Cortex Cambridge, MA, USA Editor: Leslie Pack Kaelbling Abstract We present Neural Autoregressive Distribution Estimation (NADE) models, which are neural network architectures applied to the problem of unsupervised distribution and density estimation. They leverage the probability product rule and a weight sharing scheme inspired from restricted Boltzmann machines, to yield an estimator that is both tractable and has good generalization performance. We discuss how they achieve competitive performance in modeling both binary and real-valued observations. We also present how deep NADE models can be trained to be agnostic to the ordering of input dimensions used by the autoregressive product rule decomposition. Finally, we also show how to exploit the topological structure of pixels in images using a deep convolutional architecture for NADE. Keywords: Deep Learning, Neural Networks, Density Modeling, Unsupervised Learning 1. Introduction Distribution estimation is one of the most general problems addressed by machine learning. From a good and flexible distribution estimator, in principle it is possible to solve a variety of types of inference problem, such as classification, regression, missing value imputation, and many other predictive tasks. Currently, one of the most common forms of distribution estimation is based on directed graphical models. In general these models describe the data generation process as sampling a latent state h from some prior p(h), followed by sampling the observed data x from some c 2000 Benigno Uria, Marc-Alexandre Cˆ ot´ e, Karol Gregor, Iain Murray, Hugo Larochelle. 

2 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle conditional p(x | h). Unfortunately, this approach quickly becomes intractable and requires approximations when the latent state h increases in complexity. Specifically, computing the marginal probability of the data, p(x) = h p(x | h) p(h), is only tractable under fairly constraining assumptions on p(x | h) and p(h). Another popular approach, based on undirected graphical models, gives probabilities of the form p(x) = exp {φ(x)} /Z, where φ is a tractable function and Z is a normalizing con- stant. A popular choice for such a model is the restricted Boltzmann machine (RBM), which substantially out-performs mixture models on a variety of binary datasets (Salakhutdinov and Murray, 2008). Unfortunately, we often cannot compute probabilities p(x) exactly in undirected models either, due to the normalizing constant Z. In this paper, we advocate a third approach to distribution estimation, based on autore- gressive models and feed-forward neural networks. We refer to our particular approach as Neural Autoregressive Distribution Estimation (NADE). Its main distinguishing property is that computing p(x) under a NADE model is tractable and can be computed efficiently, given an arbitrary ordering of the dimensions of x. We show that the framework is flexible and can model both binary and real-valued observations, can be made order-agnostic, and can be adapted to the case of 2D images using convolutional neural networks. In each case, we’re able to reach competitive results, compared to popular directed and undirected graphical model alternatives. 2. NADE We consider the problem of modeling the distribution p(x) of input vector observations x. For now, we will assume that the dimensions of x are binary, that is xd ∈ {0, 1} ∀d. The model generalizes to other data types, which is explored later (Section 3) and in other work (Section 8). NADE begins with the observation that any D-dimensional distribution p(x) can be factored into a product of one-dimensional distributions, in any order o (a permutation of the integers 1, . . . , D): D p(x) = p(xod | xo<d ). (1) d=1 Here o<d contains the first d − 1 dimensions in ordering o and xo<d is the corresponding subvector for these dimensions. Thus, one can define an ‘autoregressive’ generative model of the data simply by specifying a parameterization of all D conditionals p(xod | xo<d ). Frey et al. (1996) followed this approach and proposed using simple (log-)linear logistic regression models for these conditionals. This choice yields surprisingly competitive results, but are not competitive with non-linear models such as an RBM. Bengio and Bengio (2000) proposed a more flexible approach, with a single-layer feed-forward neural network for each conditional. Moreover, they allowed connections between the output of each network and the hidden layer of networks for the conditionals appearing earlier in the autoregressive ordering. Using neural networks led to some improvements in modeling performance, though at the cost of a really large model for very high-dimensional data. 2 

3 . Neural Autoregressive Distribution Estimation ... ... ... ... ... ... ... ... 500 units 784 units 784 units Figure 1: Illustration of a NADE model. In this example, in the input layer, units with value 0 are shown in black while units with value 1 are shown in white. The dashed border represents a layer pre-activation.The outputs xˆ O give predictive probabilities for each dimension of a vector xO , given elements earlier in some ordering. There is no path of connections between an output and the value being predicted, or elements of xO later in the ordering. Arrows connected together correspond to connections with shared (tied) parameters. In NADE, we also model each conditional using a feed-forward neural network. Specifi- cally, each conditional p(xod | x<d ) is parameterized as follows: p(xod = 1 | xo<d ) = sigm (V od ,· hd + bod ) (2) hd = sigm W ·,o<d xo<d + c , (3) where sigm (a) = 1/(1 + e−a ) is the logistic sigmoid, and with H as the number of hidden units, V ∈ RD×H , b ∈ RD , W ∈ RH×D , c ∈ RH are the parameters of the NADE model. The hidden layer matrix W and bias c are shared by each hidden layer hd (which are all of the same size). This parameter sharing scheme (illustrated in Figure 1) means that NADE has O(HD) parameters, rather than O(HD2 ) required if the neural networks were separate. Limiting the number of parameters can reduce the risk of over-fitting. Another advantage is that all D hidden layers hd can be computed in O(HD) time instead of O(HD2 ). Denoting the pre-activation of the dth hidden layer as ad = W ·,o<d xo<d + c, this complexity is achieved by using the recurrence h1 = sigm (a1 ) , where a1 = c (4) hd = sigm (ad ) , where ad = W ·,o<d xo<d + c = W ·,od−1 xod−1 + ad−1 (5) for d ∈ {2, . . . , D}, where Equation 5 given vector ad−1 can be computed in O(H). Moreover, the computation of Equation 2 given h is also O(H). Thus, computing p(x) from D conditional distributions (Equation 1) costs O(HD) for NADE. This complexity is comparable to that of regular feed-forward neural network models. 3 

4 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle Algorithm 1 Computation of p(x) and learning gradients for NADE. Input: training observation vector x and ordering o of the input dimensions. Output: p(x) and gradients of − log p(x) on parameters. # Computing p(x) a1 ← c p(x) ← 1 for d from 1 to D do hd ← sigm (ad ) p(xod = 1 | xo<d ) ← sigm (V od ,· hd + bod ) p(x) ← p(x) p(xod = 1 | xo<d )xod + (1 − p(xod = 1 | xo<d ))1−xod ad+1 ← ad + W ·,od xod end for # Computing gradients of − log p(x) δaD ← 0 δc ← 0 for d from D to 1 do δbod ← p(xod = 1 | xo<d ) − xod δV od ,· ← p(xod = 1 | xo<d ) − xod hd δhd ← p(xod = 1 | xo<d ) − xod V od ,· δc ← δc + δhd hd (1 − hd ) δW ·,od ← δad xod δad−1 ← δad + δhd hd (1 − hd ) end for return p(x), δb, δV , δc, δW NADE can be trained by maximum likelihood, or equivalently by minimizing the average negative log-likelihood, N N D 1 (n) 1 − log p(x )= − log p(xo(n) | xo(n) ), (6) N N d <d n=1 n=1 d=1 usually by stochastic (minibatch) gradient descent. As probabilities p(x) cost O(HD), gradients of the negative log-probability of training examples can also be computed in O(HD). Algorithm 1 describes the computation of both p(x) and the gradients of − log p(x) with respect to NADE’s parameters. 2.1 Relationship with the RBM The proposed weight-tying for NADE isn’t simply motivated by computational reasons. It also reflects the computations of approximation inference in the RBM. 4 

5 . Neural Autoregressive Distribution Estimation Denoting the energy function and distribution under an RBM as E(x, h) = −h W x − b x − c h (7) p(x, h) = exp {−E(x, h)} /Z , (8) computing all conditionals p(xod | xo<d ) = exp {−E(x, h)} /Z(xo<d ) (9) xo>d ∈{0,1}D−d h∈{0,1}H Z(xo<d ) = exp {−E(x, h)} (10) xo≥d ∈{0,1}D−d+1 h∈{0,1}H is intractable. However, these could be approximated using mean-field variational inference. Specifically, consider the conditional over xod , xo>d and h instead: p(xod , xo>d , h | xo<d ) = exp {−E(x, h)} /Z(xo<d ). (11) A mean-field approach could first approximate this conditional with a factorized distribution q(xod , xo>d , h | xo<d ) = µi (d)xod (1 − µd (d))1−xod µj (d)xoj (1 − µj (d))1−xoj j>d τk (d)hk (1 − τk (d))1−hk , (12) k where µj (d) is the marginal probability of xoj being equal to 1, given xo<d . Similarly, τk (d) is the marginal for hidden variable hk . The dependence on d comes from conditioning on xo<d , that is on the first d−1 dimensions of x in ordering o. For some d, a mean-field approximation is obtained by finding the parameters µj (d) for j ∈ {d, . . . , D} and τk (d) for k ∈ {1, . . . , H} which minimize the KL divergence between q(xod , xo>d , h | xo<d ) and p(xod , xo>d , h | xo<d ). This is usually done by finding message passing updates that each set the derivatives of the KL divergence to 0 for some of the parameters of q(xod , xo>d , h | xo<d ) given others. For some d, let us fix µj (d) = xod for j < d, leaving only µj (d) for j > d to be found. The KL-divergence develops as follows: KL(q(xod , xo>d , h | xo<d ) || p(xod , xo>d , h | xo<d )) = − q(xod , xo>d , h | xo<d ) log p(xod , xo>d , h | xo<d ) xod ,xo>d ,h + q(xod , xo>d , h | xo<d ) log q(xod , xo>d , h | xo<d ) xod ,xo>d ,h = log Z(xo<d ) − τk (d)Wk,oj µj (d) − boj µj (d) − ck τk (d) j k j k + (µj (d) log µj (d) + (1 − µj (d)) log(1 − µj (d))) j≥d + (τk (d) log τk (d) + (1 − τk (d)) log(1 − τk (d))) . k 5 

6 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle Then, we can take the derivative with respect to τk (d) and set it to 0, to obtain: ∂KL(q(xod , xo>d , h | xo<d ) || p(xod , xo>d , h | xo<d )) 0 = ∂τk (d) τk (d) 0 = −ck − Wk,oj µj (d) + log 1 − τk (d) j   τk (d)   = exp ck + Wk,oj µj (d) (13) 1 − τk (d)   j exp ck + j Wk,oj µj (d) τk (d) = 1 + exp ck + j Wk,oj µj (d)   τk (d) = sigm ck + Wk,oj µj (d) + Wk,oj xoj  . (14) j≥d j<d where in the last step we have used the fact that µj (d) = xoj for j < d. Equation 14 would correspond to the message passing updates of the hidden unit marginals τk (d) given the marginals of input µj (d). Similarly, we can set the derivative with respect to µj (d) for j ≥ d to 0 and obtain: ∂KL(q(xod , xo>d , h | xo<d ) || p(xod , xo>d , h | xo<d )) 0 = ∂µj (d) µj (d) 0 = −bod − τk (d)Wk,oj + log 1 − µj (d) k µj (d) = exp boj + τk (d)Wk,oj 1 − µj (d) k exp boj + k τk (d)Wk,oj µj (d) = 1 + exp boj + k τk (d)Wk,oj µj (d) = sigm boj + τk (d)Wk,oj . (15) k Equation 15 would correspond to the message passing updates of the input marginals µj (d) given the hidden layer marginals τk (d). The complete mean-field algorithm would thus alternate between applying the updates of Equations 14 and 15, right to left. We now notice that Equation 14 corresponds to NADE’s hidden layer computation (Equation 3) where µj (d) = 0 ∀j ≥ d. Also, Equation 15 corresponds to NADE’s output layer computation (Equation 2) where j = d, τk (d) = hd,k and W = V . Thus, in short, NADE’s forward pass is equivalent to applying a single pass of mean-field inference to approximate all the conditionals p(xod | xo<d ) of an RBM, where initially µj (d) = 0 and where a separate matrix V is used for the hidden-to-input messages. A generalization of NADE based on this connection to mean field inference has been further explored by Raiko et al. (2014). 6 

7 . Neural Autoregressive Distribution Estimation 3. NADE for non-binary observations So far we have only considered the case of binary observations xi . However, the framework of NADE naturally extends to distributions over other types of observations. In the next section, we discuss the case of real-valued observations, which is one of the most general cases of non-binary observations and provides an illustrative example of the technical considerations one faces when extending NADE to new observations. 3.1 RNADE: Real-valued NADE A NADE model for real-valued data could be obtained by applying the derivations shown in Section 2.1 to the Gaussian-RBM (Welling et al., 2005). The resulting neural network would output the mean of a Gaussian with fixed variance for each of the conditionals in Equation 1. Such a model is not competitive with mixture models, for example on perceptual datasets (Uria, 2015). However, we can explore alternative models by making the neural network for each conditional distribution output the parameters of a distribution that’s not a fixed-variance Gaussian. In particular, a mixture of one-dimensional Gaussians for each autoregressive conditional provides a flexible model. Given enough components, a mixture of Gaussians can model any continuous distribution to arbitrary precision. The resulting model can be interpreted as a sequence of mixture density networks (Bishop, 1994) with shared parameters. We call this model RNADE-MoG. In RNADE-MoG, each of the conditionals is modeled by a mixture of Gaussians: C p(xod | xo<d ) = πod ,c N (xod ; µod ,c , σo2d ,c ), (16) c=1 where the parameters are set by the outputs of a neural network: (π) exp zod ,c πod ,c = (17) C (π) c=1 exp zod ,c µod ,c =zo(µ) d ,c (18) σod ,c = exp zo(σ) d ,c (19) H (π) zo(π) d ,c =b(π) od ,c + Vod ,k,c hd,k (20) k=1 H (µ) zo(µ) d ,c =b(µ) od ,c + Vod ,k,c hd,k (21) k=1 H (σ) zo(σ) d ,c =b(σ) od ,c + Vod ,k,c hd,k (22) k=1 Parameter sharing conveys the same computational and statistical advantages as it does in the binary NADE. 7 

8 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle Different one dimensional conditional forms may be preferred, for example due to limited dataset size or domain knowledge about the form of the conditional distributions. Other choices, like single variable-variance Gaussians, sinh-arcsinh distributions, and mixtures of Laplace distributions, have been examined by Uria (2015). Training an RNADE can still be done by stochastic gradient descent on the parameters of the model with respect to the negative log-density of the training set. It was found empirically (Uria et al., 2013) that stochastic gradient descent leads to better parameter configurations when the gradient of the mean ∂µ∂J od ,c was multiplied by the standard deviation (σod ,c ). 4. Orderless and Deep NADE The fixed ordering of the variables in a NADE model makes the exact calculation of arbitrary conditional probabilities computationally intractable. Only a small subset of conditional distributions, those where the conditioned variables are at the beginning of the ordering and marginalized variables at the end, are computationally tractable. Another limitation of NADE is that a naive extension to a deep version, with multiple layers of hidden units, is computationally expensive. Deep neural networks (Bengio, 2009; LeCun et al., 2015) are at the core of state-of-the-art models for supervised tasks like image recognition (Krizhevsky et al., 2012) and speech recognition (Dahl et al., 2013). The same inductive bias should also provide better unsupervised models. However, extending the NADE framework to network architectures with several hidden layers, by introducing extra non-linear calculations between Equations (3) and (2), increases its complexity to cubic in the number of units per layer. Specifically, the cost becomes O(DH 2 L), where L stands for the number of hidden layers and can be assumed to be a small constant, D is the number of variables modeled, and H is the number of hidden units, which we assumed to be of the same order as D. This increase in complexity is caused by no longer being able to share hidden layer computations across the conditionals in Equation 1, after the non-linearity in the first layer. In this section we introduce an order-agnostic training procedure, DeepNADE, which will address both of the issues above. This procedure trains a single deep neural network that can assign a conditional distribution to any variable given any subset of the others. This network can then provide the conditionals in Equation 1 for any ordering of the input observations. Therefore, the network defines a factorial number of different models with shared parameters, one for each of the D! orderings of the inputs. At test time, given an inference task, the most convenient ordering of variables can be used. The models for different orderings will not be consistent with each other: they will assign different probabilities to a given test vector. However, we can use the models’ differences to our advantage by creating ensembles of NADE models (Section 4.1), which results in better estimators than any single NADE. Moreover, the training complexity of our procedure increases linearly with the number of hidden layers O(H 2 L), while remaining quadratic in the size of the network’s layers. We first describe the model for an L-layer neural network modeling binary variables. A conditional distribution is obtained directly from a hidden unit in the final layer: p(xod = 1 | xo<d , θ, o<d , od ) = h(L) od . (23) 8 

9 . Neural Autoregressive Distribution Estimation This hidden unit is computed from previous layers, all of which can only depend on the xo<d variables that are currently being conditioned on. We remove the other variables from the computation using a binary mask, mo<d = [11∈o<d , 12∈o<d , . . . , 1D∈o<d ], (24) which is element-wise multiplied with the inputs before computing the remaining layers as in a standard neural network: h(0) = x mo<d (25) ( ) ( ) ( −1) ( ) a =W h +b (26) h( ) = σ a( ) (27) h(L) = sigm a(L) . (28) The network is specified by a free choice of the activation function σ (·), and learnable ( ) ( −1) ( ) parameters W ( ) ∈ RH ×H and b( ) ∈ RH , where H (l) is the number of units in the -th layer. As layer zero is the masked input, H (0) = D. The final L-th layer needs to be able to provide predictions for any element (Equation 23) and so also has D units. To train a DeepNADE, the ordering of the variables is treated as a stochastic variable with a uniform distribution. Moreover, since we wish DeepNADE to provide good predictions for any ordering, we optimize the expected likelihood over the ordering of variables: J (θ) = E − log p(X | θ, o) ∝ E E − log p(x | θ, o), (29) o∈D! o∈D! x∈X where we’ve made the dependence on the ordering o and the network’s parameters θ explicit, D! stands for the set of all orderings (the permutations of D elements) and x is a uniformly sampled datapoint from the training set X . Using NADE’s expression for the density of a datapoint in Equation 1 we have D J (θ) = E E − log p(xod | xo<d , θ, o), (30) o∈D! x∈X d=1 where d indexes the elements in the ordering, o, of the variables. By moving the expectation over orderings inside the sum over the elements of the ordering, the ordering can be split in three parts: o<d (the indices of the d − 1 first dimensions in the ordering), od (the index of the d-th variable) and o>d (the indices of the remaining dimensions). Therefore, the loss function can be rewritten as: D J (θ) = E E E E − log p(xod | xo<d , θ, o<d , od , o>d ). (31) x∈X o<d od o>d d=1 The value of each of these terms does not depend on o>d . Therefore, it can be simplified as: D J (θ) = E E E − log p(xod | xo<d , θ, o<d , od ). (32) x∈X o<d od d=1 9 

10 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle In practice, this loss function will have a very high number of terms and will have to be approximated by sampling x, d and o<d . The innermost expectation over values of od can be calculated cheaply, because all of the neural network computations depend only on the masked input xo<d , and can be reused for each possible od . Assuming all orderings are equally probable, we will estimate J (θ) by: D J (θ) = − log p(xod | xo<d , θ, o<d , od ), (33) D−d+1 od which is an unbiased estimator of Equation 29. Therefore, training can be done by descent on the gradient of J (θ). D For binary observations, we use the cross-entropy scaled by a factor of D−d+1 as the training loss which corresponds to minimizing J : D J (x) = m x log h(L) + (1 − x) log 1 − h(L) . (34) D − d + 1 o≥d Differentiating this cost involves backpropagating the gradients of the cross-entropy only D from the outputs in o≥d and rescaling them by D−d+1 . The resulting training procedure resembles that of a denoising autoencoder (Vincent et al., 2008). Like the autoencoder, D outputs are used to predict D inputs corrupted by a (L) random masking process (mo<d in Equation 25). A single forward pass can compute ho≥d , which provides a prediction p(xod = 1 | xo<d , θ, o<d , od ) for every masked variable, which could be used next in an ordering starting with o<d . Unlike the autoencoder, the outputs for variables corresponding to those provided in the input (not masked out) are ignored. In this order-agnostic framework, missing variables and zero-valued observations are indistinguishable by the network. This shortcoming can be alleviated by concatenating the inputs to the network (masked variables x mo<d ) with the mask mo<d . Therefore we advise substituting the input described in Equation 25 with h(0) = concat(x mo<d , mo<d ). (35) We found this modification to be important in order to obtain competitive statistical performance (see Table 3). The resulting neural network is illustrated in Figure 2. 4.1 Ensembles of NADE models As mentioned, the DeepNADE parameter fitting procedure effectively produces a factorial number of different NADE models, one for each ordering of the variables. These models will not, in general, assign the same probability to any particular datapoint. This disagreement is undesirable if we require consistent inferences for different inference problems, as it will preclude the use of the most convenient ordering of variables for each inference task. However, it is possible to use this variability across the different orderings to our advantage by combining several models. A usual approach to improve on a particular estimator is to construct an ensemble of multiple, strong but different estimators, e.g. using bagging (Ormoneit and Tresp, 1995) or stacking (Smyth and Wolpert, 1999). The DeepNADE training procedure suggests a way of generating ensembles of NADE models: 10 

11 . Neural Autoregressive Distribution Estimation ... ... ... 784 units 784 units ... ... ... ... 500 units 500 units ... 784 units 784 units 1568 units ... 784 units Figure 2: Illustration of a DeepNADE model with two hidden layers. The dashed border represents a layer pre-activation. A mask mo<d specifies a subset of variables to condition on. A conditional or predictive probability of the remaining variables is given in the final layer. Note that the output units with a corresponding input mask of value 1 (shown with dotted contour) are effectively not involved in DeepNADE’s training loss (Equation 34). take a set of uniformly distributed orderings {o(k) }K k=1 over the input variables and use the 1 K (k) average probability K k=1 p(x | θ, o ) as an estimator. The use of an ensemble increases the test-time cost of density estimation linearly with the number of orderings used. The complexity of sampling does not change however: after one of the K orderings is chosen at random, the single corresponding NADE is sampled. Importantly, the cost of training also remains the same, unlike other ensemble methods such as bagging. Furthermore, the number of components can be chosen after training and even adapted to a computational budget on the fly. 5. ConvNADE: Convolutional NADE One drawback of NADE (and its variants so far) is the lack of a mechanism for truly exploiting the high-dimensional structure of the data. For example, when using NADE on binarized MNIST, we first need to flatten the 2D images before providing them to the model as a vector. As the spatial topology is not provided to the network, it can’t use this information to share parameters and may learn less quickly. Recently, convolutional neural networks (CNN) have achieved state-of-the-art perfor- mance on many supervised tasks related to images Krizhevsky et al. (2012). Briefly, CNNs are composed of convolutional layers, each one having multiple learnable filters. The outputs of a convolutional layer are feature maps and are obtained by the convolution on the input image (or previous feature maps) of a linear filter, followed by the addition of a bias and the application of a non-linear activation function. Thanks to the convolution, spatial 11 

12 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle structure in the input is preserved and can be exploited. Moreover, as per the definition of a convolution the same filter is reused across all sub-regions of the entire image (or previous feature maps), yielding a parameter sharing that is natural and sensible for images. The success of CNNs raises the question: can we exploit the spatial topology of the inputs while keeping NADE’s autoregressive property? It turns out we can, simply by replacing the fully connected hidden layers of a DeepNADE model with convolutional layers. We thus refer to this variant as Convolutional NADE (ConvNADE). First we establish some notation that we will use throughout this section. Without loss of generality, let the input X ∈ {0, 1}NX ×NX be a square binary image of size NX and every ( ) ( ) ( ) ( −1) ( ) convolution filter W ij ∈ RNW ×NW connecting two feature maps H i and H j also ( ) be square with their size NW varying for each layer . We also define the following mask M o<d ∈ {0, 1}NX ×NX , which is 1 for the locations of the first d − 1 pixels in the ordering o. Formally, Equation 26 is modified to use convolutions instead of dot products. Specifically for an L-layer convolutional neural network that preserves the input shape (explained below) we have (L) p(xod = 1 | xo<d , θ, o<d , od ) = vec H 1 , (36) od with (0) H1 = X M o<d (37) H( −1) ( ) ( ) ( −1) ( ) Aj = bj + Hi W ij (38) i=1 ( ) ( ) Hj = σ Aj (39) (L) (L) Hj = sigm Aj , (40) (l) where H ( ) is the number of feature maps output by the -th layer and b(l) ∈ RH , ( −1) ×H ( ) ×N ( ) ×N ( ) W ( ) ∈ RH W W , with denoting the element-wise multiplication, σ (·) being any activation function and vec (X) → x is the concatenation of every row in X. Note that H (0) corresponds to the number of channels the input images have. For notational convenience, we use to denote both “valid” convolutions and “full” convolutions, instead of introducing bulky notations to differentiate these cases. The “valid” convolutions only apply a filter to complete patches of the image, resulting in a smaller image ( ) (its shape is decreased to NX − NW + 1). Alternatively, “full” convolutions zero-pad the contour of the image before applying the convolution, thus expanding the image (its shape ( ) is increased to NX + NW − 1). Which one is used should be self-explanatory depending on the context. Note that we only use convolutions with a stride of 1. Moreover, in order for ConvNADE to output conditional probabilities as shown in (L) Equation 36, the output layer must have only one feature map H 1 , whose dimension matches the dimension of the input X. This can be achieved by carefully combining layers that use either “valid” or “full” convolutions. To explore different model architectures respecting that constraint, we opted for the following strategy. Given a network, we ensured the first half of its layers was using “valid” 12 

13 . Neural Autoregressive Distribution Estimation convolutions while the other half would use “full” convolutions. In addition to that, we made sure the network was symmetric with respect to its filter shapes (i.e. the filter shape used in layer matched the one used in layer L − ). For completeness, we wish to mention that ConvNADE can also include pooling and upsampling layers, but we did not see much improvement when using them. In fact, recent research suggests that these types of layers are not essential to obtain state-of-the-art results (Springenberg et al., 2015). The flexibility of DeepNADE allows us to easily combine both convolutional and fully connected layers. To create such hybrid models, we used the simple strategy of having two separate networks, with their last layer fused together at the end. The ‘convnet’ part is only composed of convolutional layers whereas the ‘fullnet’ part is only composed of fully connected layers. The forward pass of both networks follows respectively Equations (37)–(39) and Equations (25)–(27). Note that in the ‘fullnet’ network case, x corresponds to the input image having been flattened. In the end, the output layer g of the hybrid model corresponds to the aggregation of the last layer pre-activation of both ‘convnet’ and ‘fullnet’ networks. The conditionals are slightly modified as follows: p(xod = 1 | xo<d , θ, o<d , od ) = g od (41) (L) g = sigm vec A1 + a(L) . (42) The same training procedure as for DeepNADE model can also be used for ConvNADE. For binary observations, the training loss is similar to Equation 34, with h(L) being substi- tuted for g as defined in Equation 42. As for the DeepNADE model, we found that providing the mask M o<d as an input to the model improves performance (see Table 4). For the ‘convnet’ part, the mask was provided as an additional channel to the input layer. For the ‘fullnet’ part, the inputs were concatenated with the mask as shown in Equation 35. The final architecture is shown in Figure 3. In our experiments, we found that this type of hybrid model works better than only using convolutional layers (see Table 4). Certainly, more complex architectures could be employed but this is a topic left for future work. 6. Related Work As we mentioned earlier, the development of NADE and its extensions was motivated by the question of whether a tractable distribution estimator could be designed to match a powerful but intractable model such as the restricted Boltzmann machine. The original inspiration came from the autoregressive approach taken by fully visible sigmoid belief networks (FVSBN), which were shown by Frey et al. (1996) to be surprisingly competitive, despite the simplicity of the distribution family for its conditionals. Bengio and Bengio (2000) later proposed using more powerful conditionals, modeled as single layer neural networks. Moreover, they proposed connecting the output of each dth conditional to all of the hidden layers of the d − 1 neural networks for the preceding conditionals. More recently, Germain et al. (2015) generalized this model by deriving a simple procedure for making it deep and orderless (akin to DeepNADE, in Section 4). We compare with all of these approaches in Section 7.1. 13 

14 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle 4@5x5 (valid) 8@7x7 (valid) 4@7x7 (full) 1@5x5 (full) 28 pixels 28 pixels 28 pixels 28 pixels 24 pixels 18 pixels 24 pixels 24 pixels 18 pixels 28 pixels 28 pixels 28 pixels 24 pixels 28 pixels ... 784 units ... ... ... ... 28 pixels 500 units 500 units 784 units 28 pixels ... 1568 units Figure 3: Illustration of a ConvNADE that combines a convolutional neural network with three hidden layers and a fully connected feed-forward neural network with two hidden layers. The dashed border represents a layer pre-activation. Units with a dotted contour are not valid conditionals since they depend on themselves i.e. they were given in the input. There exists, of course, more classical and non-autoregressive approaches to tractable distribution estimation, such as mixture models and Chow–Liu trees (Chow and Liu, 1968). We compare with these as well in Section 7.1. This work also relates directly to the recently growing literature on generative neural networks. In addition to the autoregressive approach described in this paper, there exists three other types of such models: directed generative networks, undirected generative networks and hybrid networks. Work on directed generative networks dates back to the original work on sigmoid belief networks (Neal, 1992) and the Helmholtz machine (Hinton et al., 1995; Dayan et al., 1995). Helmholtz machines are equivalent to a multilayer sigmoid belief network, with each using binary stochastic units. Originally they were trained using Gibbs sampling and gradient descent (Neal, 1992), or with the so-called wake sleep algorithm (Hinton et al., 1995). More recently, many alternative directed models and training procedures have been proposed. Kingma and Welling (2014); Rezende et al. (2014) proposed the variational autoencoder (VAE), where the model is the same as the Helmholtz machine, but with real-valued (usually Gaussian) stochastic units. Importantly, Kingma and Welling (2014) identified a reparameterization trick making it possible to train the VAE in a way that resembles the training of an autoencoder. This approach falls in the family of stochastic variational inference methods, where the encoder network corresponds to the approximate variational posterior. The VAE optimizes a bound on the likelihood which is estimated using a single sample from the variational posterior, though recent work has shown that a better bound can be obtained using an importance sampling approach (Burda et al., 2016). Gregor et al. (2015) later exploited the VAE approach to develop DRAW, a directed generative model for images based on a read-write attentional mechanism. Goodfellow et al. (2014) also proposed an adversarial approach to training directed generative networks, that relies on a discriminator network simultaneously trained to distinguish between data and model samples. 14 

15 . Neural Autoregressive Distribution Estimation Generative networks trained this way are referred to as Generative Adversarial Networks (GAN). While the VAE optimizes a bound of the likelihood (which is the KL divergence between the empirical and model distributions), it can be shown that GAN optimizes the Jensen–Shannon (JS) divergence between the empirical and model distributions. Li et al. (2015) instead propose a training objective derived from Maximum Mean Discrepancy (MMD; Gretton et al., 2007). Recently, the directed generative model approach has been very successfully applied to model images (Denton et al., 2015; Sohl-Dickstein et al., 2011). The undirected paradigm has also been explored extensively for developing powerful gen- erative networks. These include the restricted Boltzmann machine (Smolensky, 1986; Freund and Haussler, 1992) and its multilayer extension, the deep Boltzmann machine (Salakhut- dinov and Hinton, 2009), which dominate the literature on undirected neural networks. Salakhutdinov and Murray (2008) provided one of the first quantitative evidence of the generative modeling power of RBMs, which motivated the original parameterization for NADE (Larochelle and Murray, 2011). Efforts to train better undirected models can vary in nature. One has been to develop alternative objectives to maximum likelihood. The proposal of Contrastive Divergence (CD; Hinton, 2002) was instrumental in the popularization of the RBM. Other proposals include pseudo-likelihood (Besag, 1975; Marlin et al., 2010), score matching (Hyv¨ arinen, 2005; Hyv¨arinen, 2007a,b), noise contrastive estimation (Gutmann and Hyv¨ arinen, 2010) and probability flow minimization (Sohl-Dickstein et al., 2011). An- other line of development has been to optimize likelihood using RobbinsMonro stochastic approximation (Younes, 1989), also known as Persistent CD (Tieleman, 2008), and develop good MCMC samplers for deep undirected models (Salakhutdinov, 2009, 2010; Desjardins et al., 2010; Cho et al., 2010). Work has also been directed towards proposing improved update rules or parameterization of the model’s energy function (Tieleman and Hinton, 2009; Cho et al., 2013; Montavon and M¨ uller, 2012) as well as improved approximate inference of the hidden layers (Salakhutdinov and Larochelle, 2010). The work of Ngiam et al. (2011) also proposed an undirected model that distinguishes itself from deep Boltzmann machines by having deterministic hidden units, instead of stochastic. Finally, hybrids of directed and undirected networks are also possible, though much less common. The most notable case is the Deep Belief Network (DBN; Hinton et al., 2006), which corresponds to a sigmoid belief network for which the prior over its top hidden layer is an RBM (whose hidden layer counts as an additional hidden layer). The DBN revived interest in RBMs, as they were required to successfully initialize the DBN. NADE thus substantially differs from this literature focusing on directed and undirected models, benefiting from a few properties that these approaches lack. Mainly, NADE does not rely on latent stochastic hidden units, making it possible to tractably compute its associated data likelihood for some given ordering. This in turn makes it possible to efficiently produce exact samples from the model (unlike in undirected models) and get an unbiased gradient for maximum likelihood training (unlike in directed graphical models). 7. Results In this section, we evaluate the performance of our different NADE models on a variety of datasets. 15 

16 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle Table 1: Statistics on the binary vector datasets of Section 7.1. Name # Inputs Train Valid. Test Adult 123 5000 1414 26147 Connect4 126 16000 4000 47557 DNA 180 1400 600 1186 Mushrooms 112 2000 500 5624 NIPS-0-12 500 400 100 1240 OCR-letters 128 32152 10000 10000 RCV1 150 40000 10000 150000 Web 300 14000 3188 32561 7.1 Binary vectors datasets We start by evaluating the performance of NADE models on a set of benchmark datasets where the observations correspond to binary vectors. These datasets were mostly taken from the LIBSVM datasets web site1 , except for OCR-letters2 and NIPS-0-12 3 . Code to download these datasets is available here: http://info.usherbrooke.ca/hlarochelle/ code/nade.tar.gz. Table 1 summarizes the main statistics for these datasets. For these experiments, we only consider tractable distribution estimators, where we can evaluate p(x) on test items exactly. We consider the following baselines: • MoB: A mixture of multivariate Bernoullis, trained using the EM algorithm. The number of mixture components was chosen from {32, 64, 128, 256, 512, 1024} based on validation set performance, and early stopping was used to determine the number of EM iterations. • RBM: A restricted Boltzmann machine made tractable by using only 23 hidden units, trained by contrastive divergence with up to 25 steps of Gibbs sampling. The validation set performance was used to select the learning rate from {0.005, 0.0005, 0.00005}, and the number of iterations over the training set from {100, 500, 1000}. • FVSBN: Fully visible sigmoid belief network, that models each conditional p(xod | xo<d ) with logistic regression. The ordering of inputs was selected randomly. Training was by stochastic gradient descent. The validation set was used for early stopping, as well as for choosing the base learning rate η ∈ {0.05, 0.005, 0.0005}, and a decreasing schedule constant γ from {0, 0.001, 0.000001} for the learning rate schedule η/(1 + γt) for the tth update. • Chow–Liu: A Chow–Liu tree is a graph over the observed variables, where the distribution of each variable, except the root, depends on a single parent node. There 1. http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/ 2. http://ai.stanford.edu/~btaskar/ocr/ 3. http://www.cs.nyu.edu/~roweis/data.html 16 

17 . Neural Autoregressive Distribution Estimation is an O(D2 ) fitting algorithm to find the maximum likelihood tree and conditional distributions (Chow and Liu, 1968). We adapted an implementation provided by Harmeling and Williams (2011), who found Chow–Liu to be a strong baseline. The maximum likelihood parameters are not defined when conditioning on events that haven’t occurred in the training set. Moreover, conditional probabilities of zero are possible, which could give infinitely bad test set performance. We re-estimated the conditional probabilities on the Chow–Liu tree using Lidstone or “add-α” smoothing: count(xd = 1 | xparent = z) + α p(xd = 1 | xparent = z) = , (43) count(xparent = z) + 2α selecting α for each dataset from {10−20 , 0.001, 0.01, 0.1} based on performance on the validation set. • MADE (Germain et al., 2015): Generalization of the neural network approach of Bengio and Bengio (2000), to multiple layers. We consider a version using a single (fixed) input ordering and another trained on multiple orderings from which an ensemble was constructed (which was inspired from the order-agnostic approach of Section 4) that we refer to as MADE-E. See Germain et al. (2015) for more details. We compare these baselines with the two following NADE variants: • NADE (fixed order): Single layer NADE model, trained on a single (fixed) randomly generated order, as described in Section 2. The sigmoid activation function was used for the hidden layer, of size 500. Much like for FVSBN, training relied on stochastic gradient descent and the validation set was used for early stopping, as well as for choosing the learning rate from {0.05, 0.005, 0.0005}, and the decreasing schedule constant γ from {0,0.001,0.000001}. • NADE-E: Single layer NADE trained according to the order-agnostic procedure described in Section 4. The rectified linear activation function was used for the hidden layer, also of size 500. Minibatch gradient descent was used for training, with minibatches of size 100. The initial learning rate, chosen among {0.016, 0.004, 0.001, 0.00025, 0.0000675}, was linearly decayed to zero over the course of 100, 000 parameter updates. Early stopping was used, using Equation 34 to get a stochastic estimate of the validation set average log-likelihood. An ensemble using 16 orderings was used to compute the test-time log-likelihood. Table 2 presents the results. We observe that NADE restricted to a fixed ordering of the inputs achieves very competitive performance compared to the baselines. However, the order-agnostic version of NADE is overall the best method, being among the top performing model for 5 datasets out of 8. The performance of fixed-order NADE is surprisingly robust to variations of the chosen input ordering. The standard deviation on the average log-likelihood when varying the ordering was small: on Mushrooms, DNA and NIPS-0-12, we observed standard deviations of 0.045, 0.05 and 0.15, respectively. However, models with different orders can do well on different test examples, which explains why ensembling can still help. 17 

18 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle Table 2: Average log-likelihood performance of tractable distribution baselines and NADE models, on binary vector datasets. The best result is shown in bold, along with any other result with an overlapping confidence interval. Model Adult Connect4 DNA Mushrooms NIPS-0-12 OCR-letters RCV1 Web MoB -20.44 -23.41 -98.19 -14.46 -290.02 -40.56 -47.59 -30.16 RBM -16.26 -22.66 -96.74 -15.15 -277.37 -43.05 -48.88 -29.38 FVSBN -13.17 -12.39 -83.64 -10.27 -276.88 -39.30 -49.84 -29.35 Chow–Liu -18.51 -20.57 -87.72 -20.99 -281.01 -48.87 -55.60 -33.92 MADE -13.12 -11.90 -83.63 -9.68 -280.25 -28.34 -47.10 -28.53 MADE-E -13.13 -11.90 -79.66 -9.69 -277.28 -30.04 -46.74 -28.25 NADE -13.19 -11.99 -84.81 -9.81 -273.08 -27.22 -46.66 -28.39 NADE-E -13.19 -12.58 -82.31 -9.69 -272.39 -27.32 -46.12 -27.87 7.2 Binary image dataset We now consider the case of an image dataset, constructed by binarizing the MNIST digit dataset, as generated by Salakhutdinov and Murray (2008). This benchmark has been a popular choice for the evaluation of generative neural network models. Here, we investigate two questions: 1. How does NADE compare to other intractable generative models? 2. Does the use of a convolutional architecture improve the performance of NADE? For these experiments, in addition to the baselines already described in Section 7.1, we consider the following: • DARN (Gregor et al., 2014): This deep generative autoencoder has two hidden layers, one deterministic and one with binary stochastic units. Both layers have 500 units (denoted as nh = 500). Adaptive weight noise (adaNoise) was either used or not to avoid the need for early stopping (Graves, 2011). Evaluation of exact test probabilities is intractable for large latent representations. Hence, Monte Carlo was used to approximate the expected description length, which corresponds to an upper bound on the negative log-likelihood. • DRAW (Gregor et al., 2015): Similar to a variational autoencoder where both the encoder and the decoder are LSTMs, guided (or not) by an attention mechanism. In this model, both LSTMs (encoder and decoder) are composed of 256 recurrent hidden units and always perform 64 timesteps. When the attention mechanism is enabled, patches (2 × 2 pixels) are provided as inputs to the encoder instead of the whole image and the decoder also produces patches (5 × 5 pixels) instead of a whole image. • Pixel RNN (Oord et al., 2016): NADE-like model for natural images that is based on convolutional and LSTM hidden units. This model has 7 hidden layers, each 18 

19 . Neural Autoregressive Distribution Estimation The The Neural Neural Autoregressive Autoregressive Distribution Distribution Estimator Estimator Figure Figure Figure 2: 2: (Left): 4: (Left):(Left): samplessamples samples from fromtrained from NADE NADE NADE on trained trained binarizedon on aa binary binary MNIST. version version (Right): of of mnist. mnist. (Middle): probabilities (Middle): propro whichfrom which eachwhich each pixeleach pixel waspixel was was sampled. sampled. sampled. (Right): (Right):Ancestral sampling visualization visualization of was of some someused of withrows of the the the same rows of of W. W. This This figure figure is is bb fixed screen. computer computer ordering used during training. screen. Algorithm set set itit toto20,Pretraining 0, to obtain:of a NADE with n hidden layers on dataset to obtain: X. References References procedure PRETRAIN(n, X) if n = 100then ∂KL(q(v ∂KL(q(vii,, v v>i >i,, h|v h|v<i<i)||p(v )||p(vii,, v v>i >i,, h|v h|v<i )) Bengio, <i)) Bengio, Y.,Y., & & Bengio, Bengio, S. S. (2000). (2000). == dimensional dimensional discrete discrete data data with with mu mu return RANDOM-ONE-HIDDEN-LAYER-NADE ∂τ ∂τkk(i) (i) else networks. networks. Advances Advances in in Neural Neural Inform Infor ττkk(i) (i) nade00←= = −c −ckk − −W PRETRAIN(n Wk,· µ(i) µ(i) k,·− + + log 1, X) log ing ing Systems Systems 12 12 (NIPS’99) (NIPS’99) (pp.(pp. 400–4 400–4 11 − − ττkk(i) (i) nade ← REMOVE-OUTPUT-LAYER(nade) Bengio, Bengio, Y., Y., Lamblin, Lamblin, P.,P., Popovici, Popovici, D., D., & ττkk(i) (i) nade ←= ADD-A-NEW-HIDDEN-LAYER(nade) = exp(c exp(ckk + +W Wk,·k,·µ(i)) µ(i)) (2007). (2007). Greedy Greedy layer-wise layer-wise training training of o 11 − − ττnade kk(i) (i) ← ADD-A-NEW-OUTPUT-LAYER(nade) Advances Advances in in Neural Neural Information Information ProPro nade ← TRAIN-ALL(nade, exp(c exp(ckk + +W Wk,· X, k,· iters = 20) µ(i)) µ(i)) Train 19 for 20 iterations. 19 (NIPS’06) (NIPS’06) (pp. (pp. 153–160). 153–160). MIT MIT P P ττkk(i) (i) = return = nade11 + + exp(c exp(ckk ++W Wk,·k,·µ(i)) µ(i)) end if    Chen,  Chen, X.X. R., R., Krishnaiah, Krishnaiah, P. P. R., R., & & Liang Liang Estimation Estimation of of multivariate multivariate binary binary dd end procedure ττkk(i) (i) = = sigm sigm  cckk + + W Wkj kjµ µjj(i) (i) + + W Wkj kjv vjj  thogonal thogonal functions. functions. Journal Journal of of Multiv Multiv j≥i j≥i j<i j<i 31, 31, 178–186. 178–186. composed of 16 units. Oord et al. (2016) proposed a novel two-dimensional Freund, Freund, Y.,Y., & & LSTM, Haussler, Haussler, D. D. (1992). (1992). A A where where namedin in the the last Diagonal last step step we BiLSTM, we have whichhave replaced replaced is used in this the the model. ma- ma-Unlike our ConvNADE, learning learning rule forthe rule for aa restricted restricted class class of of trix/vector trix/vector ordering is multiplication multiplication WWk,· fixed before training k,·µ(i) µ(i) and byby at its its explicit testexplicit time, and sum- sum-corresponds to aAdvances chines. chines. scan of thein Advances in Neural Neural Informa Informa mation mation form form and and have have used used the the fact fact that that µµjj (i) (i) == vv image in a diagonal fashion starting from a corner at the top and reachingj j for for Systemsthe Systems opposite 44 (NIPS’91) (NIPS’91) (pp. (pp. 912–919) 912–919 jj corner < < i.i. at the bottom. Morgan Morgan Kaufmann, Kaufmann, San San Mateo. Mateo. Similarly, Similarly, we we set set the the derivative derivative with with respect respect to to µµjj(i) (i) Frey, Frey, B. B. J. J. (1998). (1998). Graphical Graphical models models for for We compare these baselines with some NADE variants. The performance of a basic for jj ≥ for ≥ ii to to 00 and and obtain: obtain: ing ing and and digital digital communication. communication. MIT MIT (fixed-order, single hidden layer) NADE model is provided in Table 3 and samples are illustrated in Figure 4.∂KL(q(vMore importantly, ∂KL(q(v ii,, v v>i >i,, h|v h|v<i we <i will iifocus )||p(v )||p(v ,, v >i,,on v>i h|v h|v )) Frey, whether <i)) <i Frey, B. B. J., J., Hinton, the following Hinton, G. G. E., variants E., && Dayan, Dayan, P.P. (( 00 == achieve better test set performance: wake-sleep wake-sleep algorithm algorithm learn learn good good den den ∂µ ∂µjj(i) (i) Advances Advances in in Neural Neural Information Information ProPro µµjj(i) (i) 88 (NIPS’95) (NIPS’95) (pp. (pp. 661–670). 661–670). MIT MIT PrPr 00 = = −b −bjj − − ττ(i) (i) W W·,j·,j + + log log 19 11 − − µµjj(i) (i) MA. MA. µµjj(i) (i) Hinton, Hinton, G.G. E. E. (2002). (2002). Training Training produc produc == exp(b exp(bjj + + ττ(i)(i) W W·,j·,j)) 11 − − µµjj(i) (i) minimizing minimizing contrastive contrastive divergence. divergence. N N tion, tion, 14, 14, 1771–1800. 1771–1800. 

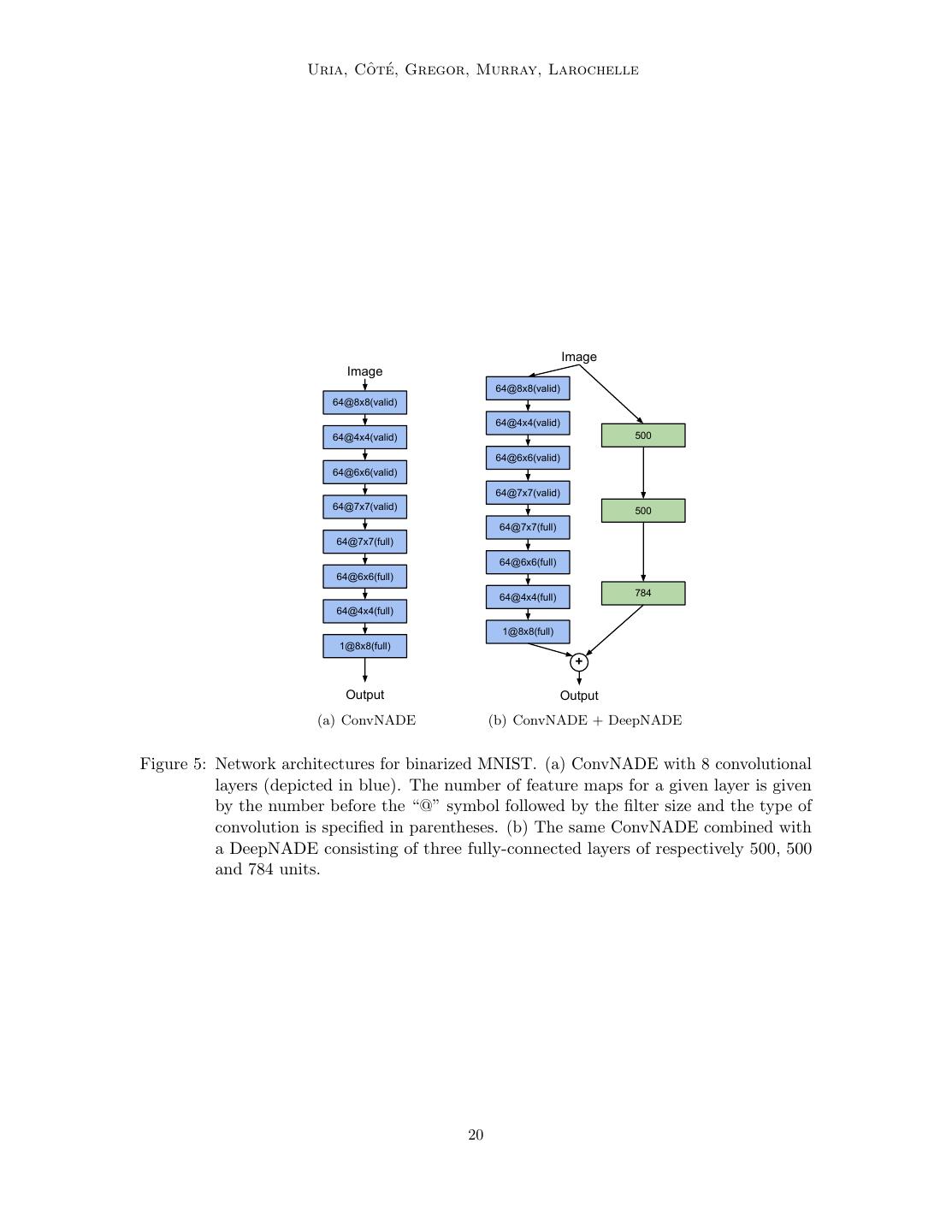
20 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle Image Image 64@8x8(valid) 64@8x8(valid) 64@4x4(valid) 64@4x4(valid) 500 64@6x6(valid) 64@6x6(valid) 64@7x7(valid) 64@7x7(valid) 500 64@7x7(full) 64@7x7(full) 64@6x6(full) 64@6x6(full) 64@4x4(full) 784 64@4x4(full) 1@8x8(full) 1@8x8(full) + Output Output (a) ConvNADE (b) ConvNADE + DeepNADE Figure 5: Network architectures for binarized MNIST. (a) ConvNADE with 8 convolutional layers (depicted in blue). The number of feature maps for a given layer is given by the number before the “@” symbol followed by the filter size and the type of convolution is specified in parentheses. (b) The same ConvNADE combined with a DeepNADE consisting of three fully-connected layers of respectively 500, 500 and 784 units. 20 

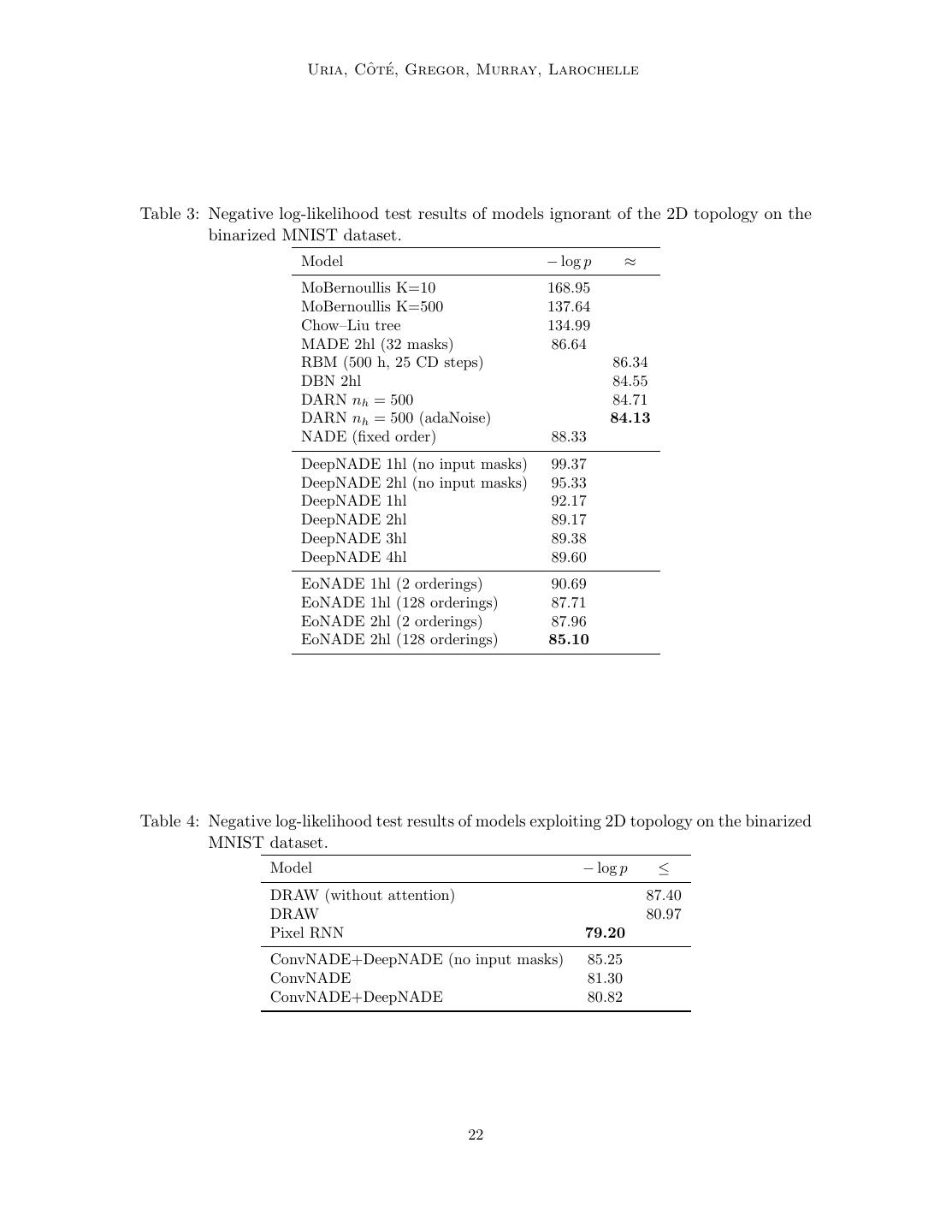
21 . Neural Autoregressive Distribution Estimation • DeepNADE: Multiple layers (1hl, 2hl, 3hl or 4hl) trained according to the order- agnostic procedure described in Section 4. Information about which inputs are masked was either provided or not (no input masks) to the model. The rectified linear activation function was used for all hidden layers. Minibatch gradient descent was used for training, with minibatches of size 1000. Training consisted of 200 iterations of 1000 parameter updates. Each hidden layer was pretrained according to Algorithm 2. We report an average of the average test log-likelihoods over ten different random orderings. • EoNADE: This variant is similar to DeepNADE except for the log-likelihood on the test set, which is instead computed from an ensemble that averages predictive probabilities over 2 or 128 orderings. To clarify, the DeepNADE results report the typical performance of one ordering, by averaging results after taking the log, and so do not combine the predictions of the models like EoNADE does. • ConvNADE: Multiple convolutional layers trained according to the order-agnostic procedure described in Section 4. The exact architecture is shown in Figure 5(a). Information about which inputs are masked was either provided or not (no input masks). The rectified linear activation function was used for all hidden layers. The Adam optimizer (Kingma and Ba, 2015) was used with a learning rate of 10−4 . Early stopping was used with a look ahead of 10 epochs, using Equation 34 to get a stochastic estimate of the validation set average log-likelihood. An ensemble using 128 orderings was used to compute the log-likelihood on the test set. • ConvNADE + DeepNADE: This variant is similar to ConvNADE except for the aggregation of a separate DeepNADE model at the end of the network. The exact architecture is shown in Figure 5(b). The training procedure is the same as with ConvNADE. Table 3 presents the results obtained by models ignorant of the 2D topology, such as the basic NADE model. Addressing the first question, we observe that the order-agnostic version of NADE with two hidden layers is competitive with intractable generative models. Moreover, examples of the ability of DeepNADE to solve inference tasks by marginalization and conditional sampling are shown in Figure 6. Now, addressing the second question, we can see from Table 4 that convolutions do improve the performance of NADE. Moreover, we observe that providing information about which inputs are masked is essential to obtaining good results. We can also see that combining convolutional and fully-connected layers helps. Even though ConvNADE+DeepNADE performs slightly worst than Pixel RNN, we note that our proposed approach is order- agnostic, whereas Pixel RNN requires a fixed ordering. Figure 7 shows samples obtained from the ConvNADE+DeepNADE model using ancestral sampling on a random ordering. 7.3 Real-valued observations datasets 21 

22 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle Table 3: Negative log-likelihood test results of models ignorant of the 2D topology on the binarized MNIST dataset. Model − log p ≈ MoBernoullis K=10 168.95 MoBernoullis K=500 137.64 Chow–Liu tree 134.99 MADE 2hl (32 masks) 86.64 RBM (500 h, 25 CD steps) 86.34 DBN 2hl 84.55 DARN nh = 500 84.71 DARN nh = 500 (adaNoise) 84.13 NADE (fixed order) 88.33 DeepNADE 1hl (no input masks) 99.37 DeepNADE 2hl (no input masks) 95.33 DeepNADE 1hl 92.17 DeepNADE 2hl 89.17 DeepNADE 3hl 89.38 DeepNADE 4hl 89.60 EoNADE 1hl (2 orderings) 90.69 EoNADE 1hl (128 orderings) 87.71 EoNADE 2hl (2 orderings) 87.96 EoNADE 2hl (128 orderings) 85.10 Table 4: Negative log-likelihood test results of models exploiting 2D topology on the binarized MNIST dataset. Model − log p ≤ DRAW (without attention) 87.40 DRAW 80.97 Pixel RNN 79.20 ConvNADE+DeepNADE (no input masks) 85.25 ConvNADE 81.30 ConvNADE+DeepNADE 80.82 22 

23 . Neural Autoregressive Distribution Estimation -61.21 -36.33 -84.40 -46.22 -96.68 -66.26 -86.37 -73.31 -93.35 -79.40 -45.84 -41.88 Figure 6: Example of marginalization and sampling. The first column shows five examples from the test set of the MNIST dataset. The second column shows the density of these examples when a random 10×10 pixel region is marginalized. The right-most five columns show samples for the hollowed region. Both tasks can be done easily with a NADE where the pixels to marginalize are at the end of the ordering. 0 Samples 50 100 150 200 0 50 100 150 200 Figure 7: (Left): samples from ConvNADE+DeepNADE trained on binarized MNIST. (Right): probabilities from which each pixel was sampled. Ancestral sampling was used with a different random ordering for each sample. 23 

24 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle In this section, we compare the statistical performance of RNADE to mixtures of Gaussians (MoG) and factor analyzers (MFA), which are surprisingly strong baselines in some tasks (Tang et al., 2012; Zoran and Weiss, 2012). 7.3.1 Low-dimensional data We start by considering three UCI datasets (Bache and Lichman, 2013), previously used to study the performance of other density estimators (Silva et al., 2011; Tang et al., 2012), namely: red wine, white wine and parkinsons. These are low dimensional datasets (see Table 5) with hard thresholds and non-linear dependencies that make it difficult to fit mixtures of Gaussians or factor analyzers. Following Tang et al. (2012), we eliminated discrete-valued attributes and an attribute from every pair with a Pearson correlation coefficient greater than 0.98. We normalized each dimension of the data by subtracting its training-subset sample mean and dividing by its standard deviation. All results are reported on the normalized data. We use full-covariance Gaussians and mixtures of factor analysers as baselines. Models were compared on their log-likelihood on held-out test data. Due to the small size of the datasets (see Table 5), we used 10-folds, using 90% of the data for training, and 10% for testing. We chose the hyperparameter values for each model by doing per-fold cross-validation, using a ninth of the training data as validation data. Once the hyperparameter values have been chosen, we train each model using all the training data (including the validation data) and measure its performance on the 10% of held-out testing data. In order to avoid overfitting, we stopped the training after reaching a training likelihood higher than the one obtained on the best validation-wise iteration of the best validation run. Early stopping was important to avoid overfitting the RNADE models. It also improved the results of the MFAs, but to a lesser degree. The MFA models were trained using the EM algorithm (Ghahramani and Hinton, 1996; Verbeek, 2005). We cross-validated the number of components and factors. We also selected the number of factors from 2, 4, . . . D, where choosing D results in a mixture of Gaussians, and the number of components was chosen among 2, 4, . . . 50. Cross-validation selected fewer than 50 components in every case. We report the performance of several RNADE models using different parametric forms for the one-dimensional conditionals: Gaussian with fixed variance (RNADE-FV), Gaussian with variable variance (RNADE-Gaussian), sinh-arcsinh distribution (RNADE-SAS), mixture of Gaussians (RNADE-MoG), and mixture of Laplace distributions (RNADE-MoL). All RNADE models were trained by stochastic gradient descent, using minibatches of size 100, for 500 epochs, each epoch comprising 10 minibatches. We fixed the number of hidden units to 50, and the non-linear activation function of the hidden units to ReLU. Three hyperparameters were cross-validated using grid-search: the number of components on each one-dimensional conditional (only applicable to the RNADE-MoG and RNADE-MoL models) was chosen from {2, 5, 10, 20}, the weight-decay (used only to regularize the input to hidden weights) from {2.0, 1.0, 0.1, 0.01, 0.001, 0}, and the learning rate from {0.1, 0.05, 0.025, 0.0125}. Learning rates were decreased linearly to reach 0 after the last epoch. 24 

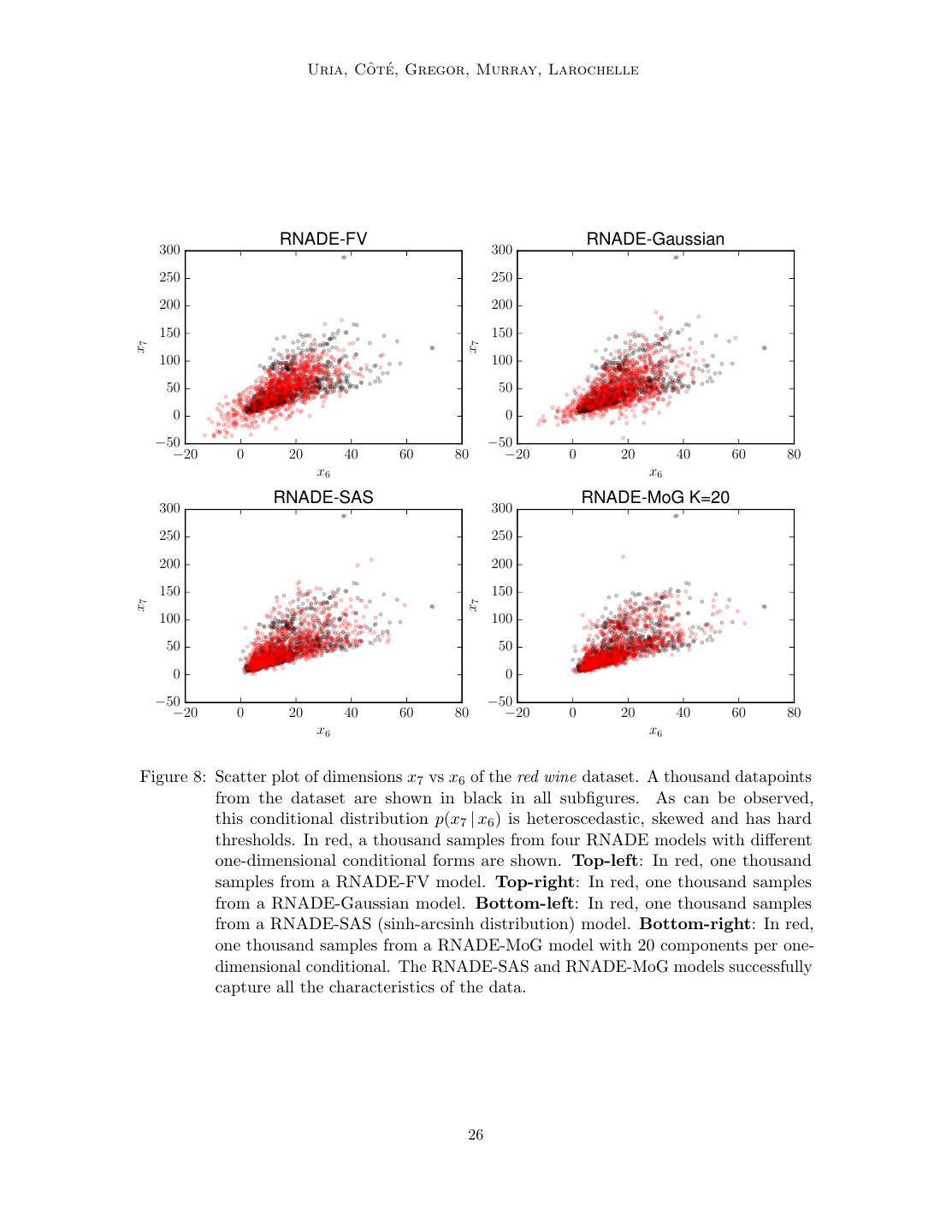
25 . Neural Autoregressive Distribution Estimation Table 5: Dimensionality and size of the UCI datasets used in Section 7.3.1 Red wine White wine Parkinsons Dimensionality 11 11 15 Total number of datapoints 1599 4898 5875 Table 6: Average test set log-likelihoods per datapoint for seven models on three UCI datasets. Performances not in bold can be shown to be significantly worse than at least one of the results in bold as per a paired t-test on the ten mean-likelihoods (obtained from each data fold), with significance level 0.05. Model Red wine White wine Parkinsons Gaussian −13.18 −13.20 −10.85 MFA −10.19 −10.73 −1.99 RNADE-FV −12.29 −12.50 −8.87 RNADE-Gaussian −11.99 −12.20 −3.47 RNADE-SAS −9.86 −11.22 −3.07 RNADE-MoG −9.36 −10.23 −0.90 RNADE-MoL −9.46 −10.38 −2.63 The results are shown in Table 6. RNADE with mixture of Gaussian conditionals was among the statistically significant group of best models on all datasets. As shown in Figure 8, RNADE-SAS and RNADE-MoG models are able to capture hard thresholds and heteroscedasticity. 7.3.2 Natural image patches We also measured the ability of RNADE to model small patches of natural images. Following the work of Zoran and Weiss (2011), we use 8-by-8-pixel patches of monochrome natural images, obtained from the BSDS300 dataset (Martin et al., 2001; Figure 9 gives examples). Pixels in this dataset can take a finite number of brightness values ranging from 0 to 255. We added uniformly distributed noise between 0 and 1 to the brightness of each pixel. We then divided by 256, making the pixels take continuous values in the range [0, 1]. Adding noise prevents deceivingly high-likelihood solutions that assign narrow high-density spikes around some of the possible discrete values. We subtracted the mean pixel value from each patch. Effectively reducing the dimen- sionality of the data. Therefore we discarded the 64th (bottom-right) pixel, which would be perfectly predictable and models could fit arbitrarily high densities to it. All of the results in this section were obtained by fitting the pixels in a raster-scan order. Experimental details follow. We trained our models by using patches randomly drawn from 180 images in the training subset of BSDS300. We used the remaining 20 images in the 25 

26 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle RNADE-FV RNADE-Gaussian 300 300 250 250 200 200 150 150 x7 x7 100 100 50 50 0 0 −50 −50 −20 0 20 40 60 80 −20 0 20 40 60 80 x6 x6 RNADE-SAS RNADE-MoG K=20 300 300 250 250 200 200 150 150 x7 x7 100 100 50 50 0 0 −50 −50 −20 0 20 40 60 80 −20 0 20 40 60 80 x6 x6 Figure 8: Scatter plot of dimensions x7 vs x6 of the red wine dataset. A thousand datapoints from the dataset are shown in black in all subfigures. As can be observed, this conditional distribution p(x7 | x6 ) is heteroscedastic, skewed and has hard thresholds. In red, a thousand samples from four RNADE models with different one-dimensional conditional forms are shown. Top-left: In red, one thousand samples from a RNADE-FV model. Top-right: In red, one thousand samples from a RNADE-Gaussian model. Bottom-left: In red, one thousand samples from a RNADE-SAS (sinh-arcsinh distribution) model. Bottom-right: In red, one thousand samples from a RNADE-MoG model with 20 components per one- dimensional conditional. The RNADE-SAS and RNADE-MoG models successfully capture all the characteristics of the data. 26 

27 . Neural Autoregressive Distribution Estimation training subset as validation data. We used 1000 random patches from the validation subset to early-stop training of RNADE. We measured the performance of each model by their log-likelihood on one million patches drawn randomly from the test subset of 100 images not present in the training data. Given the larger scale of this dataset, hyperparameters of the RNADE and MoG models were chosen manually using the performance of preliminary runs on the validation data, rather than by grid search. All RNADE models reported use ReLU activations for the hidden units. The RNADE models were trained by stochastic gradient descent, using 25 datapoints per minibatch, for a total of 1,000 epochs, each comprising 1,000 minibatches. The learning rate was initialized to 0.001, and linearly decreased to reach 0 after the last epoch. Gradient momentum with factor 0.9 was used, but initiated after the first epoch. A weight decay rate of 0.001 was applied to the input-to-hidden weight matrix only. We found that multiplying the gradient of the mean output parameters by the standard deviation improves results of the models with mixture outputs4 . RNADE training was early stopped but didn’t show signs of overfitting. Even larger models might perform better. The MoG models were trained using 1,000 iterations of minibatch EM. At each iteration 20,000 randomly sampled datapoints were used in an EM update. A step was taken from the previous parameters’ value towards the parameters resulting from the M-step: θt = (1 − η)θt−1 + ηθEM . The step size, η, was scheduled to start at 0.1 and linearly decreased to reach 0 after the last update. The training of the MoG was early-stopped and also showed no signs of overfitting. The results are shown in Table 7. We report the average log-likelihood of each model for a million image patches from the test set. The ranking of RNADE models is maintained when ordered by validation likelihood: the model with best test-likelihood would have been chosen using crossvalidation across all the RNADE models shown in the table. We also compared RNADE with a MoG trained by Zoran and Weiss (downloaded from Daniel Zoran’s website) from which we removed the 64th row and column of each covariance matrix. There are two differences in the set-up of our experiments and those of Zoran and Weiss. First, we learned the means of the MoG components, while Zoran and Weiss (2011) fixed them to zero. Second, we held-out 20 images from the training set to do early-stopping and hyperparameter optimisation, while they used the 200 images for training. The RNADE-FV model with fixed conditional variances obtained very low statistical performance. Adding an output parameter per dimension to have variable standard deviations made our models competitive with MoG with 100 full-covariance components. However, in order to obtain results superior to the mixture of Gaussians model trained by Zoran and Weiss, we had to use richer conditional distributions: one-dimensional mixtures of Gaussians (RNADE-MoG). On average, the best RNADE model obtained 3.3 nats per patch higher log-density than a MoG fitted with the same training data. In Figure 9, we show one hundred examples from the test set, one hundred examples from Zoran and Weiss’ mixture of Gaussians, and a hundred samples from our best RNADE-MoG model. Similar patterns can be observed in the three cases: uniform patches, edges, and locally smooth noisy patches. 4. Empirically, we found this to work better than regular gradients and also better than multiplying by the variances, which would provide a step with the right units. 27 

28 . ˆ te Uria, Co ´, Gregor, Murray, Larochelle Table 7: Average per-example log-likelihood of several mixture of Gaussian and RNADE models on 8×8 pixel patches of natural images. These results are reported in nats and were calculated using one million patches. Standard errors due to the finite test sample size are lower than 0.1 nats in every case. h indicates the number of hidden units in the RNADE models, and K the number of one-dimensional components for each conditional in RNADE or the number of full-covariance components for MoG. Model Test log-likelihood MoG K = 200 (Zoran and Weiss, 2012)a 152.8 MoG K = 100 144.7 MoG K = 200 150.4 MoG K = 300 150.4 RNADE-FV h = 512 100.3 RNADE-Gaussian h = 512 143.9 RNADE-Laplace h = 512 145.9 RNADE-SASb h = 512 148.5 RNADE-MoG K = 2 h = 512 149.5 RNADE-MoG K = 2 h = 1024 150.3 RNADE-MoG K = 5 h = 512 152.4 RNADE-MoG K = 5 h = 1024 152.7 RNADE-MoG K = 10 h = 512 153.5 RNADE-MoG K = 10 h = 1024 153.7 RNADE-MoL K = 2 h = 512 149.3 RNADE-MoL K = 2 h = 1024 150.1 RNADE-MoL K = 5 h = 512 151.5 RNADE-MoL K = 5 h = 1024 151.4 RNADE-MoL K = 10 h = 512 152.3 RNADE-MoL K = 10 h = 1024 152.5 a. This model was trained using the full 200 images in the BSDS training dataset, the rest of the models were trained using 180, reserving 20 for hyperparameter crossvalidation and early-stopping. b. Training an RNADE with sinh-arcsinh conditionals required the use of a starting learning rate 20 times smaller to avoid divergence during training. For this reason, this model was trained for 2000 epochs. 28 

29 . Neural Autoregressive Distribution Estimation Figure 9: Top: 100 8×8 patches from the BSDS test set. Center: 100 samples from a mixture of Gaussians with 200 full-covariance components. Bottom: 100 samples from an RNADE with 1024 hidden units and 10 Gaussian components per conditional. All data and samples were drawn randomly and sorted by their density under the RNADE. 29