DeepLab

1 . 1 DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs Liang-Chieh Chen, George Papandreou, Senior Member, IEEE, Iasonas Kokkinos, Member, IEEE, Kevin Murphy, and Alan L. Yuille, Fellow, IEEE Abstract—In this work we address the task of semantic image segmentation with Deep Learning and make three main contributions arXiv:1606.00915v2 [cs.CV] 12 May 2017 that are experimentally shown to have substantial practical merit. First, we highlight convolution with upsampled filters, or ‘atrous convolution’, as a powerful tool in dense prediction tasks. Atrous convolution allows us to explicitly control the resolution at which feature responses are computed within Deep Convolutional Neural Networks. It also allows us to effectively enlarge the field of view of filters to incorporate larger context without increasing the number of parameters or the amount of computation. Second, we propose atrous spatial pyramid pooling (ASPP) to robustly segment objects at multiple scales. ASPP probes an incoming convolutional feature layer with filters at multiple sampling rates and effective fields-of-views, thus capturing objects as well as image context at multiple scales. Third, we improve the localization of object boundaries by combining methods from DCNNs and probabilistic graphical models. The commonly deployed combination of max-pooling and downsampling in DCNNs achieves invariance but has a toll on localization accuracy. We overcome this by combining the responses at the final DCNN layer with a fully connected Conditional Random Field (CRF), which is shown both qualitatively and quantitatively to improve localization performance. Our proposed “DeepLab” system sets the new state-of-art at the PASCAL VOC-2012 semantic image segmentation task, reaching 79.7% mIOU in the test set, and advances the results on three other datasets: PASCAL-Context, PASCAL-Person-Part, and Cityscapes. All of our code is made publicly available online. Index Terms—Convolutional Neural Networks, Semantic Segmentation, Atrous Convolution, Conditional Random Fields. ✦ 1 I NTRODUCTION Deep Convolutional Neural Networks (DCNNs) [1] have employed in a fully convolutional fashion [14]. In order to pushed the performance of computer vision systems to overcome this hurdle and efficiently produce denser feature soaring heights on a broad array of high-level problems, maps, we remove the downsampling operator from the last including image classification [2], [3], [4], [5], [6] and object few max pooling layers of DCNNs and instead upsample detection [7], [8], [9], [10], [11], [12], where DCNNs trained the filters in subsequent convolutional layers, resulting in in an end-to-end manner have delivered strikingly better feature maps computed at a higher sampling rate. Filter results than systems relying on hand-crafted features. Es- upsampling amounts to inserting holes (‘trous’ in French) sential to this success is the built-in invariance of DCNNs between nonzero filter taps. This technique has a long to local image transformations, which allows them to learn history in signal processing, originally developed for the increasingly abstract data representations [13]. This invari- efficient computation of the undecimated wavelet transform ance is clearly desirable for classification tasks, but can ham- in a scheme also known as “algorithme a` trous” [15]. We use per dense prediction tasks such as semantic segmentation, the term atrous convolution as a shorthand for convolution where abstraction of spatial information is undesired. with upsampled filters. Various flavors of this idea have In particular we consider three challenges in the applica- been used before in the context of DCNNs by [3], [6], [16]. tion of DCNNs to semantic image segmentation: (1) reduced In practice, we recover full resolution feature maps by a feature resolution, (2) existence of objects at multiple scales, combination of atrous convolution, which computes feature and (3) reduced localization accuracy due to DCNN invari- maps more densely, followed by simple bilinear interpola- ance. Next, we discuss these challenges and our approach tion of the feature responses to the original image size. This to overcome them in our proposed DeepLab system. scheme offers a simple yet powerful alternative to using The first challenge is caused by the repeated combination deconvolutional layers [13], [14] in dense prediction tasks. of max-pooling and downsampling (‘striding’) performed at Compared to regular convolution with larger filters, atrous consecutive layers of DCNNs originally designed for image convolution allows us to effectively enlarge the field of view classification [2], [4], [5]. This results in feature maps with of filters without increasing the number of parameters or the significantly reduced spatial resolution when the DCNN is amount of computation. The second challenge is caused by the existence of ob- • L.-C. Chen, G. Papandreou, and K. Murphy are with Google Inc. I. Kokki- jects at multiple scales. A standard way to deal with this is nos is with University College London. A. Yuille is with the Departments to present to the DCNN rescaled versions of the same image of Cognitive Science and Computer Science, Johns Hopkins University. and then aggregate the feature or score maps [6], [17], [18]. The first two authors contributed equally to this work. We show that this approach indeed increases the perfor- 

2 . 2 mance of our system, but comes at the cost of computing The updated DeepLab system we present in this paper feature responses at all DCNN layers for multiple scaled features several improvements compared to its first version versions of the input image. Instead, motivated by spatial reported in our original conference publication [38]. Our pyramid pooling [19], [20], we propose a computationally new version can better segment objects at multiple scales, efficient scheme of resampling a given feature layer at via either multi-scale input processing [17], [39], [40] or multiple rates prior to convolution. This amounts to probing the proposed ASPP. We have built a residual net variant the original image with multiple filters that have com- of DeepLab by adapting the state-of-art ResNet [11] image plementary effective fields of view, thus capturing objects classification DCNN, achieving better semantic segmenta- as well as useful image context at multiple scales. Rather tion performance compared to our original model based than actually resampling features, we efficiently implement on VGG-16 [4]. Finally, we present a more comprehensive this mapping using multiple parallel atrous convolutional experimental evaluation of multiple model variants and layers with different sampling rates; we call the proposed report state-of-art results not only on the PASCAL VOC technique “atrous spatial pyramid pooling” (ASPP). 2012 benchmark but also on other challenging tasks. We The third challenge relates to the fact that an object- have implemented the proposed methods by extending the centric classifier requires invariance to spatial transforma- Caffe framework [41]. We share our code and models at tions, inherently limiting the spatial accuracy of a DCNN. a companion web site http://liangchiehchen.com/projects/ One way to mitigate this problem is to use skip-layers DeepLab.html. to extract “hyper-column” features from multiple network layers when computing the final segmentation result [14], [21]. Our work explores an alternative approach which we 2 R ELATED W ORK show to be highly effective. In particular, we boost our Most of the successful semantic segmentation systems de- model’s ability to capture fine details by employing a fully- veloped in the previous decade relied on hand-crafted fea- connected Conditional Random Field (CRF) [22]. CRFs have tures combined with flat classifiers, such as Boosting [24], been broadly used in semantic segmentation to combine [42], Random Forests [43], or Support Vector Machines [44]. class scores computed by multi-way classifiers with the low- Substantial improvements have been achieved by incorpo- level information captured by the local interactions of pixels rating richer information from context [45] and structured and edges [23], [24] or superpixels [25]. Even though works prediction techniques [22], [26], [27], [46], but the perfor- of increased sophistication have been proposed to model mance of these systems has always been compromised by the hierarchical dependency [26], [27], [28] and/or high- the limited expressive power of the features. Over the past order dependencies of segments [29], [30], [31], [32], [33], few years the breakthroughs of Deep Learning in image we use the fully connected pairwise CRF proposed by [22] classification were quickly transferred to the semantic seg- for its efficient computation, and ability to capture fine edge mentation task. Since this task involves both segmentation details while also catering for long range dependencies. and classification, a central question is how to combine the That model was shown in [22] to improve the performance two tasks. of a boosting-based pixel-level classifier. In this work, we The first family of DCNN-based systems for seman- demonstrate that it leads to state-of-the-art results when tic segmentation typically employs a cascade of bottom- coupled with a DCNN-based pixel-level classifier. up image segmentation, followed by DCNN-based region A high-level illustration of the proposed DeepLab model classification. For instance the bounding box proposals and is shown in Fig. 1. A deep convolutional neural network masked regions delivered by [47], [48] are used in [7] and (VGG-16 [4] or ResNet-101 [11] in this work) trained in [49] as inputs to a DCNN to incorporate shape information the task of image classification is re-purposed to the task into the classification process. Similarly, the authors of [50] of semantic segmentation by (1) transforming all the fully rely on a superpixel representation. Even though these connected layers to convolutional layers (i.e., fully convo- approaches can benefit from the sharp boundaries delivered lutional network [14]) and (2) increasing feature resolution by a good segmentation, they also cannot recover from any through atrous convolutional layers, allowing us to compute of its errors. feature responses every 8 pixels instead of every 32 pixels in The second family of works relies on using convolution- the original network. We then employ bi-linear interpolation ally computed DCNN features for dense image labeling, to upsample by a factor of 8 the score map to reach the and couples them with segmentations that are obtained original image resolution, yielding the input to a fully- independently. Among the first have been [39] who apply connected CRF [22] that refines the segmentation results. DCNNs at multiple image resolutions and then employ a From a practical standpoint, the three main advantages segmentation tree to smooth the prediction results. More of our DeepLab system are: (1) Speed: by virtue of atrous recently, [21] propose to use skip layers and concatenate the convolution, our dense DCNN operates at 8 FPS on an computed intermediate feature maps within the DCNNs for NVidia Titan X GPU, while Mean Field Inference for the pixel classification. Further, [51] propose to pool the inter- fully-connected CRF requires 0.5 secs on a CPU. (2) Accu- mediate feature maps by region proposals. These works still racy: we obtain state-of-art results on several challenging employ segmentation algorithms that are decoupled from datasets, including the PASCAL VOC 2012 semantic seg- the DCNN classifier’s results, thus risking commitment to mentation benchmark [34], PASCAL-Context [35], PASCAL- premature decisions. Person-Part [36], and Cityscapes [37]. (3) Simplicity: our sys- The third family of works uses DCNNs to directly tem is composed of a cascade of two very well-established provide dense category-level pixel labels, which makes modules, DCNNs and CRFs. it possible to even discard segmentation altogether. The 

3 . 3 Input Aeroplane Coarse DCNN Score map Atrous Convolution Final Output Fully Connected CRF Bi-linear Interpolation Fig. 1: Model Illustration. A Deep Convolutional Neural Network such as VGG-16 or ResNet-101 is employed in a fully convolutional fashion, using atrous convolution to reduce the degree of signal downsampling (from 32x down 8x). A bilinear interpolation stage enlarges the feature maps to the original image resolution. A fully connected CRF is then applied to refine the segmentation result and better capture the object boundaries. segmentation-free approaches of [14], [52] directly apply high level of activity in the benchmark’s leaderboard1 [17], DCNNs to the whole image in a fully convolutional fashion, [40], [58], [59], [60], [61], [62], [63]. Interestingly, most top- transforming the last fully connected layers of the DCNN performing methods have adopted one or both of the key into convolutional layers. In order to deal with the spatial lo- ingredients of our DeepLab system: Atrous convolution for calization issues outlined in the introduction, [14] upsample efficient dense feature extraction and refinement of the raw and concatenate the scores from intermediate feature maps, DCNN scores by means of a fully connected CRF. We outline while [52] refine the prediction result from coarse to fine by below some of the most important and interesting advances. propagating the coarse results to another DCNN. Our work End-to-end training for structured prediction has more re- builds on these works, and as described in the introduction cently been explored in several related works. While we extends them by exerting control on the feature resolution, employ the CRF as a post-processing method, [40], [59], introducing multi-scale pooling techniques and integrating [62], [64], [65] have successfully pursued joint learning of the densely connected CRF of [22] on top of the DCNN. the DCNN and CRF. In particular, [59], [65] unroll the CRF We show that this leads to significantly better segmentation mean-field inference steps to convert the whole system into results, especially along object boundaries. The combination an end-to-end trainable feed-forward network, while [62] of DCNN and CRF is of course not new but previous works approximates one iteration of the dense CRF mean field only tried locally connected CRF models. Specifically, [53] inference [22] by convolutional layers with learnable filters. use CRFs as a proposal mechanism for a DCNN-based Another fruitful direction pursued by [40], [66] is to learn reranking system, while [39] treat superpixels as nodes for a the pairwise terms of a CRF via a DCNN, significantly local pairwise CRF and use graph-cuts for discrete inference. improving performance at the cost of heavier computation. As such their models were limited by errors in superpixel In a different direction, [63] replace the bilateral filtering computations or ignored long-range dependencies. Our ap- module used in mean field inference with a faster domain proach instead treats every pixel as a CRF node receiving transform module [67], improving the speed and lowering unary potentials by the DCNN. Crucially, the Gaussian CRF the memory requirements of the overall system, while [18], potentials in the fully connected CRF model of [22] that we [68] combine semantic segmentation with edge detection. adopt can capture long-range dependencies and at the same Weaker supervision has been pursued in a number of time the model is amenable to fast mean field inference. papers, relaxing the assumption that pixel-level semantic We note that mean field inference had been extensively annotations are available for the whole training set [58], [69], studied for traditional image segmentation tasks [54], [55], [70], [71], achieving significantly better results than weakly- [56], but these older models were typically limited to short- supervised pre-DCNN systems such as [72]. In another line range connections. In independent work, [57] use a very of research, [49], [73] pursue instance segmentation, jointly similar densely connected CRF model to refine the results of tackling object detection and semantic segmentation. DCNN for the problem of material classification. However, What we call here atrous convolution was originally de- the DCNN module of [57] was only trained by sparse point veloped for the efficient computation of the undecimated supervision instead of dense supervision at every pixel. wavelet transform in the “algorithme a` trous” scheme of [15]. We refer the interested reader to [74] for early refer- Since the first version of this work was made publicly ences from the wavelet literature. Atrous convolution is also available [38], the area of semantic segmentation has pro- intimately related to the “noble identities” in multi-rate sig- gressed drastically. Multiple groups have made important nal processing, which builds on the same interplay of input advances, significantly raising the bar on the PASCAL VOC 1. http://host.robots.ox.ac.uk:8080/leaderboard/displaylb.php? 2012 semantic segmentation benchmark, as reflected to the challengeid=11&compid=6 

4 . 4 signal and filter sampling rates [75]. Atrous convolution is a Output feature term we first used in [6]. The same operation was later called Convolution dilated convolution by [76], a term they coined motivated by kernel = 3 stride = 1 the fact that the operation corresponds to regular convolu- pad = 1 tion with upsampled (or dilated in the terminology of [15]) Input feature filters. Various authors have used the same operation before (a) Sparse feature extraction for denser feature extraction in DCNNs [3], [6], [16]. Beyond mere resolution enhancement, atrous convolution allows us Convolution kernel = 3 to enlarge the field of view of filters to incorporate larger stride = 1 pad = 2 context, which we have shown in [38] to be beneficial. This rate = 2 approach has been pursued further by [76], who employ a (insert 1 zero) rate = 2 series of atrous convolutional layers with increasing rates to aggregate multiscale context. The atrous spatial pyramid (b) Dense feature extraction pooling scheme proposed here to capture multiscale objects and context also employs multiple atrous convolutional Fig. 2: Illustration of atrous convolution in 1-D. (a) Sparse layers with different sampling rates, which we however lay feature extraction with standard convolution on a low reso- out in parallel instead of in serial. Interestingly, the atrous lution input feature map. (b) Dense feature extraction with convolution technique has also been adopted for a broader atrous convolution with rate r = 2, applied on a high set of tasks, such as object detection [12], [77], instance- resolution input feature map. level segmentation [78], visual question answering [79], and optical flow [80]. We also show that, as expected, integrating into DeepLab more advanced image classification DCNNs such as the residual net of [11] leads to better results. This has also been observed independently by [81]. 3 M ETHODS downsampling convolution upsampling stride= 2 kernel=7 stride=2 3.1 Atrous Convolution for Dense Feature Extraction and Field-of-View Enlargement The use of DCNNs for semantic segmentation, or other atrous convolution dense prediction tasks, has been shown to be simply and kernel=7 rate= 2 successfully addressed by deploying DCNNs in a fully stride=1 convolutional fashion [3], [14]. However, the repeated com- bination of max-pooling and striding at consecutive layers Fig. 3: Illustration of atrous convolution in 2-D. Top row: of these networks reduces significantly the spatial resolution sparse feature extraction with standard convolution on a of the resulting feature maps, typically by a factor of 32 low resolution input feature map. Bottom row: Dense fea- across each direction in recent DCNNs. A partial remedy ture extraction with atrous convolution with rate r = 2, is to use ‘deconvolutional’ layers as in [14], which however applied on a high resolution input feature map. requires additional memory and time. We advocate instead the use of atrous convolution, originally developed for the efficient computation of the We illustrate the algorithm’s operation in 2-D through a undecimated wavelet transform in the “algorithme a` trous” simple example in Fig. 3: Given an image, we assume that scheme of [15] and used before in the DCNN context by [3], we first have a downsampling operation that reduces the [6], [16]. This algorithm allows us to compute the responses resolution by a factor of 2, and then perform a convolution of any layer at any desirable resolution. It can be applied with a kernel - here, the vertical Gaussian derivative. If one post-hoc, once a network has been trained, but can also be implants the resulting feature map in the original image seamlessly integrated with training. coordinates, we realize that we have obtained responses at Considering one-dimensional signals first, the output only 1/4 of the image positions. Instead, we can compute y[i] of atrous convolution 2 of a 1-D input signal x[i] with a responses at all image positions if we convolve the full filter w[k] of length K is defined as: resolution image with a filter ‘with holes’, in which we up- K sample the original filter by a factor of 2, and introduce zeros y[i] = x[i + r · k]w[k]. (1) in between filter values. Although the effective filter size k=1 increases, we only need to take into account the non-zero filter values, hence both the number of filter parameters and The rate parameter r corresponds to the stride with which the number of operations per position stay constant. The we sample the input signal. Standard convolution is a resulting scheme allows us to easily and explicitly control special case for rate r = 1. See Fig. 2 for illustration. the spatial resolution of neural network feature responses. 2. We follow the standard practice in the DCNN literature and use In the context of DCNNs one can use atrous convolution non-mirrored filters in this definition. in a chain of layers, effectively allowing us to compute the 

5 . 5 final DCNN network responses at an arbitrarily high resolu- Conv Conv Conv Conv tion. For example, in order to double the spatial density of kernel: 3x3 kernel: 3x3 kernel: 3x3 kernel: 3x3 computed feature responses in the VGG-16 or ResNet-101 rate: 6 rate: 12 rate: 18 rate: 24 rate = 24 networks, we find the last pooling or convolutional layer rate = 12 rate = 18 rate = 6 that decreases resolution (’pool5’ or ’conv5 1’ respectively), set its stride to 1 to avoid signal decimation, and replace all subsequent convolutional layers with atrous convolutional layers having rate r = 2. Pushing this approach all the way through the network could allow us to compute feature Atrous Spatial Pyramid Pooling responses at the original image resolution, but this ends Input Feature Map up being too costly. We have adopted instead a hybrid approach that strikes a good efficiency/accuracy trade-off, using atrous convolution to increase by a factor of 4 the Fig. 4: Atrous Spatial Pyramid Pooling (ASPP). To classify density of computed feature maps, followed by fast bilinear the center pixel (orange), ASPP exploits multi-scale features interpolation by an additional factor of 8 to recover feature by employing multiple parallel filters with different rates. maps at the original image resolution. Bilinear interpolation The effective Field-Of-Views are shown in different colors. is sufficient in this setting because the class score maps (corresponding to log-probabilities) are quite smooth, as illustrated in Fig. 5. Unlike the deconvolutional approach 3.2 Multiscale Image Representations using Atrous adopted by [14], the proposed approach converts image Spatial Pyramid Pooling classification networks into dense feature extractors without DCNNs have shown a remarkable ability to implicitly repre- requiring learning any extra parameters, leading to faster sent scale, simply by being trained on datasets that contain DCNN training in practice. objects of varying size. Still, explicitly accounting for object scale can improve the DCNN’s ability to successfully handle Atrous convolution also allows us to arbitrarily enlarge both large and small objects [6]. the field-of-view of filters at any DCNN layer. State-of-the- We have experimented with two approaches to han- art DCNNs typically employ spatially small convolution dling scale variability in semantic segmentation. The first kernels (typically 3×3) in order to keep both computation approach amounts to standard multiscale processing [17], and number of parameters contained. Atrous convolution [18]. We extract DCNN score maps from multiple (three with rate r introduces r − 1 zeros between consecutive filter in our experiments) rescaled versions of the original image values, effectively enlarging the kernel size of a k ×k filter using parallel DCNN branches that share the same param- to ke = k + (k − 1)(r − 1) without increasing the number eters. To produce the final result, we bilinearly interpolate of parameters or the amount of computation. It thus offers the feature maps from the parallel DCNN branches to the an efficient mechanism to control the field-of-view and original image resolution and fuse them, by taking at each finds the best trade-off between accurate localization (small position the maximum response across the different scales. field-of-view) and context assimilation (large field-of-view). We do this both during training and testing. Multiscale We have successfully experimented with this technique: processing significantly improves performance, but at the Our DeepLab-LargeFOV model variant [38] employs atrous cost of computing feature responses at all DCNN layers for convolution with rate r = 12 in VGG-16 ‘fc6’ layer with multiple scales of input. significant performance gains, as detailed in Section 4. The second approach is inspired by the success of the R-CNN spatial pyramid pooling method of [20], which showed that regions of an arbitrary scale can be accurately Turning to implementation aspects, there are two effi- and efficiently classified by resampling convolutional fea- cient ways to perform atrous convolution. The first is to tures extracted at a single scale. We have implemented a implicitly upsample the filters by inserting holes (zeros), or variant of their scheme which uses multiple parallel atrous equivalently sparsely sample the input feature maps [15]. convolutional layers with different sampling rates. The fea- We implemented this in our earlier work [6], [38], followed tures extracted for each sampling rate are further processed by [76], within the Caffe framework [41] by adding to the in separate branches and fused to generate the final result. im2col function (it extracts vectorized patches from multi- The proposed “atrous spatial pyramid pooling” (DeepLab- channel feature maps) the option to sparsely sample the ASPP) approach generalizes our DeepLab-LargeFOV vari- underlying feature maps. The second method, originally ant and is illustrated in Fig. 4. proposed by [82] and used in [3], [16] is to subsample the input feature map by a factor equal to the atrous convolu- tion rate r, deinterlacing it to produce r2 reduced resolution 3.3 Structured Prediction with Fully-Connected Condi- maps, one for each of the r×r possible shifts. This is followed tional Random Fields for Accurate Boundary Recovery by applying standard convolution to these intermediate A trade-off between localization accuracy and classifica- feature maps and reinterlacing them to the original image tion performance seems to be inherent in DCNNs: deeper resolution. By reducing atrous convolution into regular con- models with multiple max-pooling layers have proven most volution, it allows us to use off-the-shelf highly optimized successful in classification tasks, however the increased in- convolution routines. We have implemented the second variance and the large receptive fields of top-level nodes can approach into the TensorFlow framework [83]. only yield smooth responses. As illustrated in Fig. 5, DCNN 

6 . 6 The pairwise potential has a form that allows for efficient inference while using a fully-connected graph, i.e. when connecting all pairs of image pixels, i, j . In particular, as in [22], we use the following expression: ||pi − pj ||2 ||Ii − Ij ||2 Image/G.T. DCNN output CRF Iteration 1 CRF Iteration 2 CRF Iteration 10 θij (xi , xj ) = µ(xi , xj ) w1 exp − − 2σα2 2σβ2 Fig. 5: Score map (input before softmax function) and belief ||pi − pj ||2 map (output of softmax function) for Aeroplane. We show +w2 exp − (3) the score (1st row) and belief (2nd row) maps after each 2σγ2 mean field iteration. The output of last DCNN layer is used where µ(xi , xj ) = 1 if xi = xj , and zero otherwise, which, as input to the mean field inference. as in the Potts model, means that only nodes with dis- tinct labels are penalized. The remaining expression uses two Gaussian kernels in different feature spaces; the first, score maps can predict the presence and rough position of ‘bilateral’ kernel depends on both pixel positions (denoted objects but cannot really delineate their borders. as p) and RGB color (denoted as I ), and the second kernel Previous work has pursued two directions to address only depends on pixel positions. The hyper parameters σα , this localization challenge. The first approach is to harness σβ and σγ control the scale of Gaussian kernels. The first information from multiple layers in the convolutional net- kernel forces pixels with similar color and position to have work in order to better estimate the object boundaries [14], similar labels, while the second kernel only considers spatial [21], [52]. The second is to employ a super-pixel represen- proximity when enforcing smoothness. tation, essentially delegating the localization task to a low- Crucially, this model is amenable to efficient approxi- level segmentation method [50]. mate probabilistic inference [22]. The message passing up- We pursue an alternative direction based on coupling dates under a fully decomposable mean field approximation the recognition capacity of DCNNs and the fine-grained b(x) = i bi (xi ) can be expressed as Gaussian convolutions localization accuracy of fully connected CRFs and show in bilateral space. High-dimensional filtering algorithms that it is remarkably successful in addressing the localiza- [84] significantly speed-up this computation resulting in an tion challenge, producing accurate semantic segmentation algorithm that is very fast in practice, requiring less that 0.5 results and recovering object boundaries at a level of detail sec on average for Pascal VOC images using the publicly that is well beyond the reach of existing methods. This available implementation of [22]. direction has been extended by several follow-up papers [17], [40], [58], [59], [60], [61], [62], [63], [65], since the first version of our work was published [38]. 4 E XPERIMENTAL R ESULTS Traditionally, conditional random fields (CRFs) have We finetune the model weights of the Imagenet-pretrained been employed to smooth noisy segmentation maps [23], VGG-16 or ResNet-101 networks to adapt them to the [31]. Typically these models couple neighboring nodes, fa- semantic segmentation task in a straightforward fashion, voring same-label assignments to spatially proximal pixels. following the procedure of [14]. We replace the 1000-way Qualitatively, the primary function of these short-range Imagenet classifier in the last layer with a classifier having as CRFs is to clean up the spurious predictions of weak classi- many targets as the number of semantic classes of our task fiers built on top of local hand-engineered features. (including the background, if applicable). Our loss function Compared to these weaker classifiers, modern DCNN is the sum of cross-entropy terms for each spatial position architectures such as the one we use in this work pro- in the CNN output map (subsampled by 8 compared to duce score maps and semantic label predictions which are the original image). All positions and labels are equally qualitatively different. As illustrated in Fig. 5, the score weighted in the overall loss function (except for unlabeled maps are typically quite smooth and produce homogeneous pixels which are ignored). Our targets are the ground truth classification results. In this regime, using short-range CRFs labels (subsampled by 8). We optimize the objective function can be detrimental, as our goal should be to recover detailed with respect to the weights at all network layers by the local structure rather than further smooth it. Using contrast- standard SGD procedure of [2]. We decouple the DCNN sensitive potentials [23] in conjunction to local-range CRFs and CRF training stages, assuming the DCNN unary terms can potentially improve localization but still miss thin- are fixed when setting the CRF parameters. structures and typically requires solving an expensive dis- We evaluate the proposed models on four challenging crete optimization problem. datasets: PASCAL VOC 2012, PASCAL-Context, PASCAL- To overcome these limitations of short-range CRFs, we Person-Part, and Cityscapes. We first report the main results integrate into our system the fully connected CRF model of of our conference version [38] on PASCAL VOC 2012, and [22]. The model employs the energy function move forward to latest results on all datasets. E(x) = θi (xi ) + θij (xi , xj ) (2) i ij 4.1 PASCAL VOC 2012 where x is the label assignment for pixels. We use as unary Dataset: The PASCAL VOC 2012 segmentation benchmark potential θi (xi ) = − log P (xi ), where P (xi ) is the label [34] involves 20 foreground object classes and one back- assignment probability at pixel i as computed by a DCNN. ground class. The original dataset contains 1, 464 (train), 

7 . 7 Kernel Rate FOV Params Speed bef/aft CRF Learning policy Batch size Iteration mean IOU 7×7 4 224 134.3M 1.44 64.38 / 67.64 step 30 6K 62.25 4×4 4 128 65.1M 2.90 59.80 / 63.74 4×4 8 224 65.1M 2.90 63.41 / 67.14 poly 30 6K 63.42 3×3 12 224 20.5M 4.84 62.25 / 67.64 poly 30 10K 64.90 poly 10 10K 64.71 poly 10 20K 65.88 TABLE 1: Effect of Field-Of-View by adjusting the kernel size and atrous sampling rate r at ‘fc6’ layer. We show TABLE 2: PASCAL VOC 2012 val set results (%) (before CRF) number of model parameters, training speed (img/sec), and as different learning hyper parameters vary. Employing val set mean IOU before and after CRF. DeepLab-LargeFOV “poly” learning policy is more effective than “step” when (kernel size 3×3, r = 12) strikes the best balance. training DeepLab-LargeFOV. 1, 449 (val), and 1, 456 (test) pixel-level labeled images for 4.1.2 Improvements after conference version of this work training, validation, and testing, respectively. The dataset is augmented by the extra annotations provided by [85], After the conference version of this work [38], we have resulting in 10, 582 (trainaug) training images. The perfor- pursued three main improvements of our model, which we mance is measured in terms of pixel intersection-over-union discuss below: (1) different learning policy during training, (IOU) averaged across the 21 classes. (2) atrous spatial pyramid pooling, and (3) employment of deeper networks and multi-scale processing. 4.1.1 Results from our conference version Learning rate policy: We have explored different learn- We employ the VGG-16 network pre-trained on Imagenet, ing rate policies when training DeepLab-LargeFOV. Similar adapted for semantic segmentation as described in Sec- to [86], we also found that employing a “poly” learning rate iter power tion 3.1. We use a mini-batch of 20 images and initial policy (the learning rate is multiplied by (1− max iter ) ) learning rate of 0.001 (0.01 for the final classifier layer), is more effective than “step” learning rate (reduce the multiplying the learning rate by 0.1 every 2000 iterations. learning rate at a fixed step size). As shown in Tab. 2, We use momentum of 0.9 and weight decay of 0.0005. employing “poly” (with power = 0.9) and using the same After the DCNN has been fine-tuned on trainaug, we batch size and same training iterations yields 1.17% better cross-validate the CRF parameters along the lines of [22]. We performance than employing “step” policy. Fixing the batch use default values of w2 = 3 and σγ = 3 and we search for size and increasing the training iteration to 10K improves the best values of w1 , σα , and σβ by cross-validation on 100 the performance to 64.90% (1.48% gain); however, the total images from val. We employ a coarse-to-fine search scheme. training time increases due to more training iterations. We The initial search range of the parameters are w1 ∈ [3 : 6], then reduce the batch size to 10 and found that comparable σα ∈ [30 : 10 : 100] and σβ ∈ [3 : 6] (MATLAB notation), performance is still maintained (64.90% vs. 64.71%). In the and then we refine the search step sizes around the first end, we employ batch size = 10 and 20K iterations in order round’s best values. We employ 10 mean field iterations. to maintain similar training time as previous “step” policy. Field of View and CRF: In Tab. 1, we report experiments Surprisingly, this gives us the performance of 65.88% (3.63% with DeepLab model variants that use different field-of- improvement over “step”) on val, and 67.7% on test, com- view sizes, obtained by adjusting the kernel size and atrous pared to 65.1% of the original “step” setting for DeepLab- sampling rate r in the ‘fc6’ layer, as described in Sec. 3.1. LargeFOV before CRF. We employ the “poly” learning rate We start with a direct adaptation of VGG-16 net, using policy for all experiments reported in the rest of the paper. the original 7 × 7 kernel size and r = 4 (since we use Atrous Spatial Pyramid Pooling: We have experimented no stride for the last two max-pooling layers). This model with the proposed Atrous Spatial Pyramid Pooling (ASPP) yields performance of 67.64% after CRF, but is relatively scheme, described in Sec. 3.1. As shown in Fig. 7, ASPP slow (1.44 images per second during training). We have for VGG-16 employs several parallel fc6-fc7-fc8 branches. improved model speed to 2.9 images per second by re- They all use 3×3 kernels but different atrous rates r in the ducing the kernel size to 4 × 4. We have experimented ‘fc6’ in order to capture objects of different size. In Tab. 3, with two such network variants with smaller (r = 4) and we report results with several settings: (1) Our baseline larger (r = 8) FOV sizes; the latter one performs better. LargeFOV model, having a single branch with r = 12, Finally, we employ kernel size 3×3 and even larger atrous (2) ASPP-S, with four branches and smaller atrous rates sampling rate (r = 12), also making the network thinner by (r = {2, 4, 8, 12}), and (3) ASPP-L, with four branches retaining a random subset of 1,024 out of the 4,096 filters and larger rates (r = {6, 12, 18, 24}). For each variant in layers ‘fc6’ and ‘fc7’. The resulting model, DeepLab-CRF- we report results before and after CRF. As shown in the LargeFOV, matches the performance of the direct VGG-16 table, ASPP-S yields 1.22% improvement over the baseline adaptation (7 × 7 kernel size, r = 4). At the same time, LargeFOV before CRF. However, after CRF both LargeFOV DeepLab-LargeFOV is 3.36 times faster and has significantly and ASPP-S perform similarly. On the other hand, ASPP-L fewer parameters (20.5M instead of 134.3M). yields consistent improvements over the baseline LargeFOV The CRF substantially boosts performance of all model both before and after CRF. We evaluate on test the proposed variants, offering a 3-5% absolute increase in mean IOU. ASPP-L + CRF model, attaining 72.6%. We visualize the Test set evaluation: We have evaluated our DeepLab- effect of the different schemes in Fig. 8. CRF-LargeFOV model on the PASCAL VOC 2012 official Deeper Networks and Multiscale Processing: We have test set. It achieves 70.3% mean IOU performance. experimented building DeepLab around the recently pro- 

8 . 8 Fig. 6: PASCAL VOC 2012 val results. Input image and our DeepLab results before/after CRF. Sum-Fusion Fc8 (1x1) Fc8 Fc8 Fc8 Fc8 (1x1) (1x1) (1x1) (1x1) Fc7 (1x1) Fc7 Fc7 Fc7 Fc7 (1x1) (1x1) (1x1) (1x1) Fc6 (3x3, rate = 12) Fc6 Fc6 Fc6 Fc6 (3x3, rate = 6) (3x3, rate = 12) (3x3, rate = 18) (3x3, rate = 24) (a) Image (b) LargeFOV (c) ASPP-S (d) ASPP-L Pool5 Pool5 Fig. 8: Qualitative segmentation results with ASPP com- (a) DeepLab-LargeFOV (b) DeepLab-ASPP pared to the baseline LargeFOV model. The ASPP-L model, employing multiple large FOVs can successfully capture Fig. 7: DeepLab-ASPP employs multiple filters with differ- objects as well as image context at multiple scales. ent rates to capture objects and context at multiple scales. Method before CRF after CRF LargeFOV 65.76 69.84 ilar to what we did for VGG-16 net, we re-purpose ResNet- ASPP-S 66.98 69.73 101 by atrous convolution, as described in Sec. 3.1. On top of ASPP-L 68.96 71.57 that, we adopt several other features, following recent work of [17], [18], [39], [40], [58], [59], [62]: (1) Multi-scale inputs: TABLE 3: Effect of ASPP on PASCAL VOC 2012 val set per- We separately feed to the DCNN images at scale = {0.5, 0.75, formance (mean IOU) for VGG-16 based DeepLab model. 1}, fusing their score maps by taking the maximum response LargeFOV: single branch, r = 12. ASPP-S: four branches, r across scales for each position separately [17]. (2) Models = {2, 4, 8, 12}. ASPP-L: four branches, r = {6, 12, 18, 24}. pretrained on MS-COCO [87]. (3) Data augmentation by randomly scaling the input images (from 0.5 to 1.5) during MSC COCO Aug LargeFOV ASPP CRF mIOU training. In Tab. 4, we evaluate how each of these factors, 68.72 along with LargeFOV and atrous spatial pyramid pooling 71.27 (ASPP), affects val set performance. Adopting ResNet-101 73.28 instead of VGG-16 significantly improves DeepLab perfor- 74.87 75.54 mance (e.g., our simplest ResNet-101 based model attains 76.35 68.72%, compared to 65.76% of our DeepLab-LargeFOV 77.69 VGG-16 based variant, both before CRF). Multiscale fusion [17] brings extra 2.55% improvement, while pretraining TABLE 4: Employing ResNet-101 for DeepLab on PASCAL the model on MS-COCO gives another 2.01% gain. Data VOC 2012 val set. MSC: Employing mutli-scale inputs with augmentation during training is effective (about 1.6% im- max fusion. COCO: Models pretrained on MS-COCO. Aug: provement). Employing LargeFOV (adding an atrous con- Data augmentation by randomly rescaling inputs. volutional layer on top of ResNet, with 3×3 kernel and rate = 12) is beneficial (about 0.6% improvement). Further 0.8% improvement is achieved by atrous spatial pyramid pooling posed residual net ResNet-101 [11] instead of VGG-16. Sim- (ASPP). Post-processing our best model by dense CRF yields 

9 . 9 performance of 77.69%. Qualitative results: We provide qualitative visual com- parisons of DeepLab’s results (our best model variant) before and after CRF in Fig. 6. The visualization results obtained by DeepLab before CRF already yields excellent segmentation results, while employing the CRF further im- Image VGG-16 Bef. VGG-16 Aft. ResNet Bef. ResNet Aft. proves the performance by removing false positives and refining object boundaries. Fig. 9: DeepLab results based on VGG-16 net or ResNet- Test set results: We have submitted the result of our 101 before and after CRF. The CRF is critical for accurate final best model to the official server, obtaining test set prediction along object boundaries with VGG-16, whereas performance of 79.7%, as shown in Tab. 5. The model ResNet-101 has acceptable performance even before CRF. substantially outperforms previous DeepLab variants (e.g., DeepLab-LargeFOV with VGG-16 net) and is currently the 75 top performing method on the PASCAL VOC 2012 segmen- 70 tation leaderboard. mean IOU (%) 65 60 Method mIOU 55 ResNet aft VGG−16 aft DeepLab-CRF-LargeFOV-COCO [58] 72.7 50 ResNet bef VGG−16 bef MERL DEEP GCRF [88] 73.2 45 0 5 10 15 20 25 30 35 40 Trimap Width (pixels) CRF-RNN [59] 74.7 POSTECH DeconvNet CRF VOC [61] 74.8 (a) (b) BoxSup [60] 75.2 Context + CRF-RNN [76] 75.3 QO4mres [66] 75.5 Fig. 10: (a) Trimap examples (top-left: image. top-right: DeepLab-CRF-Attention [17] 75.7 ground-truth. bottom-left: trimap of 2 pixels. bottom-right: CentraleSuperBoundaries++ [18] 76.0 trimap of 10 pixels). (b) Pixel mean IOU as a function of the DeepLab-CRF-Attention-DT [63] 76.3 H-ReNet + DenseCRF [89] 76.8 band width around the object boundaries when employing LRR 4x COCO [90] 76.8 VGG-16 or ResNet-101 before and after CRF. DPN [62] 77.5 Adelaide Context [40] 77.8 Oxford TVG HO CRF [91] 77.9 Method MSC COCO Aug LargeFOV ASPP CRF mIOU Context CRF + Guidance CRF [92] 78.1 VGG-16 Adelaide VeryDeep FCN VOC [93] 79.1 DeepLab [38] 37.6 DeepLab-CRF (ResNet-101) 79.7 DeepLab [38] 39.6 ResNet-101 TABLE 5: Performance on PASCAL VOC 2012 test set. We DeepLab 39.6 have added some results from recent arXiv papers on top of DeepLab 41.4 DeepLab 42.9 the official leadearboard results. DeepLab 43.5 DeepLab 44.7 VGG-16 vs. ResNet-101: We have observed that DeepLab 45.7 DeepLab based on ResNet-101 [11] delivers better segmen- O2 P [45] 18.1 tation results along object boundaries than employing VGG- CFM [51] 34.4 16 [4], as visualized in Fig. 9. We think the identity mapping FCN-8s [14] 37.8 CRF-RNN [59] 39.3 [94] of ResNet-101 has similar effect as hyper-column fea- ParseNet [86] 40.4 tures [21], which exploits the features from the intermediate BoxSup [60] 40.5 layers to better localize boundaries. We further quantize this HO CRF [91] 41.3 Context [40] 43.3 effect in Fig. 10 within the “trimap” [22], [31] (a narrow band VeryDeep [93] 44.5 along object boundaries). As shown in the figure, employing ResNet-101 before CRF has almost the same accuracy along TABLE 6: Comparison with other state-of-art methods on object boundaries as employing VGG-16 in conjunction with PASCAL-Context dataset. a CRF. Post-processing the ResNet-101 result with a CRF further improves the segmentation result. DeepLab improves 2% over the VGG-16 LargeFOV. Simi- 4.2 PASCAL-Context lar to [17], employing multi-scale inputs and max-pooling Dataset: The PASCAL-Context dataset [35] provides de- to merge the results improves the performance to 41.4%. tailed semantic labels for the whole scene, including both Pretraining the model on MS-COCO brings extra 1.5% object (e.g., person) and stuff (e.g., sky). Following [35], the improvement. Employing atrous spatial pyramid pooling proposed models are evaluated on the most frequent 59 is more effective than LargeFOV. After further employing classes along with one background category. The training dense CRF as post processing, our final model yields 45.7%, set and validation set contain 4998 and 5105 images. outperforming the current state-of-art method [40] by 2.4% Evaluation: We report the evaluation results in Tab. 6. without using their non-linear pairwise term. Our final Our VGG-16 based LargeFOV variant yields 37.6% before model is slightly better than the concurrent work [93] by and 39.6% after CRF. Repurposing the ResNet-101 [11] for 1.2%, which also employs atrous convolution to repurpose 

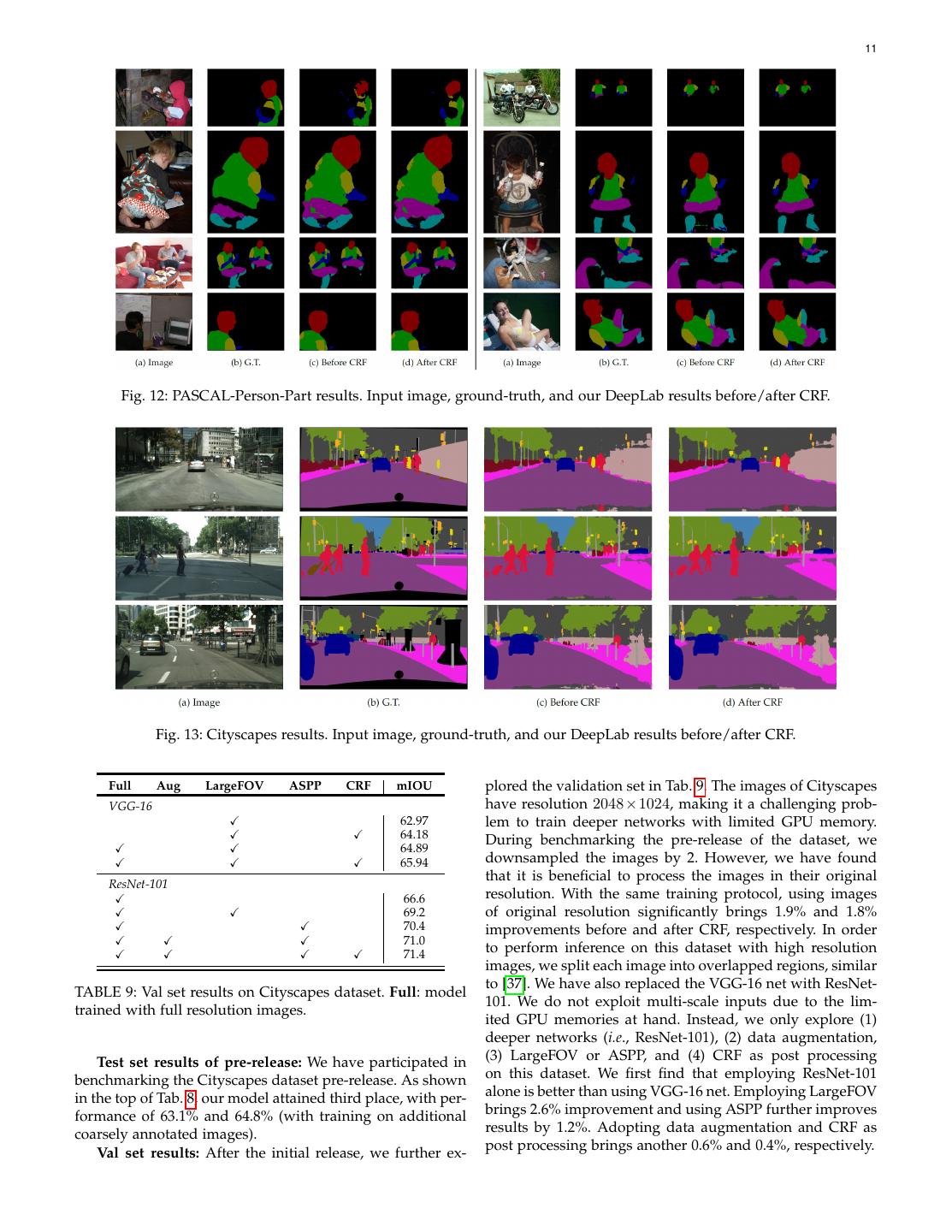
10 . 10 Fig. 11: PASCAL-Context results. Input image, ground-truth, and our DeepLab results before/after CRF. Method MSC COCO Aug LFOV ASPP CRF mIOU Method mIOU ResNet-101 pre-release version of dataset DeepLab 58.90 Adelaide Context [40] 66.4 DeepLab 63.10 FCN-8s [14] 65.3 DeepLab 64.40 DeepLab 64.94 DeepLab-CRF-LargeFOV-StrongWeak [58] 64.8 DeepLab-CRF-LargeFOV [38] 63.1 DeepLab 62.18 DeepLab 62.76 CRF-RNN [59] 62.5 DPN [62] 59.1 Attention [17] 56.39 Segnet basic [100] 57.0 HAZN [95] 57.54 Segnet extended [100] 56.1 LG-LSTM [96] 57.97 Graph LSTM [97] 60.16 official version Adelaide Context [40] 71.6 Dilation10 [76] 67.1 TABLE 7: Comparison with other state-of-art methods on DPN [62] 66.8 PASCAL-Person-Part dataset. Pixel-level Encoding [101] 64.3 DeepLab-CRF (ResNet-101) 70.4 the residual net of [11] for semantic segmentation. TABLE 8: Test set results on the Cityscapes dataset, compar- Qualitative results: We visualize the segmentation re- ing our DeepLab system with other state-of-art methods. sults of our best model with and without CRF as post pro- cessing in Fig. 11. DeepLab before CRF can already predict most of the object/stuff with high accuracy. Employing CRF, DeepLab alone yields 58.9%, significantly outperforming our model is able to further remove isolated false positives DeepLab-LargeFOV (VGG-16 net) and DeepLab-Attention and improve the prediction along object/stuff boundaries. (VGG-16 net) by about 7% and 2.5%, respectively. Incorpo- rating multi-scale inputs and fusion by max-pooling further improves performance to 63.1%. Additionally pretraining 4.3 PASCAL-Person-Part the model on MS-COCO yields another 1.3% improvement. Dataset: We further perform experiments on semantic part However, we do not observe any improvement when adopt- segmentation [98], [99], using the extra PASCAL VOC 2010 ing either LargeFOV or ASPP on this dataset. Employing annotations by [36]. We focus on the person part for the the dense CRF to post process our final output substantially dataset, which contains more training data and large varia- outperforms the concurrent work [97] by 4.78%. tion in object scale and human pose. Specifically, the dataset Qualitative results: We visualize the results in Fig. 12. contains detailed part annotations for every person, e.g. eyes, nose. We merge the annotations to be Head, Torso, Upper/Lower Arms and Upper/Lower Legs, resulting in 4.4 Cityscapes six person part classes and one background class. We only Dataset: Cityscapes [37] is a recently released large-scale use those images containing persons for training (1716 im- dataset, which contains high quality pixel-level annotations ages) and validation (1817 images). of 5000 images collected in street scenes from 50 different Evaluation: The human part segmentation results on cities. Following the evaluation protocol [37], 19 semantic PASCAL-Person-Part is reported in Tab. 7. [17] has already labels (belonging to 7 super categories: ground, construc- conducted experiments on this dataset with re-purposed tion, object, nature, sky, human, and vehicle) are used for VGG-16 net for DeepLab, attaining 56.39% (with multi-scale evaluation (the void label is not considered for evaluation). inputs). Therefore, in this part, we mainly focus on the effect The training, validation, and test sets contain 2975, 500, and of repurposing ResNet-101 for DeepLab. With ResNet-101, 1525 images respectively. 

11 . 11 Fig. 12: PASCAL-Person-Part results. Input image, ground-truth, and our DeepLab results before/after CRF. Fig. 13: Cityscapes results. Input image, ground-truth, and our DeepLab results before/after CRF. Full Aug LargeFOV ASPP CRF mIOU plored the validation set in Tab. 9. The images of Cityscapes VGG-16 have resolution 2048×1024, making it a challenging prob- 62.97 lem to train deeper networks with limited GPU memory. 64.18 During benchmarking the pre-release of the dataset, we 64.89 65.94 downsampled the images by 2. However, we have found that it is beneficial to process the images in their original ResNet-101 66.6 resolution. With the same training protocol, using images 69.2 of original resolution significantly brings 1.9% and 1.8% 70.4 improvements before and after CRF, respectively. In order 71.0 71.4 to perform inference on this dataset with high resolution images, we split each image into overlapped regions, similar to [37]. We have also replaced the VGG-16 net with ResNet- TABLE 9: Val set results on Cityscapes dataset. Full: model 101. We do not exploit multi-scale inputs due to the lim- trained with full resolution images. ited GPU memories at hand. Instead, we only explore (1) deeper networks (i.e., ResNet-101), (2) data augmentation, Test set results of pre-release: We have participated in (3) LargeFOV or ASPP, and (4) CRF as post processing benchmarking the Cityscapes dataset pre-release. As shown on this dataset. We first find that employing ResNet-101 in the top of Tab. 8, our model attained third place, with per- alone is better than using VGG-16 net. Employing LargeFOV formance of 63.1% and 64.8% (with training on additional brings 2.6% improvement and using ASPP further improves coarsely annotated images). results by 1.2%. Adopting data augmentation and CRF as post processing brings another 0.6% and 0.4%, respectively. Val set results: After the initial release, we further ex- 

12 . 12 [4] K. Simonyan and A. Zisserman, “Very deep convolutional net- works for large-scale image recognition,” in ICLR, 2015. [5] C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich, “Going deeper with convolutions,” arXiv:1409.4842, 2014. [6] G. Papandreou, I. Kokkinos, and P.-A. Savalle, “Modeling local and global deformations in deep learning: Epitomic convolution, multiple instance learning, and sliding window detection,” in (a) Image (b) G.T. (c) Before CRF (d) After CRF CVPR, 2015. [7] R. Girshick, J. Donahue, T. Darrell, and J. Malik, “Rich feature Fig. 14: Failure modes. Input image, ground-truth, and our hierarchies for accurate object detection and semantic segmenta- tion,” in CVPR, 2014. DeepLab results before/after CRF. [8] D. Erhan, C. Szegedy, A. Toshev, and D. Anguelov, “Scalable object detection using deep neural networks,” in CVPR, 2014. [9] R. Girshick, “Fast r-cnn,” in ICCV, 2015. Current test result: We have uploaded our best model to [10] S. Ren, K. He, R. Girshick, and J. Sun, “Faster r-cnn: Towards real- the evaluation server, obtaining performance of 70.4%. Note time object detection with region proposal networks,” in NIPS, 2015. that our model is only trained on the train set. [11] K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for Qualitative results: We visualize the results in Fig. 13. image recognition,” arXiv:1512.03385, 2015. [12] W. Liu, D. Anguelov, D. Erhan, C. Szegedy, and S. Reed, “SSD: Single shot multibox detector,” arXiv:1512.02325, 2015. 4.5 Failure Modes [13] M. D. Zeiler and R. Fergus, “Visualizing and understanding We further qualitatively analyze some failure modes of convolutional networks,” in ECCV, 2014. our best model variant on PASCAL VOC 2012 val set. As [14] J. Long, E. Shelhamer, and T. Darrell, “Fully convolutional net- works for semantic segmentation,” in CVPR, 2015. shown in Fig. 14, our proposed model fails to capture the [15] M. Holschneider, R. Kronland-Martinet, J. Morlet, and delicate boundaries of objects, such as bicycle and chair. P. Tchamitchian, “A real-time algorithm for signal analysis with The details could not even be recovered by the CRF post the help of the wavelet transform,” in Wavelets: Time-Frequency Methods and Phase Space, 1989, pp. 289–297. processing since the unary term is not confident enough. [16] A. Giusti, D. Ciresan, J. Masci, L. Gambardella, and J. Schmidhu- We hypothesize the encoder-decoder structure of [100], [102] ber, “Fast image scanning with deep max-pooling convolutional may alleviate the problem by exploiting the high resolution neural networks,” in ICIP, 2013. feature maps in the decoder path. How to efficiently incor- [17] L.-C. Chen, Y. Yang, J. Wang, W. Xu, and A. L. Yuille, “Attention to scale: Scale-aware semantic image segmentation,” in CVPR, porate the method is left as a future work. 2016. [18] I. Kokkinos, “Pushing the boundaries of boundary detection using deep learning,” in ICLR, 2016. 5 C ONCLUSION [19] S. Lazebnik, C. Schmid, and J. Ponce, “Beyond bags of features: Our proposed “DeepLab” system re-purposes networks Spatial pyramid matching for recognizing natural scene cate- gories,” in CVPR, 2006. trained on image classification to the task of semantic seg- [20] K. He, X. Zhang, S. Ren, and J. Sun, “Spatial pyramid pooling in mentation by applying the ‘atrous convolution’ with upsam- deep convolutional networks for visual recognition,” in ECCV, pled filters for dense feature extraction. We further extend it 2014. to atrous spatial pyramid pooling, which encodes objects as [21] B. Hariharan, P. Arbel´aez, R. Girshick, and J. Malik, “Hyper- columns for object segmentation and fine-grained localization,” well as image context at multiple scales. To produce seman- in CVPR, 2015. tically accurate predictions and detailed segmentation maps [22] ¨ and V. Koltun, “Efficient inference in fully con- P. Kr¨ahenbuhl along object boundaries, we also combine ideas from deep nected crfs with gaussian edge potentials,” in NIPS, 2011. convolutional neural networks and fully-connected condi- [23] C. Rother, V. Kolmogorov, and A. Blake, “GrabCut: Interactive foreground extraction using iterated graph cuts,” in SIGGRAPH, tional random fields. Our experimental results show that 2004. the proposed method significantly advances the state-of- [24] J. Shotton, J. Winn, C. Rother, and A. Criminisi, “Textonboost for art in several challenging datasets, including PASCAL VOC image understanding: Multi-class object recognition and segmen- tation by jointly modeling texture, layout, and context,” IJCV, 2012 semantic image segmentation benchmark, PASCAL- 2009. Context, PASCAL-Person-Part, and Cityscapes datasets. [25] A. Lucchi, Y. Li, X. Boix, K. Smith, and P. Fua, “Are spatial and global constraints really necessary for segmentation?” in ICCV, 2011. ACKNOWLEDGMENTS [26] X. He, R. S. Zemel, and M. Carreira-Perpindn, “Multiscale condi- This work was partly supported by the ARO 62250-CS, tional random fields for image labeling,” in CVPR, 2004. [27] L. Ladicky, C. Russell, P. Kohli, and P. H. Torr, “Associative FP7-RECONFIG, FP7-MOBOT, and H2020-ISUPPORT EU hierarchical crfs for object class image segmentation,” in ICCV, projects. We gratefully acknowledge the support of NVIDIA 2009. Corporation with the donation of GPUs used for this re- [28] V. Lempitsky, A. Vedaldi, and A. Zisserman, “Pylon model for search. semantic segmentation,” in NIPS, 2011. [29] A. Delong, A. Osokin, H. N. Isack, and Y. Boykov, “Fast approxi- mate energy minimization with label costs,” IJCV, 2012. R EFERENCES [30] J. M. Gonfaus, X. Boix, J. Van de Weijer, A. D. Bagdanov, J. Serrat, and J. Gonzalez, “Harmony potentials for joint classification and [1] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, “Gradient-based segmentation,” in CVPR, 2010. learning applied to document recognition,” in Proc. IEEE, 1998. [31] P. Kohli, P. H. Torr et al., “Robust higher order potentials for [2] A. Krizhevsky, I. Sutskever, and G. E. Hinton, “Imagenet classifi- enforcing label consistency,” IJCV, vol. 82, no. 3, pp. 302–324, cation with deep convolutional neural networks,” in NIPS, 2013. 2009. [3] P. Sermanet, D. Eigen, X. Zhang, M. Mathieu, R. Fergus, and [32] L.-C. Chen, G. Papandreou, and A. Yuille, “Learning a dictionary Y. LeCun, “Overfeat: Integrated recognition, localization and of shape epitomes with applications to image labeling,” in ICCV, detection using convolutional networks,” arXiv:1312.6229, 2013. 2013. 

13 . 13 [33] P. Wang, X. Shen, Z. Lin, S. Cohen, B. Price, and A. Yuille, [61] H. Noh, S. Hong, and B. Han, “Learning deconvolution network “Towards unified depth and semantic prediction from a single for semantic segmentation,” in ICCV, 2015. image,” in CVPR, 2015. [62] Z. Liu, X. Li, P. Luo, C. C. Loy, and X. Tang, “Semantic image [34] M. Everingham, S. M. A. Eslami, L. V. Gool, C. K. I. Williams, segmentation via deep parsing network,” in ICCV, 2015. J. Winn, and A. Zisserma, “The pascal visual object classes [63] L.-C. Chen, J. T. Barron, G. Papandreou, K. Murphy, and A. L. challenge a retrospective,” IJCV, 2014. Yuille, “Semantic image segmentation with task-specific edge [35] R. Mottaghi, X. Chen, X. Liu, N.-G. Cho, S.-W. Lee, S. Fidler, detection using cnns and a discriminatively trained domain R. Urtasun, and A. Yuille, “The role of context for object detection transform,” in CVPR, 2016. and semantic segmentation in the wild,” in CVPR, 2014. [64] L.-C. Chen, A. Schwing, A. Yuille, and R. Urtasun, “Learning [36] X. Chen, R. Mottaghi, X. Liu, S. Fidler, R. Urtasun, and A. Yuille, deep structured models,” in ICML, 2015. “Detect what you can: Detecting and representing objects using [65] A. G. Schwing and R. Urtasun, “Fully connected deep structured holistic models and body parts,” in CVPR, 2014. networks,” arXiv:1503.02351, 2015. [37] M. Cordts, M. Omran, S. Ramos, T. Rehfeld, M. Enzweiler, [66] S. Chandra and I. Kokkinos, “Fast, exact and multi-scale inference R. Benenson, U. Franke, S. Roth, and B. Schiele, “The cityscapes for semantic image segmentation with deep Gaussian CRFs,” dataset for semantic urban scene understanding,” in CVPR, 2016. arXiv:1603.08358, 2016. [38] L.-C. Chen, G. Papandreou, I. Kokkinos, K. Murphy, and A. L. [67] E. S. L. Gastal and M. M. Oliveira, “Domain transform for edge- Yuille, “Semantic image segmentation with deep convolutional aware image and video processing,” in SIGGRAPH, 2011. nets and fully connected crfs,” in ICLR, 2015. [68] G. Bertasius, J. Shi, and L. Torresani, “High-for-low and low-for- [39] C. Farabet, C. Couprie, L. Najman, and Y. LeCun, “Learning high: Efficient boundary detection from deep object features and hierarchical features for scene labeling,” PAMI, 2013. its applications to high-level vision,” in ICCV, 2015. [40] G. Lin, C. Shen, I. Reid et al., “Efficient piecewise training of deep [69] P. O. Pinheiro and R. Collobert, “Weakly supervised seman- structured models for semantic segmentation,” arXiv:1504.01013, tic segmentation with convolutional networks,” arXiv:1411.6228, 2015. 2014. [41] Y. Jia, E. Shelhamer, J. Donahue, S. Karayev, J. Long, R. Girshick, [70] D. Pathak, P. Kr¨ahenbuhl,¨ and T. Darrell, “Constrained convo- S. Guadarrama, and T. Darrell, “Caffe: Convolutional architecture lutional neural networks for weakly supervised segmentation,” for fast feature embedding,” arXiv:1408.5093, 2014. 2015. [42] Z. Tu and X. Bai, “Auto-context and its application to high- [71] S. Hong, H. Noh, and B. Han, “Decoupled deep neural network level vision tasks and 3d brain image segmentation,” IEEE Trans. for semi-supervised semantic segmentation,” in NIPS, 2015. Pattern Anal. Mach. Intell., vol. 32, no. 10, pp. 1744–1757, 2010. [72] A. Vezhnevets, V. Ferrari, and J. M. Buhmann, “Weakly su- [43] J. Shotton, M. Johnson, and R. Cipolla, “Semantic texton forests pervised semantic segmentation with a multi-image model,” in for image categorization and segmentation,” in CVPR, 2008. ICCV, 2011. [44] B. Fulkerson, A. Vedaldi, and S. Soatto, “Class segmentation [73] X. Liang, Y. Wei, X. Shen, J. Yang, L. Lin, and S. Yan, “Proposal- and object localization with superpixel neighborhoods,” in ICCV, free network for instance-level object segmentation,” arXiv 2009. preprint arXiv:1509.02636, 2015. [45] J. Carreira, R. Caseiro, J. Batista, and C. Sminchisescu, “Semantic [74] J. E. Fowler, “The redundant discrete wavelet transform and segmentation with second-order pooling,” in ECCV, 2012. additive noise,” IEEE Signal Processing Letters, vol. 12, no. 9, pp. [46] J. Carreira and C. Sminchisescu, “CPMC: Automatic object seg- 629–632, 2005. mentation using constrained parametric min-cuts,” PAMI, vol. 34, [75] P. P. Vaidyanathan, “Multirate digital filters, filter banks, no. 7, pp. 1312–1328, 2012. polyphase networks, and applications: a tutorial,” Proceedings of [47] P. Arbel´aez, J. Pont-Tuset, J. T. Barron, F. Marques, and J. Malik, the IEEE, vol. 78, no. 1, pp. 56–93, 1990. “Multiscale combinatorial grouping,” in CVPR, 2014. [76] F. Yu and V. Koltun, “Multi-scale context aggregation by dilated [48] J. Uijlings, K. van de Sande, T. Gevers, and A. Smeulders, convolutions,” in ICLR, 2016. “Selective search for object recognition,” IJCV, 2013. [77] J. Dai, Y. Li, K. He, and J. Sun, “R-fcn: Object detection via region- [49] B. Hariharan, P. Arbel´aez, R. Girshick, and J. Malik, “Simultane- based fully convolutional networks,” arXiv:1605.06409, 2016. ous detection and segmentation,” in ECCV, 2014. [78] J. Dai, K. He, Y. Li, S. Ren, and J. Sun, “Instance-sensitive fully [50] M. Mostajabi, P. Yadollahpour, and G. Shakhnarovich, “Feedfor- convolutional networks,” arXiv:1603.08678, 2016. ward semantic segmentation with zoom-out features,” in CVPR, [79] K. Chen, J. Wang, L.-C. Chen, H. Gao, W. Xu, and R. Nevatia, 2015. “Abc-cnn: An attention based convolutional neural network for [51] J. Dai, K. He, and J. Sun, “Convolutional feature masking for joint visual question answering,” arXiv:1511.05960, 2015. object and stuff segmentation,” arXiv:1412.1283, 2014. [80] L. Sevilla-Lara, D. Sun, V. Jampani, and M. J. Black, “Op- [52] D. Eigen and R. Fergus, “Predicting depth, surface normals tical flow with semantic segmentation and localized layers,” and semantic labels with a common multi-scale convolutional arXiv:1603.03911, 2016. architecture,” arXiv:1411.4734, 2014. [81] Z. Wu, C. Shen, and A. van den Hengel, “High-performance [53] M. Cogswell, X. Lin, S. Purushwalkam, and D. Batra, “Combining semantic segmentation using very deep fully convolutional net- the best of graphical models and convnets for semantic segmen- works,” arXiv:1604.04339, 2016. tation,” arXiv:1412.4313, 2014. [82] M. J. Shensa, “The discrete wavelet transform: wedding the a [54] D. Geiger and F. Girosi, “Parallel and deterministic algorithms trous and mallat algorithms,” Signal Processing, IEEE Transactions from mrfs: Surface reconstruction,” PAMI, vol. 13, no. 5, pp. 401– on, vol. 40, no. 10, pp. 2464–2482, 1992. 412, 1991. [83] M. Abadi, A. Agarwal et al., “Tensorflow: Large-scale [55] D. Geiger and A. Yuille, “A common framework for image machine learning on heterogeneous distributed systems,” segmentation,” IJCV, vol. 6, no. 3, pp. 227–243, 1991. arXiv:1603.04467, 2016. [56] I. Kokkinos, R. Deriche, O. Faugeras, and P. Maragos, “Computa- [84] A. Adams, J. Baek, and M. A. Davis, “Fast high-dimensional tional analysis and learning for a biologically motivated model of filtering using the permutohedral lattice,” in Eurographics, 2010. boundary detection,” Neurocomputing, vol. 71, no. 10, pp. 1798– [85] B. Hariharan, P. Arbel´aez, L. Bourdev, S. Maji, and J. Malik, 1812, 2008. “Semantic contours from inverse detectors,” in ICCV, 2011. [57] S. Bell, P. Upchurch, N. Snavely, and K. Bala, “Material recog- [86] W. Liu, A. Rabinovich, and A. C. Berg, “Parsenet: Looking wider nition in the wild with the materials in context database,” to see better,” arXiv:1506.04579, 2015. arXiv:1412.0623, 2014. [87] T.-Y. Lin et al., “Microsoft COCO: Common objects in context,” in [58] G. Papandreou, L.-C. Chen, K. Murphy, and A. L. Yuille, ECCV, 2014. “Weakly- and semi-supervised learning of a dcnn for semantic [88] R. Vemulapalli, O. Tuzel, M.-Y. Liu, and R. Chellappa, “Gaussian image segmentation,” in ICCV, 2015. conditional random field network for semantic segmentation,” in [59] S. Zheng, S. Jayasumana, B. Romera-Paredes, V. Vineet, Z. Su, CVPR, 2016. D. Du, C. Huang, and P. Torr, “Conditional random fields as [89] Z. Yan, H. Zhang, Y. Jia, T. Breuel, and Y. Yu, “Combining the best recurrent neural networks,” in ICCV, 2015. of convolutional layers and recurrent layers: A hybrid network [60] J. Dai, K. He, and J. Sun, “Boxsup: Exploiting bounding boxes to for semantic segmentation,” arXiv:1603.04871, 2016. supervise convolutional networks for semantic segmentation,” in [90] G. Ghiasi and C. C. Fowlkes, “Laplacian reconstruction and ICCV, 2015. refinement for semantic segmentation,” arXiv:1605.02264, 2016. 

14 . 14 [91] A. Arnab, S. Jayasumana, S. Zheng, and P. Torr, “Higher order Iasonas Kokkinos (S’02–M’06) obtained the potentials in end-to-end trainable conditional random fields,” Diploma of Engineering in 2001 and the Ph.D. arXiv:1511.08119, 2015. Degree in 2006 from the School of Electrical and [92] F. Shen and G. Zeng, “Fast semantic image segmentation with Computer Engineering of the National Technical high order context and guided filtering,” arXiv:1605.04068, 2016. University of Athens in Greece, and the Habili- [93] Z. Wu, C. Shen, and A. van den Hengel, “Bridging tation Degree in 2013 from Universit Paris-Est. category-level and instance-level semantic image segmentation,” In 2006 he joined the University of California at arXiv:1605.06885, 2016. Los Angeles as a postdoctoral scholar, and in [94] K. He, X. Zhang, S. Ren, and J. Sun, “Identity mappings in deep 2008 joined as faculty the Department of Applied residual networks,” arXiv:1603.05027, 2016. Mathematics of Ecole Centrale Paris (Centrale- [95] F. Xia, P. Wang, L.-C. Chen, and A. L. Yuille, “Zoom better to Supelec), working an associate professor in the see clearer: Huamn part segmentation with auto zoom net,” Center for Visual Computing of CentraleSupelec and affiliate researcher arXiv:1511.06881, 2015. at INRIA-Saclay. In 2016 he joined University College London and Face- [96] X. Liang, X. Shen, D. Xiang, J. Feng, L. Lin, and S. Yan, “Se- book Artificial Intelligence Research. His currently research activity is on mantic object parsing with local-global long short-term memory,” deep learning for computer vision, focusing in particular on structured arXiv:1511.04510, 2015. prediction for deep learning, shape modeling, and multi-task learning [97] X. Liang, X. Shen, J. Feng, L. Lin, and S. Yan, “Semantic object architectures. He has been awarded a young researcher grant by the parsing with graph lstm,” arXiv:1603.07063, 2016. French National Research Agency, has served as associate editor for [98] J. Wang and A. Yuille, “Semantic part segmentation using com- the Image and Vision Computing and Computer Vision and Image positional model combining shape and appearance,” in CVPR, Understanding Journals, serves regularly as a reviewer and area chair 2015. for all major computer vision conferences and journals. [99] P. Wang, X. Shen, Z. Lin, S. Cohen, B. Price, and A. Yuille, “Joint object and part segmentation using deep learned potentials,” in ICCV, 2015. [100] V. Badrinarayanan, A. Kendall, and R. Cipolla, “Segnet: A deep convolutional encoder-decoder architecture for image segmenta- tion,” arXiv:1511.00561, 2015. [101] J. Uhrig, M. Cordts, U. Franke, and T. Brox, “Pixel-level en- coding and depth layering for instance-level semantic labeling,” arXiv:1604.05096, 2016. [102] O. Ronneberger, P. Fischer, and T. Brox, “U-net: Convolutional Kevin Murphy was born in Ireland, grew up in networks for biomedical image segmentation,” in MICCAI, 2015. England, went to graduate school in the USA (MEng from U. Penn, PhD from UC Berkeley, Postdoc at MIT), and then became a professor at the Computer Science and Statistics Depart- ments at the University of British Columbia in Vancouver, Canada in 2004. After getting tenure, Kevin went to Google in Mountain View, Cali- fornia for his sabbatical. In 2011, he converted Liang-Chieh Chen received his B.Sc. from Na- to a full-time research scientist at Google. Kevin tional Chiao Tung University, Taiwan, his M.S. has published over 50 papers in refereed con- from the University of Michigan- Ann Arbor, and ferences and journals related to machine learning and graphical mod- his Ph.D. from the University of California- Los els. He has recently published an 1100-page textbook called “Machine Angeles. He is currently working at Google. His Learning: a Probabilistic Perspective” (MIT Press, 2012). research interests include semantic image seg- mentation, probabilistic graphical models, and machine learning. Alan L. Yuille (F’09) received the BA degree in math- ematics from the University of Cambridge in 1976. His PhD on theoretical physics, super- vised by Prof. S.W. Hawking, was approved in George Papandreou (S’03–M’09–SM’14) holds 1981. He was a research scientist in the Artificial a Diploma (2003) and a Ph.D. (2009) in Elec- Intelligence Laboratory at MIT and the Division trical Engineering and Computer Science, both of Applied Sciences at Harvard University from from the National Technical University of Athens 1982 to 1988. He served as an assistant and (NTUA), Greece. He is currently a Research Sci- associate professor at Harvard until 1996. He entist at Google, following appointments as Re- was a senior research scientist at the Smith- search Assistant Professor at the Toyota Tech- Kettlewell Eye Research Institute from 1996 to nological Institute at Chicago (2013-2014) and 2002. He joined the University of California, Los Angeles, as a full Postdoctoral Research Scholar at the University professor with a joint appointment in statistics and psychology in 2002, of California, Los Angeles (2009-2013). and computer science in 2007. He was appointed a Bloomberg Dis- His research interests are in computer vision tinguished Professor at Johns Hopkins University in January 2016. He and machine learning, with a current emphasis on deep learning. He holds a joint appointment between the Departments of Cognitive science regularly serves as a reviewer and program committee member to the and Computer Science. His research interests include computational main journals and conferences in computer vision, image processing, models of vision, mathematical models of cognition, and artificial intelli- and machine learning. He has been a co-organizer of the NIPS 2012, gence and neural network 2013, and 2014 Workshops on Perturbations, Optimization, and Statis- tics and co-editor of a book on the same topic (MIT Press, 2016).