Conditional Image Synthesis with Auxiliary Classifier GANs

1 . Conditional Image Synthesis with Auxiliary Classifier GANs Augustus Odena 1 Christopher Olah 1 Jonathon Shlens 1 Abstract several promising approaches for building image synthe- In this paper we introduce new methods for the sis models. Variational autoencoders (VAEs) maximize a improved training of generative adversarial net- variational lower bound on the log-likelihood of the train- ing data (Kingma & Welling, 2013; Rezende et al., 2014). arXiv:1610.09585v4 [stat.ML] 20 Jul 2017 works (GANs) for image synthesis. We con- struct a variant of GANs employing label condi- VAEs are straightforward to train but introduce potentially tioning that results in 128 × 128 resolution im- restrictive assumptions about the approximate posterior age samples exhibiting global coherence. We distribution (but see (Rezende & Mohamed, 2015; Kingma expand on previous work for image quality as- et al., 2016)). Autoregressive models dispense with latent sessment to provide two new analyses for assess- variables and directly model the conditional distribution ing the discriminability and diversity of samples over pixels (van den Oord et al., 2016a;b). These models from class-conditional image synthesis models. produce convincing samples but are costly to sample from These analyses demonstrate that high resolution and do not provide a latent representation. Invertible den- samples provide class information not present in sity estimators transform latent variables directly using a low resolution samples. Across 1000 ImageNet series of parameterized functions constrained to be invert- classes, 128 × 128 samples are more than twice ible (Dinh et al., 2016). This technique allows for exact as discriminable as artificially resized 32 × 32 log-likelihood computation and exact inference, but the in- samples. In addition, 84.7% of the classes have vertibility constraint is restrictive. samples exhibiting diversity comparable to real Generative adversarial networks (GANs) offer a distinct ImageNet data. and promising approach that focuses on a game-theoretic formulation for training an image synthesis model (Good- fellow et al., 2014). Recent work has shown that GANs can 1. Introduction produce convincing image samples on datasets with low variability and low resolution (Denton et al., 2015; Radford Characterizing the structure of natural images has been a et al., 2015). However, GANs struggle to generate glob- rich research endeavor. Natural images obey intrinsic in- ally coherent, high resolution samples - particularly from variances and exhibit multi-scale statistical structures that datasets with high variability. Moreover, a theoretical un- have historically been difficult to quantify (Simoncelli & derstanding of GANs is an on-going research topic (Uehara Olshausen, 2001). Recent advances in machine learning et al., 2016; Mohamed & Lakshminarayanan, 2016). offer an opportunity to substantially improve the quality of image models. Improved image models advance the state- In this work we demonstrate that that adding more structure of-the-art in image denoising (Ball´e et al., 2015), compres- to the GAN latent space along with a specialized cost func- sion (Toderici et al., 2016), in-painting (van den Oord et al., tion results in higher quality samples. We exhibit 128×128 2016a), and super-resolution (Ledig et al., 2016). Bet- pixel samples from all classes of the ImageNet dataset ter models of natural images also improve performance in (Russakovsky et al., 2015) with increased global coherence semi-supervised learning tasks (Kingma et al., 2014; Sprin- (Figure 1). Importantly, we demonstrate quantitatively that genberg, 2015; Odena, 2016; Salimans et al., 2016) and re- our high resolution samples are not just naive resizings of inforcement learning problems (Blundell et al., 2016). low resolution samples. In particular, downsampling our 128 × 128 samples to 32 × 32 leads to a 50% decrease in One method for understanding natural image statistics is to visual discriminability. We also introduce a new metric for build a system that synthesizes images de novo. There are assessing the variability across image samples and employ 1 Google Brain. Correspondence to: Augustus Odena <augus- this metric to demonstrate that our synthesized images ex- tusodena@google.com>. hibit diversity comparable to training data for a large frac- tion (84.7%) of ImageNet classes. In more detail, this work Proceedings of the 34 th International Conference on Machine is the first to: Learning, Sydney, Australia, PMLR 70, 2017. Copyright 2017 by the author(s). 

2 . Conditional Image Synthesis with Auxiliary Classifier GANs monarch butterfly goldfinch daisy redshank grey whale Figure 1. 128 × 128 resolution samples from 5 classes taken from an AC-GAN trained on the ImageNet dataset. Note that the classes shown have been selected to highlight the success of the model and are not representative. Samples from all ImageNet classes are linked later in the text. • Demonstrate an image synthesis model for all 1000 The generator is trained to minimize the second term in ImageNet classes at a 128x128 spatial resolution (or Equation 1. any spatial resolution - see Section 3). The basic GAN framework can be augmented using side • Measure how much an image synthesis model actually information. One strategy is to supply both the generator uses its output resolution (Section 4.1). and discriminator with class labels in order to produce class conditional samples (Mirza & Osindero, 2014). Class con- • Measure perceptual variability and ’collapsing’ be- ditional synthesis can significantly improve the quality of havior in a GAN with a fast, easy-to-compute metric generated samples (van den Oord et al., 2016b). Richer side (Section 4.2). information such as image captions and bounding box lo- calizations may improve sample quality further (Reed et al., • Highlight that a high number of classes is what makes 2016a;b). ImageNet synthesis difficult for GANs and provide an Instead of feeding side information to the discriminator, explicit solution (Section 4.6). one can task the discriminator with reconstructing side in- • Demonstrate experimentally that GANs that perform formation. This is done by modifying the discriminator to well perceptually are not those that memorize a small contain an auxiliary decoder network1 that outputs the class number of examples (Section 4.3). label for the training data (Odena, 2016; Salimans et al., 2016) or a subset of the latent variables from which the • Achieve state of the art on the Inception score metric samples are generated (Chen et al., 2016). Forcing a model when trained on CIFAR-10 without using any of the to perform additional tasks is known to improve perfor- techniques from (Salimans et al., 2016) (Section 4.4). mance on the original task (e.g. (Sutskever et al., 2014; Szegedy et al., 2014; Ramsundar et al., 2016)). In addi- tion, an auxiliary decoder could leverage pre-trained dis- 2. Background criminators (e.g. image classifiers) for further improving A generative adversarial network (GAN) consists of two the synthesized images (Nguyen et al., 2016). Motivated neural networks trained in opposition to one another. The by these considerations, we introduce a model that com- generator G takes as input a random noise vector z and bines both strategies for leveraging side information. That outputs an image Xf ake = G(z). The discriminator D is, the model proposed below is class conditional, but with receives as input either a training image or a synthesized an auxiliary decoder that is tasked with reconstructing class image from the generator and outputs a probability distri- labels. bution P (S | X) = D(X) over possible image sources. 1 Alternatively, one can force the discriminator to work with The discriminator is trained to maximize the log-likelihood the joint distribution (X, z) and train a separate inference network it assigns to the correct source: that computes q(z|X) (Dumoulin et al., 2016; Donahue et al., 2016). L = E[log P (S = real | Xreal )]+ E[log P (S = f ake | Xf ake )] (1) 

3 . Conditional Image Synthesis with Auxiliary Classifier GANs 3. AC-GANs spatial resolutions. The discriminator D is a deep convo- lutional neural network with a Leaky ReLU nonlinearity We propose a variant of the GAN architecture which we (Maas et al., 2013). As mentioned earlier, we find that re- call an auxiliary classifier GAN (or AC-GAN). In the AC- ducing the variability introduced by all 1000 classes of Im- GAN, every generated sample has a corresponding class la- ageNet significantly improves the quality of training. We bel, c ∼ pc in addition to the noise z. G uses both to gener- train 100 AC-GAN models – each on images from just 10 ate images Xf ake = G(c, z). The discriminator gives both classes – for 50000 mini-batches of size 100. a probability distribution over sources and a probability dis- tribution over the class labels, P (S | X), P (C | X) = Evaluating the quality of image synthesis models is chal- D(X). The objective function has two parts: the log- lenging due to the variety of probabilistic criteria (Theis likelihood of the correct source, LS , and the log-likelihood et al., 2015) and the lack of a perceptually meaningful im- of the correct class, LC . age similarity metric. Nonetheless, in later sections we at- tempt to measure the quality of the AC-GAN by building several ad-hoc measures for image sample discriminabil- ity and diversity. Our hope is that this work might provide LS = E[log P (S = real | Xreal )]+ quantitative measures that may be used to aid training and E[log P (S = f ake | Xf ake )] (2) subsequent development of image synthesis models. LC = E[log P (C = c | Xreal )]+ 4.1. Generating High Resolution Images Improves Discriminability E[log P (C = c | Xf ake )] (3) Building a class-conditional image synthesis model neces- D is trained to maximize LS + LC while G is trained to sitates measuring the extent to which synthesized images maximize LC − LS . AC-GANs learn a representation for appear to belong to the intended class. In particular, we z that is independent of class label (e.g. (Kingma et al., would like to know that a high resolution sample is not just 2014)). a naive resizing of a low resolution sample. Consider a simple experiment: pretend there exists a model that syn- Structurally, this model is not tremendously different from thesizes 32 × 32 images. One can trivially increase the existing models. However, this modification to the stan- resolution of synthesized images by performing bilinear in- dard GAN formulation produces excellent results and ap- terpolation. This would yield higher resolution images, but pears to stabilize training. Moreover, we consider the AC- these images would just be blurry versions of the low res- GAN model to be only part of the technical contributions of olution images that are not discriminable. Hence, the goal this work, along with our proposed methods for measuring of an image synthesis model is not simply to produce high the extent to which a model makes use of its given output resolution images, but to produce high resolution images resolution, methods for measuring perceptual variability of that are more discriminable than low resolution images. samples from the model, and a thorough experimental ana- lyis of a generative model of images that creates 128 × 128 To measure discriminability, we feed synthesized images samples from all 1000 ImageNet classes. to a pre-trained Inception network (Szegedy et al., 2015) and report the fraction of the samples for which the In- Early experiments demonstrated that increasing the num- ception network assigned the correct label2 . We calculate ber of classes trained on while holding the model fixed de- this accuracy measure on a series of real and synthesized creased the quality of the model outputs. The structure of images which have had their spatial resolution artificially the AC-GAN model permits separating large datasets into decreased by bilinear interpolation (Figure 2, top panels). subsets by class and training a generator and discriminator Note that as the spatial resolution is decreased, the accuracy for each subset. All ImageNet experiments are conducted decreases - indicating that resulting images contain less using an ensemble of 100 AC-GANs, each trained on a 10- class information (Figure 2, scores below top panels). We class split. summarized this finding across all 1000 ImageNet classes for the ImageNet training data (black), a 128 × 128 reso- 4. Results 2 One could also use the Inception score (Salimans et al., We train several AC-GAN models on the ImageNet data 2016), but our method has several advantages: accuracy fig- ures are easier to interpret than exponentiated KL-divergences; set (Russakovsky et al., 2015). Broadly speaking, the ar- accuracy may be assessed for individual classes; accuracy chitecture of the generator G is a series of ‘deconvolution’ measures whether a class-conditional model generated sam- layers that transform the noise z and class c into an image ples from the intended class. To compute the Inception ac- (Odena et al., 2016). We train two variants of the model ar- curacy, we modified a version of Inception-v3 supplied in chitecture for generating images at 128 × 128 and 64 × 64 https://github.com/openai/improved-gan/. 

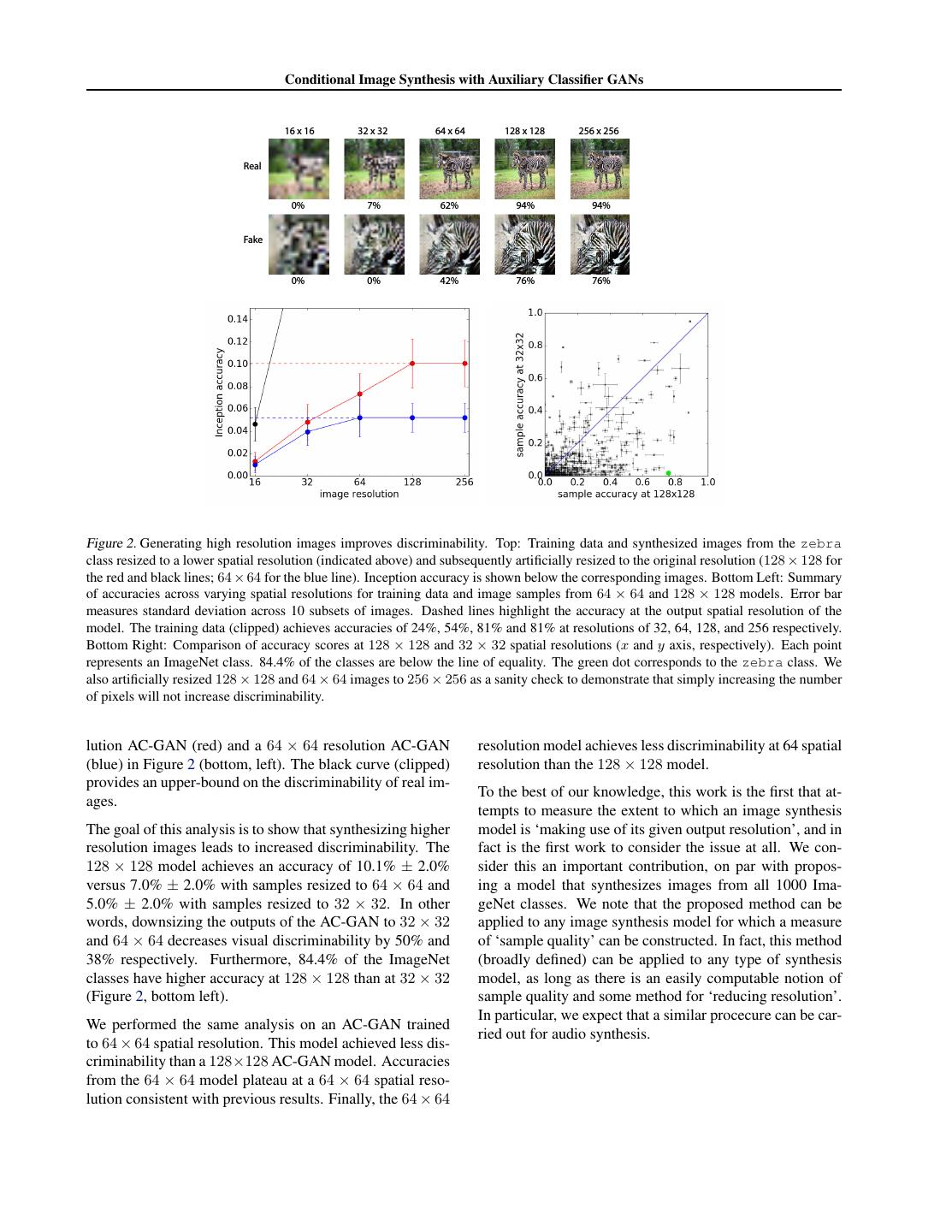
4 . Conditional Image Synthesis with Auxiliary Classifier GANs 16 x 16 32 x 32 64 x 64 128 x 128 256 x 256 Real 0% 7% 62% 94% 94% Fake 0% 0% 42% 76% 76% Figure 2. Generating high resolution images improves discriminability. Top: Training data and synthesized images from the zebra class resized to a lower spatial resolution (indicated above) and subsequently artificially resized to the original resolution (128 × 128 for the red and black lines; 64 × 64 for the blue line). Inception accuracy is shown below the corresponding images. Bottom Left: Summary of accuracies across varying spatial resolutions for training data and image samples from 64 × 64 and 128 × 128 models. Error bar measures standard deviation across 10 subsets of images. Dashed lines highlight the accuracy at the output spatial resolution of the model. The training data (clipped) achieves accuracies of 24%, 54%, 81% and 81% at resolutions of 32, 64, 128, and 256 respectively. Bottom Right: Comparison of accuracy scores at 128 × 128 and 32 × 32 spatial resolutions (x and y axis, respectively). Each point represents an ImageNet class. 84.4% of the classes are below the line of equality. The green dot corresponds to the zebra class. We also artificially resized 128 × 128 and 64 × 64 images to 256 × 256 as a sanity check to demonstrate that simply increasing the number of pixels will not increase discriminability. lution AC-GAN (red) and a 64 × 64 resolution AC-GAN resolution model achieves less discriminability at 64 spatial (blue) in Figure 2 (bottom, left). The black curve (clipped) resolution than the 128 × 128 model. provides an upper-bound on the discriminability of real im- To the best of our knowledge, this work is the first that at- ages. tempts to measure the extent to which an image synthesis The goal of this analysis is to show that synthesizing higher model is ‘making use of its given output resolution’, and in resolution images leads to increased discriminability. The fact is the first work to consider the issue at all. We con- 128 × 128 model achieves an accuracy of 10.1% ± 2.0% sider this an important contribution, on par with propos- versus 7.0% ± 2.0% with samples resized to 64 × 64 and ing a model that synthesizes images from all 1000 Ima- 5.0% ± 2.0% with samples resized to 32 × 32. In other geNet classes. We note that the proposed method can be words, downsizing the outputs of the AC-GAN to 32 × 32 applied to any image synthesis model for which a measure and 64 × 64 decreases visual discriminability by 50% and of ‘sample quality’ can be constructed. In fact, this method 38% respectively. Furthermore, 84.4% of the ImageNet (broadly defined) can be applied to any type of synthesis classes have higher accuracy at 128 × 128 than at 32 × 32 model, as long as there is an easily computable notion of (Figure 2, bottom left). sample quality and some method for ‘reducing resolution’. In particular, we expect that a similar procecure can be car- We performed the same analysis on an AC-GAN trained ried out for audio synthesis. to 64 × 64 spatial resolution. This model achieved less dis- criminability than a 128×128 AC-GAN model. Accuracies from the 64 × 64 model plateau at a 64 × 64 spatial reso- lution consistent with previous results. Finally, the 64 × 64 

5 . Conditional Image Synthesis with Auxiliary Classifier GANs hot dog promontory green apple artichoke 4.2. Measuring the Diversity of Generated Images MS-SSIM = 0.11 MS-SSIM = 0.29 MS-SSIM = 0.41 MS-SSIM = 0.90 An image synthesis model is not very interesting if it only synthesized outputs one image. Indeed, a well-known failure mode of GANs is that the generator will collapse and output a single prototype that maximally fools the discriminator (Goodfel- MS-SSIM = 0.05 MS-SSIM = 0.15 MS-SSIM = 0.08 MS-SSIM = 0.04 low et al., 2014; Salimans et al., 2016). A class-conditional model of images is not very interesting if it only outputs real one image per class. The Inception accuracy can not mea- sure whether a model has collapsed. A model that simply memorized one example from each ImageNet class would do very well by this metric. Thus, we seek a complemen- Figure 3. Examples of different MS-SSIM scores. The top and tary metric to explicitly evaluate the intra-class perceptual bottom rows contain AC-GAN samples and training data, respec- diversity of samples generated by the AC-GAN. tively. Several methods exist for quantitatively evaluating image similarity by attempting to predict human perceptual sim- to be used for measuring the quality of image compres- ilarity judgements. The most successful of these is multi- sion algorithms using a reference ‘original image’. We in- scale structural similarity (MS-SSIM) (Wang et al., 2004b; stead use it on two potentially unrelated images. We be- Ma et al., 2016). MS-SSIM is a multi-scale variant of lieve that this is acceptable for the following reasons: First: a well-characterized perceptual similarity metric that at- visual inspection seems to indicate that the metric makes tempts to discount aspects of an image that are not impor- sense - pairs with higher MS-SSIM do seem more similar tant for human perception (Wang et al., 2004a). MS-SSIM than pairs with lower MS-SSIM. Second: we restrict com- values range between 0.0 and 1.0; higher MS-SSIM values parisons to images synthesized using the same class label. correspond to perceptually more similar images. This restricts use of MS-SSIM to situations more similar to As a proxy for image diversity, we measure the MS- those in which it is typically used (it is not important which SSIM scores between 100 randomly chosen pairs of images image is the reference). Third: the metric is not ‘saturated’ within a given class. Samples from classes that have higher for our use-case. If most scores were around 0, then we diversity result in lower mean MS-SSIM scores (Figure would be more concerned about the applicability of MS- 3, left columns); samples from classes with lower diver- SSIM. Finally: The fact that training data achieves more sity have higher mean MS-SSIM scores (Figure 3, right variability by this metric (as expected) is itself evidence columns). Training images from the ImageNet training that the metric is working as intended. data contain a variety of mean MS-SSIM scores across the The second point is that the MS-SSIM metric is not in- classes indicating the variability of image diversity in Ima- tended as a proxy for the entropy of the generator distribu- geNet classes (Figure 4, x-axis). Note that the highest mean tion in pixel space, but as a measure of perceptual diversity MS-SSIM score (indicating the least variability) is 0.25 for of the outputs. The entropy of the generator output distri- the training data. bution is hard to compute and pairwise MS-SSIM scores We calculate the mean MS-SSIM score for all 1000 Ima- would not be a good proxy. Even if it were easy to com- geNet classes generated by the AC-GAN model. We track pute, we argue that it would still be useful to have a separate this value during training to identify whether the generator measure of perceptual diversity. To see why, consider that has collapsed (Figure 5, red curve). We also employ this the generator entropy will be sensitive to trivial changes metric to compare the diversity of the training images to in contrast as well as changes in the semantic content of the samples from the GAN model after training has com- the outputs. In many applications, we don’t care about this pleted. Figure 4 plots the mean MS-SSIM values for image contribution to the entropy, and it is useful to consider mea- samples and training data broken up by class. The blue line sures that attempt to ignore changes to an image that we is the line of equality. Out of the 1000 classes, we find that consider ‘perceptually meaningless’, hence the use of MS- 847 have mean sample MS-SSIM scores below that of the SSIM. maximum MS-SSIM for the training data. In other words, 84.7% of classes have sample variability that exceeds that 4.3. Generated Images are both Diverse and of the least variable class from the ImageNet training data. Discriminable There are two points related to the MS-SSIM metric and We have presented quantitative metrics demonstrating that our use of it that merit extra attention. The first point is AC-GAN samples may be diverse and discriminable but that we are ‘abusing’ the metric: it was originally intended we have yet to examine how these metrics interact. Fig- ure 6 shows the joint distribution of Inception accuracies 

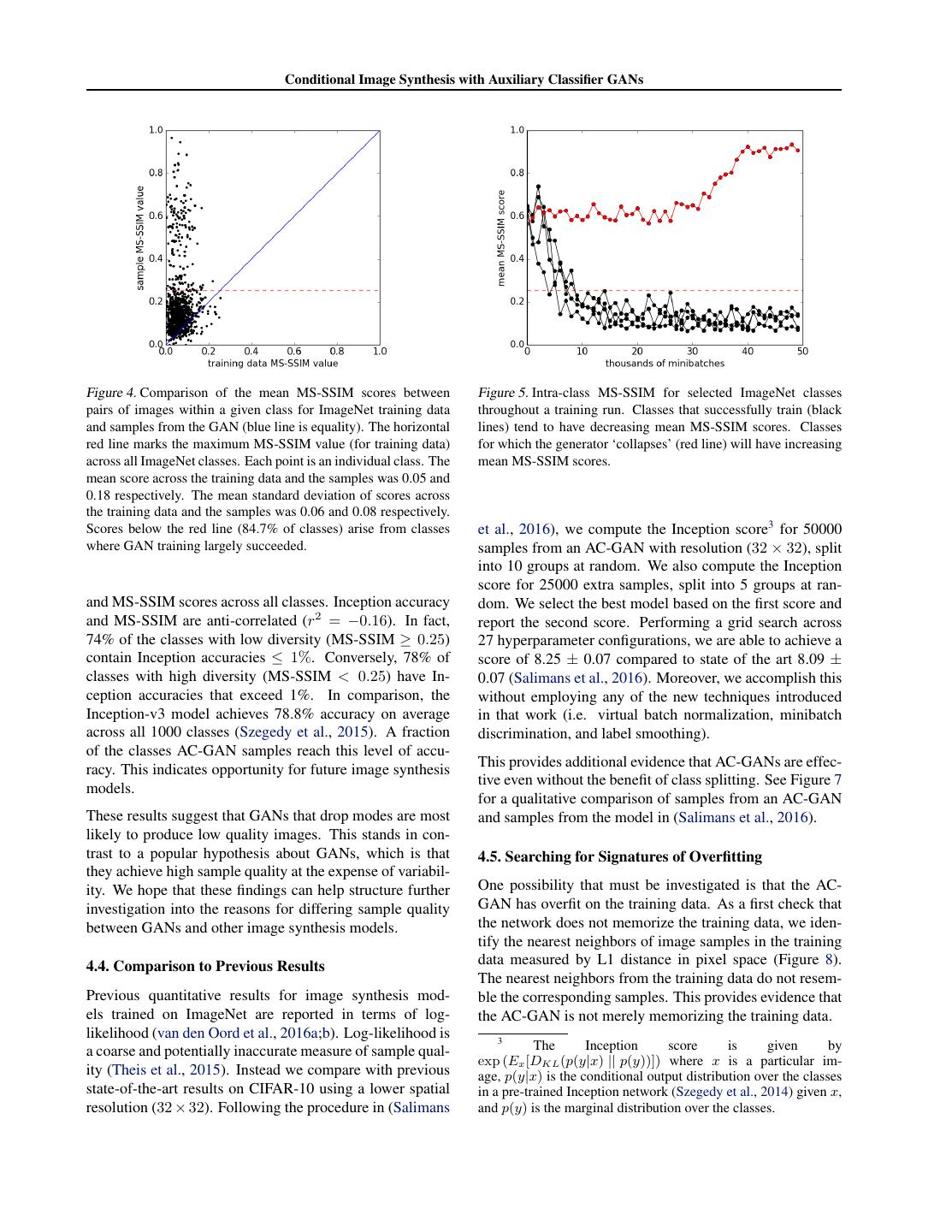
6 . Conditional Image Synthesis with Auxiliary Classifier GANs Figure 4. Comparison of the mean MS-SSIM scores between Figure 5. Intra-class MS-SSIM for selected ImageNet classes pairs of images within a given class for ImageNet training data throughout a training run. Classes that successfully train (black and samples from the GAN (blue line is equality). The horizontal lines) tend to have decreasing mean MS-SSIM scores. Classes red line marks the maximum MS-SSIM value (for training data) for which the generator ‘collapses’ (red line) will have increasing across all ImageNet classes. Each point is an individual class. The mean MS-SSIM scores. mean score across the training data and the samples was 0.05 and 0.18 respectively. The mean standard deviation of scores across the training data and the samples was 0.06 and 0.08 respectively. Scores below the red line (84.7% of classes) arise from classes et al., 2016), we compute the Inception score3 for 50000 where GAN training largely succeeded. samples from an AC-GAN with resolution (32 × 32), split into 10 groups at random. We also compute the Inception score for 25000 extra samples, split into 5 groups at ran- and MS-SSIM scores across all classes. Inception accuracy dom. We select the best model based on the first score and and MS-SSIM are anti-correlated (r2 = −0.16). In fact, report the second score. Performing a grid search across 74% of the classes with low diversity (MS-SSIM ≥ 0.25) 27 hyperparameter configurations, we are able to achieve a contain Inception accuracies ≤ 1%. Conversely, 78% of score of 8.25 ± 0.07 compared to state of the art 8.09 ± classes with high diversity (MS-SSIM < 0.25) have In- 0.07 (Salimans et al., 2016). Moreover, we accomplish this ception accuracies that exceed 1%. In comparison, the without employing any of the new techniques introduced Inception-v3 model achieves 78.8% accuracy on average in that work (i.e. virtual batch normalization, minibatch across all 1000 classes (Szegedy et al., 2015). A fraction discrimination, and label smoothing). of the classes AC-GAN samples reach this level of accu- This provides additional evidence that AC-GANs are effec- racy. This indicates opportunity for future image synthesis tive even without the benefit of class splitting. See Figure 7 models. for a qualitative comparison of samples from an AC-GAN These results suggest that GANs that drop modes are most and samples from the model in (Salimans et al., 2016). likely to produce low quality images. This stands in con- trast to a popular hypothesis about GANs, which is that 4.5. Searching for Signatures of Overfitting they achieve high sample quality at the expense of variabil- ity. We hope that these findings can help structure further One possibility that must be investigated is that the AC- investigation into the reasons for differing sample quality GAN has overfit on the training data. As a first check that between GANs and other image synthesis models. the network does not memorize the training data, we iden- tify the nearest neighbors of image samples in the training 4.4. Comparison to Previous Results data measured by L1 distance in pixel space (Figure 8). The nearest neighbors from the training data do not resem- Previous quantitative results for image synthesis mod- ble the corresponding samples. This provides evidence that els trained on ImageNet are reported in terms of log- the AC-GAN is not merely memorizing the training data. likelihood (van den Oord et al., 2016a;b). Log-likelihood is 3 a coarse and potentially inaccurate measure of sample qual- The Inception score is given by exp (Ex [DKL (p(y|x) || p(y))]) where x is a particular im- ity (Theis et al., 2015). Instead we compare with previous age, p(y|x) is the conditional output distribution over the classes state-of-the-art results on CIFAR-10 using a lower spatial in a pre-trained Inception network (Szegedy et al., 2014) given x, resolution (32 × 32). Following the procedure in (Salimans and p(y) is the marginal distribution over the classes. 

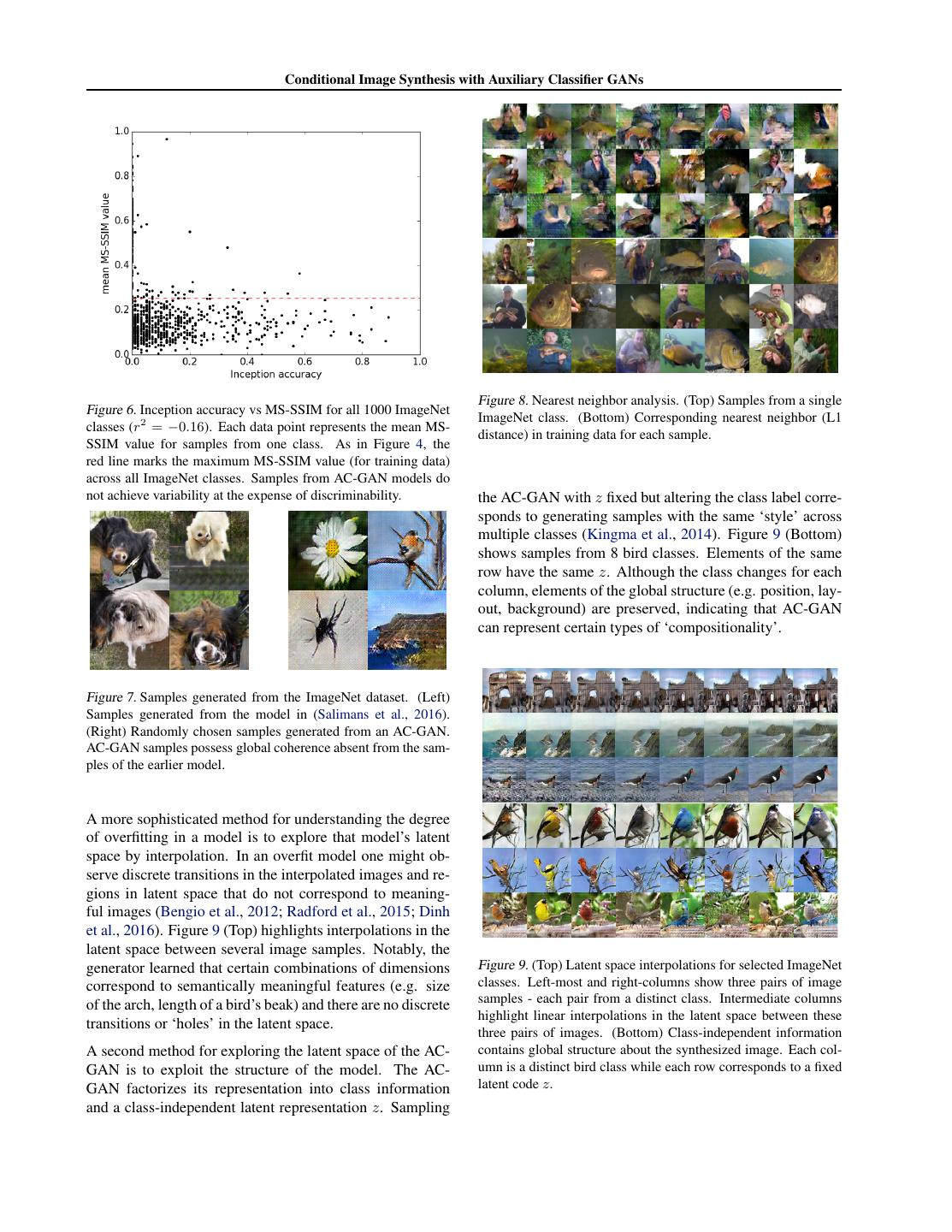
7 . Conditional Image Synthesis with Auxiliary Classifier GANs Figure 8. Nearest neighbor analysis. (Top) Samples from a single Figure 6. Inception accuracy vs MS-SSIM for all 1000 ImageNet ImageNet class. (Bottom) Corresponding nearest neighbor (L1 classes (r2 = −0.16). Each data point represents the mean MS- distance) in training data for each sample. SSIM value for samples from one class. As in Figure 4, the red line marks the maximum MS-SSIM value (for training data) across all ImageNet classes. Samples from AC-GAN models do not achieve variability at the expense of discriminability. the AC-GAN with z fixed but altering the class label corre- sponds to generating samples with the same ‘style’ across multiple classes (Kingma et al., 2014). Figure 9 (Bottom) shows samples from 8 bird classes. Elements of the same row have the same z. Although the class changes for each column, elements of the global structure (e.g. position, lay- out, background) are preserved, indicating that AC-GAN can represent certain types of ‘compositionality’. Figure 7. Samples generated from the ImageNet dataset. (Left) Samples generated from the model in (Salimans et al., 2016). (Right) Randomly chosen samples generated from an AC-GAN. AC-GAN samples possess global coherence absent from the sam- ples of the earlier model. A more sophisticated method for understanding the degree of overfitting in a model is to explore that model’s latent space by interpolation. In an overfit model one might ob- serve discrete transitions in the interpolated images and re- gions in latent space that do not correspond to meaning- ful images (Bengio et al., 2012; Radford et al., 2015; Dinh et al., 2016). Figure 9 (Top) highlights interpolations in the latent space between several image samples. Notably, the generator learned that certain combinations of dimensions Figure 9. (Top) Latent space interpolations for selected ImageNet correspond to semantically meaningful features (e.g. size classes. Left-most and right-columns show three pairs of image of the arch, length of a bird’s beak) and there are no discrete samples - each pair from a distinct class. Intermediate columns highlight linear interpolations in the latent space between these transitions or ‘holes’ in the latent space. three pairs of images. (Bottom) Class-independent information A second method for exploring the latent space of the AC- contains global structure about the synthesized image. Each col- GAN is to exploit the structure of the model. The AC- umn is a distinct bird class while each row corresponds to a fixed GAN factorizes its representation into class information latent code z. and a class-independent latent representation z. Sampling 

8 . Conditional Image Synthesis with Auxiliary Classifier GANs 4.6. Measuring the Effect of Class Splits on Image tivity to class count that is well-supported experimentally. Sample Quality. We can only note that, since the failure case that occurs when the class count is increased is ‘generator collapse’, it Class conditional image synthesis affords the opportunity seems plausible that general methods for addressing ‘gen- to divide up a dataset based on image label. In our final erator collapse’ could also address this sensitivity. model we divide 1000 ImageNet classes across 100 AC- GAN models. In this section we describe experiments that 4.7. Samples from all 1000 ImageNet Classes highlight the benefit of cutting down the diversity of classes for training an AC-GAN. We employed an ordering of the We also generate 10 samples from each of the 1000 Ima- labels and divided it into contiguous groups of 10. This geNet classes, hosted here. As far as we are aware, no other ordering can be seen in the following section, where we image synthesis work has included a similar analysis. display samples from all 1000 classes. Two aspects of the split merit discussion: the number of classes per split and 5. Discussion the intra-split diversity. We find that training a fixed model on more classes harms the model’s ability to produce com- This work introduced the AC-GAN architecture and pelling samples (Figure 10). Performance on larger splits demonstrated that AC-GANs can generate globally coher- can be improved by giving the model more parameters. ent ImageNet samples. We provided a new quantitative However, using a small split is not sufficient to achieve metric for image discriminability as a function of spatial good performance. We were unable to train a GAN (Good- resolution. Using this metric we demonstrated that our fellow et al., 2014) to converge reliably even for a split size samples are more discriminable than those from a model of 1. This raises the question of whether it is easier to train that generates lower resolution images and performs a a model on a diverse set of classes than on a similar set of naive resize operation. We also analyzed the diversity of classes: We were unable to find conclusive evidence that our samples with respect to the training data and provided the selection of classes in a split significantly affects sam- some evidence that the image samples from the majority of ple quality. classes are comparable in diversity to ImageNet data. Several directions exist for building upon this work. Much work needs to be done to improve the visual discriminabil- ity of the 128 × 128 resolution model. Although some synthesized image classes exhibit high Inception accura- cies, the average Inception accuracy of the model (10.1%± 2.0%) is still far below real training data at 81%. One im- mediate opportunity for addressing this is to augment the discriminator with a pre-trained model to perform addi- tional supervised tasks (e.g. image segmentation, (Ron- neberger et al., 2015)). Improving the reliability of GAN training is an ongoing research topic. Only 84.7% of the ImageNet classes ex- hibited diversity comparable to real training data. Training stability was vastly aided by dividing up 1000 ImageNet classes across 100 AC-GAN models. Building a single model that could generate samples from all 1000 classes Figure 10. Mean pairwise MS-SSIM values for 10 ImageNet would be an important step forward. classes plotted against the number of ImageNet classes used dur- Image synthesis models provide a unique opportunity for ing training. We fix everything except the number of classes performing semi-supervised learning: these models build trained on, using values from 10 to 100. We only report the MS- a rich prior over natural image statistics that can be lever- SSIM values for the first 10 classes to keep the scores comparable. MS-SSIM quickly goes above 0.25 (the red line) as the class count aged by classifiers to improve predictions on datasets for increases. These scores were computed using 9 random restarts which few labels exist. The AC-GAN model can perform per class count, using the same number of training steps for each semi-supervised learning by ignoring the component of the model. Since we have observed that generators do not recover loss arising from class labels when a label is unavailable from the collapse phase, the use of a fixed number of training for a given training image. Interestingly, prior work sug- steps seems justified in this case. gests that achieving good sample quality might be inde- pendent of success in semi-supervised learning (Salimans We don’t have a hypothesis about what causes this sensi- et al., 2016). 

9 . Conditional Image Synthesis with Auxiliary Classifier GANs References Ledig, C., Theis, L., Huszar, F., Caballero, J., Aitken, A., Tejani, A., Totz, J., Wang, Z., and Shi, W. Photo- Ball´e, Johannes, Laparra, Valero, and Simoncelli, Eero P. Realistic Single Image Super-Resolution Using a Gen- Density modeling of images using a generalized normal- erative Adversarial Network. ArXiv e-prints, September ization transformation. CoRR, abs/1511.06281, 2015. 2016. URL http://arxiv.org/abs/1511.06281. Bengio, Yoshua, Mesnil, Gr´egoire, Dauphin, Yann, and Ma, Kede, Wu, Qingbo, Wang, Zhou, Duanmu, Zhengfang, Rifai, Salah. Better mixing via deep representations. Yong, Hongwei, Li, Hongliang, and Zhang, Lei. Group CoRR, abs/1207.4404, 2012. URL http://arxiv. mad competition - a new methodology to compare objec- org/abs/1207.4404. tive image quality models. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June Blundell, C., Uria, B., Pritzel, A., Li, Y., Ruderman, 2016. A., Leibo, J. Z, Rae, J., Wierstra, D., and Hassabis, D. Model-Free Episodic Control. ArXiv e-prints, June Maas, Andrew, Hannun, Awni, and Ng, Andrew. Rectifier 2016. nonlinearities improve neural network acoustic models. In Proceedings of The 33rd International Conference on Chen, X., Duan, Y., Houthooft, R., Schulman, J., Machine Learning, 2013. Sutskever, I., and Abbeel, P. InfoGAN: Interpretable Representation Learning by Information Maximizing Mirza, Mehdi and Osindero, Simon. Conditional genera- Generative Adversarial Nets. ArXiv e-prints, June 2016. tive adversarial nets. CoRR, abs/1411.1784, 2014. URL http://arxiv.org/abs/1411.1784. Denton, Emily L., Chintala, Soumith, Szlam, Arthur, and Fergus, Robert. Deep generative image models using Mohamed, Shakir and Lakshminarayanan, Balaji. Learn- a laplacian pyramid of adversarial networks. CoRR, ing in implicit generative models. arXiv preprint abs/1506.05751, 2015. URL http://arxiv.org/ arXiv:1610.03483, 2016. abs/1506.05751. Dinh, Laurent, Sohl-Dickstein, Jascha, and Bengio, Nguyen, Anh Mai, Dosovitskiy, Alexey, Yosinski, Jason, Samy. Density estimation using real NVP. CoRR, Brox, Thomas, and Clune, Jeff. Synthesizing the pre- abs/1605.08803, 2016. URL http://arxiv.org/ ferred inputs for neurons in neural networks via deep abs/1605.08803. generator networks. CoRR, abs/1605.09304, 2016. URL http://arxiv.org/abs/1605.09304. Donahue, J., Kr¨ahenb¨uhl, P., and Darrell, T. Adversarial Feature Learning. ArXiv e-prints, May 2016. Odena, A. Semi-Supervised Learning with Generative Ad- versarial Networks. ArXiv e-prints, June 2016. Dumoulin, V., Belghazi, I., Poole, B., Lamb, A., Arjovsky, M., Mastropietro, O., and Courville, A. Adversarially Odena, Augustus, Dumoulin, Vincent, and Olah, Learned Inference. ArXiv e-prints, June 2016. Chris. Deconvolution and checkerboard artifacts. http://distill.pub/2016/deconv-checkerboard/, 2016. Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Radford, Alec, Metz, Luke, and Chintala, Soumith. Y. Generative Adversarial Networks. ArXiv e-prints, Unsupervised representation learning with deep con- June 2014. volutional generative adversarial networks. CoRR, abs/1511.06434, 2015. URL http://arxiv.org/ Kingma, D. P and Welling, M. Auto-Encoding Variational abs/1511.06434. Bayes. ArXiv e-prints, December 2013. Kingma, Diederik P., Rezende, Danilo Jimenez, Mohamed, Ramsundar, Bharath, Kearnes, Steven, Riley, Patrick, Web- Shakir, and Welling, Max. Semi-supervised learning ster, Dale, Konerding, David, and Pande, Vijay. Mas- with deep generative models. CoRR, abs/1406.5298, sively multitask networks for drug discovery. In Pro- 2014. URL http://arxiv.org/abs/1406. ceedings of The 33rd International Conference on Ma- 5298. chine Learning, 2016. Kingma, Diederik P., Salimans, Tim, and Welling, Max. Reed, Scott, Akata, Zeynep, Mohan, Santosh, Tenka, Improving variational inference with inverse autoregres- Samuel, Schiele, Bernt, and Lee, Honglak. Learn- sive flow. CoRR, abs/1606.04934, 2016. URL http: ing what and where to draw. arXiv preprint //arxiv.org/abs/1606.04934. arXiv:1610.02454, 2016a. 

10 . Conditional Image Synthesis with Auxiliary Classifier GANs Reed, Scott, Akata, Zeynep, Yan, Xinchen, Logeswaran, Toderici, George, Vincent, Damien, Johnston, Nick, Lajanugen, Schiele, Bernt, and Lee, Honglak. Gener- Hwang, Sung Jin, Minnen, David, Shor, Joel, and Cov- ative adversarial text-to-image synthesis. In Proceed- ell, Michele. Full resolution image compression with re- ings of The 33rd International Conference on Machine current neural networks. CoRR, abs/1608.05148, 2016. Learning, 2016b. URL http://arxiv.org/abs/1608.05148. Rezende, D. and Mohamed, S. Variational Inference with Uehara, M., Sato, I., Suzuki, M., Nakayama, K., and Mat- Normalizing Flows. ArXiv e-prints, May 2015. suo, Y. Generative Adversarial Nets from a Density Ratio Estimation Perspective. ArXiv e-prints, October Rezende, D., Mohamed, S., and Wierstra, D. Stochas- 2016. tic Backpropagation and Approximate Inference in Deep Generative Models. ArXiv e-prints, January 2014. van den Oord, A¨aron, Kalchbrenner, Nal, and Kavukcuoglu, Koray. Pixel recurrent neural net- Ronneberger, Olaf, Fischer, Philipp, and Brox, Thomas. U- works. CoRR, abs/1601.06759, 2016a. URL net: Convolutional networks for biomedical image seg- http://arxiv.org/abs/1601.06759. mentation. CoRR, abs/1505.04597, 2015. URL http: //arxiv.org/abs/1505.04597. van den Oord, A¨aron, Kalchbrenner, Nal, Vinyals, Oriol, Espeholt, Lasse, Graves, Alex, and Kavukcuoglu, Ko- Russakovsky, Olga, Deng, Jia, Su, Hao, Krause, Jonathan, ray. Conditional image generation with pixelcnn de- Satheesh, Sanjeev, Ma, Sean, Huang, Zhiheng, Karpa- coders. CoRR, abs/1606.05328, 2016b. URL http: thy, Andrej, Khosla, Aditya, Bernstein, Michael, Berg, //arxiv.org/abs/1606.05328. Alexander C., and Fei-Fei, Li. ImageNet Large Scale Visual Recognition Challenge. International Journal of Wang, Zhou, Bovik, Alan C, Sheikh, Hamid R, and Si- Computer Vision (IJCV), 115(3):211–252, 2015. doi: moncelli, Eero P. Image quality assessment: from error 10.1007/s11263-015-0816-y. visibility to structural similarity. IEEE transactions on image processing, 13(4):600–612, 2004a. Salimans, T., Goodfellow, I., Zaremba, W., Cheung, V., Radford, A., and Chen, X. Improved Techniques for Wang, Zhou, Simoncelli, Eero P, and Bovik, Alan C. Multi- Training GANs. ArXiv e-prints, June 2016. scale structural similarity for image quality assessment. In Signals, Systems and Computers, 2004. Conference Simoncelli, Eero and Olshausen, Bruno. Natural image Record of the Thirty-Seventh Asilomar Conference on, statistics and neural representation. Annual Review of volume 2, pp. 1398–1402. Ieee, 2004b. Neuroscience, 24:1193–1216, 2001. Springenberg, J. T. Unsupervised and Semi-supervised Learning with Categorical Generative Adversarial Net- works. ArXiv e-prints, November 2015. Sutskever, Ilya, Vinyals, Oriol, and V., Le Quoc. Sequence to sequence learning with neural networks. In Neural Information Processing Systems, 2014. Szegedy, Christian, Liu, Wei, Jia, Yangqing, Sermanet, Pierre, Reed, Scott E., Anguelov, Dragomir, Erhan, Dumitru, Vanhoucke, Vincent, and Rabinovich, An- drew. Going deeper with convolutions. CoRR, abs/1409.4842, 2014. URL http://arxiv.org/ abs/1409.4842. Szegedy, Christian, Vanhoucke, Vincent, Ioffe, Sergey, Shlens, Jonathon, and Wojna, Zbigniew. Rethinking the inception architecture for computer vision. CoRR, abs/1512.00567, 2015. URL http://arxiv.org/ abs/1512.00567. Theis, L., van den Oord, A., and Bethge, M. A note on the evaluation of generative models. ArXiv e-prints, Novem- ber 2015. 

11 . Conditional Image Synthesis with Auxiliary Classifier GANs A. Hyperparameters We summarize hyperparameters used for the ImageNet model in Table 1 and for the CIFAR-10 model in Table 2. Operation Kernel Strides Feature maps BN? Dropout Nonlinearity Gx (z) – 110 × 1 × 1 input Linear N/A N/A 768 × √ 0.0 ReLU Transposed Convolution 5×5 2×2 384 √ 0.0 ReLU Transposed Convolution 5×5 2×2 256 √ 0.0 ReLU Transposed Convolution 5×5 2×2 192 0.0 ReLU Transposed Convolution 5×5 2×2 3 × 0.0 Tanh D(x) – 128 × 128 × 3 input Convolution 3×3 2×2 16 × √ 0.5 Leaky ReLU Convolution 3×3 1×1 32 √ 0.5 Leaky ReLU Convolution 3×3 2×2 64 √ 0.5 Leaky ReLU Convolution 3×3 1×1 128 √ 0.5 Leaky ReLU Convolution 3×3 2×2 256 √ 0.5 Leaky ReLU Convolution 3×3 1×1 512 0.5 Leaky ReLU Linear N/A N/A 11 × 0.0 Soft-Sigmoid Optimizer Adam (α = 0.0002, β1 = 0.5, β2 = 0.999) Batch size 100 Iterations 50000 Leaky ReLU slope 0.2 Weight, bias initialization Isotropic gaussian (µ = 0, σ = 0.02), Constant(0) Table 1. ImageNet hyperparameters. A Soft-Sigmoid refers to an operation over K +1 output units where we apply a Softmax activation to K of the units and a Sigmoid activation to the remaining unit. We also use activation noise in the discriminator as suggested in (Salimans et al., 2016). 

12 . Conditional Image Synthesis with Auxiliary Classifier GANs Operation Kernel Strides Feature maps BN? Dropout Nonlinearity Gx (z) – 110 × 1 × 1 input Linear N/A N/A 384 × √ 0.0 ReLU Transposed Convolution 5×5 2×2 192 √ 0.0 ReLU Transposed Convolution 5×5 2×2 96 0.0 ReLU Transposed Convolution 5×5 2×2 3 × 0.0 Tanh D(x) – 32 × 32 × 3 input Convolution 3×3 2×2 16 × √ 0.5 Leaky ReLU Convolution 3×3 1×1 32 √ 0.5 Leaky ReLU Convolution 3×3 2×2 64 √ 0.5 Leaky ReLU Convolution 3×3 1×1 128 √ 0.5 Leaky ReLU Convolution 3×3 2×2 256 √ 0.5 Leaky ReLU Convolution 3×3 1×1 512 0.5 Leaky ReLU Linear N/A N/A 11 × 0.0 Soft-Sigmoid Generator Optimizer Adam (α = [0.0001, 0.0002, 0.0003], β1 = 0.5, β2 = 0.999) Discriminator Optimizer Adam (α = [0.0001, 0.0002, 0.0003], β1 = 0.5, β2 = 0.999) Batch size 100 Iterations 50000 Leaky ReLU slope 0.2 Activation noise standard deviation [0, 0.1, 0.2] Weight, bias initialization Isotropic gaussian (µ = 0, σ = 0.02), Constant(0) Table 2. CIFAR-10 hyperparameters. When a list is given for a hyperparameter it means that we performed a grid search using the values in the list. For each set of hyperparameters, a single AC-GAN was trained on the whole CIFAR-10 dataset. For each AC-GAN that was trained, we split up the samples into groups so that we could give some sense of the variance of the Inception Score. To the best of our knowledge, this is identical to the analysis performed in (Salimans et al., 2016).