Active Mini-Batch Sampling using Repulsive Point Processes

1 . Active Mini-Batch Sampling using Repulsive Point Processes ¨ Cheng Zhang 1 2 Cengiz Oztireli 3 Stephan Mandt 4 Giampiero Salvi 5 Abstract noise allows for larger learning rates and therefore faster convergence. For this reason, variance reduction for SGD is The convergence speed of stochastic gradient de- an active research topic. scent (SGD) can be improved by actively select- arXiv:1804.02772v1 [stat.ML] 8 Apr 2018 ing mini-batches. We explore sampling schemes Several recent works have shown that the variance of SGD where similar data points are less likely to be se- can be reduced when diversifying the data points in a mini- lected in the same mini-batch. In particular, we batch based on their features (Zhao & Zhang, 2014; Fu & prove that such repulsive sampling schemes low- Zhang, 2017; Zhang et al., 2017b). When data points are ers the variance of the gradient estimator. This coming from similar regions in feature space, their gradient generalizes recent work on using Determinantal contributions are positively correlated. Diversifying data Point Processes (DPPs) for mini-batch diversifi- points by sampling from different regions in feature space cation (Zhang et al., 2017) to the broader class de-correlates their gradient contributions, which leads to a of repulsive point processes. We first show that better gradient estimation. the phenomenon of variance reduction by diver- Another benefit of biasing the mini-batch sampling proce- sified sampling generalizes in particular to non- dure actively relates to better model performance (Chang stationary point processes. We then show that et al., 2017; Shrivastava et al., 2016; Zhang et al., 2017b). other point processes may be computationally Zhang et al. (2017b) biased the data towards a more uniform much more efficient than DPPs. In particular, we distribution, upsampling data-points in scarce regions and propose and investigate Poisson Disk sampling— downsampling data points in dense regions, leading to a frequently encountered in the computer graphics better performance during test time. Chen & Gupta (2015) community—for this task. We show empirically showed that training on simple classification tasks first, and that our approach improves over standard SGD later adding more difficult examples, leads to a clear perfor- both in terms of convergence speed as well as mance improvement compared to training on all examples final model performance. simultaneously. We refer to such schemes which modify the marginal probabilities of each data point to be selected 1 Introduction as active bias. The above results suggest that utilizing an Stochastic gradient descent (SGD) (Bottou, 2010) is key to active bias in mini-batch sampling can result in improved modern scalable machine learning. Combined with back- performance without additional computational cost. propagation, it forms the foundation to train deep neural In this work, we present a framework for active mini-batch networks (LeCun et al., 1998b). Applied to variational sampling based on repulsive point processes. The idea is inference (Hoffman et al., 2013; Zhang et al., 2017a), it simple: we specify a data selection mechanism that ac- enables the use of probabilistic graphical models on massive tively selects a mini-batch based on features of the data. data. SGD training has contributed to breakthroughs in This mechanism mimics repulsion between the data points, image classification (Krizhevsky et al., 2012) and learning meaning that it suppresses data points with similar features word-embeddings (Mikolov et al., 2013), among others. to co-occur in the same mini-batch. We use repulsive point A key limitation for the speed of convergence of SGD al- processes for this task. Finally, the chosen mini-batch is gorithms is the stochastic gradient noise. Smaller gradient used to perform a stochastic gradient step, and this scheme is repeated until convergence. 1 Microsoft Research, Cambridge, UK 2 This work was initial- ized when the author was at Disney Research, and was carried out Our framework generalizes the recently proposed mini- when the author was at KTH. 3 Disney Research, Zurich, Switzer- batch diversification based on determinantal point processes land 4 Disney Research, Los Angeles, USA 5 KTH Royal Institute (DPP) (Zhang et al., 2017b) to a much broader class of re- of Technology, Stockholm, Sweden. Correspondence to: Cheng pulsive processes, and allows users to encode any preferred Zhang <Cheng.Zhang@microsoft.com>. active bias with efficient mini-batch sampling algorithms. In more detail, our contributions are as follows: 

2 . Active Mini-Batch Sampling using Repulsive Point Processes 1. We propose to use point processes for active mini-batch Active Bias Different types of active bias in subsampling selection (Section 3). the data can improve the convergence and lead to improved • We provide a theoretical analysis which shows final performance in model training (Alain et al., 2015; that mini-batch selection with repulsive point pro- Gopal, 2016; Chang et al., 2017; Chen & Gupta, 2015; cesses may reduce the variance of stochastic gra- Shrivastava et al., 2016). As summarized in (Chang et al., dient descent. This is a strict generalization of 2017), self-paced learning biases towards easy examples in recent work which uses DPP for this task. the early learning phase. Active-learning, on the other hand, puts more emphasis on uncertain cases, and hard example • The proposed approach can accommodate point mining focuses on the difficult-to-classify examples. processes with adaptive densities and adaptive pair-wise correlations. Thus, we can use it for Chang et al. (2017) investigate a supervised setup and sam- data subsampling with an active bias. ple data points more often which have a high prediction 2. Going beyond DPPs, we propose a group of more variance. Gopal (2016) maintain a desired class distribution efficient repulsive point processes based on Poisson during mini-batch sampling. Diversified mini-batch sam- Disk Sampling (PDS). pling with DPPs (Zhang et al., 2017b) re-weights the data towards a more uniform distribution, which improves the • We propose PDS with dart throwing for mini- final performance when the data set is imbalanced. batch selection. Compared to DPPs, this improves the sampling costs from N k 3 to merely k 2 , where The choice of a good active bias depends on the data set and N is the number of data points and k is the mini- problem at hand. Our proposed method is compatible with batch size (Section 4.1). different active bias preferences. • We propose a dart-throwing method with an adap- tive disk size and adaptive densities to sample Point Processes Point processes have a long history in mini-batches with an active bias (Section 4.2). physics and mathematics, and are heavily used in computer 3. We test our proposed method on several machine learn- graphics (Macchi, 1975; Ripley, 1976; Illian et al., 2008; ing applications (Section 5) from the domains of com- ¨ Oztireli & Gross, 2012; Lavancier et al., 2015). DPPs, as a puter vision (Section 5.2, 5.3) and speech recognition group of point processes, have been introduced and used in (Section 5.4). We find increased model performance the machine learning community in recent years (Kulesza and faster convergence due to variance reduction. et al., 2012; Li et al., 2015; Kathuria et al., 2016). 2 Related Work Other types of point processes have been less explored and In this section, we briefly discuss the most relevant work for used in machine learning. There are many different repul- our proposed active mini-batch sampling method with point sive point processes, such as PDS, or Gibbs processes, with processes. We begin with reviewing the most relevant work properties similar to DPPs, but with significantly higher on diversified mini-batch sampling. Then, we discuss the sampling efficiency (Illian et al., 2008). Additionally, more benefits of subsampling schemes with an active bias, where flexible point processes with adaptive densities and interac- data are either reweighed or re-ordered. Finally, we shortly tions are well studied in computer graphics (Li et al., 2010; review the relevant aspects of point processes. Roveri et al., 2017; Kita & Miyata, 2016), but not explored much in the machine learning community. Our proposed Diversified Mini-Batch Sampling Prior research (Zhao framework is based on generic point processes. As one of & Zhang, 2014; Fu & Zhang, 2017; Zhang et al., 2017b; the most efficient repulsive point processes, we advocate Yin et al., 2017) has shown that sampling diversified mini- Poisson disk sampling in this paper. batches can reduce the variance of stochastic gradients. It is also the key to overcome the problem of the saturation of the convergence speed in the distributed setting (Yin et al., 3 Repulsive Point Processes for Variance 2017). Diversifying the data is also computationally ef- Reduction ficient for large-scale learning problems (Zhao & Zhang, 2014; Fu & Zhang, 2017; Zhang et al., 2017b). In this section, we first briefly introduce our main idea of Zhang et al. (2017b) recently proposed to use DPPs for di- using point processes for mini-batch sampling in the con- versified mini-batch sampling and drew the connection to text of the problem setting (Section 3.1) and revisit point stratified sampling (Zhao & Zhang, 2014) and clustering- processes (Section 3.2). We prove that any repulsive point based preprocessing for SGD (Fu & Zhang, 2017). A disad- process can lead to reduced gradient variances in SGD (Sec- vantage of the DPP-approach is the computational overhead. tion 3.3). Finally, we discuss the benefits of our general Besides presenting a more general theory, we provide more framework (Section 3.4). The theoretical analysis in this efficient point processes in this work. section leads to multiple practical algorithms in Section 4. 

3 . Active Mini-Batch Sampling using Repulsive Point Processes 3.2 Background on Point Processes Point processes are generative processes of collections of points in some measure space (Møller & Waagepetersen, 2004; Illian et al., 2008). They can be used to sample sub- (a) Non-Repulsive (b) Stationary (c) Non-Stationary sets of data with various properties, either from continuous spaces or from discrete sets, such as a finite dataset. In Figure 1. Examples of sampling a subset of data points. We sam- this paper, we explore different point processes to sample pled different subsets of 100 points (dark green) from a bigger set of points (light blue), using three different point processes. Panel mini-batches with different statistical properties. 1(a) shows a uniformly sampled subset. Panel 1(b) and panel 1(c) More formally, a point process P in Rd can be defined by show two examples with different repulsive point processes. considering the joint probabilities of finding points gener- 3.1 Problem Setting ated by this process in infinitesimal volumes. One way to express these probabilities is via product densities. Let xi Consider a loss function (x, θ), where θ are the model denote some arbitrary points in Rd , and Bi infinitesimal parameters, and x indicates the data. In this paper, we spheres centered at these points with volumes dxi = |Bi |. consider a modified empirical risk minimization problem Then the nth order product density (n) is defined by of the following kind, which generalize the diversified risk (n) p(x1 , · · · , xn ) = (x1 , · · · , xn )dx1 · · · dxn , from (Zhang et al., 2017b): where p(x1 , · · · , xn ) is the joint probability of having a ˆ = Exˆ ∼P [ (ˆ point of the point process P in each of the infinitesimal J(θ) x, θ)], (1) spheres Bi . We can use P to generate infinitely many point configurations, each corresponding to e.g. a mini-batch. P indicates a point process defining a distribution over sub- ˆ of the data, which will be specified below. Note that sets x For example, DPP defines this probability of sampling a this leads to a potentially biased version of the standard subset as being proportional to the determinant of a ker- empirical risk (Bottou, 2010). nel matrix. It is thus described by the nth order prod- uct density (Lavancier et al., 2012): (n) (x1 , · · · , xn ) = SGD is the most common training paradigm in scalable det[C](x1 , · · · , xn ), where det[C](x1 , · · · , xn ) is the de- machine learning. The parameter updates for minimizing terminant of the n × n sized sub-matrix of kernel matrix C Eq. 1 using SGD are with entries specified by x1 , · · · , xn . ˆ θt+1 = θt − ρt G For our analysis, we will just need the first and second = θt − 1 ρt |B| ∇ (xi , θ), B ∼ P, (2) order product density, which are commonly denoted by i∈B λ(x) := (1) (x), (x, y) := (2) (x, y). An important spe- cial case of point processes is stationary processes. For such where, B ⊂ {1, . . . , N }, a set of data indices that define the processes, the point distributions generated are translation mini-batch. G ˆ is the estimated gradient from a mini-batch. invariant, where the intensity is a constant. In contrast to standard SGD, we sample the data points not necessarily uniformly. 3.3 Point Processes for Active Mini-Batch Sampling Our scheme generalizes SGD in that the mini-batch B is Recently, Zhang et al. (2017b) investigated how to utilize selected actively. The data points chosen for each mini-batch a particular type of point process, DPP, for mini-batch di- can be considered as drawn from a point process P, which versification. Here, we generalize the theoretical results to defines probability measures over different mini-batches. arbitrary point processes, and elaborate on how the resulting Hence, each set of points B has a certain probability given formulations can be utilized for SGD based algorithms. This by P, as we will elaborate on in the next section. opens the door to exploiting a vast literature on the theory of point processes, and efficient algorithms for sampling. Figure 1 shows examples of subsets selection using differ- ent point processes. Drawing the data randomly without SGD-based algorithms commonly estimate the gradient of replacement corresponds to a point process as well, thus the objective using mini-batches of data (Section 3.1). Each standard SGD trivially belongs to the formulation above. batch, i.e. set of data points, can thus be considered as In this paper, we investigate a class of algorithms that ac- a sampled instance of an underlying point process P that tively sample mini-batches using various point processes. depends on the empirical distribution of the data, as well We explore how different point processes enable us to im- as the sampling algorithm. Our goal is to design sampling prove model performance in SGD by controlling the bias algorithms for improved learning performance by altering and variance in this estimator for the gradient. ˆ the bias and variance of the gradient estimate G(θ). 

4 . Active Mini-Batch Sampling using Repulsive Point Processes Theoretical Variance for SGD A main result of this work Figure 2. Demonstration of PDS. is the following expression for the variance of the gradient ˆ The black circles of a certain ra- estimate G(θ), derived by utilizing the theory of stochastic dius r mark regions claimed by point processes as we show in Appendix A: the collected points (red). For the 1 next iteration, if the newly sam- ˆ = varP (G) λ(x)λ(y)g(x, θ)T g(y, θ) k2 pled point falls in any of the cir- V×V cles (points colored in gray), this (x, y) point will be rejected. Otherwise, − 1 dxdy (3) λ(x)λ(y) accept. 1 + g(x, θ) 2 λ(x)dx. k2 V Here, g(x, θ) := ∇ (x, θ) is the gradient of the loss func- tion, and we assume a continous underlying space. This equation holds for general point processes with possi- bly complex interactions among points. For a sampler with factorized two-point correlation (x, y) = λ(x)λ(y), the (a) DPP (b) Poisson Disk first term vanishes. The second term is thus the variance for the case of a random sampler that samples data points Figure 3. Sampling on imbalanced dataset. We compare the sam- according to the density given by λ(x). A possible variance pling marginal probability using the toy dataset as shown in Figure reduction is therefore induced by the first term. We assume 2. The Panel (a) shows the marginal probability using DPP, and Panel (b) shows the simulated marginal probability with PDS. that the gradients are aligned, that is g(x, θ)T g(y, θ) > 0, when the data points are close to each other. This should density and alter the pair-wise interactions to encode our always be satisfied when the loss function is continuous and preference. Repulsive sampling leads to a more uniform smooth as a function of x. Repulsive point processes reduce selection of points in feature space, which may make an im- the probability to select points that are close to each other, balanced data set more balanced. Using non-stationary point (x,y) making λ(x)λ(y) − 1 < 0. In this case, the first term in processes, we can then encode our density preference for, Equation 3 is negative, leading to a reduced variance. e.g., decision boundaries. In the next section, we propose practical algorithms utilizing these benefits. 3.4 Implications for SGD 4 Poisson Disk Sampling for Active This proposed theory allows us to use any point process for mini-batch sampling, such as DPP, finite Gibbs processes, Mini-batch Sampling Poisson disk sampling (PDS), and many more (Illian et al., We adapt efficient dart throwing algorithms for fast mini- 2008). It thus offers many new directions of possible im- batch sampling. Firstly, we show how to use PDS with provement. dart throwing to sample diversified mini-batches (Section We can choose point processes with a different degree of re- 4.1) rather than using DPP. In general, we can simulate all pulsion, and computational efficiency, because any repulsive stochastic point processes with generalized dart throwing point process is able to reduce the gradient variance under ¨ and statistics, as shown in (Oztireli & Gross, 2012). the assumption that similar points have aligned gradients. Secondly, we present a dart throwing algorithm with an As discussed in (Biscio et al., 2016), DPP is a powerful adaptive disk size and an adaptive density (Section 4.2). point process that can obtain strong global repulsions, but For supervised setups, we shrink the disc size towards the it cannot achieve as high local repulsion as Poisson disc decision boundary, using the concept of the mingling in- sampling, which we will introduce in the next section. dex (Illian et al., 2008). This biases learning towards hard However, in a supervised learning setting, the gradients can examples and improves classification accuracies. change drastically around the decision boundaries. In this case, our assumption does not hold when points are simi- 4.1 Stationary Poisson Disk Sampling lar but close to the decision boundary. With the proposed PDS is one type of repulsive point process. It demonstrates framework, we can explore point processes that only repulse stronger local repulsion compared to DPP (Biscio et al., when the points are far from decision boundaries, which 2016). Typically, it is implemented with the efficient dart may further reduce the variance of stochastic gradients. throwing algorithm (Lagae & Dutr´e, 2008), and provides In general, our analysis does not enforce any assumptions point arrangements similar to those of DPP, albeit much on the point processes used. We are thus able to adapt the more efficiently. 

5 . Active Mini-Batch Sampling using Repulsive Point Processes This process dictates that the smallest distance between each pair of sample points should be at least r with respect Algorithm 1. Draw throwing for Dense PDS to some distance measure D. The second order product Input: data x, mini-batch size S, mingling index M density ρ(x, y) for PDS is zero when the distance between for all data, the parameter for categorical distribution to two points are smaller than the disk radius ||x − y|| ≤ r, sample mingling index π, disk radius r0 and converges to ρ(x, y) = λ(x)λ(y) when the two points repeat ¨ are far away (Oztireli & Gross, 2012). This makes PDS a sample a mingling index m ∼ Cat(π) (x,y) repulsive process. Thus, λ(x)λ(y) − 1 = −1 < 0 when randomly sample a point i with mingling index m if xi is not in disk of any samples then (x,y) the points are within distance r, and λ(x)λ(y) −1 = 0 insert xi to B when the points are far away. end if until S points have been accepted for the mini-batch The basic dart throwing algorithm for PDS works as follows in each iteration: 1) randomly sample a data point; 2) if it is within a distance r of any already accepted data point, reject; otherwise, accept the new point. We can also specify Depending on the mingling index, there are three different ¯ K (xi ) = 0, the region around xi situations. Firstly, if M the maximum sampling size k. This means that we termi- nate the algorithm when k points have been collected. The only includes points from the same class. This makes xi computational complexity using PDS with dart throwing1 a relatively easy point to classify. This type of points is is O(k 2 ). This is much lower than the complexity O(N k 3 ) preferred to be sampled in the early iterations for self-paced learning. Secondly, if M¯ K (xi ) > 0, this point may be close for k-DPP, where N is the number of data points in the dataset. Figure 2 demonstrates the resulting algorithm of to a decision boundary. For variance reduction, we do not using dart throwing with discrete data. In the rest of the need to repulse this type of points. Additionally, sampling paper, we refer to this version of PDS as “Vanilla PDS”. this type of points more often may help the model to refine the decision boundaries. Finally, if M ¯ K (xi ) is very high, We use a toy example shown in Figure 3 to compare DPP the point is more likely to be a hard negative. In this case, and Vanilla PDS. Figure 3(a) shows the marginal probabil- the point is mostly surrounded by points from other classes. ity of each point being sampled with DPP by means of the size of the circle. Similarly, Figure 3(b) shows the simu- Variances of Poisson Disk Sampling Utilizing the min- lated marginal probability of each data point being sampled gling index, we further explore the potential benefit of our using PDS. We can see that Vanilla PDS generates sam- method as discussed in the end of Section 3. plings similar to those with DPP. They both balance the Gradients are not necessarily aligned when points are close datasets. We show more examples on sampled mini-batches to decision boundaries. Our first simple extension, that we in Appendix B. call “Easy PDS”, sets the disk radius to r0 when the point 4.2 Poisson Disk Sampling with Adaptive Density has a mingling index Mxi = 0, while setting disk radius to 0 if Mxi > 0. Thus, only easy points (with Mxi = 0) re- To further utilize the potential benefit of our framework, we pulse. If we sample many points, “Easy PDS” is expected to propose several variations of PDS. As an example, we use sample more difficult points compared with “Vanilla PDS”. a mingling index utilizing the marker (for example class labels). We then propose: Easy PDS, where only points far For many tasks, when the data is highly structured, there are away from decision boundaries repulse, and Dense PDS, only few data points that are close to the decision boundary. where we can utilize preferences of point densities. To refine the decision boundary, inspired by hard example mining, points with a high mingling index are preferred to Mingling Index For data with markers, the mingling index be sampled more often. We thus propose the “Dense PDS” ¯ K (xi ) is defined as (Illian et al., 2008): M method summarized in Algorithm 1. Instead of drawing K darts randomly, we draw darts based on different mingling ¯ K (xi ) = 1 M 1 m(xi ) = m(xj ) , (4) indices. The mingling indices can assume K + 1 values, K j=1 where K is the number of nearest neighbors. We thus can where m(xi ) indicates the mark of the point xi . In case of specify a parameter π for a categorical distribution to sample a classification task, the mark is the class label of the point. mingling indices first. Then we randomly sample a dart M¯ K (xi ) is the ratio of points with different marks than xi which has the given mingling index. In this way, we can among its K nearest neighbors. encode our preferred density with respect to mingling index. 1 In practice, the number of accepted points can be smaller than It is straightforward to introduce an annealing mechanism the number of considered points in the dataset, as some of them in Dense PDS by using a different πn at each iteration n. will be eliminated by not satisfying the distance criteria. Inspired by self-paced learning, we can give higher density 

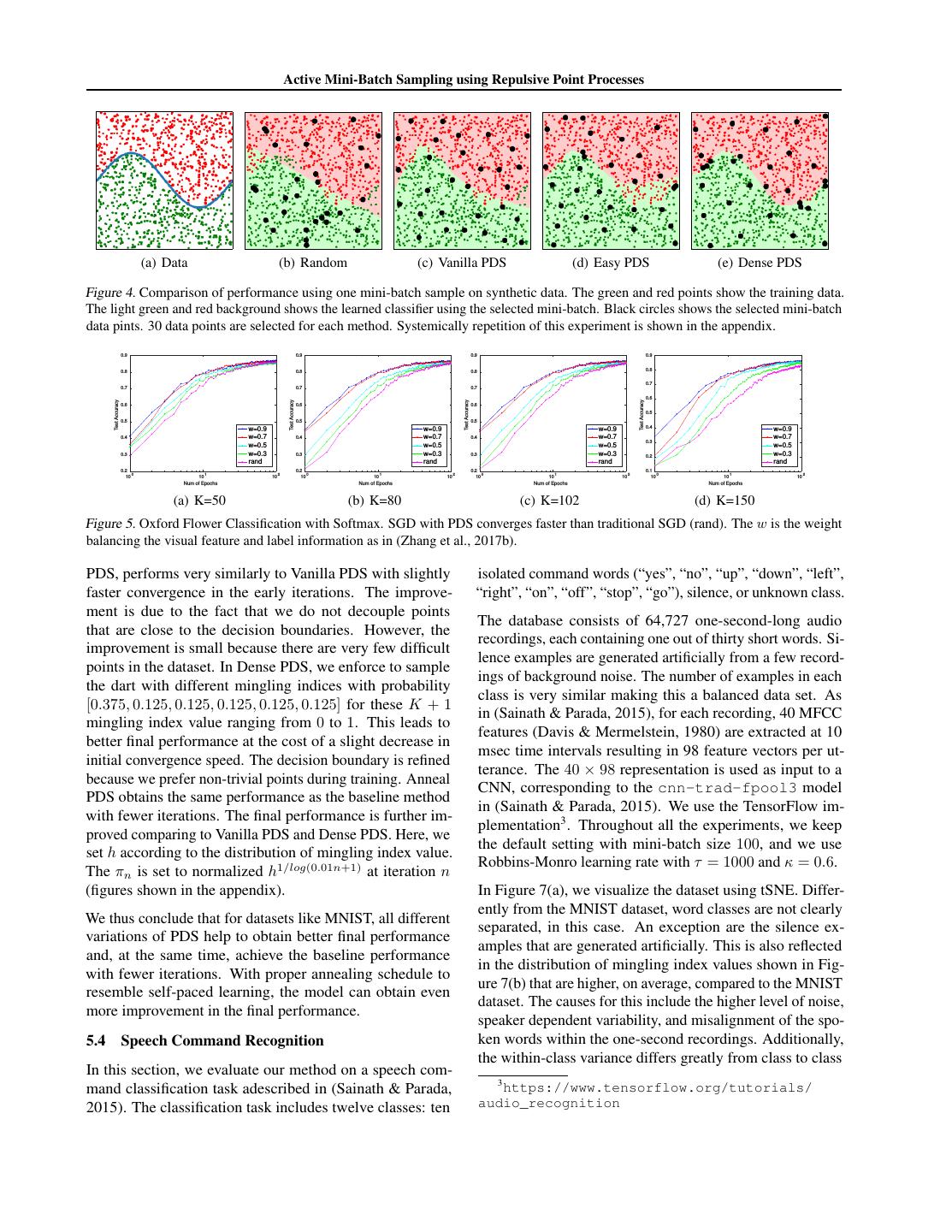
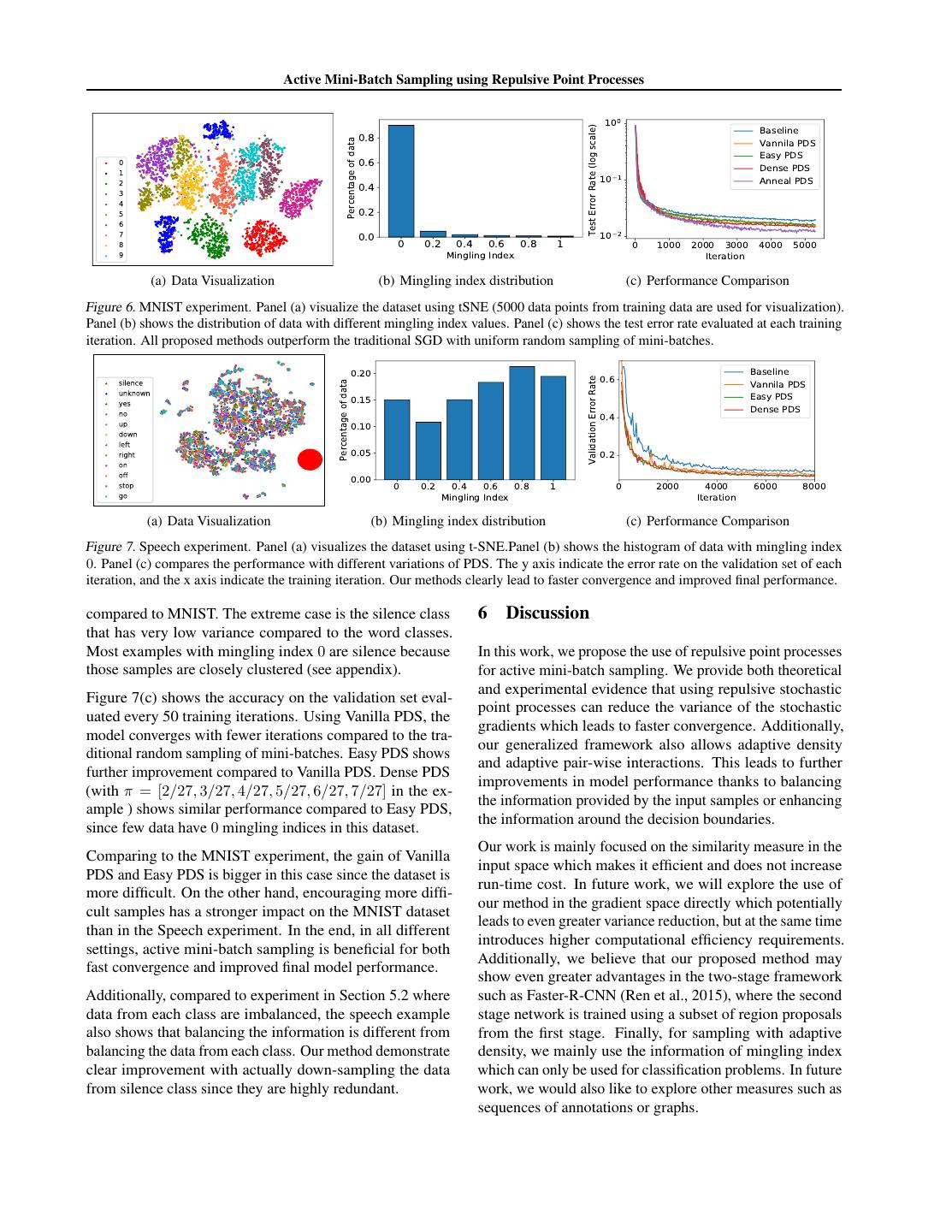
6 . Active Mini-Batch Sampling using Repulsive Point Processes to points with low mingling index in the early iterations, k 50 80 102 150 and slowly increase the density of points with high mingling k-DPP time 7.1680 29.687 58.4086 189.0303 index. We refer this method as “Anneal PDS”. Fast k-DPP 0.1032 0.3312 0.6512 1.8745 Poisson Disk 0.0461 0.0795 0.1048 0.1657 Note that our proposed method only relies on the properties of the given data instead of any model parameter. Thus, it Table 1. CPU time (sec) to sample one mini-batch. can be easily used as a pre-processing step or be parallelized from the training procedure of the specific model. with the mingling index of the points. We can see that points close to the decision boundary do not repulse. This leads 5 Experiments to potentially a more refined decision boundary comparing to Figure 4(c). Finally, Dense PDS, shown in Figure 4(e), We evaluate the performance of the proposed method in chooses more samples close to the boundary and leads to the various application scenarios showing clear improvements most precise decision boundary with a single mini-batch. compared to baseline methods in each case. We first demonstrate the behaviors of different varieties of 5.2 Oxford Flower our method using a synthetic dataset in Section 5.1. Sec- In this experiment, we evaluate the performance of our ondly, we perform the same experiment as (Zhang et al., approach on the fine-grained classification task as in (Zhang 2017b) for fine grid classification (Section 5.2). This ex- et al., 2017b) with the same experimental setting. Our goal periment shows that PDS can achieve the same behavior as is to demonstrate that vanilla PDS is able to achieve similar DPP, but with significantly improved sampling efficiency. performance as DPP but with significant improvement on Finally, we evaluate our method on two tasks with very dif- sampling efficiency. The minimum radius r is set to half of ferent properties: The first domain is image classification the median value of the distance measure D for PDS. with MNIST (Section 5.3), where the data from each class are well clustered, and the variance of data in each class is Figure 5 shows the test accuracy at the end of each epoch similar. The second domain is speech command recognition and proves that PDS leads to the same effect as DPP (for (Section 5.4). Here, data from different classes are not very references, we enclose the results from (Zhang et al., 2017b) well separated, at the same time, the within-class variance in the appendix). However, as demonstrated by Table 1, for different classes differs greatly. For both tasks, our ap- sampling using PDS is significantly faster than traditional proach shows improvements in the convergence speed and DPP (Kulesza et al., 2012), and fast k-DPP (Li et al., 2015), in the final performance compared to traditional SGD where used in the larger scale experiment in (Zhang et al., 2017b). mini-batches are sampled uniformly. 5.3 MNIST 5.1 Synthetic Data In this section we show results for hand-written digit clas- We evaluate our methods on two-dimensional synthetic sification on the MNIST dataset (LeCun et al., 1998a). We datasets to illustrate the behavior of different sampling strate- use half of the training data and the full test data. Figure 6(a) gies. Figure 4(a) shows two classes (green and red dots) visualizes the dataset using tSNE (Maaten & Hinton, 2008) separated by a wave-shaped (sine curve) decision boundary. and shows that data points from each class are well clus- tered. Thus, most data points have mingling index 0 (easy We sample one mini-batch with batch size 30 using different to classify) and only around 10% of the data have non-zero sampling methods (black circles in Figure 4(b) through 4(e)). mingling index as shown in Figure 6(b). For each method, we train a neural network classifier with one hidden layer of five units, using a single mini-batch. A standard multi-layer convolutional neural network (CNN) This model, albeit simple, is sufficient to handle the non- from tensorflow2 is used in this experiment. We use mini- linear decision boundary in the example. To visualize the batch size 100; Robbins-Monro learning rate r = (τ +n)−κ learned decision boundary, we generate test data in a dense with τ = 100 and κ = 0.6 throughout all the experiments. grid and color the prediction results. The 1 − cosine similarity is used to compute the distance, and disk radius r = 0.3 is used in the experiment. Figure 4(b) shows the result of random sampling. We can see that the mini-batch is not a good representation of the Figure 6(c) shows the test error rate evaluated after each original dataset as some random regions are more densely SGD training iteration for different mini-batch sampling or sparsely sampled. Consequently, the learned decision methods. All active sampling methods with PDS lead to boundary is very different from the ground truth. Figure 4(c) improved final performance compared to traditional SGD. shows Vanilla PDS. Because of the repulsive effect, the Vanilla PDS clearly outperforms the baseline method. Easy sampled points cover the data space more uniformly and the decision boundary is improved compared to Figure 4(b). In 2 https://www.tensorflow.org/versions/r0. Figure 4(d), we used Easy PDS, where the disk radius adapts 12/tutorials/mnist/pros/ 

7 . Active Mini-Batch Sampling using Repulsive Point Processes (a) Data (b) Random (c) Vanilla PDS (d) Easy PDS (e) Dense PDS Figure 4. Comparison of performance using one mini-batch sample on synthetic data. The green and red points show the training data. The light green and red background shows the learned classifier using the selected mini-batch. Black circles shows the selected mini-batch data pints. 30 data points are selected for each method. Systemically repetition of this experiment is shown in the appendix. 0.9 0.9 0.9 0.9 0.8 0.8 0.8 0.8 0.7 0.7 0.7 0.7 0.6 Test Accuracy Test Accuracy Test Accuracy Test Accuracy 0.6 0.6 0.6 0.5 0.5 0.5 0.5 w=0.9 w=0.9 w=0.9 0.4 w=0.9 0.4 w=0.7 0.4 w=0.7 0.4 w=0.7 w=0.7 0.3 w=0.5 w=0.5 w=0.5 w=0.5 0.3 w=0.3 0.3 w=0.3 0.3 w=0.3 0.2 w=0.3 rand rand rand rand 0.2 0.2 0.2 0.1 10 0 10 1 10 2 10 0 10 1 10 2 10 0 10 1 10 2 10 0 10 1 10 2 Num of Epochs Num of Epochs Num of Epochs Num of Epochs (a) K=50 (b) K=80 (c) K=102 (d) K=150 Figure 5. Oxford Flower Classification with Softmax. SGD with PDS converges faster than traditional SGD (rand). The w is the weight balancing the visual feature and label information as in (Zhang et al., 2017b). PDS, performs very similarly to Vanilla PDS with slightly isolated command words (“yes”, “no”, “up”, “down”, “left”, faster convergence in the early iterations. The improve- “right”, “on”, “off”, “stop”, “go”), silence, or unknown class. ment is due to the fact that we do not decouple points The database consists of 64,727 one-second-long audio that are close to the decision boundaries. However, the recordings, each containing one out of thirty short words. Si- improvement is small because there are very few difficult lence examples are generated artificially from a few record- points in the dataset. In Dense PDS, we enforce to sample ings of background noise. The number of examples in each the dart with different mingling indices with probability class is very similar making this a balanced data set. As [0.375, 0.125, 0.125, 0.125, 0.125, 0.125] for these K + 1 in (Sainath & Parada, 2015), for each recording, 40 MFCC mingling index value ranging from 0 to 1. This leads to features (Davis & Mermelstein, 1980) are extracted at 10 better final performance at the cost of a slight decrease in msec time intervals resulting in 98 feature vectors per ut- initial convergence speed. The decision boundary is refined terance. The 40 × 98 representation is used as input to a because we prefer non-trivial points during training. Anneal CNN, corresponding to the cnn-trad-fpool3 model PDS obtains the same performance as the baseline method in (Sainath & Parada, 2015). We use the TensorFlow im- with fewer iterations. The final performance is further im- plementation3 . Throughout all the experiments, we keep proved comparing to Vanilla PDS and Dense PDS. Here, we the default setting with mini-batch size 100, and we use set h according to the distribution of mingling index value. Robbins-Monro learning rate with τ = 1000 and κ = 0.6. The πn is set to normalized h1/log(0.01n+1) at iteration n (figures shown in the appendix). In Figure 7(a), we visualize the dataset using tSNE. Differ- ently from the MNIST dataset, word classes are not clearly We thus conclude that for datasets like MNIST, all different separated, in this case. An exception are the silence ex- variations of PDS help to obtain better final performance amples that are generated artificially. This is also reflected and, at the same time, achieve the baseline performance in the distribution of mingling index values shown in Fig- with fewer iterations. With proper annealing schedule to ure 7(b) that are higher, on average, compared to the MNIST resemble self-paced learning, the model can obtain even dataset. The causes for this include the higher level of noise, more improvement in the final performance. speaker dependent variability, and misalignment of the spo- 5.4 Speech Command Recognition ken words within the one-second recordings. Additionally, the within-class variance differs greatly from class to class In this section, we evaluate our method on a speech com- 3 mand classification task adescribed in (Sainath & Parada, https://www.tensorflow.org/tutorials/ 2015). The classification task includes twelve classes: ten audio_recognition 

8 . Active Mini-Batch Sampling using Repulsive Point Processes 100 Baseline Test Error Rate (log scale) 0.8 Vannila PDS Percentage of data Easy PDS 0 0.6 Dense PDS 1 2 10 1 Anneal PDS 3 0.4 4 5 0.2 6 7 0.0 0 0.2 0.4 0.6 0.8 1 10 2 8 0 1000 2000 3000 4000 5000 9 Mingling Index Iteration (a) Data Visualization (b) Mingling index distribution (c) Performance Comparison Figure 6. MNIST experiment. Panel (a) visualize the dataset using tSNE (5000 data points from training data are used for visualization). Panel (b) shows the distribution of data with different mingling index values. Panel (c) shows the test error rate evaluated at each training iteration. All proposed methods outperform the traditional SGD with uniform random sampling of mini-batches. 0.20 Baseline 0.6 Vannila PDS Validation Error Rate Percentage of data 0.15 Easy PDS Dense PDS 0.4 0.10 0.05 0.2 0.00 0 0.2 0.4 0.6 0.8 1 0 2000 4000 6000 8000 Mingling Index Iteration (a) Data Visualization (b) Mingling index distribution (c) Performance Comparison Figure 7. Speech experiment. Panel (a) visualizes the dataset using t-SNE.Panel (b) shows the histogram of data with mingling index 0. Panel (c) compares the performance with different variations of PDS. The y axis indicate the error rate on the validation set of each iteration, and the x axis indicate the training iteration. Our methods clearly lead to faster convergence and improved final performance. compared to MNIST. The extreme case is the silence class 6 Discussion that has very low variance compared to the word classes. Most examples with mingling index 0 are silence because In this work, we propose the use of repulsive point processes those samples are closely clustered (see appendix). for active mini-batch sampling. We provide both theoretical and experimental evidence that using repulsive stochastic Figure 7(c) shows the accuracy on the validation set eval- point processes can reduce the variance of the stochastic uated every 50 training iterations. Using Vanilla PDS, the gradients which leads to faster convergence. Additionally, model converges with fewer iterations compared to the tra- our generalized framework also allows adaptive density ditional random sampling of mini-batches. Easy PDS shows and adaptive pair-wise interactions. This leads to further further improvement compared to Vanilla PDS. Dense PDS improvements in model performance thanks to balancing (with π = [2/27, 3/27, 4/27, 5/27, 6/27, 7/27] in the ex- the information provided by the input samples or enhancing ample ) shows similar performance compared to Easy PDS, the information around the decision boundaries. since few data have 0 mingling indices in this dataset. Our work is mainly focused on the similarity measure in the Comparing to the MNIST experiment, the gain of Vanilla input space which makes it efficient and does not increase PDS and Easy PDS is bigger in this case since the dataset is run-time cost. In future work, we will explore the use of more difficult. On the other hand, encouraging more diffi- our method in the gradient space directly which potentially cult samples has a stronger impact on the MNIST dataset leads to even greater variance reduction, but at the same time than in the Speech experiment. In the end, in all different introduces higher computational efficiency requirements. settings, active mini-batch sampling is beneficial for both Additionally, we believe that our proposed method may fast convergence and improved final model performance. show even greater advantages in the two-stage framework Additionally, compared to experiment in Section 5.2 where such as Faster-R-CNN (Ren et al., 2015), where the second data from each class are imbalanced, the speech example stage network is trained using a subset of region proposals also shows that balancing the information is different from from the first stage. Finally, for sampling with adaptive balancing the data from each class. Our method demonstrate density, we mainly use the information of mingling index clear improvement with actually down-sampling the data which can only be used for classification problems. In future from silence class since they are highly redundant. work, we would also like to explore other measures such as sequences of annotations or graphs. 

9 . Active Mini-Batch Sampling using Repulsive Point Processes References Krizhevsky, Alex, Sutskever, Ilya, and Hinton, Geoffrey E. Imagenet classification with deep convolutional neural Alain, Guillaume, Lamb, Alex, Sankar, Chinnadhurai, networks. In Advances in neural information processing Courville, Aaron, and Bengio, Yoshua. Variance reduc- systems (NIPS), pp. 1097–1105, 2012. tion in SGD by distributed importance sampling. arXiv preprint arXiv:1511.06481, 2015. Kulesza, Alex, Taskar, Ben, et al. Determinantal point pro- cesses for machine learning. Foundations and Trends R Biscio, Christophe Ange Napol´eon, Lavancier, Fr´ed´eric, in Machine Learning, 5(2–3):123–286, 2012. et al. Quantifying repulsiveness of determinantal point processes. Bernoulli, 22(4):2001–2028, 2016. Lagae, Ares and Dutr´e, Philip. A comparison of methods for generating poisson disk distributions. In Computer Bottou, L´eon. Large-scale machine learning with stochastic Graphics Forum, volume 27, pp. 114–129. Wiley Online gradient descent. In COMPSTAT, pp. 177–186. Springer, Library, 2008. 2010. Lavancier, Fr´ed´eric, Møller, Jesper, and Rubak, Ege Hol- Chang, Haw-Shiuan, Learned-Miller, Erik, and McCallum, ger. Statistical aspects of determinantal point processes. Andrew. Active bias: Training a more accurate neural Technical report, Department of Mathematical Sciences, network by emphasizing high variance samples. arXiv Aalborg University, 2012. preprint arXiv:1704.07433, 2017. Lavancier, Fr´ed´eric, Møller, Jesper, and Rubak, Ege. Deter- Chen, Xinlei and Gupta, Abhinav. Webly supervised minantal point process models and statistical inference. learning of convolutional networks. In Proceedings of Journal of the Royal Statistical Society: Series B (Statis- the IEEE International Conference on Computer Vision tical Methodology), 77(4):853–877, 2015. (ICCV), pp. 1431–1439, 2015. LeCun, Yann, Bottou, L´eon, Bengio, Yoshua, and Haffner, Davis, Steven B and Mermelstein, Paul. Comparison of para- Patrick. Gradient-based learning applied to document metric representations for monosyllabic word recognition recognition. Proceedings of the IEEE, 86(11):2278–2324, in continuously spoken sentences. IEEE Transactions on 1998a. Acoustics, Speech, and Signal Processing, 28(4):357–366, LeCun, Yann, Bottou, L´eon, Orr, Genevieve B, and M¨uller, 1980. Klaus-Robert. Efficient backprop. In Neural networks: Fu, Tianfan and Zhang, Zhihua. CPSG-MCMC: Clustering- Tricks of the trade, pp. 9–50. Springer, 1998b. based preprocessing method for stochastic gradient Li, Chengtao, Jegelka, Stefanie, and Sra, Suvrit. Efficient MCMC. In AISTATS, 2017. sampling for k-determinantal point processes. arXiv Gopal, Siddharth. Adaptive sampling for SGD by exploit- preprint arXiv:1509.01618, 2015. ing side information. In International Conference on Li, Hongwei, Wei, Li-Yi, Sander, Pedro V, and Fu, Chi- Machine Learning (ICML), pp. 364–372, 2016. Wing. Anisotropic blue noise sampling. In ACM Trans- actions on Graphics (TOG), volume 29, pp. 167. ACM, Hoffman, Matthew D, Blei, David M, Wang, Chong, and 2010. Paisley, John. Stochastic variational inference. The Jour- nal of Machine Learning Research (JMLR), 14(1):1303– Maaten, Laurens van der and Hinton, Geoffrey. Visualizing 1347, 2013. data using t-sne. Journal of machine learning research (JMLR), 9(Nov):2579–2605, 2008. Illian, Janine, Penttinen, Antti, Stoyan, Helga, and Stoyan, Dietrich. Statistical analysis and modelling of spatial Macchi, Odile. The coincidence approach to stochastic point patterns, volume 70. John Wiley & Sons, 2008. point processes. Advances in Applied Probability, 7(1): 83–122, 1975. Kathuria, Tarun, Deshpande, Amit, and Kohli, Pushmeet. Batched gaussian process bandit optimization via deter- Mikolov, Tomas, Chen, Kai, Corrado, Greg, and Dean, Jef- minantal point processes. In Advances in Neural Infor- frey. Efficient estimation of word representations in vector mation Processing Systems, pp. 4206–4214, 2016. space. arXiv preprint arXiv:1301.3781, 2013. Kita, Naoki and Miyata, Kazunori. Multi-class anisotropic Møller, J. and Waagepetersen, R. P. Statistical inference blue noise sampling for discrete element pattern genera- and simulation for spatial point processes. Chapman & tion. The Visual Computer, 32(6-8):1035–1044, 2016. Hall/CRC, 2003, 2004. 

10 . Active Mini-Batch Sampling using Repulsive Point Processes ¨ Oztireli, A Cengiz and Gross, Markus. Analysis and synthesis of point distributions based on pair correla- tion. ACM Trans. Graph., 31(6):170:1–170:10, Novem- ber 2012. ISSN 0730-0301. Ren, Shaoqing, He, Kaiming, Girshick, Ross, and Sun, Jian. Faster R-CNN: Towards real-time object detection with region proposal networks. In Advances in neural information processing systems (NIPS), pp. 91–99, 2015. Ripley, Brian D. The second-order analysis of stationary point processes. Journal of applied probability, 13(2): 255–266, 1976. ¨ Roveri, Riccardo, Oztireli, A. Cengiz, and Gross, Markus. General point sampling with adaptive density and corre- lations. Computer Graphics Forum (Proc. Eurographics), 36(2), 2017. Sainath, Tara N. and Parada, Carolina. Convolutional neu- ral networks for small-footprint keyword spotting. In Proceedings of Interspeech, September 2015. Shrivastava, Abhinav, Gupta, Abhinav, and Girshick, Ross. Training region-based object detectors with online hard example mining. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2016. Yin, Dong, Pananjady, Ashwin, Lam, Max, Papailiopoulos, Dimitris, Ramchandran, Kannan, and Bartlett, Peter. Gra- dient diversity: a key ingredient for scalable distributed learning. In NIPS Workshop on Optimization for Machine Learning, 2017. Zhang, Cheng, B¨utepage, Judith, Kjellstr¨om, Hedvig, and Mandt, Stephan. Advances in variational inference. arXiv preprint arXiv:1711.05597, 2017a. Zhang, Cheng, Kjellstr¨om, Hedvig, and Mandt, Stephan. De- terminantal point processes for mini-batch diversification. In Conference on Uncertainty in Artificial Intelligence (UAI), 2017b. Zhao, Peilin and Zhang, Tong. Accelerating minibatch stochastic gradient descent using stratified sampling. arXiv:1405.3080, 2014. 

11 . Active Mini-Batch Sampling using Repulsive Point Processes A Derivation details Preliminary: Campbell’s Theorem A fundamental operation needed for analyzing point processes is computing expected values of sums of sampled values from functions EP [ f (xi )], where the expectation is computed over different realizations of the point process P, and x1 , · · · are the points in a given realization. Note that the number of points in a given realization is also random, and hence is often omitted for the sums. This can also be generalized to functions of more than one variable. Campbell’s theorem is a fundamental theorem that relates these sums to integrals of arbitrary functions f , and the product densities of P. In particular, we will work with sums of the form f (xi ) and ij f (xi , xj ). These are given by the following expressions: EP f (xi ) = f (x)λ(x)dx, (5) Rd where f : Rd → R, and   EP  f (xi , xj ) = f (x, y) (x, y)dxdy, (6) i=j Rd ×Rd for f : Rd × Rd → R, and under the common assumption (Illian et al., 2008) that no two points in a process can be at the same location almost surely. In practice, we typically observe sample points in a finite sub-space V ∈ Rd . For such cases, the integration domains can be replaced by V. Derivation of Gradient Variances For our derivations of bias and variance in this paper, we will need the first (1) and second (2) order product densities. The first order product density is given by (1) (x)dx = p(x). It can be shown that the expected number of points of P in a set B can be written as the integral of this expression: EP [N (B)] = B (1) (x)dx, where N (B) is the (random) number of points of the process P in set B. Hence, (1) (x) measures the local expected density of distributions generated by a point process. It is thus usually called the intensity of P and denoted by λ(x) = (1) (x). Pairwise correlations are captured by the second order product density (2) (x, y)dxdy = p(x, y). The two statistics λ(x) and (x, y) are sufficient to exactly express bias and variance of estimators for integrals or expected values. ˆ The expected value EP G(θ) , can be simply derived by utilizing the expression in Equation 5 as follows ˆ 1 1 EP G(θ) = EP g(xi , θ) = g(x, θ)λ(x)dx. (7) k i V k The λ(x) is fundamentally related to the assumed underlying distribution pdata (x) for the observed data-points. If the sampler does not introduce additional adaptivity, e.g. random sampling, then λ(x) is directly proportional to pdata (x). We can also compute the variance of the gradient estimate G ˆ using the point processes framework. The variance of a ˆ multi-dimensional random variable can be written as varP (G) = tr[covP (G)]ˆ = ˆ ˆ m varP (Gm ), where Gm denotes the th m component of G. ˆ The variance for each dimension is given by varP (G ˆ m ) = EP [Gˆ ] − (E[G 2 ˆ m ]) . These terms can 2 m be written in terms of λ and by utilizing Equations 6, and 5, respectively, as follows   ˆ2 1 EP Gm = EP  2 gm (xi , θ)gm (xj , θ) k ij   1 1 2 = EP  2 gm (xi , θ)gm (xj , θ) + EP gm (xi , θ) k k2 i (8) i=j 1 = gm (x, θ)gm (y, θ) (x, y)dxdy k2 V×V 1 2 + 2 gm (x, θ)λ(x)dx, k V 

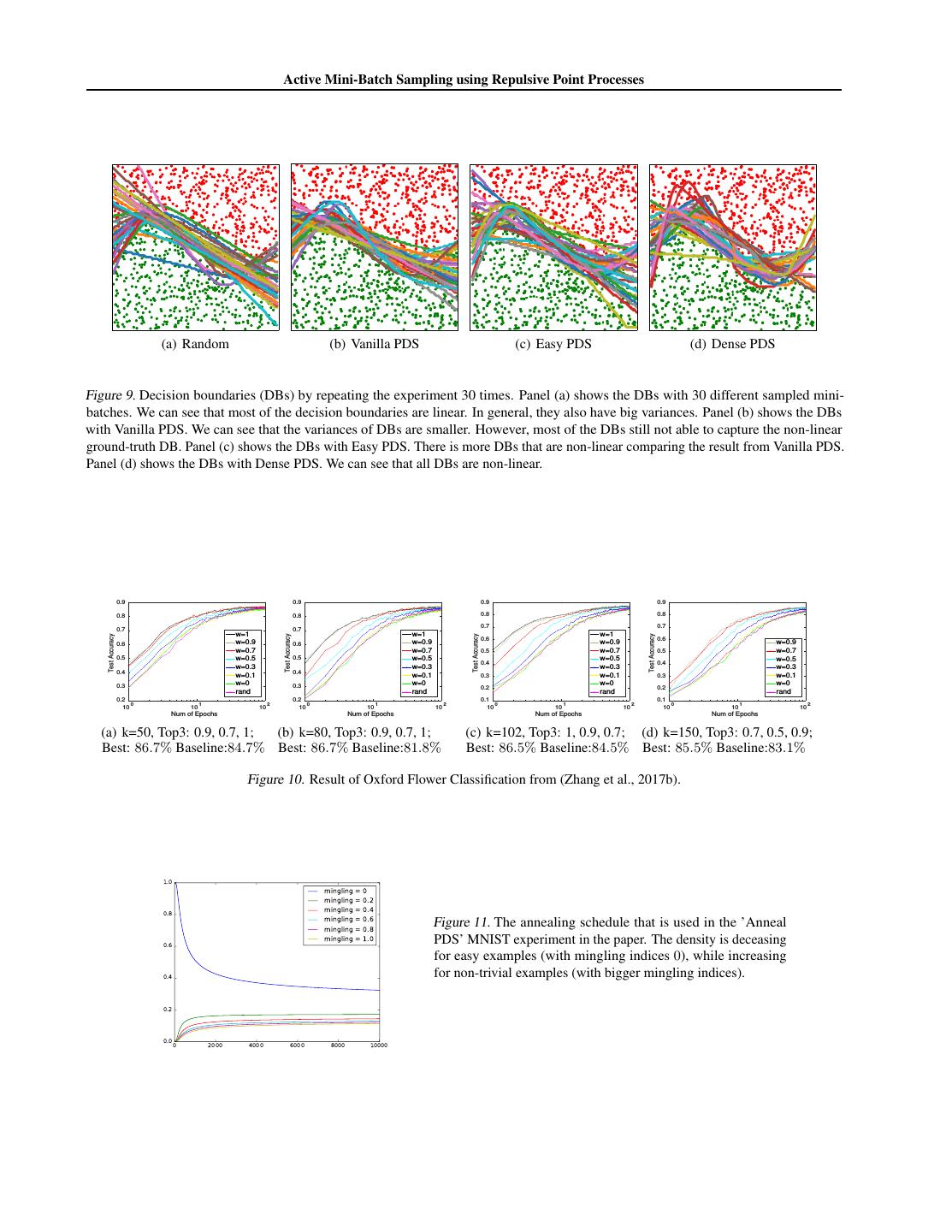
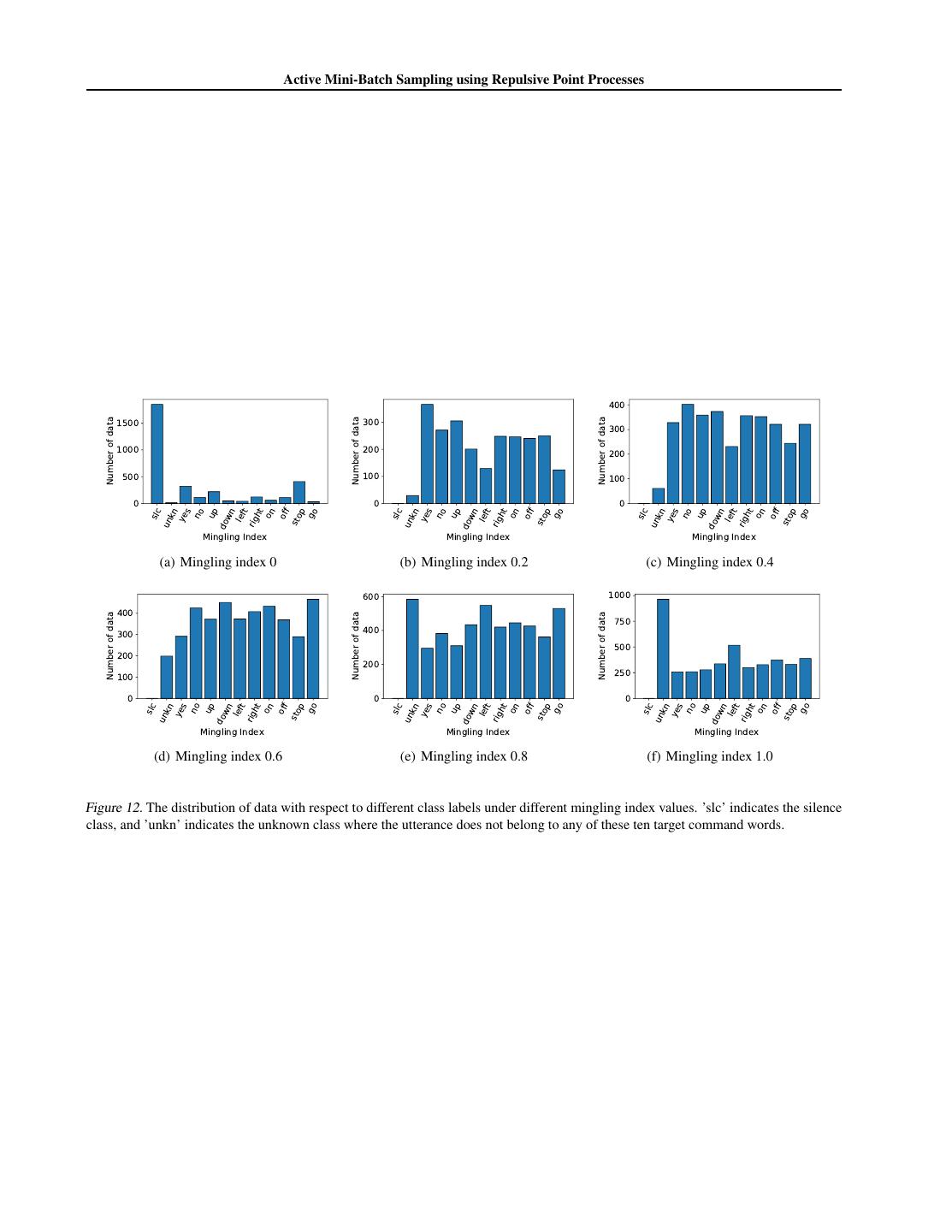
12 . Active Mini-Batch Sampling using Repulsive Point Processes 2 2 ˆm 1 EP G = gm (x, θ)λ(x)dx k V (9) 1 = 2 gm (x, θ)gm (y, θ)λ(x)λ(y)dxdy k V×V ˆ Finally, summing over all dimensions, we can get the following formula for the variance of G ˆ = 1 (x, y) varP (G) λ(x)λ(y)g(x, θ)T g(y, θ) − 1 dxdy k2 V×V λ(x)λ(y) (10) 1 + 2 g(x, θ) 2 λ(x)dx. k V B Additional Figures Figure 8 shows examples of samples using DPP and using Poisson disk sampling (by dart throwing). 2 2 2 2 1.8 1.8 1.8 1.8 1.6 1.6 1.6 1.6 1.4 1.4 1.4 1.4 1.2 1.2 1.2 1.2 1 1 1 1 0.8 0.8 0.8 0.8 0.6 0.6 0.6 0.6 0.4 0.4 0.4 0.4 0.2 0.2 0.2 0.2 0 0 0 0 0 0.5 1 1.5 2 0 0.5 1 1.5 2 0 0.5 1 1.5 2 0 0.5 1 1.5 2 (a) DPP exp 1 (b) DPP exp 2 (c) DPP exp 3 (d) DPP exp 4 2 2 2 2 1.8 1.8 1.8 1.8 1.6 1.6 1.6 1.6 1.4 1.4 1.4 1.4 1.2 1.2 1.2 1.2 1 1 1 1 0.8 0.8 0.8 0.8 0.6 0.6 0.6 0.6 0.4 0.4 0.4 0.4 0.2 0.2 0.2 0.2 0 0 0 0 0 0.5 1 1.5 2 0 0.5 1 1.5 2 0 0.5 1 1.5 2 0 0.5 1 1.5 2 (e) Poisson Disk exp 1 (f) Poisson Disk exp 2 (g) Poisson Disk exp 3 (h) Poisson Disk exp 4 Figure 8. Examples of sampled data points. The first row are sampled using DPP and the second row are sampled with Poisson Disk sampling. The green dots are the training data and the black circles indicated that the data point has been sampled. As a comparison to our result with efficient Poisson Disk Sampling in Figure 5 in the paper, we provided the original result from (Zhang et al., 2017b) for the same experiment setting here in the supplement as shown in Figure 10. Figure 11 shows the annealing parameter that is used in the MNIST experiment in Section 5.3. The original distribution of data with different mingling indices is h = [0.9017, 0.0474, 0.0212, 0.013, 0.0096, 0.0071]. We uses an annealing schedule where πn is set to normalized h1/log(0.01n+1) . In this way, data with mingling index 0 (easy examples) are sampled more often in the early iterations during training. Figure 12 shows the distributions of data with different mingling index over these twelve classes. We can see that most points with mingling indices 0 are from the “silence” class where the data are artificially constructed from background noise. Data from other classes, in general, have higher mingling indices, since they are not well separated as shown in the t-SNE plot in the paper. Additionally, we can see in Figure 12 (b) that most data points with mingling index 1 are from the “unknown” class, that is the noisiest class because it corresponds to a number of different words. 

13 . Active Mini-Batch Sampling using Repulsive Point Processes (a) Random (b) Vanilla PDS (c) Easy PDS (d) Dense PDS Figure 9. Decision boundaries (DBs) by repeating the experiment 30 times. Panel (a) shows the DBs with 30 different sampled mini- batches. We can see that most of the decision boundaries are linear. In general, they also have big variances. Panel (b) shows the DBs with Vanilla PDS. We can see that the variances of DBs are smaller. However, most of the DBs still not able to capture the non-linear ground-truth DB. Panel (c) shows the DBs with Easy PDS. There is more DBs that are non-linear comparing the result from Vanilla PDS. Panel (d) shows the DBs with Dense PDS. We can see that all DBs are non-linear. 0.9 0.9 0.9 0.9 0.8 0.8 0.8 0.8 0.7 0.7 0.7 0.7 w=1 w=1 w=1 Test Accuracy Test Accuracy Test Accuracy Test Accuracy 0.6 0.6 0.6 w=0.9 0.6 w=0.9 w=0.9 w=0.9 w=0.7 w=0.7 0.5 w=0.7 0.5 w=0.7 0.5 w=0.5 0.5 w=0.5 w=0.5 w=0.5 0.4 0.4 w=0.3 w=0.3 w=0.3 w=0.3 0.4 0.4 w=0.1 w=0.1 0.3 w=0.1 0.3 w=0.1 0.3 w=0 0.3 w=0 w=0 w=0 0.2 0.2 rand rand rand rand 0.2 0.2 0.1 0.1 10 0 10 1 10 2 10 0 10 1 10 2 10 0 10 1 10 2 10 0 10 1 10 2 Num of Epochs Num of Epochs Num of Epochs Num of Epochs (a) k=50, Top3: 0.9, 0.7, 1; (b) k=80, Top3: 0.9, 0.7, 1; (c) k=102, Top3: 1, 0.9, 0.7; (d) k=150, Top3: 0.7, 0.5, 0.9; Best: 86.7% Baseline:84.7% Best: 86.7% Baseline:81.8% Best: 86.5% Baseline:84.5% Best: 85.5% Baseline:83.1% Figure 10. Result of Oxford Flower Classification from (Zhang et al., 2017b). 1.0 mingling = 0 mingling = 0.2 0.8 mingling = 0.4 mingling = 0.6 Figure 11. The annealing schedule that is used in the ’Anneal mingling = 0.8 mingling = 1.0 PDS’ MNIST experiment in the paper. The density is deceasing 0.6 for easy examples (with mingling indices 0), while increasing 0.4 for non-trivial examples (with bigger mingling indices). 0.2 0.0 0 2000 4000 6000 8000 10000 

14 . Active Mini-Batch Sampling using Repulsive Point Processes 400 1500 300 Number of data Number of data Number of data 300 1000 200 200 500 100 100 0 0 0 slc n yes no up n left t on off stop go slc n yes no up n left t on off stop go slc n yes no up n left t on off stop go righ righ righ unk dow unk dow unk dow Mingling Index Mingling Index Mingling Index (a) Mingling index 0 (b) Mingling index 0.2 (c) Mingling index 0.4 600 1000 400 750 Number of data Number of data Number of data 300 400 500 200 200 100 250 0 0 0 slc n yes no up n left t on off stop go slc n yes no up n left t on off stop go slc n yes no up n left t on off stop go righ righ righ unk dow unk dow unk dow Mingling Index Mingling Index Mingling Index (d) Mingling index 0.6 (e) Mingling index 0.8 (f) Mingling index 1.0 Figure 12. The distribution of data with respect to different class labels under different mingling index values. ’slc’ indicates the silence class, and ’unkn’ indicates the unknown class where the utterance does not belong to any of these ten target command words.