Unsupervised Learning: Neighbor Embedding

1 .Unsupervised Learning: Neighbor Embedding 

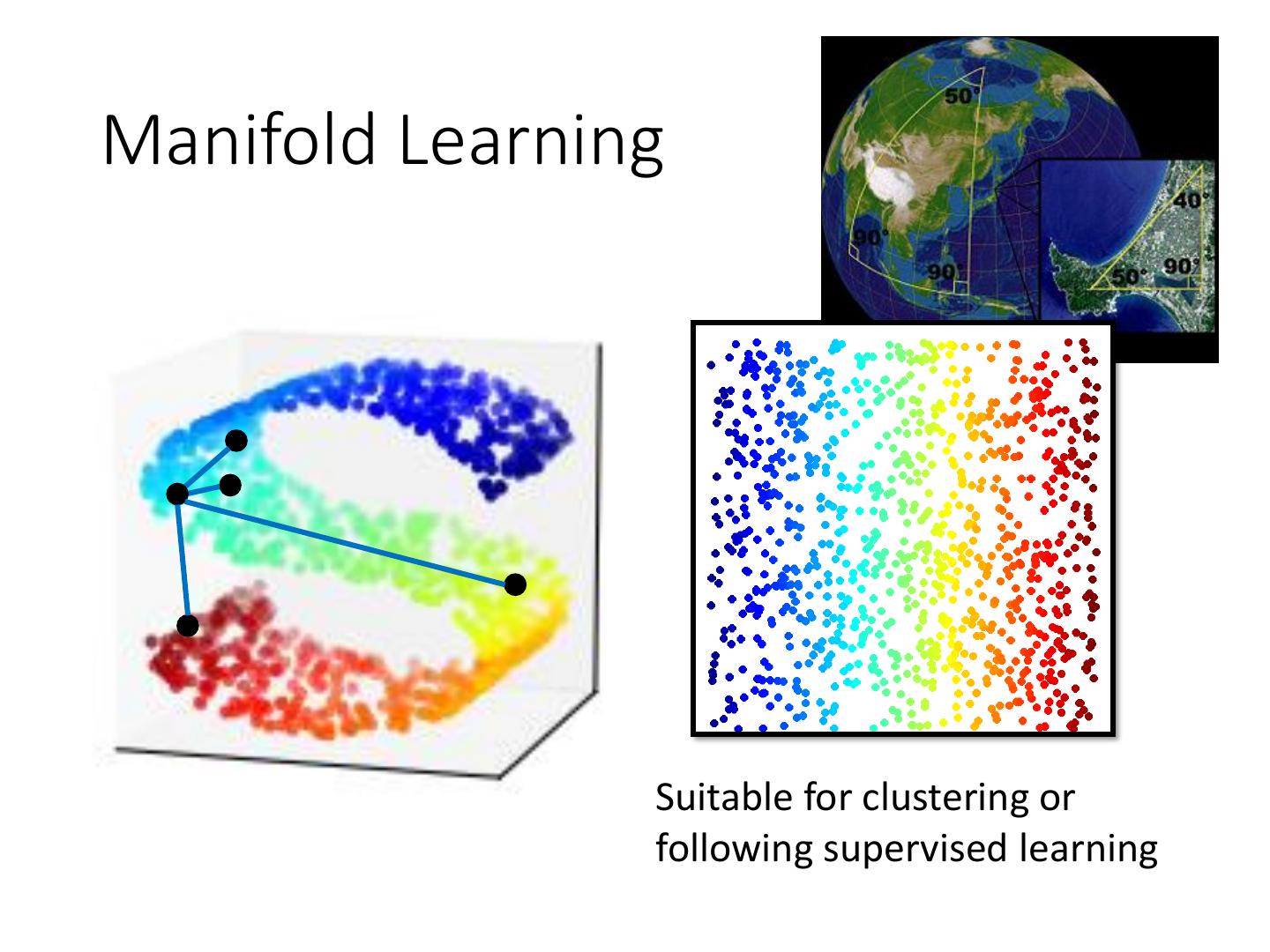
2 .Manifold Learning Suitable for clustering or following supervised learning 

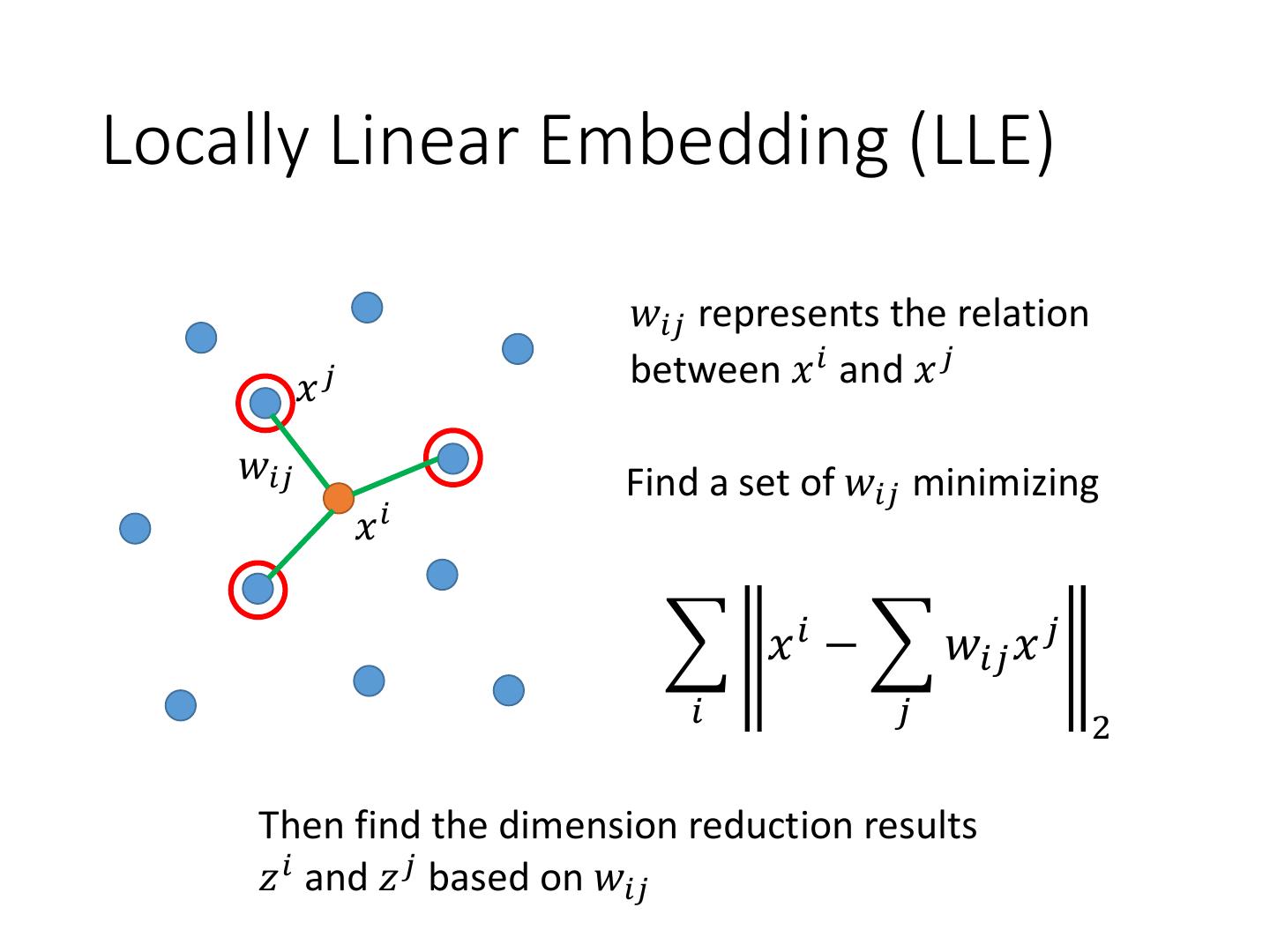
3 .Locally Linear Embedding (LLE) 𝑤𝑖𝑗 represents the relation 𝑥𝑗 between 𝑥 𝑖 and 𝑥 𝑗 𝑤𝑖𝑗 Find a set of 𝑤𝑖𝑗 minimizing 𝑥𝑖 ෍ 𝑥 𝑖 − ෍ 𝑤𝑖𝑗 𝑥 𝑗 𝑖 𝑗 2 Then find the dimension reduction results 𝑧 𝑖 and 𝑧 𝑗 based on 𝑤𝑖𝑗 

4 .LLE Find a set of 𝑧 𝑖 minimizing Keep 𝑤𝑖𝑗 unchanged ෍ 𝑧 𝑖 − ෍ 𝑤𝑖𝑗 𝑧 𝑗 𝑖 𝑗 2 𝑥𝑗 𝑤𝑖𝑗 𝑧𝑗 𝑧𝑖 𝑥𝑖 𝑤𝑖𝑗 Original Space New (Low-dim) Space 

5 . LLE 𝑧 𝑖 ,𝑧 𝑗 𝑥 𝑖 ,𝑥 𝑗 𝑤𝑖𝑗 𝑤𝑖𝑗 Source of image: http://feetsprint.blogspot.tw/2016 /02/blog-post_29.html 

6 .LLE Lawrence K. Saul, Sam T. Roweis, “Think Globally, Fit Locally: Unsupervised Learning of Low Dimensional Manifolds”, JMLR, 2013 

7 .Laplacian Eigenmaps • Graph-based approach Distance defined by graph approximate the distance on manifold Construct the data points as a graph 

8 . similarity If connected Laplacian Eigenmaps 𝑤𝑖,𝑗 = 0 otherwise • Review in semi-supervised learning: If 𝑥 1 and 𝑥 2 are close in a high density region, 𝑦ො 1 and 𝑦ො 2 are probably the same. 𝐿 = ෍ 𝐶 𝑦 𝑟 , 𝑦ො 𝑟 +𝜆𝑆 𝑥𝑟 As a regularization term 1 2 𝑆 = ෍ 𝑤𝑖,𝑗 𝑦 𝑖 − 𝑦 𝑗 = 𝒚𝑇 𝐿𝒚 2 𝑖,𝑗 L: (R+U) x (R+U) matrix S evaluates how smooth your label is Graph Laplacian 𝐿 =𝐷−𝑊 

9 .Laplacian Eigenmaps • Dimension Reduction: If 𝑥 1 and 𝑥 2 are close in a high density region, 𝑧1 and 𝑧 2 are close to each other. 1 2 𝑆 = ෍ 𝑤𝑖,𝑗 𝑧 𝑖 − 𝑧 𝑗 2 𝑖,𝑗 Any problem? How about 𝑧 𝑖 = 𝑧 𝑗 = 𝟎? Giving some constraints to z: If the dim of z is M, Span{z1, z2, … zN} = RM Spectral clustering: clustering on z Belkin, M., Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Advances in neural information processing systems . 2002 

10 .T-distributed Stochastic Neighbor Embedding (t-SNE) • Problem of the previous approaches • Similar data are close, but different data may collapse LLE on MNIST LLE on COIL-20 

11 . t-SNE x z Compute similarity between Compute similarity between all all pairs of x: 𝑆 𝑥 𝑖 , 𝑥 𝑗 pairs of z: 𝑆′ 𝑧 𝑖 , 𝑧 𝑗 𝑆 𝑥𝑖, 𝑥 𝑗 𝑆′ 𝑧 𝑖 , 𝑧 𝑗 𝑃 𝑥 𝑗 |𝑥 𝑖 = 𝑄 𝑧 𝑗 |𝑧 𝑖 = σ𝑘≠𝑖 𝑆 𝑥 𝑖 , 𝑥 𝑘 σ𝑘≠𝑖 𝑆′ 𝑧 𝑖 , 𝑧 𝑘 Find a set of z making the two distributions as close as possible 𝐿 = ෍ 𝐾𝐿 𝑃 ∗ |𝑥 𝑖 ||𝑄 ∗ |𝑧 𝑖 𝑖 𝑗 |𝑥 𝑖 𝑃 𝑥 = ෍ ෍ 𝑃 𝑥 𝑗 |𝑥 𝑖 𝑙𝑜𝑔 𝑄 𝑧 𝑗 |𝑧 𝑖 𝑖 𝑗 

12 . Ignore 𝜎 for simplicity t-SNE –Similarity Measure SNE: 𝑆 𝑥𝑖, 𝑥 𝑗 𝑆′ 𝑧 𝑖 , 𝑧 𝑗 = 𝑒𝑥𝑝 − 𝑧 𝑖 − 𝑧 𝑗 2 = 𝑒𝑥𝑝 − 𝑥 𝑖 − 𝑥 𝑗 2 t-SNE: 𝑆′ 𝑧 𝑖 , 𝑧 𝑗 = 1ൗ1 + 𝑧 𝑖 − 𝑧 𝑗 2 1ൗ1 + 𝑧 𝑖 − 𝑧 𝑗 2 𝑒𝑥𝑝 − 𝑥 𝑖 − 𝑥 𝑗 2 𝑥𝑖 − 𝑥 𝑗 2 , 𝑧 𝑖 − 𝑧 𝑗 2 

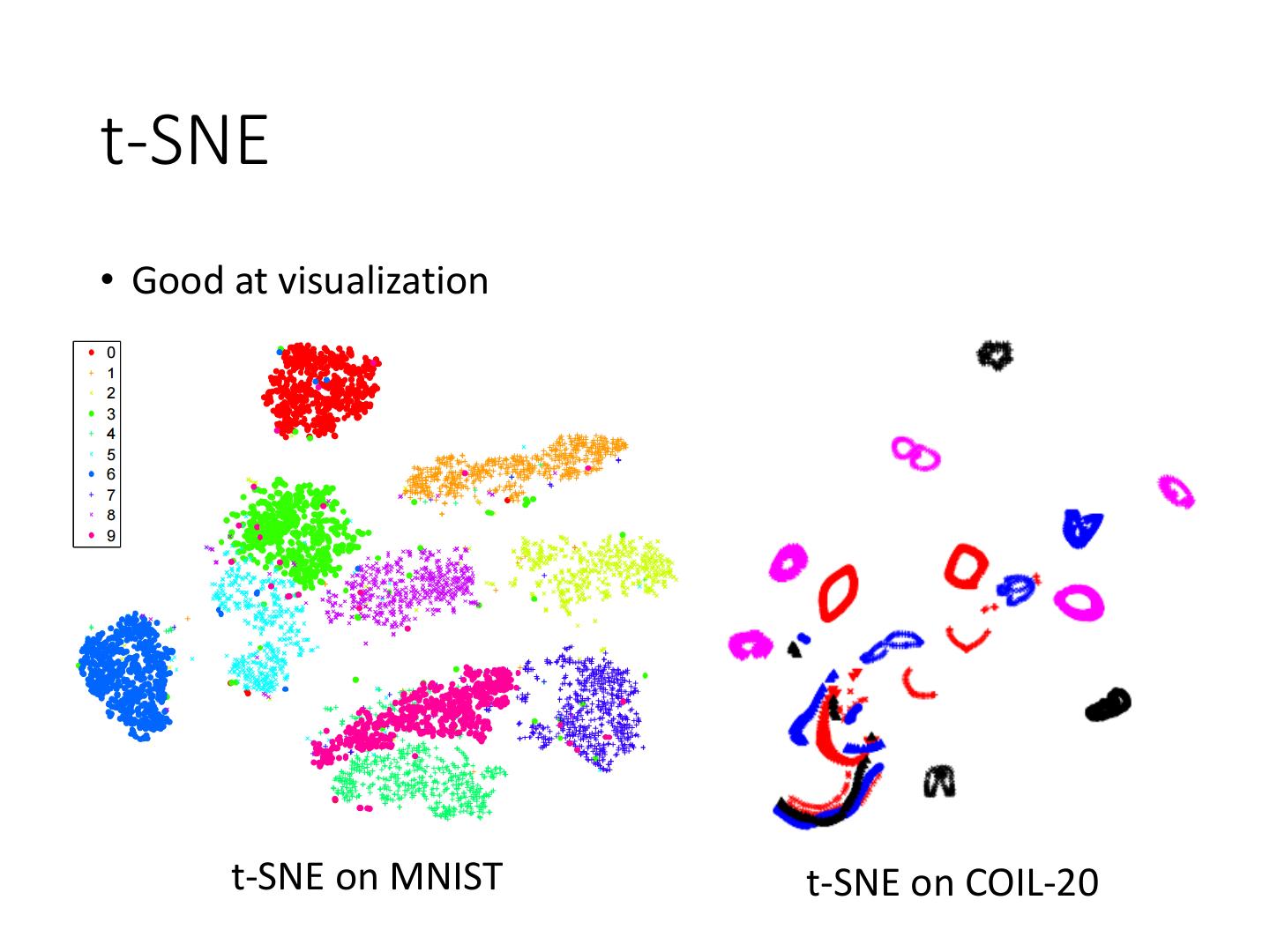
13 .t-SNE • Good at visualization t-SNE on MNIST t-SNE on COIL-20 

14 .

15 .To learn more … • Locally Linear Embedding (LLE): [Alpaydin, Chapter 6.11] • Laplacian Eigenmaps: [Alpaydin, Chapter 6.12] • t-SNE • Laurens van der Maaten, Geoffrey Hinton, “Visualizing Data using t-SNE”, JMLR, 2008 • Excellent tutorial: https://github.com/oreillymedia/t-SNE-tutorial