Recurrent Neural Network (RNN)

1 .Recurrent Neural Network (RNN) 

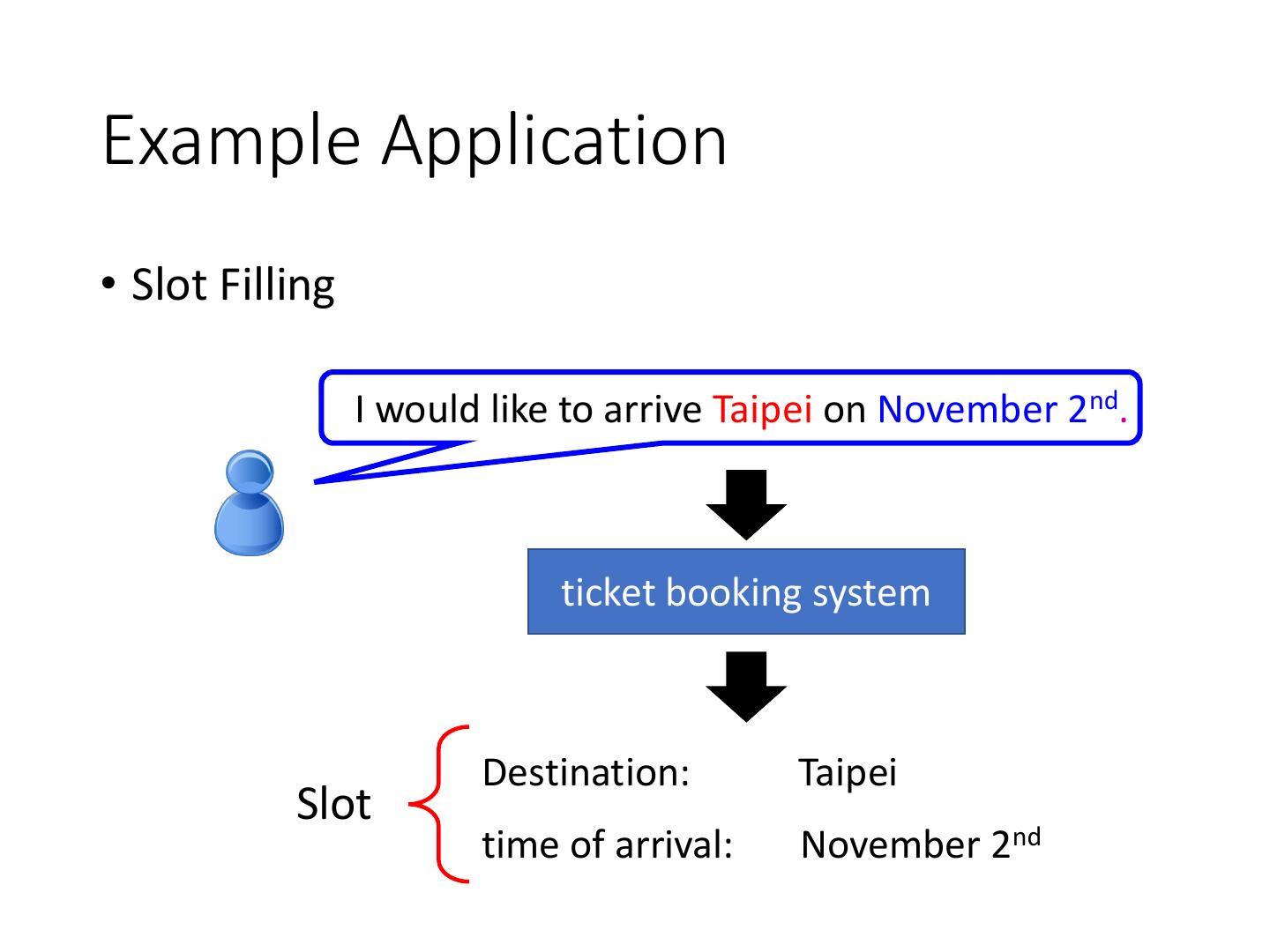
2 .Example Application • Slot Filling I would like to arrive Taipei on November 2nd. ticket booking system Destination: Taipei Slot time of arrival: November 2nd 

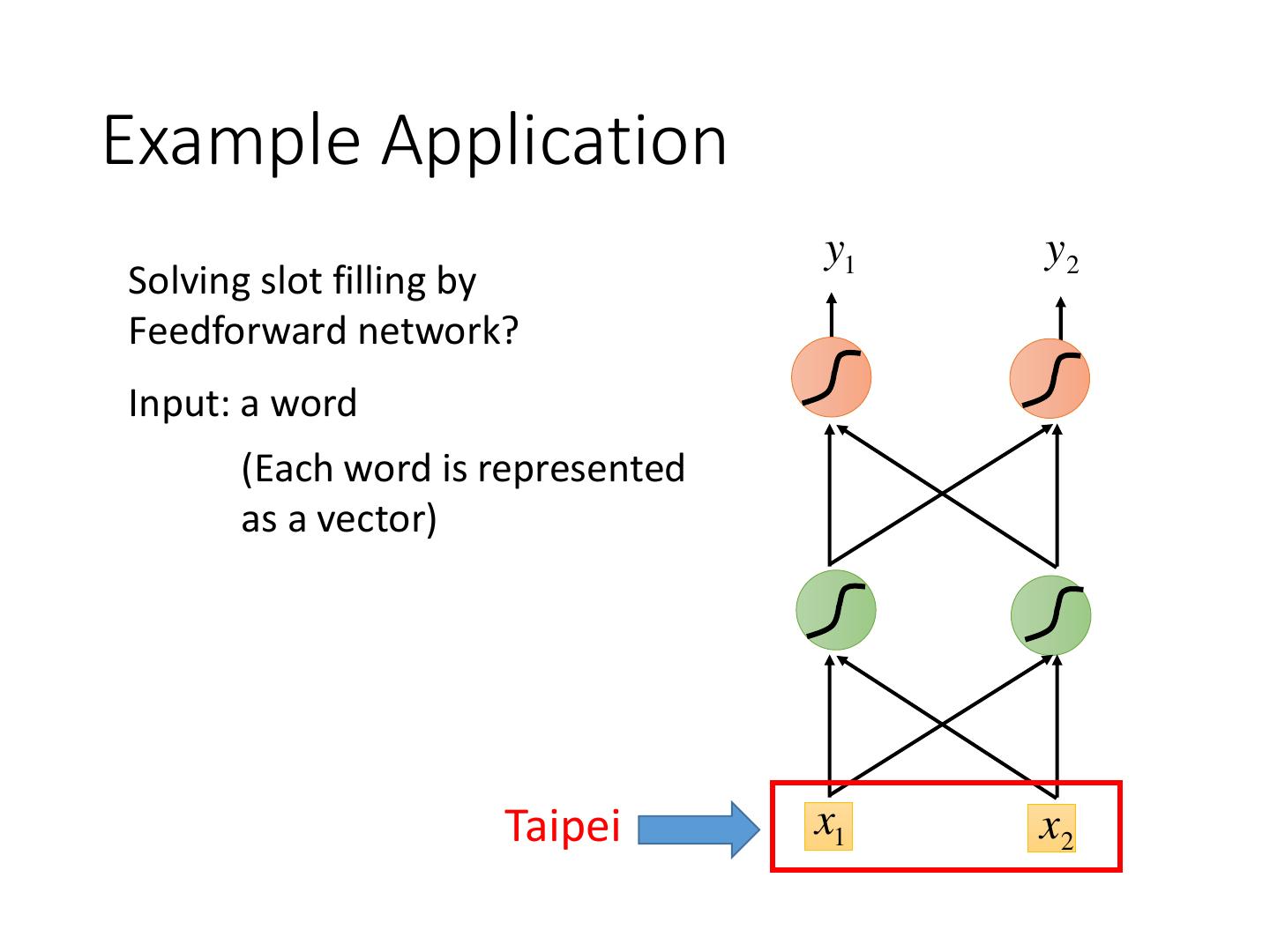
3 .Example Application y1 y2 Solving slot filling by Feedforward network? Input: a word (Each word is represented as a vector) Taipei x1 x2 

4 . 1-of-N encoding How to represent each word as a vector? 1-of-N Encoding lexicon = {apple, bag, cat, dog, elephant} The vector is lexicon size. apple = [ 1 0 0 0 0] Each dimension corresponds bag = [ 0 1 0 0 0] to a word in the lexicon cat = [ 0 0 1 0 0] The dimension for the word dog = [ 0 0 0 1 0] is 1, and others are 0 elephant = [ 0 0 0 0 1] 

5 . Beyond 1-of-N encoding Dimension for “Other” Word hashing apple 0 a-a-a 0 bag 0 a-a-b 0 … … cat 0 a-p-p 1 dog 0 … … 26 X 26 X 26 elephant 0 p-l-e 1 … … … p-p-l 1 “other” 1 … … w = “apple” w = “Gandalf” w = “Sauron” 5 

6 .Example Application time of dest departure y1 y2 Solving slot filling by Feedforward network? Input: a word (Each word is represented as a vector) Output: Probability distribution that the input word belonging to the slots Taipei x1 x2 

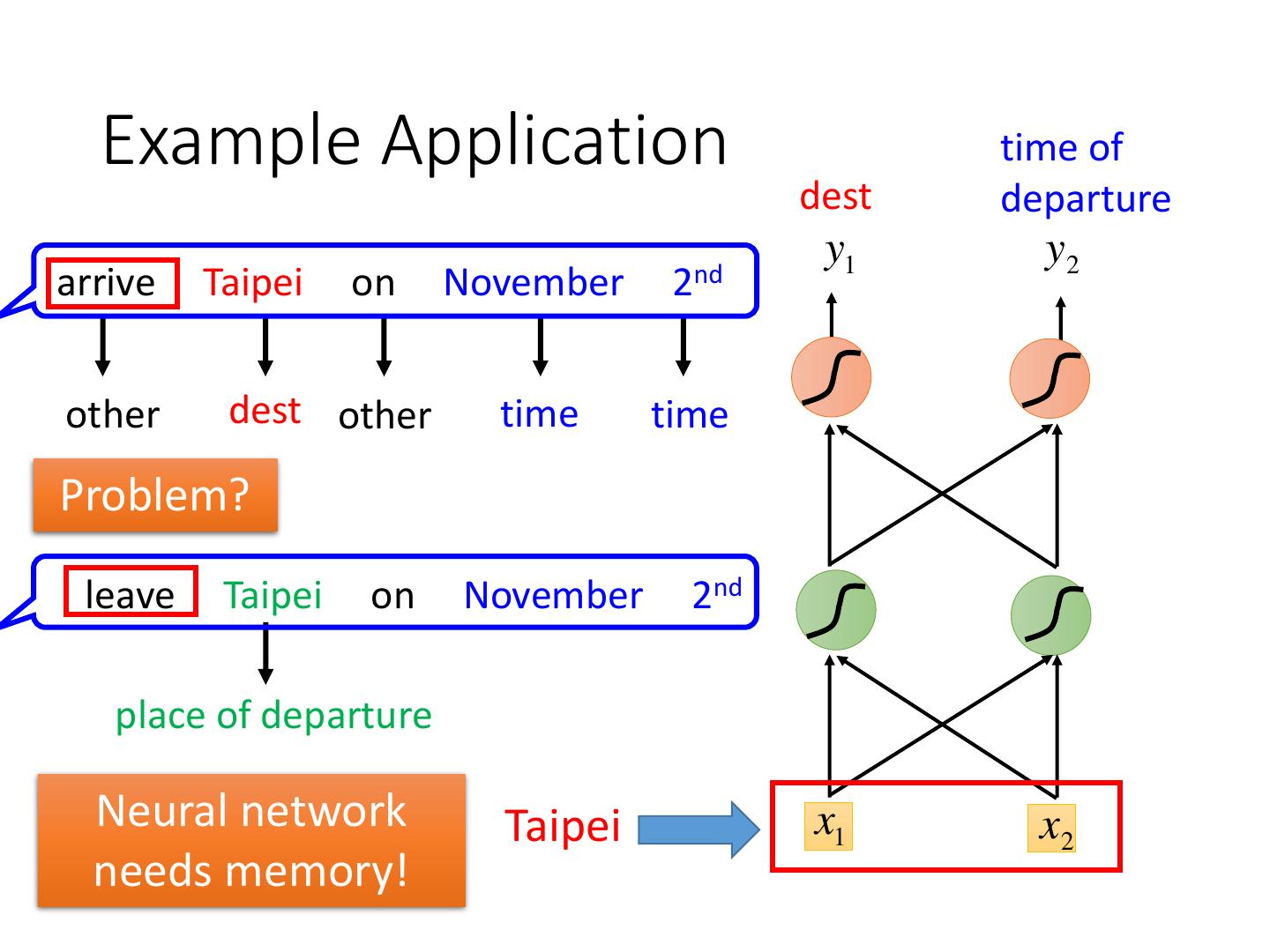
7 . Example Application time of dest departure y1 y2 arrive Taipei on November 2nd other dest other time time Problem? leave Taipei on November 2nd place of departure Neural network Taipei x1 x2 needs memory! 

8 .Recurrent Neural Network (RNN) y1 y2 The output of hidden layer are stored in the memory. store a1 a2 Memory can be considered x1 x2 as another input. 

9 . Input sequence: 1 1 2 …… 1 1 2 Example 4 output sequence: 4 y1 y2 4 4 store 2 2 given Initial a01 a02 values All the weights are “1”, no bias x11 x12 All activation functions are linear 

10 . Input sequence: 1 1 2 …… 1 1 2 Example 4 12 output sequence: 4 12 y1 y2 12 12 store 6 6 a21 a22 All the weights are “1”, no bias x11 x12 All activation functions are linear 

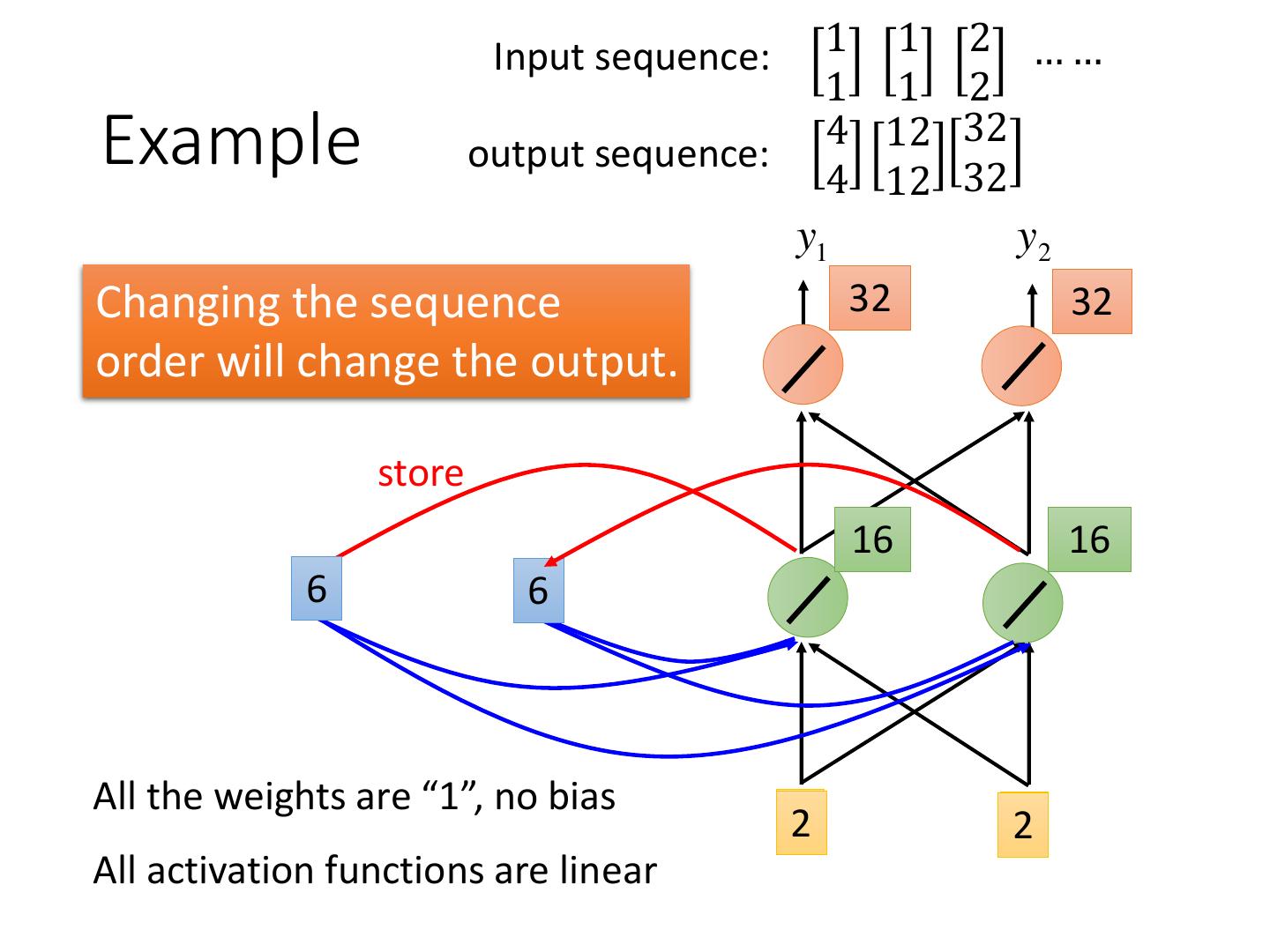
11 . Input sequence: 1 1 2 …… 1 1 2 Example 4 12 32 output sequence: 4 12 32 y1 y2 Changing the sequence 32 32 order will change the output. store 16 16 a61 a62 All the weights are “1”, no bias x21 x22 All activation functions are linear 

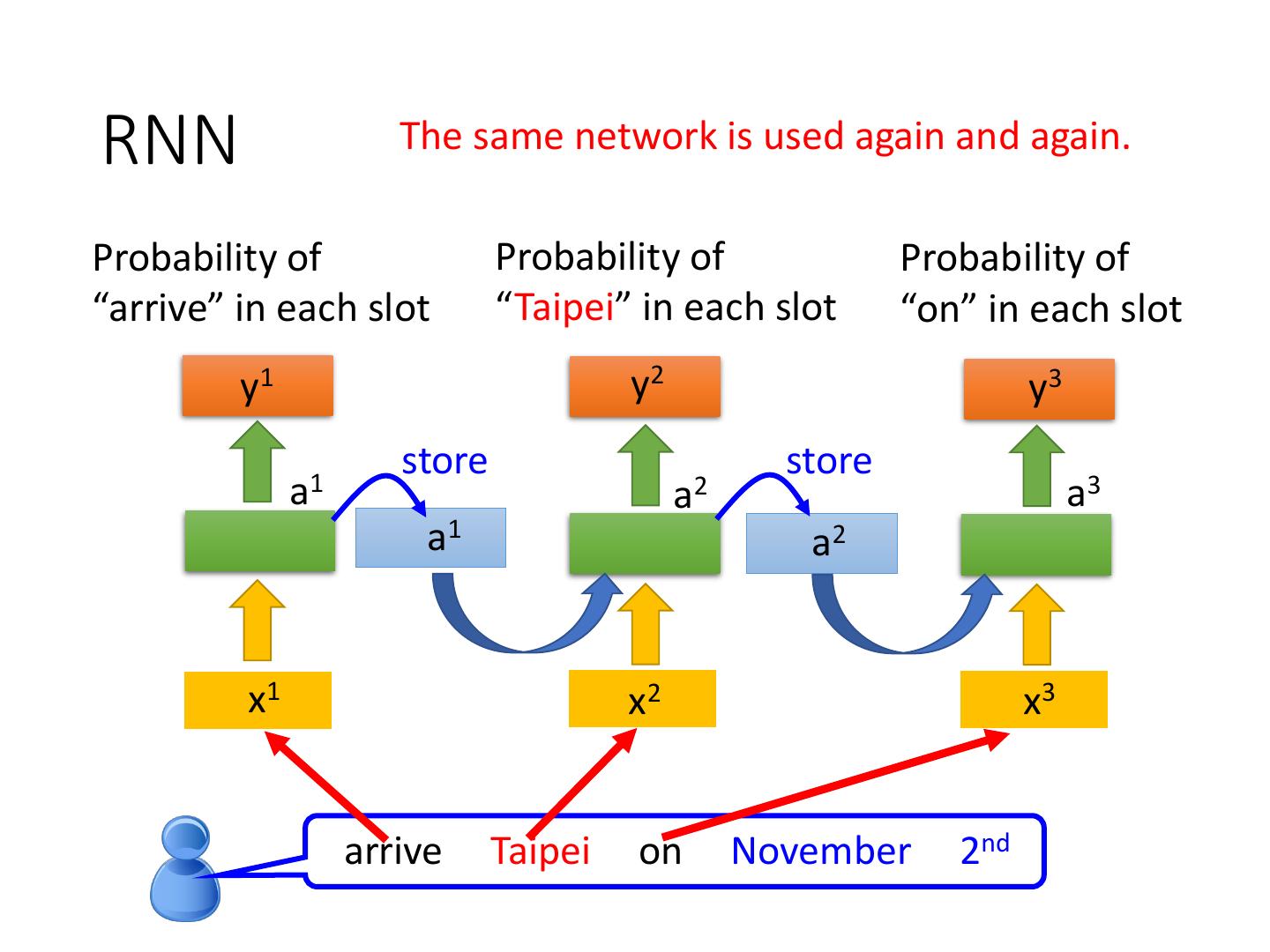
12 .RNN The same network is used again and again. Probability of Probability of Probability of “arrive” in each slot “Taipei” in each slot “on” in each slot y1 y2 y3 store store a1 a2 a3 a1 a2 x1 x2 x3 arrive Taipei on November 2nd 

13 . RNN Different Prob of “leave” Prob of “Taipei” Prob of “arrive” Prob of “Taipei” in each slot in each slot in each slot in each slot y1 y2 …… y1 y2 …… store store a1 a2 a1 a2 a1 …… a1 …… x1 x2 …… x1 x2 …… leave Taipei arrive Taipei The values stored in the memory is different. 

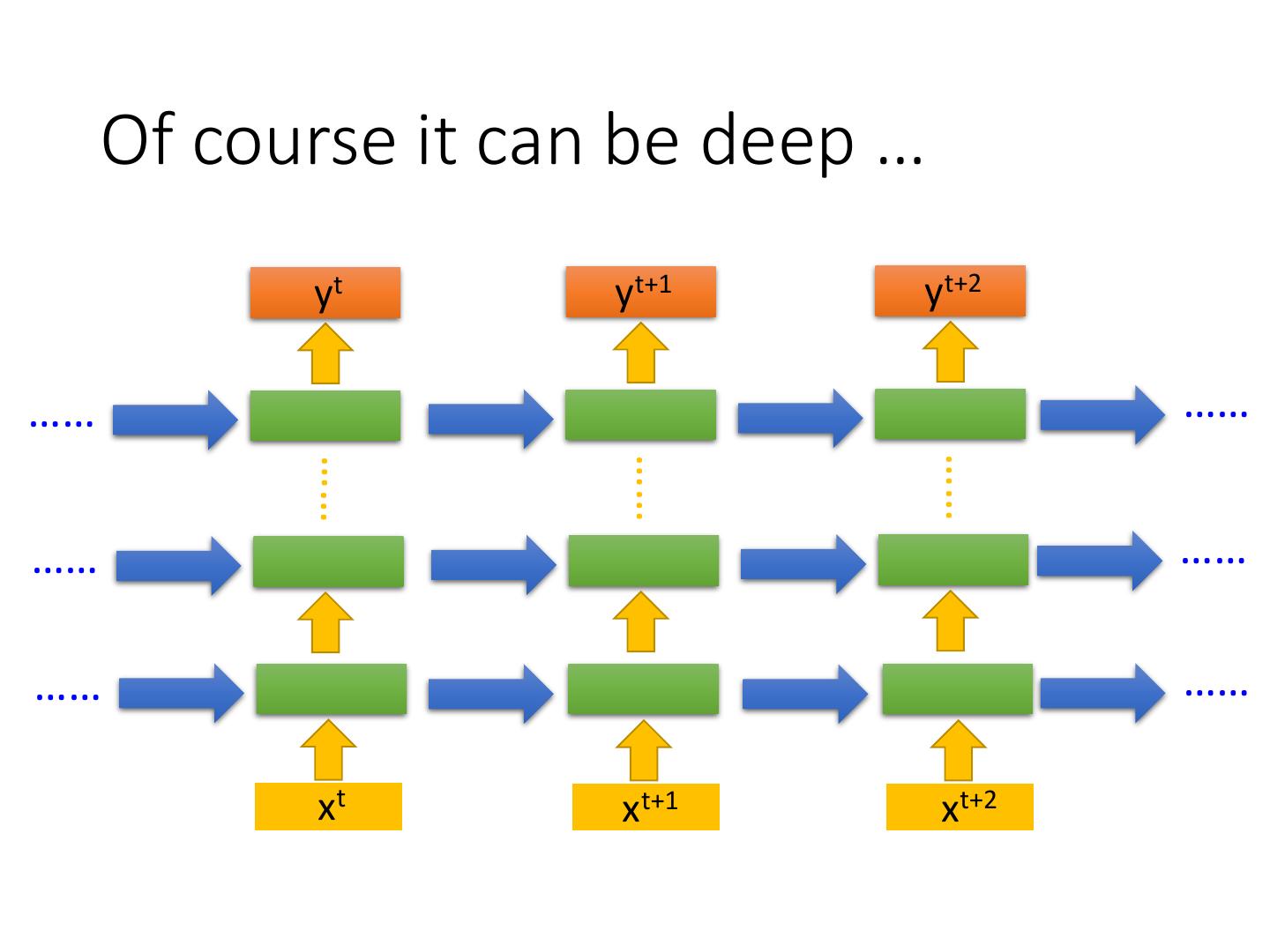
14 . Of course it can be deep … yt yt+1 yt+2 …… …… …… …… …… …… …… …… …… xt xt+1 xt+2 

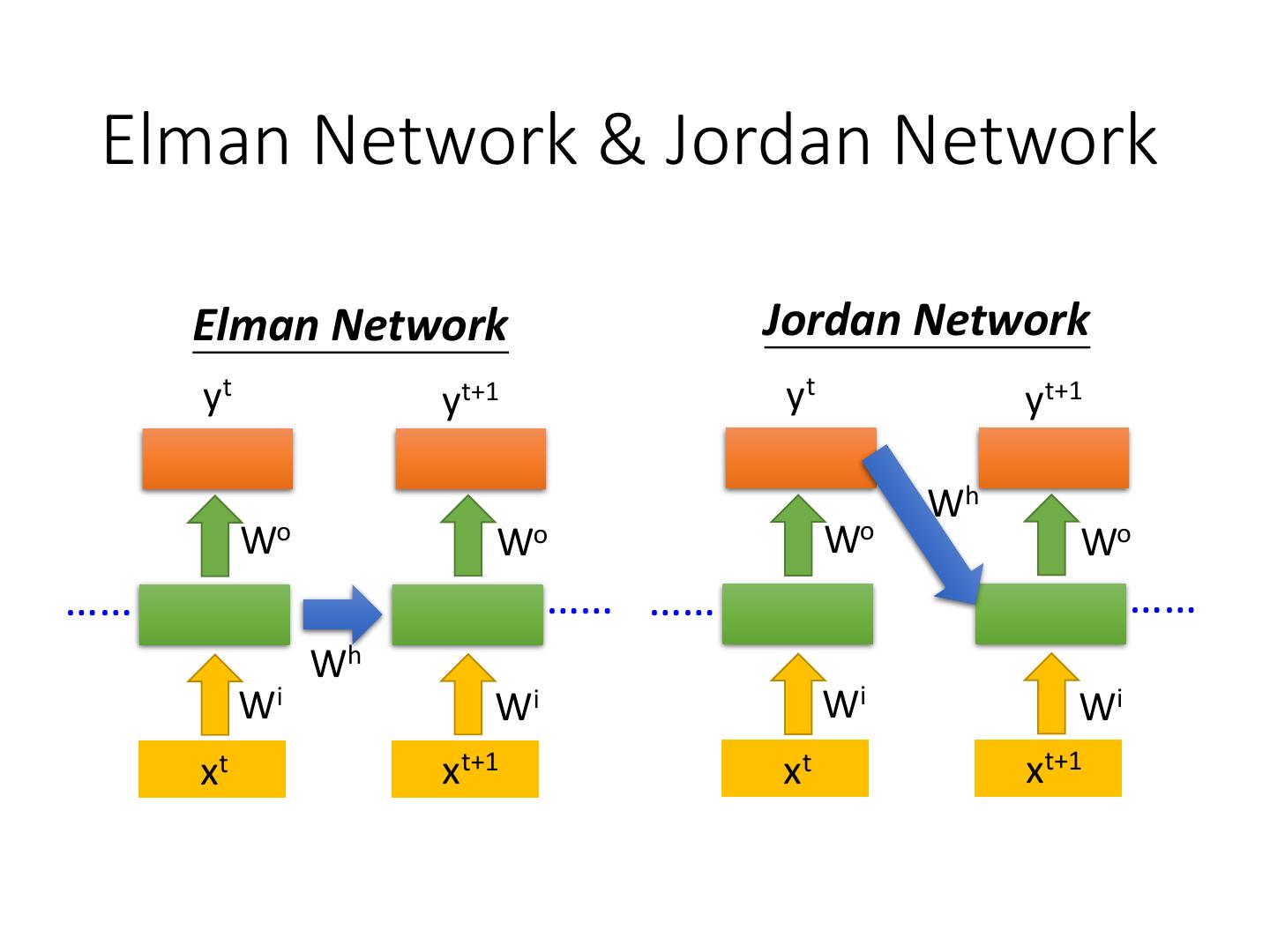
15 . Elman Network & Jordan Network Elman Network Jordan Network yt yt+1 yt yt+1 Wh Wo Wo Wo Wo …… …… …… …… Wh Wi Wi Wi Wi xt xt+1 xt xt+1 

16 . Bidirectional RNN xt xt+1 xt+2 …… …… yt yt+1 yt+2 …… …… xt xt+1 xt+2 

17 . Long Short-term Memory (LSTM) Other part of the network Special Neuron: Signal control Output Gate 4 inputs, the output gate 1 output (Other part of the network) Memory Forget Signal control Cell Gate the forget gate (Other part of the network) Signal control Input Gate LSTM the input gate (Other part of the network) Other part of the network 

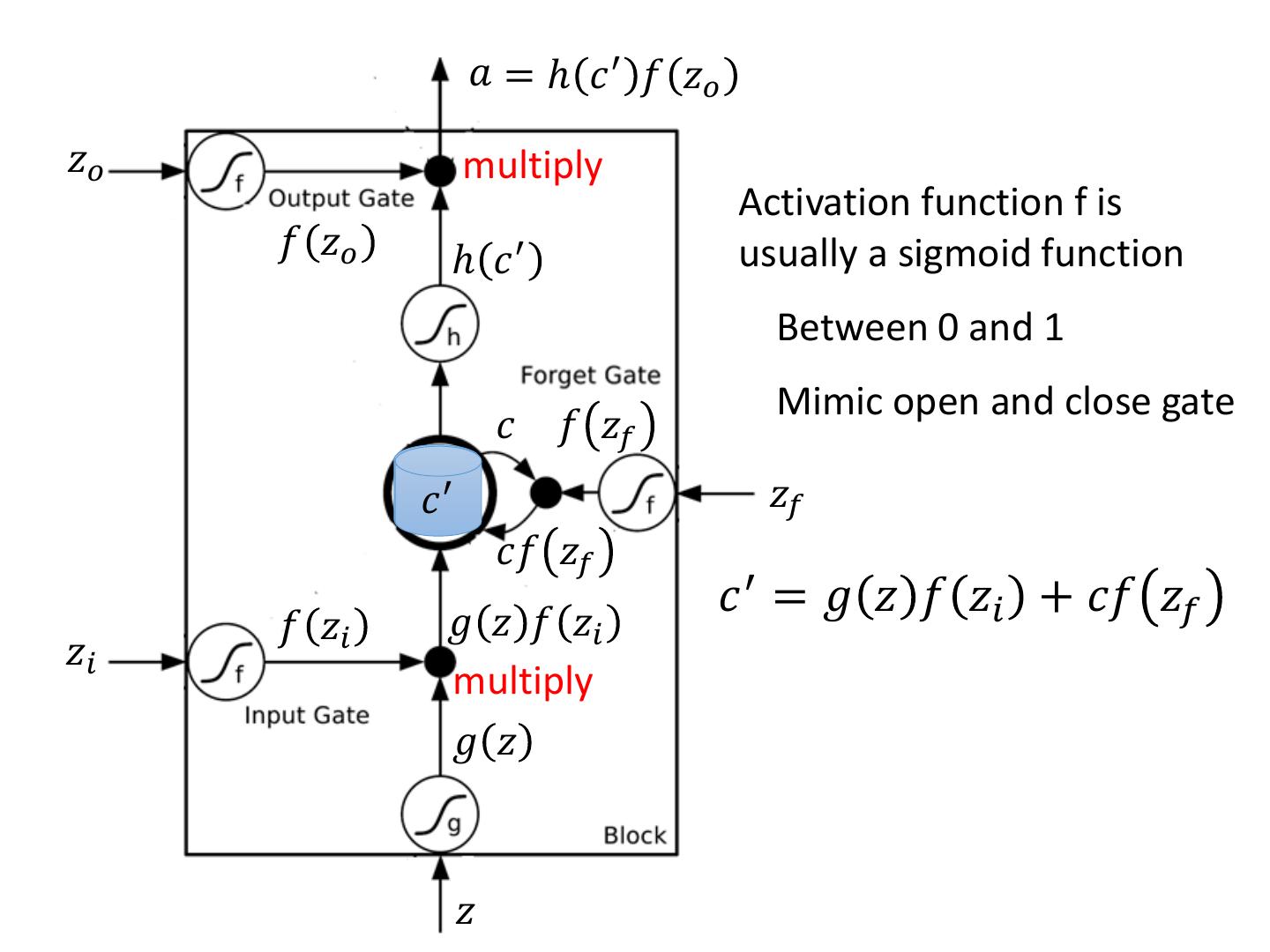
18 . 𝑎 = ℎ 𝑐 ′ 𝑓 𝑧𝑜 𝑧𝑜 multiply Activation function f is 𝑓 𝑧𝑜 ℎ 𝑐′ usually a sigmoid function Between 0 and 1 Mimic open and close gate 𝑐 𝑓 𝑧𝑓 𝑐c′ 𝑧𝑓 𝑐𝑓 𝑧𝑓 𝑔 𝑧 𝑓 𝑧𝑖 𝑐 ′ = 𝑔 𝑧 𝑓 𝑧𝑖 + 𝑐𝑓 𝑧𝑓 𝑓 𝑧𝑖 𝑧𝑖 multiply 𝑔 𝑧 𝑧 

19 .LSTM - Example 0 0 3 3 7 7 7 0 6 𝑥1 1 3 2 4 2 1 3 6 1 𝑥2 0 1 0 1 0 0 -1 1 0 𝑥3 0 0 0 0 0 1 0 0 1 𝑦 0 0 0 0 0 7 0 0 6 When x2 = 1, add the numbers of x1 into the memory When x2 = -1, reset the memory When x3 = 1, output the number in the memory. 

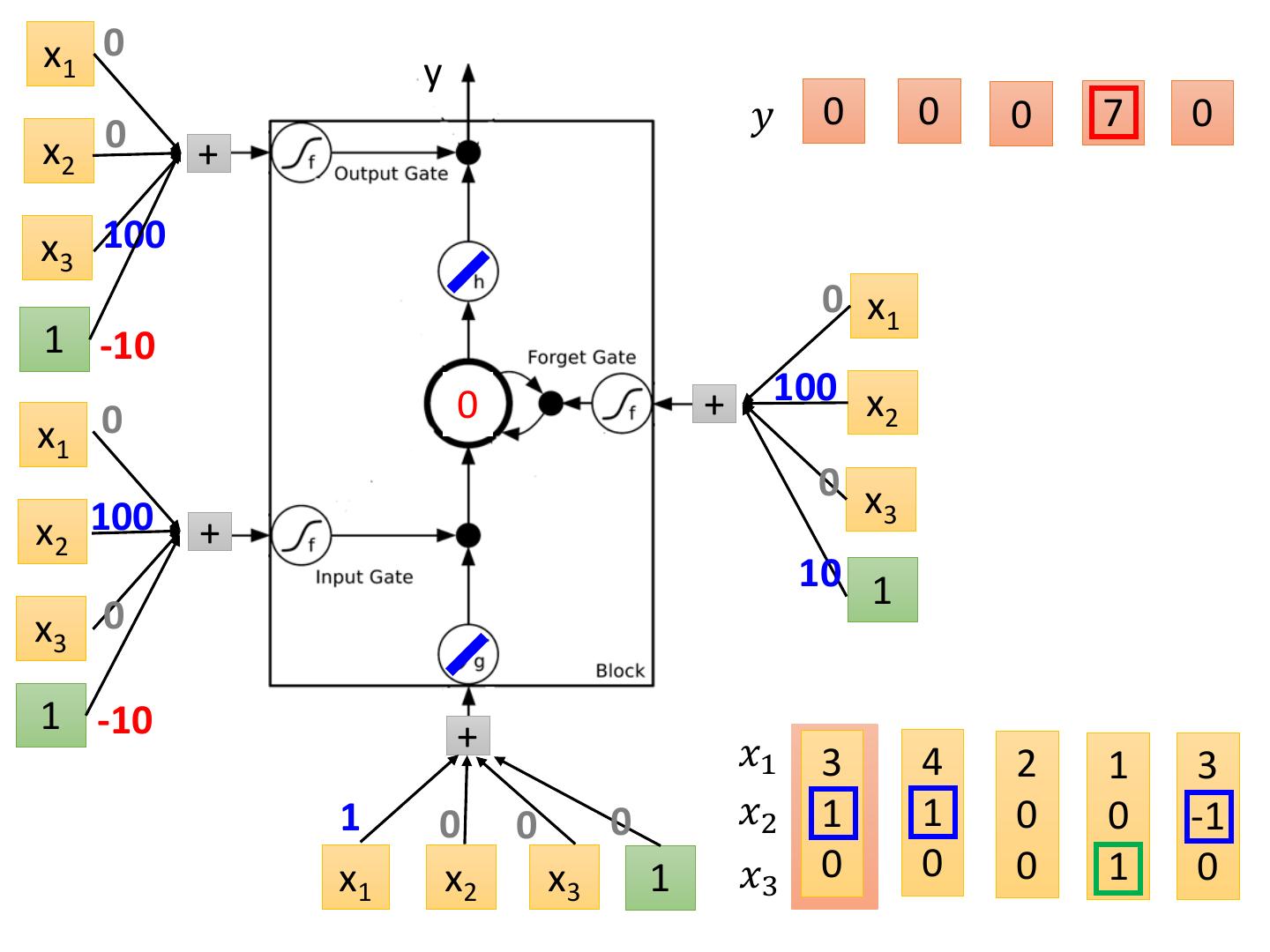
20 .x1 0 y 0 𝑦 0 0 0 7 0 x2 + x3 100 0 x1 1 -10 0 + 100 x x1 0 2 0 x x2 100 3 + 10 1 x3 0 1 -10 + 𝑥1 3 4 2 1 3 1 0 0 0 𝑥2 1 1 0 0 -1 x1 x2 x3 1 𝑥3 0 0 0 1 0 

21 .3 0 y ≈0 𝑦 0 0 0 7 0 1 0 + ≈0 3 0 100 0 3 1 -10 30 + 100 1 3 0 ≈1 0 0 ≈1 3 1 100 + 3 10 1 0 0 1 -10 + 𝑥1 3 4 2 1 3 1 0 0 0 𝑥2 1 1 0 0 -1 3 1 0 1 𝑥3 0 0 0 1 0 

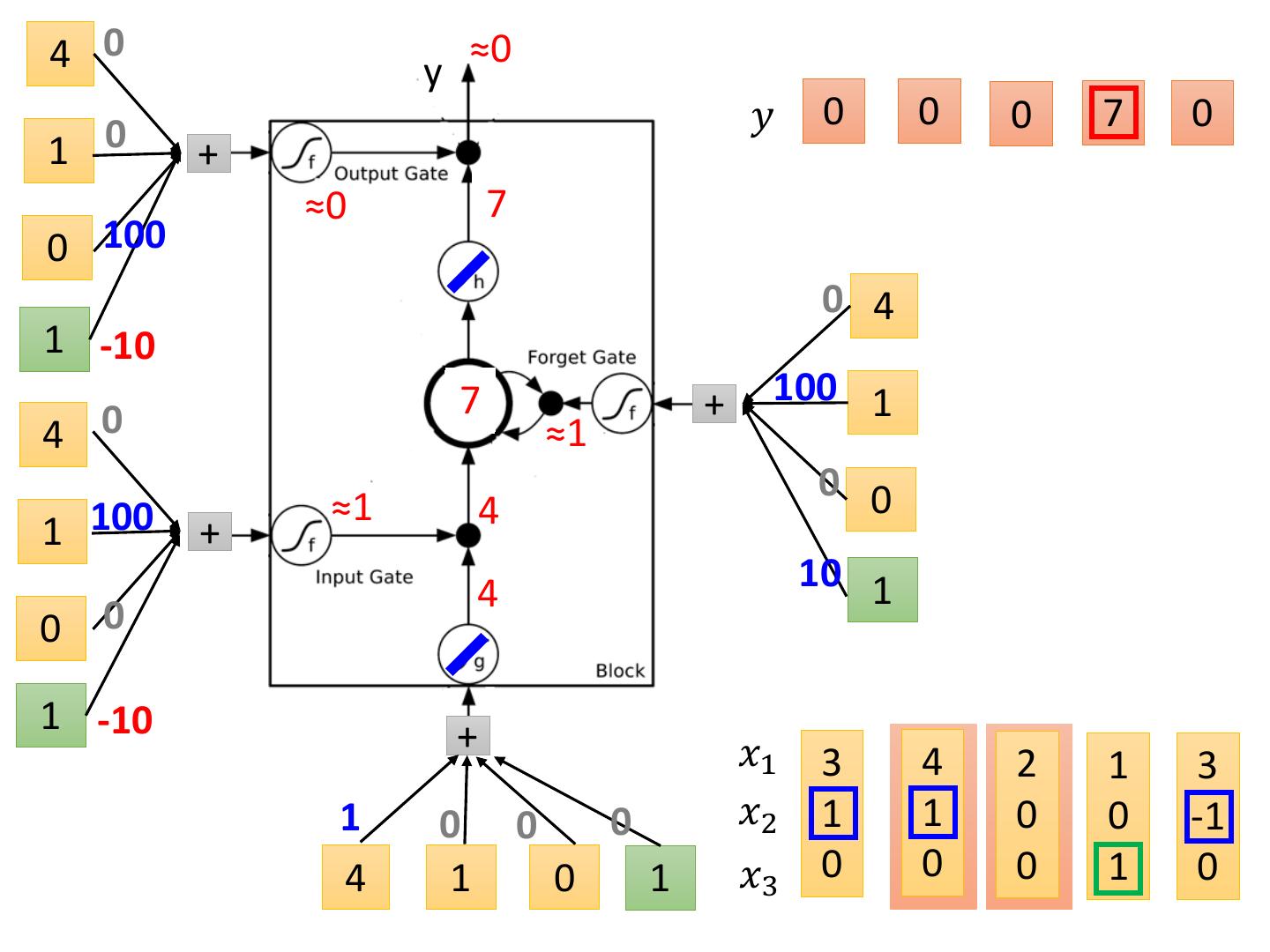
22 .4 0 y ≈0 𝑦 0 0 0 7 0 1 0 + ≈0 7 0 100 0 4 1 -10 37 + 100 1 4 0 ≈1 0 0 ≈1 4 1 100 + 4 10 1 0 0 1 -10 + 𝑥1 3 4 2 1 3 1 0 0 0 𝑥2 1 1 0 0 -1 4 1 0 1 𝑥3 0 0 0 1 0 

23 .2 0 y ≈0 𝑦 0 0 0 7 0 0 0 + ≈0 7 0 100 0 2 1 -10 7 + 100 0 2 0 ≈1 0 0 ≈0 0 0 100 + 2 10 1 0 0 1 -10 + 𝑥1 3 4 2 1 3 1 0 0 0 𝑥2 1 1 0 0 -1 2 0 0 1 𝑥3 0 0 0 1 0 

24 .1 0 y ≈7 𝑦 0 0 0 7 0 0 0 + ≈1 7 1 100 0 1 1 -10 7 + 100 0 1 0 ≈1 0 1 ≈0 0 0 100 + 1 10 1 1 0 1 -10 + 𝑥1 3 4 2 1 3 1 0 0 0 𝑥2 1 1 0 0 -1 1 0 1 1 𝑥3 0 0 0 1 0 

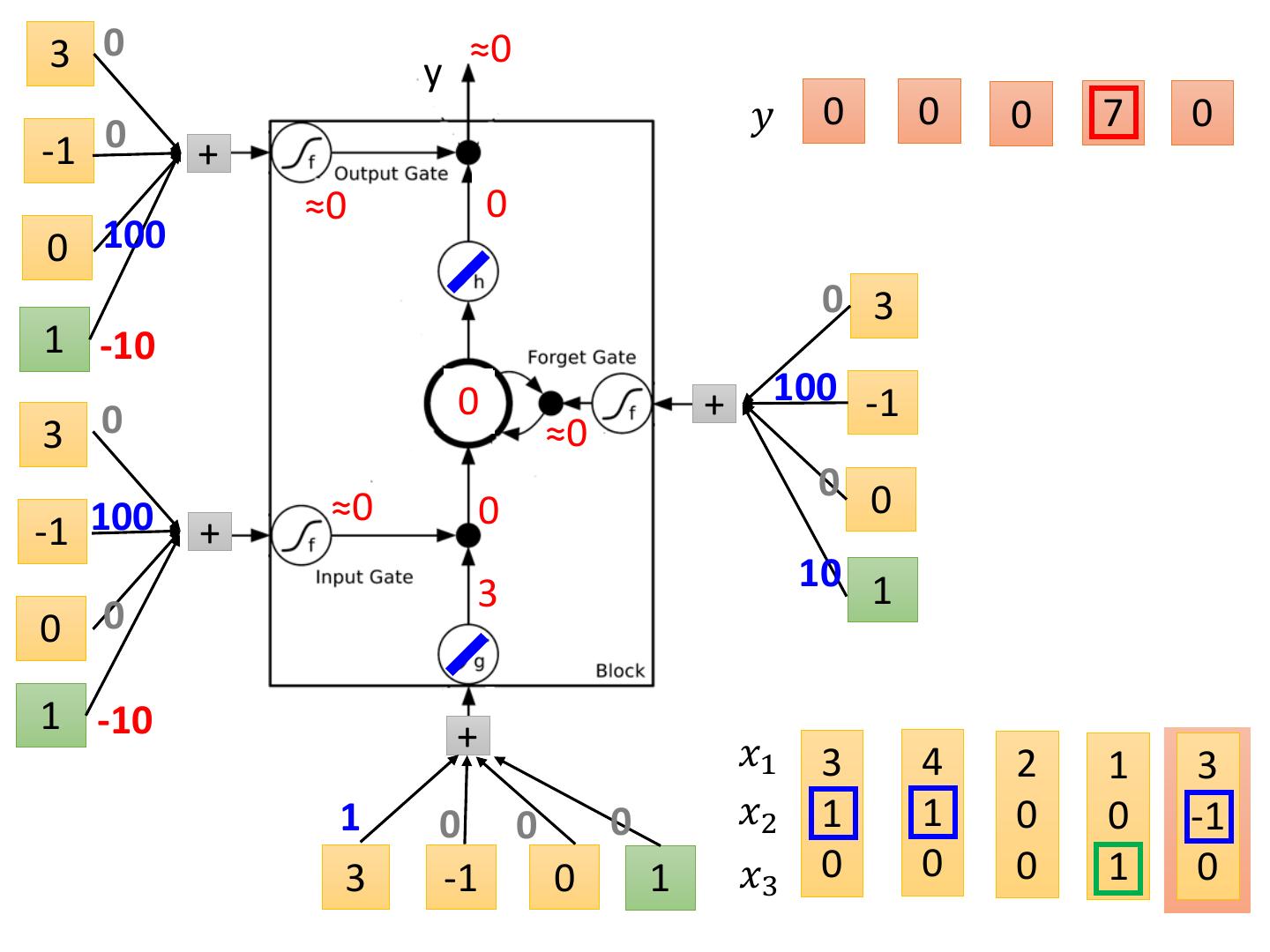
25 .3 0 y ≈0 𝑦 0 0 0 7 0 -1 0 + ≈0 0 0 100 0 3 1 -10 07 + 100 -1 3 0 ≈0 0 0 ≈0 0 -1 100 + 3 10 1 0 0 1 -10 + 𝑥1 3 4 2 1 3 1 0 0 0 𝑥2 1 1 0 0 -1 3 -1 0 1 𝑥3 0 0 0 1 0 

26 .Original Network: Simply replace the neurons with LSTM …… …… 𝑎1 𝑎2 𝑧1 𝑧2 x1 x2 Input 

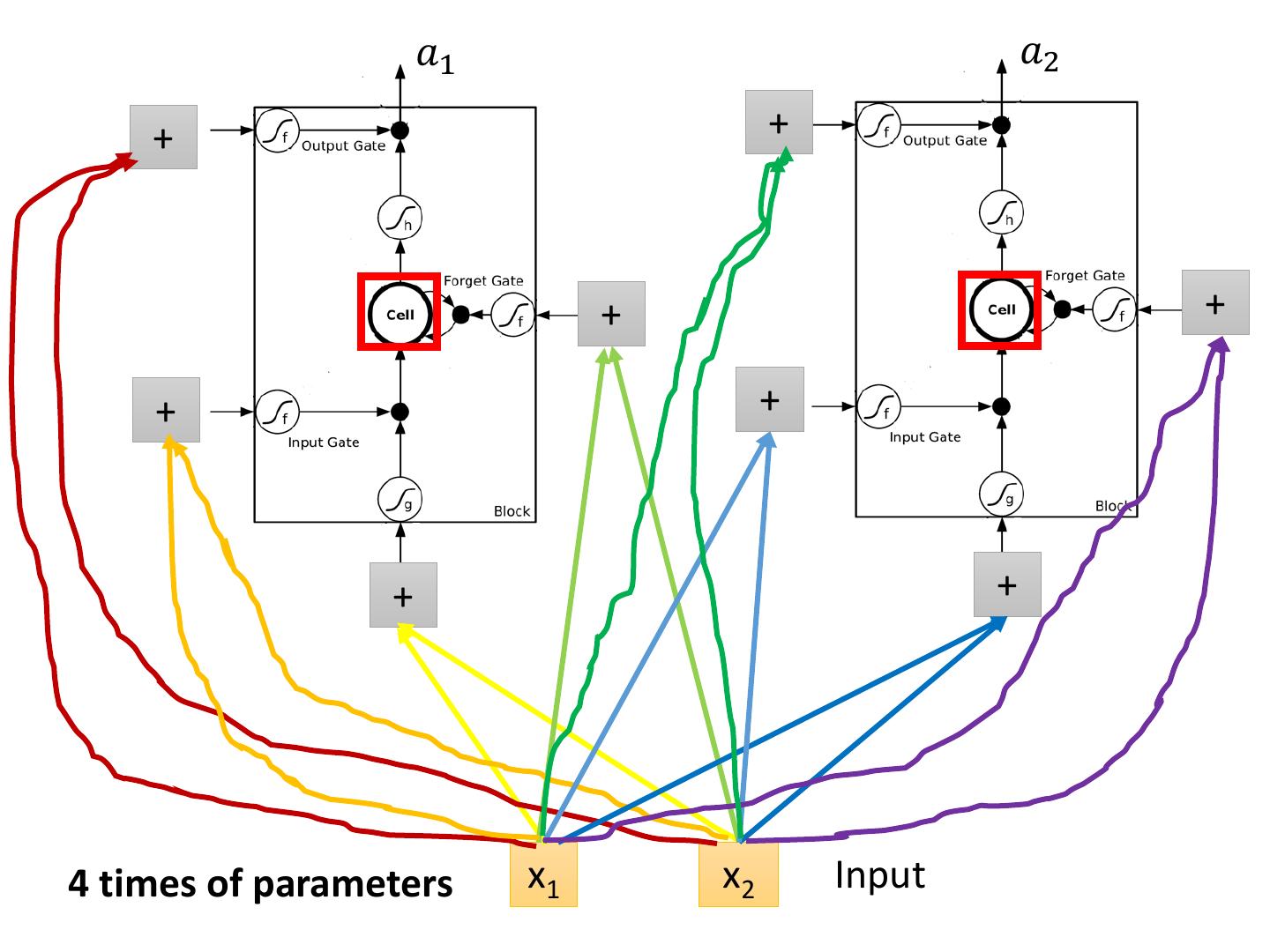
27 . 𝑎1 𝑎2 + + + + + + + + 4 times of parameters x1 x2 Input 

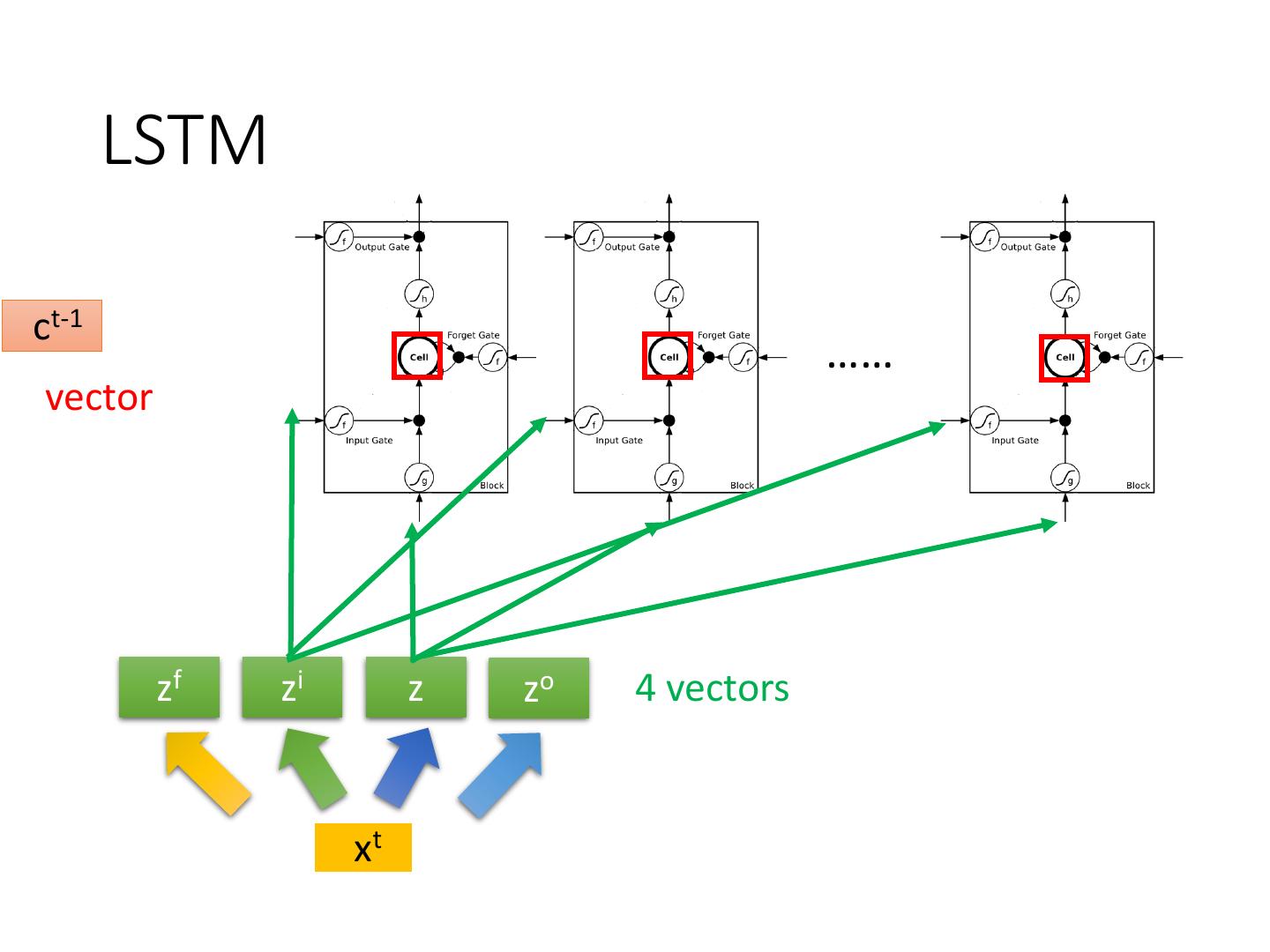
28 . LSTM ct-1 …… vector zf zi z zo 4 vectors xt 

29 . LSTM yt zo ct-1 × ＋ × × zf zi zf zi z zo xt z